A Comprehensive Flow–Mass–Thermal–Electrochemical Coupling Model for a VRFB Stack and Its Application in a Stack Temperature Control Strategy
Abstract
1. Introduction
2. VRFB Multi-Physics Stack Model
- Due to forced convection, the temperature and concentration of the electrolyte are uniformly distributed within a cell and a tank [14].
- In the charge–discharge process, oxygen and hydrogen evolution reactions do not occur [14].
- The self-discharge reactions on both sides of the membrane are instantaneous [12].
- The conductivities of various components are constant [12].
- The electrolyte volume remains constant [12].
- Sulfuric acid is fully ionized [2].
2.1. Mass Balance
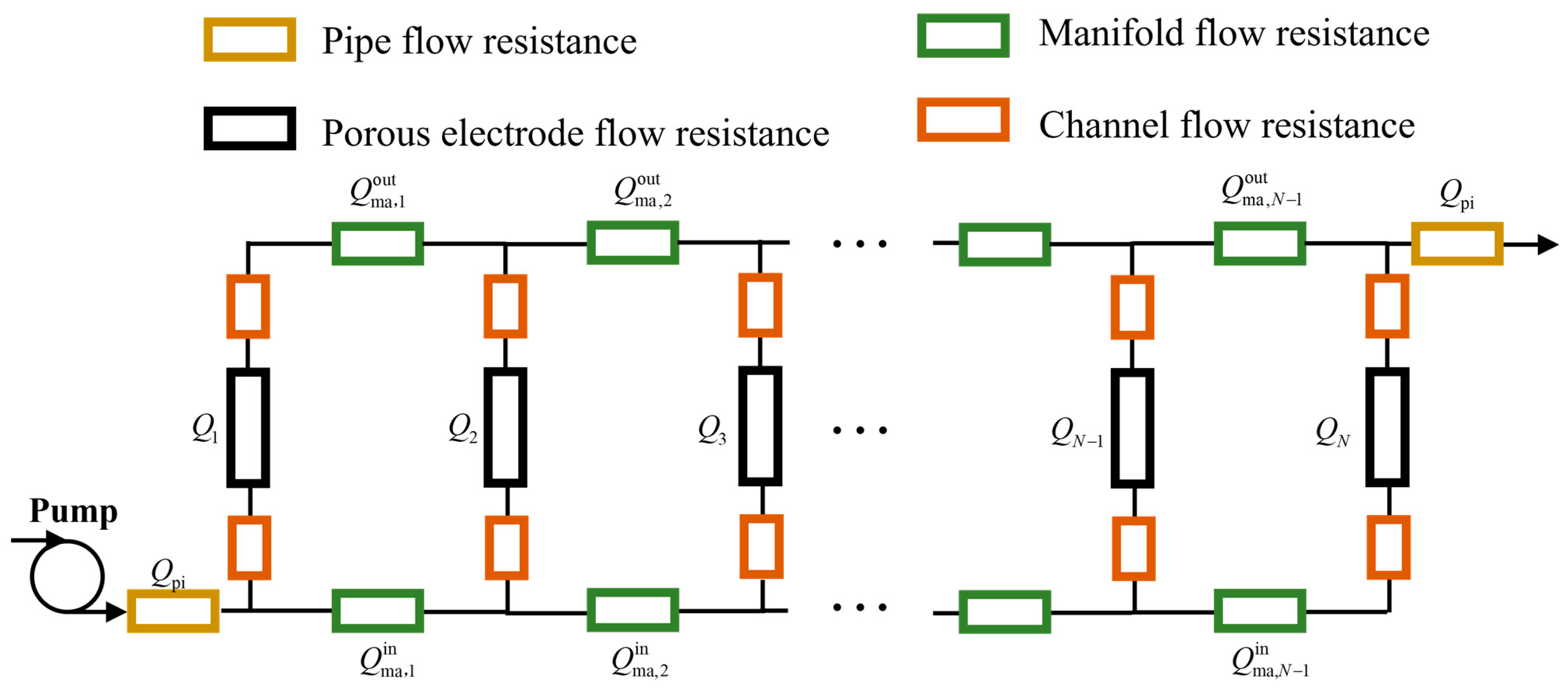
2.2. Electrolyte Flow Network Model
2.3. Shunt Current
2.4. Electrochemical Reaction
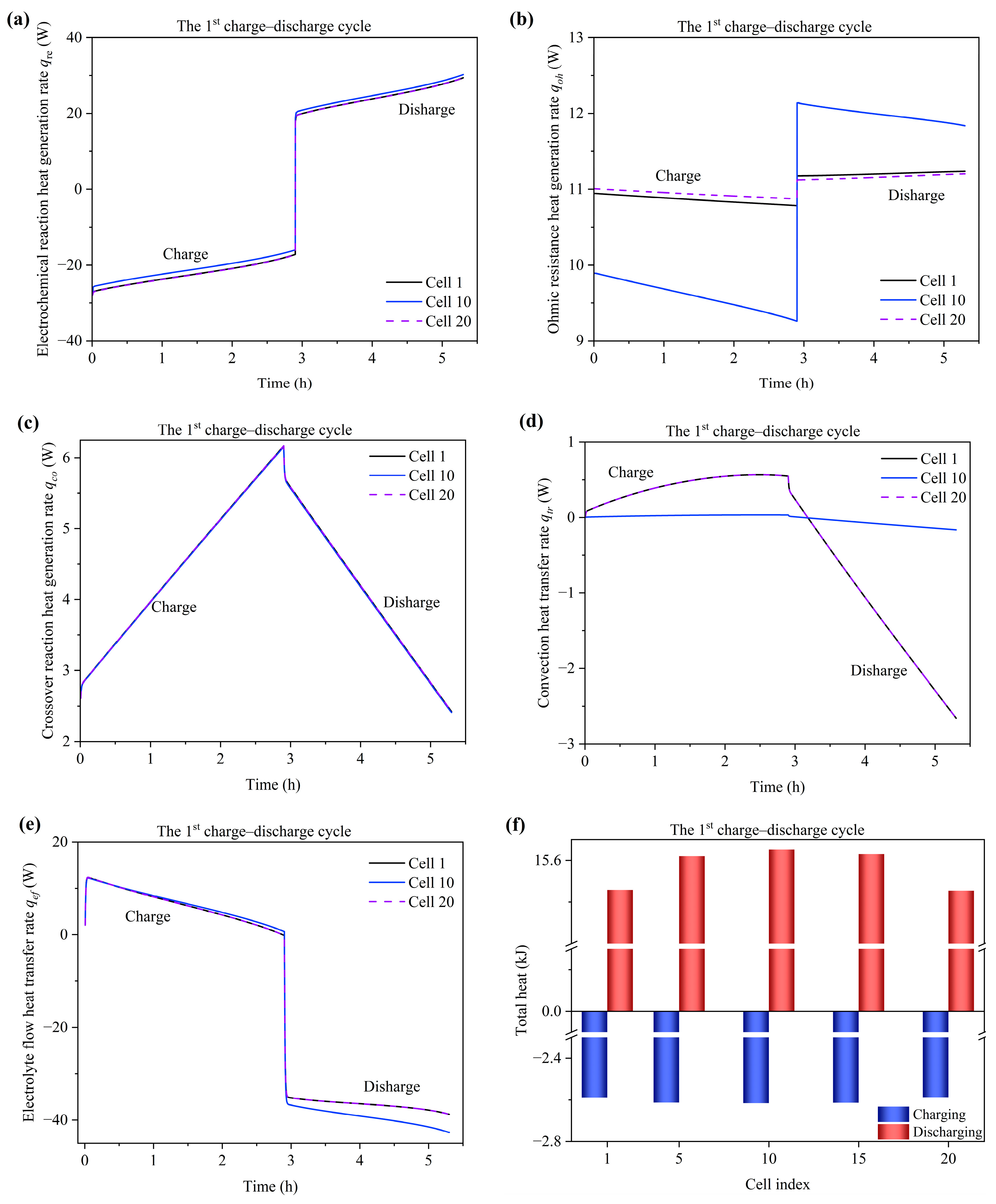
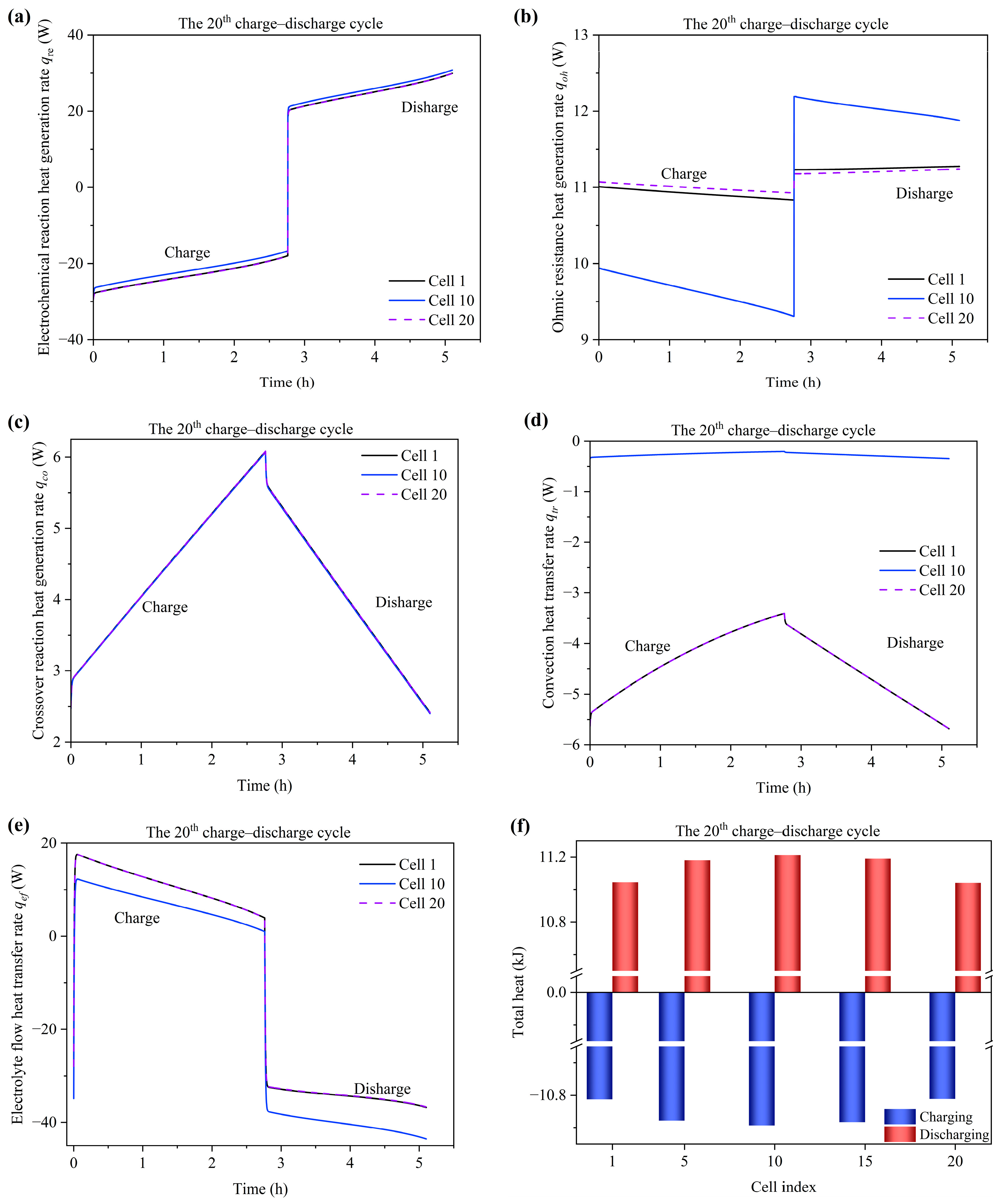
2.5. Energy Balance
3. Model Validation and Physical Parameters Distribution
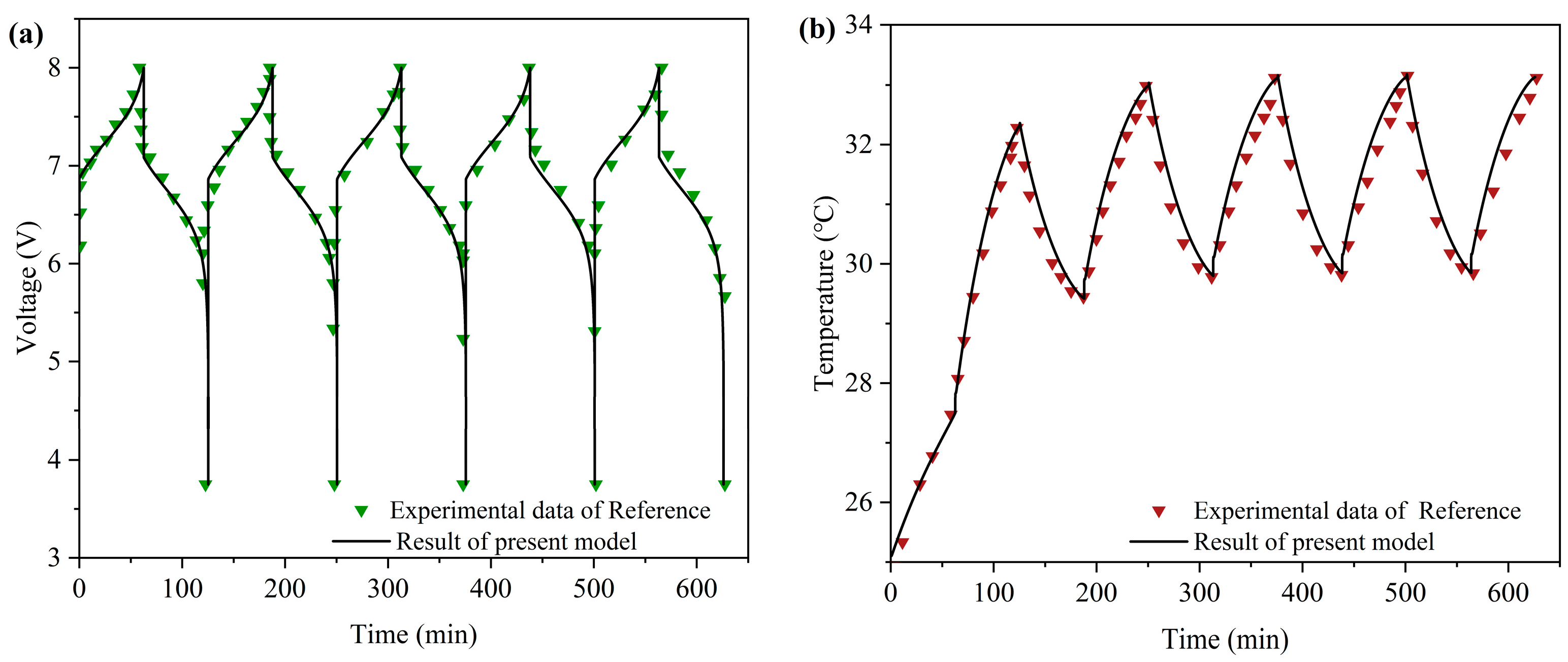
3.1. Model Validation
3.2. Flow Rate Distribution in Stack
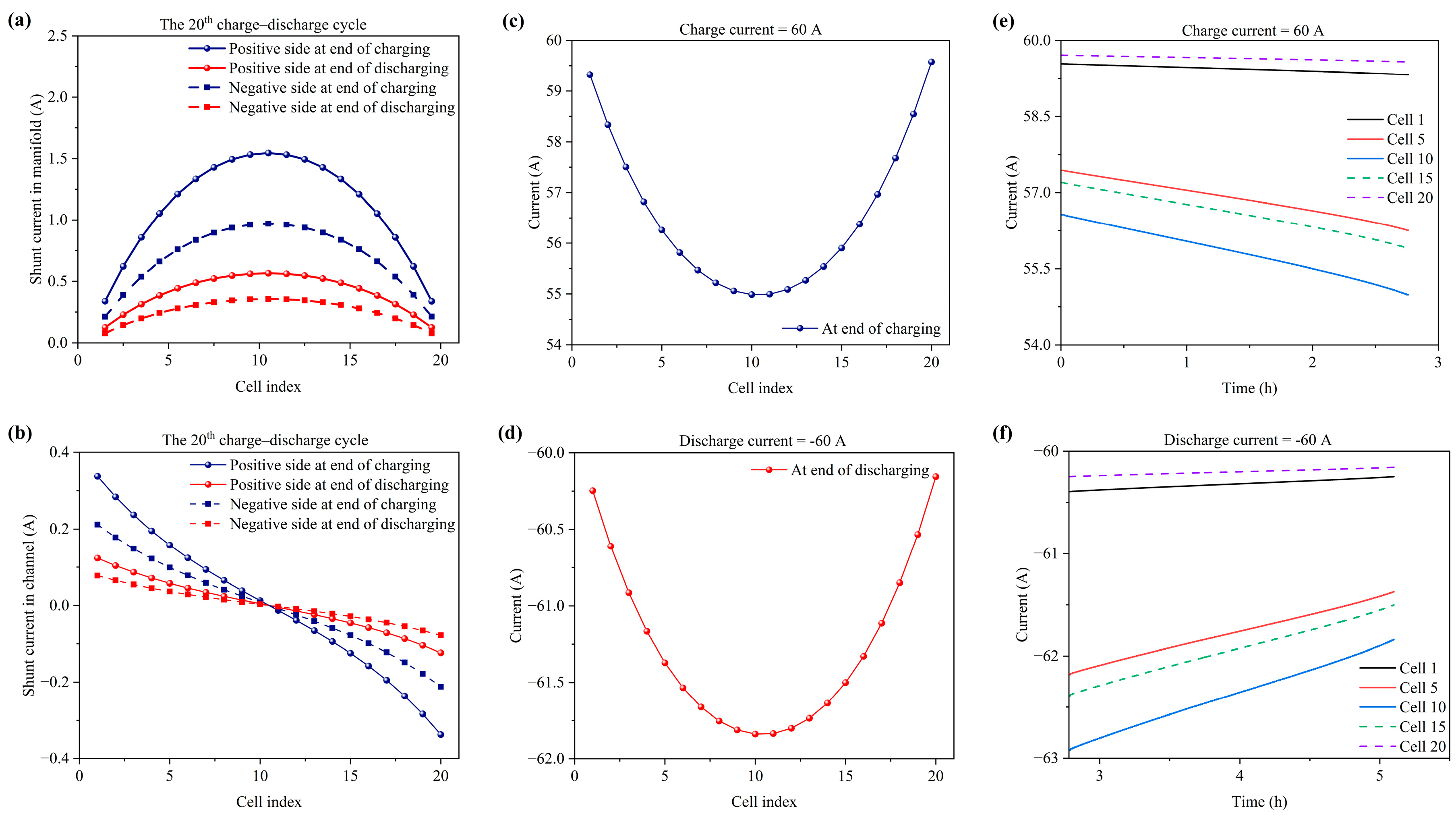
3.3. Current Variation and Distribution in Stack
3.4. Voltage Variation and Distribution in Stack
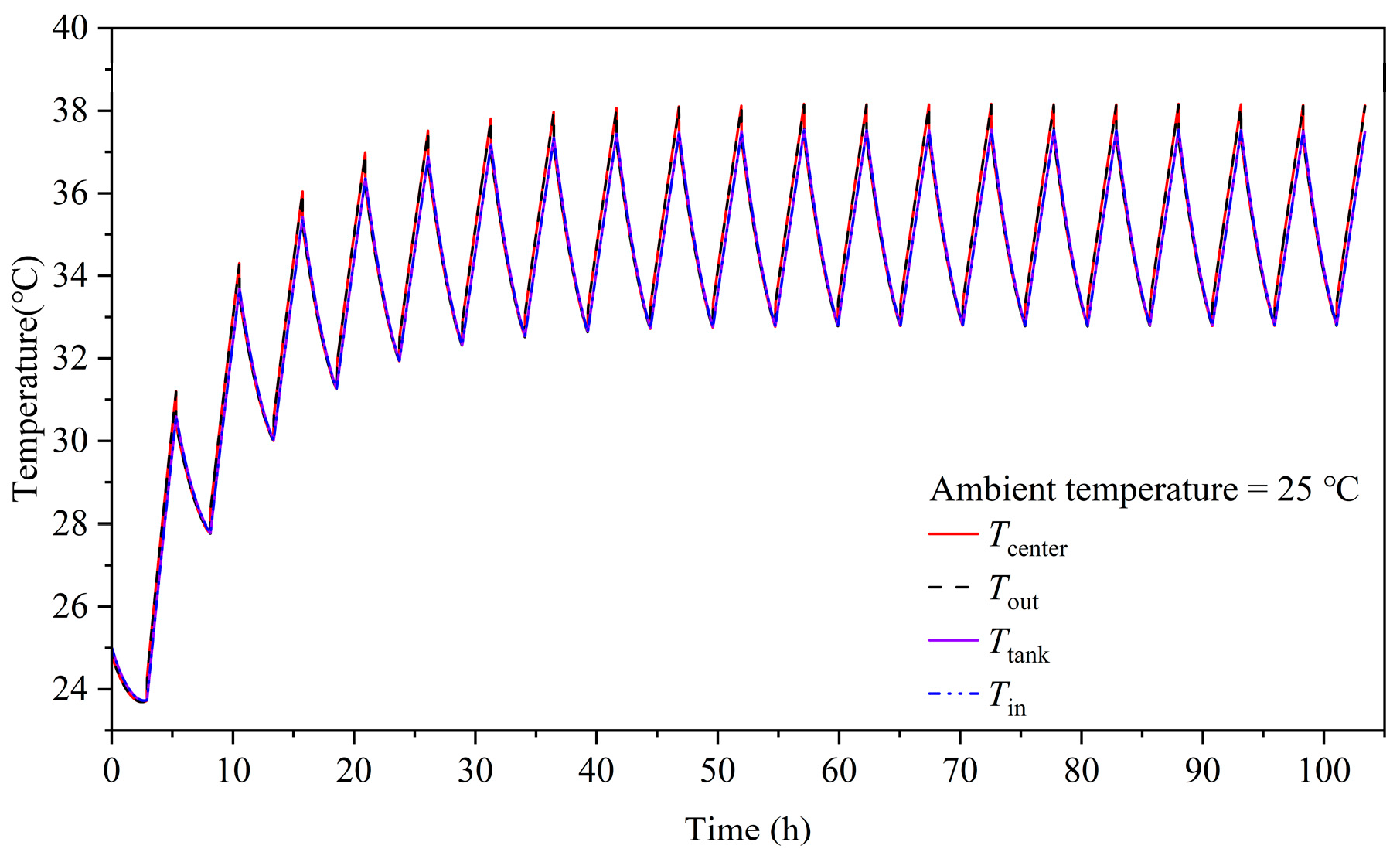
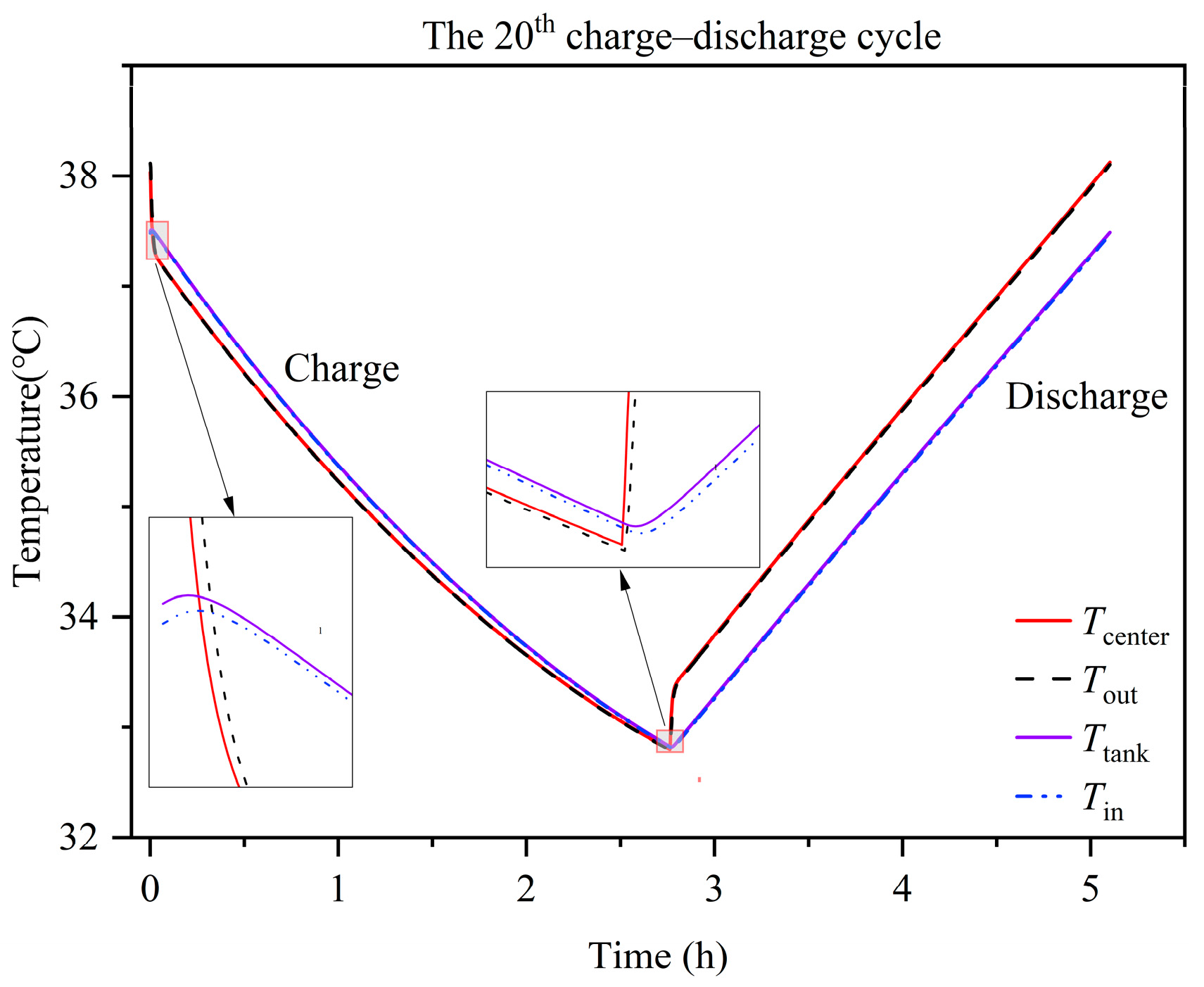
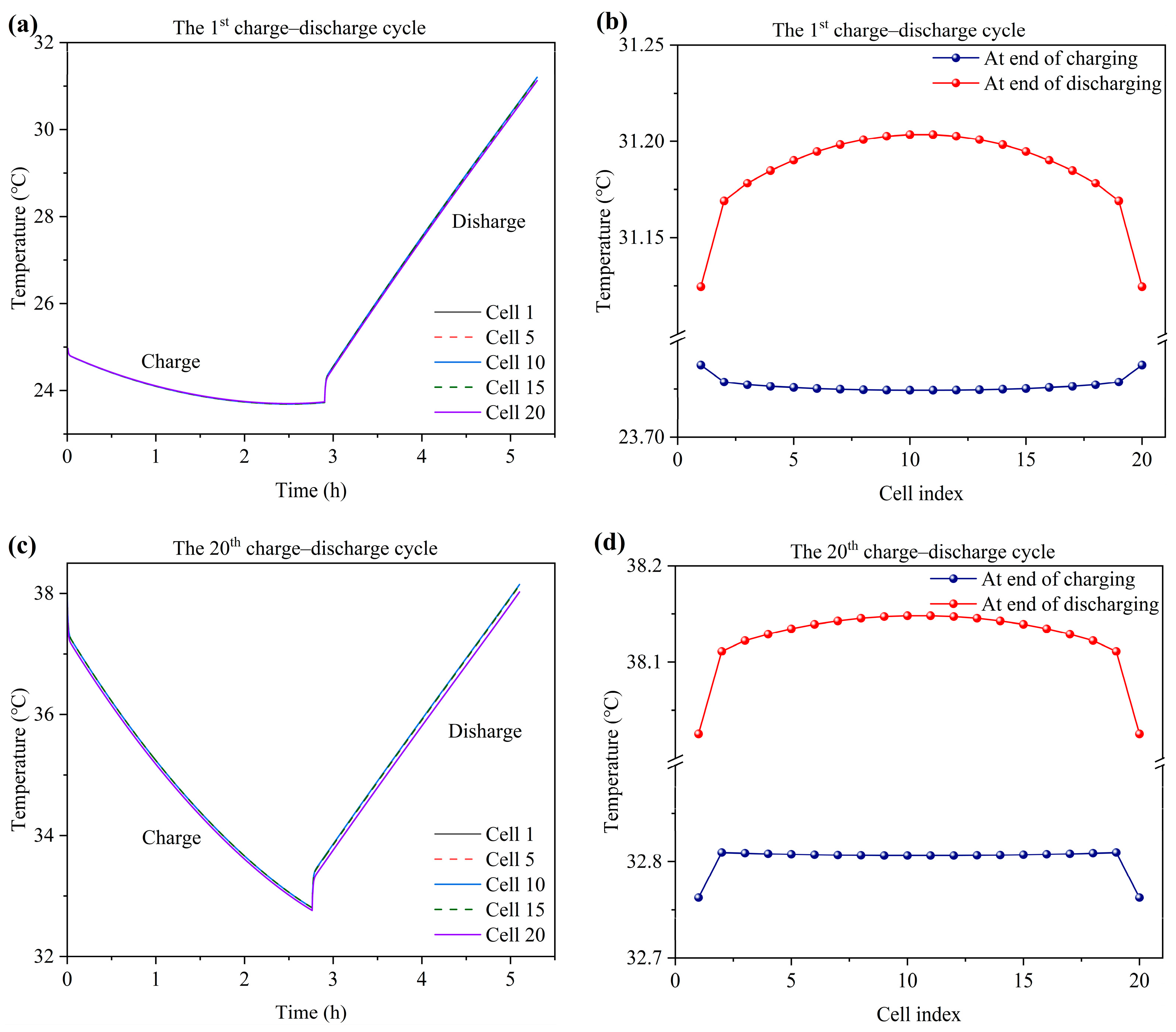
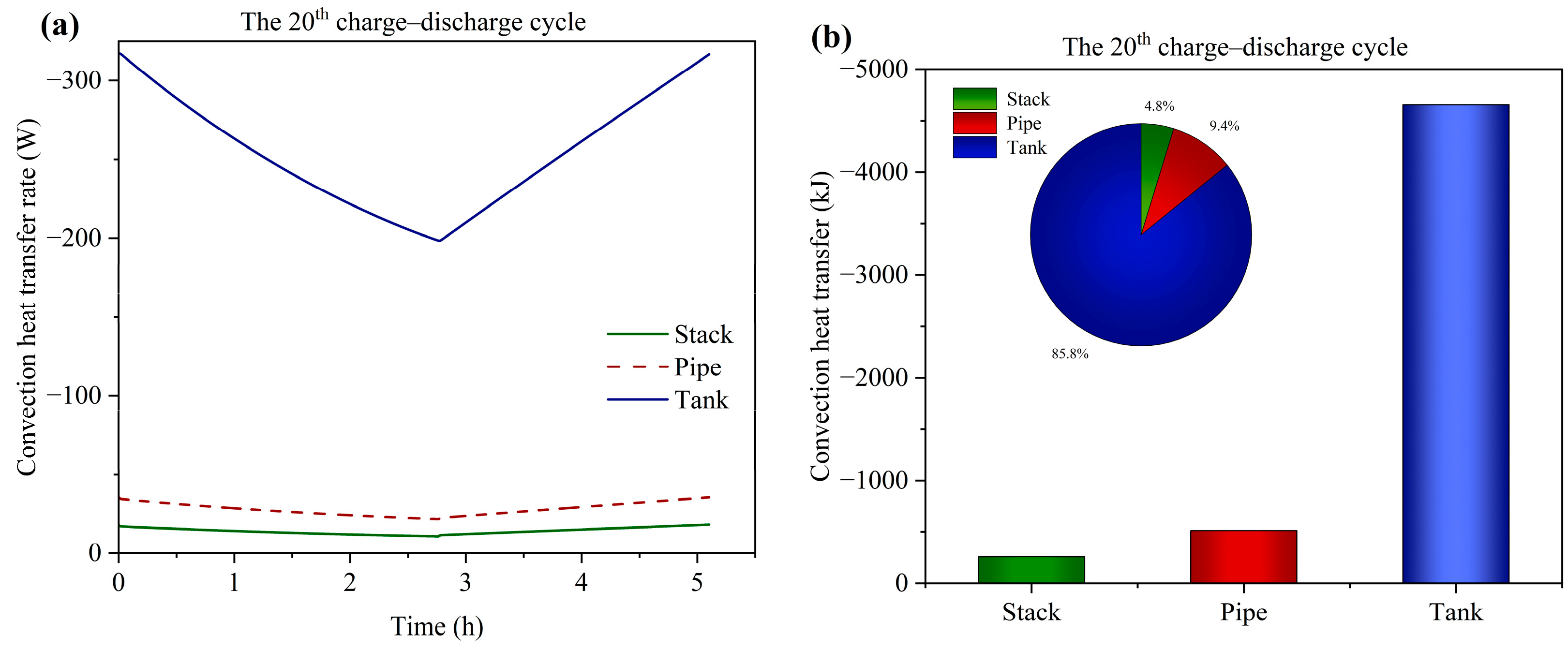
3.5. Temperature Variation and Distribution
4. VRFB Cooling Control Strategy
4.1. Room Gas Flow Cooling Control Model
- The temperatures of the room ground and walls are the same.
- The air mass in the room remains constant.
- In the room, the VRFB system is the only heat source.
- The temperature of the room changes instantly in the initial stage.
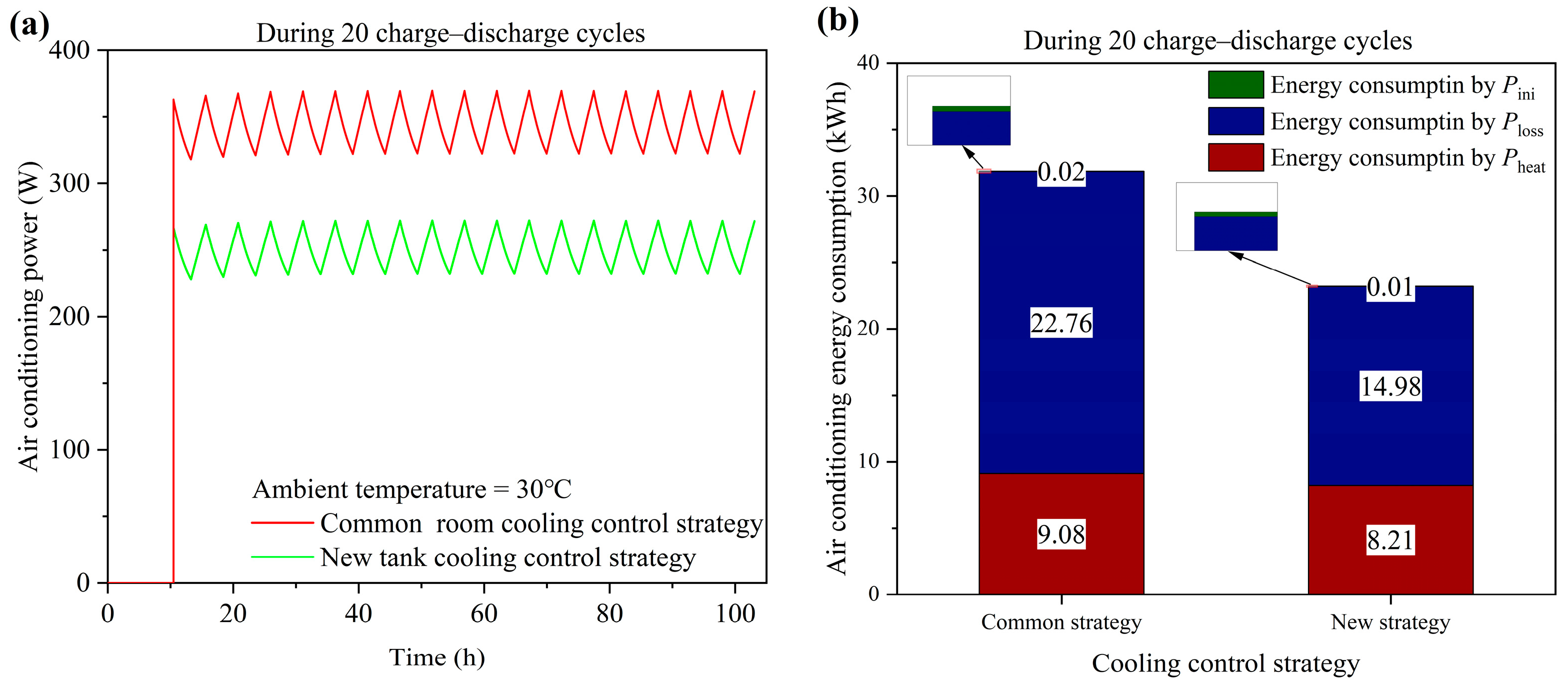
4.2. Common Room Cooling Control Strategy
4.3. New Tank Cooling Control Strategy
5. Conclusions
- The electrolyte flow rate exhibits non-uniform distribution across the cells in the stack. The end cells (1st and 20th cells) possess the highest flow rate and the center cell (10th and 11th cells) possesses the lowest flow rate.
- The shunt currents in the manifolds are largest at the center cell (10th and 11th cells) and lowest at the end cells (1st and 20th cells), and the shunt currents in the channels change direction across the cells in the stack, which can be attributed to the highest voltage of the 1st cell and the lowest voltage of the 20th cell in a series arrangement. In addition, the shunt currents in the positive side are higher than those in the negative side due to the lower resistance in the positive electrolyte.
- At the end of the charging and discharging process, the outermost end cells (1st and 20th cells) possess the lowest charging voltage and the highest discharging voltage due to having the highest flow rate and enough active species. The center cells (10th and 11th cells) show the worst charge–discharge performance due to having the lowest flow rate and a lack of active species.
- At the alternating point between the charge and discharge process, the temperature variation of the tank is hysteretic when compared with the stack. Moreover, the temperature of the end cells (1st and 20th cells) experiences a sharper decrease compared to the middle cells due to the large degree of heat dissipation from the endplate to the environment. The temperature of the stack is mainly influenced by the electrochemical reaction and electrolyte flow heat transfer between the cell and tank. Heat generation from the ohmic resistance is an intermediate influencing factor. Heat generation from the crossover reaction and convection heat transfer between the cell and environment are the least impactful factors.
- The temperature of the stack will exceed 40 °C during the charge–discharge cycles when operating at 60 A and an ambient temperature of 30 °C. To keep the stack temperature below 40 °C, a new tank cooling strategy is proposed and saves 27.18% of the air conditioning energy consumption during 20 charge–discharge cycles.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variables | |
| A | Cross-sectional area or surface area, m2 |
| c | Concentration, mol L−1 |
| C | Friction coefficient |
| Cp | Electrolyte specific heat capacity, J kg−1 K−1 |
| d | Membrane thickness, m |
| df | Carbon fiber diameter, m |
| Dh | Hydraulic diameter, m |
| E | Voltage, V |
| f | Darcy friction factor |
| F | Faraday’s constant, C mol−1 |
| H | Height, m |
| ΔH | Enthalpy change of crossover chemical reaction, J mol−1 |
| i | Current density, A m−2 |
| I | Current, A |
| k | Diffusion coefficient, m2 s−1 |
| k+ | Reaction rate constant of positive, m s−1 |
| k− | Reaction rate constant of negative, m s−1 |
| km | Mass transfer coefficient, m s−1 |
| KCK | Kozeny–Carman constant |
| L | Length, m |
| N | Total cell number |
| P | Energy consumption, kWh |
| ΔP | Pressure drop, Pa |
| q | Heat rate, W |
| Q | Flow rate of electrolyte, m3 s−1 |
| R | Gas constant, J mol−1 K−1 |
| R | Resistance, Ω |
| Rf | Flow resistance, Pa m−3 s |
| S | Cross-sectional area of membrane, m2 |
| ΔSΘ | Molar reaction entropy, J mol−1 K−1 |
| SΘ | Standard molar entropy, J mol−1 K−1 |
| T | Temperature, K |
| U | Heat transfer coefficient, W m−2 K−1 |
| V | Volume, m3 |
| W | Width, m |
| z | Number of reaction electrons |
| Greek | |
| α | Charge transfer coefficient |
| σ | Conductivity, S m−1 |
| μ | Dynamic viscosity of electrolyte, m2 s−1 |
| ρ | Density of electrolyte, kg m−3 |
| ε | Porosity of porous electrode |
| η | Overpotential, V |
| Subscripts | |
| 0 | Stand condition |
| 2 | V2+ |
| 3 | V3+ |
| 4 | VO2+ |
| 5 | VO2+ |
| II | Equation (3) |
| III | Equation (4) |
| IV | Equation (5) |
| V | Equation (6) |
| a | Activation |
| ac | Air conditioning |
| air | Air |
| app | Applied |
| c | Concentration |
| cell | Cell |
| center | Center cell of stack |
| ch | Channel |
| co | Crossover reaction |
| con | Contact |
| e | Electrode |
| ef | Electrolyte flow |
| el | Electrolyte |
| end | End of stack |
| f | Friction |
| H2+ | H2+ |
| H2O | H2O |
| heat | Heat transfer between VRFB and room |
| hf | Hydraulic friction |
| i | Species index |
| in | Inlet |
| ini | Initial process |
| loss | Heat transfer between environment and room |
| m | Membrane |
| ma | Manifold |
| n | n-th cell |
| OCV | Open-circuit voltage |
| oh | Ohmic resistance |
| out | Outlet |
| pipe | Pipe |
| re | Electrochemical reaction |
| SO42− | SO42− |
| stack | Stack |
| tank | Tank |
| tr | Heat transfer |
| x | Direction x |
| y | Direction y |
| z | Direction z |
| Superscripts | |
| + | Positive side |
| − | Negative side |
| in | Inlet |
| out | Outlet |
References
- Shi, X.; Zheng, Y.; Lei, Y.; Xue, W.; Yan, G.; Liu, X.; Cai, B.; Tong, D.; Wang, J. Air quality benefits of achieving carbon neutrality in China. Sci. Total Environ. 2021, 795, 148784. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Y.-H.; Zhang, Z.-K.; Dou, P.-Y.; Xu, Q.; Yang, W.-W. Consistency analysis and resistance network design for vanadium redox flow battery stacks with a cell-resolved stack model. Int. J. Green Energy 2023, 20, 166–180. [Google Scholar] [CrossRef]
- Ren, J.; Wei, L.; Wang, Z.; Yue, Q.; Liu, B.; Jia, G.; Fan, X.; Zhao, T. An electrochemical-thermal coupled model for aqueous redox flow batteries. Int. J. Heat Mass Transf. 2022, 192, 122926. [Google Scholar] [CrossRef]
- Kazacos, M.; Cheng, M.; Skyllas-Kazacos, M. Vanadium redox cell electrolyte optimization studies. J. Appl. Electrochem. 1990, 20, 463–467. [Google Scholar] [CrossRef]
- Trovò, A.; Guarnieri, M. Standby thermal management system for a kW-class vanadium redox flow battery. Energy Convers. Manag. 2020, 226, 113510. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; McCann, J.; Li, Y.; Bao, J.; Tang, A. The Mechanism and Modelling of Shunt Current in the Vanadium Redox Flow Battery. ChemistrySelect 2016, 1, 2249–2256. [Google Scholar] [CrossRef]
- Wandschneider, F.T.; Röhm, S.; Fischer, P.; Pinkwart, K.; Tübke, J.; Nirschl, H. A multi-stack simulation of shunt currents in vanadium redox flow batteries. J. Power Sources 2014, 261, 64–74. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Non-isothermal modelling of the all-vanadium redox flow battery. Electrochim. Acta 2009, 55, 78–89. [Google Scholar] [CrossRef]
- Tang, A.; Ting, S.; Bao, J.; Skyllas-Kazacos, M. Thermal modelling and simulation of the all-vanadium redox flow battery. J. Power Sources 2012, 203, 165–176. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Thermal modelling of battery configuration and self-discharge reactions in vanadium redox flow battery. J. Power Sources 2012, 216, 489–501. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Skyllas-Kazacos, M.; Xiong, B. Dynamic thermal-hydraulic modeling and stack flow pattern analysis for all-vanadium redox flow battery. J. Power Sources 2014, 260, 89–99. [Google Scholar] [CrossRef]
- Trovò, A.; Saccardo, A.; Giomo, M.; Guarnieri, M. Thermal modeling of industrial-scale vanadium redox flow batteries in high-current operations. J. Power Sources 2019, 424, 204–214. [Google Scholar] [CrossRef]
- Kirk, E.H.; Fenini, F.; Oreiro, S.N.; Bentien, A. Temperature-Induced Precipitation of V2O5 in Vanadium Flow Batteries—Revisited. Batteries 2021, 7, 87. [Google Scholar] [CrossRef]
- Han, S.; Tan, L. Thermal and efficiency improvements of all vanadium redox flow battery with novel main-side-tank system and slow pump shutdown. J. Energy Storage 2020, 28, 101274. [Google Scholar] [CrossRef]
- Wang, H.; Soong, W.L.; Pourmousavi, S.A.; Zhang, X.; Ertugrul, N.; Xiong, B. Thermal dynamics assessment of vanadium redox flow batteries and thermal management by active temperature control. J. Power Sources 2023, 570, 233027. [Google Scholar] [CrossRef]
- Yan, Y.; Li, Y.; Skyllas-Kazacos, M.; Bao, J. Modelling and simulation of thermal behaviour of vanadium redox flow battery. J. Power Sources 2016, 322, 116–128. [Google Scholar] [CrossRef]
- Tang, A.; McCann, J.; Bao, J.; Skyllas-Kazacos, M. Investigation of the effect of shunt current on battery efficiency and stack temperature in vanadium redox flow battery. J. Power Sources 2013, 242, 349–356. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, J.; Wang, P.; Skyllas-Kazacos, M.; Xiong, B.; Badrinarayanan, R. A comprehensive equivalent circuit model of all-vanadium redox flow battery for power system analysis. J. Power Sources 2015, 290, 14–24. [Google Scholar] [CrossRef]
- Ye, Q.; Hu, J.; Cheng, P.; Ma, Z. Design trade-offs among shunt current, pumping loss and compactness in the piping system of a multi-stack vanadium flow battery. J. Power Sources 2015, 296, 352–364. [Google Scholar] [CrossRef]
- Trovò, A.; Picano, F.; Guarnieri, M. Comparison of energy losses in a 9 kW vanadium redox flow battery. J. Power Sources 2019, 440, 227144. [Google Scholar] [CrossRef]
- Xiao, W.; Tan, L. Control strategy optimization of electrolyte flow rate for all vanadium redox flow battery with consideration of pump. Renew. Energy 2019, 133, 1445–1454. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Studies on pressure losses and flow rate optimization in vanadium redox flow battery. J. Power Sources 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Jirabovornwisut, T.; Kheawhom, S.; Chen, Y.-S.; Arpornwichanop, A. Optimal operational strategy for a vanadium redox flow battery. Comput. Chem. Eng. 2020, 136, 106805. [Google Scholar] [CrossRef]
- Kim, D.K.; Yoon, S.J.; Lee, J.; Kim, S. Parametric study and flow rate optimization of all-vanadium redox flow batteries. Appl. Energy 2018, 228, 891–901. [Google Scholar] [CrossRef]
- Shah, A.A.; Tangirala, R.; Singh, R.; Wills, R.G.A.; Walsh, F.C. A Dynamic Unit Cell Model for the All-Vanadium Flow Battery. J. Electrochem. Soc. 2011, 158, A671. [Google Scholar] [CrossRef]
- Yue, M.; Lv, Z.; Zheng, Q.; Li, X.; Zhang, H. Battery assembly optimization: Tailoring the electrode compression ratio based on the polarization analysis in vanadium flow batteries. Appl. Energy 2019, 235, 495–508. [Google Scholar] [CrossRef]
- Wang, Q.; Qu, Z.G.; Jiang, Z.Y.; Yang, W.W. Experimental study on the performance of a vanadium redox flow battery with non-uniformly compressed carbon felt electrode. Appl. Energy 2018, 213, 293–305. [Google Scholar] [CrossRef]
- Hietaharju, P.; Ruusunen, M.; Leiviskä, K. A Dynamic Model for Indoor Temperature Prediction in Buildings. Energies 2018, 11, 1477. [Google Scholar] [CrossRef]
- Kim, N.-K.; Shim, M.-H.; Won, D. Building Energy Management Strategy Using an HVAC System and Energy Storage System. Energies 2018, 11, 2690. [Google Scholar] [CrossRef]






| Symbol | Parameter | Value |
|---|---|---|
| We × He × Le | Electrode dimension | 30 cm × 20 cm × 0.4 cm [12] |
| d | Membrane thickness | 5 × 10−5 m [12] |
| Ama × Lma | Manifold dimension | 7.065 cm2 × 2 cm [18,19] |
| Hch × Wch × Lch | Channel dimension | 4 mm × 10 mm × 50 mm [2,19] |
| Api × Lpi | Pipe dimension | 7.065 cm2 × 2 m [18,20] |
| Atank × Htank | Tank dimension | 0.24 m2 × 1 m [10] |
| Symbol | Parameter | Value |
|---|---|---|
| N | Number of cells | 20 |
| R | Gas constant | 8.314 J mol−1 K−1 |
| F | Faraday’s constant | 96,485 |
| c | Total vanadium concentration | 1.7 mol L−1 |
| Vtank | Volume of electrolyte in tank | 100 L |
| Cp | Electrolyte specific heat capacity | 3200 J kg−1 K−1 [12] |
| ρ | Density of electrolyte | 1354 kg m−3 [12] |
| μ | Dynamic viscosity of electrolyte | 4.928 × 10−3 Pa s [19] |
| k2 | Transmembrane diffusion coefficient of V2+ | 8.768 × 10−12 m2 s−1 [15] |
| k3 | Transmembrane diffusion coefficient of V3+ | 3.222 × 10−12 m2 s−1 [15] |
| k4 | Transmembrane diffusion coefficient of VO2+ | 6.825 × 10−12 m2 s−1 [15] |
| k5 | Transmembrane diffusion coefficient of VO2+ | 5.897 × 10−12 m2 s−1 [15] |
| D2 | Diffusion coefficient of V2+ | 2.4 × 10−10 m2 s−1 [2] |
| D3 | Diffusion coefficient of V3+ | 2.4 × 10−10 m2 s−1 [2] |
| D4 | Diffusion coefficient of VO2+ | 3.9 × 10−10 m2 s−1 [2] |
| D5 | Diffusion coefficient of VO2+ | 3.9 × 10−10 m2 s−1 [2] |
| Diffusion coefficient of H+ | 9.312 × 10−9 m2 s−1 [2] | |
| Diffusion coefficient of SO42− | 1.065 × 10−9 m2 s−1 [2] | |
| σ2 | Conductivity of V2+ | 27.5 S m−1 [12] |
| σ3 | Conductivity of V3+ | 17.5 S m−1 [12] |
| σ4 | Conductivity of VO2+ | 27.5 S m−1 [12] |
| σ5 | Conductivity of VO2+ | 41.3 S m−1 [12] |
| σe | Conductivity of electrode | 1000 S m−1 [2] |
| σm | Conductivity of membrane | 7.3 S m−1 [2] |
| ε | Porosity | 0.87 [27] |
| df | Carbon fiber diameter | 11.94 × 10−6 m [27] |
| KCK | Carman–Kozeny constant | 4.89 [27] |
| k+ | Standard rate constant of positive reaction | 6.8 × 10−7 m s−1 [20] |
| k− | Standard rate constant of positive reaction | 2.6 × 10−6 m s−1 [20] |
| Ux | Heat transfer coefficient of cell in direction x | 21.67 W m−2 K−1 [12] |
| Uy | Heat transfer coefficient of cell in direction y | 2.413 W m−2 K−1 [12] |
| Uz | Heat transfer coefficient of cell in direction z | 1.376 W m−2 K−1 [12] |
| Uend | Heat transfer coefficient of end cell in direction x | 2.877 W m−2 K−1 [12] |
| Upipe | Heat transfer coefficient of pipe | 3.667 W m−2 K−1 [12] |
| Utank | Heat transfer coefficient of tank | 5.734 W m−2 K−1 [12] |
| Standard molar entropy of V2+ | −130.0 J mol−1 K−1 [15] | |
| Standard molar entropy of V3+ | −230.0 J mol−1 K−1 [15] | |
| Standard molar entropy of VO2+ | −133.9 J mol−1 K−1 [15] | |
| Standard molar entropy of VO2+ | −42.3 J mol−1 K−1 [15] | |
| Standard molar entropy of H2O | 69.9 J mol−1 K−1 [15] | |
| Standard molar entropy of H+ | 0 J mol−1 K−1 [15] | |
| ΔHII | Enthalpy of reaction in Equation (3) | −220.03 kJ mol−1 [3] |
| ΔHIII | Enthalpy of reaction in Equation (4) | −64.40 kJ mol−1 [3] |
| ΔHIV | Enthalpy of reaction in Equation (5) | −91.23 kJ mol−1 [3] |
| ΔHV | Enthalpy of reaction in Equation (6) | −246.86 kJ mol−1 [3] |
| Symbol | Parameter | The Common Strategy | The New Strategy |
|---|---|---|---|
| H × L × W | Cooling control room dimension | 3 m × 3 m × 2 m | 2 m × 2 m × 2 m |
| Awall | Total surface of walls | 42 m2 | 24 m2 |
| Uwall | Total heat transfer coefficient of room | 5.32 W m−2 K−1 [15] | 5.32 W m−2 K−1 [15] |
| Cair | Heat capacity of air | 1020 J kg−1 K−1 | 1020 J kg−1 K−1 |
| Mair | Air mass inside cooling control room | 23 kg | 10 kg |
| EER | Energy efficiency ratio | 3 [15] | 3 [15] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, C.; Lu, M.; Ma, Q.; Su, H.; Yang, W.; Xu, Q. A Comprehensive Flow–Mass–Thermal–Electrochemical Coupling Model for a VRFB Stack and Its Application in a Stack Temperature Control Strategy. Batteries 2024, 10, 347. https://doi.org/10.3390/batteries10100347
Yin C, Lu M, Ma Q, Su H, Yang W, Xu Q. A Comprehensive Flow–Mass–Thermal–Electrochemical Coupling Model for a VRFB Stack and Its Application in a Stack Temperature Control Strategy. Batteries. 2024; 10(10):347. https://doi.org/10.3390/batteries10100347
Chicago/Turabian StyleYin, Chen, Mengyue Lu, Qiang Ma, Huaneng Su, Weiwei Yang, and Qian Xu. 2024. "A Comprehensive Flow–Mass–Thermal–Electrochemical Coupling Model for a VRFB Stack and Its Application in a Stack Temperature Control Strategy" Batteries 10, no. 10: 347. https://doi.org/10.3390/batteries10100347
APA StyleYin, C., Lu, M., Ma, Q., Su, H., Yang, W., & Xu, Q. (2024). A Comprehensive Flow–Mass–Thermal–Electrochemical Coupling Model for a VRFB Stack and Its Application in a Stack Temperature Control Strategy. Batteries, 10(10), 347. https://doi.org/10.3390/batteries10100347













