Real-Time Lithium Battery Aging Prediction Based on Capacity Estimation and Deep Learning Methods
Abstract
:1. Introduction
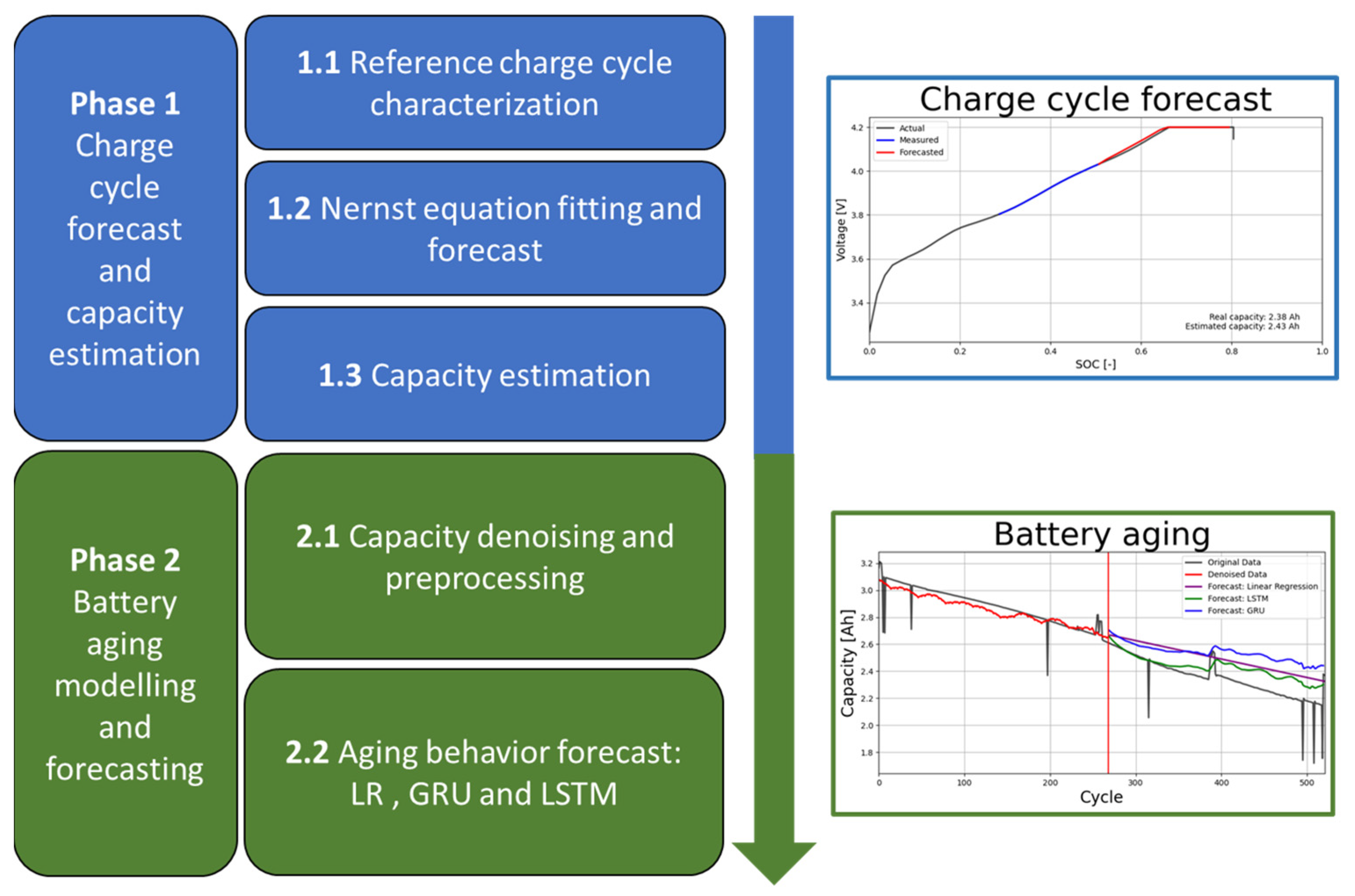
2. Methodology
- Phase 1.1.
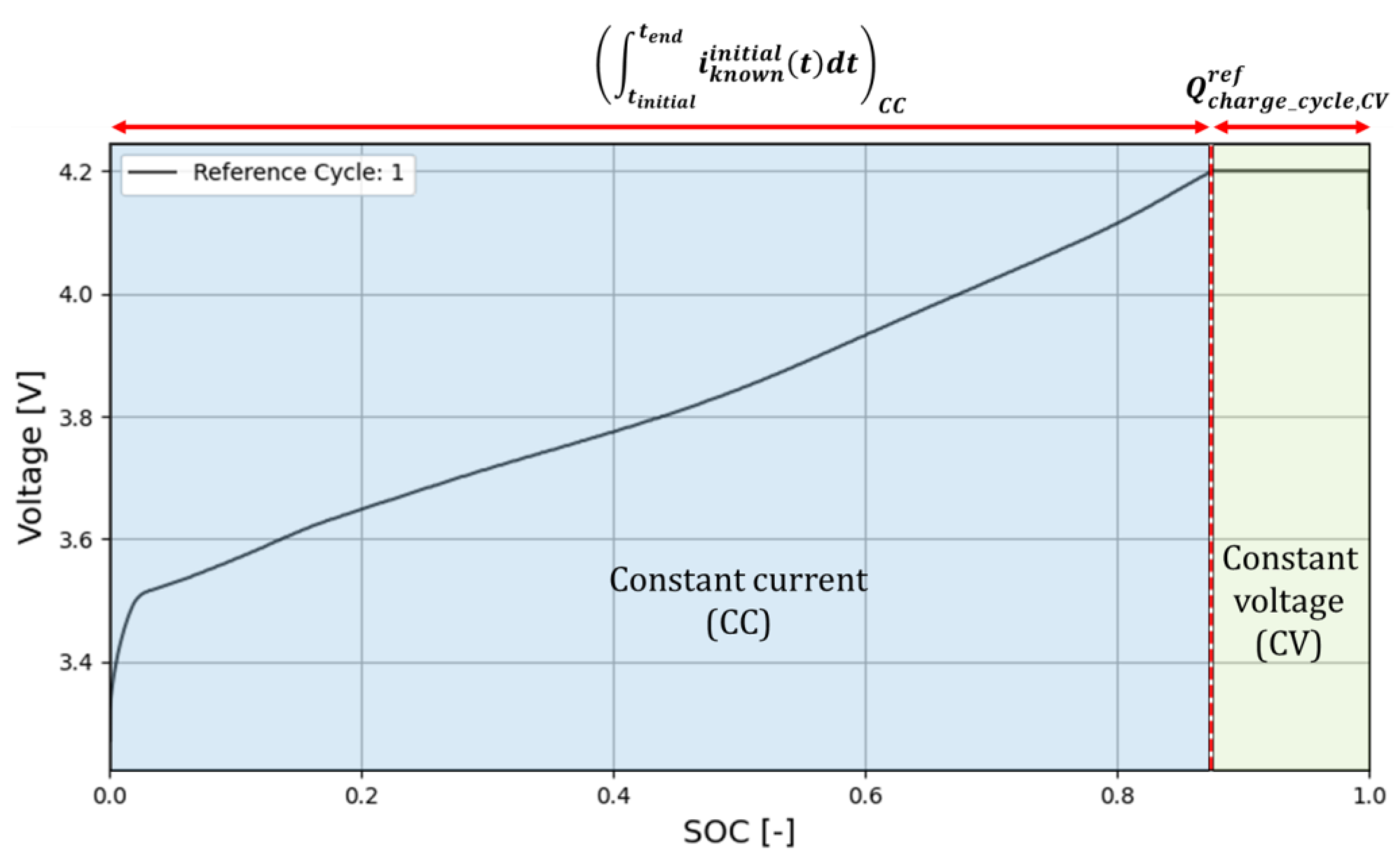
- Reference charge cycle characterization. Several (SOC(t), v(t)) data points of the voltage–SOC curve of the battery are acquired, together with the input charge in the constant voltage (CV) stage of the reference charge cycle, i.e., when the battery is brand new. The initial or reference cycle determines the reference capacity of the battery.
- Phase 1.2.
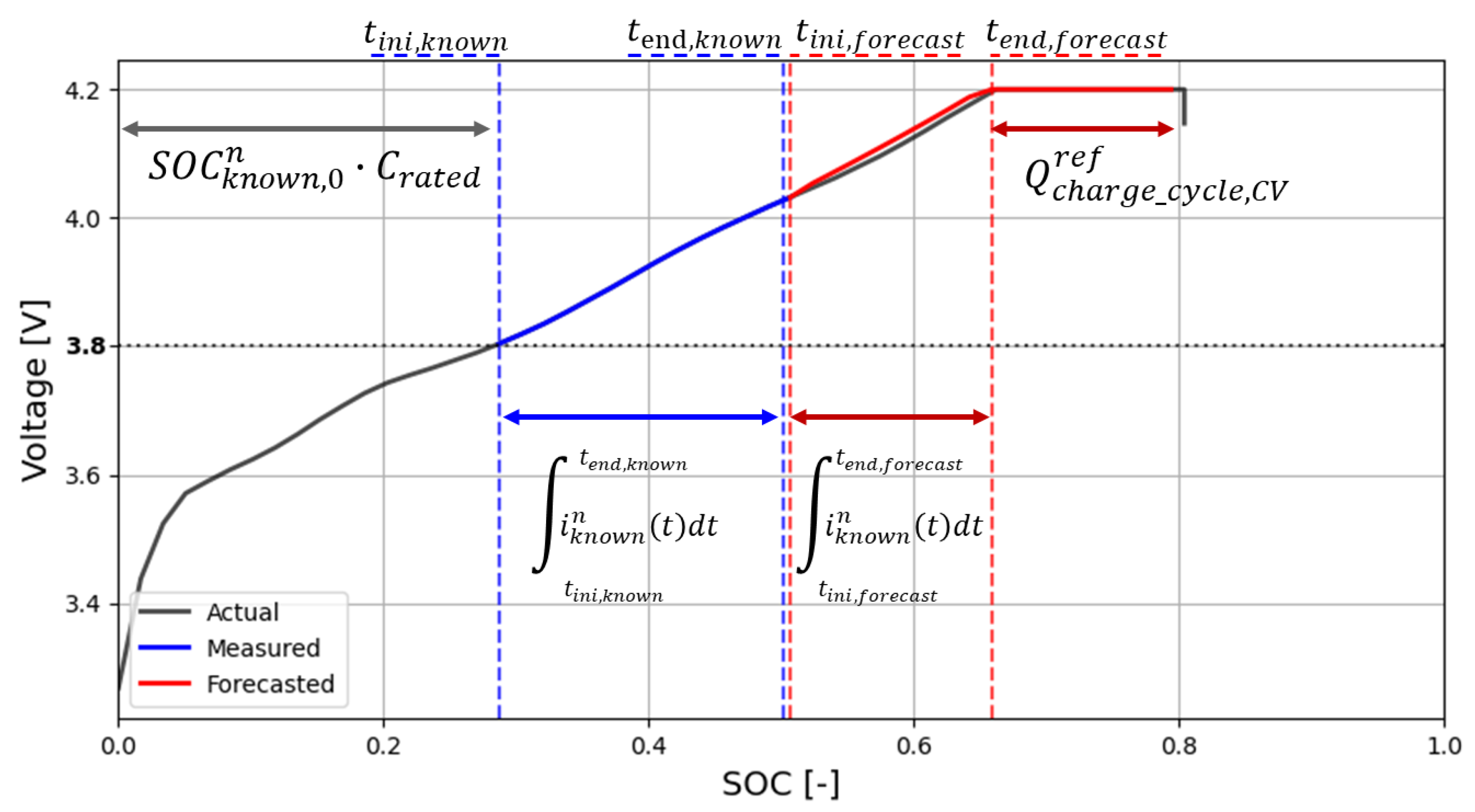
- Nernst equation fitting and forecasting. During the constant current (CC) stage of a generic charge cycle over the lifetime of the battery, a few data points (SOC(t), v(t)) corresponding to a portion of the generic charge cycle are used to fit the Nernst equation and forecast the behavior of the voltage–SOC curve during the remaining charge period.
- Phase 1.3.
- Capacity estimation. The total charge that the battery can hold in a given cycle (cycle capacity) is estimated based on the forecasted charge cycle and the reference cycle data.
- Phase 2.1.
- Phase 2.1 Capacity denoising and preprocessing. To improve the accuracy of the forecasting techniques in future steps, the time-series data of the calculated cycle capacity are denoised using a discrete wavelet filter. In this step, various algorithms are applied to preprocess the input data of the forecast models.
- Phase 2.2.
- Phase 2.2 Aging behavior forecast. Using the processed data from the previous steps as input, linear regression (LR), a long short-term memory neural network (LSTM-RNN), and a gated recurrent unit neural network (GRU-RNN) are used to predict the aging behavior and degradation of the battery.
2.1. Phase 1.1. Reference Charge Cycle Characterization
2.2. Phase 1.2. Nernst Equation Fitting and Forecast
2.3. Phase 1.3. Capacity Estimation
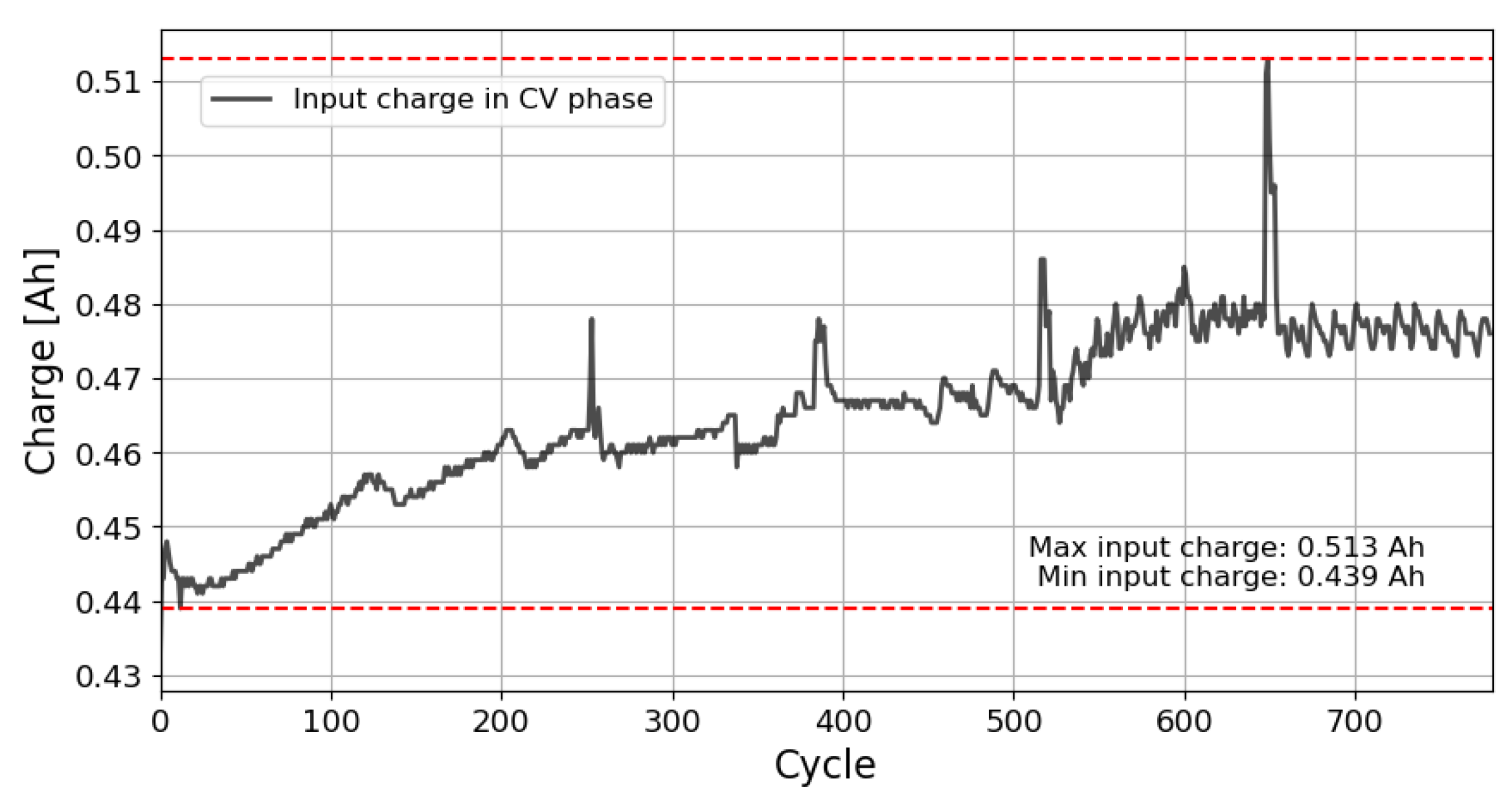
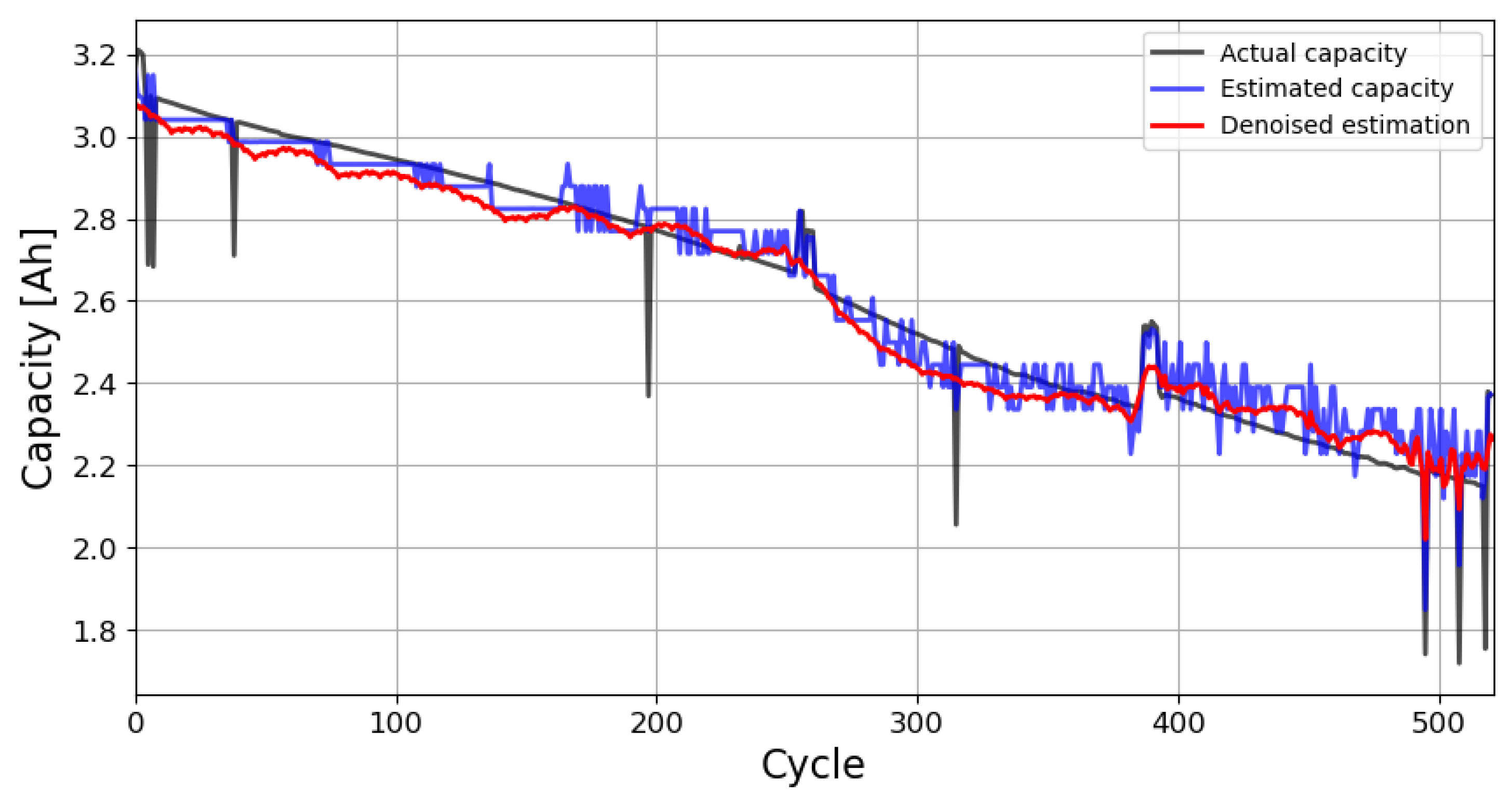
2.4. Phase 2.1. Capacity Denoising and Preprocessing
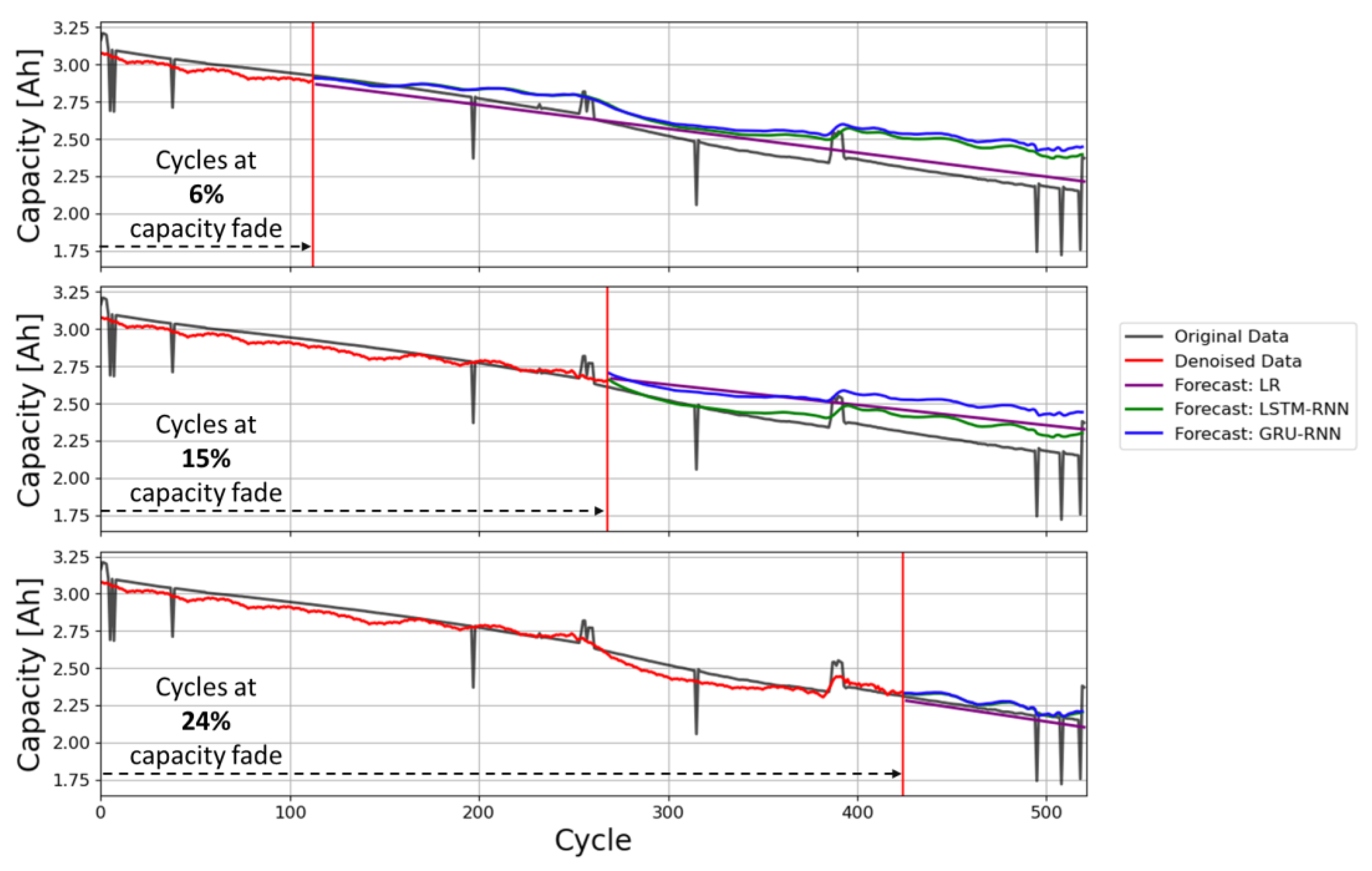
2.5. Phase 2.2. Aging Behavior Forecast
3. Data Description
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Term | Symbol | Unit |
| Battery capacity | C | Ah |
| Reference battery capacity (fresh battery) | Cref | Ah |
| Remaining battery capacity at cycle n | Ah | |
| Constant current phase | CC | - |
| Constant voltage phase | CV | - |
| Battery charge | Q | C |
| Max. battery charge | Qmax | C |
| Rated or nominal battery charge | Qrated | C |
| Remaining battery charge | Qremaining | C |
| Reference battery charge (fresh battery) | Qref | C |
| Current | i | A |
| Generalized least squares | GLS | - |
| Gated recurrent unit | GRU | - |
| Linear regression | LR | - |
| Long short-term memory | LSTM | - |
| State of charge | SOC | - |
| Initial state of charge | SOC0 | - |
| State of health | SOH | - |
| Remaining useful life | RUL | h |
| Internal cell resistance | R | Ω |
| Radial neural network | RNN | - |
| Cell voltage | v | V |
Appendix A

References
- Huang, Y. The discovery of cathode materials for lithium-ion batteries from the view of interdisciplinarity. Interdiscip. Mater. 2022, 1, 323–329. [Google Scholar] [CrossRef]
- Spitthoff, L.; Øyre, E.S.; Muri, H.I.; Wahl, M.; Gunnarshaug, A.F.; Pollet, B.G.; Lamb, J.J.; Burheim, O.S. Thermal management of lithium-ion batteries. In Micro-Optics and Energy: Sensors for Energy Devices; Springer: Berlin/Heidelberg, Germany, 2020; pp. 183–194. [Google Scholar]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.I.; Stroe, A.I.; Teodorescu, R. An Overview and Comparison of Online Implementable SOC Estimation Methods for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Gao, F. Lithium polymer battery state-of-charge estimation based on adaptive unscented kalman filter and support vector machine. IEEE Trans. Power Electron. 2016, 31, 2226–2238. [Google Scholar] [CrossRef]
- Tao, R.; Gu, Y.; Sharma, J.; Hong, K.; Li, J. A conformal heat-drying direct ink writing 3D printing for high-performance lithium-ion batteries. Mater. Today Chem. 2023, 32, 101672. [Google Scholar] [CrossRef]
- Teodorescu, R.; Sui, X.; Vilsen, S.B.; Bharadwaj, P.; Kulkarni, A.; Stroe, D.I. Smart Battery Technology for Lifetime Improvement. Batteries 2022, 8, 169. [Google Scholar] [CrossRef]
- Zhu, J.; Xu, W.; Knapp, M.; Dewi Darma, M.S.; Mereacre, L.; Su, P.; Hua, W.; Liu-Théato, X.; Dai, H.; Wei, X.; et al. A method to prolong lithium-ion battery life during the full life cycle. Cell Reports Phys. Sci. 2023, 4, 101464. [Google Scholar] [CrossRef]
- Ruan, H.; Barreras, J.V.; Engstrom, T.; Merla, Y.; Millar, R.; Wu, B. Lithium-ion battery lifetime extension: A review of derating methods. J. Power Sources 2023, 563, 232805. [Google Scholar] [CrossRef]
- Jin, S.; Huang, X.; Sui, X.; Wang, S.; Teodorescu, R.; Stroe, D.I. Overview of Methods for Battery Lifetime Extension. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021. [Google Scholar]
- Harper, G.; Sommerville, R.; Kendrick, E.; Driscoll, L.; Slater, P.; Stolkin, R.; Walton, A.; Christensen, P.; Heidrich, O.; Lambert, S.; et al. Recycling lithium-ion batteries from electric vehicles. Nature 2019, 575, 75–86. [Google Scholar] [CrossRef]
- Woody, M.; Arbabzadeh, M.; Lewis, G.M.; Keoleian, G.A.; Stefanopoulou, A. Strategies to limit degradation and maximize Li-ion battery service lifetime—Critical review and guidance for stakeholders. J. Energy Storage 2020, 28, 101231. [Google Scholar] [CrossRef]
- Chung, C.H.; Jangra, S.; Lai, Q.; Lin, X. Optimization of Electric Vehicle Charging for Battery Maintenance and Degradation Management. IEEE Trans. Transp. Electrif. 2020, 6, 958–969. [Google Scholar] [CrossRef]
- Shen, L.; Li, J.; Meng, L.; Zhu, L.; Shen, H.T. Transfer Learning-based State of Charge and State of Health Estimation for Li-ion Batteries: A Review. IEEE Trans. Transp. 2023. [Google Scholar] [CrossRef]
- Koleti, U.R. Fast Charging Strategies in Lithium-Ion Batteries: Detection and Control of Lithium Plating; University of Warwick: Coventry, UK, 2020. [Google Scholar]
- de la Vega, J.; Riba, J.R.; Ortega-Redondo, J.A. Mathematical Modeling of Battery Degradation Based on Direct Measurements and Signal Processing Methods. Appl. Sci. 2023, 13, 4938. [Google Scholar] [CrossRef]
- Wenzl, H. BATTERIES|Capacity. In Encyclopedia of Electrochemical Power Sources; Newnes: Sebastopol, CA, USA, 2009; pp. 395–400. [Google Scholar]
- Peng, J.; Meng, J.; Chen, D.; Liu, H.; Hao, S.; Sui, X.; Du, X. A Review of Lithium-Ion Battery Capacity Estimation Methods for Onboard Battery Management Systems: Recent Progress and Perspectives. Batteries 2022, 8, 229. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, C. Fundamentals and Application of Lithium-Ion Batteries in Electric Drive Vehicles; Sons, J.W., Ed.; Wiley: Singapore, 2015. [Google Scholar]
- IEC IEC 62660-2:2018; Secondary Lithium-Ion Cells for the Propulsion of Electric Road Vehicles—Part 2: Reliability and Abuse Testing. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- ISO ISO 6469-1:2019; Electrically Propelled Road Vehicles—Safety Specifications—Part 1: Rechargeable Energy Storage System (RESS). ISO: Geneva, Switzerland, 2019.
- IEEE IEEE Std 450-2020; Recommended Practice for Maintenance, Testing, and Replacement of Vented Lead-Acid Batteries for Stationary Applications. IEEE: Piscataway Township, NJ, USA, 2020.
- Meng, J.; Cai, L.; Luo, G.; Stroe, D.I.; Teodorescu, R. Lithium-ion battery state of health estimation with short-term current pulse test and support vector machine. Microelectron. Reliab. 2018, 88–90, 1216–1220. [Google Scholar] [CrossRef]
- Song, Y.; Li, L.; Peng, Y.; Liu, D. Lithium-Ion Battery Remaining Useful Life Prediction Based on GRU-RNN. In Proceedings of the 2018 12th International Conference on Reliability, Maintainability, and Safety (ICRMS), Shanghai, China, 17–19 October 2018; pp. 317–322. [Google Scholar]
- Park, K.; Choi, Y.; Choi, W.J.; Ryu, H.Y.; Kim, H. LSTM-Based Battery Remaining Useful Life Prediction with Multi-Channel Charging Profiles. IEEE Access 2020, 8, 20786–20798. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, Y.; Zhang, B.; Liu, M.; Wang, J.; Liu, C.; Hao, X.; Kowal, J.; Zhao, J.; Zhu, Y.; et al. Review of State Estimation and Remaining Useful Life Prediction Methods for Lithium–Ion Batteries. Sustainability 2023, 15, 5014. [Google Scholar]
- MaximIntegrated. MAX1726x ModelGauge m5 EZ User Guide; MaximIntegrated: San Jose, CA, USA, 2018. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Hussein, A.A.H.; Batarseh, I. An overview of generic battery models. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Wang, Y.; Meng, D.; Chang, Y.; Zhou, Y.; Li, R.; Zhang, X. Research on online parameter identification and SOC estimation methods of lithium-ion battery model based on a robustness analysis. Int. J. Energy Res. 2021, 45, 21234–21253. [Google Scholar] [CrossRef]
- Pavković, D.; Kasać, J.; Krznar, M.; Cipek, M. Adaptive Constant-Current/Constant-Voltage Charging of a Battery Cell Based on Cell Open-Circuit Voltage Estimation. World Electr. Veh. J. 2023, 14, 155. [Google Scholar] [CrossRef]
- Meng, J.; Azib, T.; Yue, M. Early-Stage end-of-Life prediction of lithium-Ion battery using empirical mode decomposition and particle filter. Proc. Inst. Mech. Eng. Part A J. Power Energy 2023. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J.; Zhao, Y. Wavelet Based Denoising for the Estimation of the State of Charge for Lithium-Ion Batteries. Energies 2018, 11, 1144. [Google Scholar] [CrossRef]
- Dogan, A.; Cidem Dogan, D. A Review on Machine Learning Models in Forecasting of Virtual Power Plant Uncertainties. Arch. Comput. Methods Eng. 2023, 30, 2081–2103. [Google Scholar] [CrossRef]
- Kwon, S.J.; Han, D.; Choi, J.H.; Lim, J.H.; Lee, S.E.; Kim, J. Remaining-useful-life prediction via multiple linear regression and recurrent neural network reflecting degradation information of 20Ah LiNixMnyCo1−x−yO2 pouch cell. J. Electroanal. Chem. 2020, 858, 113729. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Preger, Y.; Barkholtz, H.M.; Fresquez, A.; Campbell, D.L.; Juba, B.W.; Romàn-Kustas, J.; Ferreira, S.R.; Chalamala, B. Degradation of Commercial Lithium-Ion Cells as a Function of Chemistry and Cycling Conditions. J. Electrochem. Soc. 2020, 167, 120532. [Google Scholar] [CrossRef]
- Available online: https://www.batteryarchive.org/ (accessed on 27 November 2023).
- Lu, J.; Xiong, R.; Tian, J.; Wang, C.; Hsu, C.W.; Tsou, N.T.; Sun, F.; Li, J. Battery degradation prediction against uncertain future conditions with recurrent neural network enabled deep learning. Energy Storage Mater. 2022, 50, 139–151. [Google Scholar] [CrossRef]
- Costa, N.; Sánchez, L.; Anseán, D.; Dubarry, M. Li-ion battery degradation modes diagnosis via Convolutional Neural Networks. J. Energy Storage 2022, 55, 105558. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Cao, L.; Gopaluni, B.; Cao, Y. Long Short-Term Memory Network with Transfer Learning for Lithium-ion Battery Capacity Fade and Cycle Life Prediction. Appl. Energy 2023, 350, 121660. [Google Scholar] [CrossRef]
- Lee, G.R.; Gommers, R.; Waselewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python package for wavelet analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Matlab Introduction to Wavelet Families. Available online: https://www.mathworks.com/help/wavelet/gs/introduction-to-the-wavelet-families.html (accessed on 17 December 2023).
| Cathode Chemistry | NCA | NMC |
|---|---|---|
| Manufacturer | Panasonic | LG Chem |
| Manufacturer PN | NCR18650B | 18650HG2 |
| Battery type | 18650 | 18650 |
| Nominal capacity [Ah] | 3.2 | 3 |
| Nominal voltage [V] | 3.6 | 3.6 |
| Voltage range [V] | 2.5 to 4.2 | 2 to 4.2 |
| Max discharge current [A] | 6 | 20 |
| Temperature range [°C] | 0 to 45 | −5 to 50 |
| Charge C-rate | 0.5C | 0.5C |
| Discharge C-rate | 0.5C/1C/2C | 0.5C/1C/2C |
| Test temperature [°C] | 15 °C/25 °C/35 °C | 15 °C/25 °C/35 °C |
| Depth of discharge | 0% to 100% | 0% to 100% |
| Tambient | 15 °C | 25 °C | 35 °C | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cathode | NCA | NMC | NCA | NMC | NCA | NMC | ||||||||
| C-Rate | 1 | 2 | 1 | 2 | 0.5 | 1 | 2 | 0.5 | 1 | 2 | 1 | 2 | 1 | 2 |
| Average max. difference [Ah] | 0.08 | 0.10 | 0.04 | 0.03 | 0.05 | 0.06 | 0.08 | 0.21 | 0.14 | 0.09 | 0.09 | 0.09 | 0.07 | 0.07 |
| Average max. difference [%] * | 2.73 | 3.41 | 1.46 | 1.08 | 0.44 | 2.03 | 2.62 | 7.14 | 4.63 | 3.06 | 2.50 | 2.80 | 2.38 | 2.38 |
| Tambient | 15 °C | 25 °C | 35 °C | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cathode | NCA | NMC | NCA | NMC | NCA | NMC | |||||||||
| V | C-Rate | 1 | 2 | 1 | 2 | 0.5 | 1 | 2 | 0.5 | 1 | 2 | 1 | 2 | 1 | 2 |
| 3.7 | RMSE | 0.11 | 0.12 | 0.11 | 0.07 | 0.09 | 0.09 | 0.11 | 0.35 | 0.34 | 0.17 | 0.18 | 0.17 | 0.17 | 0.16 |
| MAPE | 4.46 | 5.16 | 5.27 | 3.05 | 2.54 | 3.16 | 3.78 | 13.80 | 13.78 | 7.02 | 5.71 | 6.40 | 6.61 | 6.15 | |
| 3.8 | RMSE | 0.06 | 0.11 | 0.07 | 0.04 | 0.04 | 0.06 | 0.1 | 0.18 | 0.21 | 0.22 | 0.09 | 0.12 | 0.17 | 0.21 |
| MAPE | 2.23 | 4.08 | 1.81 | 1.4 | 1.34 | 1.75 | 2.77 | 6.26 | 7.23 | 9.05 | 2.18 | 3.86 | 6.69 | 8.23 | |
| 3.9 | RMSE | 0.04 | 0.05 | 0.13 | 0.12 | 0.05 | 0.07 | 0.08 | 0.11 | 0.07 | 0.11 | 0.12 | 0.14 | 0.13 | 0.15 |
| MAPE | 1.14 | 1.89 | 6.30 | 5.84 | 1.87 | 2.32 | 3.02 | 2.67 | 2.82 | 4.54 | 3.99 | 5.55 | 5.22 | 5.62 | |
| Forecast Errors Calculated at the Cycle Corresponding to 6% Capacity Fade | ||||||||||||||||
| TAmb | 15 °C | 25 °C | 35 °C | |||||||||||||
| Cathode | NCA | NMC | NCA | NMC | NCA | NMC | ||||||||||
| C-Rate | 1 | 2 | 1 | 2 | 0.5 | 1 | 2 | 0.5 | 1 | 2 | 1 | 2 | 1 | 2 | Average | |
| LR | RMSE | 0.09 | 0.13 | 0.19 | 0.19 | 0.17 | 0.13 | 0.14 | 0.16 | 0.26 | 0.24 | 0.23 | 0.20 | 0.22 | 0.28 | 0.19 |
| MAPE | 3.54 | 5.14 | 9.68 | 9.41 | 6.10 | 4.77 | 5.51 | 6.57 | 10.50 | 10.55 | 7.75 | 7.71 | 9.29 | 11.49 | 7.72 | |
| GRU | RMSE | 0.48 | 0.80 | 0.29 | 0.27 | 0.05 | 0.28 | 0.38 | 0.75 | 0.40 | 0.30 | 0.15 | 0.31 | 0.34 | 0.15 | 0.35 |
| MAPE | 19.20 | 40.47 | 13.61 | 10.48 | 1.59 | 9.70 | 15.66 | 28.82 | 15.60 | 10.63 | 4.65 | 11.15 | 12.30 | 5.60 | 14.25 | |
| LSTM | RMSE | 0.08 | 0.15 | 0.17 | 0.11 | 0.10 | 0.08 | 0.11 | 0.14 | 0.24 | 0.24 | 0.16 | 0.16 | 0.20 | 0.27 | 0.16 |
| MAPE | 3.09 | 5.66 | 8.63 | 5.28 | 3.40 | 2.83 | 3.27 | 5.87 | 9.68 | 10.57 | 4.92 | 5.59 | 8.18 | 11.11 | 6.29 | |
| Forecast Errors Calculated at the Cycle Corresponding to 15% Capacity Fade | ||||||||||||||||
| TAmb | 15 °C | 25 °C | 35 °C | |||||||||||||
| Cathode | NCA | NMC | NCA | NMC | NCA | NMC | ||||||||||
| C-Rate | 1 | 2 | 1 | 2 | 0.5 | 1 | 2 | 0.5 | 1 | 2 | 1 | 2 | 1 | 2 | Average | |
| LR | RMSE | 0.05 | 0.12 | 0.05 | 0.03 | 0.06 | 0.06 | 0.12 | 0.15 | 0.19 | 0.2 | 0.14 | 0.15 | 0.17 | 0.21 | 0.12 |
| MAPE | 1.7 | 3.84 | 2.16 | 1.54 | 2.49 | 2.03 | 3.79 | 6.21 | 7.34 | 8.93 | 4.33 | 5.74 | 7.18 | 8.35 | 4.69 | |
| GRU | RMSE | 0.24 | 0.3 | 0.28 | 0.32 | 0.1 | 0.21 | 0.12 | 0.18 | 0.12 | 0.33 | 0.15 | 0.41 | 0.14 | 0.1 | 0.21 |
| MAPE | 10.38 | 13.95 | 14.85 | 15.25 | 3.82 | 8.03 | 4.05 | 7.43 | 4.8 | 14.16 | 4.89 | 17.67 | 5.26 | 3.09 | 9.12 | |
| LSTM | RMSE | 0.04 | 0.15 | 0.06 | 0.02 | 0.03 | 0.07 | 0.12 | 0.14 | 0.16 | 0.21 | 0.12 | 0.15 | 0.15 | 0.19 | 0.12 |
| MAPE | 1.51 | 5.53 | 2.69 | 0.78 | 0.86 | 2.21 | 3.57 | 5.85 | 6.28 | 9.12 | 3.3 | 5.84 | 6.12 | 7.75 | 4.39 | |
| Forecast Errors Calculated at the Cycle Corresponding to 24% Capacity Fade | ||||||||||||||||
| TAmb | 15 °C | 25 °C | 35 °C | |||||||||||||
| Cathode | NCA | NMC | NCA | NMC | NCA | NMC | ||||||||||
| C-Rate | 1 | 2 | 1 | 2 | 0.5 | 1 | 2 | 0.5 | 1 | 2 | 1 | 2 | 1 | 2 | Average | |
| LR | RMSE | 0.04 | 0.15 | 0.06 | 0.02 | 0.01 | 0.07 | 0.15 | 0.12 | 0.12 | 0.21 | 0.09 | 0.15 | 0.11 | 0.19 | 0.11 |
| MAPE | 1.83 | 5.1 | 3.23 | 0.88 | 0.43 | 2.67 | 5.71 | 4.86 | 5.16 | 9.28 | 2.8 | 5.85 | 4.69 | 7.41 | 4.28 | |
| GRU | RMSE | 0.09 | 0.24 | 0.06 | 0.17 | 0.05 | 0.13 | 0.13 | 0.13 | 0.08 | 0.2 | 0.1 | 0.21 | 0.09 | 0.17 | 0.13 |
| MAPE | 3.88 | 12.12 | 3.07 | 8.93 | 1.61 | 5.18 | 2.49 | 5.71 | 3.12 | 9.25 | 3.62 | 8.23 | 3.72 | 6.66 | 5.54 | |
| LSTM | RMSE | 0.05 | 0.17 | 0.08 | 0.02 | 0.02 | 0.06 | 0.15 | 0.12 | 0.11 | 0.22 | 0.08 | 0.17 | 0.12 | 0.2 | 0.11 |
| MAPE | 2.04 | 6.48 | 4.64 | 0.78 | 0.63 | 2.34 | 4.62 | 5.24 | 4.79 | 9.9 | 2.41 | 7.47 | 4.87 | 7.76 | 4.57 | |
| Method | Average Computation Time per Cycle [s] |
|---|---|
| Capacity estimation | 0.00158 |
| DWT denoising | 0.00053 |
| LR | 0.00188 |
| GRU | 19.28116 |
| LSTM | 21.13642 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de la Vega, J.; Riba, J.-R.; Ortega-Redondo, J.A. Real-Time Lithium Battery Aging Prediction Based on Capacity Estimation and Deep Learning Methods. Batteries 2024, 10, 10. https://doi.org/10.3390/batteries10010010
de la Vega J, Riba J-R, Ortega-Redondo JA. Real-Time Lithium Battery Aging Prediction Based on Capacity Estimation and Deep Learning Methods. Batteries. 2024; 10(1):10. https://doi.org/10.3390/batteries10010010
Chicago/Turabian Stylede la Vega, Joaquín, Jordi-Roger Riba, and Juan Antonio Ortega-Redondo. 2024. "Real-Time Lithium Battery Aging Prediction Based on Capacity Estimation and Deep Learning Methods" Batteries 10, no. 1: 10. https://doi.org/10.3390/batteries10010010
APA Stylede la Vega, J., Riba, J.-R., & Ortega-Redondo, J. A. (2024). Real-Time Lithium Battery Aging Prediction Based on Capacity Estimation and Deep Learning Methods. Batteries, 10(1), 10. https://doi.org/10.3390/batteries10010010






