Ferromagnetic Resonance in Magnetic Oxide Nanoparticules: A Short Review of Theory and Experiment
Abstract
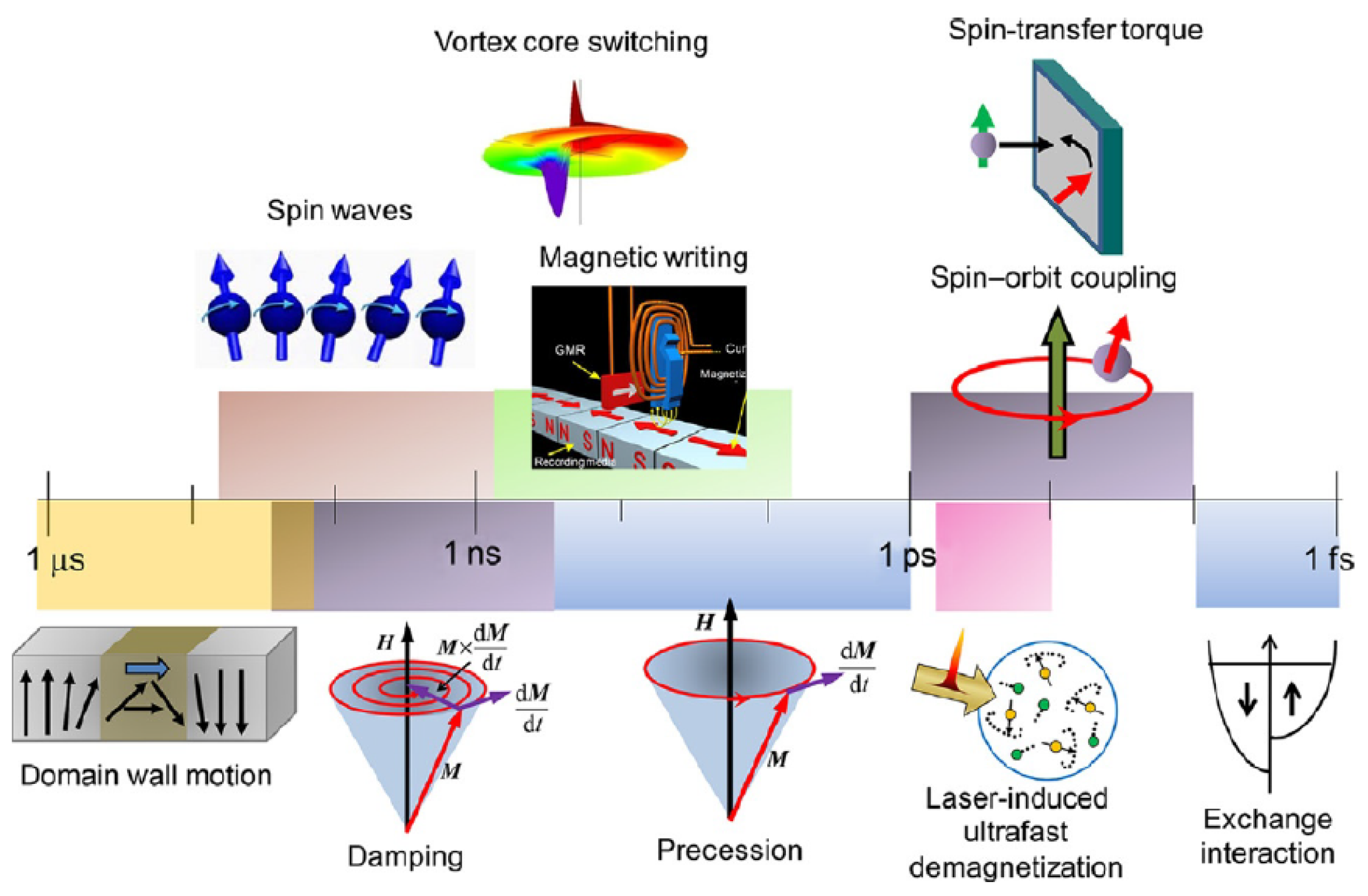
1. Introduction
2. Ferromagnetic Resonance
3. Methods of Synthesis
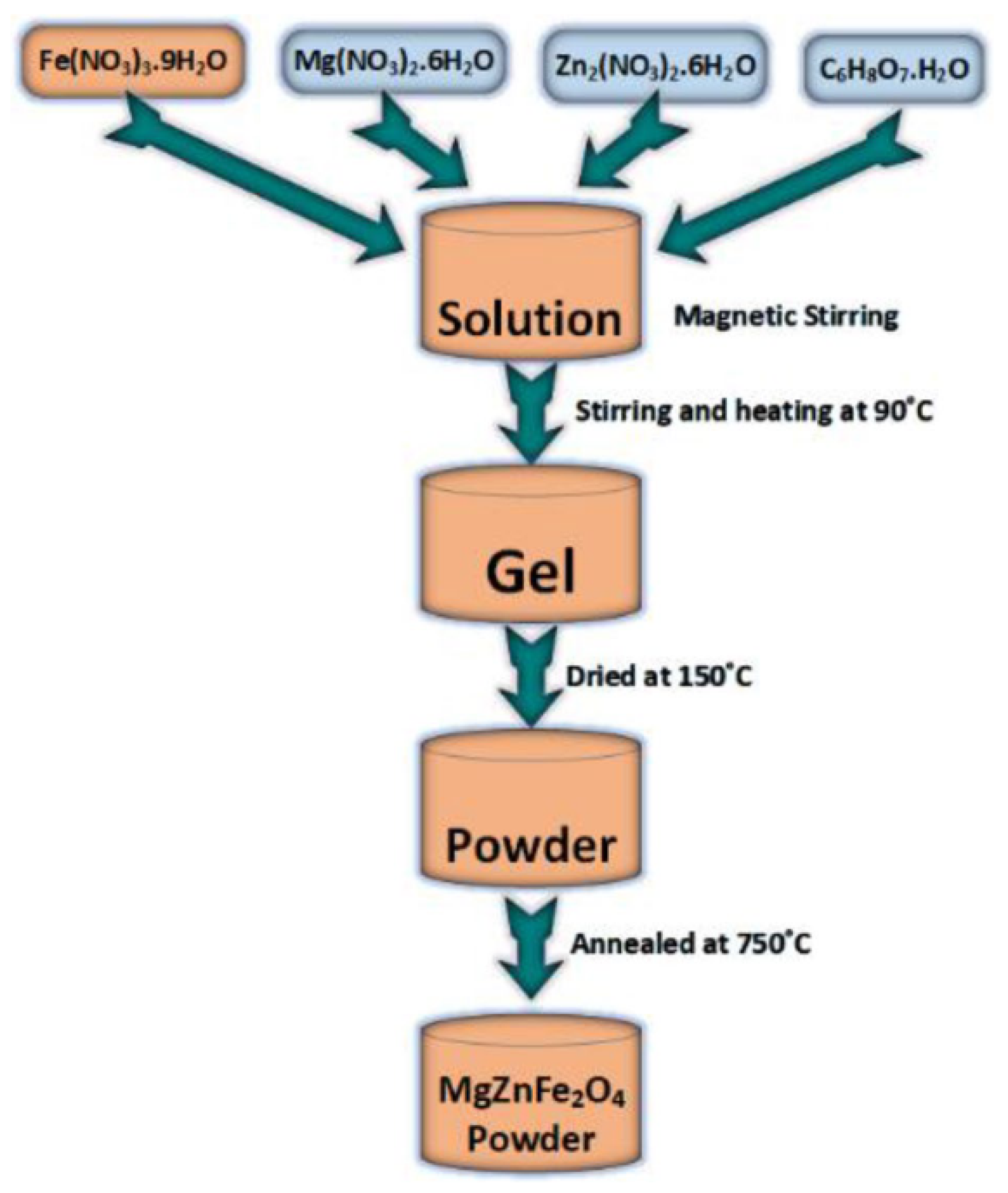
3.1. Sol-Gel Technique
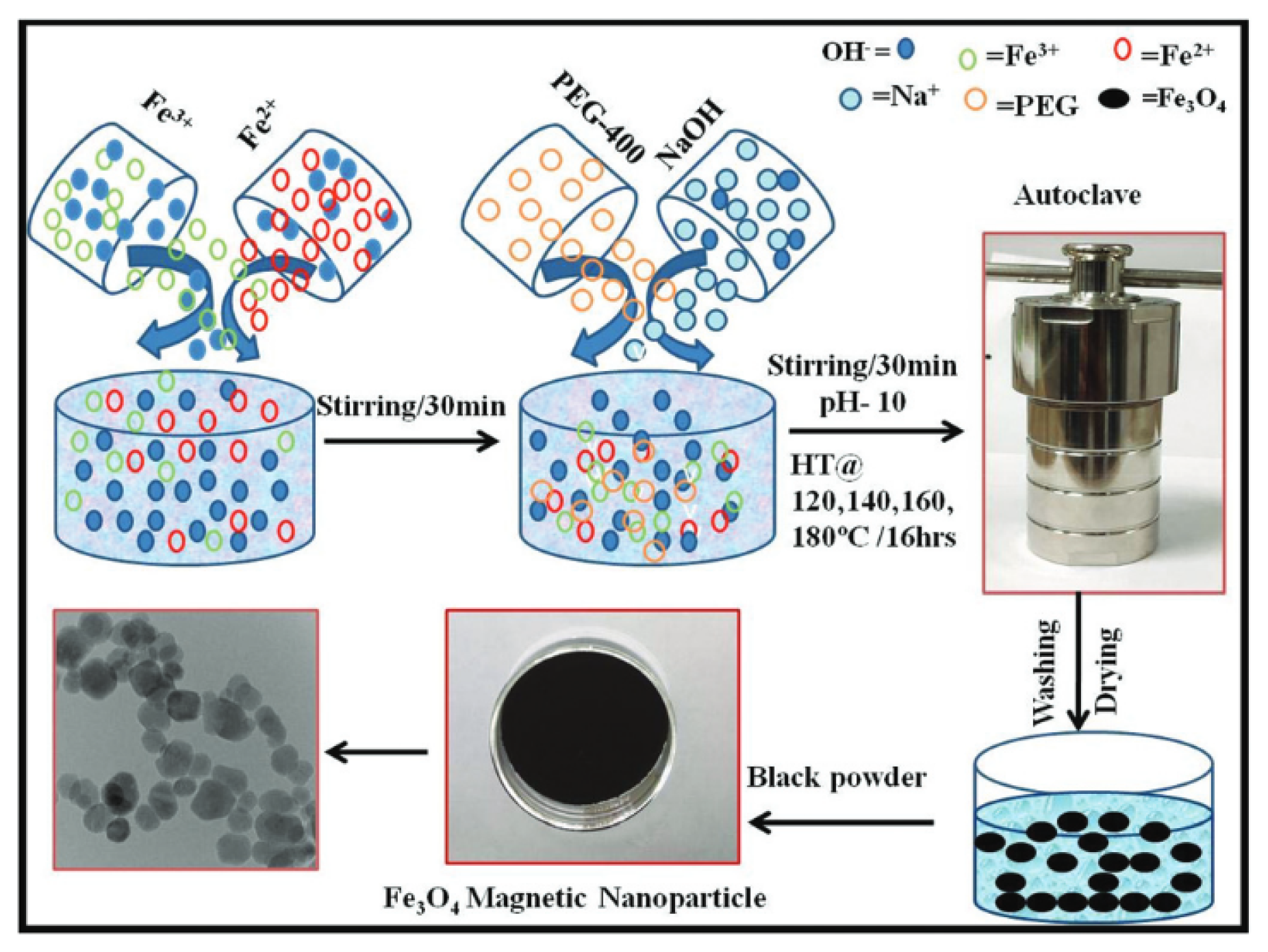
3.2. Hydrothermal Technique
4. Aspects of Ferromagnetic Resonance in Magnetic Nanoparticle Assemblies
4.1. General Theory of Ferromagnetic Resonance
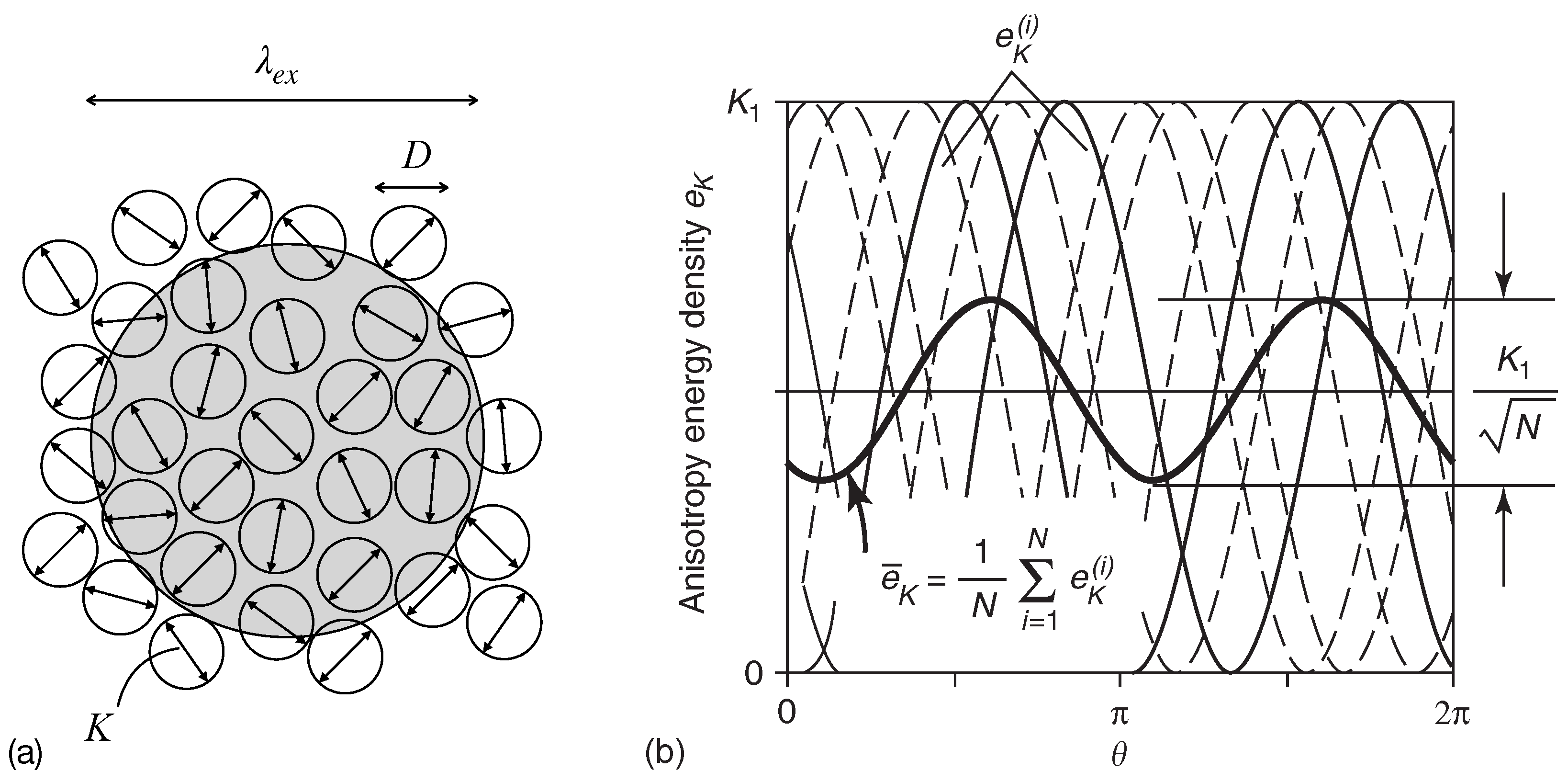
4.2. Contributions to the Free Energy in Magnetic Nanoparticle Systems
4.3. Ferromagnetic Resonance in Magnetic Nanoparticle Assemblies
4.4. Superparamagnetism and Its Effect on the Ferromagnetic Resonance of Magnetic Nanoparticles
4.5. FMR Linewidth
5. A Compilation of Experimental Studies on FMR
5.1. Effect of Temperature
5.2. Doping Effect
5.3. Other Effects
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schmool, D.S. Ferromagnetic Resonance in Nanometric Magnetic Systems; Elsevier: Amsterdam, The Netherlands, 2016; p. 19. [Google Scholar]
- Gazeau, F.; Bacri, J.; Gendron, F.; Perzynski, R.; Raikher, Y.; Stepanov, V.; Dubois, E. Magnetic resonance of ferrite nanoparticles: Evidence of surface effects. J. Magn. Magn. Mater. 1998, 186, 175–187. [Google Scholar] [CrossRef]
- Arbab, A.; Tufail, S.; Rehmat, U.; Pingfan, Z.; Manlin, G.; Muhammad, O.; Zhiqiang, T.; YuKui, R. Review on Recent Progress in Magnetic Nanoparticles: Synthesis, Characterization, and Diverse Applications. Front. Chem. 2021, 9, 629054. [Google Scholar]
- kianfar, E. Magnetic Nanoparticles in Targeted Drug Delivery: A Review. J. Supercond. Nov. Magn. 2021, 34, 1709–1735. [Google Scholar] [CrossRef]
- Mitchell, E.; Gupta, R.K.; Mensah-Darkwa, K.; Kumar, D.; Ramasamy, K.; Gupta, B.K.; Kahol, P. Facile synthesis and morphogenesis of superparamagnetic iron oxide nanoparticles for high-performance supercapacitor applications. N. J. Chem. 2014, 38, 4344. [Google Scholar] [CrossRef]
- Chhaganlal, G.A.; Pradeep, R.; Yu-Chen, Y.; Tai-Yue, L.; Chi-Yuan, W.; Hayakawa, Y.; Yun, W.S. Understanding the Magnetic Memory Effect in Fe-Doped NiO Nanoparticles for the Development of Spintronic Devices. ACS Appl. Nano Mater. 2019, 2, 278–290. [Google Scholar]
- Hirohata, A.; Takanashi, K. Future perspectives for spintronic devices. J. Phys. D Appl. Phys. 2014, 47, 193001. [Google Scholar] [CrossRef]
- Puebla, J.; Kim, J.; Kondou, K.; Yoshichika, O. Spintronic devices for energy-efficient data storage and energy harvesting. Commun. Mater. 2020, 1, 24. [Google Scholar] [CrossRef]
- Barla, P.; Joshi, V.K.; Bhat, S. Spintronic devices: A promising alternative to CMOS devices. J. Comput. Electron. 2021, 20, 805–837. [Google Scholar] [CrossRef]
- Barman, A.; Haldar, A. Time-Domain Study of Magnetization Dynamics in Magnetic Thin Films and Micro- and Nanostructures. Solid State Phys. 2014, 65, 1–108. [Google Scholar]
- Sima, M.; Fatemeh, Z.S.; Mussa, F.S.; Mehdi, S.G.; Abolfazl, A. Current methods for synthesis of magnetic nanoparticles. Artif. Cells Nanomed. Biotechnol. 2016, 44, 722–734. [Google Scholar]
- Jing, X.; Haibin, Y.; Wuyou, F.; Kai, D.; Yongming, S.; Jiuju, C.; Yi, Z.; Minghui, L.; Guangtian, Z. Preparation and magnetic properties of magnetite nanoparticles by sol–gel method. J. Magn. Magn. Mater. 2007, 309, 307–311. [Google Scholar]
- Atiqur, R.M.; Tariqul, I.M.; Jit, S.M.S.; Samsuzzaman, M.; Samsuzzaman, M.E.H. Synthesis and characterization of Mg–Zn ferrite based flexible microwave composites and its application as SNG metamaterial. Sci. Rep. 2021, 11, 7654. [Google Scholar]
- Pessoa, M.; Moscon, P.; Melo, R.; Franco, A.; Morais, P. A comprehensive study of Co1-xNixFe2O4 nanoparticles fabricated via three different synthetic methods. Mater. Res. Express 2019, 6, 125068. [Google Scholar] [CrossRef]
- Prashant, K.; Khanduri, H.; Saurabh, P.; Arjun, S.; Basheed, G.A.; Pant, R.P. Temperature selectivity for single phase hydrothermal synthesis of PEG-400 coated magnetite nanoparticles. Dalton Trans. 2020, 49, 8672–8683. [Google Scholar]
- Arkadýev, V.K. The Reflection of Electric Waves from a Wire. Sov. Phys.-JETP 1913, 45A, 45312. [Google Scholar]
- Landau, L. Über die Elektrodynamik der Kristallgitter. Phys. Z. Der Sowjetunion 1935, 8, 165. [Google Scholar]
- Vonsovskii, V. Ferromagnetic Resonance; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Smit, J.; Beljers, H.G. Ferromagnetic Hysteresis in Single Crystals of Hematite (Fe2O3). Philips Res. Rep. 1955, 10, 113–130. [Google Scholar]
- Farle, M. Magnetic nanoparticles: Synthesis, protection, functionalization, and application. Rep. Prog. Phys. 1998, 61, 755–788. [Google Scholar] [CrossRef]
- Osborn, J.A. Demagnetizing Factors of the General Ellipsoid. Phys. Rev. 1945, 67, 351. [Google Scholar] [CrossRef]
- MacDonald, J.R. Ferromagnetic Resonance and the Internal Field in Ferromagnetic Materials. Proc. Phys. Soc. A 1951, 64, 968. [Google Scholar] [CrossRef]
- Slay, D.; Cao, D.; Ferré, E.C.; Charilaou, M. Ferromagnetic resonance of superparamagnetic nanoparticles: The effect of dipole–dipole interactions. J. Appl. Phys. 2021, 130, 113902. [Google Scholar] [CrossRef]
- Skomski, R.; Hadjipanayis, G.C.; Sellmyer, D.J. Effective Demagnetizing Factors of Complicated Particle Mixtures. IEEE Trans. Magn. 2007, 43, 6. [Google Scholar] [CrossRef]
- Schmool, D.S. Nanotechnologies: The Physics of Nanomaterials. In The Physics of Surfaces and Nanofabrication Techniques; Apple Academic Press (CRC Press, Taylor and Francis Group): Cambridge, MA, USA, 2021; Volume 1. [Google Scholar]
- Kachkachi, H.; Dimian, M. Hysteretic properties of a magnetic particle with strong surface anisotropy. Phys. Rev. B 2002, 66, 174419. [Google Scholar] [CrossRef]
- Kachkachi, M.; Bonet, E. Surface-induced cubic anisotropy in nanomagnets. Phys. Rev. B 2006, 73, 224402. [Google Scholar] [CrossRef]
- Jamet, M.; Wernsdorfer, W.; Thirion, C.; Dupuis, V.; Mélinon, P.; Pérez, A.; Mailly, D. Magnetic anisotropy in single clusters. Phys. Rev. B 2004, 69, 024401. [Google Scholar] [CrossRef]
- Bodker, F.; Mørup, S.; Linderoth, S. Surface effects in metallic iron nanoparticles. Phys. Rev. Lett. 1994, 72, 282. [Google Scholar] [CrossRef]
- Herzer, G.M. (Ed.) Properties and Applications of Nanocrystalline Alloys from Amorphous Precursors; NATO ARW Series; Kluwer: Alphen aan den Rijn, The Netherlands, 2005; p. 15234. [Google Scholar]
- Herzer, G. Nanocrystalline Soft Magnetic Alloys. In Handbook of Magnetic Material; Buchow, K.H.J., Ed.; 1997; Volume 10, pp. 415–462. [Google Scholar]
- Alben, R.; Becker, J.J.; Chi, M.C. Random anisotropy in amorphous ferromagnets. JAP 1978, 49, 1653–1658. [Google Scholar] [CrossRef]
- Chudnovsky, E.M.; Saslow, W.M.; Serota, R.A. Ordering in ferromagnets with random anisotropy. Phys. Rev. B 1986, 33, 251. [Google Scholar] [CrossRef]
- Suzuki, K.; Herzer, G. Soft Magnetic Nanostructures and Applications. In Advanced Magnetic Nanostructures; Springer: Lincoln, NE, USA, 2006. [Google Scholar]
- Cacciola, G.; Berdie, J. Surface effects on the wetting properties of nanofluids. Acta Phys. Pol. A 2016, 129, 88–91. [Google Scholar] [CrossRef]
- Schmool, D.S.; Schmalzl, K. Ferromagnetic resonance in magnetic nanoparticle assemblies. J. Non-Cryst. Solids 2007, 353, 738–742. [Google Scholar] [CrossRef]
- Schmool, D.S.; Schmalzl, K. Magnetic dipolar interaction in nanoparticle systems: Theory, simulation and ferromagnetic resonance. In Advances in Nanoscale Magnetism; Springer: Berlin/Heidelberg, Germany, 2009; pp. 321–326. [Google Scholar]
- Schmool, D.S.; Rocha, R.; Sousa, J.B.; Santos, J.A.M.; Kakazei, G.N.; Garitaonandia, J.S.; Lezama, L. The role of dipolar interactions in magnetic nanoparticles: Ferromagnetic resonance in discontinuous magnetic multilayers. J. Appl. Phys. 2007, 101, 103907. [Google Scholar] [CrossRef]
- Netzelmann, U. Magnetic susceptibility of YBa2Cu3O7 single crystals. JAP 1990, 68, 1800–1806. [Google Scholar]
- Dubowik, J.; Rakowski, M.; Baran, M. Anisotropic magnetic susceptibility of TmSe. Phys. Rev. B 1996, 54, 1088–1092. [Google Scholar] [CrossRef]
- Kakazei, G.N.; Pleshchev, V.G.; Poltavtsev, S.V. Magnetic properties of quasicrystals AlNiCo and AlCuFe. JAP 1999, 85, 5654–5657. [Google Scholar]
- Morup, S.; Christensen, M.; Bechgaard, K. Magnetic nanoparticles: Synthesis, stabilization, functionalization, characterization, and applications. Beilstein J. Nanotechnol. 2010, 1, 182–210. [Google Scholar]
- Néel, L. Théorie du trainage magnétique des ferromagnétiques en grains fins avec applications aux terres cuites. Années de Géophysique 1949, 5, 99–136. [Google Scholar]
- Brown, W.F. Thermal fluctuations of a single-domain particle. Phys. Rev. 1963, 130, 1677. [Google Scholar] [CrossRef]
- Chantrell, R. W; Wohlfarths, E.P. Rate Dependence of the Field-Cooled Magnetisation of a Fine Particle System. Phys. Status Solidi 1985, 91, 619–626. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A Mechanism of Magnetic Hysteresis in Heterogeneous Alloys. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1948, 240, 599–642. [Google Scholar] [CrossRef]
- Tannous, C.; Gieraltowski, J. The Stoner–Wohlfarth model of ferromagnetism. Eur. J. Phys. 2008, 29, 475. [Google Scholar] [CrossRef]
- Guardia, P.; Batlle-Brugal, B.; Roca, A.G.; Iglesias, O.; Morales, M.P.; Serna, C.J.; Labarta, A.; Batlle, X. Surfactant effects in magnetite nanoparticles of controlled size. J. Magn. Magn. Mater. 2007, 316, e756–e759. [Google Scholar] [CrossRef]
- Antoniak, C.; Lindner, J.; Farle, M. Magnetic anisotropy and its temperature dependence in iron-rich FexPt1-x nanoparticles. Europhys. Lett. 2005, 70, 250. [Google Scholar] [CrossRef]
- Dormann, J.L.; Bessais, L.; Fiorani, D. A dynamic study of small interacting particles: Superparamagnetic model and spin-glass laws. J. Phys. C Solid State Phys. 1988, 21, 2015. [Google Scholar] [CrossRef]
- Shtrikman, S.; Wohlfarth, E. The theory of the Vogel-Fulcher law of spin glasses. Phys. Lett. A 1981, 85, 467–470. [Google Scholar] [CrossRef]
- Djurberg, C.; Svedlindh, P.; Nordblad, P.; Hansen, M.F.; Bødker, F.; Mørup, S. Dynamics of an Interacting Particle System: Evidence of Critical Slowing Down. Phys. Rev. Lett. 1997, 79, 5154–5157. [Google Scholar] [CrossRef]
- Toulemon, D.; Mircea, V.R.; Schmool, D.; Garitaonandia, J.S.; Lezama, L.; Cattoen, X.; Begin-Colin, S.; Pichon, B.P. Iron Oxide Nanoparticles: Enhanced Collective Magnetic Properties Induced by the Controlled Assembly of Iron Oxide Nanoparticles in Chains. Adv. Funct. Mater. 2016, 26, 2583. [Google Scholar] [CrossRef]
- Charilaou, M. Ferromagnetic resonance of biogenic nanoparticle-chains. JAP 2017, 122, 063903. [Google Scholar] [CrossRef]
- Steen, M.; Elisabeth, T. Superparamagnetic relaxation of weakly interacting particles. Phys. Rev. Lett. 1994, 72, 3278–3281. [Google Scholar]
- Pereira, A.M.; Pereira, C.; Silva, A.S.; Schmool, D.S.; Freire, C.; Greneche, J.M.; Araujo, J.P. Unravelling the effect of interparticle interactions and surface spin canting in γ-Fe2O3SiO2 superparamagnetic nanoparticles. JAP 2011, 109, 114319. [Google Scholar]
- de Biasi, R.S.; Devezas, T.C. Anisotropy field of small magnetic particles as measured by resonance. JAP 1978, 49, 2466–2469. [Google Scholar] [CrossRef]
- Berger, R.; Kliava, J.; Bissey, J.C.; Baietto, V. Superparamagnetic resonance of annealed iron-containing borate glass. J. Phys. Condens. Matter 1998, 10, 8559. [Google Scholar] [CrossRef]
- Berger, R.; Kliava, J. Size and shape distribution of magnetic nanoparticles in disordered systems: Computer simulations of superparamagnetic resonance spectra. J. Magn. Magn. Mater. 1999, 205, 328–342. [Google Scholar]
- Heinrich, B. Spin relaxation in magnetic metallic layers and multilayers. In Ultrathin Magnetic Structures III: Fundamentals of Nanomagnetism; Bland, J.A.C., Heinrich, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; p. 143. [Google Scholar]
- Vittoria, C.; Barker, R.C.; Yelon, A. Anisotropic Ferromagnetic Resonance Linewidth in Ni Platelets. Phys. Rev. Lett. 1967, 19, 792. [Google Scholar] [CrossRef]
- Evgeny, G.; Miroslav, S.; Mingxi, W.; Liudmila, A.; Dmitrii, M.; Ekaterina, K.; Vasilii, L.; Evgeny, A.; Boris, G.; Oleg, B.; et al. Tuning the particle size, natural ferromagnetic resonance frequency and magnetic properties of -Fe 2 O 3 nanoparticles prepared by a rapid sol–gel method. J. Mater. Chem. C 2021, 9, 6173–6179. [Google Scholar]
- Jin, J.; Ohkoshi, S.I.; Hashimoto, K. Giant Coercive Field of Nanometer Sized Iron Oxide. Adv. Mater. 2004, 12, 48–51. [Google Scholar] [CrossRef]
- Pessoa, M.; Proveti, J.; Pelegrini, F.; Moscon, P. Ferromagnetic resonance lines of annealed Ni ferrites. Phys. B Condens. Matter 2019, 558, 20–23. [Google Scholar] [CrossRef]
- Tsay, F.D.; Chan, S.; Manatt, S.L. Ferromagnetic resonance of lunar samples. Geochim. Cosmochim. Acta 1971, 35, 865–875. [Google Scholar] [CrossRef]
- Mantilla, J.; Felix, L.L.; Rodriguez, M.; Aragon1, F.; Morais, P.; Coaquira, J.; Kuzmann, E.; de Oliveira, A.; Gonzalez, I.; Macedo, W.; et al. Washing effect on the structural and magnetic properties of NiFe2O4 nanoparticles synthesized by chemical sol-gel method. Mater. Chem. Phys. 2018, 211, 1–17. [Google Scholar]
- Gandhi, A.C.; Lin, J.C. Magnetic resonance study of exchange-biased Ni/NiO nanoparticles. J. Phys. Condens. Matter 2017, 29, 215802. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, A.C.; Lin, J.C. Exchange bias in finite sized NiO nanoparticles with Ni clusters. J. Magn. Magn. Mater. 2017, 424, 221–225. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Stepanov, V.I. The effect of thermal fluctuations on the FMR line shape in dispersed ferromagnets. Sov. Phys. JETP 1992, 75, 764. [Google Scholar]
- Hernández-Gómez, P.; Valente, M.A.; Graça, M.P.F.; Muñoz, J.M. Synthesis, structural characterization and broadband ferromagnetic resonance in Li ferrite nanoparticles. J. Alloys Compd. 2018, 765, 186–192. [Google Scholar] [CrossRef]
- Azzawi, S.; Hindmarch, A.T.; Atkinson, D. Magnetic damping phenomena in ferromagnetic thin-films and multilayers. J. Phys. D Appl. Phys. 2017, 50, 473001. [Google Scholar] [CrossRef]
- Castel, V.; Youssef, J.B.; Brosseau, C. Broadband ferromagnetic resonance measurements in Ni/ZnO and Niy-Fe2O3 nanocomposites. J. Nanomater. 2007, 27437, 16. [Google Scholar]
- Hernandez-Gomez, P.; Munoz, J.; Valente, M. Field-induced microwave absorption in Ni ferrite nanoparticles. IEEE Trans. Magn. 2010, 46, 475–478. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Song, L.; Zhao, M.; Wang, J.; Luo, H. A study on the coercivity and the magnetic anisotropy of the lithium ferrite nanocrystallite. J. Phys. D Appl. Phys. 1996, 29, 2574. [Google Scholar] [CrossRef]
- Hernandez Gomez, P.; Munoz, J.M.; Valente, M.A.; Graça, M.P.F. Broadband ferromagnetic resonance in Mn doped Li ferrite nanoparticles. Mater. Res. Bull. 2019, 112, 432–437. [Google Scholar] [CrossRef]
- White, O.; Patton, C. Magnetic properties of lithium ferrite microwave materials. J. Magn. Magn. Mater. 1978, 9, 299–317. [Google Scholar] [CrossRef]
- Argentina, B.G.; Courtney, W.; Dionne, G.; Temme, D. Lithium ferrites for microwave devices. IEEE Trans. Magn. 1972, 8, 83–94. [Google Scholar]
- Datt, G.; Kotabageb, C.; Abhyankar, A.C. Ferromagnetic resonance of NiCoFe2O4 nanoparticles and microwave absorption properties of flexible NiCoFe2O4–carbon black/poly(vinyl alcohol) composites. Phys. Chem. Chem. Phys. 2017, 19, 20699–20712. [Google Scholar] [CrossRef]
- Yanez-Vilar, S.; Sanchez-Andujar, M.; Gomez-Aguirre, C.; Mira, J.; Senaris-Rodriguez, M.; Castro-Garcia, S. A simple solvothermal synthesis of MFe2O4 (M=Mn, Co and Ni) nanoparticles. J. Solid State Chem. 2009, 182, 2685–2690. [Google Scholar] [CrossRef]
- Dutta, P.; Manivannan, A.; Seehra, M.; Shah, N.; Huffman, G. Magnetic properties of nearly defect-free maghemite nanocrystals. Phys. Rev. B 2004, 70, 174428. [Google Scholar] [CrossRef]
- Weil, J.A.; Bolton, J.R. Electron Paramagnetic Resonance Elementary Theory and Practical Applications, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Datt, G.; Bishwas, M.S.; Raja, M.M.; Abhyankar, A.C. Observation of magnetic anomalies in onestep solvothermally synthesized nickel–cobalt ferrite nanoparticles. Nanoscale 2016, 8, 5200–5213. [Google Scholar] [CrossRef] [PubMed]
- Chien-Yie, T.; Yi-Chun, C.; Yung-Kuan, T. Investigation on structural, magnetic, and FMR properties for hydrothermally-synthesized magnesium-zinc ferrite nanoparticles. Phys. B Condens. Matter 2019, 570, 29–34. [Google Scholar]
- Gama, L.; Hernandez, E.; Cornejo, D.; Costa, A.; Rezendea, S.; Kiminami, R.; Costa, A. Magnetic and structural properties of nanosize Ni–Zn–Crferrite particles synthesized by combustion reaction. J. Magn. Magn. Mater. 2007, 317, 29–33. [Google Scholar] [CrossRef]
- Angadi, V.J.; Choudhury, L.; Sadhana, K.; Liu, H.L.; Sandhya, R.; Matteppanavar, S.; Rudraswamy, B.; Pattar, V.; Anavekar, R.V.; Praveena, K. Structural, electrical and magnetic properties of Sc3+ doped Mn-Zn ferrite nanoparticles. J. Magn. Magn. Mater. 2017, 424, 1–11. [Google Scholar] [CrossRef]
- Sharma, V.; Kumari, S.; Kuanr, B.K. Rare earth doped M-type hexaferrites; ferromagnetic resonance and magnetization dynamics. AIP Adv. 2018, 8, 056232. [Google Scholar] [CrossRef]
- Bastrukov, S.; Khoo, J.Y.; Lukiyanchuk, B.; Molodtsova, I. Micromagnetic theory of spin relaxation and ferromagnetic resonance in multilayered metallic films. arXiv 2012, arXiv:1210.2609. [Google Scholar]
- Spasova, M.; Wiedwald, U.; Ramchal, R.; Farle, M.; Hilgendorff, M.; Giersig, M. Magnetic properties of arrays of interacting Co nanocrystals. J. Magn. Magn. Mater. 2002, 240, 40–43. [Google Scholar] [CrossRef]
- Amstad, E.; Fischer, H.; Gehring, A.U.; Textor, M.; Reimhul, E. Magnetic Decoupling of Surface Fe3+ in Magnetite Nanoparticles upon Nitrocatechol-Anchored Dispersant Binding. Chem. Eur. J. 2011, 17, 7396–7398. [Google Scholar] [CrossRef]
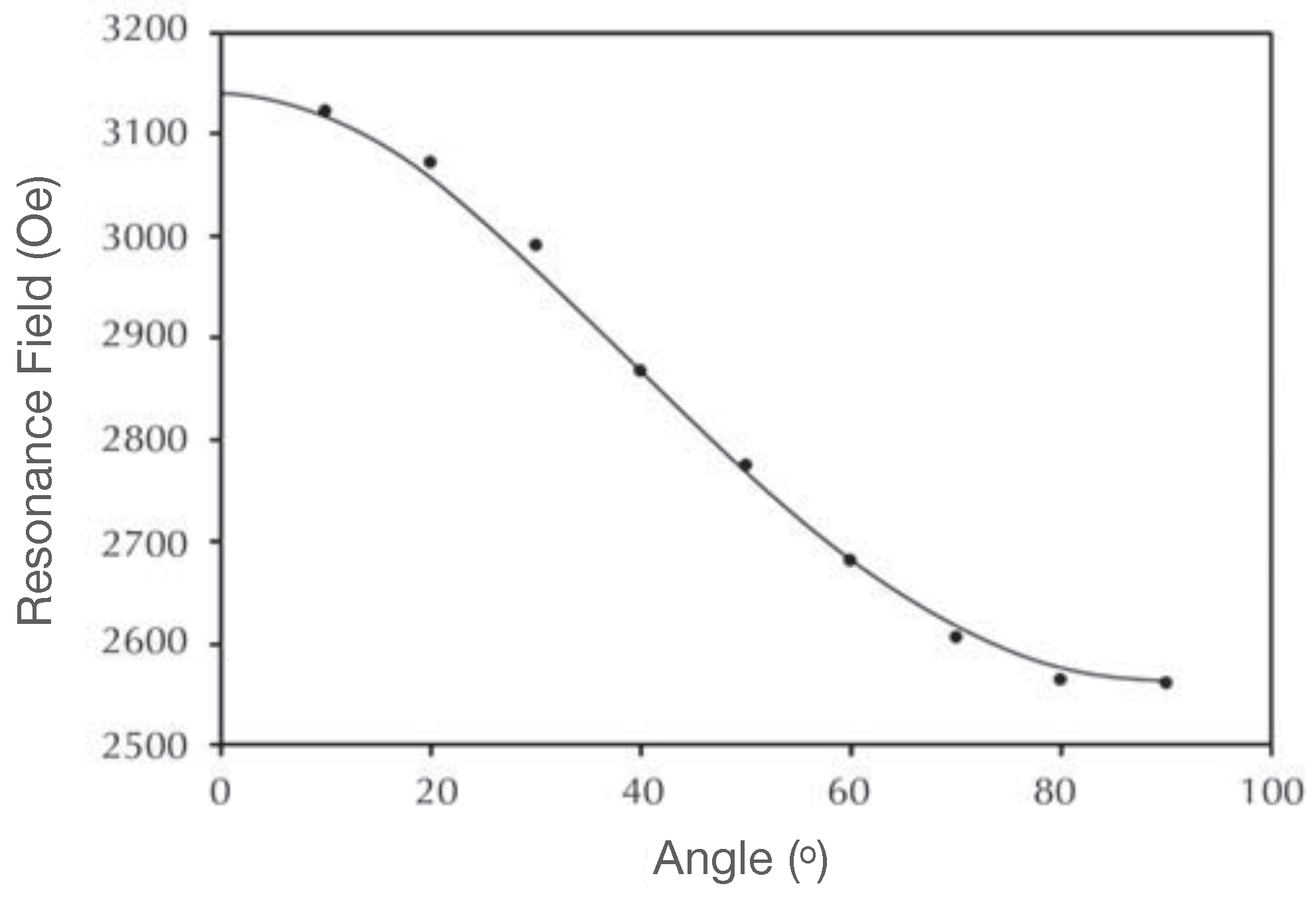
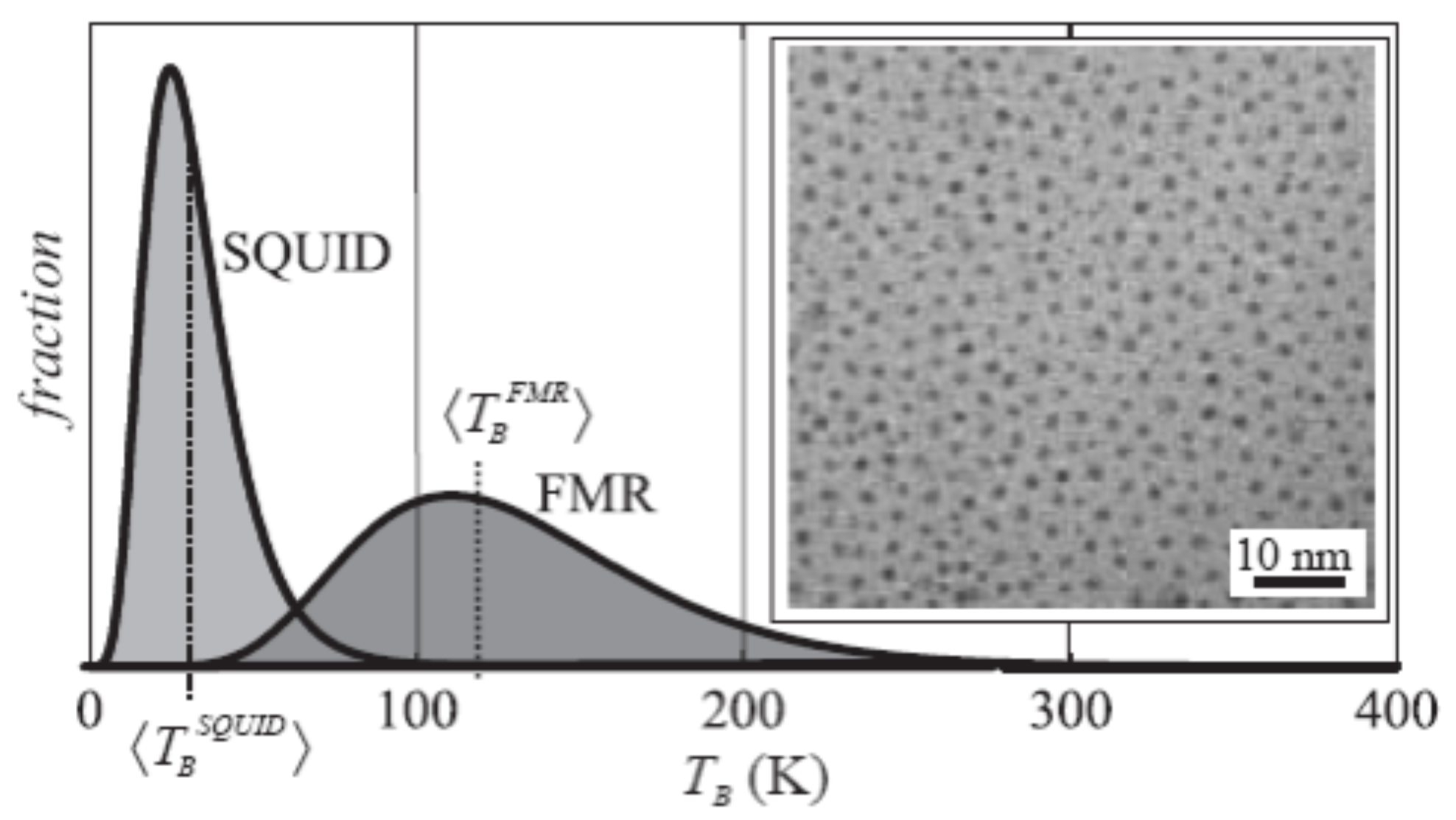



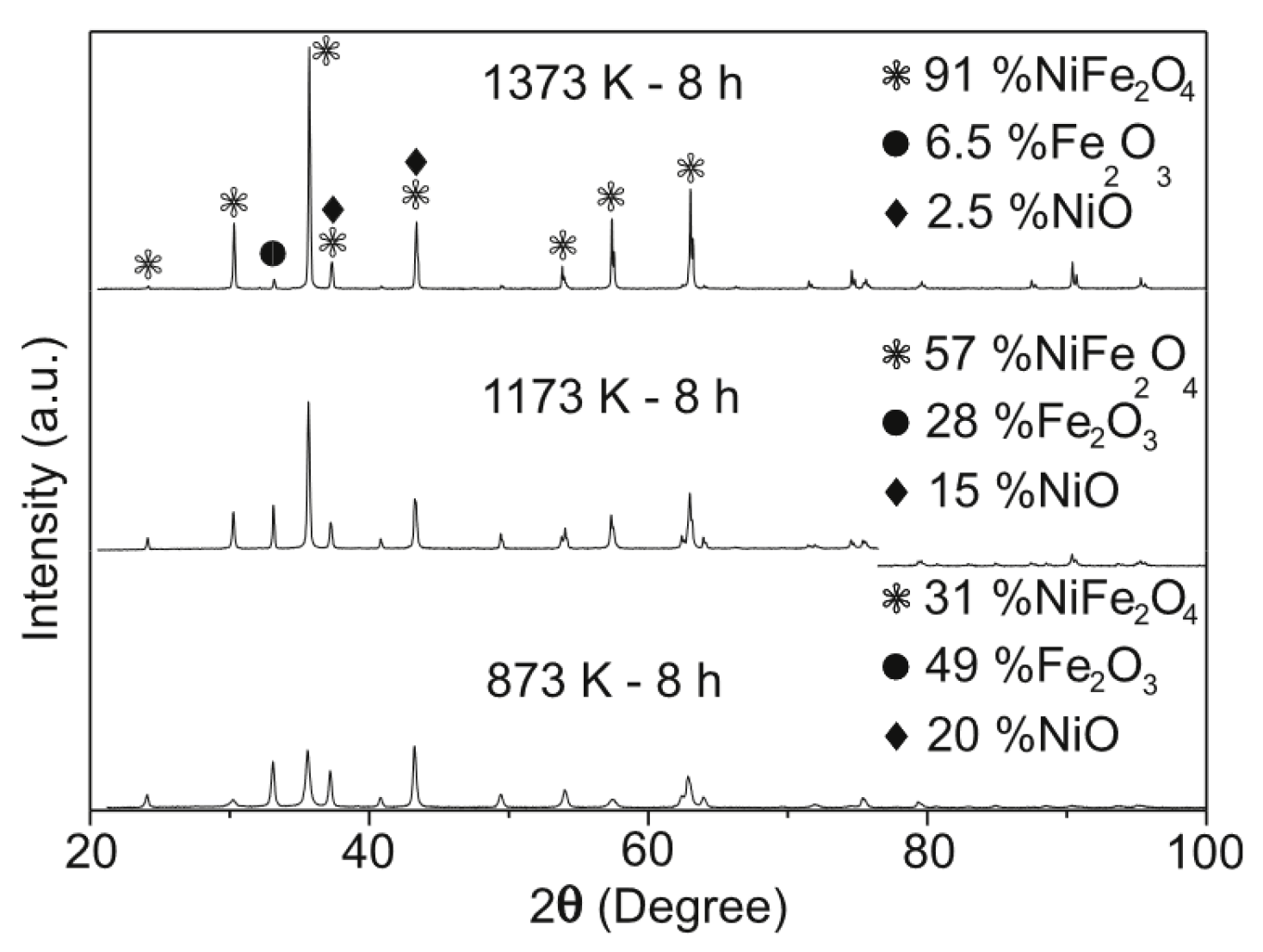
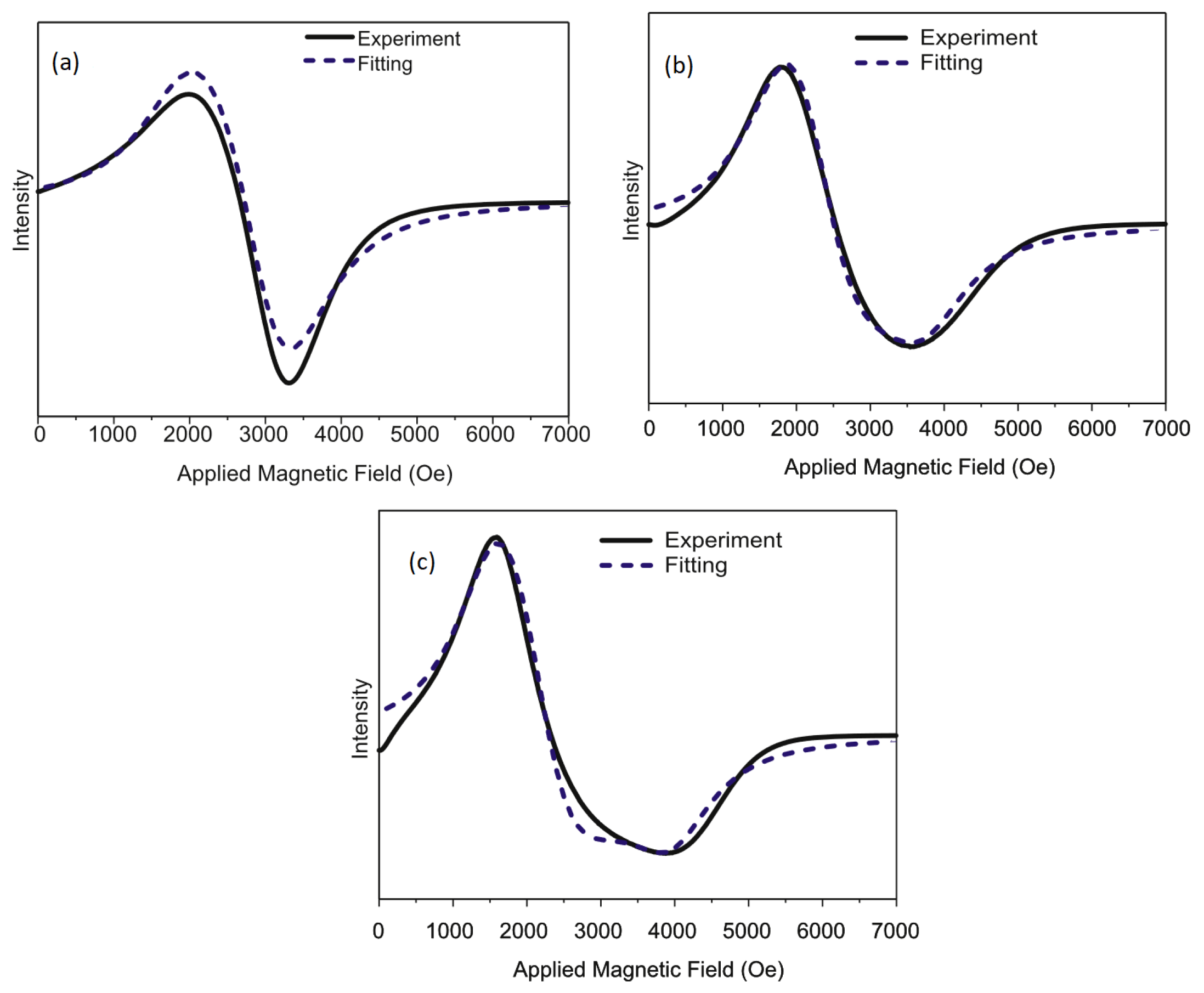

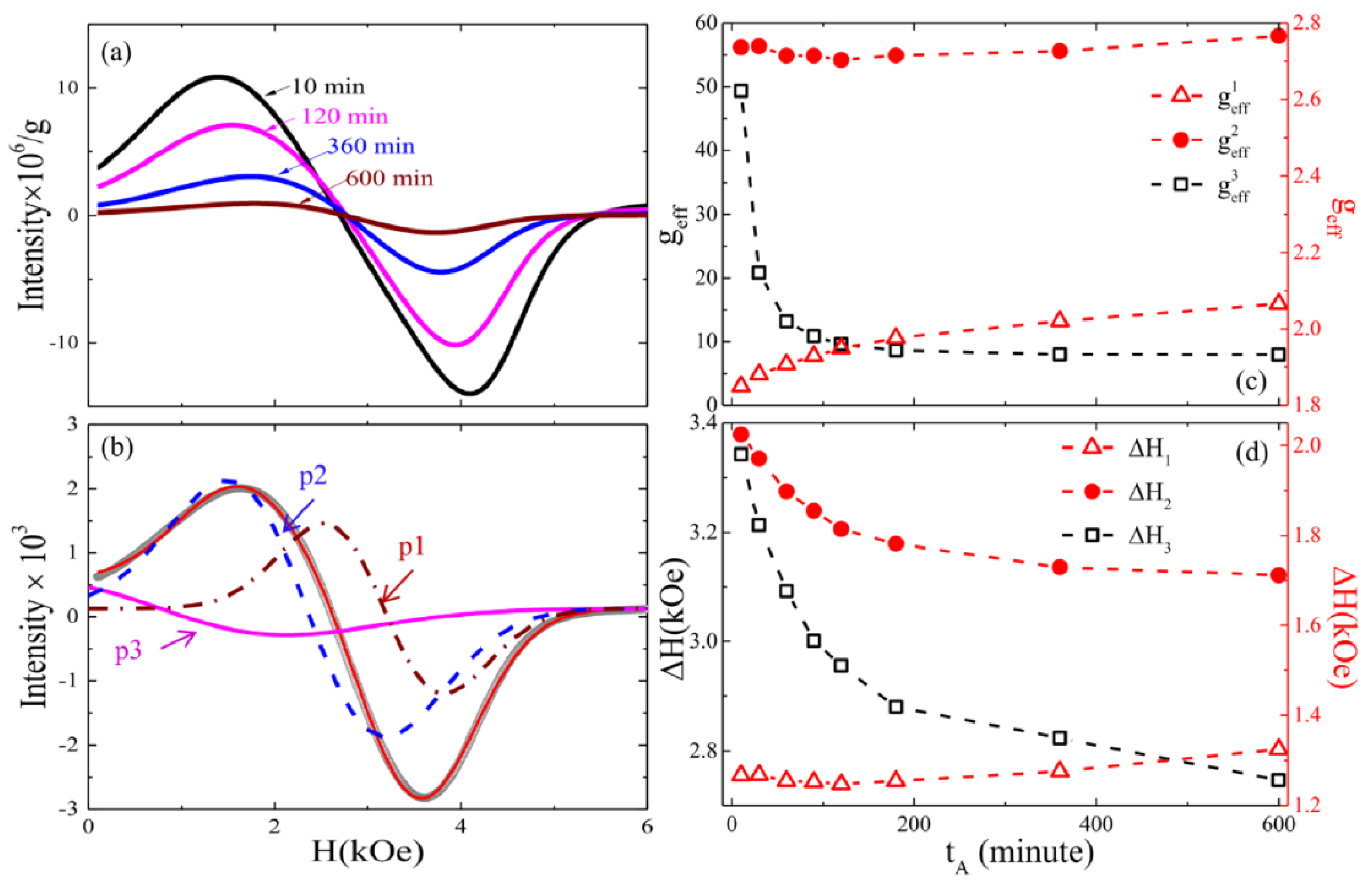
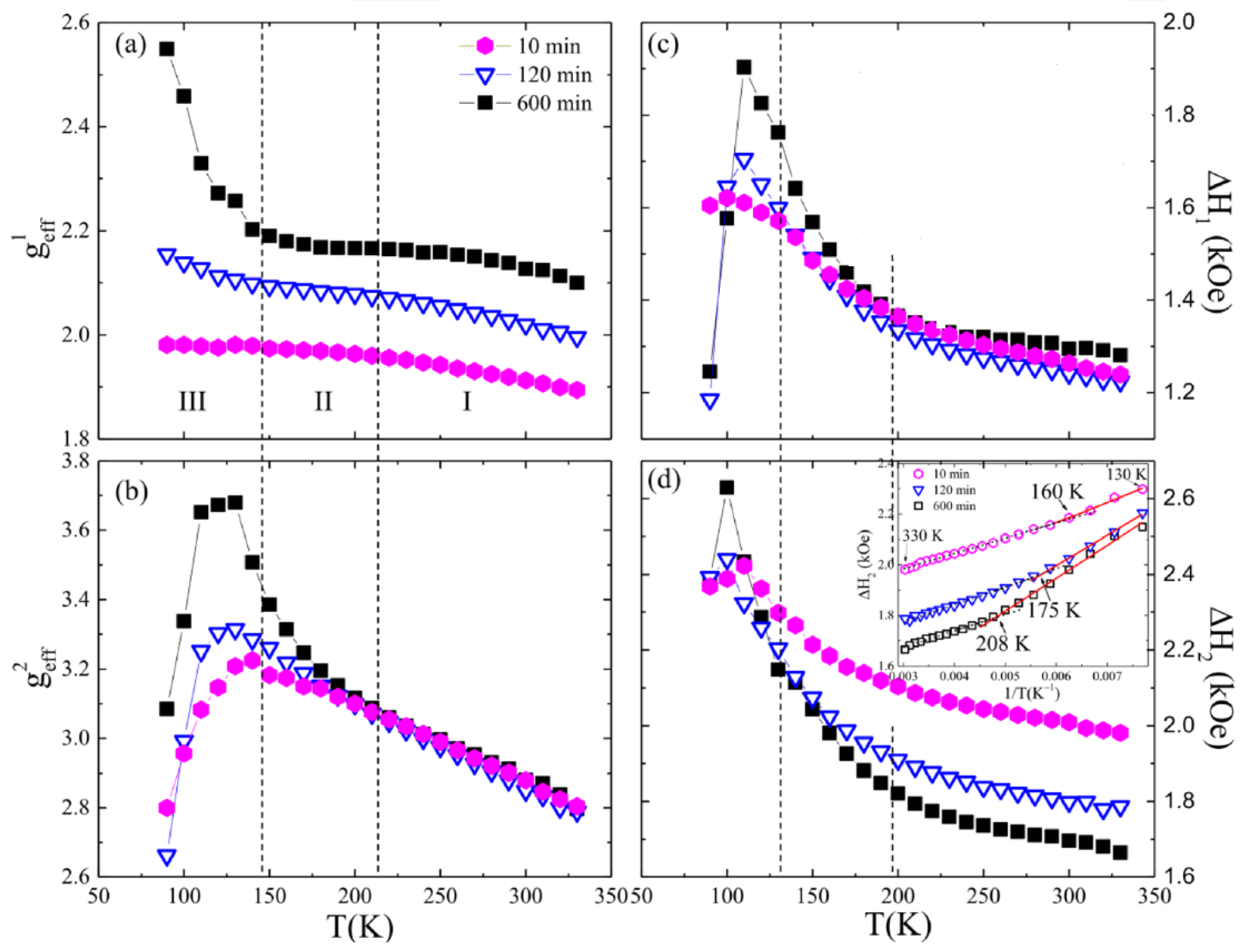

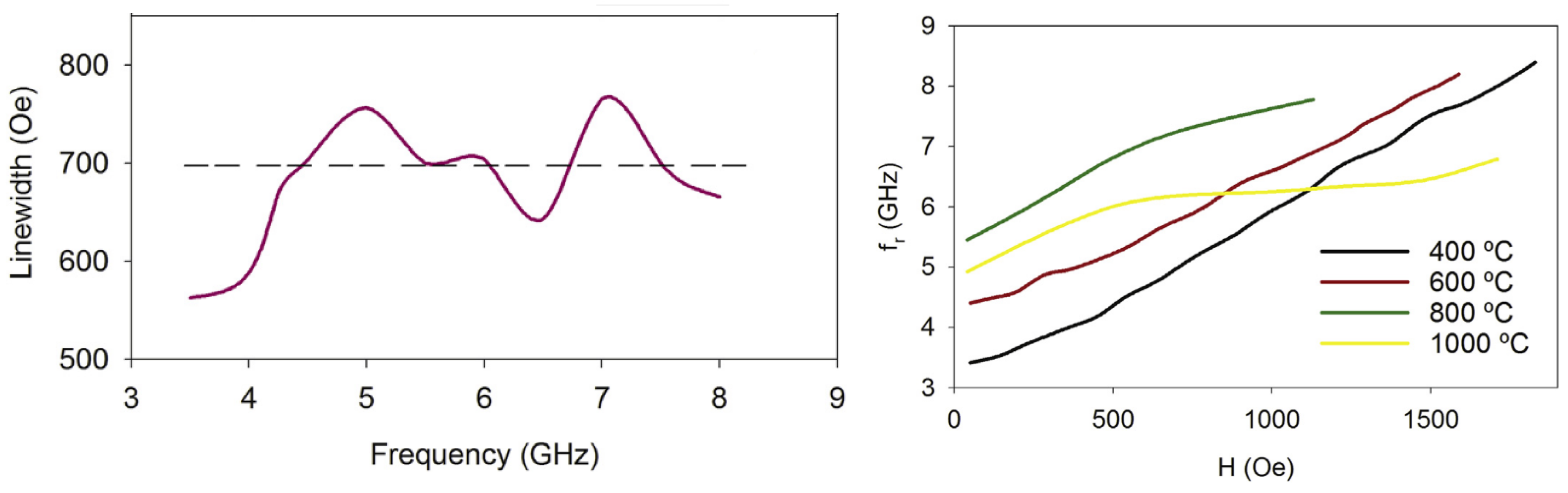
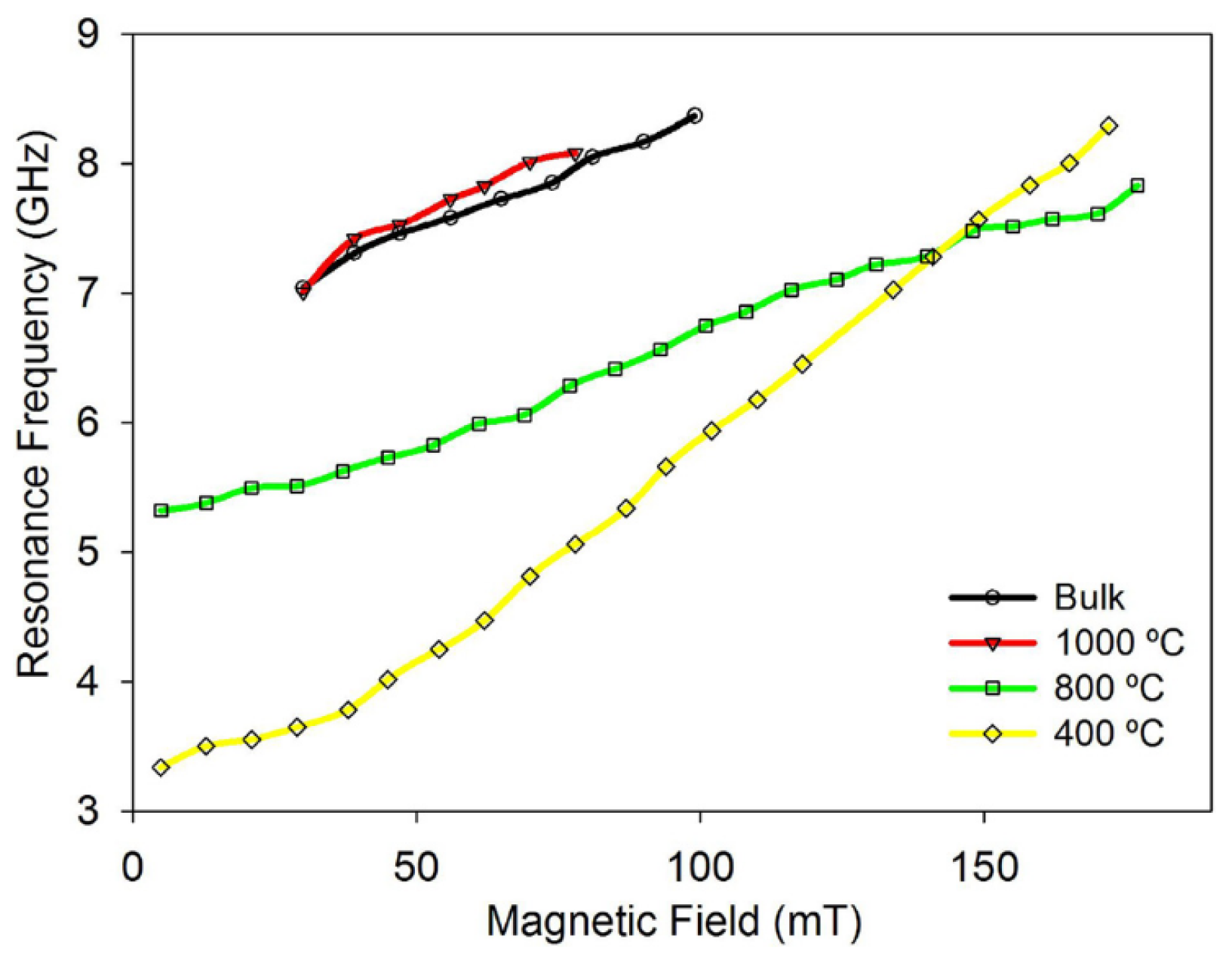
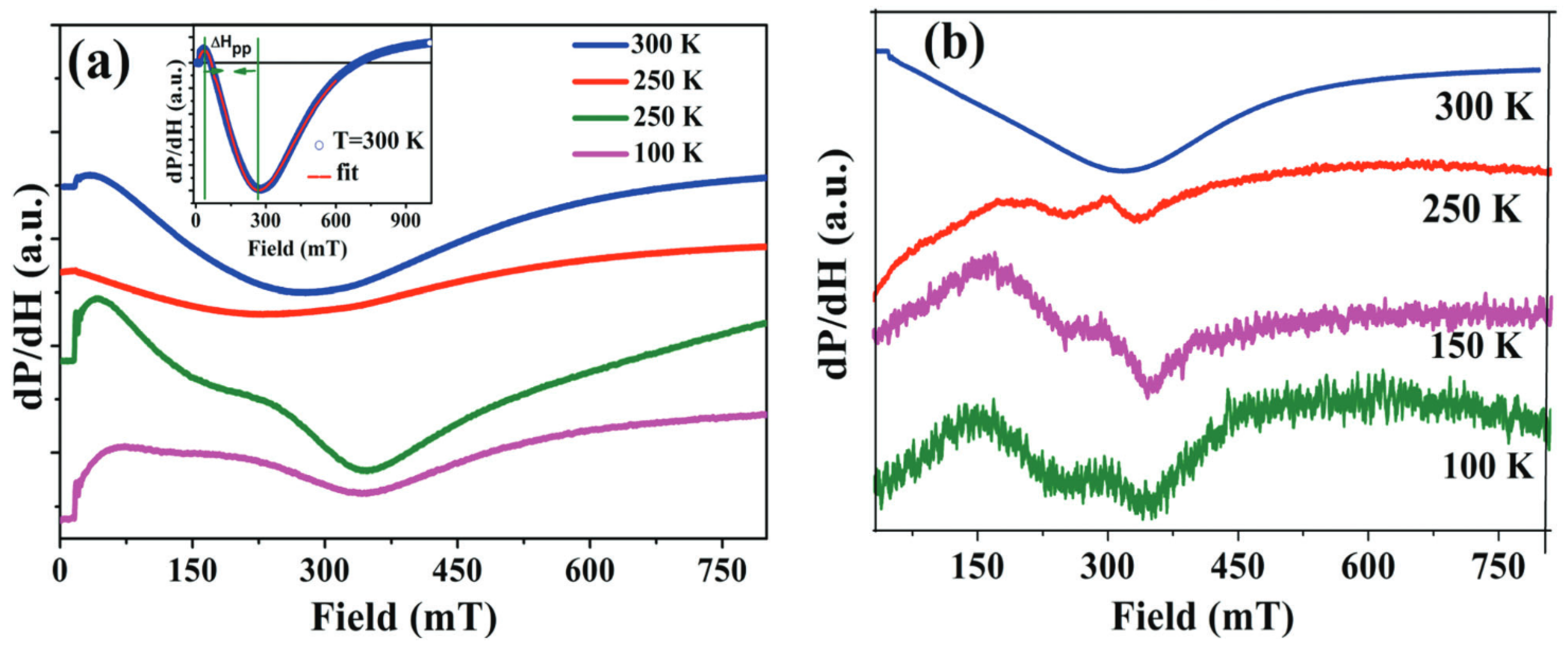
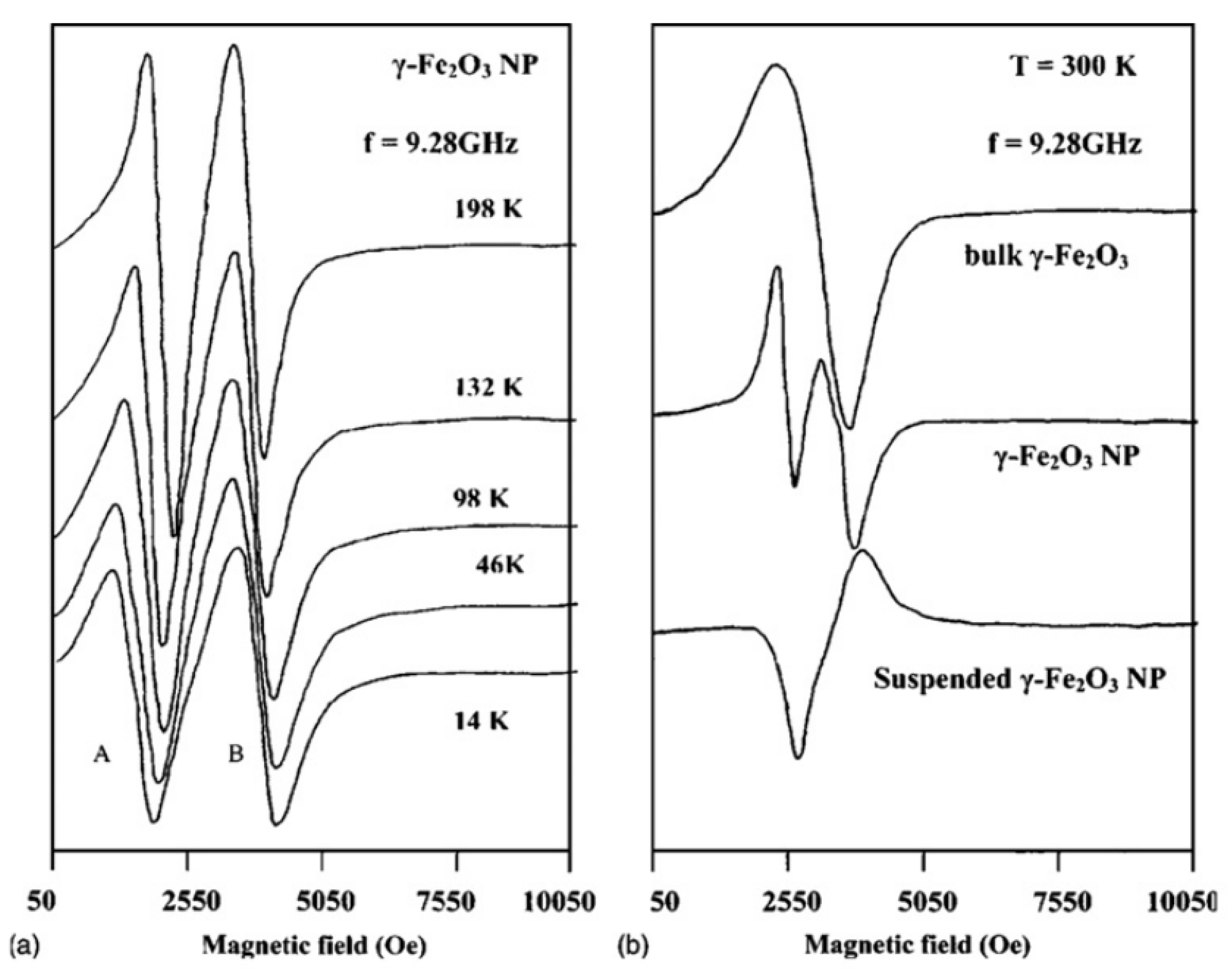

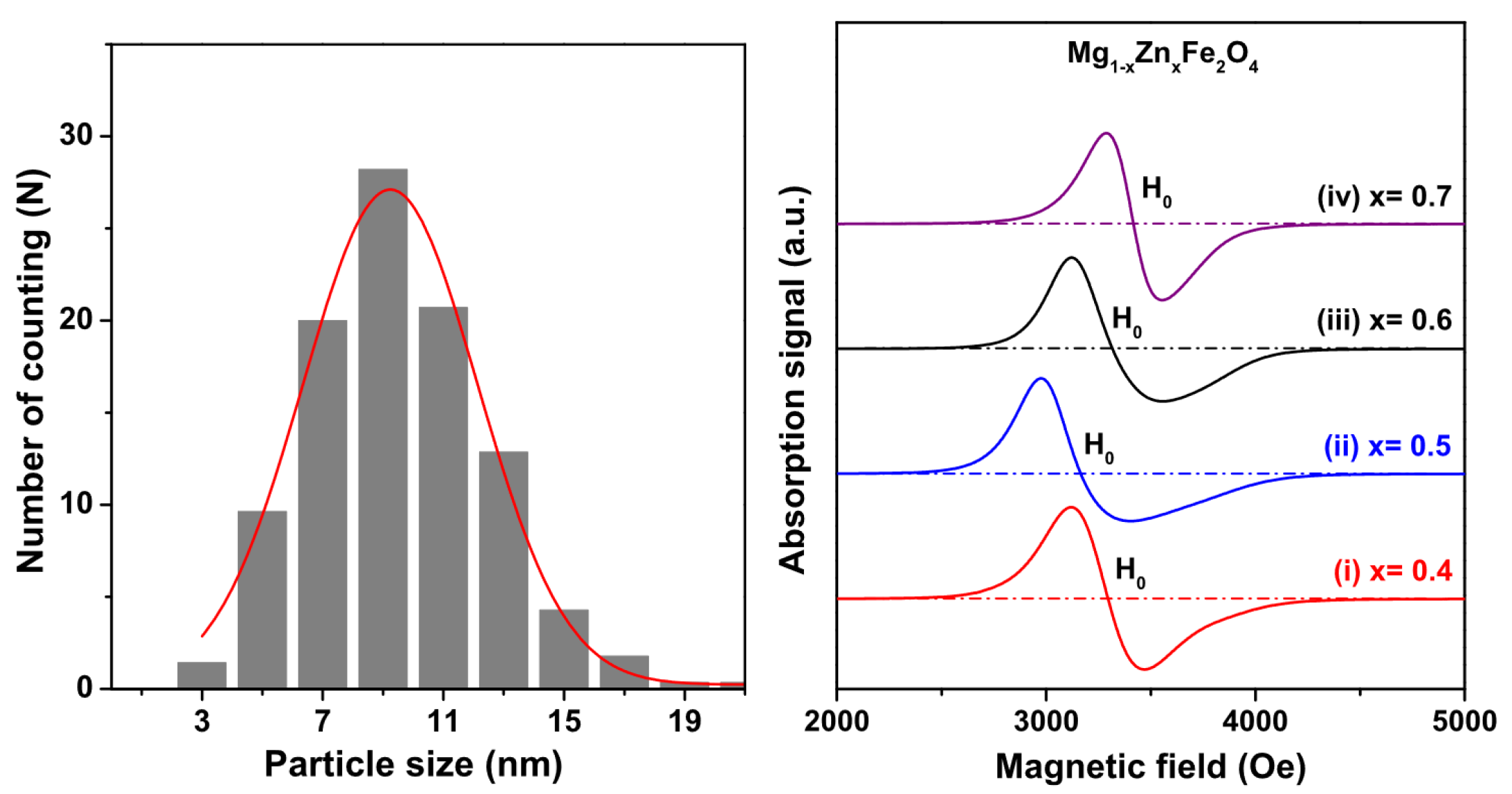


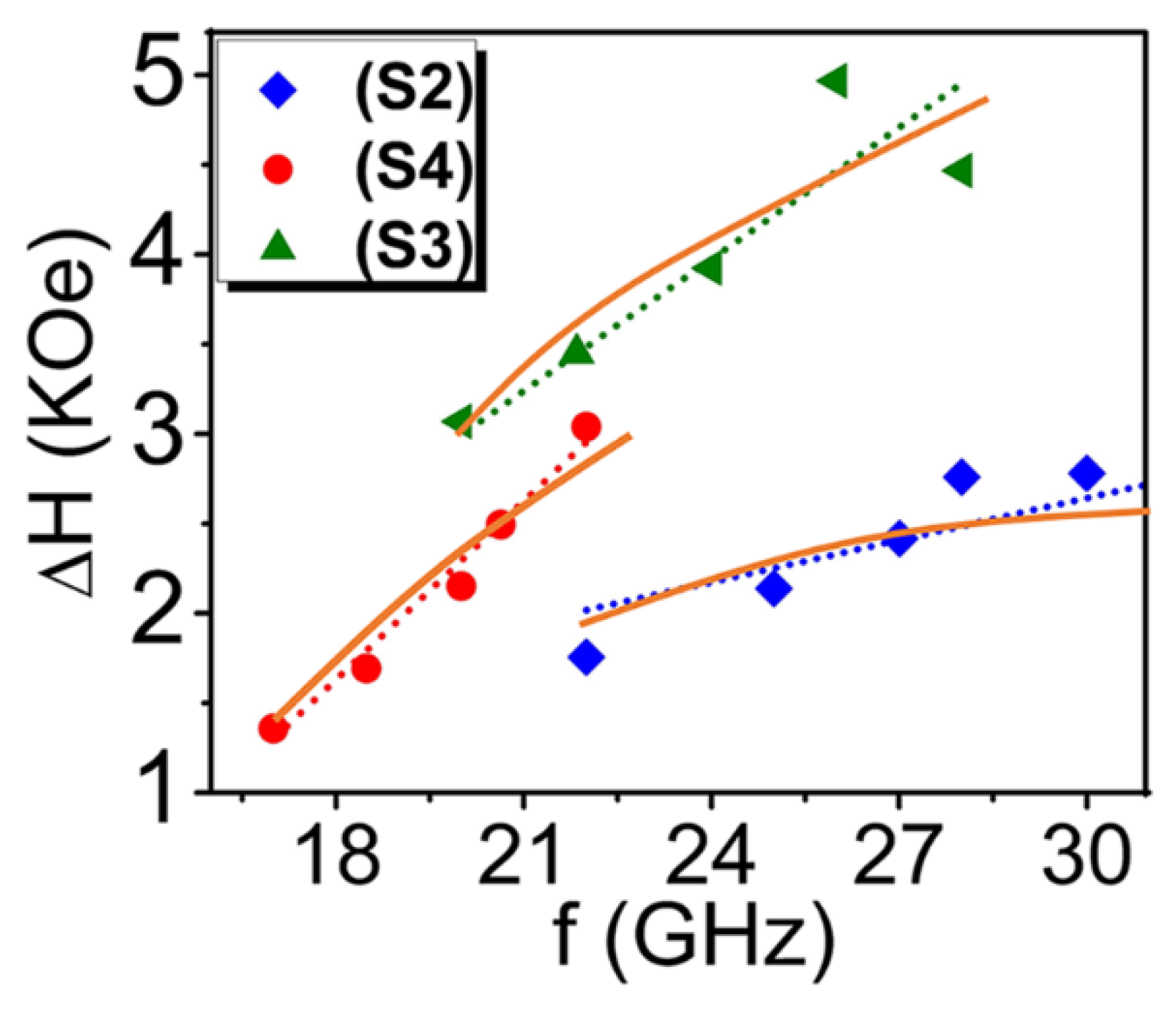
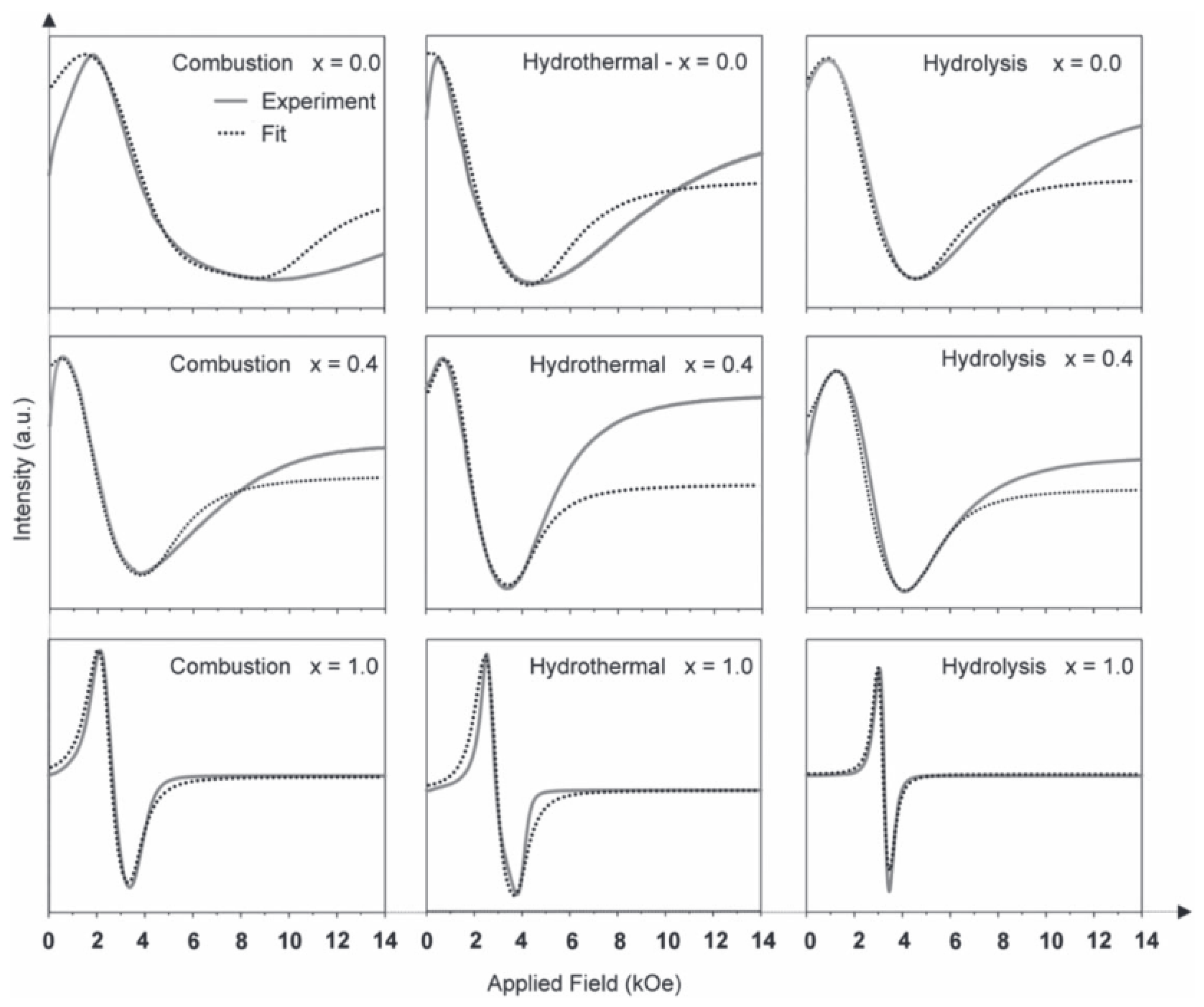
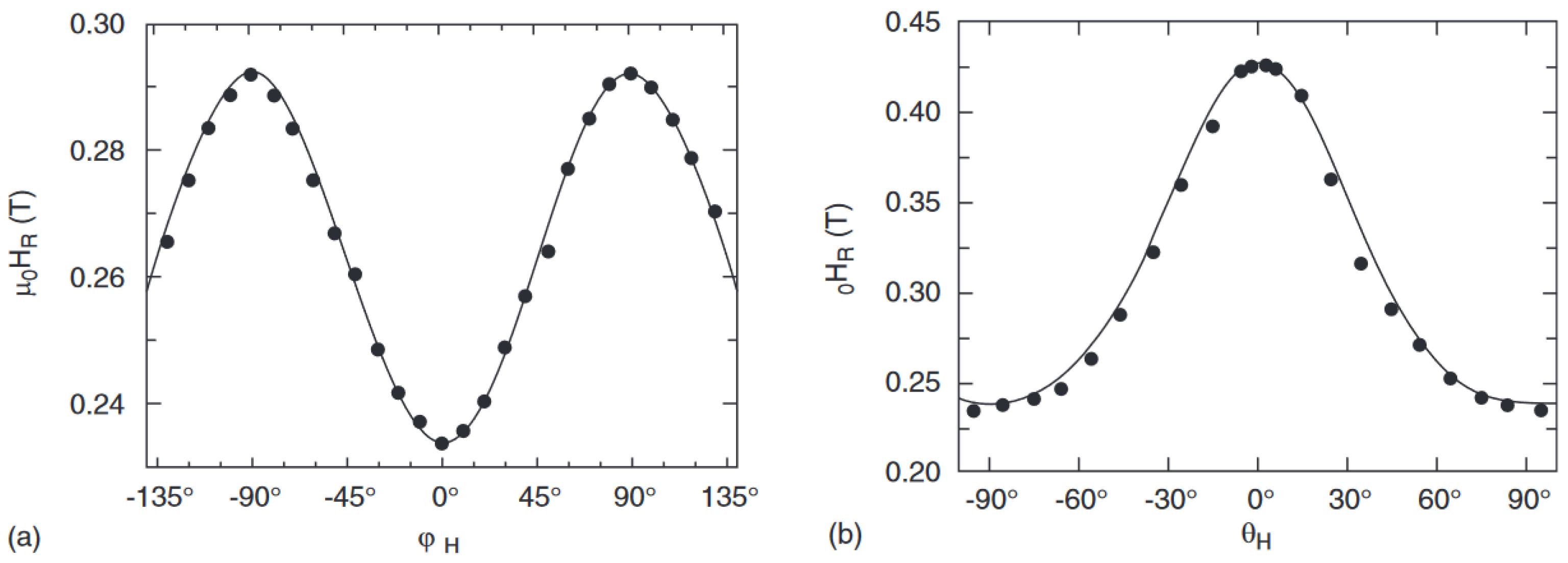
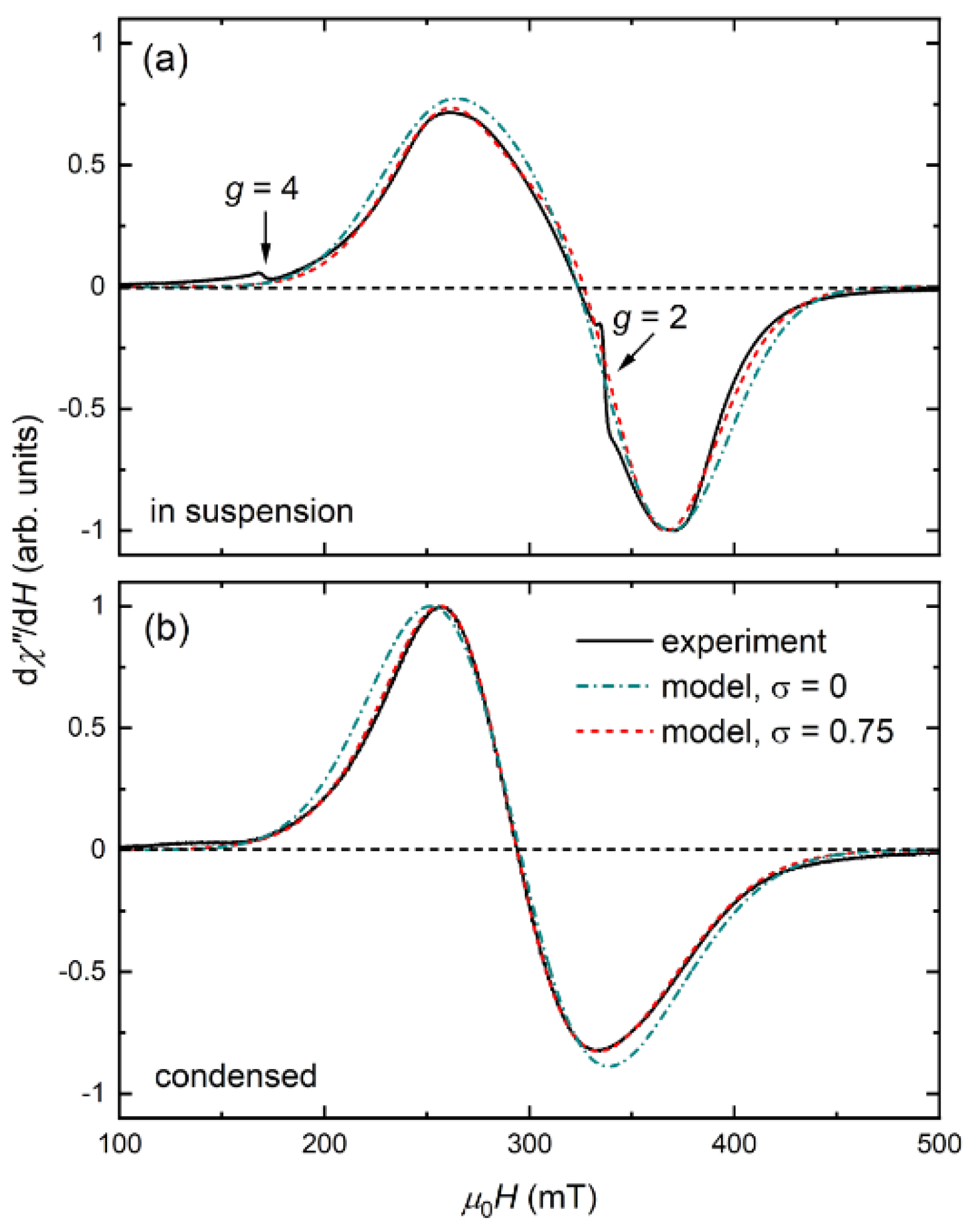
| Sample | G-Factor | (Oe) | (Oe) |
|---|---|---|---|
| 600 °C | 2.6 | 1640 | 680 |
| 900 °C | 2.6 | 1500 | −1200 |
| 1100 °C | 2.7 | 900 | −1400 |
| ap-NCF | an-NCF | |||||
|---|---|---|---|---|---|---|
| Temp (K) | (Oe) | (Oe) | (Oe) | (Oe) | ||
| 100 | 1700 | 2700 | 3.78 | 2350 | 2000 | 3.73 |
| 150 | 2000 | 3000 | 3.21 | 2450 | 1820 | 2.62 |
| 250 | 1300 | 2300 | 4.94 | 2550 | 1400 | 2.51 |
| 300 | 1400 | 2900 | 4.59 | 2500 | 2700 | 2.57 |
| Zn Content (x) | (Oe) | (Oe) | G-Factor |
|---|---|---|---|
| x = 0.4 | 3295 | 350 | 2.14 |
| x = 0.5 | 3166 | 350 | 2.23 |
| x = 0.6 | 3317 | 435 | 2.13 |
| x = 0.7 | 3418 | 265 | 2.06 |
| Sc Content (x) | (Oe) | (Oe) | G-Factor |
|---|---|---|---|
| x = 0.00 | 3211 | 987 | 2.25 |
| x = 0.01 | 3265 | 936 | 2.19 |
| x = 0.03 | 3211 | 670 | 2.11 |
| x = 0.05 | 3211 | 603 | 2.05 |
| LLG Model | Modified LLG Model | |||||
|---|---|---|---|---|---|---|
| Sample | (kOe) | (GHz/kOe) | (GHz/kOe) | |||
| 1.53 | 3.48 | 2.89 | 1.76 | 2.58 | 2.79 | |
| 0.76 | 5.56 | 2.86 | 1.36 | 6.11 | 2.84 | |
| 4.32 | 7.61 | 2.91 | 6.14 | 3.45 | 2.90 | |
| D (nm) | G-Factor | (Oe) | (Oe) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | C | HT | FH | C | HT | FH | C | HT | FH | C | HT | FH |
| 0.0 | 52 | 16 | 8.9 | 1.5 | 3.25 | 2.65 | −4600 | −2445 | −2165 | 7660 | 4075 | 3610 |
| 0.4 | 35 | 36 | 9.3 | 3.35 | 3.40 | 2.65 | −1968 | −1620 | −1660 | 3280 | 2700 | 2765 |
| 1.0 | 33 | 80 | 5.5 | 2.62 | 2.32 | 2.19 | −747 | −769 | −252 | 1245 | 1282 | 420 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benguettat-El Mokhtari, I.; Schmool, D.S. Ferromagnetic Resonance in Magnetic Oxide Nanoparticules: A Short Review of Theory and Experiment. Magnetochemistry 2023, 9, 191. https://doi.org/10.3390/magnetochemistry9080191
Benguettat-El Mokhtari I, Schmool DS. Ferromagnetic Resonance in Magnetic Oxide Nanoparticules: A Short Review of Theory and Experiment. Magnetochemistry. 2023; 9(8):191. https://doi.org/10.3390/magnetochemistry9080191
Chicago/Turabian StyleBenguettat-El Mokhtari, Ibtissem, and David S. Schmool. 2023. "Ferromagnetic Resonance in Magnetic Oxide Nanoparticules: A Short Review of Theory and Experiment" Magnetochemistry 9, no. 8: 191. https://doi.org/10.3390/magnetochemistry9080191
APA StyleBenguettat-El Mokhtari, I., & Schmool, D. S. (2023). Ferromagnetic Resonance in Magnetic Oxide Nanoparticules: A Short Review of Theory and Experiment. Magnetochemistry, 9(8), 191. https://doi.org/10.3390/magnetochemistry9080191







