Magnetic and Magnetocaloric Properties of Nano- and Polycrystalline Bulk Manganites La0.7Ba(0.3−x)CaxMnO3 (x ≤ 0.25)
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation
2.3. Structural Characterization
2.4. Electrical and Magnetic Properties
3. Results
3.1. Structural Analysis
3.2. Oxygen Content
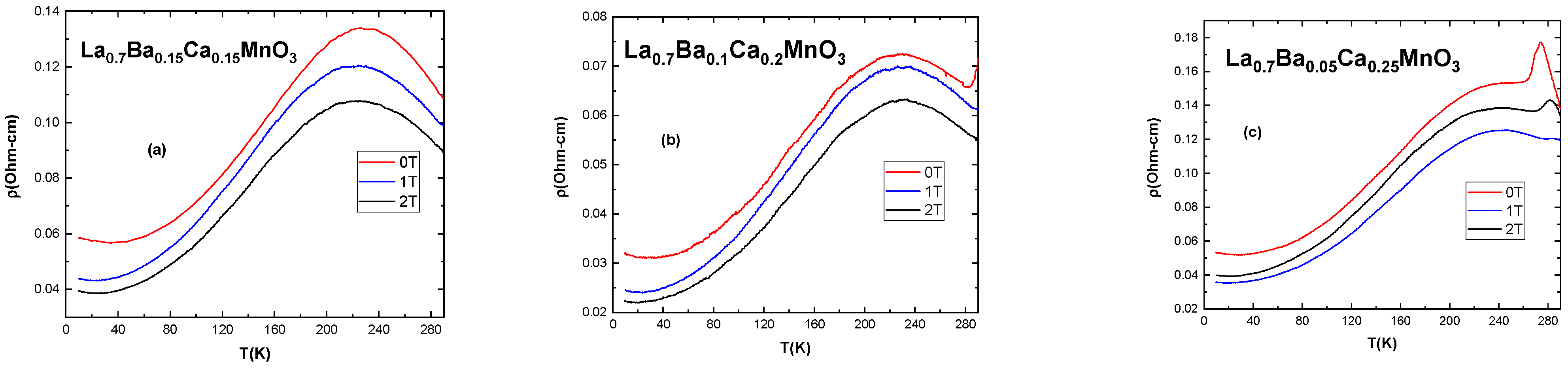
3.3. Electrical Measurements
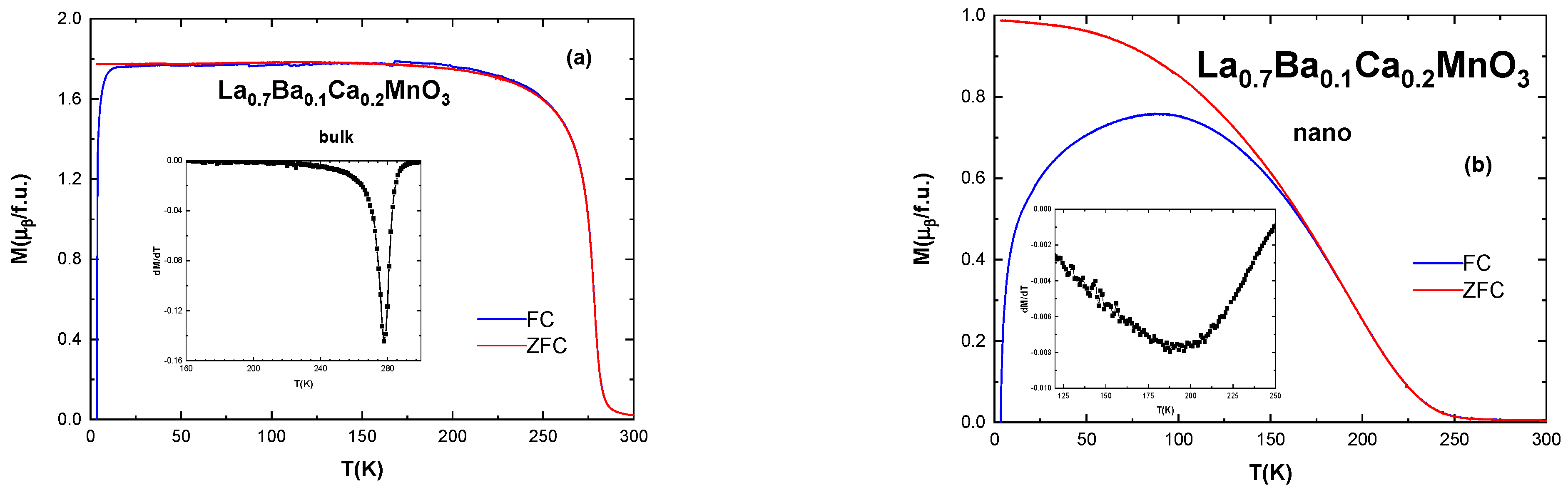
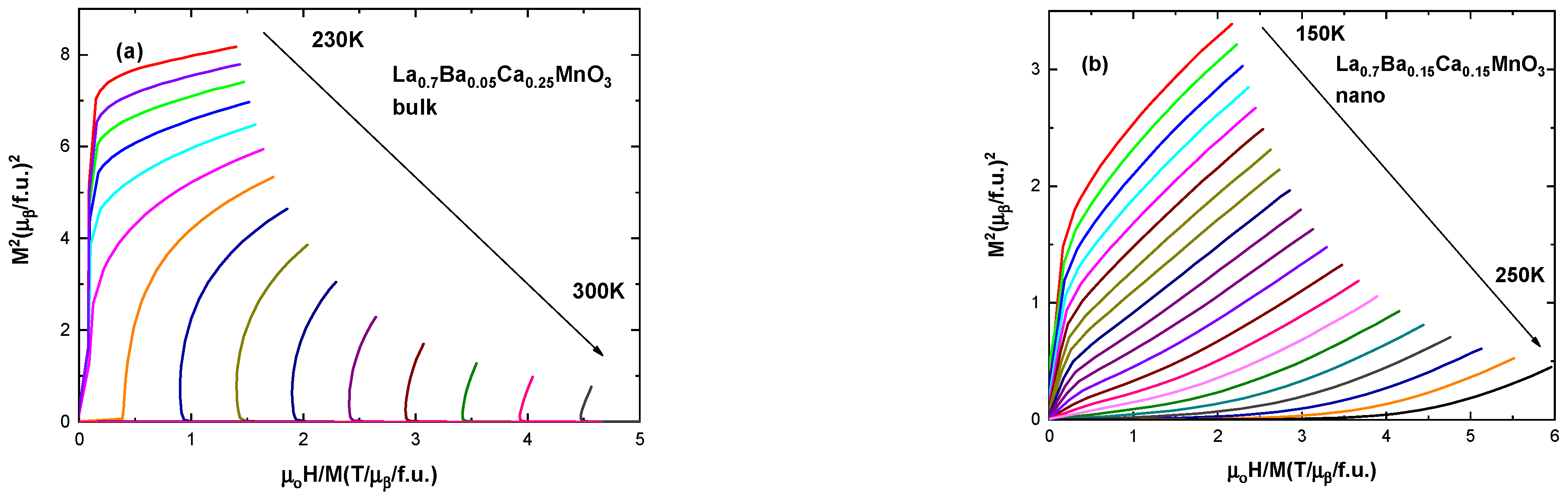
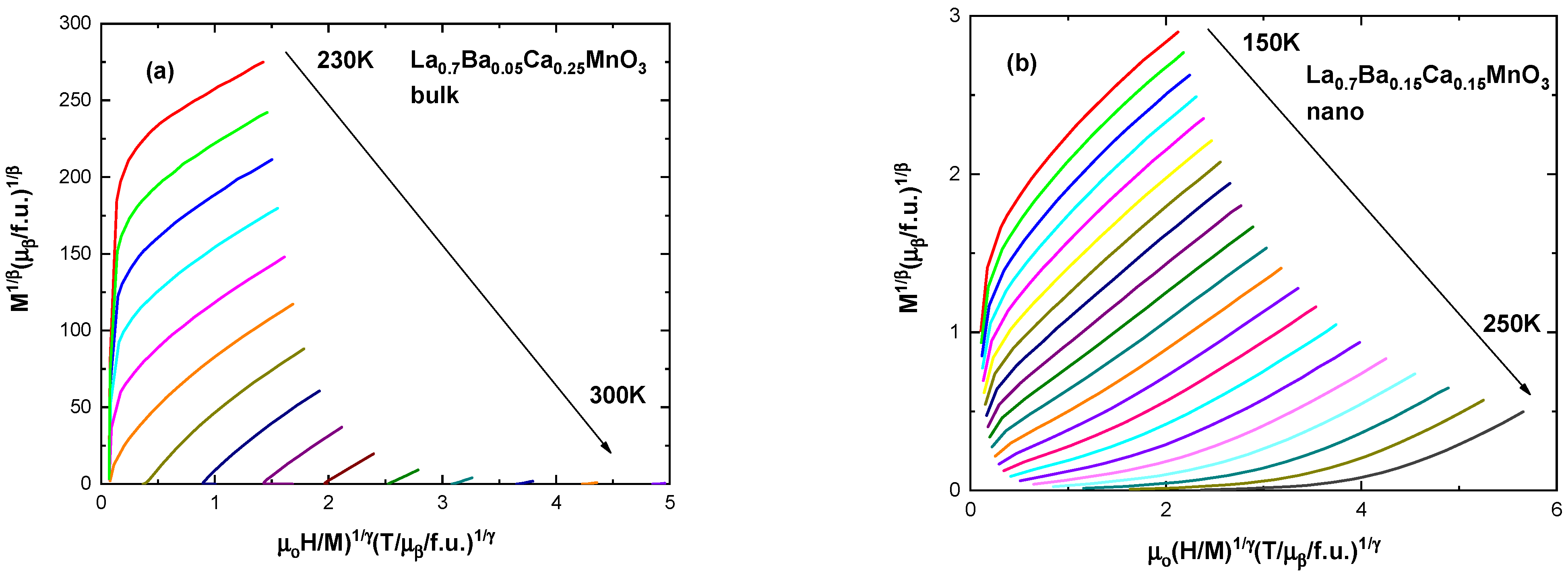
3.4. Magnetic Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rote, D.M.; Hoffert, M.I.; Caldeira, K. Encyclopedia of Energy: Magnetic Levitation; Climate Change and Energy; Elsevier Science: Amsterdam, The Netherlands, 2004; Volume 1, pp. 359–380, 691–703. [Google Scholar]
- Salazar-Munoz, V.E.; Lobo Guerrero, A.; Palomares-Sanchez, S.A. Review of magnetocaloric properties in lanthanum manganites. J. Magn. Magn. Mater. 2022, 562, 169787. [Google Scholar] [CrossRef]
- Dagotto, E.; Hotta, T.; Moreo, A. Colossal Magnetoresistant Materials: The Key Role of Phase Separation. Phys. Rep. 2001, 344, 1–153. [Google Scholar] [CrossRef]
- Rostamnejadi, A.; Venkatesan, M.; Alaria, J.; Boese, M.; Kameli, P.; Salamati, H.; Coey, J.M.D. Conventional and Inverse Magnetocaloric Effects in La0.45Sr0.55MnO3 Nanoparticles. J. Appl. Phys. 2011, 110, 043905. [Google Scholar] [CrossRef]
- Varvescu, A.; Deac, I.G. Critical Magnetic Behavior and Large Magnetocaloric Effect in Pr0.67Ba0.33MnO3 Perovskite Manganite. Phys. B Condens. Matter 2015, 470–471, 96–101. [Google Scholar] [CrossRef]
- Pavarini, E.; Koch, E.; Anders, F.; Jarrell, M. Correlated Electrons: From Models to Materials Modeling and Simulation; Forschungszentrum Julich: Aachen, Germany, 2012; Volume 2, pp. 18–21. ISBN 978-3-89336-796-2. [Google Scholar]
- Coey, J.M.D.; Viret, M.; Von Molnár, S. Mixed-Valence Manganites. Adv. Phys. 1999, 48, 167–293. [Google Scholar] [CrossRef]
- Badea, C.; Tetean, R.; Deac, I.G. Suppression of Charge and Antiferromagnetic Ordering in Ga-doped La0.4Ca0.6MnO3. Rom. J. Phys. 2018, 63, 604. [Google Scholar]
- Trukhanov, S.V.; Trukhanov, A.V.; Stepin, S.G.; Szymczak, H.; Botez, C.E. Effect of the size factor on the magnetic properties of manganite La 0.50Ba0.50MnO3. Phys. Solid State 2008, 50, 5. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Botez, C.E.; Szymczak, H. Magnetic properties of the La0.50Ba0.50MnO3 nanomanganites. In Solid State Phenomena; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2009; Volume 152–153. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, X.; Dong, F.; Wang, Y.; Wang, H.; Tan, W.; Huo, D. The Magnetic Properties and Magnetocaloric Effect of Pr0.7Sr0.3MnO3 Thin Film Grown on SrTiO3 Substrate. Materials 2023, 16, 75. [Google Scholar] [CrossRef]
- Moutis, N.; Panagiotopoulos, I.; Pissas, M.; Niarchos, D. Structural and magnetic properties of La0.67(BaxCa1−x)0.33MnO3 perovskites (0 < ~x < ~1). Phys. Rev. B 1999, 59, 2. [Google Scholar] [CrossRef]
- Tali, R. Determination of Average Oxidation State of Mn in ScMnO3 and CaMnO3 by Using Iodometric Titration. Damascus Univ. J. Basic Sci. 2007, 23, 9–19. [Google Scholar]
- Ehsani, M.H.; Kameli, P.; Ghazi, M.E.; Razavi, F.S.; Taheri, M. Tunable magnetic and magnetocaloric properties of La0.6Sr0.4MnO3 nanoparticles. J. Appl. Phys. 2013, 114, 223907. [Google Scholar] [CrossRef]
- Raju, K.; Manjunathrao, S.; Venugopal Reddy, P. Correlation between Charge, Spin and Lattice in La-Eu-Sr Manganites. J. Low Temp. Phys. 2012, 168, 334–349. [Google Scholar] [CrossRef]
- Dagotto, E. Nanoscale Phase Separation and Colossal Magnetoresistance, 1st ed.; Springer Science & Business Media: New York, NY, USA, 2002; pp. 271–284. [Google Scholar]
- Rao, C.N.R. Perovskites. In Encyclopedia of Physical Science and Technology; Elsevier: Amsterdam, The Netherlands, 2003; pp. 707–714. [Google Scholar]
- Nath, D.; Singh, F.; Das, R. X-Ray Diffraction Analysis by Williamson-Hall, Halder-Wagner and Size-Strain Plot Methods of CdSe Nanoparticles—A Comparative Study. Mater. Chem. Phys. 2020, 239, 2764–2772. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Fedotova, V.V.; Trukhanov, A.V.; Stepin, S.G.; Szymczak, H. Synthesis and structure of nanocrystalline La0.50Ba0.50MnO3. Crystallogr. Rep. 2008, 53, 7. [Google Scholar] [CrossRef]
- Licci, F.; Turilli, G.; Ferro, P. Determination of Manganese Valence in Complex La-Mn Perovskites. J. Magn. Magn. Mater. 1996, 164, L268–L272. [Google Scholar] [CrossRef]
- Saw, A.K.; Channagoudra, G.; Hunagund, S.; Hadimani, R.L.; Dayal, V. Study of transport, magnetic and magnetocaloric properties in Sr2+ substituted praseodymium manganite. Mater. Res. Express 2020, 7, 016105. [Google Scholar] [CrossRef]
- Deac, I.G.; Tetean, R.; Burzo, E. Phase Separation, Transport and Magnetic Properties of La2/3A1/3Mn1−XCoxO3, A = Ca, Sr (0.5 ≤ x ≤ 1). Phys. B Condens. Matter 2008, 403, 1622–1624. [Google Scholar] [CrossRef]
- Panwar, N.; Pandya, D.K.; Agarwal, S.K. Magneto-Transport and Magnetization Studies of Pr2/3Ba1/3MnO3:Ag2O Composite Manganites. J. Phys. Condens. Matter 2007, 19, 456224. [Google Scholar] [CrossRef]
- Panwar, N.; Pandya, D.K.; Rao, A.; Wu, K.K.; Kaurav, N.; Kuo, Y.K.; Agarwal, S.K. Electrical and Thermal Properties of Pr 2/3(Ba1-XCsx)1/3MnO 3 Manganites. Eur. Phys. J. B 2008, 65, 179–186. [Google Scholar] [CrossRef]
- Ibrahim, N.; Rusop, N.A.M.; Rozilah, R.; Asmira, N.; Yahya, A.K. Effect of grain modification on electrical transport properties and electroresistance behavior of Sm0.55Sr0.45MnO3. Int. J. Eng. Technol. 2018, 7, 113–117. [Google Scholar]
- Atanasov, R.; Bortnic, R.; Hirian, R.; Covaci, E.; Frentiu, T.; Popa, F.; Deac, I.G. Magnetic and Magnetocaloric Properties of Nano- and Polycrystalline Manganites La(0.7−x)EuxBa0.3MnO3. Materials 2022, 15, 7645. [Google Scholar] [CrossRef] [PubMed]
- Brinza, E. Electrical and Magnetocaloric Properties of the La0.7Ba0.3−xCaxMnO3 Compounds. Diploma Thesis, Babes-Bolyai University, Cluj-Napoca, Romania, 2022. [Google Scholar]
- Kubo, K.; Ohata, N. A Quantum Theory of Double Exchange. J. Phys. Soc. Jpn. 1972, 33, 21–32. [Google Scholar] [CrossRef]
- Arun, B.; Suneesh, M.V.; Vasundhara, M. Comparative Study of Magnetic Ordering and Electrical Transport in Bulk and Nano-Grained Nd0.67Sr0.33MnO3 Manganites. J. Magn. Magn. Mater. 2016, 418, 265–272. [Google Scholar] [CrossRef]
- Peters, J.A. Relaxivity of Manganese Ferrite Nanoparticles. Prog. Nucl. Magn. Reson. Spectrosc. 2020, 120, 72–94. [Google Scholar] [CrossRef]
- Banerjee, B.K. On a Generalised Approach to First and Second Order Magnetic Transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Jeddi, M.; Gharsallah, H.; Bejar, M.; Bekri, M.; Dhahri, E.; Hlil, E.K. Magnetocaloric Study, Critical Behavior and Spontaneous Magnetization Estimation in La0.6Ca0.3Sr0.1MnO3 Perovskite. RSC Adv. 2018, 8, 9430–9439. [Google Scholar] [CrossRef]
- Arrott, A. Criterion for Ferromagnetism from Observations of Magnetic Isotherms. Phys. Rev. 1957, 108, 1394–1396. [Google Scholar] [CrossRef]
- Arrott, A.; Noakes, J.E. Approximate Equation of State for Nickel Near Its Critical Temperature. Phys. Rev. Lett. 1967, 19, 786–789. [Google Scholar] [CrossRef]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Oxford University Press: Oxford, UK, 1987; pp. 7–10. [Google Scholar]
- Fisher, M.E.; Ma, S.K.; Nickel, B.G. Critical Exponents for Long-Range Interactions. Phys. Rev. Lett. 1972, 29, 917. [Google Scholar] [CrossRef]
- Pathria, R.K.; Beale, P.D. Phase Transitions: Criticality, Universality, and Scaling. In Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 2022; pp. 417–486. [Google Scholar]
- Vadnala, S.; Asthana, S. Magnetocaloric effect and critical field analysis in Eu substituted La0.7−xEuxSr0.3MnO3 (x = 0.0, 0.1, 0.2, 0.3) manganites. J. Magn. Magn. Mater. 2018, 446, 68–79. [Google Scholar] [CrossRef]
- Kim, D.; Revaz, B.; Zink, B.L.; Hellman, F.; Rhyne, J.J.; Mitchell, J.F. Tri-critical Point and the Doping Dependence of the Order of the Ferromagnetic Phase Transition of La1−xCaxMnO3. Phys. Rev. Lett. 2002, 89, 227202. [Google Scholar] [CrossRef] [PubMed]
- Pelka, R.; Konieczny, P.; Fitta, M.; Czapla, M.; Zielinski, P.M.; Balanda, M.; Wasiutynski, T.; Miyazaki, Y.; Inaba, A.; Pinkowicz, D.; et al. Magnetic systems at criticality: Different signatures of scaling. Acta Phys. Pol. 2013, 124, 977. [Google Scholar] [CrossRef]
- Majumder, D.D.; Majumder, D.D.; Karan, S. Magnetic Properties of Ceramic Nanocomposites. In Ceramic Nanocomposites; Banerjee, R., Manna, I., Eds.; Woodhead Publishing Series in Composites Science and Engineering; Elsevier: Amsterdam, The Netherlands, 2013; pp. 51–91. [Google Scholar] [CrossRef]
- Souca, G.; Iamandi, S.; Mazilu, C.; Dudric, R.; Tetean, R. Magnetocaloric Effect and Magnetic Properties of Pr1−XCexCo3 Compounds. Stud. Univ. Babeș-Bolyai Phys. 2018, 63, 9–18. [Google Scholar] [CrossRef]
- Zverev, V.; Tishin, A.M. Magnetocaloric Effect: From Theory to Practice. In Reference Module in Materials Science and Material Engineering; Elsevier: Amsterdam, The Netherlands, 2016; pp. 5035–5041. [Google Scholar] [CrossRef]
- Griffith, L.D.; Mudryk, Y.; Slaughter, J.; Pecharsky, V.K. Material-based figure of merit for caloric materials. J. Appl. Phys. 2018, 123, 034902. [Google Scholar] [CrossRef]
- Deac, I.G.; Vladescu, A. Magnetic and magnetocaloric properties of Pr1−xSrxCoO3 cobaltites. J. Magn. Magn. Mater. 2014, 365, 1–7. [Google Scholar] [CrossRef]
- Naik, V.B.; Barik, S.K.; Mahendiran, R.; Raveau, B. Magnetic and Calorimetric Investigations of Inverse Magnetocaloric Effect in Pr0.46Sr0.54MnO3. Appl. Phys. Lett. 2011, 98, 112506. [Google Scholar] [CrossRef]
- Gong, Z.; Xu, W.; Liedienov, N.A.; Butenko, D.S.; Zatovsky, I.V.; Gural’skiy, I.A.; Wei, Z.; Li, Q.; Liu, B.; Batman, Y.A.; et al. Expansion of the multifunctionality in off-stoichiometric manganites using post-annealing and high pressure: Physical and electrochemical studies. Phys Chem. Chem. Phys. 2002, 24, 21872–21885. [Google Scholar] [CrossRef]
- Sandeman, K.G. Magnetocaloric materials: The search for new systems. Scr. Mater. 2012, 67, 566–571. [Google Scholar] [CrossRef]
- Smith, A.; Bahl, A.C.R.H.; Bjørk, R.; Engelbrecht, K.; Kaspar, K.; Nielsen, K.K.; Pryds, N. Materials challenges for high performance magnetocaloric refrigeration devices. Adv. Energy Mater. 2012, 2, 1288–1318. [Google Scholar] [CrossRef]
- Kitanovski, A.; Tusek, J.; Tomc, U.; Plaznik, U.; Ozbolt, M.; Poredos, A. Magentocaloric Energy Conversion: From Theory to Applications, 1st ed.; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Mazumdar, D.; Das, K.; Das, I. Study of magnetocaloric effect and critical exponents in polycrystalline La0.4Pr0.3Ba0.3MnO3 compounds. J. Appl. Phys. 2020, 127, 093902. [Google Scholar] [CrossRef]
- Wang, C.L.; Liu, J.; Mudryk, Y.; Zhu, Y.J.; Fu Bin Long, Y.; Pecharsky, V.K. Magnetic and magnetocaloric properties of DyCo2Cx alloys. J. Alloys Compd. 2019, 777, 152–156. [Google Scholar] [CrossRef]
- Souca, G. Magnetic Properties and Magnetocaloric Effect on Selected Rare Earth-Transition Metal Intermetallic Compounds. Ph. D. Thesis, Babes-Bolyai University, Cluj-Napoca, Romania, 2022; pp. 101–103. [Google Scholar]
- Hueso, L.E.; Sande, P.; Miguéns, D.R.; Rivas, J.; Rivadulla, F.; López-Quintela, M.A. Tuning of the magnetocaloric effect in nanoparticles synthesized by sol–gel techniques. J. Appl. Phys. 2002, 91, 9943–9947. [Google Scholar] [CrossRef]
- Anis, B.; Tapas, S.; Banerjee, S.; Das, I. Magnetocaloric properties of nanocrystalline Pr0.65(Ca0.6Sr0.4)0.35MnO3. J. Appl. Phys. 2008, 103, 013912. [Google Scholar] [CrossRef]




| Ca Content | Bulk Samples | Fit (Χ2) | Nanocrystalline Samples | Fit (Χ2) | Space Group | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | V (Å3) | a (Å) | b (Å) | c (Å) | V (Å3) | ||||
| X = 0 | 5.533(2) | 5.533(2) | 13.519(6) | 358.3(2) | 1.54 | 5.526(3) | 5.526(3) | 13.48(12) | 356.6(5) | 1.9 | R-3c |
| X = 0.15 | 5.509(4) | 5.509(4) | 13.42(14) | 352.8(6) | 1.54 | 5.502(9) | 5.502(9) | 13.44(27) | 352.4(9) | 1.53 | R-3c |
| X = 0.2 | 5.499(5) | 5.499(5) | 13.41(2) | 351.2(6) | 1.67 | 5.487(8) | 5.487(8) | 13.41(24) | 349.8(9) | 1.64 | R-3c |
| X = 0.25 | 5.492(4) | 5.467(5) | 7.727(8) | 232.0(4) | 1.64 | 5.509(3) | 5.505(2) | 7.802(3) | 236.(157) | 1.68 | Pbnm |
| Ca Content (Bulk) | t (Tolerance Factor) | Mn-O1 (Mn-O2) (Å) | Mn-O1-Mn (Mn-O2-Mn) (°) | Average Particle Diameter (μm) | Williamson–Hall Size (nm) | Average Rietveld Size (nm) | Strain |
|---|---|---|---|---|---|---|---|
| x = 0 | 0.926 | 1.9643 (4) | 168.36 (3) | 1.1 | 110.05 | 111.1 | 0.0018 |
| x = 0.15 | 0.91 | 1.9531 (5) | 169.31 (3) | 1 | 83.15 | 91.18 | 0.0019 |
| x = 0.2 | 0.905 | 1.9515 (5) | 168.35 (6) | 0.9 | 62.81 | 89.99 | 0.0016 |
| x = 0.25 | 0.9 | 1.9327 (6) (1.9473 (6)) | 180(168.61 (6)) | 1.5 | 120.95 | 132.45 | 0.0019 |
| Ca Content (Nano) | Mn-O1 (Mn-O2) (Å) | Mn-O1-Mn (Mn-O2-Mn) (°) | Average Particle Diameter (nm) | Williamson–Hall Size (nm) | Average Rietveld Size (nm) | Strain |
|---|---|---|---|---|---|---|
| x = 0 | 1.9616 (6) | 168.35 (9) | 46.6 | 36.23 | 18.14 | 0.0022 |
| x = 0.15 | 1.9687 (4) | 161.98 (5) | 35.6 | 27.98 | 16.41 | 0.0022 |
| x = 0.2 | 1.9632 (4) | 161.98 (8) | 45.9 | 32.67 | 17.65 | 0.0019 |
| x = 0.25 | 1.9514 (7) (1.9577 (7)) | 180 (168.58 (8)) | 55.4 | 54.6 | 23.28 | 0.0024 |
| Ca content | Average Mn3+ Ratio | Standard Deviation | Relative Standard Deviation (%) | Average Oxygen Content |
|---|---|---|---|---|
| x = 0 bulk | 0.7306 | 0.0159 | 2.18 | O2.98±0.02 |
| x = 0.15 bulk | 0.7817 | 0.015 | 1.92 | O2.96±0.01 |
| x = 0.2 bulk | 0.7616 | 0.0306 | 4.01 | O2.97±0.02 |
| x = 0.25 bulk | 0.7852 | 0.006 | 0.76 | O2.96±0.01 |
| x = 0 nano | 0.6813 | 0.0086 | 1.26 | O3.01±0.01 |
| x = 0.15 nano | 0.6707 | 0.0178 | 2.65 | O3.02±0.02 |
| x = 0.2 nano | 0.6766 | 0.009 | 1.33 | O3.01±0.01 |
| x = 0.25 nano | 0.6689 | 0.0207 | 3.09 | O3.02±0.02 |
| Compound (Bulk) | Tc (K) | Tp1 (K) | Tp2 (K) | ρpeak (Ωcm) in 0 T | MRMax (%) (1 T) at Tp | MRMax (%) (2 T) at Tp | MRMax (%) (1 T) at 10K | MRMax (%) (2 T) at 10K |
|---|---|---|---|---|---|---|---|---|
| La0.7Ba0.3MnO3 [21] | 340 | 295 | 0.693 | 5.8 | 12.9 | 27.03 | 32.11 | |
| La0.7Ba0.15Ca0.15MnO3 | 308 | 226 | 0.134 | 10.18 | 19.72 | 25.12 | 32.59 | |
| La0.7Ba0.1Ca0.2MnO3 | 279 | 226 | 0.073 | 3.42 | 12.99 | 23.78 | 30.97 | |
| La0.7Ba0.05Ca0.25MnO3 | 261 | 230 | 274 | 0.177 | 9.2 (22.04) | 18.1 (31.94) | 24.94 | 33.05 |
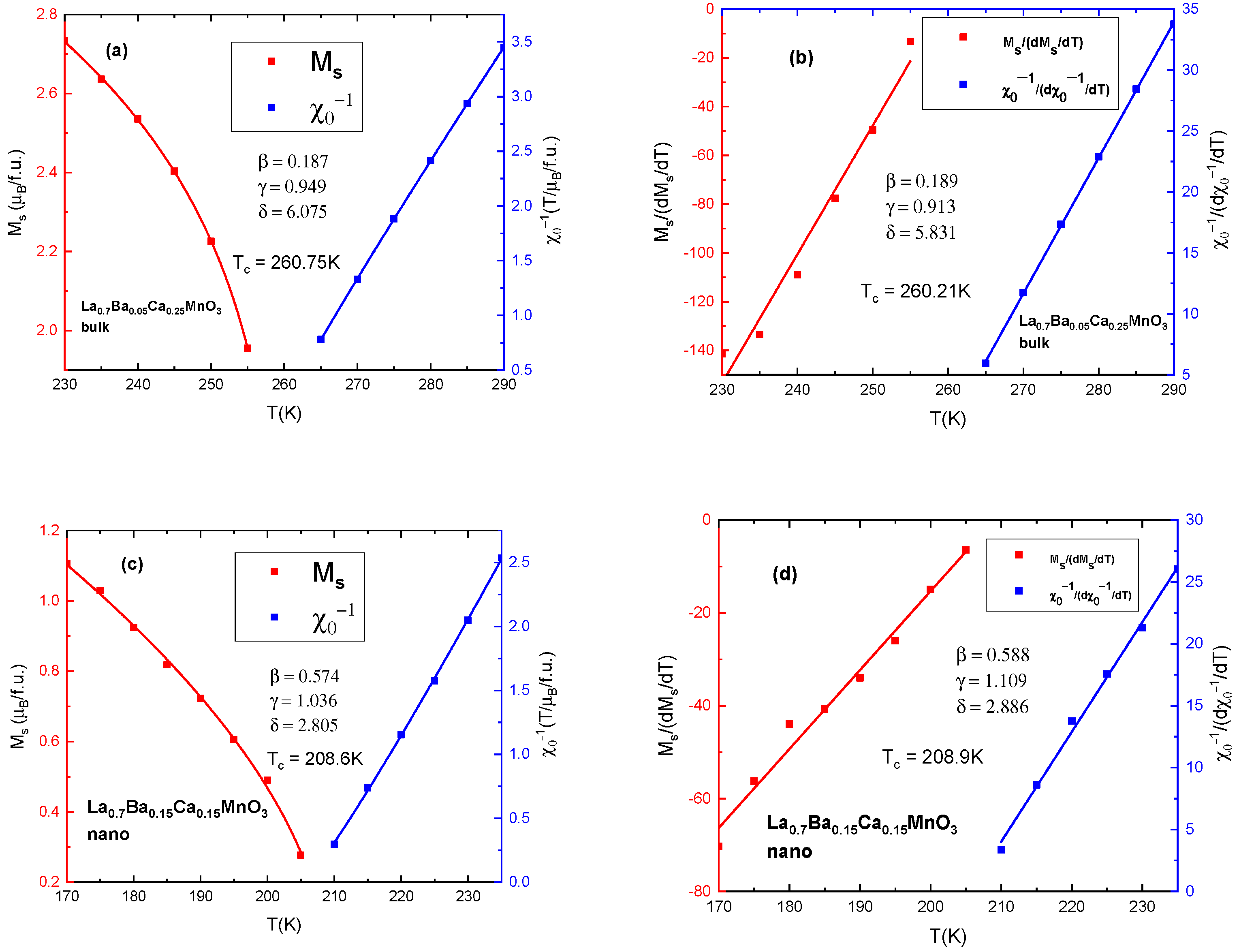
| Compound | γ | β | δ | Tc (K) | |
|---|---|---|---|---|---|
| x = 0 | bulk | 1.065 | 0.288 | 4.69 | 340 [26] |
| x = 0.15 | bulk | 0.958 | 0.238 | 5.025 | 308 |
| x = 0.2 | bulk | 0.979 | 0.245 | 4.996 | 279 |
| x = 0.25 | bulk | 0.949 | 0.187 | 6.075 | 261 |
| x = 0 | nano | 1.823 | 0.493 | 4.698 | 263 [26] |
| x= 0.15 | nano | 1.036 | 0.574 | 2.805 | 210 |
| x = 0.2 | nano | 1.022 | 0.555 | 2.838 | 185 |
| x = 0.25 | nano | 0.985 | 0.623 | 2.581 | 130 |
| Mean-field model | 1 | 0.5 | 3 | ||
| 3D Heisenberg model | 1.366 | 0.355 | 4.8 | ||
| Ising model | 1.24 | 0.325 | 4.82 | ||
| Tricritical mean-field model | 1 | 0.25 | 5 | ||
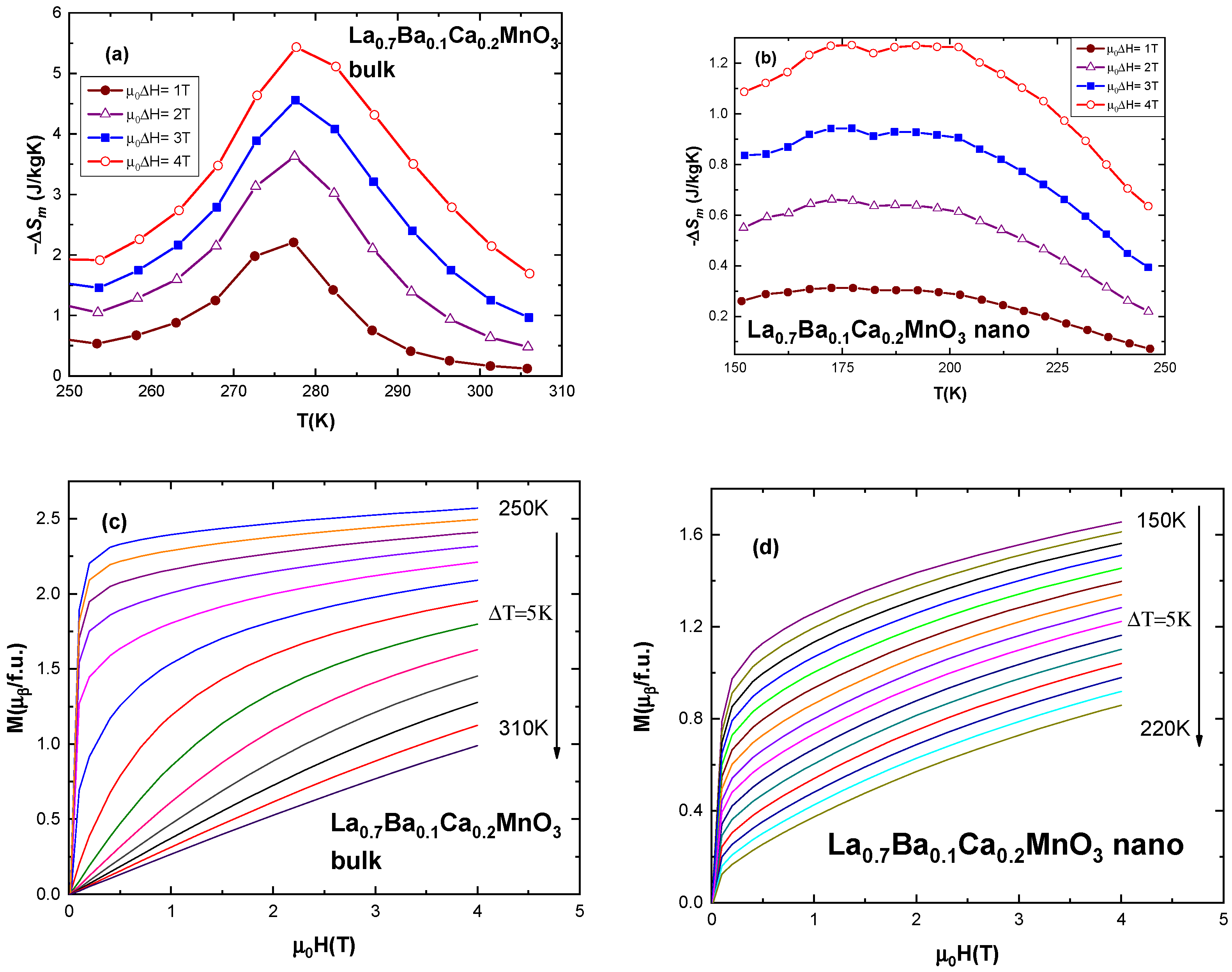
| Compound (Bulk) | TC (K) | Ms (μB/f.u.) | Hci (Oe) | |ΔSM| (J/kgK) μ0ΔH = 1 T | |ΔSM| (J/kgK) μ0ΔH = 4 T | RCP (S) (J/kg) μ0ΔH = 1 T | RCP (S) (J/kg) μ0ΔH = 4 T | Refs |
|---|---|---|---|---|---|---|---|---|
| La0.7Ba0.3MnO3 | 340 | 4.04 | 200 | 1.33 | 3.5 | 53.7 | 158.4 | [26,27] |
| La0.7Ba0.15Ca0.15MnO3 | 308 | 3.612 | 150 | 2.04 | 4.37 | 38.74 | 140.43 | This work |
| La0.7Ba0.1Ca0.2MnO3 | 279 | 3.676 | 110 | 2.29 | 5.43 | 41.26 | 184.69 | This work |
| La0.7Ba0.05Ca0.25MnO3 | 261 | 3.758 | 100 | 3.66 | 7.01 | 40.24 | 182.37 | This work |
| La0.7Ca0.3MnO3 | 256 | 1.38 | 41 | [5] | ||||
| La0.7Sr0.3MnO3 | 365 | - | 4.44 (5 T) | 128 (5 T) | [5] | |||
| La0.6Nd0.1Ca0.3MnO3 | 233 | 1.95 | 37 | [5] | ||||
| Gd5Si2Ge2 | 276 | - | 18 (5 T) | - | 535 (5 T) | [5] | ||
| Gd | 293 | 2.8 | 35 | [5] |
| Compound (Nano) | Tc (K) | Ms (μB/f.u.) | Hci (Oe) | |ΔSM| (J/kgK) μ0ΔH = 1 T | |ΔSM| (J/kgK) μ0ΔH = 4 T | RCP(S) (J/kg) μ0ΔH = 1 T | RCP(S) (J/kg) μ0ΔH = 4 T | Refs |
|---|---|---|---|---|---|---|---|---|
| La0.7Ba0.3MnO3 | 263 | 2.79 | 4800 | 1.04 | 1.37 | 105.4 | 130.1 | [26,27] |
| La0.7Ba0.15Ca0.15MnO3 | 210 | 2.547 | 370 | 0.33 | 1.31 | 33.7 | 144.1 | This work |
| La0.7Ba0.1Ca0.2MnO3 | 185 | 2.389 | 440 | 0.32 | 1.28 | 35.2 | 153.6 | This work |
| La0.7Ba0.05Ca0.25MnO3 | 130 | 710 | 0.05 | 0.27 | 6.1 | 40.5 | This work | |
| La0.67Ca0.33MnO3 | 260 | - | 0.97 (5 T) | 27 (5 T) | [54] | |||
| Pr0.65(Ca0.6Sr0.4)0.35MnO3 | 220 | 0.75 | 21.8 | [55] | ||||
| La0.6Sr0.4MnO3 | 365 | 1.5 | 66 | [14] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atanasov, R.; Brinza, E.; Bortnic, R.; Hirian, R.; Souca, G.; Barbu-Tudoran, L.; Deac, I.G. Magnetic and Magnetocaloric Properties of Nano- and Polycrystalline Bulk Manganites La0.7Ba(0.3−x)CaxMnO3 (x ≤ 0.25). Magnetochemistry 2023, 9, 170. https://doi.org/10.3390/magnetochemistry9070170
Atanasov R, Brinza E, Bortnic R, Hirian R, Souca G, Barbu-Tudoran L, Deac IG. Magnetic and Magnetocaloric Properties of Nano- and Polycrystalline Bulk Manganites La0.7Ba(0.3−x)CaxMnO3 (x ≤ 0.25). Magnetochemistry. 2023; 9(7):170. https://doi.org/10.3390/magnetochemistry9070170
Chicago/Turabian StyleAtanasov, Roman, Ecaterina Brinza, Rares Bortnic, Razvan Hirian, Gabriela Souca, Lucian Barbu-Tudoran, and Iosif Grigore Deac. 2023. "Magnetic and Magnetocaloric Properties of Nano- and Polycrystalline Bulk Manganites La0.7Ba(0.3−x)CaxMnO3 (x ≤ 0.25)" Magnetochemistry 9, no. 7: 170. https://doi.org/10.3390/magnetochemistry9070170
APA StyleAtanasov, R., Brinza, E., Bortnic, R., Hirian, R., Souca, G., Barbu-Tudoran, L., & Deac, I. G. (2023). Magnetic and Magnetocaloric Properties of Nano- and Polycrystalline Bulk Manganites La0.7Ba(0.3−x)CaxMnO3 (x ≤ 0.25). Magnetochemistry, 9(7), 170. https://doi.org/10.3390/magnetochemistry9070170






