Abstract
A new mixed-valence one-dimensional coordination polymer of formula {[CoII(MeOH)2][(μ-NC)2CoIII(dmphen)(CN)2]2}n·2nH2O (1) was obtained by reacting the Ph4P[CoII(dmphen)(CN)3] metalloligand (dmphen = 2,9-dimethyl-1,10-phenanthroline and Ph4P+ = tetraphenylphosphonium ion) with cobalt(II) acetate tetrahydrate. The structural analysis shows the formation of a neutral 4,2-ribbon-like chain of vertex-sharing cyanido-bridged {CoIII2CoII2} squares in which the metalloligand underwent an oxidation process and a reorganization to form {CoIII(dmphen)(CN)4}− linkers that coordinate to the [CoII(MeOH)2]2+ units through single cyanido ligands. Both cobalt(II) and Co(III) cations are six-coordinated in distorted octahedral environments. The shortest intrachain distance between the paramagnetic cobalt(II) ions is 7.36 Å, a value which is shorter than the shortest interchain one (10.36 Å). Variable-temperature (1.9–300 K) static (dc) magnetic measurements for 1 indicate the occurrence of magnetically isolated high-spin cobalt(II) ions with a D value of +67.0 cm−1. Dynamic alternating current (ac) magnetic measurements between 2.0–13 K reveal that 1 exhibits slow magnetic relaxation under non-zero applied dc fields, being thus a new example of field-induced SIM with easy-plane magnetic anisotropy. Theoretical calculations by CASSCF/NEVPT2 on 1 support the results from magnetometry. The relaxation of the magnetization occurs in the ground state under external dc fields through a two-phonon Raman process and one intra-Kramers mechanism.
1. Introduction
Cyanido spacers represent a prolific platform in metal assembling for magnetic molecule-based materials such as single-molecule magnets (SMMs), single-ion magnets (SIMs) or single-chain magnets (SCMs) which are very appealing systems considering their potential use in molecular electronics [1,2]. We focused on cyanido-bridged heterometallic complexes which exhibit slow relaxation of the magnetization, and which were successfully obtained through the rational bottom-up approach involving the use of cyanido-bearing metalloligands against highly anisotropic species [3,4,5,6,7,8]. Complex cations of 3d (MnIII, CoII) and 4f (DyIII, YbIII, TbIII) metal centers or heterometallic phenoxo-bridged d-f units ({NiIILnIII} and {CuIILnIII}) behave as SIMs or SMMs fragments, with four-, six- or eight-coordinate homo- and heteroleptic cyanide-containing complex anions such as [CoIII(CN)6]3−, [CoIII(AA)(CN)4]−, [FeII(AA)2(CN)2], [Co2III(2,5-dpp)(CN)8]2−, [NiII(CN)4]2−, [PtIVBr2(CN)4]2−, [MIV(CN)8]4− and [MIV(AA)CN)6]2−, being used as diamagnetic linkers (M = Mo, W; AA = bidentate ligand; 2,5-dpp = 2,5-bis(2-pyridyl)pyrazine) [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Most of the heterometallic compounds reported are of the mixed d-f type, where a cyanido building block of a diamagnetic transition metal ion (S = 0) coordinates through the cyanide bridges to an anisotropic LnIII complex cation: (i) a 3D network of SMMs, {[DyIII(H2O)2][CoIII(CN)6]}n · 2.2nH2O [13]; (ii) several one-dimensional (1D) coordination polymers of SMMs whose general formula is {[DyIII(MeOH)4][FeII(AA)(CN)2]}(CF3SO3)3 · nMeOH [16]; (iii) and discrete complexes, such as a pentanuclear emissive SMM, {[DyIII(H2O)3(tmpo)3]2[PtIVBr2(CN)4]3} · 2H2O [20], a heterobinuclear field-induced SMM, [YbIIICoIII(CN)6(bpyO2)2(H2O)3] · 4H2O [15], a heterotrimetallic decanuclear square showing SMM behavior, [(MoIV(CN)8)2(CuIILTbIII)4]4+ [21], and a metallocyclic molecular nanomagnet, {[NiII(Me2valpn)]2DyIII(H2O)Co(CN)6}2⋅ 8H2O⋅2DMF⋅6CH3CN [12] [tmpo = trimethylphosphine oxide, bpyO2 = 2,2′-bipyridine-N,N’-dioxide; H2L = N,N’-bis(3-methoxysalicylidene)ethylenediamine and H2Me2valpn = N,N’-bis(3-methoxysalicylidene)-2,2-dimethyl-1,3-diaminopropane]. Fewer examples of d nodes acting as SIMs or SMMs within heterometallic coordination compounds are known: the honeycomb structure {[CoII(TODA)3][CoIII(CN)6]2 · 9H2O}n [10], the tubular 1D motif [CoII(LN3O2)]6[CoIII(CN)6]4 · 26H2O [11], the chain of SIMs with seven-coordinate iron(II) ions {[FeII(H2DAPBH)][NiII(CN)4]}n [19], and 1D compounds behaving as SMMs with formulas {[CoII(bpp)(H2O)][WIV(CN)8]}n·6nH2O [24] and [CoII(CH3OH)2(DMSO)2(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·4nCH3OH [17] {TODA = 1,4,10-trioxa-7,13-diazacyclopentadecane; LN3O2 = 2,13-dimethyl-3,12,18-triaza-6,9-dioxabicyclo-[12.3.1]octadeca-1(18),2,12,14,16-pentaene, H2DAPBH = 2,6-diacetylpyridine bis-benzoylhydrazone and bpp = 2,6-di(1-pyrazolyl)pyridine}.
Redox labile cyanido building blocks have been described in the literature [25,26,27,28,29]. In this respect, we reported several heterometallic complexes which were obtained by using the heteroleptic cyanide-bearing [WV(bpy)(CN)6]− or [CoII(dmphen)(CN)3]− complexes as building blocks for metal assembling, processes that were accompanied by a reduction from WV to WIV or an oxidation from CoII to CoIII to form more stable species as nodes within the {NiIIDyIIIWIV} [22] and {CoIIIMnIII} [9] coordination polymers, respectively. The [WV(bpy)(CN)6]− species underwent reduction to form a 2D network of SMMs in which diamagnetic W(IV) spacers connected the {NiIIDyIII} nodes, whereas the Co(II) ion within the [CoII(dmphen)(CN)3]− complex anion was oxidized, turning into the [CoIII(dmphen)(CN)4]− linker in the resulting {CoIIIMnIII} chain of SIMs.
Herein, we describe the preparation and magneto-structural study of a 4,2-ribbon-like chain of the formula {[CoII(MeOH)2][(μ-NC)2CoIII(dmphen)(CN)2]2}n·2nH2O (1) where vertex-sharing {CoIII2CoII2}n squares and field-induced slow relaxation of the magnetization occur. Remarkably, the low-spin [CoII(dmphen)(CN)3]− species which is used as a metalloligand for fully solvated cobalt(II) ions undergoes an oxidation process and a reorganization into the more stable diamagnetic [CoIII(dmphen)(CN)4]− unit in 1.
2. Results and Discussion
2.1. Synthesis, IR Spectroscopy and Powder X-ray Diffraction
In previous works, we explored the use of the low-spin [CoII(dmphen)(CN)3]− complex anion as a metalloligand for the [MnIII(salen)(H2O)]+ complex cation [9,30]. This complex-as-ligand strategy afforded two heterobimetallic chains of formulas {[MnIII(salen)(μ-NC)2CoIII(dmphen)(CN)2]}n [9] and {[MnIII(salen)(μ-NC)2CoII(dmphen)(CN)]·2H2O}n [30]. The oxidation of the Co(II) ion to Co(III) occurred in the formation of the first one, a process that could be explained by taking into account the oxidizing activity of the [MnIII(salen)(H2O)]+ complex cation. Single crystals of the neutral {MnIIICoIII} chain were grown in a test tube by slow diffusion, after a few weeks. As far as the second chain is concerned, the kinetic factor was most likely determinant in its formation because single crystals formed within a day. In the present report, the reaction between [CoII(dmphen)(CN)3]− and Co(CH3COO)2·4H2O in the methanol afforded orange crystals of 1 by slow evaporation of the resulting solution in the open air after five days. The oxidation of the cobalt(II) ion from the cyanide-bearing metalloligand to cobalt(III) in 1 is favored by the strong ligand field character of the dmphen and cyanide ligands that would stabilize the [CoIII(dmphen)(CN)4]− unit in this 1D compound.
The FTIR spectrum of 1 shows two strong bands at 2172 and 2128 cm−1 which are attributed to the stretching vibrations of the bridging and terminal cyanido ligands, respectively (Figure S1). The fact that these peaks are observed at 2171 and 2140 cm−1 in the infrared spectra of the related {CoIIIMnIII} and [MnII(MAC)(μ-NC)2Co2III(μ-2,5-dpp)(CN)6]n·7nH2O chains [9,31] and that the stretching vibration of the terminal cyanide for PPh4[CoIII(4,4′-dmbipy)(CN)4] (4,4′dmbipy = 4,4′-dimethyl-2,2′-bipyridine) occurs at 2130 cm−1 [9], supports the coexistence of the bridging cyanide between Co(II) and Co(III) and terminal cyanide ligands at Co(III) in 1. The peaks at 1627, 1598 and 1562 cm−1 would correspond to the C=Ndmphen bond vibration and the ring-stretching modes of the dmphen ligand. Finally, the strong intensity peak at 442 cm–1 is most likely due to the vibrations of the CoII-O bond. All these spectroscopic features are sustained by the X-ray crystal structure of 1. Additionally, the purity of the bulk sample is confirmed by the agreement between its PXRD pattern and the calculated one from the single crystal X-ray diffraction (Figure S2). The powder XRD was performed on a fresh sample, the compound losing crystallinity over time.
2.2. Description of the Structure
Compound 1 crystallizes in the triclinic system, spatial group P-1 and its structure consists of neutral chains of vertex-sharing squares of formula {[CoII(MeOH)2][(μ-NC)2CoIII(dmphen)(CN)2]2}n·2nH2O (1). The asymmetric unit is made up by a cyanido-bridged {CoIIICoII} unit, where the [CoIII(dmphen)(CN)4]− metalloligand coordinates to a diaquacobalt(II) ion through a single cyanido group (Figure 1, left).
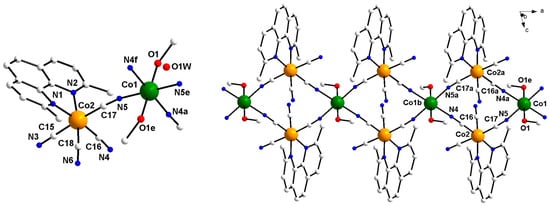
Figure 1.
(Left) View of the asymmetric unit of 1 with the atom numbering. (Right) View of a fragment of the neutral chain of 1. The water molecules were not represented for the sake of clarity [symmetry code: (a) = 1 − x, 1 − y, −z; (b) = −1 + x, y, z; (e) = 2 − x, 1 − y, −z; (f) = 1 + x, y, z].
Further, each metalloligand connects to another CoII ion to give {CoIII2CoII2} squares, sharing the CoII ions as vertices. In such a way, a neutral, 4,2-ribbon-like chain, running parallel to the crystallographic b axis, results (Figure 1, right). This type of topology was observed in previously reported heterobimetallic chains obtained by using [MIII(L’)(CN)4]− (M = Cr and Fe; L’ = bipy and phen) [32,33,34,35,36,37], [Cr(ampy)(CN)4]− (ampy = 2-aminomethylpyridine) [33], [FeIII(bpym)(CN)4]− (bpym = 2,2′-bipyrimidine) [38], [FeIII(4,4′-dmbpy)(CN)4]− [39,40,41] and [FeIII(dbphen)(CN)4]− (dbphen = 5,6-dibromo-1,10-phenanthroline) [42] as building blocks towards fully solvated transition metal ions.
Selected bond lengths and angles for 1 are listed in Table 1. The cobalt(II) ion in 1 (Co1) is surrounded by four cyanide-nitrogen atoms building the equatorial plane and two trans-positioned methanol molecules in the axial positions, the whole set of donor atoms defining a slightly distorted octahedral geometry. In this respect, the estimated ChSM value for the environment of the Co1 atom is 0.016 (a zero value corresponds to the ideal octahedron as predicted by the SHAPE program; see Table S1 and Figure S3) [43,44]. The values of the equatorial Co1-Ncyanide bond lengths are 2.102(5) and 2.129(6) Å for Co1-N5 and Co1-N4a, respectively, while those of the axial Co1-OMeOH bond distances are of 2.125(5) Å (Co1-O1), these structural features accounting for the octahedral distortion. The values of the Co1-N-C bond angles cover the wide range between 169.5(5) and 176.5(6)° for C16-N4-Co1b and C17-N5-Co1, respectively.

Table 1.
Main bond lengths (Å) and angles (deg) for 1 *.
The Co(III) ions from the crystallographically independent [CoIII(dmphen)(CN)4]− metalloligand (Co2) is also six-coordinated by a didentate dmphen molecule and four cyanide-carbon atoms in a somewhat more distorted octahedral environment than the cobalt(II) ion [estimated ChSM values through the SHAPE program of 0.459 (Co2); see Table S1 and Figure S3]. The main source of this distortion is the reduced value of the bite angle of the chelating dmphen, of 82.7(2)°. The Co2-Ccyanide bond distances cover the range 1.872(7)–1.922(7) Å, values that agree with those previously reported for other cyanido-based cobalt(III) complexes [9,17,31,45,46]. The Co2-Ndmphen bond lengths [2.034(5), 2.011(5) Å, are longer than those of the Co2-Ccyanide, as expected. The Co2-C-Ncyanide bond angles are close to linearity, their values varying in the range between 174.4(6) (Co2-C16-N4) and 178.8(6)° (Co2-C15-N3).
The cobalt atoms within each square unit of 1 form angles at the corners which deviate slightly from the ideal value of 90° (ca. 91.93 and 88.04° for Co1b-Co2a-Co1 and Co2a-Co1b-Co2, respectively). Very close intermetallic distances are found along the edges of the {CoIII2CoII2} squares, ca. 5.13 Å both for Co1···Co2 and Co1···Co2a [symmetry code: (a) = 1 − x, 1− y, −z; (b) = −1 + x, y, z]. The values of the shortest intra- and interchain distances between the paramagnetic cobalt(II) ions are 7.38 (Co1…Co1b) and 10.92 Å (Co1…Co1d), respectively [symmetry code: (d) = x, 1 + y, z].
The neutral chains in 1 are further interconnected through hydrogen bonds involving the coordinated methanol molecules, two peripheral cyanide ligands and the water molecules of crystallization leading to a supramolecular 2D network that grows in the crystallographic ac plane (Figure 2 and Table S2). Supramolecular π-π stacking interactions between dmphen ligands from adjacent chains (value of the centroid···centroid distance of ca. 3.59 Å) contribute to the stabilization of this supramolecular network (Figure S4).
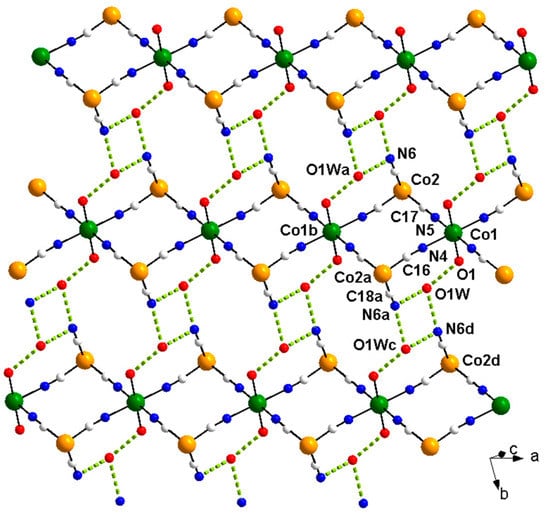
Figure 2.
A view of a fragment of the hydrogen bonding pattern (dashed lines) in 1. The dmphen molecules were omitted for the sake of clarity [symmetry code: (a) = 1 − x, 1 − y, −z; (b) = −1 + x, y, z; (c) = 1 − x, 2 − y, −z; (d) = x, 1 + y, z].
2.3. Static (dc) Magnetic Properties
The dc magnetic properties of compound 1, as the χMT against T plot (χM being the magnetic susceptibility per CoIII2CoII unit), are shown in Figure 3. At room temperature, χMT is equal to 2.81 cm3 mol−1 K, a value which is as expected for a magnetically diluted high-spin cobalt(II) ion with a significant orbital angular momentum [47]. The cobalt(III) ions in 1 are diamagnetic. Upon cooling, χMT continuously decreases to reach a value of 1.62 cm3 mol−1 K at 1.9 K. There is no maximum of the magnetic susceptibility in the χM vs. T plot. The observed decrease in χMT could be due to the thermal depopulation of the higher Kramer doublets of the high-spin cobalt(II) ion and/or to antiferromagnetic interactions between the paramagnetic cobalt(II) ions. This last possibility is to be ruled out because of the large cobalt(II)···cobalt(II) distance (shortest intra- and interchain values of ca. 7.36 and 10.36 Å, respectively).
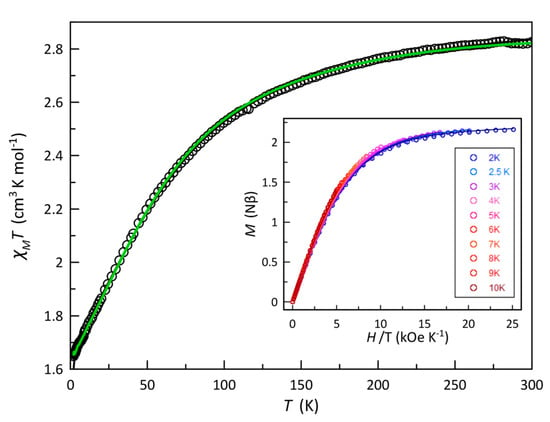
Figure 3.
χMT against T for 1: (empty circles) experimental; (solid line) best-fit curves to the experimental data by using the parameters reported in the text for the first order spin-orbit coupling. The inset shows the reduced M vs. H plot, the solid lines being the best-fit curves in the temperature range from 2.0 to 10 K (from blue to red colors) through the zfs approach (see text).
Having in mind these features, we treated the magnetic data of 1 through the Hamiltonian Equation (1):
H = −αλLCoSCo + ∆[Lz,CoSCo − L(L + 1)/3] + βH(geSCo − αLCo)
The first term in this Hamiltonian describes the spin-orbit coupling (SOC) where λ is the spin-orbit coupling parameter and α is an orbital reduction factor defined as α = Aκ. κ represents the reduction in the orbital momentum caused by the delocalization of the unpaired electrons on the ligands covalency. The A parameter takes values of 3/2 and 1 in the weak and strong crystal field limits, respectively, and it considers the admixture of the upper 4T1g(4P) state into the 4T1g(4F) ground state. The second term models the axial splitting of the 4T1g ground state of the ideal Oh symmetry of the cobalt(II) ion into singlet 4A2 and doublet 4E levels, ∆ being the energy gap between these levels. The 4A2 and 4E levels split in turn by second-order SOC, leading to two and four Kramers doublets. Finally, the third term corresponds to the Zeeman interaction, which includes both spin and orbital contributions. The best-fit parameters of the magnetic data of 1 from the whole temperature range explored through the VPMAG program [48] are α = 1.24, λ = −163 cm−1 and ∆ = +553 cm−1 with F = 8.0 × 10−6 (F is the agreement factor defined as ∑[Pexp–Pcalcd]2/∑[Pexp]2, where P is the physical property under study). The obtained values of α, λ and ∆ for 1 are in the range of those previously reported for other six-coordinate high-spin cobalt(II) complexes [17,49,50,51,52,53,54,55,56,57].
Due to the strong axial distortion of the cobalt(II) ion, both structurally (see Table 1) and magnetically (∆ = +553 cm−1), an important reduction in the orbital momentum is expected. Therefore, a spin Hamiltonian currently used to simultaneously fit the χMT vs. T and M against T plots, which is based on the assumption that the zero-field splitting (zfs) of S = 3/2 is dominant, can be applied. The corresponding Hamiltonian is expressed by Equation (2)
where S, D, and E are the ground spin state and axial and transverse anisotropies, respectively, β is the Bohr magneton and H is the applied dc field. If E = 0 (a case where the rhombic distortion is neglected), 2D for 1 corresponds to the energy gap between the ±1/2 and ±3/2 doublets arising from the second order SOC of the quartet ground state of the axially distorted octahedral cobalt(II) ion. As the M vs. H/T curves for 1 in the temperature range from 2.0 to 9 K quasi collapse (see inset of Figure 3), a large value of D is predicted. The simultaneous analysis of the variable-temperature magnetic susceptibility and magnetization data under different applied dc fields and temperatures of 1 through the VPMAG package [48] led to the following best-fit parameters: D = +67.0 cm−1, E/D = 0.13, g// = 2.44, g⊥ = 2.51 and TIP = 930 × 10−6 cm3 mol−1 with F = 7.6 × 10−6. The simulated curves with these values match well the experimental data in the temperature ranges explored. When we started with a negative value of D, no reasonable results were obtained. Consequently, this system can be considered as a doublet at low temperatures. The positive sign of the zfs parameter arises from the interaction between the ground and excited electronic states coupled through the SOC and illustrates the strong easy-plane anisotropy of the high-spin cobalt(II) in 1. The value of D for 1 lies within the range of those reported for other examples of SIMs with six-coordinate cobalt(II) ions [17,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70].
Hzfs+Zeeman = D[Sz2 − S(S + 1)] + E(Sx2 − Sy2) + βH[g//Sz + g⊥(Sx + Sy)]
2.4. Theoretical Calculations
To confirm the validity of the results from magnetometry for 1, theoretical CASSCF/NEVPT2 calculations were carried out. Owing to the high disorder observed in 1, two different geometries for the CoII coordination sphere can be extracted (Table S3). Given that each CoII ion is surrounded by four CoIII ions, the model that introduces all electronic effects on the cobalt(II) center is too large to be calculated at a moderate computational cost. Therefore, a simpler model was built by substituting the CoIII ions and their surroundings with a simple proton, which simulates the presence of a positively charged entity bound to the cyanide bridging ligands that decrease the magnitude of its ligand field (just as the CoIII ion does in the actual system). The sign and magnitude of the computed value of D for the two mononuclear models (+42.9 and +62.7 cm–1 for A and B, respectively) agree with the one from magnetometry. To be more precise, the result extracted from experimental data is close to the calculated ones. A similar case occurs with the calculated E/D ratio, which takes high (0.179) and low (0.050) values for the first high- and second low-rhombic distorted models. Consequently, from magnetometry where only a single geometry for the CoII coordination sphere is considered, an intermediate value (that is 0.13) very close to the theoretical mean one (0.115) is found for the E/D ratio. The calculated components for the g-tensor show an axial magnetic anisotropy in both models with a parallel contribution lower than the perpendicular one (gz = 2.057, gy = 2.418, gx = 2.524, g⊥ = 2.471, and gz = 2.062, gy = 2.505, gx = 2.610, g⊥ = 2.560 for the A and B models, respectively), whereas A points to a smaller value of D (|gz − g⊥| (0.414 and 0.498) and a larger rhombicity (|gx − gy|/|gz − g⊥| = 0.256 and 0.211). 4T1g is the ground term for a high-spin d7 configuration of a CoII ion in an octahedral environment. Due to geometric or ligand-field distortions, it splits into three states; one of them is the ground state and the other two are the closest excited states (ca. 1490 and 990 cm–1 for A and B). For this type of compound, the interaction between these excited states and the ground one contributes mainly to the zfs, which is also observed for the A and B models with estimated contributions to D [+42.1 (A) and +56.0 cm–1 (B)], which are somewhat above 90% of the calculated total value.
According to the geometry of the CoII coordination sphere in 1, with four bridged cyanide ligands building a plane and two O-donor solvent molecules on the axial sites, the z-axis of the zfs tensor is placed on this O-Co-O vector and the four cyanide-nitrogen atoms form the equatorial plane (Figure S5). It is worth noting that some deviations from the axial axis occur due to several distortions of the octahedral coordination sphere.
2.5. Dynamic (ac) Magnetic Properties
Alternating current (ac) magnetic susceptibility measurements for 1 were carried out in the temperature range from 2.0 to 10 K to investigate its magnetization dynamics. No frequency dependence was observed for the ac components in the absence of a magnetic field (Hdc), a feature which is usually attributed to a fast relaxation by quantum tunneling of magnetization (QTM). However, for easy-plane magnetic anisotropy (D > 0) as in 1, no energy barrier arises from the zfs to govern the magnetic relaxation. Instead, the swift spin reversal in the absence of Hdc is associated with the enabled direct pass between the two MS components of the ground ±1/2 Kramers doublet. Such a mechanism is known as an intra-Kramer (IK) relaxation [71]. Although an IK can suppress the occurrence of the slow magnetic relaxation phenomenon, it becomes less efficient when applying an external dc magnetic field. Therefore, frequency-dependent χM′ and χM″ signals are observed under Hdc of 2.5 and 5.0 kOe (Figure 4 and Figure S6), in agreement with a slow magnetic relaxation process typical of high-spin cobalt(II) SIMs.
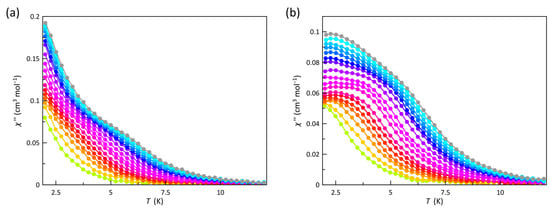
Figure 4.
Temperature dependence of χM″ of 1 under Hdc of 2.5 (a) and 5.0 kOe (b) at ±5 Oe oscillating field in the frequency range from 0.3 to 10 kHz (from green to grey). The solid lines are only eye guides.
Two relaxation processes can be distinguished from the χM″ vs. T curves (Figure 4). They occur at blocking temperatures (TB) close enough to superimpose and, consequently, no clear maxima are appreciated. It is possible to identify one process being predominant at higher temperatures (TB > 5.0 K) that shifts towards lower TB values by decreasing the frequency of the oscillating magnetic field (ν) and another process which seems to be temperature-independent occurring at lower temperatures (TB < 4.0 K). In these cases, where no maxima can be discerned, the approximation to calculate the magnetic relaxation times (τ) of τ = 1/2πν at T = Tmax cannot be applied. Therefore, the best way to extract this parameter is the joint analysis of the χM′ and χM″ vs. ν curves (Figure S7a,b) through the generalized Debye model [Equations (3) and (4)], which also takes into account the static and infinite magnetic susceptibilities (χS and χT) as well as the exponential factor that describes the broadness of the spectra (α) [72]:
We tried to use a double relaxation model to analyze both the aforementioned lower- and higher-temperature distinct processes, where each process was considered additive and independent. However, it resulted in overparameterization, and no reliable data could be extracted from this approach. Alternatively, the contribution of the temperature-independent process was omitted because of a lack of accuracy derived from its very low TB values (below 2.0 K). This method allowed us to obtain a good set of magnetic parameters for the higher-temperature process that reproduces well the χM′ and χM″ vs. ν curves (Figure S7a,b), as well as the Argand plots (Figure S7c). For that, the data of temperatures below 3.5 (Hdc = 5.0 kOe) or 4.5 K (Hdc = 2.5 kOe) were discarded in the analysis. The relatively high values of α at these temperatures (0.26 and 0.40 for Hdc = 2.5 and 5.0 kOe, respectively) and how they continuously decrease down to 0.13 at 7.0 K, support the occurrence of additional relaxation processes that become less relevant when the temperature increases, as predicted from a qualitative analysis of the χM′ and χM″ against T plots.
The values of τ are displayed in the form of ln τ vs. ln T plots in Figure 5. Satisfactory least-squares fits of the experimental data were obtained through Equation (5)
which expresses a double spin reversal mechanism involving a two-phonon Raman and an IK relaxation prevailing at higher and lower temperatures, respectively. As expected, the values of the C and n Raman coefficients are very similar regardless of Hdc (Table S4). Moreover, the values of n between 6 and 7 (6.7 and 6.5 under Hdc fields of 2.5 and 5.0 kOe, respectively) indicate that acoustic phonons are involved in the Raman spin-lattice relaxation. Even though the τIK values are close, a slight decrease was observed when we increased Hdc, revealing that the spin reversal through this mechanism becomes faster. This is the opposite trend which should be expected for the greater splitting of the ground ±1/2 Kramers doublet promoted by a higher Hdc. Several circumstances may explain this feature, but the limited precision in determining τ (as denoted by the standard deviations in Figure 5), the influence of the low-temperature parallel process or even the arising of faster secondary mechanisms of relaxation that depend differently on Hdc, such as the one-phonon direct mechanism (τ–1 = AT), are most likely the main sources of this deviation.
τ–1 = τIK–1 + τRAMAN–1 = τIK–1 + CTn
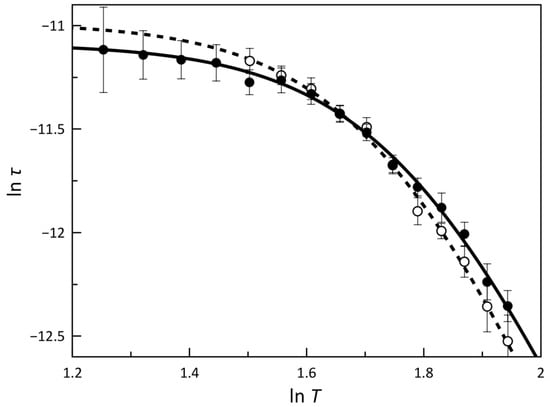
Figure 5.
ln τ vs. ln T plots for 1 under Hdc of 2.5 (open circles) and 5.0 kOe (filled circles). The solid and dashed lines are the best-fit curves through Equation (5) (see text). Vertical error bars denote the standard deviations.
3. Materials and Methods
3.1. Materials and General Methods
The chemicals used as well as the solvents were of reagent grade and were purchased from commercial sources. Ph4P[Co(dmphen)(CN)3]·4H2O was prepared as described in the literature [45]. Elemental analyses (C, H, N) were performed on a Perkin Elmer 2400 analyzer. IR spectra were carried out on a FTIR Bruker Tensor V-37 spectrophotometer using KBr pellets in the range from 4000 to 400 cm−1.
Caution! The high toxicity of the cyanides means that great caution is required in their use. The syntheses were carried out at a mmol scale, in a well-ventilated hood. The waste was treated with solutions of NaClO and NaOH to transform the cyanide into cyanate.
3.2. Preparation of {[CoII(MeOH)2][(μ-NC)2CoIII(dmphen)(CN)2]2}n·2nH2O (1)
A solution of 0.082 g (0.11 mmol) of Ph4P[Co(dmphen)(CN)3]·4H2O in 15 mL methanol was poured into a methanolic solution (20 mL) of 0.04 g (0.22 mmol) Co(CH3COO)2·4H2O, with a few drops of acetic acid. The orange solution formed was left undisturbed for five days. X-ray quality orange prism-like crystals were obtained. Yield: ca. 55% (1). Anal. Calcd for C38H36N12Co3O4 (1): C, 26.82; H, 1.06; N, 21.40. Found: C, 26.87; H, 1.02; N, 21.32%. IR (KBr/cm−1): 3438s, 2172vs and 2128s [νCNcyanide], 1627s [νC=N], 1429vs, 1378s, 1159m, 863vs, 729s, 442s.
3.3. Physical Measurements
Direct current (dc) magnetic susceptibility measurements (1.9–300 K) under applied dc magnetic fields of 5000 G (T ≥ 50 K) and 100 G (1.9 ≤ T ≤ 50 K) and variable-field (0–5 T) magnetization measurements (2.0–10 K) on crushed crystals of 1 (mixed with grease to avoid the crystallite orientation) were carried out with a Quantum Design SQUID magnetometer. Variable-temperature (2.0–12 K) alternating current (ac) magnetic susceptibility measurements under different applied dc magnetic fields in the range 0 to 2500 G were performed for 1 by using a Quantum Design Physical Property Measurement System (PPMS). The magnetic susceptibility data of both compounds were corrected for the diamagnetism of the constituent atoms and the sample holder (a plastic bag). Powder X-ray diffraction (XPRD) measurements were done on a PANalytical Empyrean X-ray diffractometer using Cu-Kα radiation (α = 1.5418 Å), in which the X-ray tube was operated at 40 kV and 30 mA ranging from 5 to 30°.
3.4. Computational Details
The parameters that determine the axial (D) and rhombic (E) components of the local zero-field splitting (zfs) of 1 were estimated from theoretical calculations based on a second-order N-electron valence state perturbation theory (CASSCF/NEVPT2) [73,74,75], which often provides accurate values of the nearby excited states energies and for the zfs tensor of mononuclear first-row transition metal complexes. As a starting wavefunction, one found from a previous complete active space (CAS) calculation was used. Calculations were carried out on the experimental geometries with version 4.0.1 of the ORCA programme [76], using the def2-TZVP basis set proposed by Ahlrichs [77,78] and the auxiliary TZV/C Coulomb fitting basis sets [79,80,81]. The contributions to zfs from 10 quartet and 20 doublet excited states generated from an active space with seven electrons in five d orbitals were included using an effective Hamiltonian. The RIJCOSX method was used combining resolution of the identity (RI) and “chain of spheres” COSX approximations for the Coulomb and exchange terms, respectively [82,83,84].
3.5. X-ray Data Collection and Structure Refinement
X-ray quality single crystals of 1 were measured on an Oxford Diffraction XCALIBUR Eos CCD diffractometer equipped with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å). The crystals were positioned 40 mm from the CCD detector and 248 frames were measured each for 125 s over a 1° scan width. The determination of the unit cell and data integration was established by using the CrysAlis package of Oxford Diffraction [85]. Multi-scan correction for absorption was applied. The structure was solved with the program SHELXT using the intrinsic phasing method and refined by the full-matrix least-squares method on F2 with SHELXL [86,87]. Olex2 was used as an interface to the SHELX programs [88]. All hydrogen atoms attached were introduced in idealized positions and refined using a riding model. The structural images were obtained with a Diamond 4 program [89]. The unit cell parameters and refinement conditions for 1 are given in Table 2. The supplementary crystallographic data can be obtained free of charge via www.ccdc.cam.ac.uk/conts/retrieving.html or deposit@ccdc.ca.ac.uk accessed on 25 March 2023, CCDC-2252204 (1)

Table 2.
Crystal data and structure refinement for 1.
4. Conclusions
Our attempts to explore the coordination ability of the low-spin [CoII(dmphen)(CN)3]− complex anion to fully solvated metal cations provided the 4,2-ribbon-like chain of formula {[CoII(MeOH)2][(μ-NC)2CoIII(dmphen)(CN)2]2}n·2nH2O (1) where the low-spin cobalt(II) ion from the starting metalloligand underwent oxidation to diamagnetic cobalt(III) together with a reorganization of its environment. This phenomenon was observed previously in the reaction of the same low-spin cobalt(II) building block with the preformed [MnIII(salen)(H2O)]+ complex cation. In contrast to what occurs in 1, a heterobimetallic zigzag chain of formula {[MnIII(salen)(μ-NC)CoIII(dmphen)(CN)3]}n resulted in this last case, the oxidant being the manganese(III) from the complex cation. Static (dc) and dynamic (ac) magnetic measurements reveal that 1 is a new example of a field-induced SIM with an easy-plane anisotropy, the positive sign and size of D from magnetometry being substantiated by theoretical calculations. The analysis of the relaxation of the magnetization at low temperatures of 1 obeys a combination of an intra-Kramers mechanism and a Raman process.
Supplementary Materials
The information is available online at https://www.mdpi.com/article/10.3390/magnetochemistry9050130/s1, Figure S1: FTIR spectrum, Figure S2: Experimental and calculated PXRD patterns, Figure S3: Coordination polyhedra of the cobalt atoms; Figure S4: A view of the interchain π-π stacking in the crystallographic ab plane; Figure S5: Relative orientation of the experimental coordination sphere of models A (left) and B (right) and the calculated D tensor, Figure S6: Temperature dependence of χM′ under applied static fields of 2.5 (a) and 5.0 kOe (b) with a ±5.0 G oscillating field at frequencies in the range 0.3–10 kHz, Figure S7: Frequency dependence of χM′ (a) and χM″ (b) and Argand plots (c) under magnetic fields of 2.5 (left) and 5.0 kOe (right) at ±5.0 Oe oscillating field in the temperature ranges 4.5–7.0 and 3.5–7.0 K, respectively, Table S1: Results of the SHAPE analysis for CoIIIC4N2 and CoIIN4O2 chromophores, Table S2: Hydrogen bonding pattern. Table S3: Atomic coordinates (Å) for the A and B models based on the experimental geometry. Table S4: Selected parameters from the least-squares fit of the ac susceptibility data.
Author Contributions
M.-G.A. and D.V. prepared the compounds and grew the single crystals; S.S. performed the X-ray diffraction experiments; N.M. carried out the cryomagnetic measurements; F.L. and J.C. analyzed the magnetic data; J.C. was in charge of the theoretical calculations; M.-G.A. and M.J. conceived and designed the experiments; all authors contributed to the writing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from the Romanian National Authority for Scientific Research CNCS-UEFISCDI (Projects PN-III-P1-1.1-TE-2019-0352), the Spanish MINECO (PID2019-109735GB-I00), Unidad de Excelencia María de Maetzu CEX2019-000919-M and Generalitat Valenciana (AICO2021/295) is gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article or Supplementary Material.
Acknowledgments
The authors would like to thank Renato Rabelo of the ICMol for his unselfish help with the analysis of the ac data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sieklucka, B.; Pinkowicz, D. (Eds.) Molecular Magnetic Materials; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]
- Ferrando-Soria, J.; Vallejo, J.; Castellano, M.; Martínez-Lillo, J.; Pardo, E.; Cano, J.; Castro, I.; Lloret, F.; Ruiz-García, R.; Julve, M. Molecular Magnetism, quo vadis? A historical perspective from a coordination chemist viewpoint. Coord. Chem. Rev. 2017, 339, 17–103. [Google Scholar] [CrossRef]
- Lescouëzec, R.; Toma, L.M.; Vaissermann, J.; Verdaguer, M.; Delgado, F.S.; Ruiz-Pérez, C.; Lloret, F.; Julve, M. Design of single chain magnets through cyanide-bearing six-coordinate complexes. Coord. Chem. Rev. 2005, 249, 2691–2729. [Google Scholar] [CrossRef]
- Wang, S.; Ding, X.-H.; Zuo, J.-L.; You, X.-Z.; Huang, W. Tricyanometalate molecular chemistry: A type of versatile building blocks for the construction of cyanide-bridged molecular architectures. Coord. Chem. Rev. 2011, 255, 1713–1732. [Google Scholar] [CrossRef]
- Wang, S.; Ding, X.-H.; Li, Y.-H.; Huang, W. Dicyanometalate chemistry: A type of versatile building block for the construction of cyanide-bridged molecular architectures. Coord. Chem. Rev. 2012, 256, 439–464. [Google Scholar] [CrossRef]
- Li, Y.-H.; He, W.-R.; Ding, X.-H.; Wang, S.; Cui, L.-F.; Huang, W. Cyanide-bridged assemblies constructed from capped tetracyanometalate building blocks [MA(ligand)(CN)4]1-/2- (MA = Fe or Cr). Coord. Chem. Rev. 2012, 256, 2795–2815. [Google Scholar] [CrossRef]
- Jeon, I.-R.; Clérac, R. Controlled association of single-molecule magnets (SMMs) into coordination networks: Towards a new generation of magnetic materials. Dalton Trans. 2012, 41, 9569–9586. [Google Scholar] [CrossRef]
- Wang, J.-H.; Li, Z.-Y.; Yamashita, M.; Bu, X.-H. Recent progress on cyano-bridged transition-metal-based single-molecule magnets and single-ion magnets. Coord. Chem. Rev. 2021, 428, 213617. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Marino, N.; de Munno, G.; Lloret, F.; Julve, M. {CoIIIMnIII}n corrugated chains based on heteroleptic cyanido metalloligands. RSC Adv. 2015, 5, 95410–95420. [Google Scholar] [CrossRef]
- Shao, D.; Zhou, Y.; Pi, Q.; Shen, F.-X.; Yang, S.-R.; Zhang, S.-L.; Wang, X.-Y. Two-dimensional frameworks formed by pentagonal bipyramidal cobalt(II) ions and hexacyanometallates: Antiferromagnetic ordering, metamagnetism and slow magnetic relaxation. Dalton Trans. 2017, 46, 9088–9096. [Google Scholar] [CrossRef]
- Shao, D.; Shi, L.; Shena, F.-X.; Wang, X.-Y. A cyano-bridged coordination nanotube showing field-induced slow magnetic relaxation. CrystEngComm 2017, 19, 5707–5711. [Google Scholar] [CrossRef]
- Liu, M.-J.; Hu, K.-Q.; Liu, C.-M.; Cui, A.-L.; Kou, H.-Z. Metallocyclic Ni4Ln2M2 single-molecule magnets. Dalton Trans. 2017, 46, 6544–6552. [Google Scholar] [CrossRef]
- Xin, Y.; Wang, J.; Zychowicz, M.; Zakrzewski, J.J.; Nakabayashi, K.; Sieklucka, B.; Chorazy, S.; Ohkoshi, S.I. Dehydration–Hydration Switching of Single-Molecule Magnet Behavior and Visible Photoluminescence in a Cyanido-Bridged DyIIICoIII Framework. J. Am. Chem. Soc. 2019, 141, 18211–18220. [Google Scholar] [CrossRef]
- Wang, J.; Zakrzewski, J.J.; Heczko, M.; Zychowicz, M.; Nakagawa, K.; Nakabayashi, K.; Sieklucka, B.; Chorazy, S.; Ohkoshi, S.I. Proton Conductive Luminescent Thermometer Based on Near-Infrared Emissive {YbCo2} Molecular Nanomagnets. J. Am. Chem. Soc. 2020, 142, 3970–3979. [Google Scholar] [CrossRef]
- Karachousos-Spiliotakopoulos, K.; Tangoulis, V.; Panagiotou, N.; Tasiopoulos, A.; Moreno-Pineda, E.; Wernsdorfer, W.; Schulze, M.; Botas, A.M.P.; Carlos, L.D. Luminescence thermometry and field induced slow magnetic relaxation based on a near infrared emissive heterometallic complex. Dalton Trans. 2022, 51, 8208–8216. [Google Scholar] [CrossRef]
- Liberka, M.; Zychowicz, M.; Zychowicz, W.; Chorazy, S. Neutral dicyanidoferrate(II) metalloligands for the rational design of dysprosium(III) single-molecule magnets. Chem. Commun. 2022, 58, 6381–6384. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Bentama, A.; Lloret, F.; Cano, J.; Julve, M. X-ray structure and magnetic properties of heterobimetallic chains based on the use of an octacyanidodicobalt(III) complex as metalloligand. Magnetochemistry 2020, 6, 66. [Google Scholar] [CrossRef]
- Jiménez, J.-R.; Xu, B.; El Said, H.; Li, Y.; Bardeleben, J.; Chamoreau, L.-M.; Lescouëzec, R.; Shova, S.; Visinescu, D.; Alexandru, M.-G.; et al. Field-induced Single Ion Magnet behaviour in discrete and one-dimensional complexes containing the bis(1-methylimidazol-2-yl)ketone]-containing cobalt(II) building units. Dalton Trans. 2021, 50, 16353–16363. [Google Scholar] [CrossRef]
- Bar, A.K.; Pichon, C.; Gogoi, N.; Duhayon, C.; Ramaseshac, S.; Sutter, J.-P. Single-ion magnet behaviour of heptacoordinated Fe(II) complexes: On the importance of supramolecular organization. Chem. Commun. 2015, 51, 3616–3619. [Google Scholar] [CrossRef]
- Puzan, A.; Zychowicz, M.; Wang, J.; Zakrzewski, J.J.; Reczyński, M.; Ohkoshi, S.I.; Chorazy, S. Tunable magnetic anisotropy in luminescent cyanido-bridged {Dy2Pt3} molecules incorporating heteroligand PtIV linkers. Dalton Trans. 2021, 50, 16242–16253. [Google Scholar] [CrossRef]
- Long, J.; Chamoreau, L.-M.; Marvaud, V. Heterotrimetallic 3d-4d-4f decanuclear metal-capped square showing single-molecule magnet behavior. Dalton Trans. 2010, 39, 2188–2190. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Lloret, F.; Julve, M.; Andruh, M. Two-Dimensional Coordination Polymers Constructed by [NiIILnIII] Nodes and [WIV(bpy)(CN)6]2- Spacers: A Network of [NiIIDyIII] Single Molecule Magnets. Inorg. Chem. 2013, 52, 11627–11637. [Google Scholar] [CrossRef] [PubMed]
- Jankowski, R.; Zakrzewski, J.J.; Surma, O.; Ohkoshi, S.I.; Chorazy, S.; Sieklucka, B. Near-infrared emissive Er(III) and Yb(III) molecular nanomagnets in metal–organic chains functionalized by octacyanidometallates(IV). Inorg. Chem. Front. 2019, 6, 2423–2434. [Google Scholar] [CrossRef]
- Charytanowicz, T.; Jankowski, R.; Zychowicz, M.; Chorazy, S.; Sieklucka, B. The rationalized pathway from field-induced slow magnetic relaxation in CoII–WIV chains to single-chain magnetism in isotopological CoII–WV analogues. Inorg. Chem. Front. 2022, 9, 1152–1170. [Google Scholar] [CrossRef]
- Podgajny, R.; Chmel, N.P.; Bałanda, M.; Tracz, P.; Gaweł, B.; Zajac, D.; Sikora, M.; Kapusta, C.; Łasocha, W.; Wasiutynski, T.; et al. Exploring the formation of 3D ferromagnetic cyano-bridged CuII2+x{CuII4[WV(CN)8]4−2x[WIV(CN)8]2x}·yH2O networks. J. Mater. Chem. 2007, 17, 3308–3314. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Wei, J.; Li, Y.-Z.; Guo, J.-S.; Song, Y. Two trinuclear copper(II)-octacyanometalate(IV) bimetallic complexes coordinated with chiral ligands. J. Mol. Struct. 2008, 875, 198–204. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, T.-W.; Xiao, H.-P.; Li, Y.-Z.; Song, Y.; You, X.-Z. Diamond- and Graphite-Like Octacyanometalate-Based Polymers Induced by Metal Ions. Chem. Eur. J. 2009, 15, 7648–7655. [Google Scholar] [CrossRef]
- Qian, J.; Yoshikawa, H.; Zhang, J.; Zhao, H.; Awaga, K.; Zhang, C. Heterobimetallic Tungsten/Molybdenum(IV)−Copper(II) MOFs Constructed by a Unique 2D → 3D Architecture and Exhibiting New Topology and Magnetic Properties. Cryst. Growth Des. 2009, 9, 5351–5355. [Google Scholar] [CrossRef]
- Qian, J.; Zhao, H.; Wei, H.; Li, J.; Zhang, J.; Yoshikawa, H.; Awaga, K.; Zhang, C. Two 3D coordination assemblies with same cluster configuration showing different magnetic behaviors: A ferromagnetic {[W(CN)8Co2(DMF)8][NO3]}n and a paramagnetic {W(CN)8Cu2(py)8}n. CrystEngComm 2011, 13, 517–523. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Lloret, F.; Julve, M. Synthesis, crystal structure and magnetic properties of a cyanide-bridged heterometallic {CoIIMnIII} chain. Dalton Trans. 2017, 46, 39–43. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Marino, N.; Visinescu, D.; De Munno, G.; Andruh, M.; Bentama, A.; Lloret, F.; Julve, M. A novel octacyanido dicobalt(III) building block for the construction of heterometallic compounds. New J. Chem. 2019, 43, 6675–6682. [Google Scholar] [CrossRef]
- Toma, L.; Lescouëzec, R.; Vaissermann, J.; Delgado, F.S.; Ruiz-Pérez, C.; Carrasco, R.; Cajo, J.; Lloret, F.; Julve, M. Nuclearity Controlled Cyanide-Bridged Bimetallic CrIII-MnII Compounds: Synthesis, Crystal Structures, Magnetic Properties and Theoretical Calculations. Chem. Eur. J. 2004, 10, 6130–6145. [Google Scholar] [CrossRef]
- Toma, L.; Lescouëzec, R.; Vaissermann, J.; Herson, P.; Marvaud, V.; Lloret, F.; Julve, M. [CrIII(L)(CN4)]−: A new building block in designing cyanide-bridged 4,2-ribbon-like chains {[CrIII(L)(CN)4]2Mn(H2O)2}· nH2O} [L = 2-aminomethylpyridine (n = 6) and 1,10-phenanthroline (n = 4)]. New J. Chem. 2005, 29, 210–219. [Google Scholar] [CrossRef]
- Lescouëzec, R.; Lloret, F.; Julve, M.; Vaissermann, J.; Verdaguer, M.; Llusar, R.; Uriel, S. [Fe(Phen)(CN)4)]−: A Versatile Building Block for the Design of Heterometallic Systems. Crystal Structures and Magnetic Properties of PPh4[Fe(Phen)(CN)4]·2H2O and [{Fe(Phen)(CN)4}2Mn(H2O)2]·4H2O] [Phen = 1,10-Phenanthroline; M = Mn(II) and Zn(II)]. Inorg. Chem. 2001, 40, 2065–2072. [Google Scholar] [CrossRef]
- Lescouëzec., R.; Vaissermann, J.; Ruiz-Pérez, C.; Lloret, F.; Carrasco, R.; Julve, M.; Verdaguer, M.; Dromzée, Y.; Gatteschi, D.; Wernsdorfer, W. Cyanide-Bridged Iron(III)-Cobalt(II) Double Zigzag Ferromagnetic Chains: Two New Molecular Magnetic Nanowires. Angew. Chem. Int. Ed. Engl. 2003, 42, 1483–1486. [Google Scholar] [CrossRef]
- Toma, L.M.; Delgado, F.S.; Ruiz-Pérez, C.; Carrasco, R.; Cano, J.; Lloret, F.; Julve, M. Synthesis, crystal structures and magnetic properties of single and double cyanide-bridged bimetallic FeIII2CuII zigzag chains. Dalton Trans. 2004, 2836–2846. [Google Scholar] [CrossRef]
- Toma, L.M.; Lescouëzec, R.; Uriel, S.; Llusar, R.; Ruiz-Pérez, C.; Vaissermann, J.; Lloret, F.; Julve, M. 4,2-Ribbon like ferromagnetic cyano-bridged FeIII2NiII chains: A magneto-structural study. Dalton Trans. 2007, 33, 3690–3698. [Google Scholar] [CrossRef]
- Toma, L.M.; Lescouëzec, R.; Pasán, J.; Ruiz-Pérez, C.; Vaissermann, J.; Cano, J.; Carrasco, R.; Wernsdorfer, W.; Lloret, F.; Julve, M. [Fe(bpym)(CN)4]−: A New Building Block for Designing Single-Chain Magnets. J. Am. Chem. Soc. 2006, 128, 4842–4853. [Google Scholar] [CrossRef]
- Wen, H.-R.; Wang, C.-F.; Song, Y.; Li, Y.-Z.; Zuo, J.-L.; You, X.-Z. Syntheses, structures and magnetic properties of heterometallic FeIII2MII (M = Cu, Mn) chains based on tetracyanometallate building units. Inorg. Chim. Acta 2009, 362, 1485–1490. [Google Scholar] [CrossRef]
- Toma, L.M.; Ruiz-Pérez, C.; Lloret, F.; Julve, M. Slow Relaxation of the Magnetization in a 4,4-Wavelike FeIII2CoII Heterobimetallic Chain. Inorg. Chem. 2012, 51, 1216–1218. [Google Scholar] [CrossRef]
- Toma, L.M.; Pasán, J.; Ruiz-Pérez, C.; Lloret, F.; Julve, M. [FeIII(dmphen)(CN)4]−: A new building block for designing single-chain magnets. Dalton Trans. 2012, 41, 13716–13726. [Google Scholar] [CrossRef]
- Kang, L.C.; Chen, X.; Wang, C.F.; Zhou, X.-H.; Zuo, J.-L.; You, X.-Z. Syntheses, structures and magnetic properties of heterometallic complexes based on a new tetracyanometallate precursor. Inorg. Chim. Acta 2009, 362, 5195–5202. [Google Scholar] [CrossRef]
- Llunell, M.; Casanova, D.; Cirera, J.; Bofill, J.M.; Alemany, P.; Alvarez, S.; Pinsky, M.; Avnir, D. Shape: Continuous Shape Measures of Polygonal and Polyhedral Molecular Fragments, 1.1b; University of Barcelona: Barcelona, Spain, 2005. [Google Scholar]
- Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. The Rich Stereochemistry of Eight-Vertex Polyhedra: A Continuous Shape Measures Study. Chem. Eur. J. 2005, 11, 1479–1494. [Google Scholar] [CrossRef] [PubMed]
- Alexandru, M.-G.; Visinescu, D.; Marino, N.; De Munno, G.; Vallejo, J.; Lloret, F.; Julve, M. Cyanido-Bearing Cobalt (II/III) Metalloligands–Synthesis, Crystal Structure, and Magnetic Properties. Eur. J. Inorg. Chem. 2014, 27, 4564–4572. [Google Scholar] [CrossRef]
- Alexandru, M.-G.; Visinescu, D.; Shova, S.; Stiriba, S.-E.; Cano, J.; Lloret, F.; Julve, M. Slow relaxation of the magnetization in a [CoIIIMnIII] heterometallic brick-wall network. Polyhedron 2021, 200, 115118. [Google Scholar] [CrossRef]
- Carlin, R.L. Magnetochemistry; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Cano, J. VPMAG; University of Valencia: Valencia, Spain, 2003. [Google Scholar]
- De Munno, G.; Julve, M.; Lloret, F.; Faus, J.; Caneschi, A. 2,2′-Bipyrimidine (bipym)-bridged Dinuclear Complexes. Part 4.1 Synthesis, Crystal Structure and Magnetic Properties of [Co2(H2O)8(bipym)](NO3)4, [Co2(H2O)8(bipym)][SO4]2.2H2O and [Co2(bipym)3(NCS)4]. J. Chem. Soc. Dalton Trans. 1994, 8, 1175–1183. [Google Scholar] [CrossRef]
- Sakiyama, H.; Ito, R.; Kumagai, H.; Inoue, K.; Sakamoto, M.; Nishida, Y.; Yamasaki, M. Dinuclear Cobalt(II) Complexes of an Acyclic Phenol-Based Dinucleating Ligand with four Methoxyethyl Chelating Arms-First Magnetic Analyses in an Axially Distorted Octahedral Field. Eur. J. Inorg. Chem. 2001, 8, 2027–2032. [Google Scholar] [CrossRef]
- Herrera, J.M.; Bleuzen, A.; Dromzée, Y.; Julve, M.; Lloret, F.; Verdaguer, M. Crystal Structures and Magnetic Properties of Two Octacyaniotungstate(IV) and Cobalt(II) Three-Dimensional Bimetallic Frameworks. Inorg. Chem. 2003, 42, 7052–7059. [Google Scholar] [CrossRef]
- Mishra, V.; Lloret, F.; Mukherjee, R. Coordination versatility of 1,3-bis [3-(2-pyridyl)pyrazol-1-yl]propane: Co(II) and Ni(II) complexes. Inorg. Chim. Acta 2006, 359, 4053–4062. [Google Scholar] [CrossRef]
- Lloret, F.; Julve, M.; Cano, J.; Ruiz-García, R.; Pardo, E. Magnetic properties of six-coordinated high-spin cobalto(II) complexes. Theoretical background and its applications. Inorg. Chim. Acta 2008, 361, 3432–3445. [Google Scholar] [CrossRef]
- Fabelo, O.; Pasán, J.; Lloret, F.; Julve, M.; Ruiz-Pérez, C. 1,24,5-Benzenetetracarboxylate- and 2,2′-Bipyrimidine-Containing Cobalt(II) Coordination Polymers. Preparation, Crystal Structure, and Magnetic Properties. Inorg. Chem. 2008, 47, 3568–3576. [Google Scholar] [CrossRef]
- Fabelo, O.; Pasán, J.; Cañadillas-Delgado, L.; Delgado, F.S.; Lloret, F.; Julve, M.; Ruiz-Pérez, C. Cobalt(II) Sheet-Like Systems Based on Diacetic Ligands: From Subtle Structural Variances to Different Magnetic Behaviors. Inorg. Chem. 2009, 48, 6086–6095. [Google Scholar] [CrossRef]
- Świtlicka-Olszewska, A.; Machura, B.; Kruszynski, R.; Cano, J.; Toma, L.M.; Lloret, F.; Julve, M. Single-ion magnet behavior in mononuclear and two-dimensional dicyanamide-containing coblat(II) complexes. Dalton Trans. 2016, 45, 10181–10193. [Google Scholar] [CrossRef]
- Świtlicka, A.; Klemens, T.; Machura, B.; Vallejo, J.; Cano, J.; Lloret, F.; Julve, M. Field-induced slow magnetic relaxation in pseudooctahedral cobalto(II) complexes with positive axial and large rhombic anisotropy. Dalton Trans. 2019, 48, 1404–1417. [Google Scholar] [CrossRef]
- Vallejo, J.; Castro, I.; Ruiz-García, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef]
- Peng, Y.; Mereacre, V.; Anson, C.E.; Zhang, Y.; Bodenstein, T.; Fink, K.; Powell, A.K. Field-Induced Co(II) Single-Ion Magnets with mer-Directing Ligands but Ambiguous Coordination Geometry. Inorg. Chem. 2017, 56, 6056–6066. [Google Scholar] [CrossRef]
- Villa-Pérez, C.; Oyarzabal, I.; Echeverria, G.A.; Valencia-Uribe, G.C.; Seco, J.M.; Soria, D.B. Single-Ion Magnets Based on Mononuclear Cobalt(II) Complexes with Sulfadiazines. Eur. J. Inorg. Chem. 2016, 29, 4835–4841. [Google Scholar] [CrossRef]
- Rajnák, C.; Titiš, J.; Moncol, J.; Renz, F.; Boca, R. Field-Supported Slow Magnetic Relaxation in Hexacoordinate CoII Complexes with Easy Plane Anisotropy. Eur. J. Inorg. Chem. 2017, 11, 1520–1525. [Google Scholar] [CrossRef]
- Valigura, D.; Rajnák, C.; Moncol, J.; Titiš, J.; Boca, R. A mononuclear Co(II) complex formed from pyridinedimethanol with manifold slow relaxation channels. Dalton Trans. 2017, 46, 10950–10956. [Google Scholar] [CrossRef]
- Sertphon, D.; Murray, K.S.; Phonsn, W.; Jover, J.; Ruiz, E.; Telfer, S.G.; Alkas, A.; Harding, P.; Harding, D.J. Slow relaxation of magnetization in a bis-mer-tridentate octahedral Co (II) complex. Dalton Trans. 2018, 47, 859–867. [Google Scholar] [CrossRef]
- Váhovská, L.; Vitushkina, S.; Potocnák, I.; Travnicek, Z.; Herchel, R. Effect of linear and non-linear pseudohalides on the structural and magnetic proerties of Co(II) hexacoordinate single-molecule magnet. Dalton Trans. 2018, 47, 1498–1512. [Google Scholar] [CrossRef]
- Vallejo, J.; Viciano-Chumillas, M.; Lloret, F.; Julve, M.; Castro, I.; Krzystek, J.; Ozerov, M.; Armentano, D.; De Munno, G.; Cano, J. Coligand Effects on the Field-Induced Double Slow Magnetic Relaxation in Six-Coordinate Cobalt(II) Single-Ion Magnets (SIMs) with Positive Magnetic Anisotropy. Inorg. Chem. 2019, 58, 15726–15740. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Tian, D.; Ferrando-Soria, J.; Cano, J.; Yin, L.; Ouyang, Z.; Wang, Z.; Luo, S.; Liu, X.; Pardo, E. Modulation of the magnetic anisotropy of octahedral cobalto(II) single-ion magnets by fine tuning the axial coordination microenvironment. Inorg. Chem. Front. 2019, 6, 848–856. [Google Scholar] [CrossRef]
- Chahine, A.Y.; Phonsn, W.; Murray, K.S.; Turner, D.R.; Batten, S.R. Coordination polymers of a bis-isophthalate bridging ligand with single molecule magnet behaviour of the CoII analogue. Dalton Trans. 2020, 49, 5241–5249. [Google Scholar] [CrossRef] [PubMed]
- Świtlicka, A.; Machura, B.; Kruszynski, R.; Moliner, N.; Carbonell, J.M.; Cano, J.; Lloret, F.; Julve, M. Magneto-structural diversity of Co(II) compounds with 1-benzylimidazole induced by linear pseudohalide colignads. Inorg. Chem. Front. 2020, 7, 4535–4552. [Google Scholar] [CrossRef]
- Shao, D.; Xu, F.-X.; Yin, L.; Li, H.-Q.; Sun, Y.-C.; Ouyang, Z.-W.; Wang, Z.-X.; Zhang, Y.-Q.; Wang, X.-Y. Fine-Tuning of Structural Distortion and Magnetic Anisotropy by Organosulfonates in Octahedral Cobalt(II) Complexes. Chin. J. Chem. 2022, 40, 2193–2202. [Google Scholar] [CrossRef]
- Sahu, P.K.; Kharel, R.; Shome, S.; Goswami, S.; Konar, S. Understanding the unceasing evolution of Co(II) based single-ion magnets. Coord. Chem. Rev. 2023, 475, 214871. [Google Scholar] [CrossRef]
- Rabelo, R.; Toma, L.; Moliner, N.; Julve, M.; Lloret, F.; Pasán, J.; Ruiz-Pérez, C.; Ruiz-García, R.; Cano, J. Electroswitching of the Single-Molecule Magnet Behaviour in an Octahedral Spin Crossover Cobalt(II) Complex with a Redox-Active Pyridinediimine Ligand. Chem. Commun. 2020, 56, 12242–12245. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics. I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wires Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995, 242, 652–660. [Google Scholar] [CrossRef]
- Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc. 1997, 97, 119–124. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Izsák, R.; Neese, F.J. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef]
- Izsák, R.; Hansen, A.; Neese, F. The resolution of identity and chain of spheres approximations for the LPNO-CCSD singles Fock term. Mol. Phys. 2012, 110, 2413–2417. [Google Scholar] [CrossRef]
- CrysAlisPro Software System v42; Rigaku Corporation: Oxford, UK, 2015.
- Sheldrick, G.M. SHELXT—Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. Sect. A Found. Crystallogr. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. A complete structure solution, refinement and general all round good thing Olex2. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Putz, H.; Brandenburg, K. Diamond—Crystal and Molecular Structure Visualization, Crystal Impact. Bonn, Germany. Available online: https://www.crystalimpact.com/diamond (accessed on 30 October 2014).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).