Evidence of Hysteresis Free Ferromagnetic Nature and Significant Magnetocaloric Parameters in FeNi Binary Alloy
Abstract
1. Introduction
2. Materials and Method
3. Results and Discussion
3.1. Structural Study
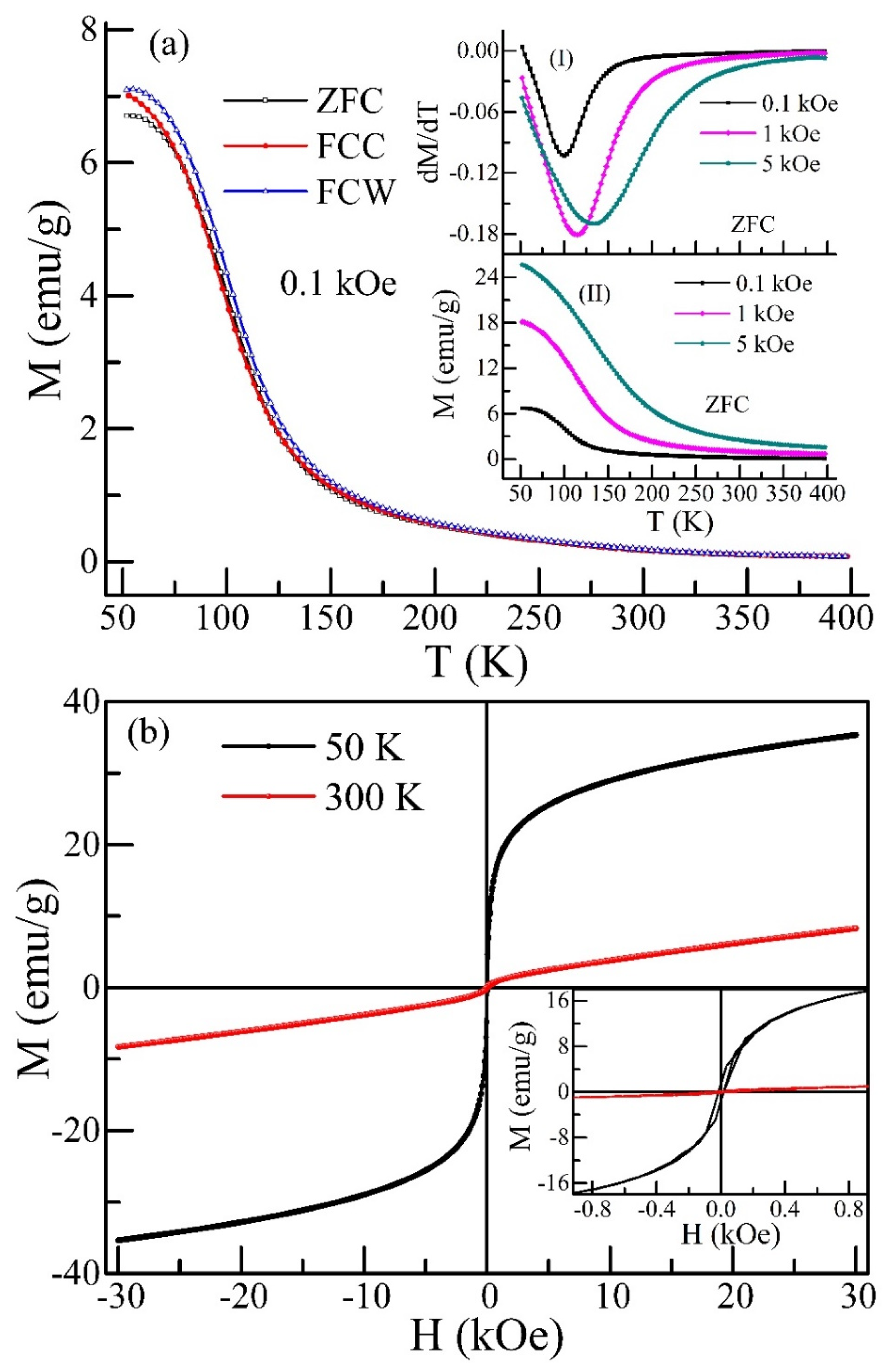
3.2. Magnetization Study
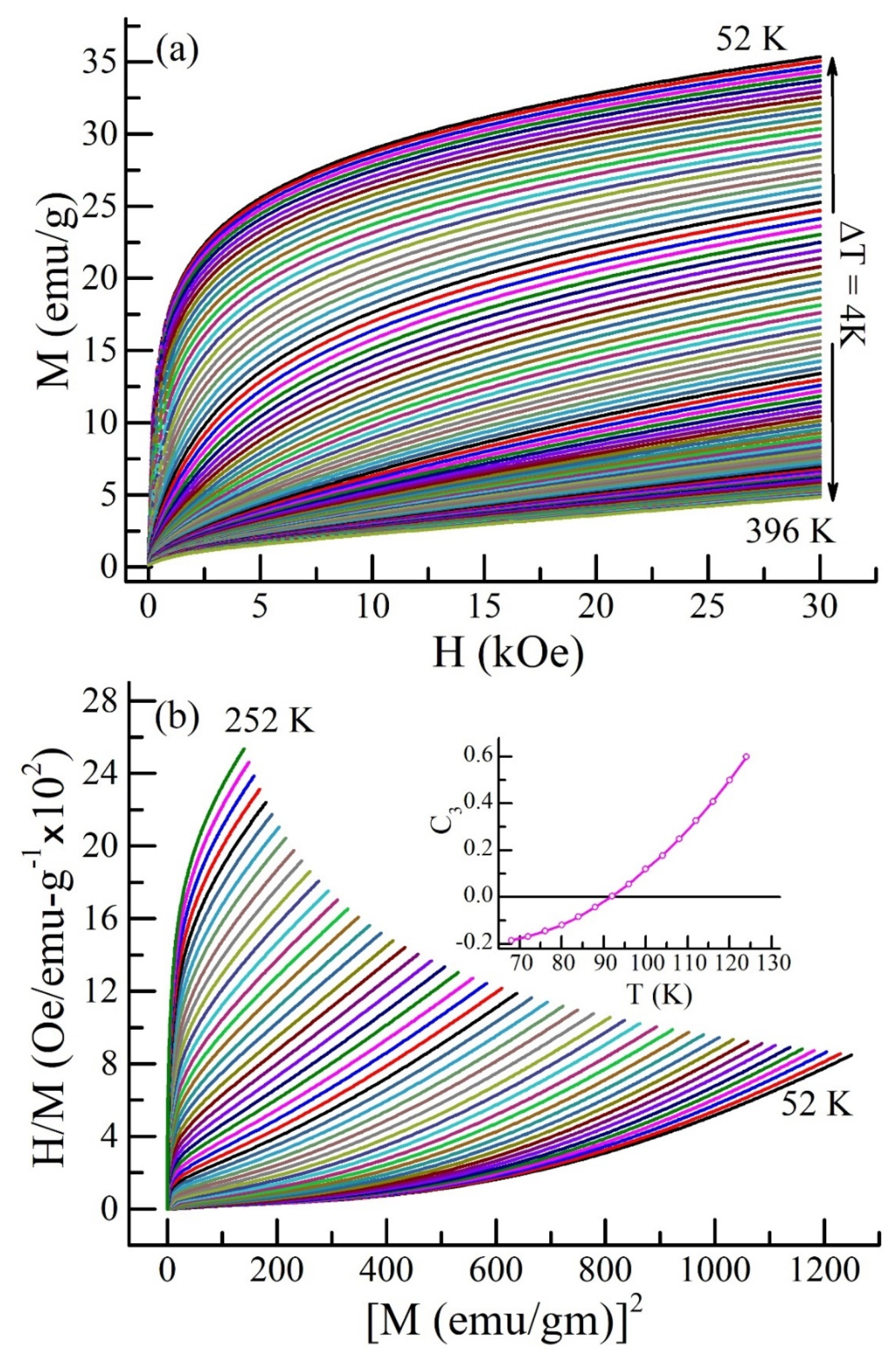
3.3. Arrott Plot Study
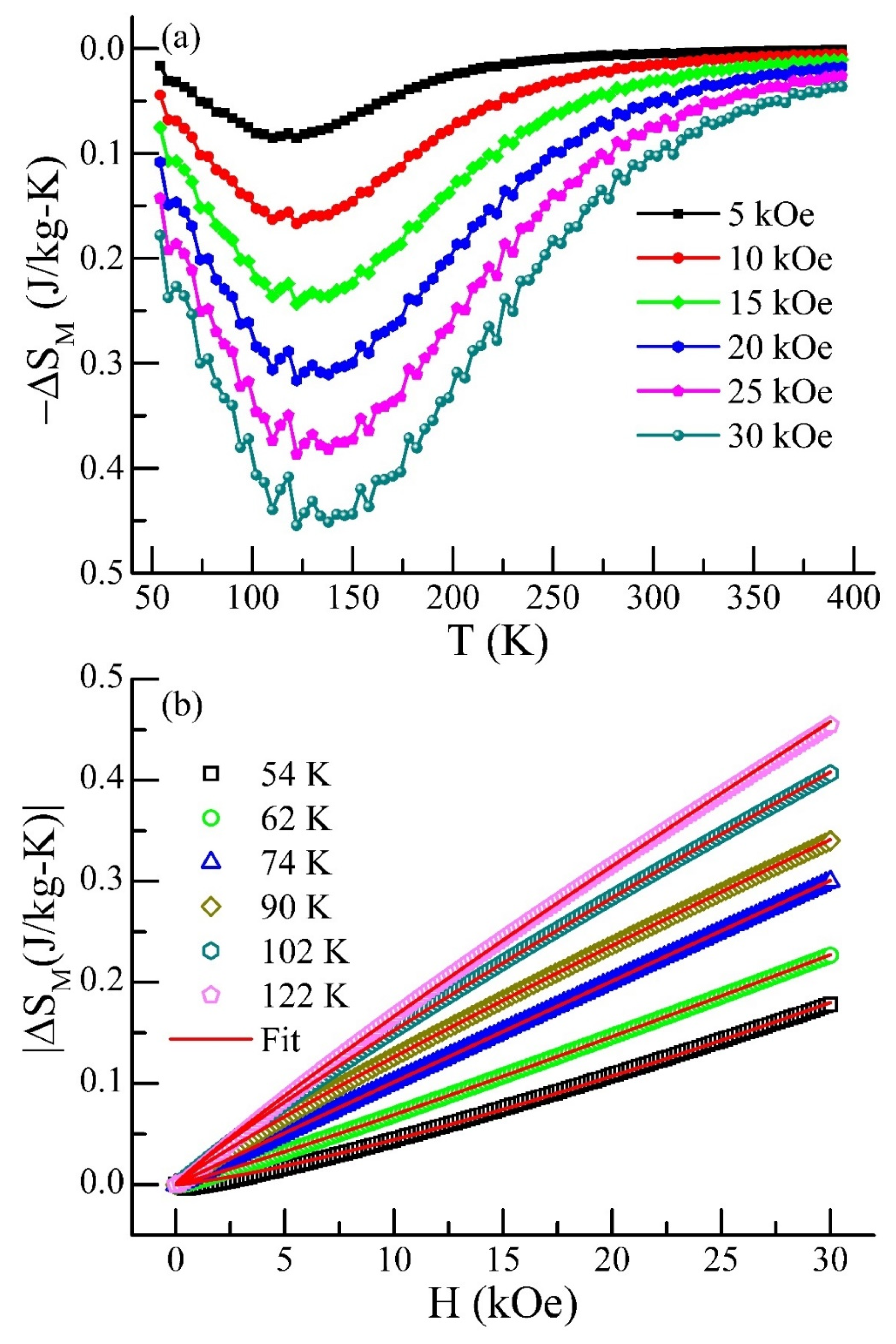
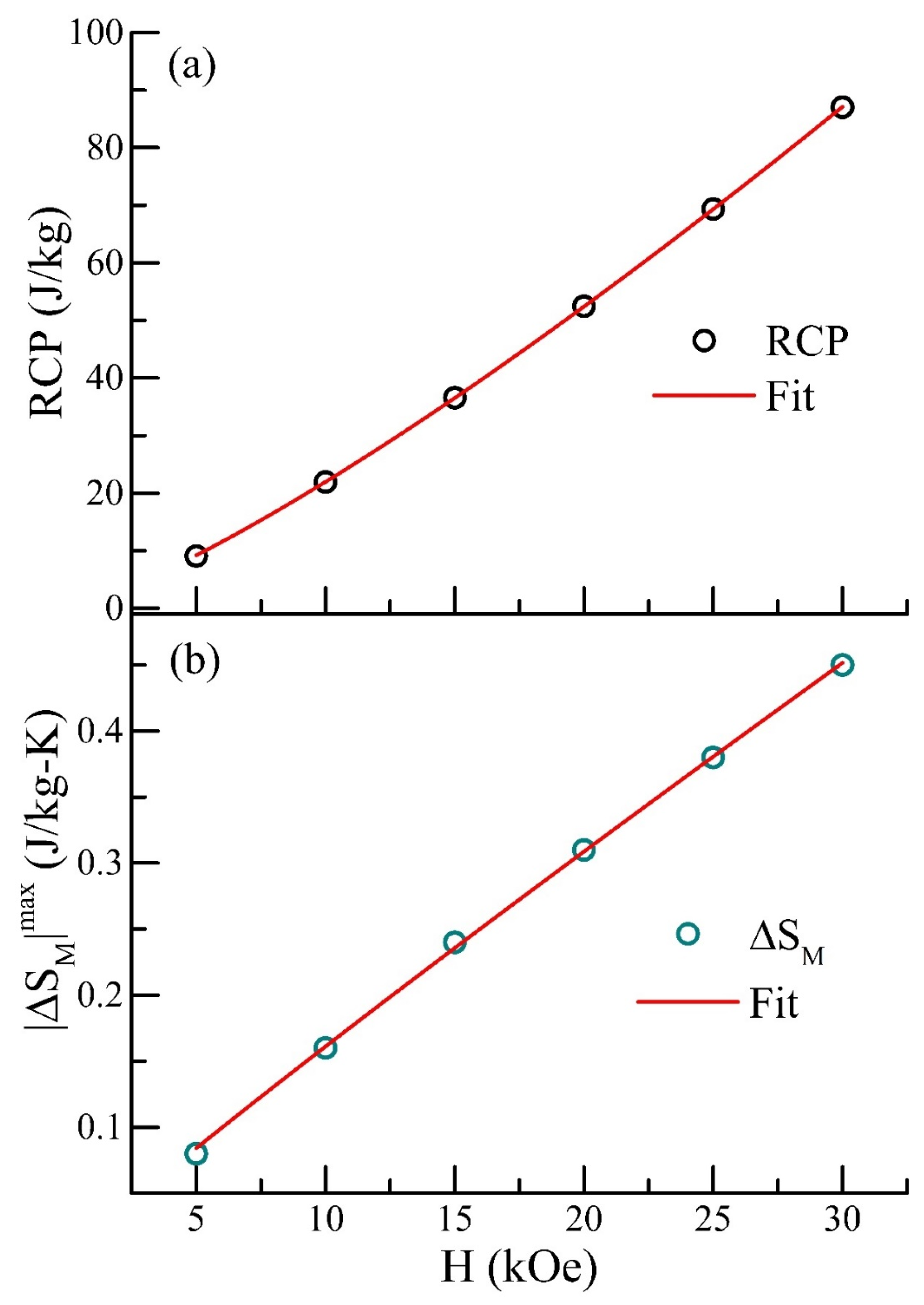
3.4. Magnetocaloric Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; CRS Press: Boca Raton, FL, USA; Taylor and Francis Group: Didcot, UK, 2003; ISBN 978-1-4200-3337-3. [Google Scholar]
- Pecharsky, V.K.; Gschneidner, K.A. Advanced magnetocaloric materials: What does the future hold? Int. J. Refrig. 2006, 29, 1239–1249. [Google Scholar] [CrossRef]
- Bruck, E. Developments in magnetocaloric refrigeration. J. Phys. D Appl. Phys. 2005, 38, R381. [Google Scholar] [CrossRef]
- Kitanovski, A.; Tusek, J.; Tomc, U.; Plaznik, U.; Ozbolt, M.; Poredos, A. Magnetocaloric Energy Conversion: From Theory to Applications; Springer International Publishing: Basel, Switzerland, 2015; ISBN 978-3-319-08741-2. [Google Scholar]
- Olivera, N.A.; Ranke, P.J. Theoretical aspects of the magnetocaloric effect. Phys. Rep. 2010, 489, 89–159. [Google Scholar] [CrossRef]
- Ucar, H.; Ipus, J.J.; Laughlin, D.E.; McHenry, M.E. Tuning the Curie temperature in γ -FeNi nanoparticles for magnetocaloric applications by controlling the oxidation kinetics. J. Appl. Phys. 2013, 113, 17A918. [Google Scholar] [CrossRef]
- Oliveira, N.A. Magnetocaloric effect in transition metals-based compounds: A theoretical approach: A theoretical approach. Eur. Phys. J. B Condens. Matter Complex Syst. 2004, 40, 259–264. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Opus, J.J.; Law, J.Y.; Moreno, L.M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Romero, J.; Ferreiro, R.; De Miguel, A.; Romero, M. Magnetocaloric effect: A review of the thermodynamic cycles in magnetic refrigeration. Renew. Sustain. Energy Rev. 2013, 17, 74–82. [Google Scholar] [CrossRef]
- Phan, M.-H.; Yu, S.-C. Review of the magnetocaloric effect in manganite materials. J. Magn. Magn. Mater. 2007, 308, 325–340. [Google Scholar] [CrossRef]
- Chaudhary, V.; Chen, X.; Ramanujan, R.V. Iron and manganese based magnetocaloric materials for near room temperature thermal management. Prog. Mater. Sci. 2019, 100, 64–98. [Google Scholar] [CrossRef]
- Xu, P.; Hub, L.; Zhang, Z.; Wang, H.; Li, L. Electronic structure, magnetic properties and magnetocaloric performance in rare earths (RE) based RE2BaZnO5 (RE = Gd, Dy, Ho, and Er) compounds. Acta Mater. 2022, 236, 118114. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Hu, L.; Wang, X.; Li, L.; Yan, M. Excellent magnetocaloric performance in the carbide compounds RE2Cr2C3 (RE = Er, Ho, and Dy) and their composites. Mater. Today Phys. 2022, 27, 100786. [Google Scholar] [CrossRef]
- Lyubina, J. Magnetocaloric materials for energy efficient cooling. J. Phys. D Appl. Phys. 2017, 50, 053002. [Google Scholar] [CrossRef]
- Sharma, M.K.; Mukherjee, K. Evidence of large magnetic cooling power and double glass transition in Tb5Pd2. J. Magn. Magn. Mater. 2018, 466, 317–322. [Google Scholar] [CrossRef]
- Sharma, M.K.; Yadav, K.; Mukherjee, K. Complex magnetic behaviour and evidence of superspin glass state in the binary intermetallic compound Er5Pd2. J. Phys. Condens. Matter 2018, 30, 215803. [Google Scholar] [CrossRef] [PubMed]
- Biswas, A.; Chandra, S.; Samanta, T.; Phan, M.H.; Das, I.; Srikanth, H. The universal behavior of inverse magnetocaloric effect in antiferromagnetic materials. J. Appl. Phys. 2013, 113, 17A902. [Google Scholar] [CrossRef]
- Sharma, M.K.; Mukherjee, K. Magnetic and universal magnetocaloric behavior of rare-earth substituted DyFe0.5Cr0.5O3. J. Magn. Magn. Mater. 2017, 444, 178–183. [Google Scholar] [CrossRef]
- Sharma, M.K.; Kaur, G.; Mukherjee, K. Nature of glassy magnetic state in magnetocaloric materials Dy5Pd2-xNix (x = 0 and 1) and universal scaling analysis of R5Pd2 (R = Tb, Dy and Er). J. Alloys Compd. 2019, 782, 10–16. [Google Scholar] [CrossRef]
- Xuexi Zhang, X.; Zhang, H.; Qian, M.; Geng, L. Enhanced magnetocaloric efect in Ni-Mn-Sn-Co alloys with two successive magnetostructural transformations. Sci. Rep. 2018, 8, 8235. [Google Scholar] [CrossRef]
- Sarkar, S.K.; Babu, P.D.; Biswas, A.; Siruguri, V.; Krishnan, M. Giant magnetocaloric effect from reverse martensitic transformation in Ni-Mn-Ga-Cu ferromagnetic shape memory alloys. J. Alloys Compd. 2016, 670, 281–288. [Google Scholar] [CrossRef]
- Umetsu, R.Y.; Kusakari, Y.; Kanomata, T.; Suga, K.; Sawai, Y.; Kindo, K.; Oikawa, K.; Kainuma, R.; Ishida, K. Metamagnetic behaviour under high magnetic fields in Ni50Mn50−xInx (x = 14.0 and 15.6) shape memory alloys. J. Phys. D Appl. Phys. 2009, 42, 075003. [Google Scholar] [CrossRef]
- Chaudhary, V.; Ramanujan, R.V. Magnetic and structural properties of high relative cooling power (Fe70Ni30)92Mn8 magnetocaloric nanoparticles. J. Phys. D Appl. Phys. 2015, 48, 305003. [Google Scholar] [CrossRef]
- Ucar, H.; Craven, M.; Laughlin, D.E.; McHenry, M.E. Effect of Mo addition on structure and magnetocaloric effect in γ-FeNi nanocrystals. J. Electron. Mater. 2014, 43, 137–141. [Google Scholar] [CrossRef]
- Chaudhary, V.; Ramanujan, R.V. Magnetocaloric Properties of Fe-Ni-Cr Nanoparticles for Active Cooling. Sci. Rep. 2016, 6, 35156. [Google Scholar] [CrossRef] [PubMed]
- Sarlar, K.; Tekgul, A.; Küçük, N.; Etemoğlu, A.B. Structural and magnetocaloric properties of FeNi high entropy alloys. Phys. Scr. 2021, 96, 125847. [Google Scholar] [CrossRef]
- Kurlyandskaya, G.V.; Bhagat, S.M.; Bagazeev, A.V.; Medvedev, A.I.; Ballesteros, A.; Beketov, I.V.; Safronov, A.P. Structure, magnetic and microwave properties of FeNi invar nanoparticles obtained by electrical explosion of wire in different preparation conditions. J. Phys. Chem. Solids 2016, 98, 255–262. [Google Scholar] [CrossRef]
- Chaudhary, V.; Ramanujan, R.V. High Relative Cooling Power in a Multiphase Magnetocaloric FeNiB Alloy. IEEE Magn. Lett. 2015, 6, 6700104. [Google Scholar] [CrossRef]
- Paduani, C.; Krause, J.C. Local magnetic properties of γ-Fe-Mn alloys. Phys. Rev. B 1998, 58, 175–179. [Google Scholar] [CrossRef]
- Kumari, K.; Kumar, A.; Shin, M.; Kumar, S.; Huh, S.H.; Koo, B.H. Investigating the magnetocrystalline anisotropy and the exchange bias through interface efects of nanocrystalline FeCo. J. Korean Phys. Soc. 2021, 79, 1180–1189. [Google Scholar] [CrossRef]
- Kumari, K.; Kumar, A.; Koo, B.H. Investigating the origin of exchange bias efect in ferromagnetic FeNi nanoparticles prepared via controlled synthesis. Appl. Nanosci. 2021, 1–9. [Google Scholar] [CrossRef]
- Ghisari, K.; Oh, J.T.; Javapour, S. The effect of heat treatment on the structure and magnetic properties of mechanically alloyed Fe—45%Ni nanostructured powders. J. Alloys Compd. 2011, 509, 1020–1024. [Google Scholar] [CrossRef]
- Sharma, M.K.; Kumar, A.; Kumari, K.; Park, S.-J.; Yadav, N.; Huh, S.-H.; Koo, B.-H. Structural, Magnetic, and Magnetocaloric Studies of Ball-Milled Fe100−xTx (T = Ni and Mn) Alloy. Appl. Sci. 2022, 12, 9098. [Google Scholar] [CrossRef]
- Vas’kovskiy, V.O.; Lepalovskij, V.N.; Gor’kovenko, A.N.; Kulesh, N.A.; Savin, P.A.; Svalov, A.V.; Stepanova, E.A.; Shchegoleva, N.N.; Yuvchenko, A.A. Fe20Ni80/Fe50Mn50 Film Magnetoresistive Medium. Tech. Phys. 2015, 60, 116–122. [Google Scholar] [CrossRef]
- Gor’kovenko, A.N.; Lepalovskij, V.N.; Savin, P.A.; Vas’kovskiy, V.O. Effect of Technological Conditions on the Magnetic and Magnetoresistive Properties of Fe20Ni80/Fe50Mn50 Films. Bull. Russ. Acad. Sci. Phys. 2014, 78, 925–926. [Google Scholar] [CrossRef]
- Swartzendruber, L.J.; Itkin, V.P.; Alcock, C.B. The Fe-Ni (Iron-Nickel) system. J. Phase Equilibria Diffus. 1991, 12, 288–312. [Google Scholar] [CrossRef]
- Miettinen, J.; Lilova, K.; Vassilev, G. Thermodynamic Description of Ternary Fe-B-X Systems. Part 3: Fe-B-Mn. Arch. Metall. Mater. 2014, 59, 1481–1485. [Google Scholar] [CrossRef]
- Miettinen, J.; Lilova, K.; Vassilev, G. Thermodynamic description of ternary Fe-B-X systems. Part 2: Fe-B-Ni. Arch. Metall. Mater. 2014, 59, 609–614. [Google Scholar] [CrossRef]
- Witusiewicz, V.T.; Sommer, F.; Mittemeijer, E.J. Reevaluation of the Fe-Mn Phase Diagram. J. Phase Equilibria Diffus. 2004, 25, 346–354. [Google Scholar] [CrossRef]
- Sun, X.; Zhu, X.; Ruan, Y.R.; Ding, Z.L.; Song, W.H.; Zhao, B.C.; Ma, Y.Q. NiFe2 and its nitride g-NiFe2N derived from NiFe2O4: Magnetostriction, thermal expansion, resistivity and corrosion resistance. Mater. Res. Bull. 2017, 89, 245–252. [Google Scholar] [CrossRef]
- Valenzuela, J.L.; Valderruten, J.F.; Alcázar, G.P.; Colorado, H.D.; Romero, J.J.; González, J.M.; Greneche, J.M.; Marco, J.F. Low temperature study of mechanically alloyed Fe67.5Ni32.5 Invar sample. J. Magn. Magn. Mater. 2015, 385, 83–87. [Google Scholar] [CrossRef]
- Abdu, Y.A.; Ericsson, T.; Annersten, H. Coexisting antiferromagnetism and ferromagnetism in mechanically alloyed Fe-rich Fe–Ni alloys: Implications regarding the Fe–Ni phase diagram below 400 °C. J. Magn. Magn. Mater. 2004, 280, 395–403. [Google Scholar] [CrossRef]
- Rancourt, D.G.; Hargraves, P.; Lamarch, G. Microstructure and Low Temperature Magnetism of Fe-Ni Invar Alloys. J. Magn. Magn. Mater. 1990, 87, 71–82. [Google Scholar] [CrossRef]
- Rancourt, D.G.; Scorzelli, R.B. Low spin γ-Fe-Ni(γLS) proposed as a new minerala in Fe-Ni bearing meteorites: Epitaxial intergrowth of γLS and tetrataenite as a possible equilibrium state at 20–40 at% Ni. J. Magn. Magn. Matter. 1995, 150, 30–36. [Google Scholar] [CrossRef]
- Kumar, A.; Kumari, K.; Sharma, M.K.; Vij, A.; Kumar, S.; Huh, S.H.; Koo, B.H. Chemically inducing room temperature spin-crossover in double layered magnetic refrigerants Pr1.4+xSr1.6-xMn2O7 (0.0 ≤ x ≤ 0.5). J. Mater. Sci. Technol. 2022, 124, 232–242. [Google Scholar] [CrossRef]
- Rodriguez-Carvajal, J. FULLPROF: A Program for Rietveld Refinement and Pattern Matching Analysis. In Abstracts of the Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr; IUCr: Toulouse, France, 1990; p. 127. [Google Scholar]
- Rodriguez-Carvajal, J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Phys. B 1993, 192, 55–69; Recent Developments of the Program FULLPROF, in Commission on Powder Diffraction (IUCr). Newsletter 2001, 26, 12–19. [Google Scholar] [CrossRef]
- Rodríguez, V.P.; Rojas-Ayala, C.; Medina, J.M.; Cabrera, P.P.; Quispe-Marcatoma, J.; Landauro, C.V.; Rojas Tapia, J.; Baggio-Saitovitch, E.M.; Passamani, E.C. Fe50Ni50 synthesized by high energy ball milling: A systematic study using X-ray diffraction, EXAFS and Mössbauer methods. Mater. Charact. 2019, 149, 249–254. [Google Scholar] [CrossRef]
- Reuter, K.B.; Williams, D.B.; Goldstein, J.I. Determination of the Fe–Ni phase diagram below 400 °C. Metall. Mater. Trans. A 1989, 20, 719–725. [Google Scholar] [CrossRef]
- Byshkin, M.; Hou, M. Phase transformations and segregation in Fe–Ni alloys and nanoalloys. J. Mater. Sci. 2012, 47, 5784–5793. [Google Scholar] [CrossRef]
- Dung Nguyen-Trong, D.; Pham-Huu, K.; Nguyen-Tri, P. Simulation on the Factors Affecting the Crystallization Process of FeNi Alloy by Molecular Dynamics. ACS Omega 2019, 4, 14605–14612. [Google Scholar] [CrossRef]
- Nguyen, T.D. Influence of impurity concentration, atomic number, temperature and tempering time on microstructure and phase transformation of Ni1−xFex (x = 0.1, 0.3, 0.5) nanoparticles. Mod. Phys. Lett. B 2018, 32, 1850204. [Google Scholar]
- Huck, B.; Hesse, J. Search for Reentrant Spin Glass Phenomenon in the “Classic” FeNi-Invar. J. Magn. Magn. Mater. 1987, 70, 425–426. [Google Scholar] [CrossRef]
- Rancourt, D.G.; Hargraves, P.; Lamarch, G. Reentrant Magnetism, Antiferromagnetism, and Domain Wall Pinning in Nominally Ferromagnetic Fe-Ni Invar. J. Magn. Magn. Mater. 1989, 78, 129–152. [Google Scholar] [CrossRef]
- Banerjee, B.K. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Liu, X.B.; Altounian, Z. Magnetocaloric effect in (Er1-xGdx)Co2 pseudobinary compounds. J. Magn. Magn. Mater. 2005, 292, 83–88. [Google Scholar] [CrossRef]
- Olivier Toulemonde, O.; Roussel, P.; Isnard, O.; Andre, G.; Mentre, O. Spin-Flop Transition and Magnetocaloric Effect through Disconnected Magnetic Blocks in CoIII/CoIV Oxybromides. Chem. Mater. 2010, 22, 3807–3816. [Google Scholar] [CrossRef]
- M’nassri, R. Magnetocaloric effect and its implementation in critical behaviour study of La0.67Ca0.33Mn0.9Fe0.1O3. Bull. Mater. Sci. 2016, 39, 551–557. [Google Scholar] [CrossRef]
- Franco, V.; Blazquez, J.S.; Conde, A. Field dependence of the magnetocaloric effect in materials with a second order phase transition: A master curve for the magnetic entropy change. Appl. Phys. Lett. 2006, 89, 222512. [Google Scholar] [CrossRef]
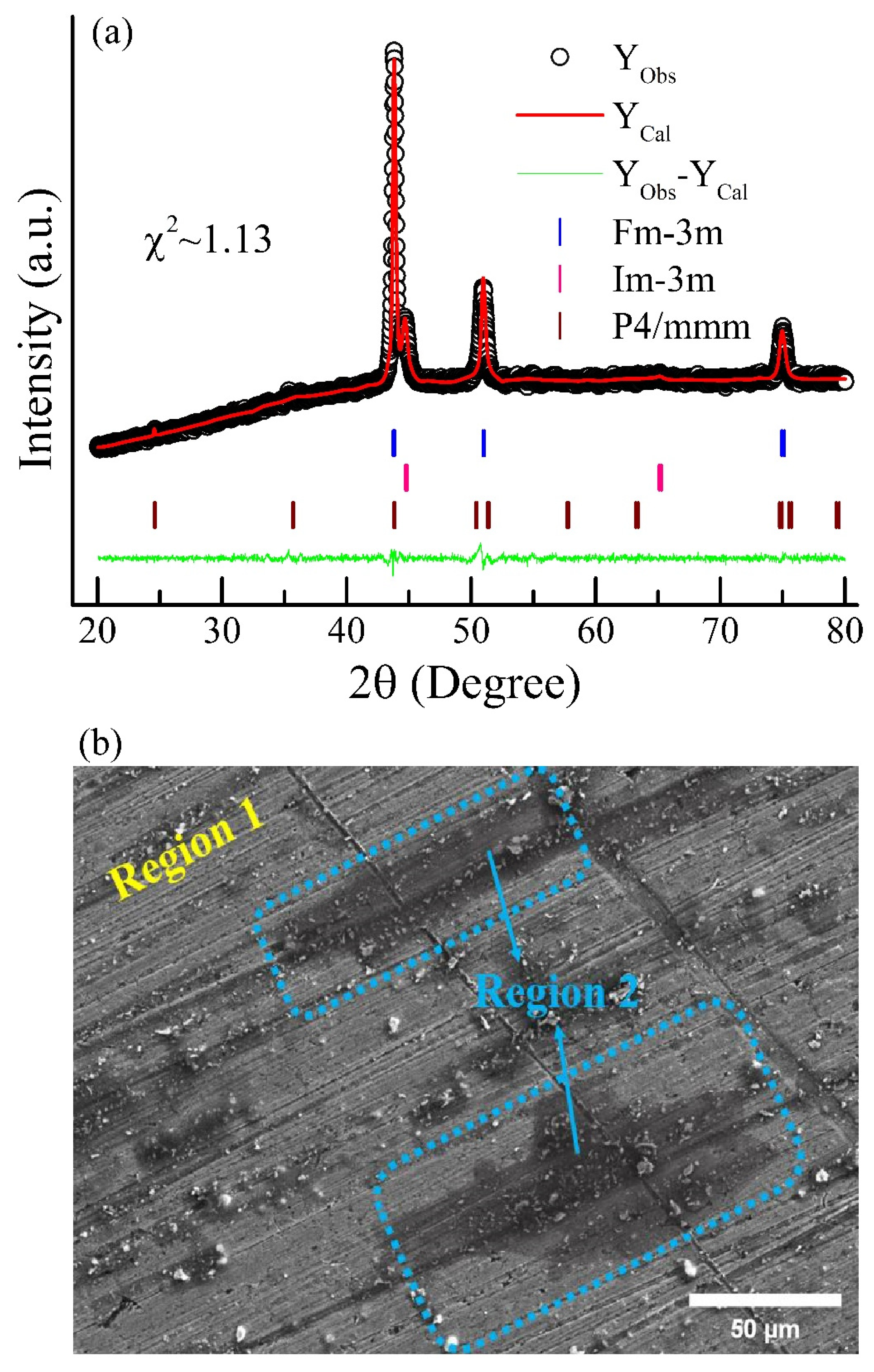
| Refined Parameters | Cubic Fm-3m (Fe65Ni35) | Cubic Im-3m (Fe70Ni30) | Tetragonal I4/mmm (FeNi) |
|---|---|---|---|
| a (Å) | 3.5818(4) | 2.8630(5) | 2.5161(3) |
| b (Å) | 2.5161(3) | ||
| c (Å) | 3.6212(4) | ||
| Phase fraction (%) | 61.96(0.93) | 36.49(0.59) | 1.55(0.25) |
| Goodness-of-fit | 1.13 | ||
| Bragg R-factor | 2.31 | 2.1 | 10.51 |
| RF-factor | 1.10 | 1.2 | 12.13 |
| Element | Line Type | K Ratio | Wt% | Wt% Sigma |
|---|---|---|---|---|
| Region 1 | ||||
| Fe | K series | 0.02858 | 69.15 | 0.57 |
| Ni | K series | 0.01178 | 30.85 | 0.57 |
| Region 2 | ||||
| Fe | K series | 0.02700 | 74.73 | 0.51 |
| Ni | K series | 0.00844 | 25.27 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, M.K.; Kumar, A.; Kumari, K.; Park, S.-J.; Yadav, N.; Huh, S.-H.; Koo, B.-H. Evidence of Hysteresis Free Ferromagnetic Nature and Significant Magnetocaloric Parameters in FeNi Binary Alloy. Magnetochemistry 2023, 9, 8. https://doi.org/10.3390/magnetochemistry9010008
Sharma MK, Kumar A, Kumari K, Park S-J, Yadav N, Huh S-H, Koo B-H. Evidence of Hysteresis Free Ferromagnetic Nature and Significant Magnetocaloric Parameters in FeNi Binary Alloy. Magnetochemistry. 2023; 9(1):8. https://doi.org/10.3390/magnetochemistry9010008
Chicago/Turabian StyleSharma, Mohit K., Akshay Kumar, Kavita Kumari, Su-Jeong Park, Naveen Yadav, Seok-Hwan Huh, and Bon-Heun Koo. 2023. "Evidence of Hysteresis Free Ferromagnetic Nature and Significant Magnetocaloric Parameters in FeNi Binary Alloy" Magnetochemistry 9, no. 1: 8. https://doi.org/10.3390/magnetochemistry9010008
APA StyleSharma, M. K., Kumar, A., Kumari, K., Park, S.-J., Yadav, N., Huh, S.-H., & Koo, B.-H. (2023). Evidence of Hysteresis Free Ferromagnetic Nature and Significant Magnetocaloric Parameters in FeNi Binary Alloy. Magnetochemistry, 9(1), 8. https://doi.org/10.3390/magnetochemistry9010008









