Simulation and Theory of Classical Spin Hopping on a Lattice
Abstract
:1. Introduction
2. Theory
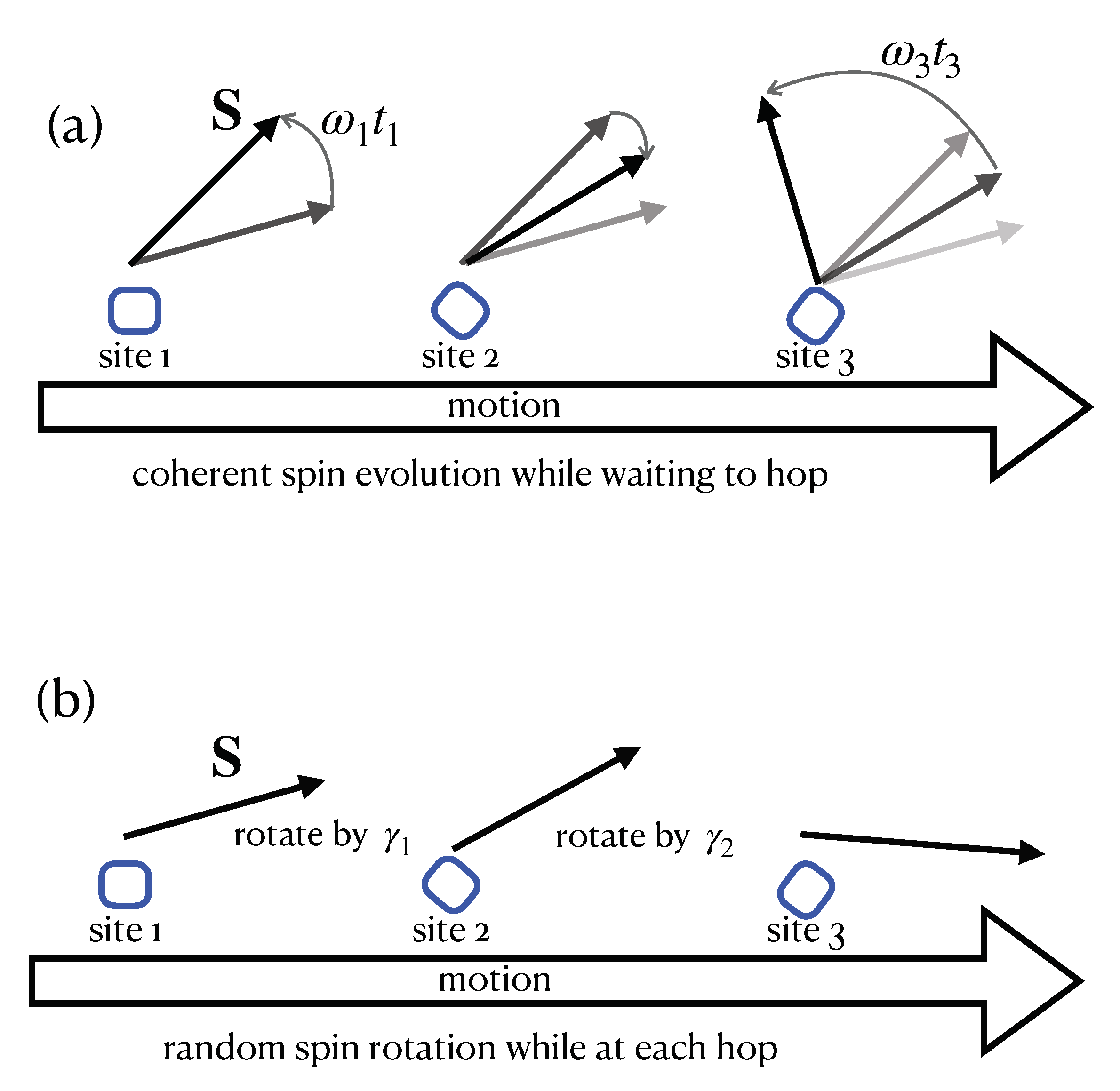
2.1. Spin Evolution
2.2. Strong Collision Approximation
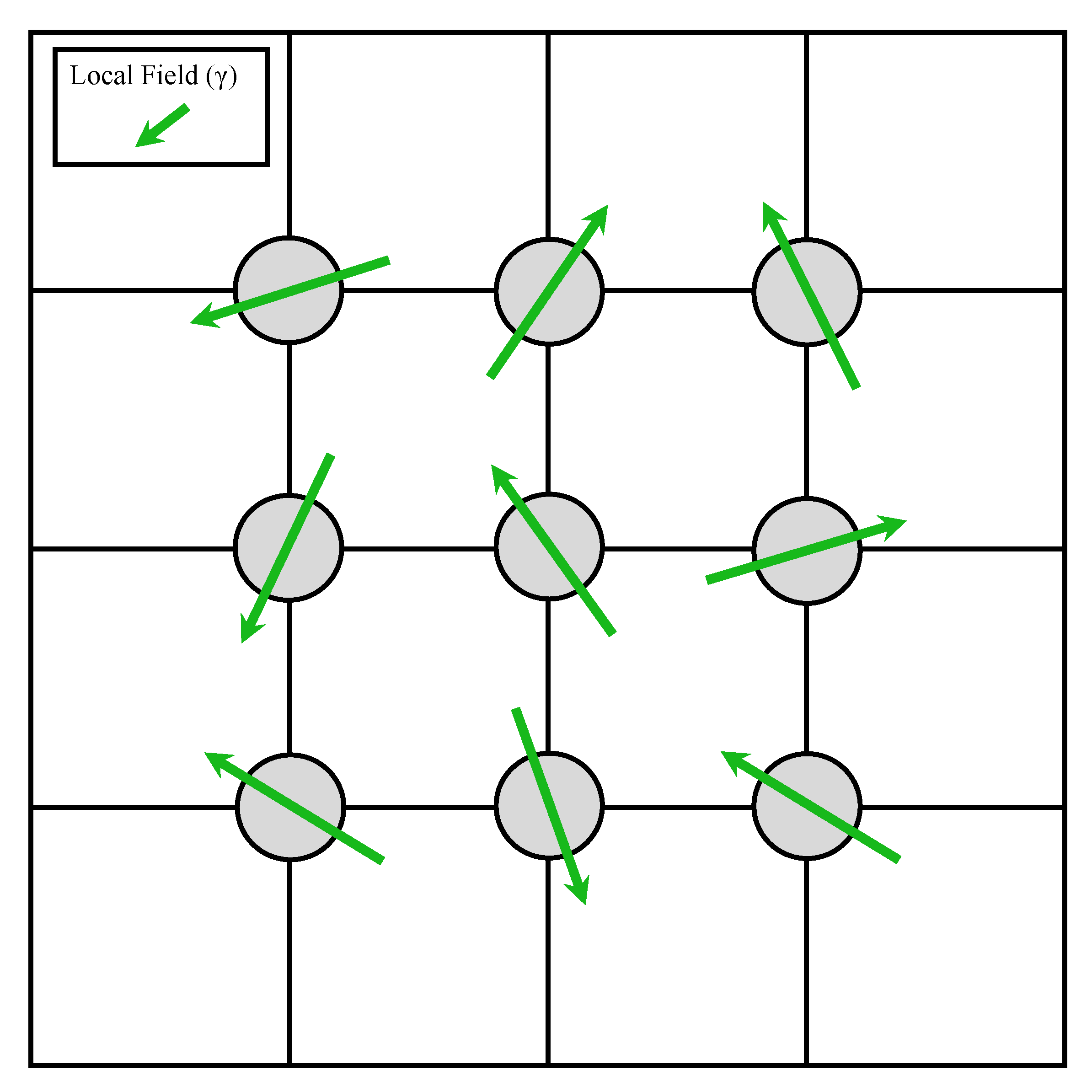
2.3. Non-Disordered Model
2.4. Hopping Models
2.5. Multiple Trapping Model
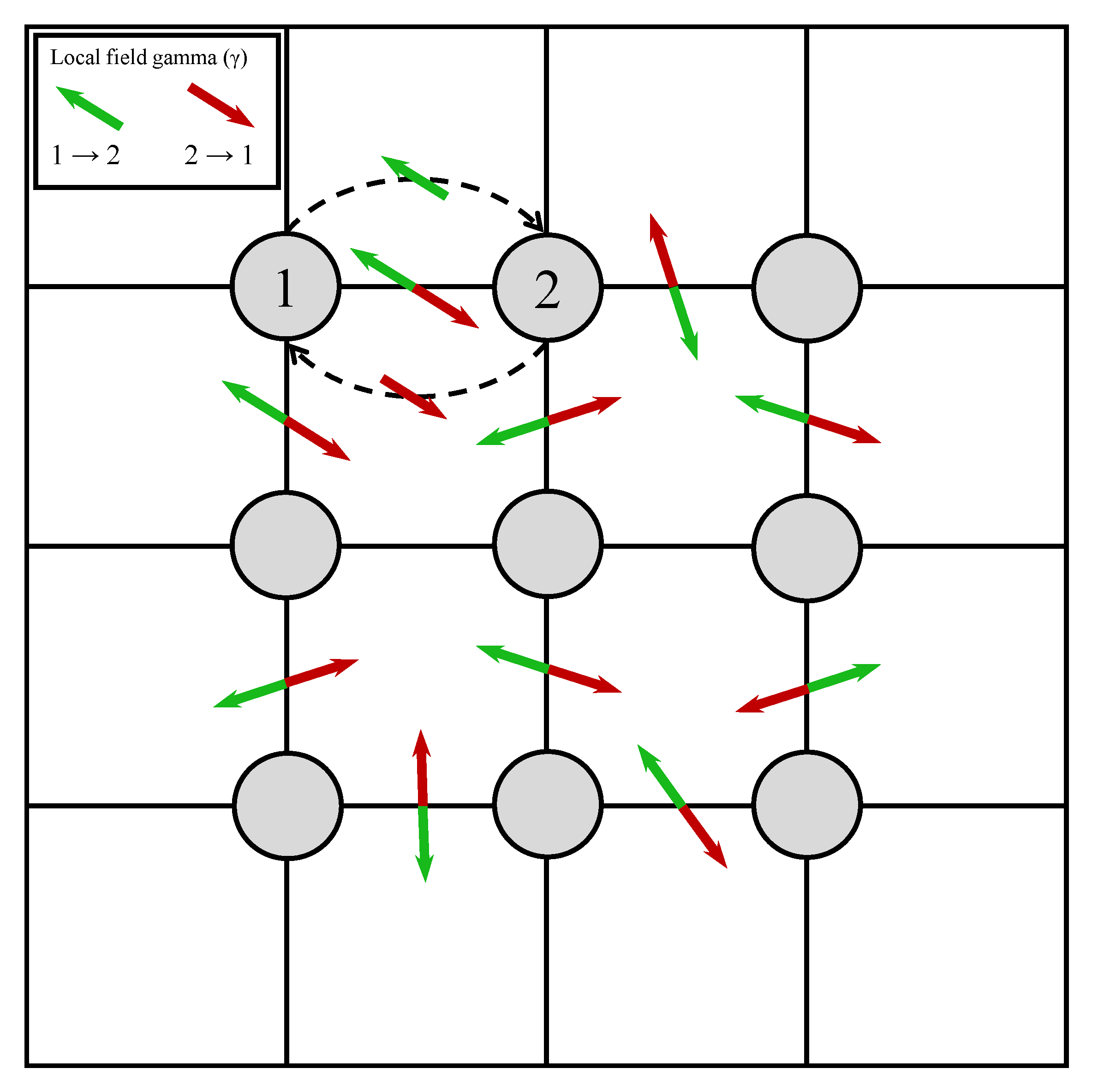
2.6. Multiple Hopping Model
2.6.1. Local Field Correlations
2.6.2. Local Field Magnitude
3. Results
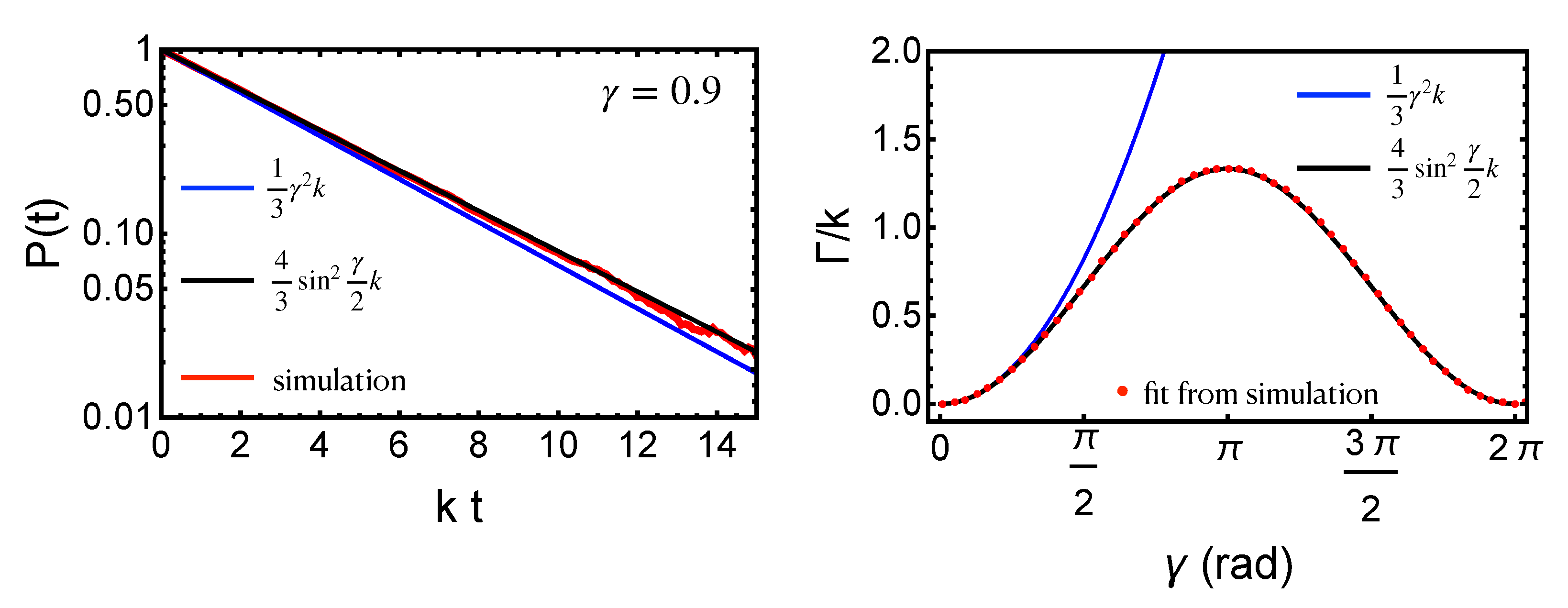
3.1. Zero Disorder
3.2. Finite Disorder
4. Discussion
4.1. Evaluating the Models
4.2. Shortcomings of the Classical Spin Model
5. Materials and Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MT | Multiple Trapping |
| MH | Multiple Hopping |
References
- Yafet, Y. g Factors and Spin-Lattice Relaxation of Conduction Electrons. Solid State Phys. 1963, 14, 2–98. [Google Scholar]
- Meier, F.; Zachachrenya, B.P. Optical Orientation: Modern Problems in Condensed Matter Science; North-Holland: Amsterdam, The Netherlands, 1984; Volume 8. [Google Scholar]
- Ziese, M.; Thornton, M.J. (Eds.) Spin Electronics; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2001; Volume 569. [Google Scholar]
- Awschalom, D.D.; Samarth, N.; Loss, D. (Eds.) Semiconductor Spintronics and Quantum Computation; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Samarth, N. An Introduction to Semiconductor Spintronics. Solid State Phys. 2004, 58, 1–72. [Google Scholar]
- Dediu, V.; Murgia, M.; Matacotta, F.C.; Taliani, C.; Barbanera, S. Room temperature spin polarized injection in organic semiconductor. Solid State Commun. 2002, 122, 181–184. [Google Scholar] [CrossRef]
- Xiong, Z.H.; Wu, D.; Vardeny, Z.V.; Shi, J. Giant magnetoresistance in organic spin-valves. Nature 2004, 427, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Bobbert, P.A.; Wagemans, W.; Oost, F.W.A.; Koopmans, B.; Wohlgenannt, M. Theory for spin diffusion in disordered organic semiconductors. Phys. Rev. Lett. 2009, 102, 156604. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.D.; Hukic-Markosian, G.; Wang, F.; Wojcik, L.; Li, X.G.; Ehrenfreund, E.; Vardeny, Z.V. Isotope effect in spin response of π-conjugated polymer films and devices. Nat. Mater. 2010, 9, 345. [Google Scholar] [CrossRef]
- Baker, W.J.; Keevers, T.L.; Lupton, J.M.; McCamey, D.R.; Boehme, C. Slow hopping and spin dephasing of Coulombically bound polaron pairs in an organic semiconductor at room temperature. Phys. Rev. Lett. 2012, 108, 267601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rybicki, J.; Lin, R.; Wang, F.; Wohlgenannt, M.; He, C.; Sanders, T.; Suzuki, Y. Tuning the performance of organic spintronic devices using x-ray generated traps. Phys. Rev. Lett. 2012, 109, 076603. [Google Scholar] [CrossRef] [Green Version]
- Harmon, N.J.; Flatté, M.E. Distinguishing spin relaxation mechanisms in organic semiconductors. Phys. Rev. Lett. 2013, 110, 176602. [Google Scholar] [CrossRef]
- Tian, Q.; Xie, S. Spin injection and transport in organic materials. Micromachines 2019, 10, 596. [Google Scholar] [CrossRef] [Green Version]
- Schulten, K.; Wolynes, P.G. Semiclassical description of electron spin motion in radicals including the effect of electron hopping. J. Chem. Phys. 1978, 68, 3292. [Google Scholar] [CrossRef]
- Deotare, P.B.; Chang, W.; Hontz, E.; Congreve, D.N.; Shi, L.; Reusswig, P.D.; Modtland, B.; Bahlke, M.E.; Lee, C.K.; Willard, A.P.; et al. Nanoscale transport of charge-transfer states in organic donor?acceptor blends. Nat. Mater. 2015, 14, 1130–1134. [Google Scholar] [CrossRef]
- Ritz, T.; Wiltschko, R.; Wiltschko, R.; Hore, P.J.; Rodgers, C.T.; Stapput, K.; Thalau, P.; Timmel, C.R.; Wiltschk, W. Magnetic Compass of Birds Is Based on a Molecule with Optimal Directional Sensitivity. Biophys. J. 2009, 96, 3451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cochrane, C.J.; Lenahan, P.M. Zero-field detection of spin dependent recombination with direct observation of electron nuclear hyperfine interactions in the absence of an oscillating electromagnetic field. J. Appl. Phys. 2012, 112, 123714. [Google Scholar] [CrossRef]
- Harmon, N.J.; McMillan, S.R.; Ashton, J.P.; Lenahan, P.M.; Flatté, M.E. Coherent Detection of Single or Few Defects. IEEE Trans. Nucl. Sci. 2020, 67, 1669–1673. [Google Scholar] [CrossRef]
- Kehr, K.W.; Honig, G.; Richter, D. Stochastic theory of spin depolarization of muons diffusing in the presence of traps. Z. Phys. B 1978, 32, 49. [Google Scholar] [CrossRef]
- Czech, R.K. Spin depolarization for one-dimensional random walk. Phys. Rev. Lett. 1984, 53, 3–6. [Google Scholar] [CrossRef]
- Czech, R. Spin depolarization by random walks in lattice gases. J. Chem. Phys. 1989, 91, 2506. [Google Scholar] [CrossRef]
- Czech, R. Number of distinct sites visited by random walks in lattice gases. J. Chem. Phys. 1989, 91, 2498. [Google Scholar] [CrossRef]
- Smilga, V.; Belousov, Y.M. The Muon Method in Science; Nova Science Publishers: New York, NY, USA, 1994. [Google Scholar]
- Yaouanc, A.; de Rèotier, P.D. Muon Spin Rotation, Relaxation, and Resonance; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Ghandi, K.; Clark, I.P.; Lord, J.S.; Cottrell, S.P. Laser-muon spin spectroscopy in liquids: A technique to study the excited state chemistry of transients. Phys. Chem. Chem. Phys. 2007, 9, 353–359. [Google Scholar] [CrossRef]
- Foy, M.L.G.; Heiman, N.; Kossler, W.J.; Stronach, C.E. Precession of Positive Muons in Nickel and Iron. Phys. Rev. Lett. 1973, 30, 1064–1067. [Google Scholar] [CrossRef]
- Reid, I.D.; Azuma, T.; Roduner, E. Surface-adsorbed free radicals observed by positive-muon avoided-level-crossing resonance. Nature 1990, 345, 328–330. [Google Scholar] [CrossRef]
- Kubo, R.; Tomita, K. A General Theory of Magnetic Resonance Absorption. J. Phys. Soc. Jpn. 1954, 9, 888–919. [Google Scholar] [CrossRef]
- Abragam, A. Principles of Nuclear Magnetism; Oxford Science Publications: Oxford, UK, 1961. [Google Scholar]
- Adhikari, P.; Harmon, N.J. Spin diffusion in organic semiconductors. 2021; unpublished. [Google Scholar]
- Landi, A.; Borrelli, R.; Capobianco, A.; Velardo, A.; Peluso, A. Hole Hopping Rates in Organic Semiconductors: A Second-Order Cumulant Approach. J. Chem. Theory Comput. 2018, 14, 1594–1601. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.G. Spin-orbit coupling, spin relaxation, and spin diffusion in organic solids. Phys. Rev. Lett. 2011, 106, 106602. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.G. Spin-orbit coupling and its effects in organic solids. Phys. Rev. B 2012, 85, 115201. [Google Scholar] [CrossRef] [Green Version]
- Harmon, N.J.; Flatté, M.E. Spin Relaxation in Materials Lacking Coherent Charge Transport. Phys. Rev. B 2014, 90, 115203. [Google Scholar] [CrossRef] [Green Version]
- Shumilin, A.V.; Kabanov, V.V. Kinetic equations for hopping transport and spin relaxation in a random magnetic field. Phys. Rev. B 2015, 92, 014206. [Google Scholar] [CrossRef] [Green Version]
- McMillan, S.R.; Harmon, N.J.; Flatté, M.E. Steric Paper. 2021; unpublished. [Google Scholar]
- Merkulov, I.A. Electron spin relaxation by nuclei in semiconductor quantum dots. Phys. Rev. B 2002, 65, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hayano, R.S.; Uemura, Y.J.; Imazato, J.; Yamazaki, T.; Kubo, R. Zero and low field spin relaxation studied by positive muons. Phys. Rev. B 1979, 20, 850. [Google Scholar] [CrossRef]
- Montroll, E.W.; Weiss, G.H. Random walks on lattices. II. J. Math. Phys. 1965, 6, 167. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- Baranovskii, S.D. Theoretical description of charge transport in disordered organic semiconductors. Phys. Stat. Solidi B 2014, 251, 487. [Google Scholar] [CrossRef]
- GWR and Talbot Numerical Inverse Laplace Transform Methods. Available online: http://library.wolfram.com/infocenter/ (accessed on 10 March 2021).
- Valkó, P.P.; Abate, J. Comparison of sequence accelerators for the Gaver method of numerical Laplace transform inversion. Comput. Math. Appl. 2004, 48, 629. [Google Scholar] [CrossRef] [Green Version]
- Abate, J.; Valkó, P.P. Multi-precision Laplace Transform inversion. Int. J. Numer. Meth. Eng. 2004, 60, 979. [Google Scholar] [CrossRef]
- Hartenstein, B.; Bassler, H.; Jakobs, A.; Kehr, K.W. Comparison between multiple trapping and multiple hopping transport in random medium. Phys. Rev. B 1996, 54, 8574. [Google Scholar] [CrossRef] [PubMed]
- Harmon, N.J.; Flatté, M.E. Organic magnetoresistance from deep traps. J. Appl. Phys. 2014, 116, 043707. [Google Scholar] [CrossRef] [Green Version]
- Voget-Grote, U.; Stuke, J.; Wagner, H. Electron spin resonance of amorphous silicon. AIP Conf. Proc. 1976, 31, 91. [Google Scholar]
- Movaghar, B.; Schweitzer, L. ESR and conductivity in amorphous germanium and silicon. Phys. Stat. Solidi B 1977, 80, 491. [Google Scholar] [CrossRef]
- Dersch, H.; Stuke, J.; Beichler, J. Electron Spin Resonance of Doped Glow-Discharge Amorphous Silicon. Phys. Stat. Solidi B 1981, 105, 265. [Google Scholar] [CrossRef]
- Dersch, H.; Stuke, J.; Beichler, J. Temperature dependence of ESR spectra of doped a-Si:H. Phys. Stat. Solidi B 1981, 107, 307. [Google Scholar] [CrossRef]
- Pfister, G.; Scher, H. Dispersive (non-Gaussian) transient transport in disordered solids. Adv. Phys. 1978, 27, 747. [Google Scholar] [CrossRef]
- Borsenberger, P.M.; Pautmeier, L.T.; Bassler, H. Nondispersive-to-dispersive charge-transport transition in disordered molecular solids. Phys. Rev. B 1992, 46, 12145. [Google Scholar] [CrossRef] [PubMed]

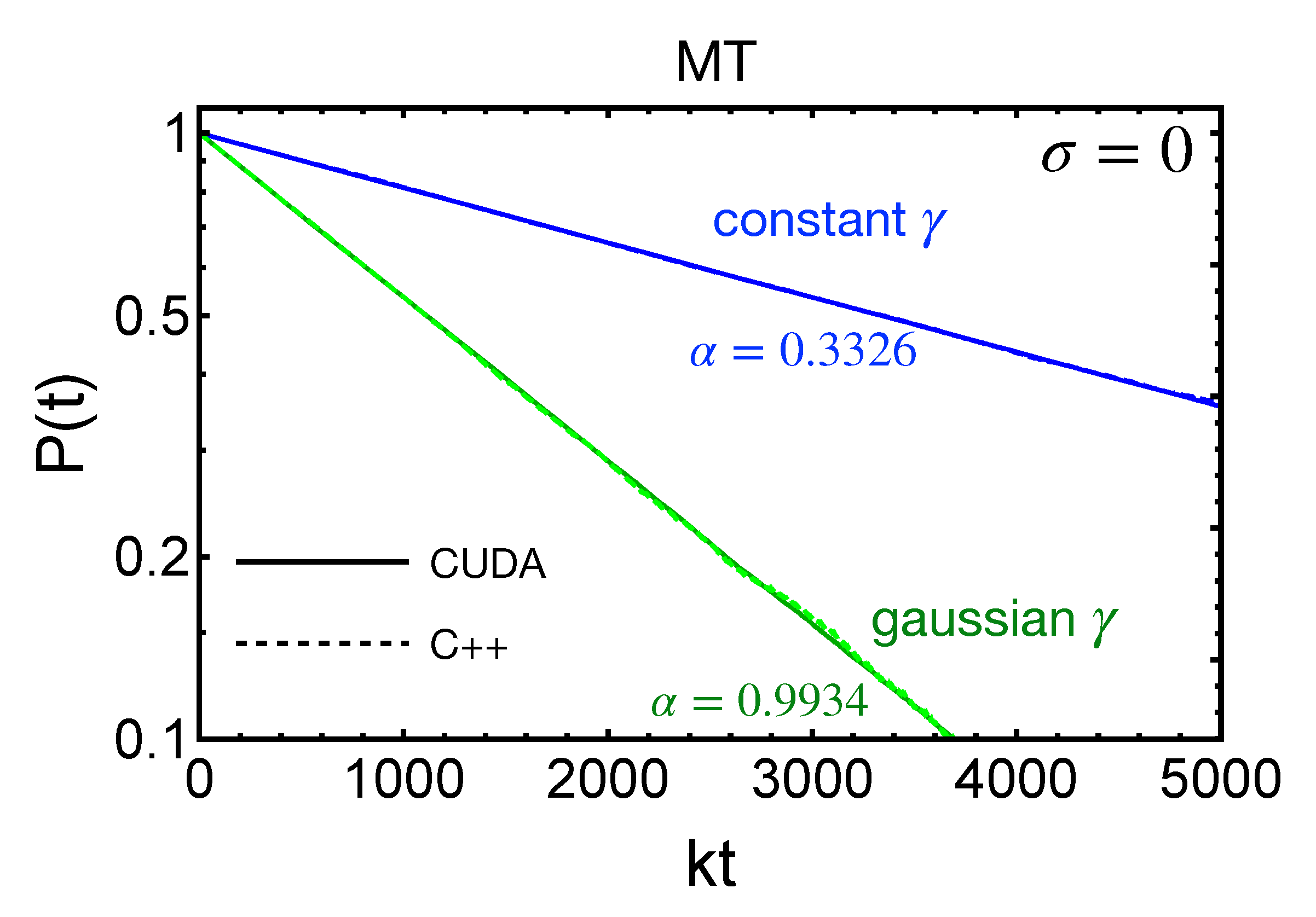
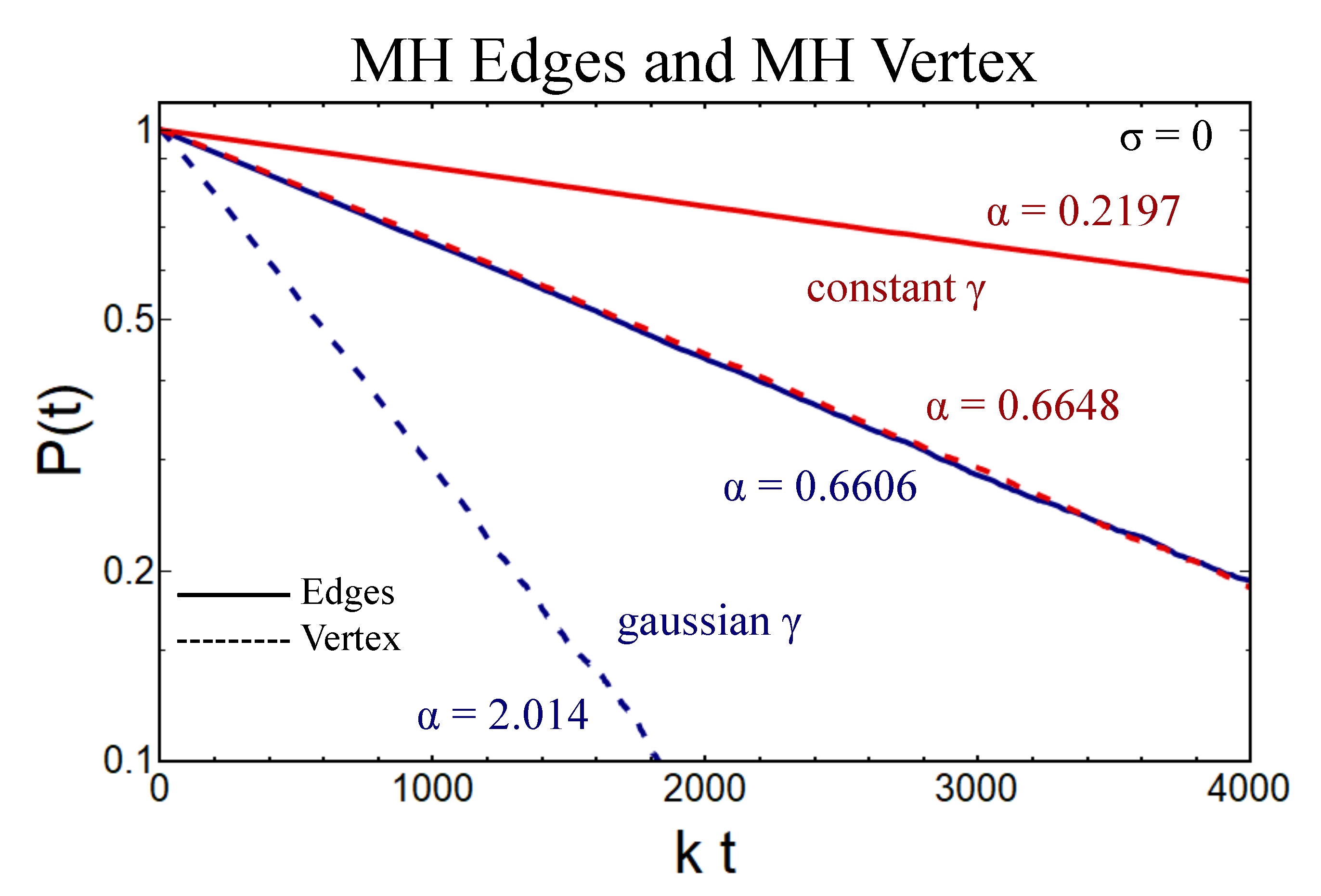



| α | MT | MH |
|---|---|---|
| Gaussian | 1 | – |
| Gaussian-vertex | – | 2.014∼2 |
| Gaussian-edge | – | 2/3 |
| constant | 1/3 | – |
| constant-vertex | – | 0.6606∼2/3 |
| constant-edge | – | 2/9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerst, R.; Becerra Silva, R.; Harmon, N.J. Simulation and Theory of Classical Spin Hopping on a Lattice. Magnetochemistry 2021, 7, 88. https://doi.org/10.3390/magnetochemistry7060088
Gerst R, Becerra Silva R, Harmon NJ. Simulation and Theory of Classical Spin Hopping on a Lattice. Magnetochemistry. 2021; 7(6):88. https://doi.org/10.3390/magnetochemistry7060088
Chicago/Turabian StyleGerst, Richard, Rodrigo Becerra Silva, and Nicholas J. Harmon. 2021. "Simulation and Theory of Classical Spin Hopping on a Lattice" Magnetochemistry 7, no. 6: 88. https://doi.org/10.3390/magnetochemistry7060088
APA StyleGerst, R., Becerra Silva, R., & Harmon, N. J. (2021). Simulation and Theory of Classical Spin Hopping on a Lattice. Magnetochemistry, 7(6), 88. https://doi.org/10.3390/magnetochemistry7060088






