Deciphering the Structural Characterization, Hirshfeld Surface Analysis, Raman Studies, and Temperature-Dependent Magnetodielectric Properties of BiMn2O5
Abstract
1. Introduction
2. Experimental Section
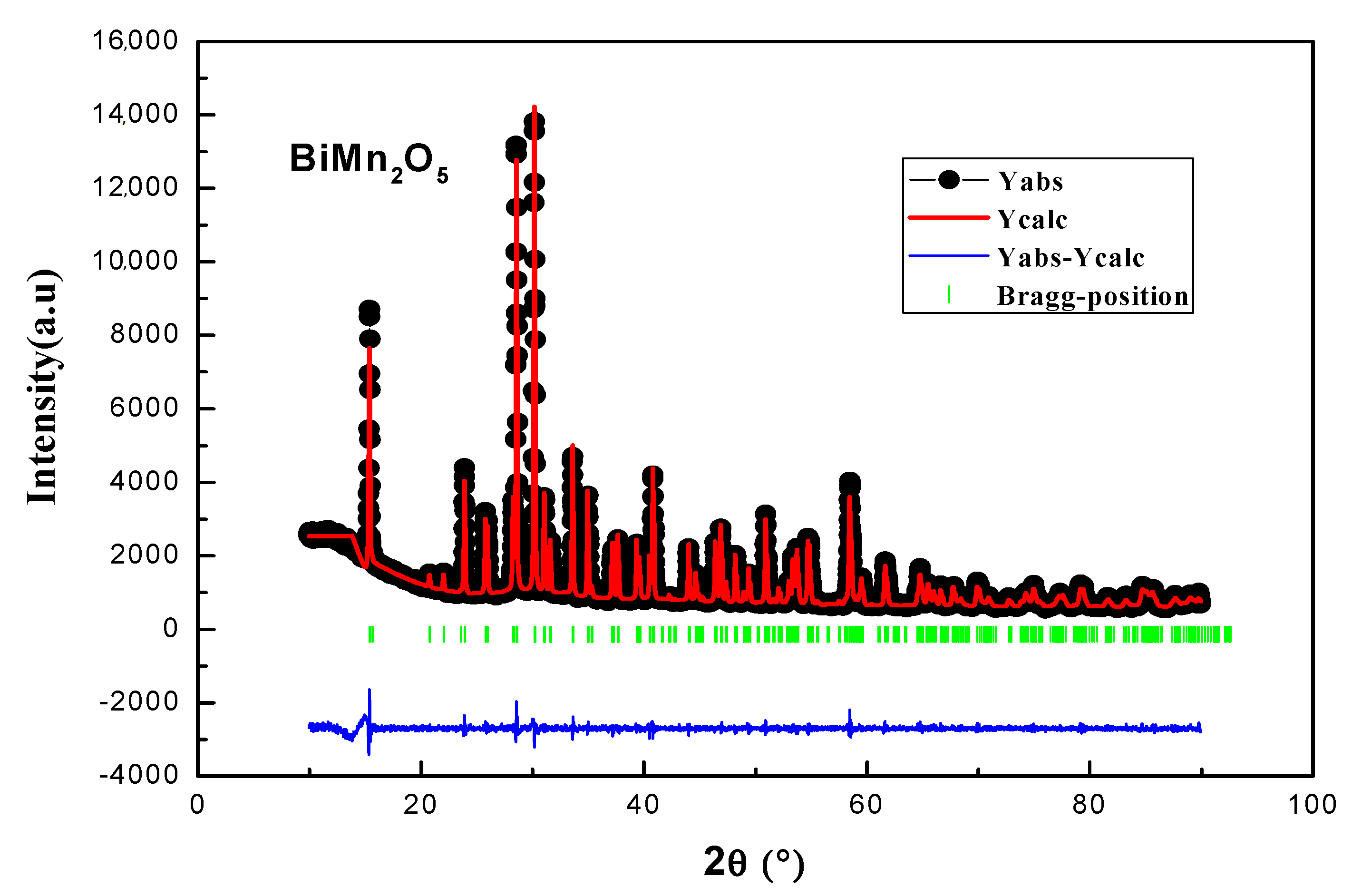
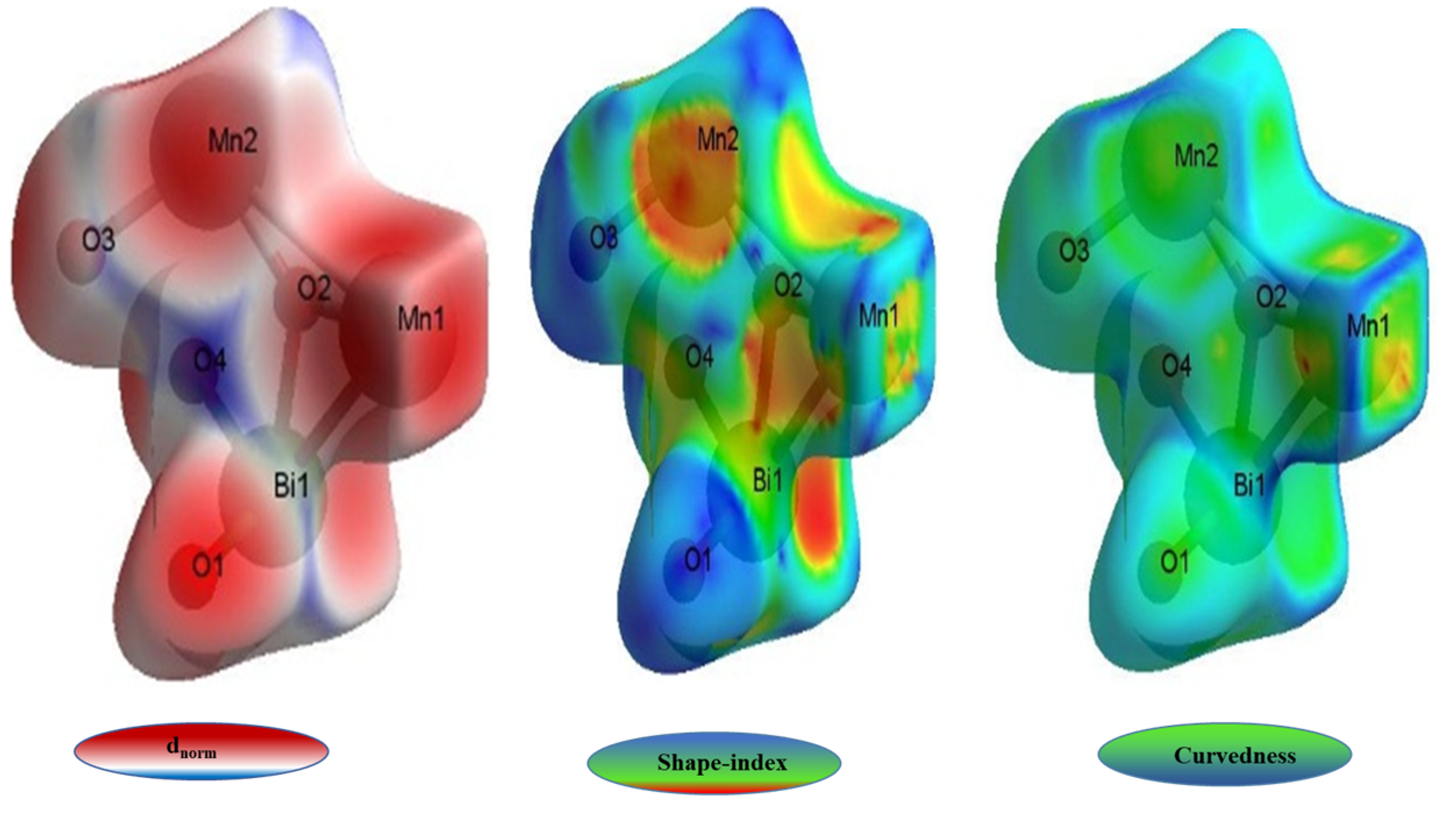
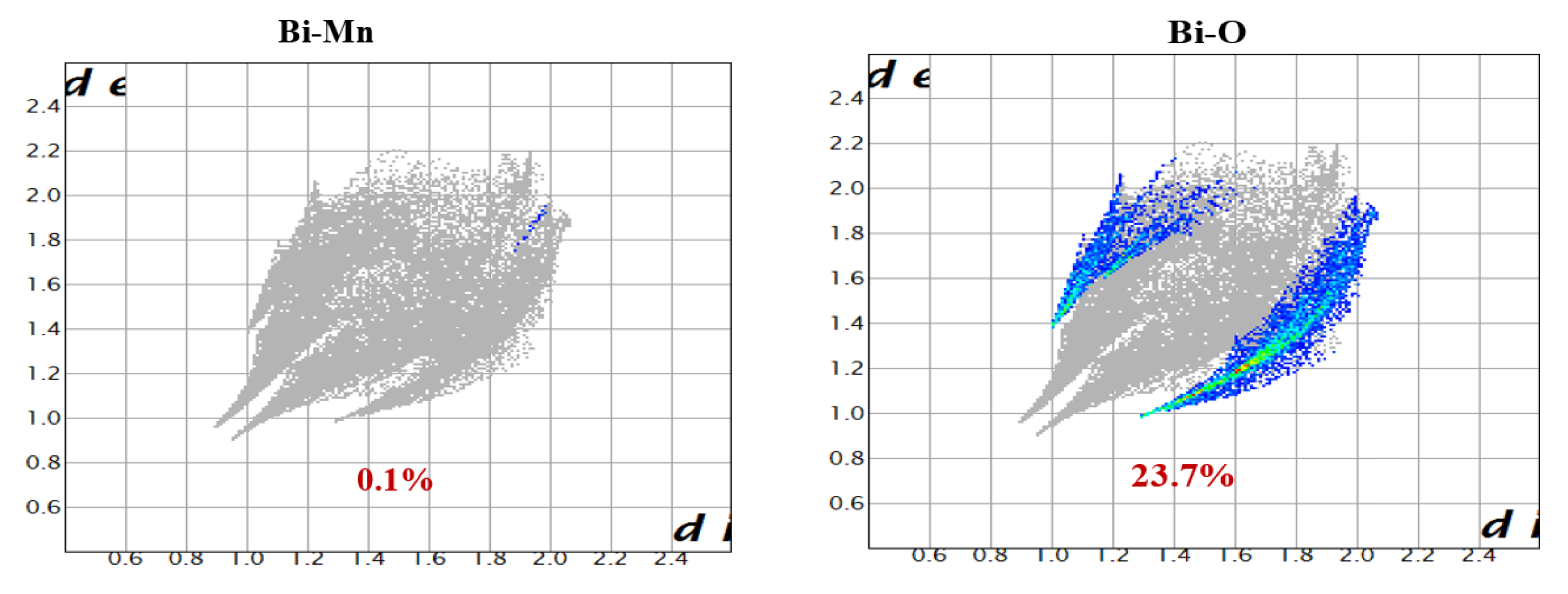
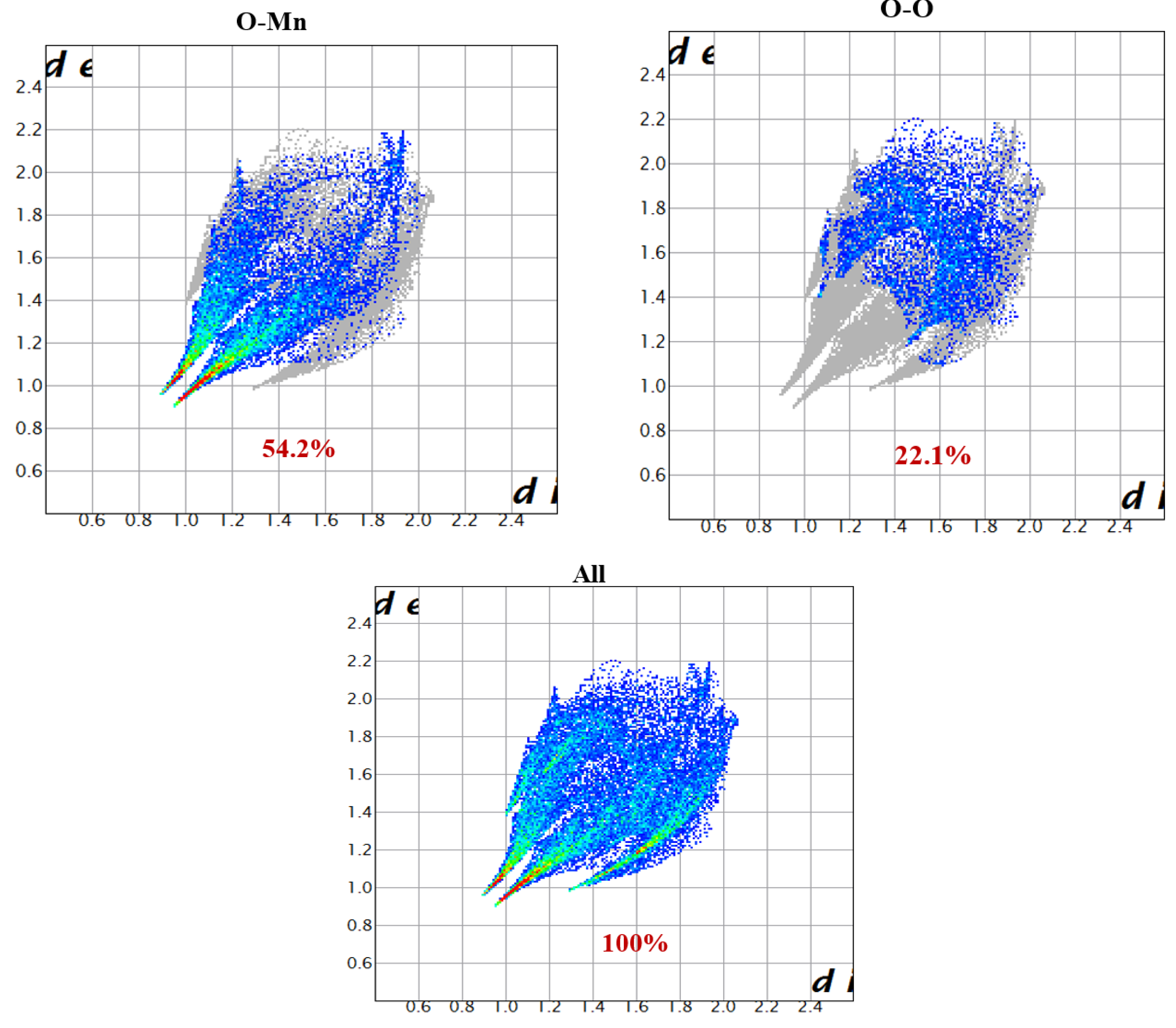
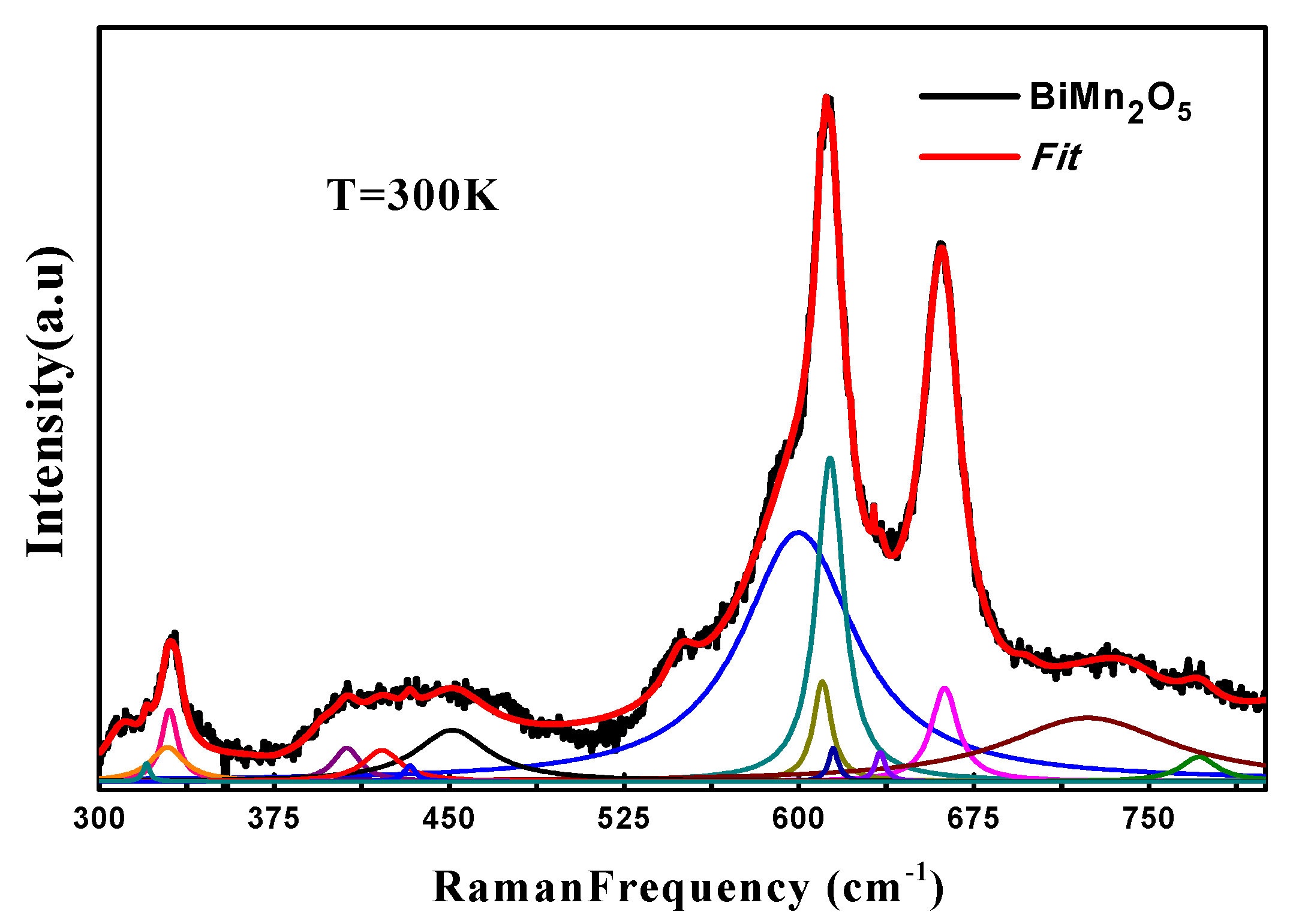
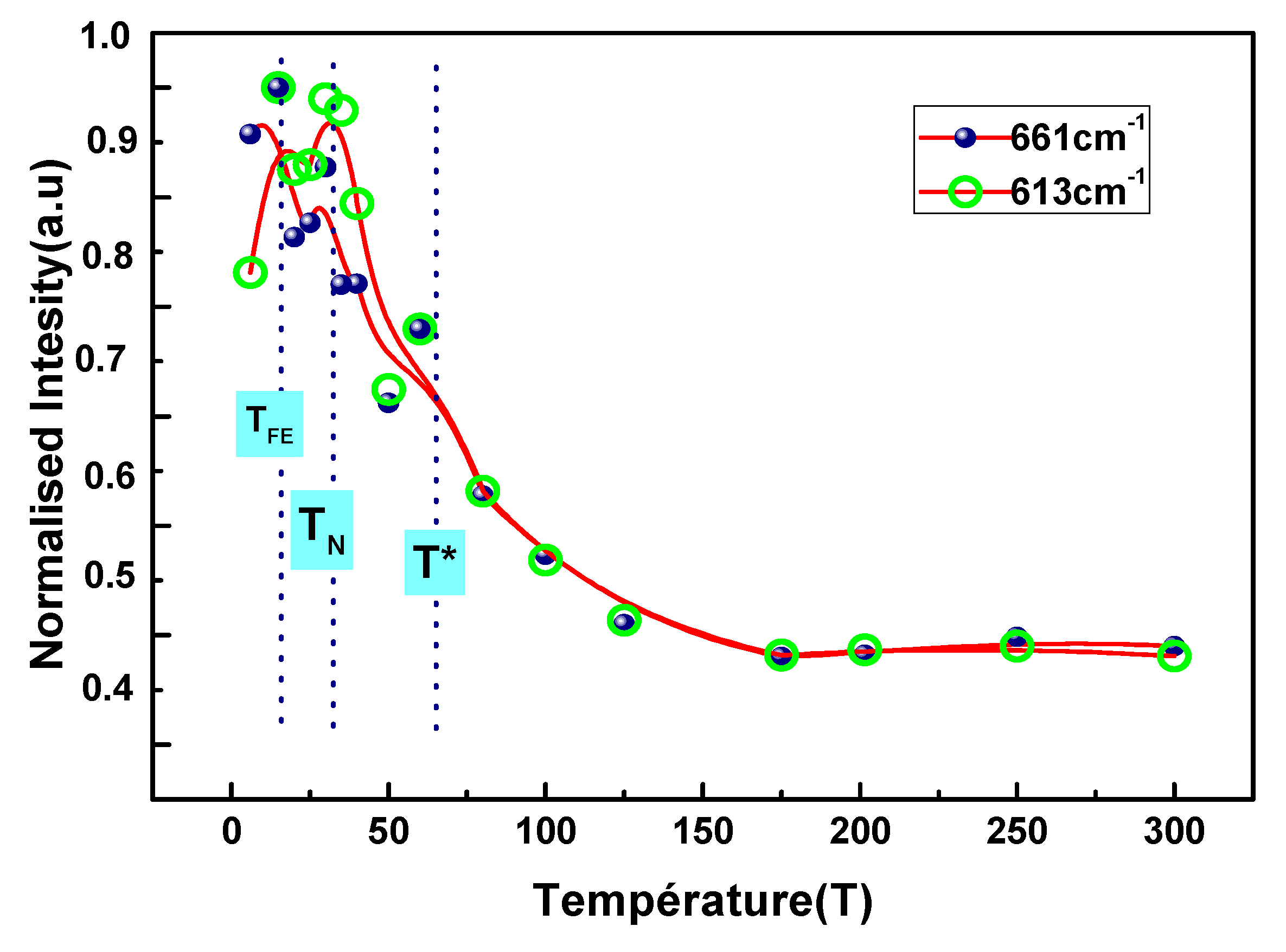
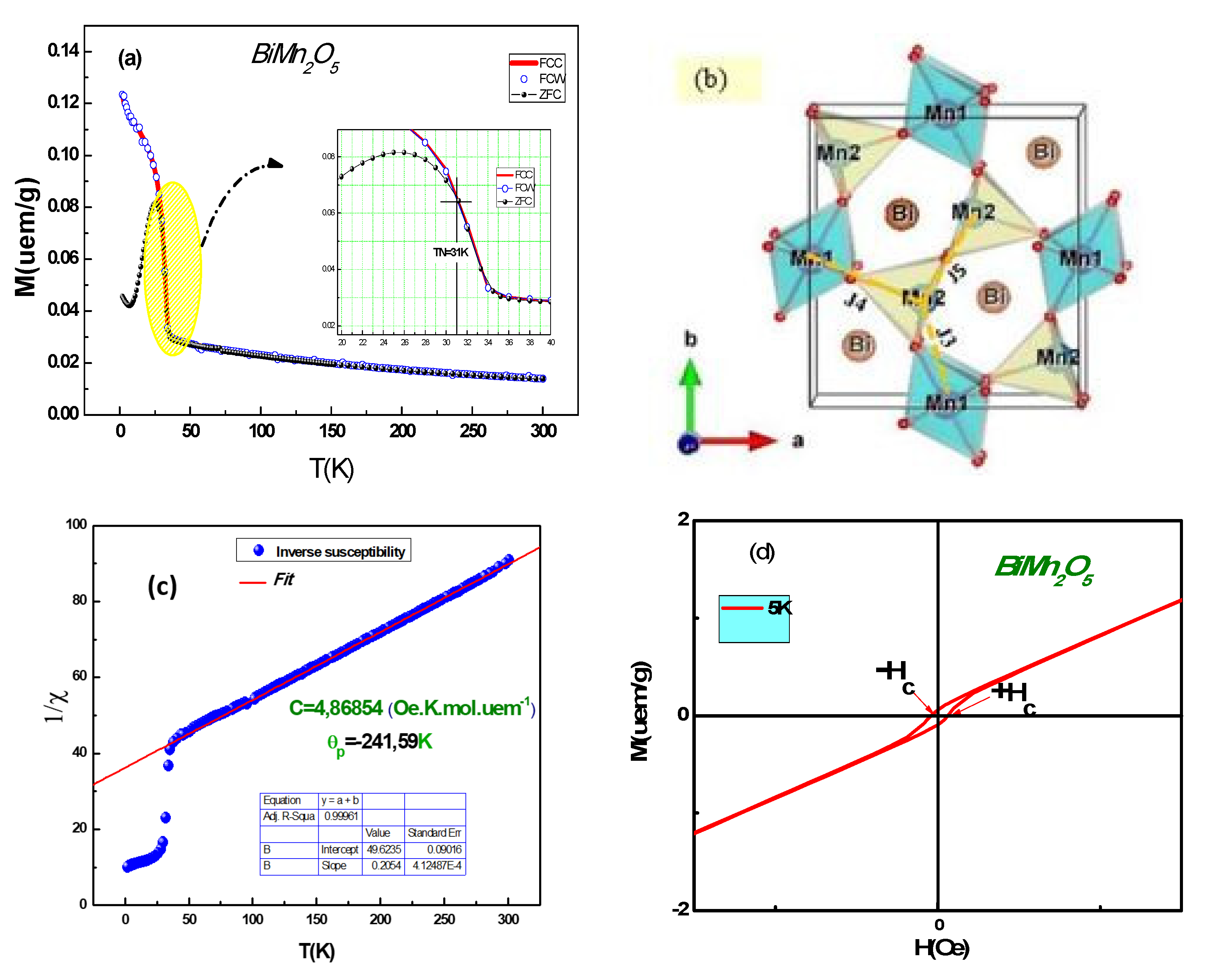
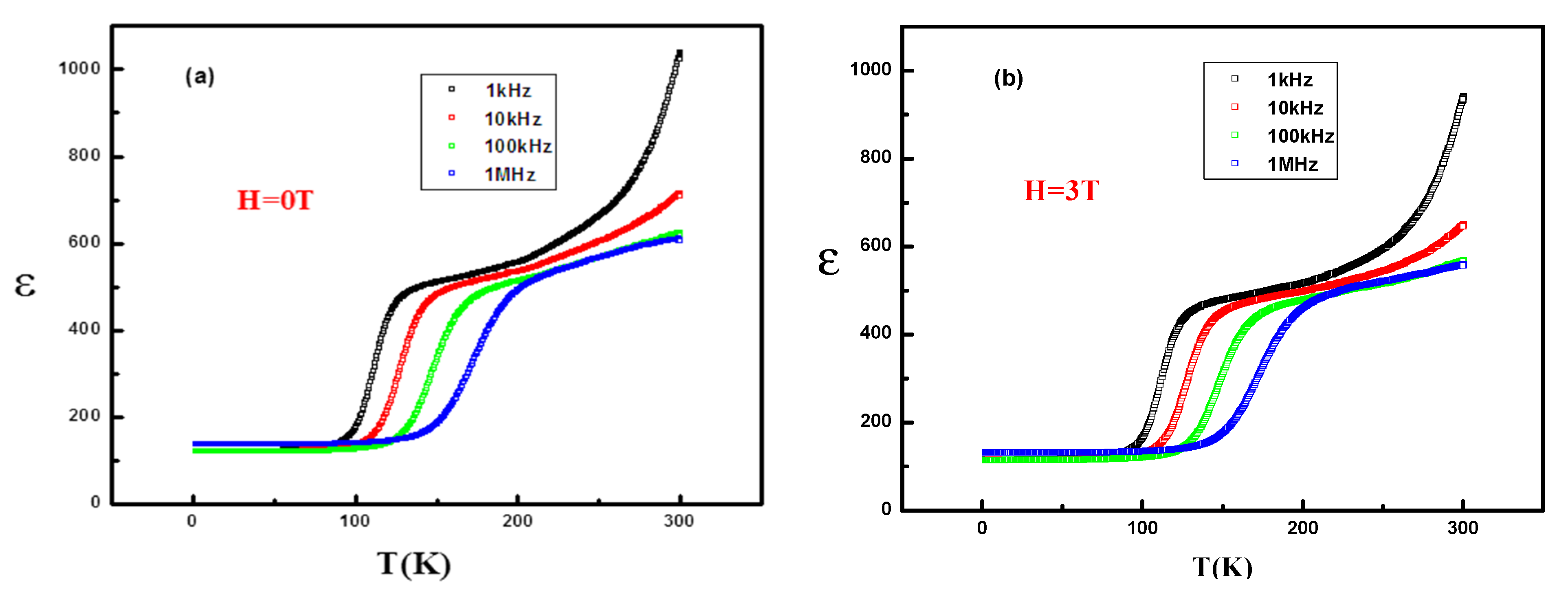
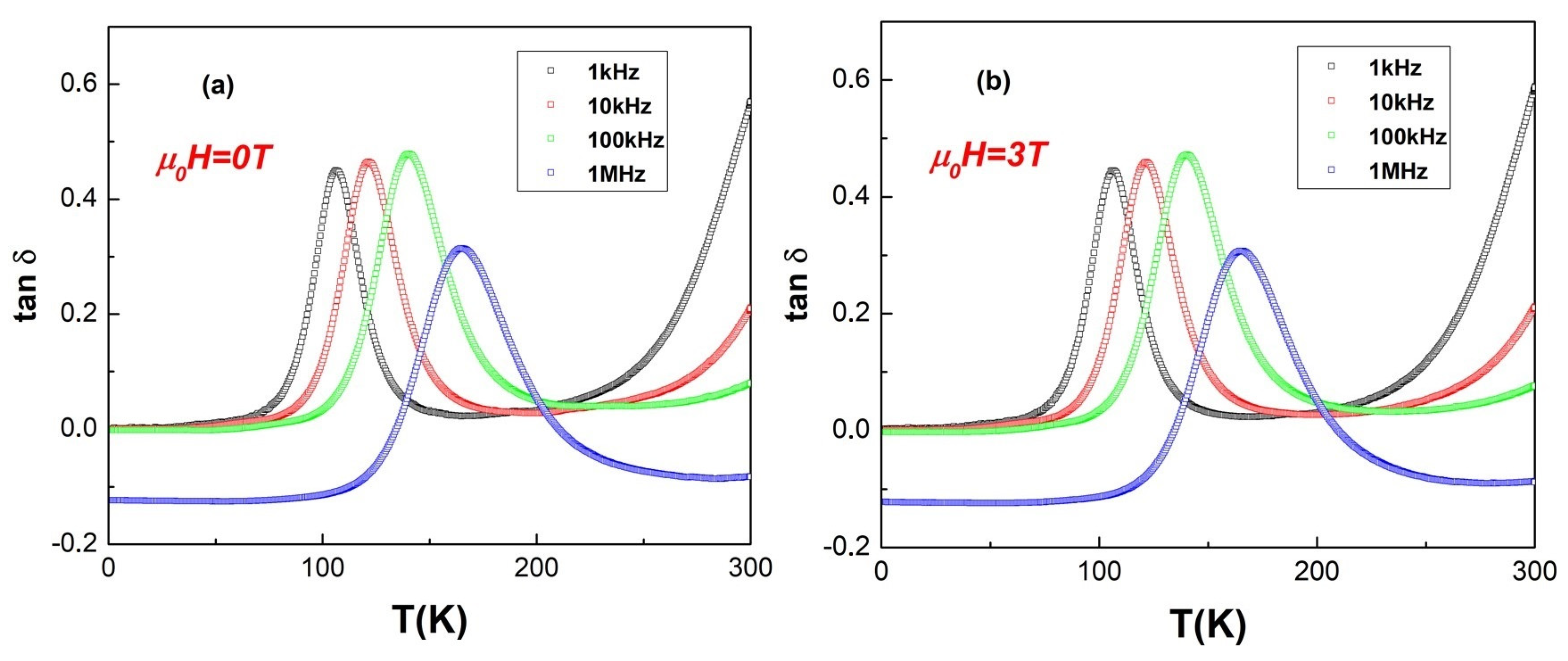
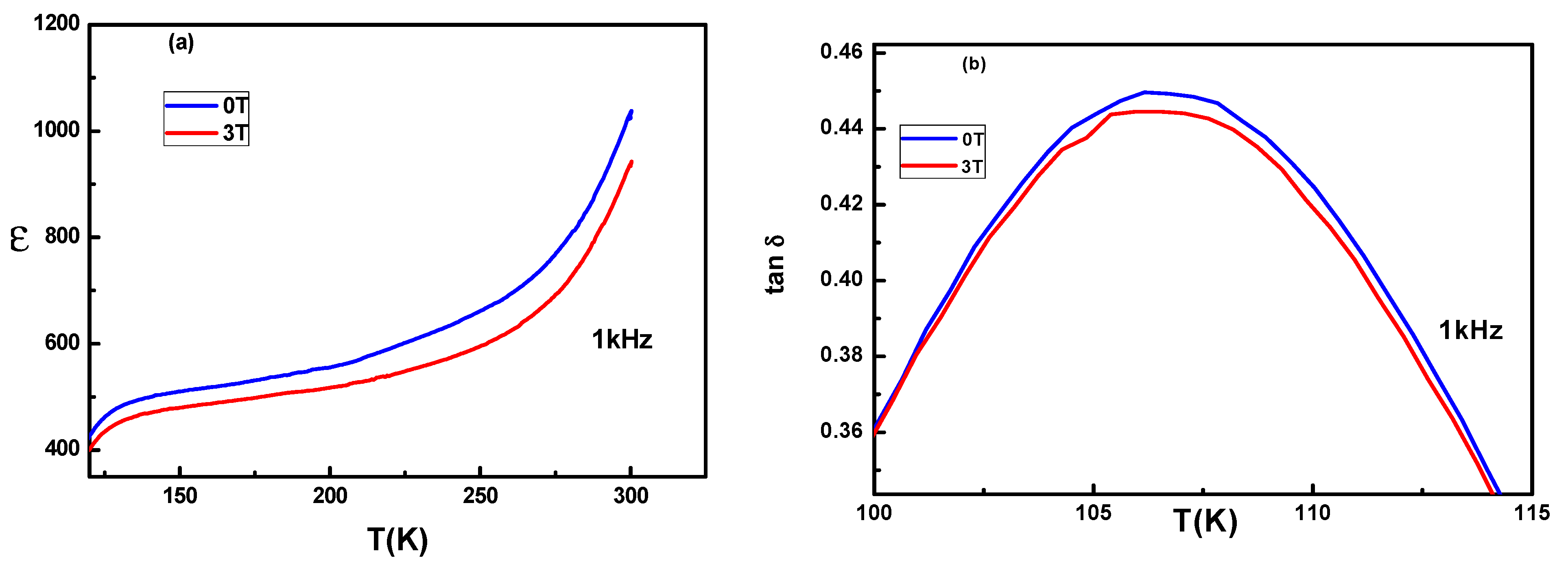
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smolenskii, G.A.; Chupis, I.E. Ferroelectromagnets. J. Sov. Phys. Uspekhi 1982, 25, 475. [Google Scholar] [CrossRef]
- Venevtsev, Y.N.; Gagulin, V.V. Search, design and investigation of seignettomagnetic oxides. J. Ferroelectr. 1994, 162, 23. [Google Scholar] [CrossRef]
- Aizu, K. Possible Species of Ferromagnetic, Ferroelectric, and Ferroelastic Crystals. J. Phys. Rev. B 1970, 2, 754. [Google Scholar] [CrossRef]
- Schmid, H. Multi-ferroic magnetoelectrics. J. Ferroelectr. 1994, 162, 317. [Google Scholar] [CrossRef]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. J. Nat. 2003, 426, 55. [Google Scholar] [CrossRef]
- Hur, N.; Park, S.; Sharma, P.A.; Ahn, J.S.; Guha, S.; Cheong, S.-W. Electric polarization reversal and memory in a multiferroic material induced by magnetic fields. J. Nat. 2004, 429, 392. [Google Scholar] [CrossRef]
- Lawes, G.; Harris, A.B.; Kimura, T.; Rogado, N.; Cava, R.J.; Aharony, A.; Entin-Wohlman, O.; Yildirim, T.; Kenzelmann, M.; Broholm, C.; et al. Magnetically Driven Ferroelectric Order in Ni3V2O8. J. Phys. Rev. Lett. 2005, 95, 087205. [Google Scholar] [CrossRef]
- Kimura, T.; Lawes, G.; Ramirez, A.P. Electric Polarization Rotation in a Hexaferrite with Long-Wavelength Magnetic Structures. J. Phys. Rev. Lett. 2005, 94, 137201. [Google Scholar] [CrossRef] [PubMed]
- Erenstein, W.; Mathur, N.D.; Scott, J.F. Multiferroic and magnetoelectric materials. J. Nat. 2006, 442, 759. [Google Scholar] [CrossRef]
- Hill, N.A. Why Are There so Few Magnetic Ferroelectrics. J. Phys. Chem. B 2000, 104, 6694. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Cheong, S.-W.; Ramesh, R. Multiferroics: Past, present, and future. J. Phys. Today 2010, 63, 38. [Google Scholar] [CrossRef]
- Khomskii, D. Classifying multiferroics: Mechanisms and effects. Physics 2009, 2, 20. [Google Scholar] [CrossRef]
- Zhao, H.J.; Ren, W.; Yang, Y.; Íñiguez, J.; Chen, X.M.; Bellaiche, L. Near room-temperature multiferroic materials with tunable ferromagnetic and electrical properties. J. Nat. Commun. 2014, 5, 4021. [Google Scholar] [CrossRef] [PubMed]
- Dey, K.; Indra, A.; De, D.; Majumdar, S.; Giri, S. Magnetoelectric Coupling, Ferroelectricity, and Magnetic Memory Effect in Double Perovskite La3Ni2NbO9. ACS Appl. Mater. Interfaces 2016, 8, 12901. [Google Scholar] [CrossRef] [PubMed]
- Katsufuji, T.; Takagi, H. Coupling between magnetism and dielectric properties in quantum paraelectric EuTiO3. J. Phys. Rev. B 2001, 64, 054415. [Google Scholar] [CrossRef]
- Felhi, H.; Lahouli, R.; Smari, M.; Rahmouni, H.; Khirouni, K.; Dhahri, E. Study of the structural, electric and dielectric proprieties of Bi1-xNdxMn2O5 (x=0, x=0.1 and x=0.2). J. Mol. Strut. 2019, 1179, 1. [Google Scholar] [CrossRef]
- Felhi, H.; Smari, M.; Bajorek, A.; Nouri, K.; Dhahri, E.; Bessais, L. Controllable synthesis, XPS investigation and magnetic property of multiferroic BiMn2O5 system: The role of neodyme doping. J. Prog. Nat. Sci. Mater. 2019, 29, 178. [Google Scholar] [CrossRef]
- Yin, L.H.; Yuan, B.; Chen, J.; Zhang, D.M.; Zhang, Q.L.; Yang, J.; Dai, J.M.; Song, W.H.; Sun, J.Y.P. Dielectric relaxations and magnetodielectric response in BiMn2O5 single crystaApp. J. Phys. Lett. 2013, 103, 152908. [Google Scholar]
- Muñoz, A.; Alonso, J.A.; Casais, M.T.; MartínezLopez, M.J.; Martínez, J.L.; Fernadez-Díaz, M.T. Magnetic structure and properties ofBiMn2O5oxide: A neutron diffraction study. J. Phys. Rev. B 2002, 65, 1444423. [Google Scholar] [CrossRef]
- Mansouri, S.; Jandl, S.; Balli, M.; Fournier, P.; Ishii, Y.; Kimura, H.; Orlita, M.; Chaker, M. Origin of the enhanced ferroelectricity in multiferroic SmMn2O5. J. Phys. Rev. B 2019, 100, 085147. [Google Scholar] [CrossRef]
- Hemberger, J.; Lobina, S.; von Nidda, H.A.K.; Ivanov, V.Y.; Mukhin, A.A.; Balbashov, A.M.; Loidl, A. Complex interplay of 3d and 4f magnetism inLa1−xGdxMnO3. J. Phys. Rev. B 2004, 70, 024414. [Google Scholar] [CrossRef]
- Wolff, S.K.; Grimwood, D.J.; McKinnon, J.J.; Turner, M.J.; Jayatilaka, D.; Spackman, M.A. Crystal Explorer Version 3.1; University of Western Australia: Perth, Australia, 2012. [Google Scholar]
- Koenderink, J.J.; van Doorn, A.J. Surface shape and curvature scales. J. Image Vis. Comput. 1992, 557, 10. [Google Scholar] [CrossRef]
- Hajbi, M.; Abdi, M.; Loukil, M. Synthesis, crystal structure, Hirshfeld surface analysis, spectroscopic studies, electric and dielectric properties of the new Hg(II) complex with N,N-dimethy-p-toluidine ligand: [C9H14N]HgCl3. J. Ion. 2018, 24, 2355. [Google Scholar] [CrossRef]
- Nuzhnyy, D.; Petzelt, J.; Kamba, S.; Marti, X.; Cechal, T.; Brooks, C.M.; Schlom, D.G. Infrared phonon spectroscopy of a compressively strained (001) SrTiO3 film grown on a (110) NdGaO3 substrate. J. Phys. Condens. Matter 2011, 23, 045901. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, D.L.; Bauman, R.P.; Porto, S.P.S. Normal mode determination in crystals. J. Raman Spectrosc. 1981, 10, 253. [Google Scholar] [CrossRef]
- Litvinchuk, A.P. Spin-phonon study of EuMn2O5 nanorods. J. Magn. Magn. Mater. 2009, 321, 2373. [Google Scholar] [CrossRef]
- Choi, Y.J.; Zhang, C.L.; Lee, N.; Cheong, S.-W. Cross-Control of Magnetization and Polarization by Electric and Magnetic Fields with Competing Multiferroic and Weak-Ferromagnetic Phases. J. Phys. Rev. Lett. 2010, 105, 097201. [Google Scholar] [CrossRef]
- Kumar, M.; Yadav, K.L. Study of dielectric, magnetic, ferroelectric and magnetoelectric properties in the PbMnxTi1−xO3 system at room temperature. J. Phys. Condens. Matter 2007, 19, 242202. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Flores, A.F.; Granado, E.; Martinho, H.; Urbano, R.R.; Rettori, C.; Golovenchits, E.I.; Sanina, V.A.; Oseroff, S.B.; Park, S.; Cheong, S.-W. Anomalous phonon shifts in the paramagnetic phase of multiferroic RMn2O5 (R=Bi, Eu, Dy): Possible manifestations of unconventional magnetic correlations. J. Phys. Rev. B 2006, 73, 104411. [Google Scholar] [CrossRef]
- Chapon, L.C.; Blake, G.R.; Gutmann, M.J.; Park, S.; Hur, N.; Radaelli, P.G.; Cheong, S.W. Structural Anomalies and Multiferroic Behavior in Magnetically Frustrated TbMn2O5. Phys. Rev. Lett. 2004, 93, 177402. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241. [Google Scholar] [CrossRef]
- Sergienko, A.; Dagotto, E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. J. Phys. Rev. B 2006, 73, 094434. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Sahoo, S.; Barik, S.K.; Puli, V.S.; Misra, P.; Katiyar, R.S. Studies on magnetoelectric coupling in PFN-NZFO composite at room temperature. J. Appl. Phys. 2014, 115, 194105. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons, Inc.: East Suite Bridgewater, NJ, USA, 2004. [Google Scholar]
- Fier, I.; Walmsley, L.; Souza, J.A. Relaxor behavior in multiferroic BiMn2O5 ceramics. J. Appl. Phys. 2011, 110, 084101. [Google Scholar] [CrossRef]
- Peliz-Barranco, A.; Caldern-Piar, F.; Garca-Zaldvar, O.; Gonzlez-Abreu, Y. Relaxor behaviour in ferroelectric ceramics. In Advances in Ferroelectrics; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Axelrod, E.; Puzenko, A.; Haruvy, Y.; Reisfeld, R.; Feldman, Y. Negative dielectric loss phenomenon in porous sol–gel glasses. J. Non Cryst. Solids 2006, 352, 4166. [Google Scholar] [CrossRef]
- Chandrasekhar, K.D.; Das, A.K.; Venimadhav, A. Spin glass behaviour and extrinsic origin of magnetodielectric effect in non-multiferroic La2NiMnO6 nanoparticles. J. Phys. Condens. Matter 2012, 24, 376003. [Google Scholar] [CrossRef] [PubMed]


| D2h | E | C2 (z) | C2 (y) | C2 (x) | i | σ (xy) | σ (xz) | σ (yz) |
|---|---|---|---|---|---|---|---|---|
| Ag | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 ,, |
| B1g | 1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 xy |
| B2g | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 xz |
| B3g | 1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 yz |
| Au | 1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 |
| B1u | 1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 x |
| B2u | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 y |
| B3u | 1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 z |
| Modes Ag (cm−1) | Modes B1g (cm−1) | Modes B2g (cm−1) | Modes B3g (cm−1) | ||||
|---|---|---|---|---|---|---|---|
| Calc | Exp (300 K) | Calc | Exp (300 K) | Calc | Exp (300 K) | Calc | Exp (300 K) |
| 175 193 198 279 348 415 442 523 565 610 657 708 754 | 414 566 612 661 | 137 174 213 292 331 411 443 467 508 597 608 700 750 | 330 406 433 599 609 697 723 | 72 179 221 259 322 332 416 455 471 536 577 | 320 339 421 451 534 | 63 177 225 262 283 367 412 431 476 546 573 | 379 433 549 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Felhi, H.; Smari, M.; Mansouri, S.; Massoudi, J.; Dhahri, E. Deciphering the Structural Characterization, Hirshfeld Surface Analysis, Raman Studies, and Temperature-Dependent Magnetodielectric Properties of BiMn2O5. Magnetochemistry 2021, 7, 68. https://doi.org/10.3390/magnetochemistry7050068
Felhi H, Smari M, Mansouri S, Massoudi J, Dhahri E. Deciphering the Structural Characterization, Hirshfeld Surface Analysis, Raman Studies, and Temperature-Dependent Magnetodielectric Properties of BiMn2O5. Magnetochemistry. 2021; 7(5):68. https://doi.org/10.3390/magnetochemistry7050068
Chicago/Turabian StyleFelhi, Houda, Mourad Smari, Saber Mansouri, Jalel Massoudi, and Essebti Dhahri. 2021. "Deciphering the Structural Characterization, Hirshfeld Surface Analysis, Raman Studies, and Temperature-Dependent Magnetodielectric Properties of BiMn2O5" Magnetochemistry 7, no. 5: 68. https://doi.org/10.3390/magnetochemistry7050068
APA StyleFelhi, H., Smari, M., Mansouri, S., Massoudi, J., & Dhahri, E. (2021). Deciphering the Structural Characterization, Hirshfeld Surface Analysis, Raman Studies, and Temperature-Dependent Magnetodielectric Properties of BiMn2O5. Magnetochemistry, 7(5), 68. https://doi.org/10.3390/magnetochemistry7050068







