Finding the Limits of Magnetic Hyperthermia on Core-Shell Nanoparticles Fabricated by Physical Vapor Methods
Abstract
1. Introduction
2. Results
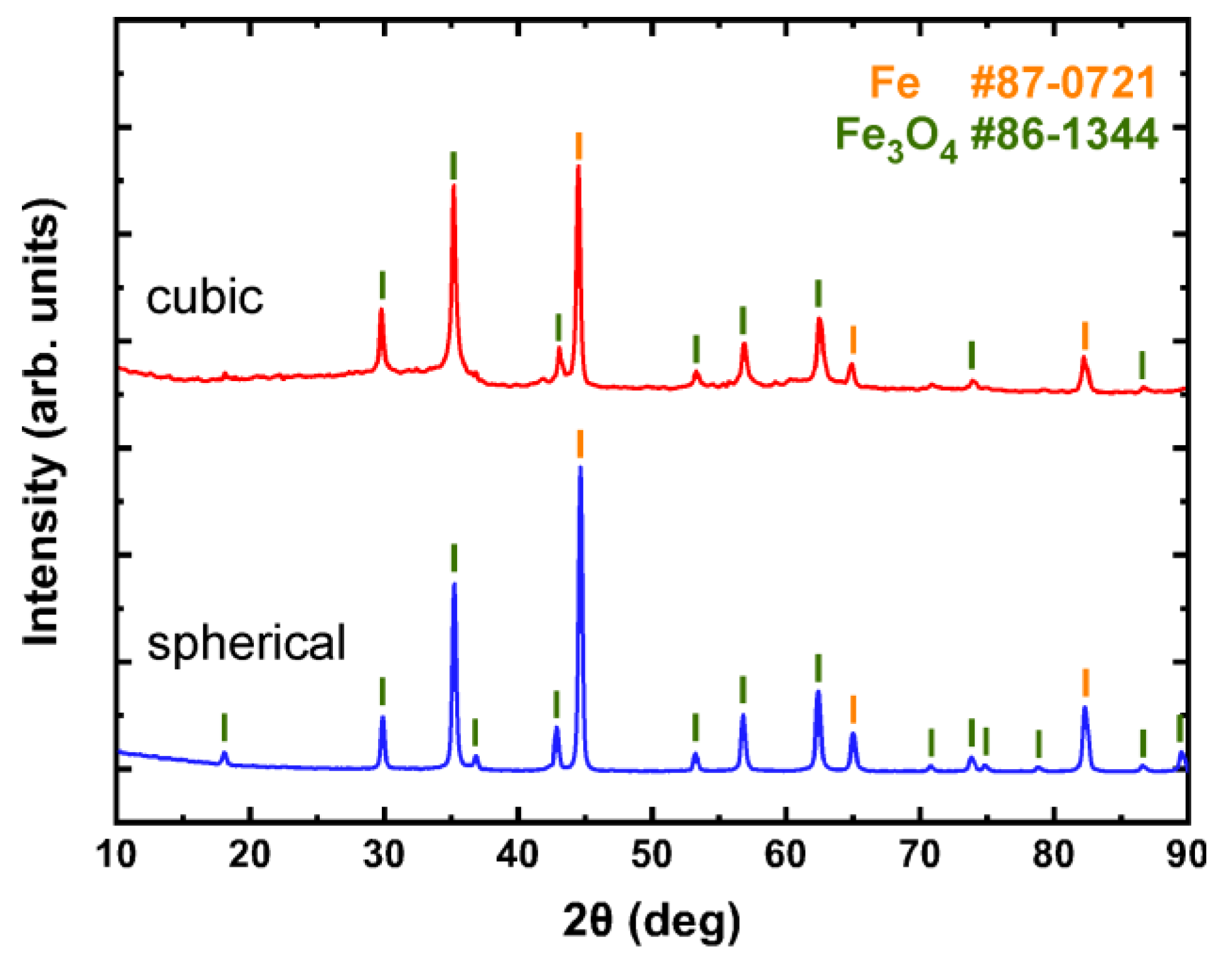
2.1. Structure and Morphology
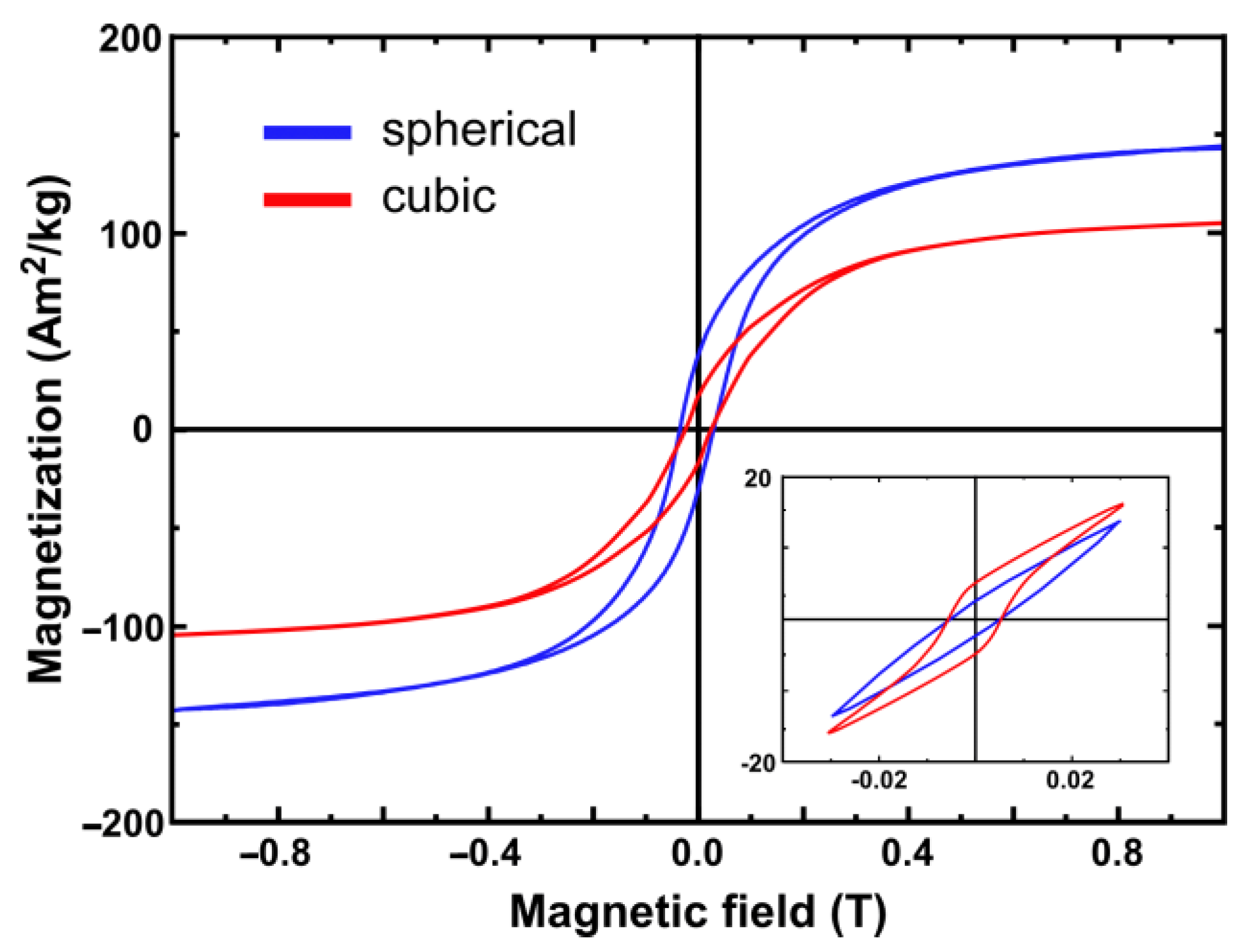
2.2. Magnetism and Heating Efficiency
3. Discussion
3.1. Effect of Geometry
3.2. Comparison with Other Core-Shell Systems
3.3. Perspectives
4. Materials and Methods
4.1. Nanoparticles Preparation
4.2. Characterization
4.3. Theoretical Estimations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kok, H.P.; Cressman, E.N.K.; Ceelen, W.; Brace, C.L.; Ivkov, R.; Grüll, H.; ter Haar, G.; Wust, P.; Crezee, J. Heating technology for malignant tumors: A review. Int. J. Hyperth. 2020, 37, 711–741. [Google Scholar] [CrossRef]
- Gilchrist, R.K.; Medal, R.; Shorey, W.D.; Hanselman, R.C.; Parrot, J.C.; Taylor, C.B. Selective inductive heating of lymph nodes. Ann. Surg. 1957, 146, 596–606. [Google Scholar] [CrossRef] [PubMed]
- Etemadi, H.; Plieger, P.G. Magnetic Fluid Hyperthermia Based on Magnetic Nanoparticles: Physical Characteristics, Historical Perspective, Clinical Trials, Technological Challenges, and Recent Advances. Adv. Ther. 2020, 3, 2000061. [Google Scholar] [CrossRef]
- Conde-Leboran, I.; Baldomir, D.; Martinez-Boubeta, C.; Chubykalo-Fesenko, O.; Del Puerto Morales, M.; Salas, G.; Cabrera, D.; Camarero, J.; Teran, F.J.; Serantes, D. A Single Picture Explains Diversity of Hyperthermia Response of Magnetic Nanoparticles. J. Phys. Chem. C 2015, 119, 15698–15706. [Google Scholar] [CrossRef]
- Tong, S.; Zhu, H.; Bao, G. Magnetic iron oxide nanoparticles for disease detection and therapy. Mater. Today 2019, 31, 86–99. [Google Scholar] [CrossRef]
- Simeonidis, K.; Martinez-Boubeta, C.; Serantes, D.; Ruta, S.; Chubykalo-Fesenko, O.; Chantrell, R.; Oró-Solé, J.; Balcells, L.; Kamzin, A.S.; Nazipov, R.A.; et al. Controlling Magnetization Reversal and Hyperthermia Efficiency in Core-Shell Iron-Iron Oxide Magnetic Nanoparticles by Tuning the Interphase Coupling. ACS Appl. Nano Mater. 2020, 3, 4465–4476. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Su, D.; Wu, K.; Wang, J.P. High-moment magnetic nanoparticles. J. Nanoparticle Res. 2020, 22, 1–16. [Google Scholar] [CrossRef]
- Balcells, L.; Stanković, I.; Konstantinović, Z.; Alagh, A.; Fuentes, V.; López-Mir, L.; Oró, J.; Mestres, N.; García, C.; Pomar, A.; et al. Spontaneous in-flight assembly of magnetic nanoparticles into macroscopic chains. Nanoscale 2019, 11, 14194–14202. [Google Scholar] [CrossRef]
- Serantes, D.; Baldomir, D.; Martinez-Boubeta, C.; Simeonidis, K.; Angelakeris, M.; Natividad, E.; Castro, M.; Mediano, A.; Chen, D.X.; Sanchez, A.; et al. Influence of dipolar interactions on hyperthermia properties of ferromagnetic particles. J. Appl. Phys. 2010, 108, 073918. [Google Scholar] [CrossRef]
- Martinez-Boubeta, C.; Simeonidis, K.; Makridis, A.; Angelakeris, M.; Iglesias, O.; Guardia, P.; Cabot, A.; Yedra, L.; Estradé, S.; Peiró, F.; et al. Learning from Nature to Improve the Heat Generation of Iron-Oxide Nanoparticles for Magnetic Hyperthermia Applications. Sci. Rep. 2013, 3, 1652. [Google Scholar] [CrossRef]
- Tong, S.; Quinto, C.A.; Zhang, L.; Mohindra, P.; Bao, G. Size-Dependent Heating of Magnetic Iron Oxide Nanoparticles. ACS Nano 2017, 11, 6808–6816. [Google Scholar] [CrossRef]
- Davis, H.C.; Kang, S.; Lee, J.H.; Shin, T.H.; Putterman, H.; Cheon, J.; Shapiro, M.G. Nanoscale Heat Transfer from Magnetic Nanoparticles and Ferritin in an Alternating Magnetic Field. Biophys. J. 2020, 118, 1502–1510. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Boubeta, C.; Simeonidis, K.; Serantes, D.; Conde-Leborán, I.; Kazakis, I.; Stefanou, G.; Peña, L.; Galceran, R.; Balcells, L.; Monty, C.; et al. Adjustable hyperthermia response of self-assembled ferromagnetic Fe-MgO core-shell nanoparticles by tuning dipole-dipole interactions. Adv. Funct. Mater. 2012. [Google Scholar] [CrossRef]
- Serantes, D.; Simeonidis, K.; Angelakeris, M.; Chubykalo-Fesenko, O.; Marciello, M.; Del Puerto Morales, M.; Baldomir, D.; Martinez-Boubeta, C. Multiplying magnetic hyperthermia response by nanoparticle assembling. J. Phys. Chem. C 2014, 118, 5927–5934. [Google Scholar] [CrossRef]
- Bondarenko, A.V.; Holmgren, E.; Li, Z.W.; Ivanov, B.A.; Korenivski, V. Chaotic dynamics in spin-vortex pairs. Phys. Rev. B 2019, 99. [Google Scholar] [CrossRef]
- Snoeck, E.; Gatel, C.; Lacroix, L.M.; Blon, T.; Lachaize, S.; Carrey, J.; Respaud, M.; Chaudret, B. Magnetic configurations of 30 nm iron nanocubes studied by electron holography. Nano Lett. 2008, 8, 4293–4298. [Google Scholar] [CrossRef]
- López-Conesa, L.; Martínez-Boubeta, C.; Serantes, D.; Estradé, S.; Peiró, F. Mapping the Magnetic Coupling of Self-Assembled Fe3O4 Nanocubes by Electron Holography. Materials 2021, 14, 774. [Google Scholar] [CrossRef]
- Usov, N.A.; Nesmeyanov, M.S.; Tarasov, V.P. Magnetic vortices as efficient nano heaters in magnetic nanoparticle hyperthermia. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef]
- McClurg, G.O. Magnetic Field Distributions for a Sphere and for an Ellipsoid. Am. J. Phys. 1956, 24, 496–499. [Google Scholar] [CrossRef]
- Munoz-Menendez, C.; Conde-Leboran, I.; Serantes, D.; Chantrell, R.; Chubykalo-Fesenko, O.; Baldomir, D. Distinguishing between heating power and hyperthermic cell-treatment efficacy in magnetic fluid hyperthermia. Soft Matter 2016, 12, 8815–8818. [Google Scholar] [CrossRef]
- Munoz-Menendez, C.; Serantes, D.; Ruso, J.M.; Baldomir, D. Towards improved magnetic fluid hyperthermia: Major-loops to diminish variations in local heating. Phys. Chem. Chem. Phys. 2017, 19, 14527–14532. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-H.; Jang, J.-T.; Choi, J.-S.; Moon, S.H.; Noh, S.-H.; Kim, J.-W.; Kim, J.-G.; Kim, I.-S.; Park, K.I.; Cheon, J. Exchange-coupled magnetic nanoparticles for efficient heat induction. Nat. Nanotechnol. 2011, 6, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Noh, S.H.; Na, W.; Jang, J.T.; Lee, J.H.; Lee, E.J.; Moon, S.H.; Lim, Y.; Shin, J.S.; Cheon, J. Nanoscale magnetism control via surface and exchange anisotropy for optimized ferrimagnetic hysteresis. Nano Lett. 2012, 12, 3716–3721. [Google Scholar] [CrossRef] [PubMed]
- Moon, S.H.; Noh, S.H.; Lee, J.H.; Shin, T.H.; Lim, Y.; Cheon, J. Ultrathin Interface Regime of Core-Shell Magnetic Nanoparticles for Effective Magnetism Tailoring. Nano Lett. 2017, 17, 800–804. [Google Scholar] [CrossRef]
- Pardo, A.; Pelaz, B.; Gallo, J.; Bañobre-López, M.; Parak, W.J.; Barbosa, S.; Del Pino, P.; Taboada, P. Synthesis, Characterization, and Evaluation of Superparamagnetic Doped Ferrites as Potential Therapeutic Nanotools. Chem. Mater. 2020, 32, 2220–2231. [Google Scholar] [CrossRef]
- Lavorato, G.C.; Das, R.; Alonso Masa, J.; Phan, M.-H.; Srikanth, H. Hybrid magnetic nanoparticles as efficient nanoheaters in biomedical applications. Nanoscale Adv. 2021. [Google Scholar] [CrossRef]
- Vamvakidis, K.; Mourdikoudis, S.; Makridis, A.; Paulidou, E.; Angelakeris, M.; Dendrinou-Samara, C. Magnetic hyperthermia efficiency and MRI contrast sensitivity of colloidal soft/hard ferrite nanoclusters. J. Colloid Interface Sci. 2018, 511, 101–109. [Google Scholar] [CrossRef]
- Phadatare, M.R.; Meshram, J.V.; Gurav, K.V.; Kim, J.H.; Pawar, S.H. Enhancement of specific absorption rate by exchange coupling of the core-shell structure of magnetic nanoparticles for magnetic hyperthermia. J. Phys. D Appl. Phys. 2016, 49. [Google Scholar] [CrossRef]
- Hammad, M.; Nica, V.; Hempelmann, R. Synthesis and Characterization of Bi-Magnetic Core/Shell Nanoparticles for Hyperthermia Applications. IEEE Trans. Magn. 2017, 53. [Google Scholar] [CrossRef]
- Fabris, F.; Lima, E.; De Biasi, E.; Troiani, H.E.; Vásquez Mansilla, M.; Torres, T.E.; Fernández Pacheco, R.; Ibarra, M.R.; Goya, G.F.; Zysler, R.D.; et al. Controlling the dominant magnetic relaxation mechanisms for magnetic hyperthermia in bimagnetic core-shell nanoparticles. Nanoscale 2019, 11, 3164–3172. [Google Scholar] [CrossRef]
- Nica, V.; Caro, C.; Páez-Muñoz, J.M.; Leal, M.P.; Garcia-Martin, M.L. Bi-magnetic core-shell CoFe2 O4 @MnFe2 O4 nanoparticles for in vivo theranostics. Nanomaterials 2020, 10, 907. [Google Scholar] [CrossRef]
- Sanna Angotzi, M.; Mameli, V.; Cara, C.; Musinu, A.; Sangregorio, C.; Niznansky, D.; Xin, H.L.; Vejpravova, J.; Cannas, C. Coupled hard-soft spinel ferrite-based core-shell nanoarchitectures: Magnetic properties and heating abilities. Nanoscale Adv. 2020, 2, 3191–3201. [Google Scholar] [CrossRef]
- Darwish, M.S.A.; Kim, H.; Lee, H.; Ryu, C.; Lee, J.Y.; Yoon, J. Engineering core-shell structures of magnetic ferrite nanoparticles for high hyperthermia performance. Nanomaterials 2020, 10, 991. [Google Scholar] [CrossRef] [PubMed]
- Carrião, M.S.; Bakuzis, A.F. Mean-field and linear regime approach to magnetic hyperthermia of core-shell nanoparticles: Can tiny nanostructures fight cancer? Nanoscale 2016, 8, 8363–8377. [Google Scholar] [CrossRef]
- Wang, L.; Yan, Y.; Wang, M.; Yang, H.; Zhou, Z.; Peng, C.; Yang, S. An integrated nanoplatform for theranostics via multifunctional core-shell ferrite nanocubes. J. Mater. Chem. B 2016, 4, 1908–1914. [Google Scholar] [CrossRef] [PubMed]
- Albarqi, H.A.; Wong, L.H.; Schumann, C.; Sabei, F.Y.; Korzun, T.; Li, X.; Hansen, M.N.; Dhagat, P.; Moses, A.S.; Taratula, O.; et al. Biocompatible Nanoclusters with High Heating Efficiency for Systemically Delivered Magnetic Hyperthermia. ACS Nano 2019, 13, 6383–6395. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Zhang, H.; Liu, Y.; Sun, F.; Yu, X.; Li, X.; Zhang, L.; Wang, L.; Mao, K.; Wang, G.; et al. Maximizing Specific Loss Power for Magnetic Hyperthermia by Hard–Soft Mixed Ferrites. Small 2018, 14. [Google Scholar] [CrossRef]
- Pardo, A.; Yáñez, S.; Piñeiro, Y.; Iglesias-Rey, R.; Al-Modlej, A.; Barbosa, S.; Rivas, J.; Taboada, P. Cubic Anisotropic Co- And Zn-Substituted Ferrite Nanoparticles as Multimodal Magnetic Agents. ACS Appl. Mater. Interfaces 2020, 12, 9017–9031. [Google Scholar] [CrossRef]
- Lavorato, G.C.; Das, R.; Xing, Y.; Robles, J.; Litterst, F.J.; Baggio-Saitovitch, E.; Phan, M.H.; Srikanth, H. Origin and Shell-Driven Optimization of the Heating Power in Core/Shell Bimagnetic Nanoparticles. ACS Appl. Nano Mater. 2020, 3, 1755–1765. [Google Scholar] [CrossRef]
- Kallumadil, M.; Tada, M.; Nakagawa, T.; Abe, M.; Southern, P.; Pankhurst, Q.A. Suitability of commercial colloids for magnetic hyperthermia. J. Magn. Magn. Mater. 2009, 321, 1509–1513. [Google Scholar] [CrossRef]
- Makridis, A.; Curto, S.; Van Rhoon, G.C.; Samaras, T.; Angelakeris, M. A standardisation protocol for accurate evaluation of specific loss power in magnetic hyperthermia. J. Phys. D Appl. Phys. 2019, 52, 255001. [Google Scholar] [CrossRef]
- Asimakidou, T.; Makridis, A.; Veintemillas-Verdaguer, S.; Morales, M.P.; Kellartzis, I.; Mitrakas, M.; Vourlias, G.; Angelakeris, M.; Simeonidis, K. Continuous production of magnetic iron oxide nanocrystals by oxidative precipitation. Chem. Eng. J. 2020, 393, 124593. [Google Scholar] [CrossRef]
- Chalkidou, A.; Simeonidis, K.; Angelakeris, M.; Samaras, T.; Martinez-Boubeta, C.; Balcells, L.; Papazisis, K.; Dendrinou-Samara, C.; Kalogirou, O. In vitro application of Fe/MgO nanoparticles as magnetically mediated hyperthermia agents for cancer treatment. J. Magn. Magn. Mater. 2011, 323, 775–780. [Google Scholar] [CrossRef]
- Rubia-Rodríguez, I.; Santana-Otero, A.; Spassov, S.; Tombácz, E.; Johansson, C.; De La Presa, P.; Teran, F.J.; Morales, M.D.P.; Veintemillas-Verdaguer, S.; Thanh, N.T.K.; et al. Whither magnetic hyperthermia? A tentative roadmap. Materials 2021, 14, 706. [Google Scholar] [CrossRef] [PubMed]
- Lanier, O.L.; Korotych, O.I.; Monsalve, A.G.; Wable, D.; Savliwala, S.; Grooms, N.W.F.; Nacea, C.; Tuitt, O.R.; Dobson, J. Evaluation of magnetic nanoparticles for magnetic fluid hyperthermia. Int. J. Hyperth. 2019, 36, 687–701. [Google Scholar] [CrossRef] [PubMed]
- Rao, M.; Krishnamurthy, H.R.; Pandit, R. Magnetic hysteresis in two model spin systems. Phys. Rev. B 1990, 42. [Google Scholar] [CrossRef] [PubMed]
- Hergt, R.; Dutz, S. Magnetic particle hyperthermia-biophysical limitations of a visionary tumour therapy. J. Magn. Magn. Mater. 2007, 311, 187–192. [Google Scholar] [CrossRef]
- Bakoglidis, K.D.; Simeonidis, K.; Sakellari, D.; Stefanou, G.; Angelakeris, M. Size-dependent mechanisms in AC magnetic hyperthermia response of iron-oxide nanoparticles. IEEE Trans. Magn. 2012, 48, 1320–1323. [Google Scholar] [CrossRef]
- Hergt, R.; Hiergeist, R.; Hilger, I.; Kaiser, W.A.; Lapatnikov, Y.; Margel, S.; Richter, U. Maghemite nanoparticles with very high AC-losses for application in RF-magnetic hyperthermia. J. Magn. Magn. Mater. 2004, 270, 345–357. [Google Scholar] [CrossRef]
- Robles, J.; Das, R.; Glassell, M.; Phan, M.H.; Srikanth, H. Exchange-coupled Fe3O4/CoFe2O4 nanoparticles for advanced magnetic hyperthermia. AIP Adv. 2018, 8. [Google Scholar] [CrossRef]
- Mehdaoui, B.; Meffre, A.; Carrey, J.; Lachaize, S.; Lacroix, L.M.; Gougeon, M.; Chaudret, B.; Respaud, M. Optimal size of nanoparticles for magnetic hyperthermia: A combined theoretical and experimental study. Adv. Funct. Mater. 2011, 21, 4573–4581. [Google Scholar] [CrossRef]
- Torche, P.; Munoz-Menendez, C.; Serantes, D.; Baldomir, D.; Livesey, K.L.; Chubykalo-Fesenko, O.; Ruta, S.; Chantrell, R.; Hovorka, O. Thermodynamics of interacting magnetic nanoparticles. Phys. Rev. B 2020, 101, 224429. [Google Scholar] [CrossRef]
- Das, R.; Alonso, J.; Nemati Porshokouh, Z.; Kalappattil, V.; Torres, D.; Phan, M.H.; Garaio, E.; García, J.Á.; Sanchez Llamazares, J.L.; Srikanth, H. Tunable High Aspect Ratio Iron Oxide Nanorods for Enhanced Hyperthermia. J. Phys. Chem. C 2016, 120, 10086–10093. [Google Scholar] [CrossRef]
- Gandia, D.; Gandarias, L.; Rodrigo, I.; Robles-García, J.; Das, R.; Garaio, E.; García, J.Á.; Phan, M.H.; Srikanth, H.; Orue, I.; et al. Unlocking the Potential of Magnetotactic Bacteria as Magnetic Hyperthermia Agents. Small 2019, 15. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Lv, Y.; Herng, T.S.; Xu, X.; Xia, W.; Zhang, T.; Fang, J.; Xiao, W.; Ding, J. Orientation mediated enhancement on magnetic hyperthermia of Fe3 O4 nanodisc. Adv. Funct. Mater. 2015, 25, 812–820. [Google Scholar] [CrossRef]
- Liu, X.L.; Yang, Y.; Ng, C.T.; Zhao, L.Y.; Zhang, Y.; Bay, B.H.; Fan, H.M.; Ding, J. Magnetic Vortex Nanorings: A New Class of Hyperthermia Agent for Highly Efficient in Vivo Regression of Tumors. Adv. Mater. 2015, 27, 1939–1944. [Google Scholar] [CrossRef] [PubMed]
- Hugounenq, P.; Levy, M.; Alloyeau, D.; Lartigue, L.; Dubois, E.; Cabuil, V.; Ricolleau, C.; Roux, S.; Wilhelm, C.; Gazeau, F.; et al. Iron oxide monocrystalline nanoflowers for highly efficient magnetic hyperthermia. J. Phys. Chem. C 2012, 116, 15702–15712. [Google Scholar] [CrossRef]
- Simeonidis, K.; Viñas, S.L.; Wiedwald, U.; Ma, Z.; Li, Z.-A.; Spasova, M.; Patsia, O.; Myrovali, E.; Makridis, A.; Sakellari, D.; et al. A versatile large-scale and green process for synthesizing magnetic nanoparticles with tunable magnetic hyperthermia features. RSC Adv. 2016, 53107–53117. [Google Scholar] [CrossRef]
- Fortin, J.-P.; Wilhelm, C.; Servais, J.; Ménager, C.; Bacri, J.-C.; Gazeau, F. Size-sorted anionic iron oxide nanomagnets as colloidal mediators for magnetic hyperthermia. J. Am. Chem. Soc. 2007, 129, 2628–2635. [Google Scholar] [CrossRef]
- Lanier, O.L.; Monsalve, A.G.; McFetridge, P.S.; Dobson, J. Magnetically triggered release of biologics. Int. Mater. Rev. 2019, 64, 63–90. [Google Scholar] [CrossRef]
- Simeonidis, K.; Martinez-Boubeta, C.; Balcells, L.; Monty, C.; Stavropoulos, G.; Mitrakas, M.; Matsakidou, A.; Vourlias, G.; Angelakeris, M. Fe-based nanoparticles as tunable magnetic particle hyperthermia agents. J. Appl. Phys. 2013, 114. [Google Scholar] [CrossRef]
- Martinez-Boubeta, C.; Simeonidis, K.; Amarantidis, S.; Angelakeris, M.; Balcells, L.; Monty, C. Scaling up the production of magnetic nanoparticles for biomedical applications: Cost-effective fabrication from basalts. Phys. Status Solidi Curr. Top. Solid State Phys. 2014, 11, 1053–1058. [Google Scholar] [CrossRef]
- Balcells, L.; Martínez-Boubeta, C.; Cisneros-Fernández, J.; Simeonidis, K.; Bozzo, B.; Oró-Sole, J.; Bagués, N.; Arbiol, J.; Mestres, N.; Martínez, B. One-Step Route to Iron Oxide Hollow Nanocuboids by Cluster Condensation: Implementation in Water Remediation Technology. ACS Appl. Mater. Interfaces 2016, 8, 28599–28606. [Google Scholar] [CrossRef] [PubMed]
- Joint Center for Powder Diffraction Studies (Ed.) Powder Diffraction File, 2004th ed.; International Centre for Diffraction Data: Newtown Square, PA, USA, 2004. [Google Scholar]
- Bellizzi, G.; Bucci, O.M.; Chirico, G. Numerical assessment of a criterion for the optimal choice of the operative conditions in magnetic nanoparticle hyperthermia on a realistic model of the human head. Int. J. Hyperth. 2016, 32, 688–703. [Google Scholar] [CrossRef]
- Dennis, C.L.; Krycka, K.L.; Borchers, J.A.; Desautels, R.D.; Van Lierop, J.; Huls, N.F.; Jackson, A.J.; Gruettner, C.; Ivkov, R. Internal Magnetic Structure of Nanoparticles Dominates Time-Dependent Relaxation Processes in a Magnetic Field. Adv. Funct. Mater. 2015, 25, 4300–4311. [Google Scholar] [CrossRef]
- Conde-Leborán, I.; Serantes, D.; Baldomir, D. Orientation of the magnetization easy axes of interacting nanoparticles: Influence on the hyperthermia properties. J. Magn. Magn. Mater. 2015, 380, 321–324. [Google Scholar] [CrossRef]
- Arciniegas, M.P.; Castelli, A.; Brescia, R.; Serantes, D.; Ruta, S.; Hovorka, O.; Satoh, A.; Chantrell, R.; Pellegrino, T. Unveiling the Dynamical Assembly of Magnetic Nanocrystal Zig-Zag Chains via In Situ TEM Imaging in Liquid. Small 2020, 16. [Google Scholar] [CrossRef]
- Balakrishnan, P.B.; Silvestri, N.; Fernandez-Cabada, T.; Marinaro, F.; Fernandes, S.; Fiorito, S.; Miscuglio, M.; Serantes, D.; Ruta, S.; Livesey, K.; et al. Exploiting Unique Alignment of Cobalt Ferrite Nanoparticles, Mild Hyperthermia, and Controlled Intrinsic Cobalt Toxicity for Cancer Therapy. Adv. Mater. 2020, 32. [Google Scholar] [CrossRef]
- García-Otero, J.; Porto, M.; Rivas, J.; Bunde, A. Influence of the cubic anisotropy constants on the hysteresis loops of single-domain particles: A Monte Carlo study. J. Appl. Phys. 1999, 85, 2287–2292. [Google Scholar] [CrossRef]
- Johnson, C.E.; Brown, W.F. Stoner-Wohlfarth Calculation on Particle with Both Magnetocrystalline and Shape Anisotropy. J. Appl. Phys. 1959, 30, S320–S322. [Google Scholar] [CrossRef]



| AC Field (kA/m) | Specific Loss Power (W/g) | |
|---|---|---|
| Spherical | Cubic | |
| 24 | 62 (±4) | 83 (±4) |
| 40 | 156 (±8) | 292 (±11) |
| 48 | 278 (±12) | 374 (±13) |
| Reference | System | Size (nm) | Frequency (kHz) | SLP (W/g) |
|---|---|---|---|---|
| [22] | CoFe2O4@MnFe2O4 | 15 | 500 | 2280 |
| [23] | ZnFe2O4/CoFe2O4 | 70 | 500 | 10,600 |
| [24] | CoFe2O4@MnFe2O4 | 30 | 500 | 10,810 |
| [25] | (Zn,Co,Mn)Fe2O4 | 9 | 850 | 97 |
| [27] | MnFe2O4@CoFe2O4 | 81 | 765 | 525 |
| [28] | CoFe2O4@(Ni,Zn)Fe2O4 | 10 | 265 | 25 |
| [29] | (Zn,Co)Fe2O4@MnFe2O4 | 11 | 1955 | 520 |
| [30] | Fe3O4@(Zn,Co)Fe2O4 | 9.4 | 817 | 190 |
| [31] | CoFe2O4@MnFe2O4 | 14.4 | 1950 | 320 |
| [32] | CoFe2O4@Fe3O4 | 12.8 | 183 | 59 |
| [33] | Fe3O4@(Zn,Co)Fe2O4 | 13 | 97 | 380 |
| [35] | (Zn,Co)Fe2O4@(Zn,Mn)Fe2O4 | 7.6 | 200 | 1343 |
| [36] | (Co,Mn)Fe2O4 | 15 | 420 | 1718 |
| [37] | (Co,Mn)Fe2O4 | 22 | 380 | 3417 |
| [38] | Zn-doped Fe3O4 | 40 | 293 | 1675 |
| [39] | Fe3O4@(Co,Zn)Fe2O4 | 18 | 309 | 2400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez-Boubeta, C.; Simeonidis, K.; Oró, J.; Makridis, A.; Serantes, D.; Balcells, L. Finding the Limits of Magnetic Hyperthermia on Core-Shell Nanoparticles Fabricated by Physical Vapor Methods. Magnetochemistry 2021, 7, 49. https://doi.org/10.3390/magnetochemistry7040049
Martinez-Boubeta C, Simeonidis K, Oró J, Makridis A, Serantes D, Balcells L. Finding the Limits of Magnetic Hyperthermia on Core-Shell Nanoparticles Fabricated by Physical Vapor Methods. Magnetochemistry. 2021; 7(4):49. https://doi.org/10.3390/magnetochemistry7040049
Chicago/Turabian StyleMartinez-Boubeta, Carlos, Konstantinos Simeonidis, Judit Oró, Antonios Makridis, David Serantes, and Lluis Balcells. 2021. "Finding the Limits of Magnetic Hyperthermia on Core-Shell Nanoparticles Fabricated by Physical Vapor Methods" Magnetochemistry 7, no. 4: 49. https://doi.org/10.3390/magnetochemistry7040049
APA StyleMartinez-Boubeta, C., Simeonidis, K., Oró, J., Makridis, A., Serantes, D., & Balcells, L. (2021). Finding the Limits of Magnetic Hyperthermia on Core-Shell Nanoparticles Fabricated by Physical Vapor Methods. Magnetochemistry, 7(4), 49. https://doi.org/10.3390/magnetochemistry7040049








