Eliashberg Theory of a Multiband Non-Phononic Spin Glass Superconductor
Abstract
1. Introduction
2. The Model
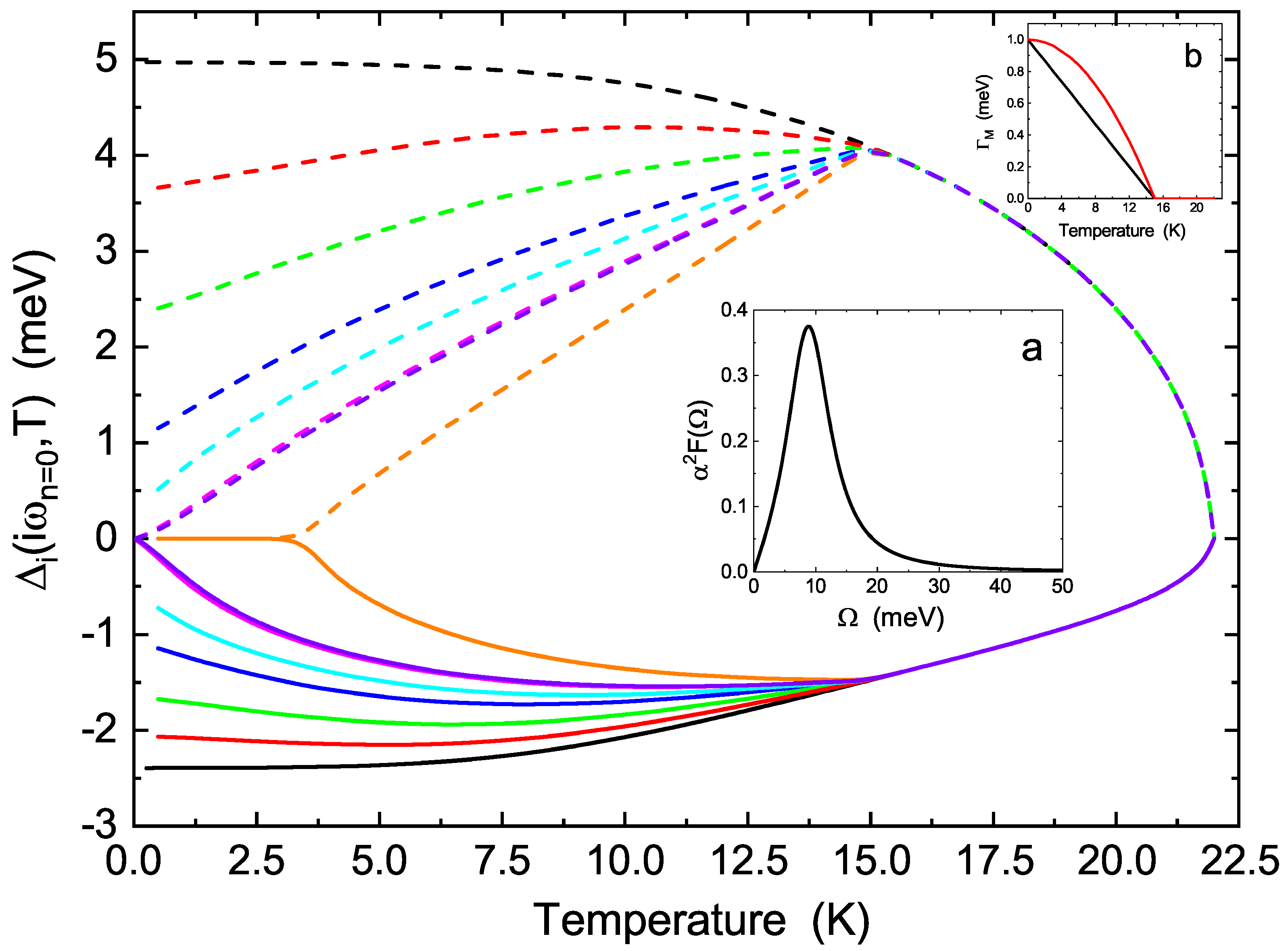
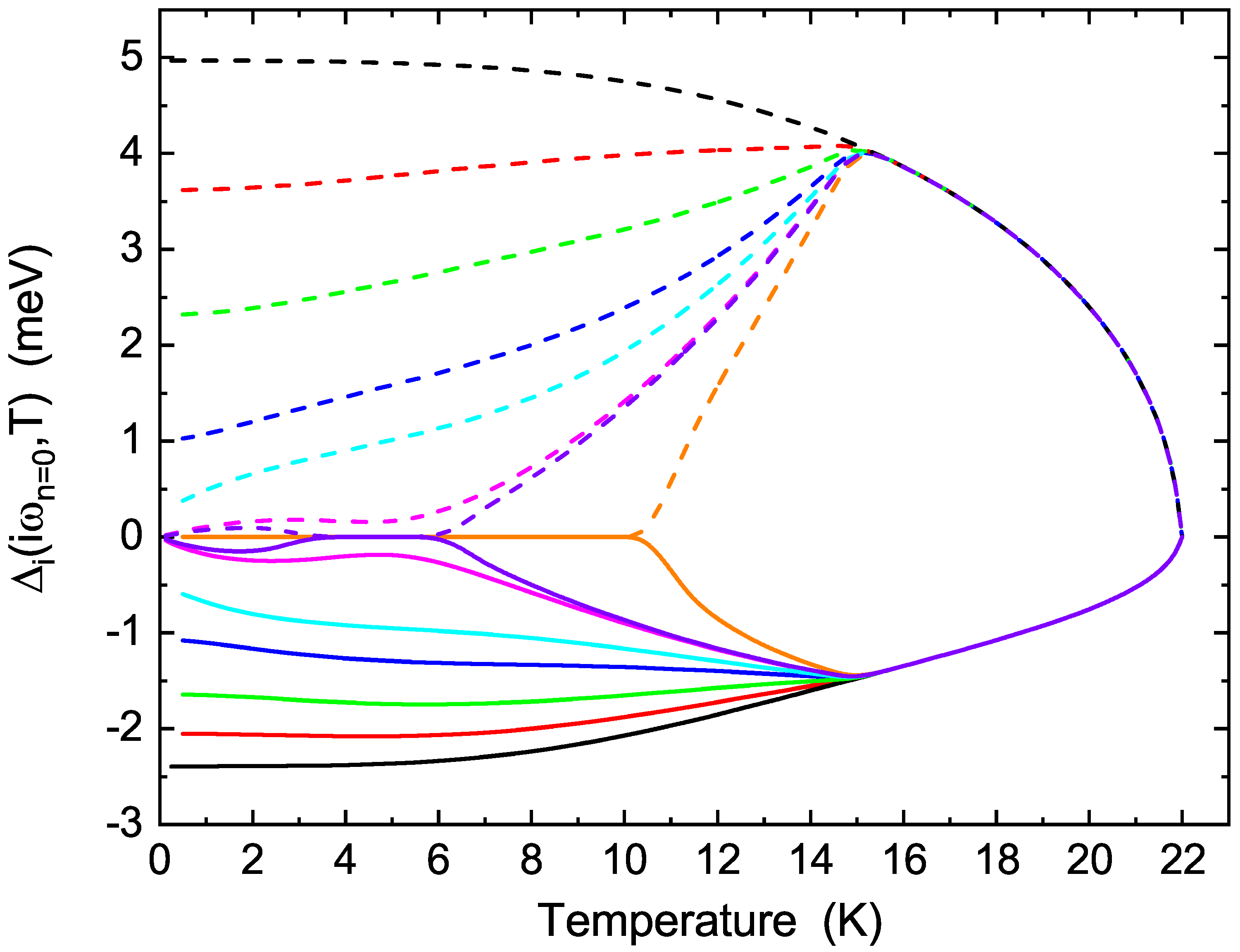
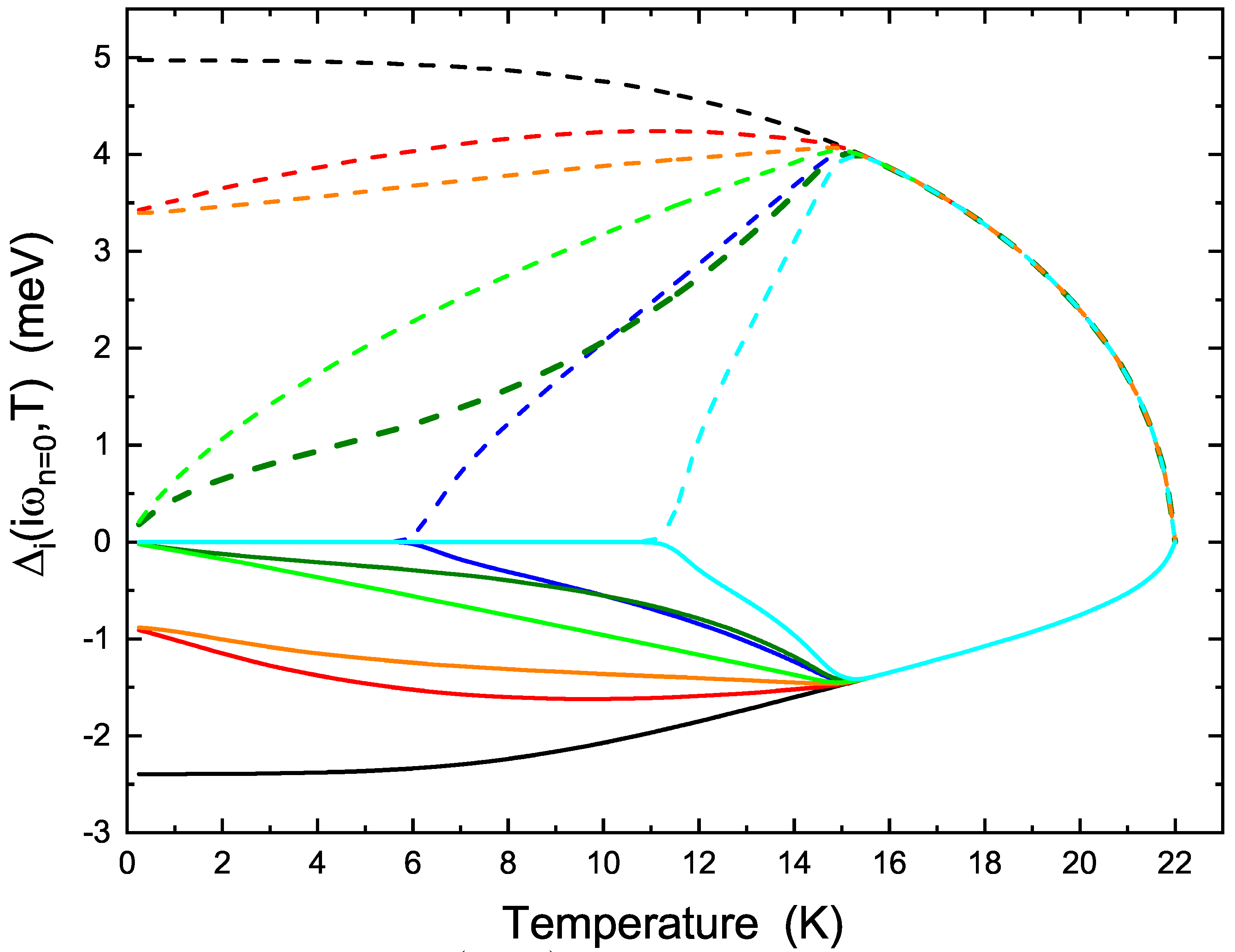
3. Calculation of Superconducting Gaps
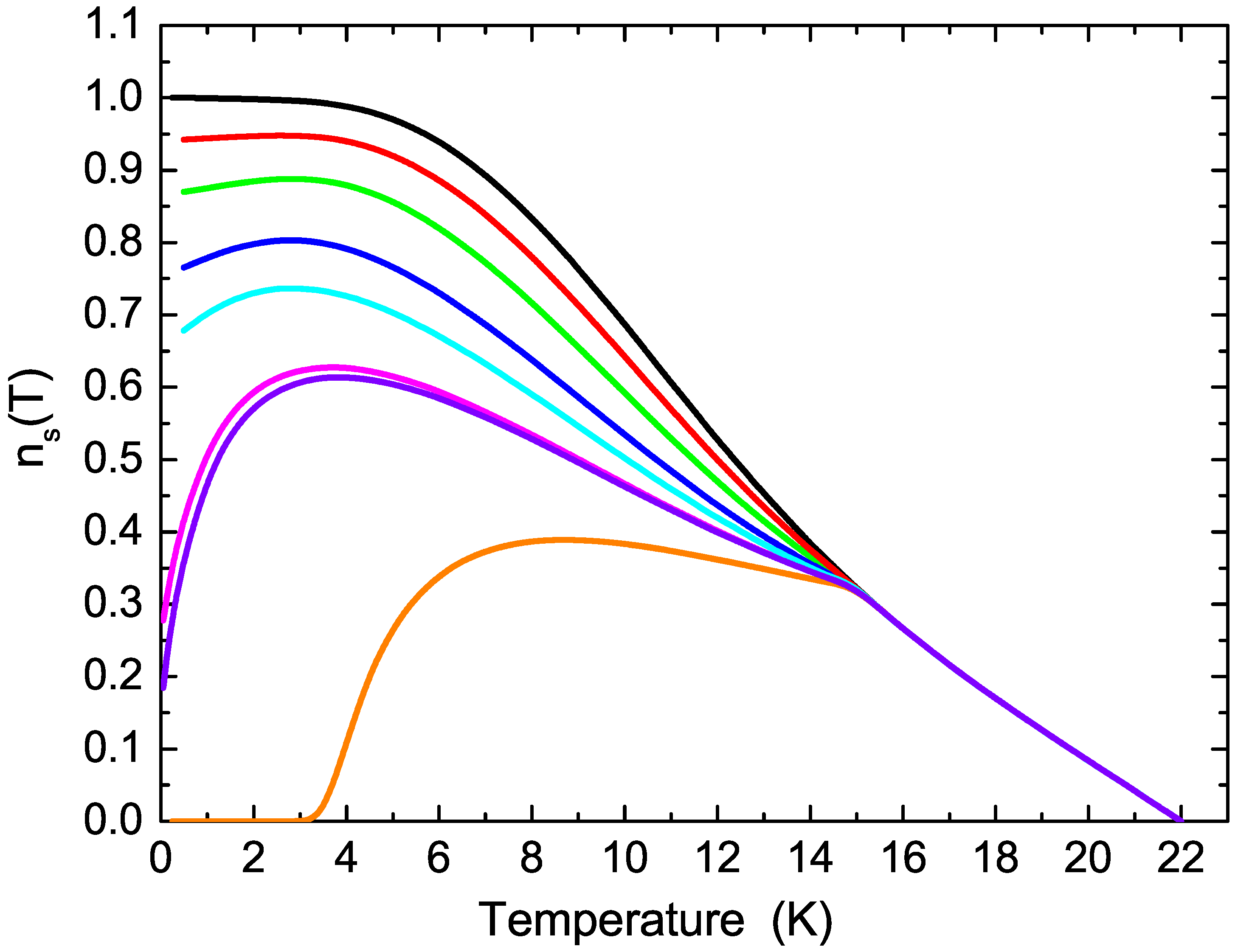
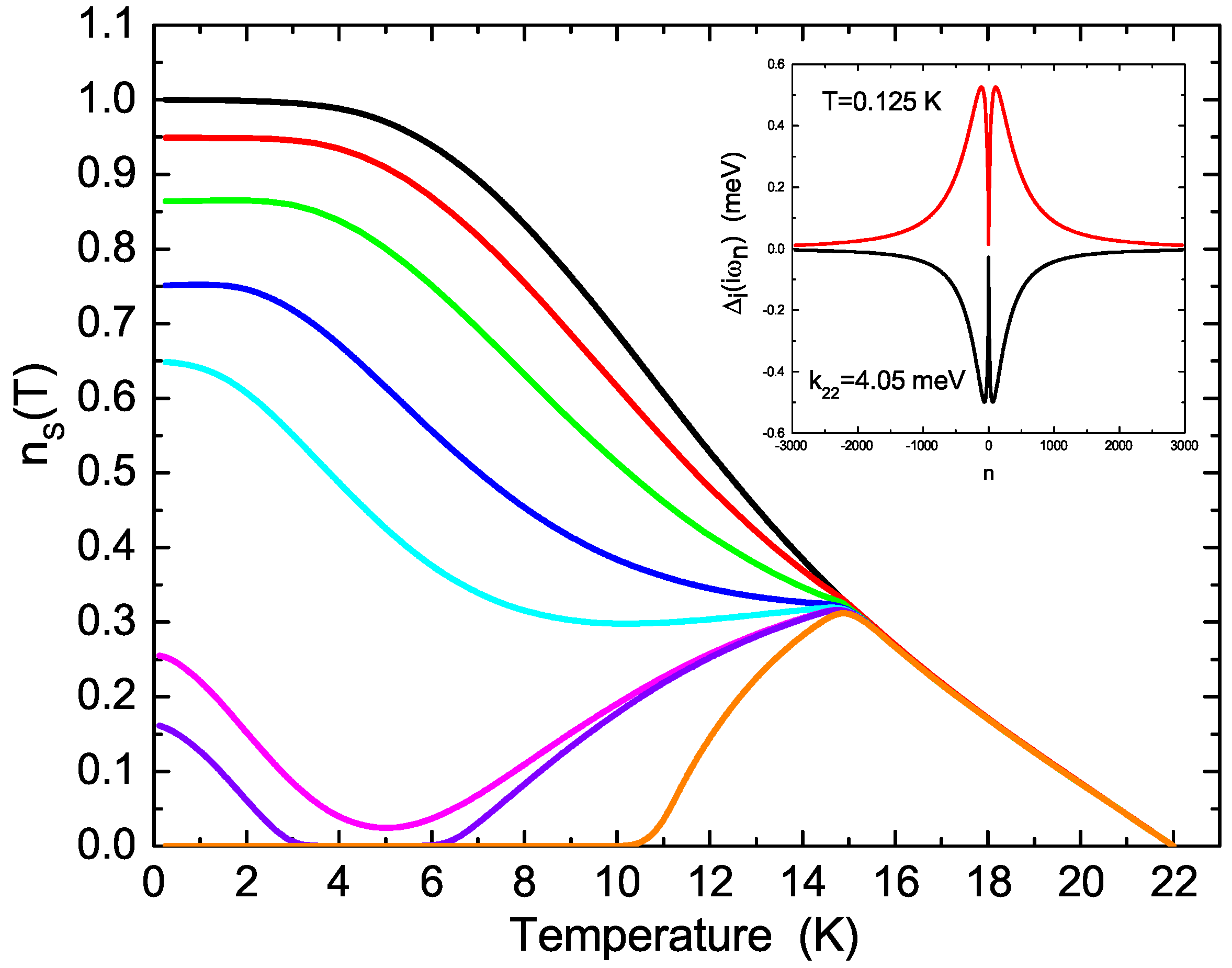
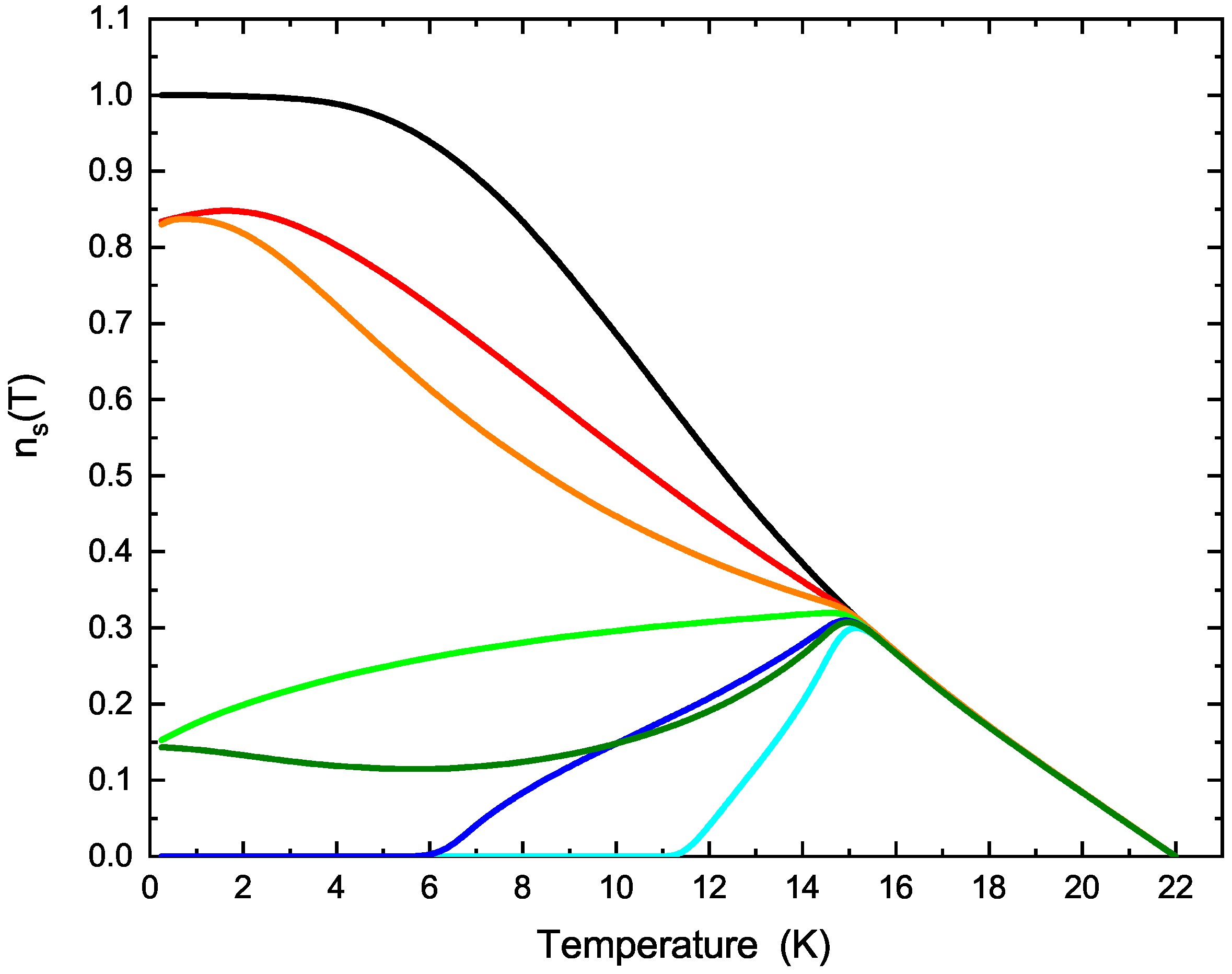
4. Calculation of the Penetration Depth
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Nandi, S.; Jin, W.T.; Xiao, Y.; Su, Y.; Price, S.; Shukla, D.K.; Strempfer, J.; Jeevan, H.S.; Gegenwart, P.; Bruckel1, T. Coexistence of superconductivity and ferromagnetism in P-doped EuFe2As2. Phys. Rev. B 2014, 89, 014512. [Google Scholar] [CrossRef]
- Ghigo, G.; Torsello, D.; Gozzelino, L.; Tamegai, T.; Veshchunov, I.S.; Pyon, S.; Jiao, W.; Cao, G.-H.; Grebenchuk, S.Y.; Golovchanskiy, I.A.; et al. Microwave analysis of the interplay between magnetism and superconductivity in EuFe2(As1-xPx)2 single crystals. Phys. Rev. Res. 2019, 1, 033110. [Google Scholar] [CrossRef]
- Jin, W.T.; Xiao, Y.; Su, Y.; Nandi, S.; Jiao, W.H.; Nisbet, G.; Demirdis, S.; Cao, G.H.; Bruckel1, T. Magnetic polarization of Ir in underdoped nonsuperconducting Eu(Fe0.94Ir0.06)2As2. Phys. Rev. B 2016, 93, 024517. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.-B.; Tang, Z.-T.; Jiang, H.; Wang, Z.-C.; Ablimit, A.; Jiao, W.-H.; Tao, Q.; Feng, C.-M.; Xu, Z.-A.; et al. Superconductivity and ferromagnetism in hole-doped RbEuFe4As4. Phys. Rev. B 2016, 93, 214503. [Google Scholar] [CrossRef]
- Zapf, S.; Jeevan, H.S.; Ivek, T.; Pfister, F.; Klingert, F.; Jiang, S.; Wu, D.; Gegenwart, P.; Kremer, R.K.; Dressel, M. EuFe2(As1-xPx)2: Reentrant Spin Glass and Superconductivity. Phys. Rev. Lett. 2013, 110, 237002. [Google Scholar] [CrossRef]
- Neubauer, D.; Pronin, A.V.; Zapf, S.; Merz, J.; Jeevan, H.S.; When-He, J.; Gegenwart, P.; Guang-Han, C.; Dressel, M. Optical properties of superconducting EuFe2(As1-xPx)2. Phys. Status Solidi B 2017, 254, 1600148. [Google Scholar] [CrossRef]
- Zapf, S.; Dressel, M. Europium-based iron pnictides: A unique laboratory for magnetism, superconductivity and structural effects. Rep. Prog. Phys. 2017, 80, 016501. [Google Scholar] [CrossRef]
- Ghigo, G.; Torsello, D.; Gerbaldo, R.; Gozzelino, L.; Pyon, S.; Veshchunov, I.S.; Tamegai, T.; Cao, G.-H. Effects of proton irradiation on the magnetic superconductor EuFe2(As1-xPx)2. SUST 2020, 33, 094011. [Google Scholar]
- Mezard, M.; Parisi, G.; Virasoro, M. Spin Glass Theory and Beyond: An Introduction to the Replica Method and Its Applications; World Scientific Publishing Company: Singapore, 1987. [Google Scholar]
- Davidov, D.; Davidov, D.; Mydosh, J.A.; Nieuwenhuys, G.J.; Baberschke, K. Coexistence of superconductivity and spin glass magnetic freezing. J. Phys. F 1977, 7, L47. [Google Scholar] [CrossRef]
- Bud’ko, S.L.; Strand, J.D.; Anderson, N.E., Jr.; Ribeiro, R.A.; Canfield, P.C. Evolution from long-range order to Kondo lattice in Gd1-xYbxNi2B2C. Phys. Rev. B 2003, 68, 104417. [Google Scholar] [CrossRef]
- Bud’ko, S.L.; Kogan, V.G.; Hodovanets, H.; Ran, S.; Moser, S.A.; Lampe, M.J.; Canfield, P.C. Evolution of ground state and upper critical field in R1-xGdxNi2B2C (R=Lu,Y): Coexistence of superconductivity and spin-glass state. Phys.Rev. B 2010, 82, 174513. [Google Scholar] [CrossRef]
- Nass, M.J.; Levin, K.; Grest, G.S. Magnetic Fine Structure in Superconducting Tunneling: Spin-Glass Superconductors. Phys. Rev. Lett. 1980, 45, 2070. [Google Scholar] [CrossRef]
- Nass, M.J.; Levin, K.; Grest, G.S. Coexistence of magnetism and superconductivity: Tunneling characteristics of magnetic superconductors. Phys. Rev. B 1981, 23, 1111. [Google Scholar] [CrossRef]
- Nass, M.J.; Levin, K.; Grest, G.S. Impurity and spin-fluctuation effects in antiferromagnetic superconductors. Phys. Rev. B 1982, 25, 4541. [Google Scholar] [CrossRef]
- Stephan, W.; Carbotte, J.P. Spin-glass superconductor: Thermodynamics. J. Low Temp. Phys. 1991, 83, 131. [Google Scholar] [CrossRef]
- Schachinger, E.; Stephan, W.; Carbotte, J.P. Quasiparticle density of states for a spin-glass superconductor. Phys. Rev. B 1988, 37, 5003. [Google Scholar] [CrossRef]
- Nicol, E.J.; Carbotte, J.P. Thermodynamic and electromagnetic properties of a spin-glass superconductor. Phys. Rev. B 1992, 45, 10509. [Google Scholar] [CrossRef]
- Gonzalez, A.P.; Nicol, E.J.; Carbotte, J.P. Upper critical field of a spin-glass superconductor. Phys. Rev. B 1992, 45, 5055. [Google Scholar] [CrossRef]
- Hoshino, S.; Werner, P. Superconductivity from Emerging Magnetic Moments. Phys. Rev. Lett. 2015, 115, 247001. [Google Scholar] [CrossRef]
- Steiner, K.; Hoshino, S.; Nomura, Y.; Werner, P. Long-range orders and spin/orbital freezing in the two-band Hubbard model. Phys. Rev. B 2016, 94, 075107. [Google Scholar] [CrossRef]
- Hoshino, S.; Werner, P. Spontaneous Orbital-Selective Mott Transitions and the Jahn-Teller Metal of A3C60. Phys. Rev. Lett. 2017, 118, 177002. [Google Scholar] [CrossRef]
- Werner, P.; Hoshino, S.; Shinaoka, H. Spin-freezing perspective on cuprates. Phys. Rev. B 2016, 94, 245134. [Google Scholar] [CrossRef]
- Werner, P.; Chen, X.; Gull, E. Ferromagnetic spin correlations in the two-dimensional Hubbard model. Phys. Rev. Research 2020, 2, 023037. [Google Scholar] [CrossRef]
- Mazin, I.I.; Schmalian, J. Pairing symmetry and pairing state in ferropnictides: Theoretical overview. Phys. C 2009, 469, 614. [Google Scholar] [CrossRef]
- Hirschfeld, P.J.; Korshunov, M.M.; Mazin, I.I. Gap symmetry and structure of Fe-based superconductors. Rep. Prog. Phys. 2011, 74, 124508. [Google Scholar] [CrossRef]
- Torsello, D.; Ummarino, G.A.; Gozzelino, L.; Tamegai, T.; Ghigo, G. Comprehensive Eliashberg analysis of microwave conductivity and penetration depth of K-, Co-, and P-substituted BaFe2As2. Phys. Rev. B 2019, 99, 134518. [Google Scholar] [CrossRef]
- Graser, S.; Maier, T.A.; Hirschfeld, P.J.; Scalapino, D.J. Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. New J. Phys. 2009, 11, 025016. [Google Scholar] [CrossRef]
- Korshunov, M.M.; Togushova, Y.N.; Dolgov, O.V. Impurities in multiband superconductors. Phys. Uspekhi 2016, 59, 1211. [Google Scholar] [CrossRef]
- Koizumi, H. Explanation of Superfluidity Using the Berry Connection for Many-Body Wave Functions. J. Supercond. Nov. Magn. 2020, 33, 1697. [Google Scholar] [CrossRef]
- Koizumi, H. Possible Occurrence of Superconductivity by the π-flux Dirac String Formation Due to Spin-Twisting Itinerant Motion of Electrons. Symmetry 2020, 12, 776. [Google Scholar] [CrossRef]
- Koizumi, H. Reversible superconducting-normal phase transition in a magnetic field and the existence of topologically protected loop currents that appear and disappear without Joule heating. EPL 2020, 131, 37001. [Google Scholar] [CrossRef]
- Kim, T.K.; Pervakov, K.S.; Evtushinsky, D.V.; Jung, S.W.; Poelchen, G.; Kummer, K.; Vlasenko, V.A.; Pudalov, V.M.; Roditchev, D.; Stolyarov, V.S.; et al. When superconductivity does not fear magnetism: Insight into electronic structure of RbEuFe4As4. arXiv 2008, arXiv:2008.00736v1. [Google Scholar]
- Mazin, I.I.; Singh, D.J.; Johannes, M.D.; Du, M.H. Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO1-xFx. Phys. Rev. Lett. 2008, 101, 057003. [Google Scholar] [CrossRef]
- Charnukha, A.; Dolgov, O.V.; Golubov, A.A.; Matiks, Y.; Sun, D.L.; Lin, C.T.; Keimer, B.; Boris, A.V. Eliashberg approach to infrared anomalies induced by the superconducting state of Ba0.68K0.32Fe2As2 single crystals. Phys. Rev. B 2011, 84, 174511. [Google Scholar] [CrossRef]
- Torsello, D.; Cho, K.; Joshi, K.R.; Ghimire, S.; Ummarino, G.A.; Nusran, N.M.; Tanatar, M.A.; Meier, W.R.; Xu, M.; Bud’ko, S.L.; et al. Analysis of the London penetration depth in Ni-doped CaKFe4As4. Phys. Rev. B 2019, 100, 094513. [Google Scholar] [CrossRef]
- Eliashberg, G.M. Interation between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP 1960, 11, 696. [Google Scholar]
- Chubukov, A.V.; Pines, D.; Schmalian, J. A Spin Fluctuation Model for d-Wave Superconductivity. In Superconductivity Volume II. Superconductivity:Novel Superconductors; Bennemann, K.H., Ketterson, J.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Chapter 22; p. 1349. [Google Scholar]
- Manske, D.; Eremin, I.; Bennemann, K.H. Electronic Theory for Superconductivity in High-Tc Cuprates and Sr2RuO4. In Superconductivity Volume II. Superconductivity:Novel Superconductors; Bennemann, K.H., Ketterson, J.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Chapter 23; p. 1415. [Google Scholar]
- Torsello, D.; Ummarino, G.A.; Gerbaldo, R.; Gozzelino, L.; Ghigo, G. Eliashberg Analysis of the Electrodynamic Response of Ba(Fe1-xRhx)2As2 Across the s± to s++ Order Parameter Transition. J. Supercond. Nov. Magn. 2020, 33, 2319–2324. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Tortello, M.; Daghero, D.; Gonnelli, R.S. Three-band s± Eliashberg theory and the superconducting gaps of iron pnictides. Phys. Rev. B 2009, 80, 172503. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Tortello, M.; Daghero, D.; Gonnelli, R.S. Predictions of Multiband s± Strong-Coupling Eliashberg Theory Compared to Experimental Data in Iron Pnictides. J. Supercond. Nov. Magn. 2011, 24, 247. [Google Scholar] [CrossRef]
- Ummarino, G.A. Multiband s± Eliashberg theory and temperature-dependent spin-resonance energy in iron pnictide superconductors. Phys. Rev. B 2011, 83, 092508. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Galasso, S.; Sanna, A. A phenomenological multiband Eliashberg model for LiFeAs. J. Phys. Condens. Matter 2013, 25, 205701. [Google Scholar] [CrossRef][Green Version]
- Ummarino, G.A. Phenomenology of CaKFe4As4 explained in the framework of four bands Eliashberg theory. Phys. C 2016, 529, 50. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Muratov, A.V.; Kadyrov, L.S.; Gorshunov, B.P.; Richter, S.; Thomas, A.A.; Huhne, R.; Aleshchenko, Y.A. THz electrodynamics of BaFe1.91Ni0.09As2 film analyzed in the framework of multiband Eliashberg theory. Supercond. Sci. Technol. 2020, 33, 075005. [Google Scholar] [CrossRef]
- Boeri, L.; Calandra, M.; Mazin, I.I.; Dolgov, O.V.; Mauri, F. Effects of magnetism and doping on the electron-phonon coupling in BaFe2As2. Phys. Rev. B 2010, 82, 020506. [Google Scholar] [CrossRef]
- Inosov, D.S.; Park, J.T.; Bourges, P.; Sun, D.L.; Sidis, Y.; Schneidewind, A.; Hradil, K.; Haug, D.; Lin, C.T.; Keimer, B.; et al. Normal-State Spin Dynamics and Temperature-Dependent Spin Resonance Energy in an Optimally Doped Iron Arsenide Superconductor. Nat. Phys. 2010, 6, 178. [Google Scholar] [CrossRef]
- Ghigo, G.; Torsello, D.; Ummarino, G.A.; Gozzelino, L.; Tanatar, M.A.; Prozorov, R.; Canfield, P.C. Disorder-Driven Transition from s± to s++ Superconducting Order Parameter in Proton Irradiated Ba(Fe1-xRhx)2As2 Single Crystals. Phys. Rev. Lett. 2018, 121, 107001. [Google Scholar] [CrossRef]
- Paglione, J.; Greene, R.L. High-temperature superconductivity in iron-based materials. Nat. Phys. 2010, 6, 645. [Google Scholar] [CrossRef]
- Inosov, D.S.; Park, J.T.; Charnukha, A.; Li, Y.; Boris, A.V.; Keimer, B.; Hinkov, V. Crossover from weak to strong pairing in unconventional superconductors. Phys. Rev. B 2011, 83, 214520. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Galasso, S.; Pecchio, P.; Daghero, D.; Gonnelli, R.S.; Kurth, F.; Iida, K.; Holzapfel, B. Resistivity in Ba(FeCo)As: Comparison of thin films and single crystals. Phys. Status Solidi B 2015, 252, 821–827. [Google Scholar] [CrossRef][Green Version]
- Aleshchenko, Y.A.; Muratov, A.V.; Ummarino, G.A.; Richter, S.; Thomas, A.A.; Huhne, R. Optical and hidden transport properties of BaFe1.91Ni0.09As2 film. J. Phys. Condens. Matter, 2020; 32. [Google Scholar] [CrossRef]
- Torsello, D.; Gerbaldo, R.; Gozzelino, L.; Tanatar, M.; Prozorov, R.; Canfield, P.C.; Ghigo, G. Electrodynamic response of Ba(Fe1-xRhx)2As2 across the s± to s++ order parameter transition. Eur. Phys. J. Spec. Top. 2019, 228, 719. [Google Scholar] [CrossRef]
- Golubov, A.A.; Dolgov, O.V.; Boris, A.V.; Charnukha, A.; Sun, D.L.; Lin, C.T.; Shevchun, A.F.; Korobenko, A.V.; Trunin, M.R.; Zverev, V.N. Normal state resistivity of Ba1-xKxFe2As2: Evidence for multiband strong-coupling behavior. JETP Lett. 2011, 94, 333–337. [Google Scholar] [CrossRef][Green Version]
- Seiichiro, O.; Hiroshi, K. Violation of Anderson’s theorem for the sign-reversing s-wave state of iron-pnictide superconductors. Phys. Rev. Lett. 2009, 103, 177001. [Google Scholar]
- Prozorov, R.; Ko’nczykowski, M.; Tanatar, M.A.; Thaler, A.; Bud’ko, S.L.; Canfield, P.C.; Mishra, V.; Hirschfeld, P.J. Effect of Electron Irradiation on Superconductivity in Single Crystals of Ba(Fe1-xRux)2As2 (x=0.24). Phys. Rev. X 2014, 4, 041032. [Google Scholar]
- Mizukami, Y.; Konczykowski, M.; Kawamoto, Y.; Kurata, S.; Kasahara, S.; Hashimoto, K.; Mishra, V.; Kreisel, A.; Wang, Y.; Hirschfeld, P.J.; et al. Disorder-induced topological change of the superconducting gap structure in iron pnictides. Nature Commun. 2014, 5, 5657. [Google Scholar] [CrossRef] [PubMed]
- Efremov, D.V.; Drechsler, S.; Rosner, H.; Grinenko, V.; Dolgov, O.V. A multiband Eliashberg approach to iron based superconductors. Physica Status Solidi B 2017, 254, 1600828. [Google Scholar] [CrossRef]
- Korshunov, M.M.; Efremov, D.V.; Golubov, A.A.; Dolgov, O.V. Unexpected impact of magnetic disorder on multiband superconductivity. Phys. Rev. B 2014, 90, 134517. [Google Scholar] [CrossRef]
- Torsello, D.; Ummarino, G.A.; Bekaert, J.; Gozzelino, L.; Gerbaldo, R.; Tanatar, M.A.; Canfield, P.C.; Prozorov, R.; Ghigo, G. Effects of disorder induced by heavy-ion irradiation on (Ba1-xKx)Fe2As2 single crystals, within the three-band Eliashberg s± wave model. Sci. Rep. 2017, 7, 13029. [Google Scholar]
- Dolgov, O.V.; Mazin, I.I.; Parker, D.; Golubov, A.A. Two-band BCS mechanism of superconductivity in a Ba(Fe0.9Co0.1)2As2 high-temperature superconductor. Phys. Rev. B 2009, 79, 060502R. [Google Scholar] [CrossRef]
- Hemmida, M.; von Nidda, H.-A.K.; Gunther, A.; Loidl, A.; Leithe-Jasper, A.; Schnelle, W.; Rosner, H.; Sichelschmidt, J. Probing the density of states in EuFe2-xRuxAs2. Phys. Rev. B 2014, 90, 205105. [Google Scholar] [CrossRef]
- Shestakov, V.A.; Korshunov, M.M.; Dolgov, O.V. Temperature-Dependent s±⟷s++ Transitions in the Multiband Model for Fe-Based Superconductors with Impurities. Symmetry 2018, 10, 323. [Google Scholar] [CrossRef]
- Ummarino, G.A. Effects of magnetic impurities on two-band superconductor. J. Supercond. Nov. Magn. 2007, 20, 639. [Google Scholar] [CrossRef][Green Version]
- Golubov, A.A.; Brinkman, A.; Dolgov, O.V.; Kortus, J.; Jepsen, O. Multiband model for penetration depth in MgB2. Phys. Rev. B 2002, 66, 054524. [Google Scholar] [CrossRef]
- Torsello, D.; Ummarino, G.A.; Bekaert, J.; Gozzelino, L.; Gerbaldo, R.; Tanatar, M.A.; Canfield, P.C.; Prozorov, R.; Ghigo, G. Tuning the Intrinsic Anisotropy with Disorder in the CaKFe4As4 Superconductor. Phys. Rev. Appl. 2020, 13, 064046. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ummarino, G.A. Eliashberg Theory of a Multiband Non-Phononic Spin Glass Superconductor. Magnetochemistry 2020, 6, 51. https://doi.org/10.3390/magnetochemistry6040051
Ummarino GA. Eliashberg Theory of a Multiband Non-Phononic Spin Glass Superconductor. Magnetochemistry. 2020; 6(4):51. https://doi.org/10.3390/magnetochemistry6040051
Chicago/Turabian StyleUmmarino, Giovanni Alberto. 2020. "Eliashberg Theory of a Multiband Non-Phononic Spin Glass Superconductor" Magnetochemistry 6, no. 4: 51. https://doi.org/10.3390/magnetochemistry6040051
APA StyleUmmarino, G. A. (2020). Eliashberg Theory of a Multiband Non-Phononic Spin Glass Superconductor. Magnetochemistry, 6(4), 51. https://doi.org/10.3390/magnetochemistry6040051




