Abstract
A one-dimensional coordination polymer was synthesized employing hepta-coordinate CoII as nodes and dicyanamide as linkers. Detailed direct current (DC) and alternating current (AC) magnetic susceptibility measurements reveal the presence of field-induced slow magnetic relaxation behavior of the magnetically isolated seven-coordinate CoII center with an easy-plane magnetic anisotropy. Detailed ab initio calculations were performed to understand the magnetic relaxation processes. To our knowledge, the reported complex represents the first example of slow magnetic relaxation in a one-dimensional coordination polymer constructed from hepta-coordinate CoII nodes and dicyanamide linkers.
1. Introduction
In the past few decades, the design and synthesis of coordination polymers (CPs) have attracted significant attention because of their different structural dimensionalities (1D, 2D and 3D), interesting topologies and potential applications [1,2,3,4]. The metal ions in CPs are the source of some interesting physical properties including magnetism apart from their structural role. In recent years, rapid developments in the field of single molecule magnets (SMMs) have been observed because of their applications in data storage, quantum computing, and spintronic [5,6,7]. The smallest possible SMMs are known as single ion magnets (SIMs), where slow magnetic relaxation occurs from a single metal center [8]. The most interesting feature of single ion magnets (SIMs) lies in the possible tuning of their magnetic anisotropy through the regulation of the coordination number and ligand field. Along with the lanthanides-based SIMs [9,10,11,12,13,14], there has been significant research interest in transition metal-based SIMs [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. In the family of 3D-SIMs, CoII-based complexes draw significant attention because of their non-integer spin ground state, which decreases the probability of quantum tunneling of magnetization (QTM) [38]. Most of the CoII-based SIMs reported so far concern mononuclear complexes and less interest has been given for making CoII-containing CPs. In 2014, Andruh et al. first reported two CoII-based 2D CPs using linear and angular ligands simultaneously where the well-separated six-coordinated CoII centers behave as SIMs [39]. In 2015, Gao et al. also reported a one-dimensional CoII CP in which the independently six-coordinated CoII ions feature SIM behaviour [40]. The abovementioned examples were based on magnetically separated octahedral CoII ions, but less attention has been given to prepare hepta-coordinate CoII centers as building blocks for the construction of 1D CoII-based single-ion-magnet. In recent times, it has been observed that the hepta-coordinate CoII SIMs are very attractive candidates due to their large magnetic anisotropy [41,42,43,44,45,46,47,48,49,50]. Furthermore, these systems can serve as excellent building blocks for the preparation of larger clusters due to the labile axial ligands. Huang et al. reported the first example of field induced SIM behavior of pentagonal-bipyramidal CoII complex [42]. The positive sign of D parameter was verified by experimentally and theoretically [41,42,43,44,45,46,47] and further confirmed by high-field electron paramagentic resonance (HFEPR) [49]. In the case of a pentagonal-bipyramidal CoII system, the spin-orbit coupling between ground electronic states with two excited electronic states results in the easy plane magnetic anisotropy. Therefore, significant efforts have been made in order to modulate the easy plane magnetic anisotropy by modulation of the coordination environment of various pentagonal-bipyramidal CoII complexes [43,45]. In our earlier report on pentagonal-bipyramidal CoII complexes [41], we showed that either by employing a better σ donor axial ligand or by using a symmetric equatorial ligand, it is possible to decrease the magnitude of the D parameters as well as the energy barrier. Both experimental and ab initio calculations disclosed that the sign of the D parameter is generally unaffected by the change in coordination environments, whereas the appropriate weak σ-donor axial ligand can be able to considerably increase the magnitude of the D parameter in pentagonal-bipyramidal CoII complex [41].
Inspired by the aforementioned consideration, we prepared a CoII-based 1D coordination polymer, [Co(H3daps)(dca)]·(MeOH)2·(MeCN) (1, where H4daps = 2,6-bis(1-salicyloylhydrazonoethyl) pyridine and dca = dicyanamide) employing hepta-coordinate CoII as nodes and dicyanamide as linkers in which the well-separated seven-coordinated CoII centers behave as SIMs. The magnetic study reveals field-induced slow relaxation behavior of the magnetically isolated seven-coordinate CoII centers with an easy-plane magnetic anisotropy.
2. Results and Discussion
The reaction of H4daps ligand with methanolic solution of Co(ClO4)2·H2O and aqueous solution of NaN(CN)2 under ambient condition gave complex 1. The final reaction was filtered after additional stirring for 3 h and then was kept for crystallization, which gave X-ray quality red crystals of complex 1 (for details procedure, see Materials and Methods section). Single-crystal X-ray analysis revealed that complex 1 crystallized in the orthorhombic Pbca space group (Table S1). The CoII center is ligated around the equatorial plane by a pentadentate H4daps ligand and the axial positions are occupied by the cyano N atoms of two crystallographically equivalent {N(CN)2} units (Figure 1). The two N atoms of the bridging {N(CN)2} moiety binds to CoII center in a cis-μ2-N-coordination mode, resulting in an anti-configuration for the zigzag one-dimensional (1D) framework. Systematic analysis of the coordination geometry around the metal using SHAPE 2.1 [51] reveals that the seven-coordinate CoII center displays a distorted pentagonal bipyramid coordination geometry (Figure S1) with a minimum CShM value of 0.244 (Table S2). The ligand bite angles range from 71.27(3)° (for Npyridyl–Co–N) to 76.82(4)° (for O–Co–O) (Table S3). The shortest intra-chain Co···Co distance is 7.980(3) Å, whereas the shortest inter-chain Co···Co distance equals 10.674(2) Å. The chains run parallel to the crystallographic c-axis (Figure 1). Lattice methanol molecules are involved in intermolecular hydrogen bonding with the carbonyl oxygen atoms and phenoxy oxygen atoms of the ligand (Table S4). Additionally, there are significant π-interactions and hydrogen-bonding networks between the chains and the interstitial solvent molecules (methanol and acetonitrile), which also supports the formation of a supramolecular two dimensional arrangement (Figures S2–S4). The large intra and inter-chain Co···Co distances play a significant role to make them magnetically isolated seven-coordinate CoII centers and allows us to measure the single ion magnetic behavior.
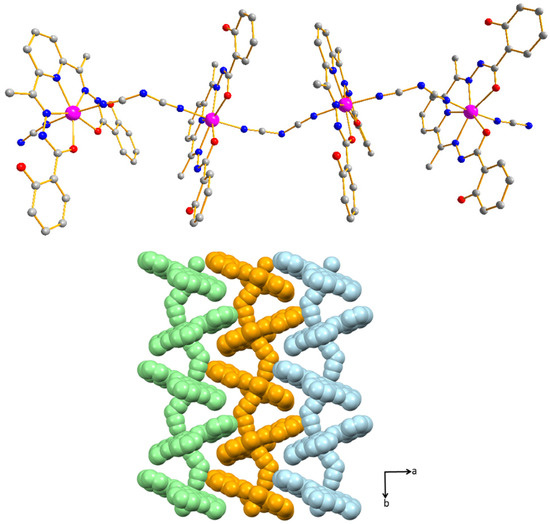
Figure 1.
View of the molecular structure of complex 1 (top panel). Color codes: Co (magenta), O (red), N (blue), C (gray). Hydrogen atoms are omitted for clarity; Helical arrangement of 1 along the c axis (bottom panel).
Phase purity of complex 1 was confirmed by the good agreement of the bulk phase powder X-ray diffraction patterns which matches well with the simulated ones from crystal structure data (Figure S5). Magnetic susceptibility measurements were performed under direct current (DC) and an applied field of 0.1 T. At room temperature, the experimental χMT value (χM = molar magnetic susceptibility) of 2.76 cm3 K mol−1 is larger than the spin-only value (1.875 cm3 mol−1 K, S = 3/2, g = 2) for a high-spin CoII ion but falls well in the range of 2.1–3.4 cm3 mol−1 K as expected for a highly anisotropic CoII ion with a significant orbital contribution [52]. Upon cooling from 300 K, the χMT value remains constant down to 150 K, below which it drastically decreases and reaches a value of 1.61 cm3 mol−1 K at 2 K (Figure 2).
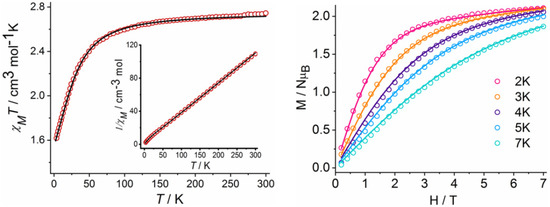
Figure 2.
χMT vs. T plot measured at 0.1 T for complex 1 (left). The black line is the best fit; M/NμB vs. H plots for complex 1 (right) at the indicated temperatures. The solid lines are the best fit.
The decrease in the χMT curves at low temperatures may be due to the intrinsic magnetic anisotropy of the CoII ions. Reduced magnetization data (M/NμB vs. H) were collected, and they reached the highest value of 2.15 NμB at 2 K and 7 T (Figure 2). This value is well below the theoretical saturation value of 3.3 for S = 3/2 system (g = 2.2). The magnetization values do not saturate even at the highest available fields and the M/NμB vs. H/T plots show that all isotherm magnetization plots do not collapse on the same master curve, indicating that the system has a strong magnetic anisotropy (Figure S6). The spin Hamiltonian of Equation (1) is used to define the magnetic anisotropy qualitatively.
where J is the exchange interaction between two adjacent CoII centers; μB, S and B represent the Bohr magneton, spin (S = 3/2) and magnetic field vectors, respectively; D and E terms represent the single-ion axial and rhombic ZFS parameters. The PHI code [53] was used in order to calculate the anisotropy parameter by simultaneously fitting the susceptibility and the magnetization data. The best fit gave D = 41.3(5) cm−1, E = 0.81(3) cm−1 and gx = 2.29, gy = 2.21, gz = 1.98 and very weak antiferromagnetic exchange interaction, J = −0.004 cm−1. The positive sign of the D parameter also agrees well with the other previously reported seven-coordinate CoII complexes (Table S5) [41,42,43,44,45,46,47,48,49,50].
To further analyze the electronic structure and magnetic anisotropy of the complex, we performed quantum chemical calculation with ORCA 4.0 and MOLCAS 8.2 [54,55] (see Computational details). However, it has been observed that MOLCAS calculations show slightly higher anisotropic parameters (D and E) as compared to the ORCA calculations. This is because the dynamic correlation effect was employed (by NEVPT2) in ORCA, whereas we were unable to perform the CASPT2 calculations due to the limitation of our computational facility. The calculations show that the strong spin orbit coupling between the spin-free states reduces the energy of the spin-orbit states (Table S6). The ZFS parameters disclose that the lowest energy Kramers doublets (KDs) lead to easy-plane magnetic anisotropy as the gx and gy components of the g tensor are higher than the gz components (Table 1). This is also in good agreement with the positive sign of D as estimated from the fitting of the experimental DC data shown in Table 1. For the CoII system with axial anisotropy, the spin state with S = 3/2 splits in two Kramers doublets ±1/2 and ±3/2. The negative D stabilized ±3/2 doublets and the positive D stabilized ±1/2 doublets, which is also reflected in the anisotropy of the ground state (gx = 5.21, gy = 4.37, gz = 1.97) Kramers doublets (S = 1/2) as obtained from ab initio calculation for the studied complex (Figure 3 and Table S7). Furthermore, the first excited state KDs is axial in nature (±3/2), as the anisotropy is very close to the ideal value (gx = 0, gy = 0, gz = 6, Table S6). In order to check the electronic transition and the splitting of the d orbital (Figure 3), we employed the ab initio ligand field theory (AILFT) approach by ORCA [16,26].

Table 1.
ORCA/CASSCF, ORCA/CASSCF+NEVPT2 and MOLCAS/CASSCF+RASSI-SO computed D, |E| and main values of gx,y,z from the pseudospin Hamiltonian w.r.t. = 3/2 for complex 1.
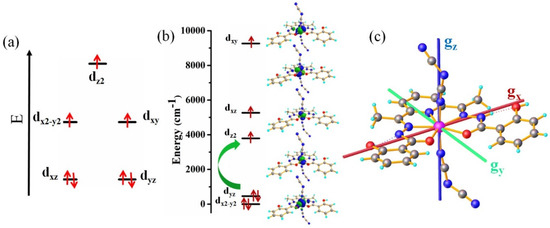
Figure 3.
The splitting of the d-orbital on ideal PBP geometry (a); AILFT computed d-orbital splitting diagram (b) and orientation of the ground state anisotropy axis for complex 1 (c).
It is well known that if the ground and excited state have the same multiplicity and coupled through the or part of the SOC operator, then they lead to positive or negative contribution to D. Usually, in the ideal PBP geometry, the electronic configuration for Co(II) d7 system reveals that the electronic excitation occurs between the different ml values of the d orbitals and results in easy-plane magnetic anisotropy (positive D) as reported in the literature (Figure 3a) [41,42,43,44,45,46,47,48,49,50]. In the studied complex, we found that the ground and excited states are multi configurational and none of them can be expressed by single determinant. It has been also observed that the quartet ground state wave functions is more dominated (53%) by an electronic configuration of (dxz)1 (dyz)2 (dxy)1 (dx2−y2)2 (dz2)1, which is also reflected in d-orbital splitting obtained from the AILFT (Figure 3b). However, the presence of the multiconfigurational nature of the wave function of the electronic states leads to the strong mixing among d orbitals for which the orbital splitting differs from the expected for ideal PBP geometry. On the other hand, the first excited state is dominated (31%) by an electronic configuration of (dxz)1 (dyz)1 (dxy)1 (dx2−y2)2 (dz2)2. Thus, the ground and excited states differ only by the occupation of dyz and dz2 orbitals. In this case, the first excitation involved the transition between different ml level from dyz to dz2 orbital (Figure 3b,c), which induces a coupling through the part of the SOC operator, results in positive D value. Similarly, the contribution to D from the third and fourth excited states are also positive and much higher as compare to other states, whereas the large positive and negative contributions of E are from the third and fourth excited states, respectively (Table S8). It has been observed that both the same spin multiplicity and different multiplicity states contribute to the overall D value.
To investigate the dynamic magnetic behavior of complex 1, the alternating current (ac) susceptibility measurements were performed with the temperature and frequency range of 2–10 K and 1–750 Hz respectively. No out-of-phase (χM″) signal on AC susceptibility was observed in the absence of an external magnetic field. This is probably due to strong QTM which leads to fast relaxation, as commonly observed in transition metal based SMMs [15]. Therefore, to reduce the QTM and check the optimum field, we measured the ac susceptibility at 2 K temperature to different external fields. The χM″ shows peak maxima around 0.22 T (Figure S7) and the AC susceptibility measurement was again performed for the same field.
However, no clear peak maxima were observed in the temperature as well as frequency dependence above 2 K within the frequency range of 1–800 Hz (Figure 4b).
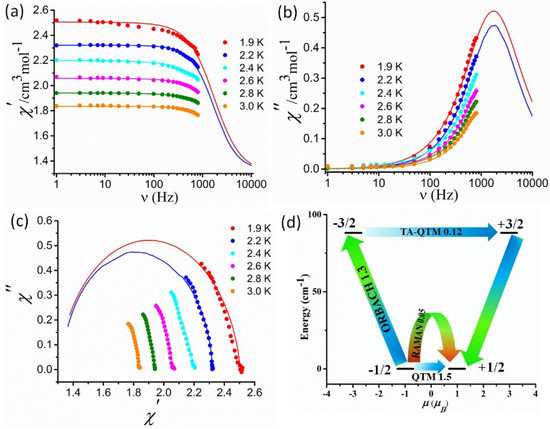
Figure 4.
The frequency dependence of the in-phase (χM′) (a) and out-of-phase (χM″) (b) AC magnetic susceptibility plots under 0.22 T external field; Cole-Cole plot complex 1 (c). Solid lines represent the best fit; lowest two Kramers’ doublets and ab initio computed relaxation mechanism of complex 1 (d). The values shown in the arrows indicate the matrix elements of the transition magnetic moments (above 0.1 an efficient spin relaxation mechanism is expected).
This demonstrates the significant effect of QTM on the slow relaxation process, even under the most optimal DC field, and it is very common for CoII-based SMMs, as reported earlier [46,47,56,57]. Although we have limitation in our instrument (frequency range 0–800 Hz) but the extrapolation of the frequency dependence plots up to 10,000 Hz using the Debye model shows clear peak maxima in both χM′ and χM″ (Figure 4). This indicates the presence of field-induced slow relaxation of magnetization in complex 1. The semicircle nature of the Cole-Cole plot [58,59,60,61] obtained from both χM′ and χM″ reveals the single relaxation process and the generalized Debye model was used to extract the magnetization relaxation time (τ) with the associated width of the distribution (α) which displays narrow distribution of relaxation time (α = 0.21–0.09). Furthermore, the fitting of the Arrhenius plot using ln(τ) = ln(τ0) + Ueff/KT equation gives Ueff = 9.9 K (6.88 cm−1) and τ0 = 5.3 × 10−6 s (Figure S8). The obtained barrier for spin reversal process is much lower than the energy of the first excited states (88 cm−1). This clearly indicates that the relaxation process does not follow the Orbach process. Furthermore, to analyze the relaxation dynamics, we used the Single_Aniso module of MOLCAS (Figure 4d). It was found that the matrix element of the transition moment between the ground state KDs is somewhat larger (1.5 μB) than the required value (0.1 μB) for efficient relaxation.
Thus, it can be said that QTM plays a major role in the dynamic magnetic behavior of complex 1. On the other hand, the energy of the first exited state lies around 88 cm−1, which also quite large as compared to the observed energy barrier. This means that the relaxation process in 1 also follows some shortcut path through virtual states, called the Raman process, and results in barrier relaxation. So, in complex 1, the magnetization relaxation process is mainly controlled by QTM and the Raman process, as QTM cannot be suppressed completely as it is also dependent on some other factor such as hyperfine interaction, dipole–dipole interaction, etc. Furthermore, the second and third excited states have much higher energy (2189 and 2662 cm−1) and demagnetization does not follow this path.
3. Materials and Methods
Magnetic measurements were performed using a Quantum Design SQUID-VSM magnetometer The measured values were corrected for the experimentally measured contribution of the sample holder, while the derived susceptibilities were corrected for the diamagnetic contribution of the sample, estimated from Pascal’s tables [62]. Elemental analysis was performed on Elementar Microvario Cube Elemental Analyzer. The infrared spectroscopy (IR) spectrum was recorded on KBr pellets with a Perkin-Elmer spectrometer. Powder X-ray diffraction (PXRD) data were collected on a PANalytical EMPYREAN instrument using Cu-Kα radiation.
Synthesis of ligand: H4daps was prepared by a simple hydrazine condensation reaction of one equivalent 2,6-diacetylpyridine with two equivalents of 2-salicyloylhydrazide in methanol according to a previously reported procedure [63].
Synthesis of complex 1: H4daps (43 mg, 0.1 mmol) was dissolved in 5 mL of MeCN; then, triethylamine (10 mg, 0.1 mmol) was added dropwise to it. Then, 5 mL methanolic solution of Co(ClO4)2·H2O (36 mg, 0.1 mmol) was added and the reaction mixture stirred. Then, 5 mL aqueous solution of NaN(CN)2 (9 mg, 0.1 mmol) was added to the above reaction mixture. The whole mixture forms a red color and stirred for 3 h. Then, the solution was filtered and kept for slow evaporation for 3 days and gave X-ray quality red crystals of [Co(H3daps)(dca)]·(MeOH)2·(MeCN) (1). These were washed with ether, and the yield was calculated as 53%. Anal. Calcd for C29H31CoN9O6: C, 52.73; H, 4.73; N, 19.08%. Found: C, 52.80; H, 4.82; N, 19.15%. IR (KBr pellet, 4000−400 cm−1) ν/cm−1: 3422, 3073, 2917, 2818, 2175, 1529, 1384, 1318, 1289, 1076, 1028, 713.
Intensity data were collected on a Brüker APEX-II CCD diffractometer using a graphite monochromated Mo-Kα radiation (λ = 0.71073 Å) at 296 K. Data collection was performed using φ and ω scans. The structure was solved using direct methods followed by full matrix least square refinements against F2 (all data HKLF 4 format) using SHELXTL [64]. Subsequent difference Fourier synthesis and least-square refinement revealed the positions of the remaining non-hydrogen atoms. Determinations of the crystal system, orientation matrix, and cell dimensions were performed according to the established procedures. Lorentz polarization and multi–scan absorption correction was applied. Non-hydrogen atoms were refined with independent anisotropic displacement parameters and hydrogen atoms were placed geometrically and refined using the riding model. All calculations were carried out using SHELXL 97 [65], PLATON 99 [66], and WinGX systemVer−1.64 [67]. Crystallographic data for complex 1 are summarized in Table S1.
All the calculations were performed using ORCA 4.0 [54] and MOLCAS 8.2 [55] software packages on the experimentally determined X-ray structure without optimization. In ORCA 4.0 we performed both the calculations CASSCF and CASSCF+NEVPT2 (Method of dynamic correlation effect), whereas only CASSCF/RASSI-SO/SINGLE_ANISO type calculations were performed. All the calculations were carried out with scalar relativistic effect with ZORA (zeroth-order regular approximation) in ORCA. We used the def2-TZVPP basis set for Co, def2-TZVP for N, O and def2-SV(P) for other atoms. An auxiliary def2/JK Coulomb fitting basis set was used during the calculation. The quasi-degenerate perturbation theory (QDPT) approach was used to introduce the spin-orbit coupling effects. We considered CAS (7,5) where 7 electrons in 5 ‘d’ orbital and computed 10 quartets and 40 doublet. For the effect of dynamic correlation, we employed N-electron valence perturbation theory (NEVPT2) on top of the CASSCF wave functions. Both the zero-field splitting parameter (D) and transverse anisotropy (E) were calculated from second order perturbation theory and an effective Hamiltonian approach (EHA). For MOLCAS calculations, all atoms were described by the ANO-RCC basis sets of functions ([ANO-RCC-VTZP] for Co, [ANO-RCC-VTZ] for O, N and [ANO-RCC-VDZ] for C, H) including the relativistic effects within Douglas Kroll Hess Hamiltonian [68,69]. To save computational time and disk space, the Cholesky decomposition [70] of two-electron integrals has been used. In CASSCF [71] method 7 electrons in 5 ‘d’ orbital was used to calculate all states (10 quartets and 40 doublets). The RASSI program was used to introduce spin orbit coupling by mixing of the optimized states in previous calculations. We were unable to performed CASPT2 calculations due to limitations in Computational facility. The SINGLE_ANISO [72] program was used to calculate the magnetic properties and the parameters of the pseudo-spin Hamiltonians describing the zero-field splitting.
4. Conclusions
In summary, SIM-type field-induced slow relaxation behavior of the magnetically isolated seven-coordinate CoII centers in a 1D coordination polymer is reported. The easy-plane magnetic anisotropy was confirmed from both experimental and ab initio theoretical calculations. Besides reporting the single-ion-magnetic behavior with seven-coordinate CoII centers, the present work also provides a new route to the design and synthesis of a stable magnetic material based on a mononuclear complex unit and toward the construction of multifunctional coordination polymer materials.
Supplementary Materials
The following are available online at https://www.mdpi.com/2312-7481/6/4/45/s1. Table S1: X-ray Crystallographic Data and Refinement Parameters for complex 1. Figure S1: Distorted pentagonal bipyramid coordination geometry around the CoII center in 1. Table S2: Summary of SHAPE analysis for complex 1. Table S3: Bond distances (Å) and bond angles (˚) around CoII center found in complex 1. Figure S2: A view of supramolecular 2D arrangement of complex 1 through intermolecular H-bonding and CH⋯π interactions. Figure S3: A view of de-solvated framework of 1 emphasizing the supramolecular interactions. Figure S4: Helical 1D arrangement of complex 1 along the c axis. Table S4: H-bond parameters found in complex 1. Figure S5: PXRD for complex 1. Figure S6: M/NμB vs. H/T plots at the indicated temperatures for complex 1. The solid lines are the best fit. Table S5: Magnetic anisotropy (D parameters) and SIM parameters for previously reported seven-coordinated CoII SIMs in the literature. Table S6: Ab initio calculated energies (cm−1) of the lowest states (S = 3/2) of complex 1. Table S7: Ab initio calculated magnetic anisotropy in the ground state and first excited state (w.r.t. S = 1/2) for complex 1. Table S8: Energy of the first four excited states (cm−1) and their contribution to the D and E values in cm−1 at CAS(7,5) NEVPT2 level by ORCA. Figure S7: Frequency dependency of out-of-phase susceptibility at different external magnetic field (0–0.9 T) and 2 K temperature. Figure S8: ln(τ) vs. 1/T plot for complex 1.
Author Contributions
A.K.M. designed the project and performed all the experiments; A.K.M. solved the crystal structures and collected and analyzed the magnetic data; A.M. performed the theoretical calculations; A.K.M., A.M. and S.K. wrote the paper; S.K. supervised the overall project. All authors have read and agreed to the published version of the manuscript.
Funding
A.M. thanks IISER Bhopal for SRF fellowship. S.K. thanks SERB (Project No. CRG/2018/00072), Government of India and IISER Bhopal for generous financial and infrastructural support. The high-performance computing (HPC) facility at IISER Bhopal is gratefully acknowledged for the computational work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Batten, S.R.; Murray, K.S. Structure and magnetism of coordination polymers containing dicyanamide and tricyanomethanide. Coord. Chem. Rev. 2003, 246, 103–130. [Google Scholar] [CrossRef]
- Andruh, M. Oligonuclear complexes as tectons in crystal engineering: Structural diversity and magnetic properties. Chem. Commun. 2007, 2565. [Google Scholar] [CrossRef] [PubMed]
- Carranza, J.; Brennan, C.; Sletten, J.; Lloret, F.; Julve, M. Three one-dimensional systems with end-to-end dicyanamide bridges between copper(ii) centres: Structural and magnetic properties. J. Chem. Soc. Dalton Trans. 2002, 16, 3164–3170. [Google Scholar] [CrossRef]
- Mondal, A.K.; Khatua, S.; Tomar, K.; Konar, S. Field-Induced Single-Ion-Magnetic Behavior of Octahedral CoII in a Two-Dimensional Coordination Polymer. Eur. J. Inorg. Chem. 2016, 3545–3552. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Aromí, G.; Aguilá, D.; Gamez, P.; Luis, F.; Roubeau, O. Design of magnetic coordination complexes for quantum computing. Chem. Soc. Rev. 2012, 41, 537–546. [Google Scholar] [CrossRef]
- Zheng, Y.Z.; Zheng, Z.; Chen, X.M. A symbol approach for classification of molecule-based magnetic materials exemplified by coordination polymers of metal carboxylates. Coord. Chem. Rev. 2014, 258, 1–15. [Google Scholar] [CrossRef]
- Dey, A.; Kalita, P.; Chandrasekhar, V. Lanthanide(III)-Based Single-Ion Magnets. ACS Omega 2018, 3, 9462–9475. [Google Scholar] [CrossRef]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef]
- Goswami, S.; Mondal, A.K.; Konar, S. Nanoscopic molecular magnets. Inorg. Chem. Front. 2015, 2, 687–712. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Liu, J.-L.; Ungur, L.; Liu, J.; Li, Q.-W.; Wang, L.-F.; Ni, Z.-P.; Chibotaru, L.F.; Chen, X.-M.; Tong, M.-L. Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets. J. Am. Chem. Soc. 2016, 138, 2829–2837. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Understanding the Magnetic Anisotropy toward Single-Ion Magnets. Acc. Chem. Res. 2016, 49, 2381–2389. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Guo, Y.N.; Tang, J. Recent advances in dysprosium-based single molecule magnets: Structural overview and synthetic strategies. Coord. Chem. Rev. 2013, 257, 1728–1763. [Google Scholar] [CrossRef]
- Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coca, S.; Aravena, D.; Morales, R.; Ruiz, E. Large magnetic anisotropy in mononuclear metal complexes. Coord. Chem. Rev. 2015, 289, 379–392. [Google Scholar] [CrossRef]
- Habib, F.; Luca, O.R.; Vieru, V.; Shiddiq, M.; Korobkov, I.; Gorelsky, S.I.; Takase, M.K.; Chibotaru, L.F.; Hill, S.; Crabtree, R.H.; et al. Influence of the Ligand Field on Slow Magnetization Relaxation versus Spin Crossover in Mononuclear Cobalt Complexes. Angew. Chem. Int. Ed. 2013, 52, 11290–11293. [Google Scholar] [CrossRef]
- Bar, A.K.; Pichon, C.; Sutter, J. Magnetic anisotropy in two- to eight-coordinated transition−metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. [Google Scholar] [CrossRef]
- Woods, T.J.; Ballesteros-Rivas, M.F.; Gómez-Coca, S.; Ruiz, E.; Dunbar, K.R. Relaxation Dynamics of Identical Trigonal Bipyramidal Cobalt Molecules with Different Local Symmetries and Packing Arrangements: Magnetostructural Correlations and ab inito Calculations. J. Am. Chem. Soc. 2016, 138, 16407–16416. [Google Scholar] [CrossRef]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Investigation of easy plane magnetic anisotropy in P-ligand square-pyramidal CoII single ion magnets. Chem. Commun. 2017, 53, 5338–5341. [Google Scholar] [CrossRef]
- Mondal, A.K.; Sundararajan, M.; Konar, S. A new series of tetrahedral Co(II) complexes [CoLX2] (X = NCS, Cl, Br, I) manifesting single-ion magnet features. Dalton Trans. 2018, 47, 3745–3754. [Google Scholar] [CrossRef]
- Mathonière, C.; Lin, H.-J.; Siretanu, D.; Clérac, R.; Smith, J.M. Photoinduced Single-Molecule Magnet Properties in a Four-Coordinate Iron(II) Spin Crossover Complex. J. Am. Chem. Soc. 2013, 135, 19083–19086. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Mathonière, C.; Jeon, I.-R.; Rouzières, M.; Ozarowski, A.; Aubrey, M.L.; Gonzalez, M.I.; Clérac, R.; Long, J.R. Tristability in a Light-Actuated Single-Molecule Magnet. J. Am. Chem. Soc. 2013, 135, 15880–15884. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Goswami, T.; Misra, A.; Konar, S. Probing the Effects of Ligand Field and Coordination Geometry on Magnetic Anisotropy of Pentacoordinate Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2017, 56, 6870–6878. [Google Scholar] [CrossRef]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Quantitative Estimation of Ising-Type Magnetic Anisotropy in a Family of C3-Symmetric CoII Complexes. Chem. Eur. J. 2017, 23, 12550–12558. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.-N.; Du, J.-Z.; Zhang, Y.-Q.; Leng, X.-B.; Yang, M.-W.; Jiang, S.-D.; Wang, Z.-X.; Ouyang, Z.-W.; Deng, L.; Wang, B.-W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef]
- Jurca, T.; Farghal, A.; Lin, P.H.; Korobkov, I.; Murugesu, M.; Richeson, D.S. Single-Molecule Magnet Behavior with a Single Metal Center Enhanced through Peripheral Ligand Modifications. J. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Long, J.R. Slow magnetic relaxation at zero field in the tetrahedral complex [Co(SPh)4]2−. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef]
- Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.E.; Varzatskii, O.A.; Voloschin, Y.Z.; Winpenny, R.E.P. A trigonal prismatic mononuclear cobalt(II) complex showing single-molecule magnet behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef]
- Vaidya, S.; Upadhyay, A.; Singh, S.K.; Langley, S.K.; Walsh, J.P.S.; Murray, K.S.; Rajaraman, G.; Shanmugam, M. A synthetic strategy for switching the single ion anisotropy in tetrahedral cobalt(II) complexes. Chem. Commun. 2015, 51, 3739–3742. [Google Scholar] [CrossRef]
- Cahier, B.; Perfetti, M.; Zakhia, G.; Naoufal, D.; ElKhatib, F.; Guillot, R.; Rivière, E.; Sessoli, R.; Barra, A.L.; Guihéry, N.; et al. Magnetic Anisotropy in Pentacoordinate NiII and CoII Complexes: Unraveling Electronic and Geometrical Contributions. Chem. Eur. J. 2017, 23, 3648–3657. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.-H.; Wang, J.; Chen, X.-T.; Xue, Z.-L. Slow magnetic relaxation in five-coordinate spin-crossover cobalt(II) complexes. Chem. Commun. 2017, 53, 9304–9307. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Single-ion magnetic anisotropy in a vacant octahedral Co(II) complex. Dalton Trans. 2019, 48, 25–29. [Google Scholar] [CrossRef]
- Schweinfurth, D.; Sommer, M.G.; Atanasov, M.; Demeshko, S.; Hohloch, S.; Meyer, F.; Neese, F.; Sarkar, B. The Ligand Field of the Azido Ligand: Insights into Bonding Parameters and Magnetic Anisotropy in a Co(II)-Azido Complex. J. Am. Chem. Soc. 2015, 137, 1993–2005. [Google Scholar] [CrossRef] [PubMed]
- Ruamps, R.; Batchelor, L.J.; Guillot, R.; Zakhia, G.; Barra, A.-L.; Wernsdorfer, W.; Guihéry, N.; Mallah, T. Ising-type magnetic anisotropy and single molecule magnet behaviour in mononuclear trigonal bipyramidal Co(II) complexes. Chem. Sci. 2014, 5, 3418–3424. [Google Scholar] [CrossRef]
- Shao, F.; Cahier, B.; Rivière, E.; Guillot, R.; Guihéry, N.; Campbell, V.E.; Mallah, T. Structural Dependence of the Ising-type Magnetic Anisotropy and of the Relaxation Time in Mononuclear Trigonal Bipyramidal Co(II) Single Molecule Magnets. Inorg. Chem. 2017, 56, 1104–1111. [Google Scholar] [CrossRef]
- Murrie, M. Cobalt(II) single-molecule magnets. Chem. Soc. Rev. 2010, 39, 1986–1995. [Google Scholar] [CrossRef]
- Ion, A.E.; Nica, S.; Madalan, A.M.; Shova, S.; Vallejo, J.; Julve, M.; Lloret, F.; Andruh, M. Two-dimensional Coordination Polymers Constructed Using, Simultaneously, Linear and Angular Spacers and cobalt(II) Nodes. New Examples of Networks of Single-Ion Magnets. Inorg. Chem. 2015, 54, 16–18. [Google Scholar] [CrossRef]
- Zhu, Y.-Y.; Zhu, M.-S.; Yin, T.-T.; Meng, Y.-S.; Wu, Z.-Q.; Zhang, Y.-Q.; Gao, S. Cobalt(II) Coordination Polymer Exhibiting Single-Ion-Magnet-Type Field-Induced Slow Relaxation Behavior. Inorg. Chem. 2015, 54, 3716–3718. [Google Scholar] [CrossRef]
- Mondal, A.K.; Mondal, A.; Dey, B.; Konar, S. Influence of the Coordination Environment on Easy-Plane Magnetic Anisotropy of Pentagonal Bipyramidal Cobalt(II) Complexes. Inorg. Chem. 2018, 57, 9999–10008. [Google Scholar] [CrossRef]
- Huang, X.-C.; Zhou, C.; Shao, D.; Wang, X.-Y. Field-Induced Slow Magnetic Relaxation in Cobalt(II) Compounds with Pentagonal Bipyramid Geometry. Inorg. Chem. 2014, 53, 12671–12673. [Google Scholar] [CrossRef] [PubMed]
- Shao, D.; Zhang, S.-L.; Shi, L.; Zhang, Y.-Q.; Wang, X.-Y. Probing the Effect of Axial Ligands on Easy-Plane Anisotropy of Pentagonal-Bipyramidal Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2016, 55, 10859–10869. [Google Scholar] [CrossRef] [PubMed]
- Ruamps, R.; Batchelor, L.J.; Maurice, R.; Gogoi, N.; Jiménez-Lozano, P.; Guihéry, N.; de Graaf, C.; Barra, A.L.; Sutter, J.-P.; Mallah, T. Origin of the Magnetic Anisotropy in Heptacoordinate NiII and CoII Complexes. Chem. Eur. J. 2013, 19, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Dey, M.; Dutta, S.; Sarma, B.; Deka, R.C.; Gogoi, N. Modulation of the coordination environment: A convenient approach to tailor magnetic anisotropy in seven coordinate Co(II) complexes. Chem. Commun. 2016, 52, 753–756. [Google Scholar] [CrossRef]
- Mondal, A.; Kharwar, A.K.; Konar, S. Sizeable Effect of Lattice Solvent on Field Induced Slow Magnetic Relaxation in Seven Coordinated CoII Complexes. Inorg. Chem. 2019, 58, 10686–10693. [Google Scholar] [CrossRef]
- Drahoš, B.; Herchel, R.; Travniček, Z. Impact of Halogenido Coligands on Magnetic Anisotropy in Seven-Coordinate Co(II) Complexes. Inorg. Chem. 2017, 56, 5076–5088. [Google Scholar] [CrossRef]
- Habib, F.; Korobkov, I.; Murugesu, M. Exposing the intermolecular nature of the second relaxation pathway in a mononuclear cobalt(II) single-molecule magnet with positive anisotropy. Dalton Trans. 2015, 44, 6368–6373. [Google Scholar] [CrossRef]
- Chen, L.; Chen, S.-Y.; Sun, Y.-C.; Guo, Y.-M.; Yu, L.; Chen, X.-T.; Wang, Z.-X.; Ouyang, Z.-W.; Song, Y.; Xue, Z.-L. Slow magnetic relaxation in mononuclear seven-coordinate cobalt(II) complexes with easy plane anisotropy. Dalton Trans. 2015, 44, 11482–11490. [Google Scholar] [CrossRef]
- Higgins, R.F.; Livesay, B.N.; Ozumerzifon, T.J.; Joyce, J.P.; Rappé, A.K.; Shores, M.P. A family of related Co(II) terpyridine compounds exhibiting field induced single-molecule magnet properties. Polyhedron 2018, 143, 193–200. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Mabbs, F.E.; Machin, D.J. Magnetism and Transition Metal. Complexes; Dover Publications: Mineola, NY, USA, 2008. [Google Scholar]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Karlström, G.; Lindh, R.; Malmqvist, P.-Å.; Roos, B.O.; Ryde, U.; Veryazov, V.; Widmark, P.-O.; Cossi, M.; Schimmelpfennig, B.; Neogrady, P.; et al. MOLCAS: A program package for computational chemistry. Comput. Matter Sci. 2003, 28, 222–239. [Google Scholar] [CrossRef]
- Mondal, A.K.; Mondal, A.; Konar, S. Field Induced Single Ion Magnetic Behaviour in Square-Pyramidal Cobalt(II) Complexes with Easy-Plane Magnetic Anisotropy. Magnetochemistry 2019, 5, 12–22. [Google Scholar] [CrossRef]
- Shi, L.; Shao, D.; Wei, H.-Y.; Wang, X.-Y. Two Interpenetrated Cobalt(II) Metal−Organic Frameworks with Guest-Dependent Structures and Field-Induced Single-Ion Magnet Behaviors. Cryst. Growth Des. 2018, 18, 5270–5278. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Xue, S.; Guo, Y.N.; Zhao, L.; Zhang, P.; Tang, J. Unique Y-shaped lanthanide aggregates and single-molecule magnet behaviour for the Dy4 analogue. Dalton Trans. 2014, 43, 1564–1570. [Google Scholar] [CrossRef]
- Xu, G.F.; Wang, Q.L.; Gamez, P.; Ma, Y.; Clerac, R.; Tang, J.; Yan, S.P.; Cheng, P.; Liao, D.Z. A promising new route towards single-molecule magnets based on the oxalate ligand. Chem. Commun. 2010, 46, 1506–1508. [Google Scholar] [CrossRef]
- Mondal, A.K.; Parmar, V.S.; Konar, S. Modulating the Slow Relaxation Dynamics of Binuclear Dysprosium(III) Complexes through Coordination Geometry. Magnetochemistry 2016, 2, 35–43. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH Publishers: Weinheim, Germany, 1993. [Google Scholar]
- Naskar, S.; Mishra, D.; Chattopadhyay, S.K.; Corbella, M.; Blake, A.J. Versatility of 2,6-diacetylpyridine (dap) hydrazones in stabilizing uncommon coordination geometries of Mn(II): Synthesis, spectroscopic, magnetic and structural characterization. Dalton Trans. 2005, 2428–2435. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXTL Program. for the Solution of Crystal of Structures; University of Göttingen: Göttingen, Germany, 1993. [Google Scholar]
- Sheldrick, G.M. SHELXL 97, Program. for Crystal Structure Refinement; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
- Spek, A.L. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX suite for small-molecule single-crystal crystallography. J. Appl. Crystallogr. 1999, 32, 837–838. [Google Scholar] [CrossRef]
- Douglas, M.; Kroll, N.M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Reiher, M. Relativistic Douglas–Kroll–Hess theory. WIREs Comput. Mol. Sci. 2012, 2, 139–149. [Google Scholar] [CrossRef]
- Aquilante, F.; Malmqvist, P.-Å.; Pedersen, T.B.; Ghosh, A.; Roos, B.O. Cholesky Decomposition-Based Multiconfiguration Second-Order Perturbation Theory (CD-CASPT2): Application to the Spin-State Energetics of CoIII(diiminato)(NPh). J. Chem. Theory Comput. 2008, 4, 694–702. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Sigbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112–064133. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).