How to Quench Ferromagnetic Ordering in a CN-Bridged Ni(II)-Nb(IV) Molecular Magnet? A Combined High-Pressure Single-Crystal X-Ray Diffraction and Magnetic Study
Abstract
1. Introduction
2. Results and Discussion
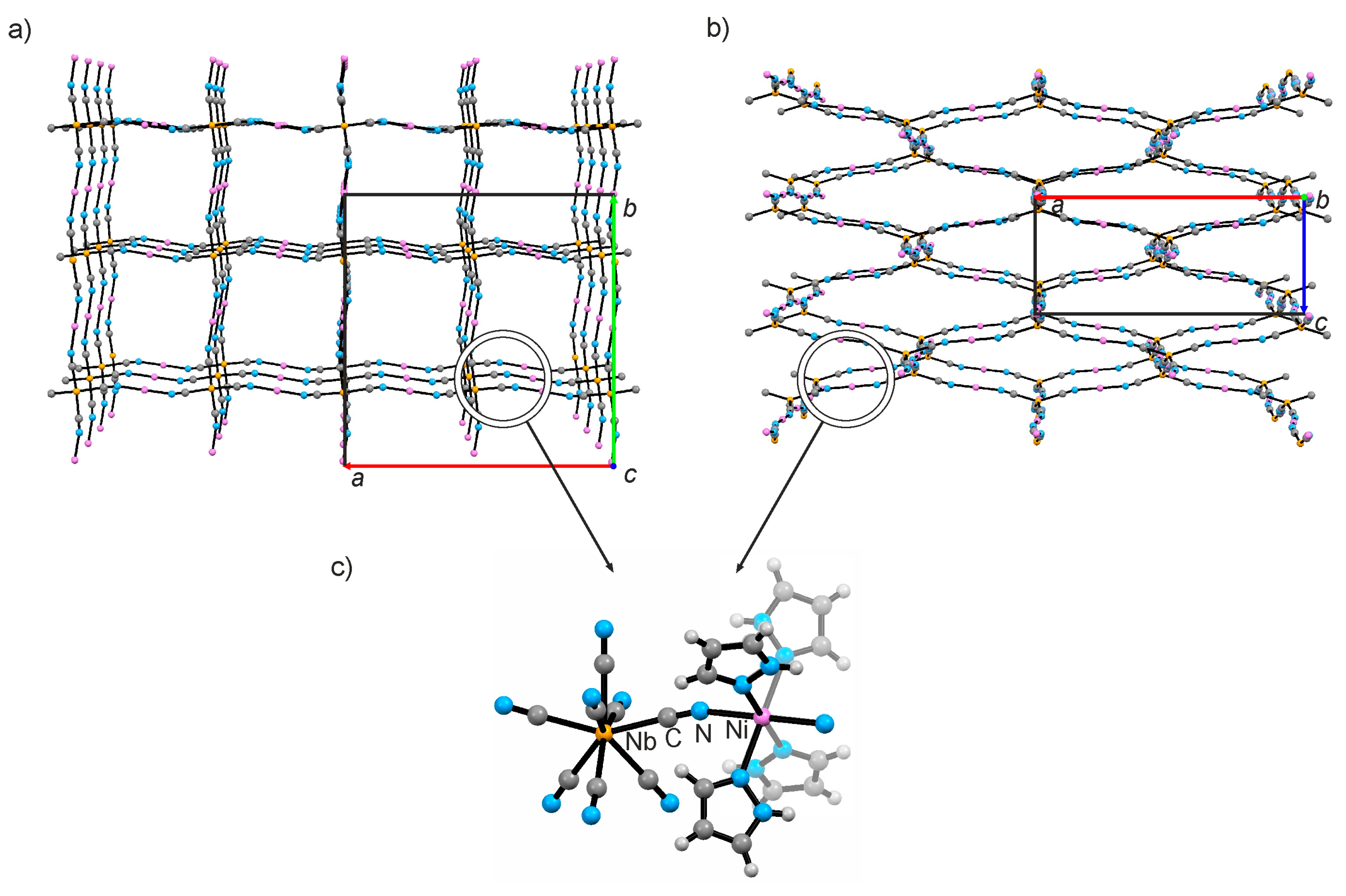
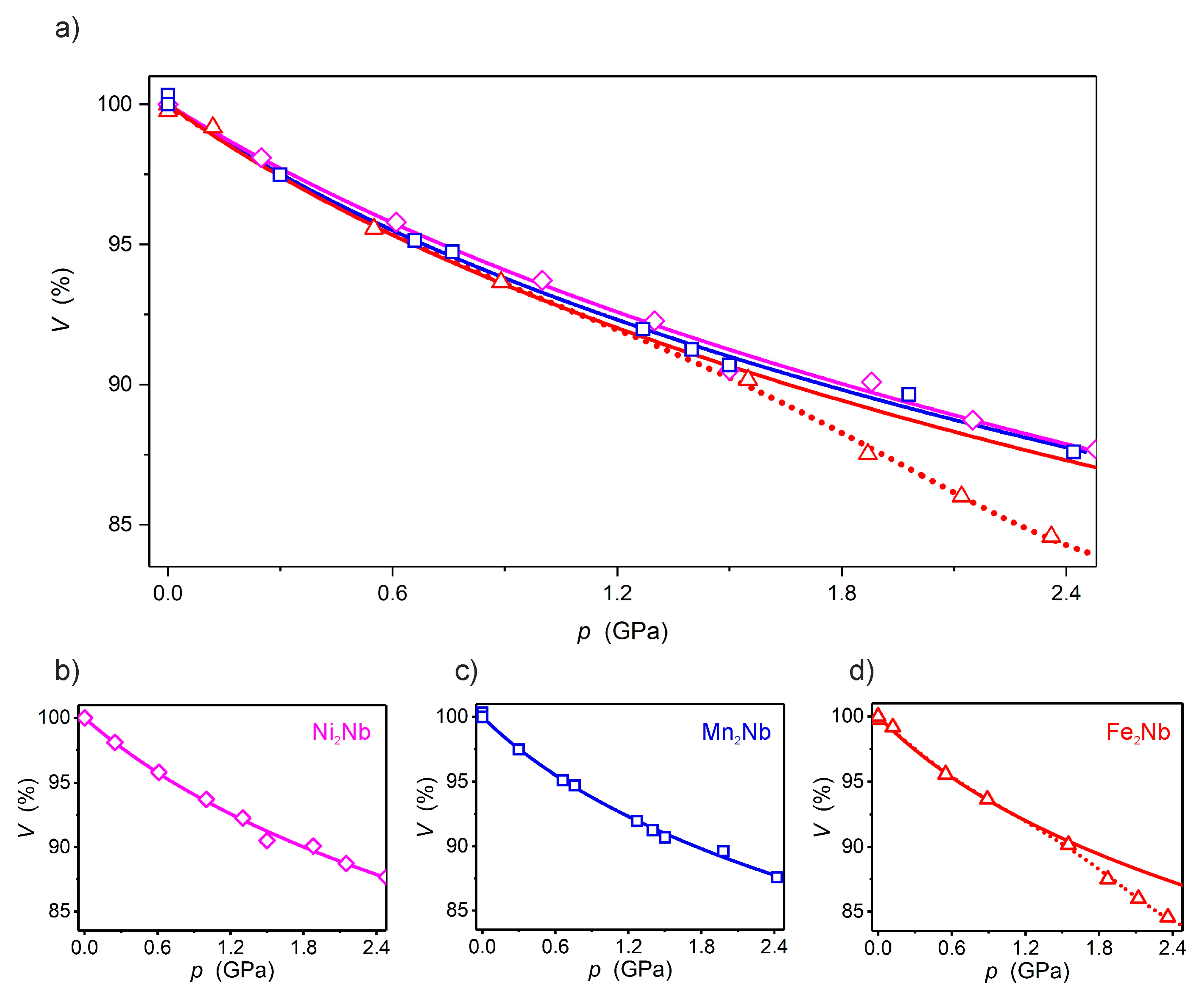
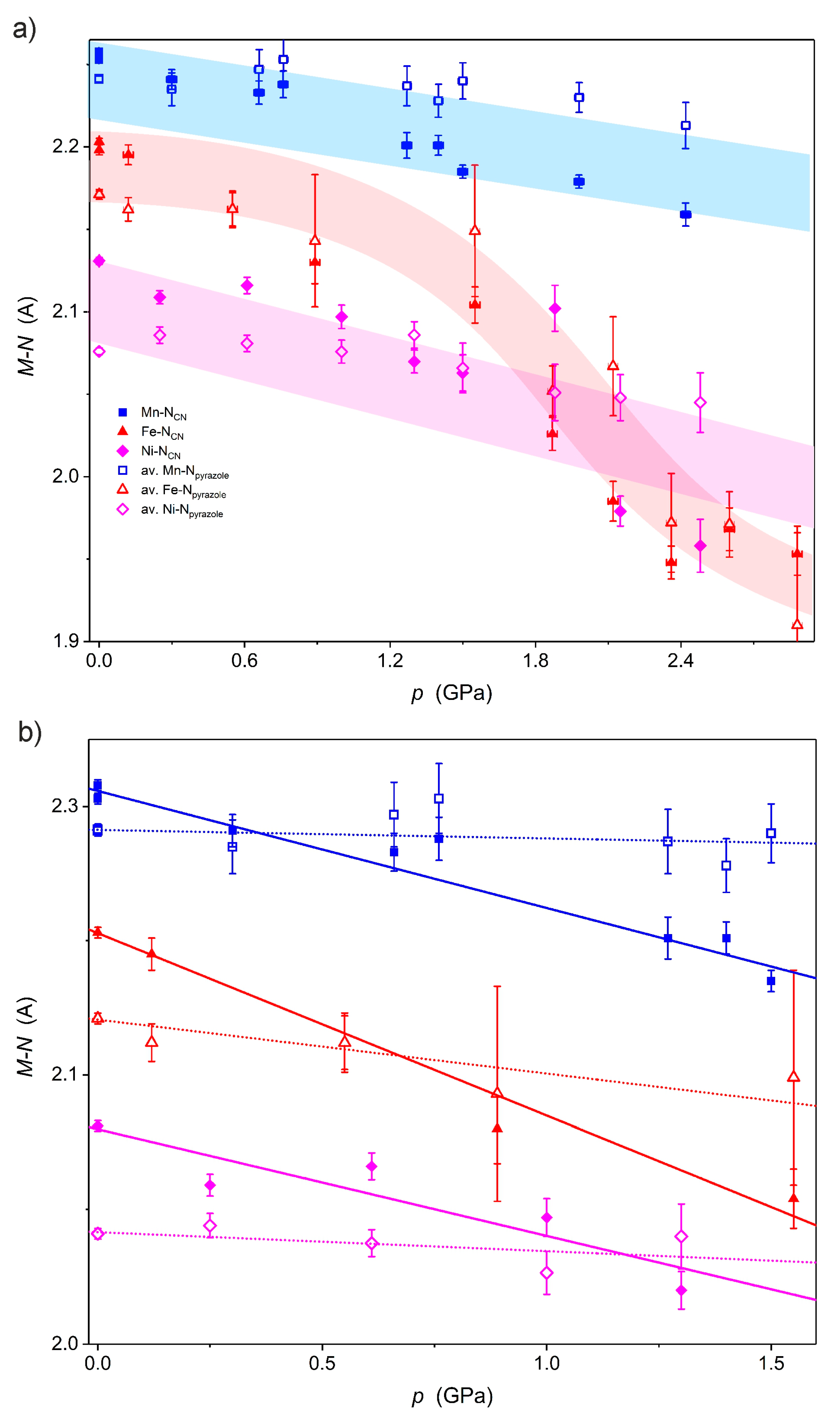
2.1. X-ray Crystal Structure Description under High Pressure
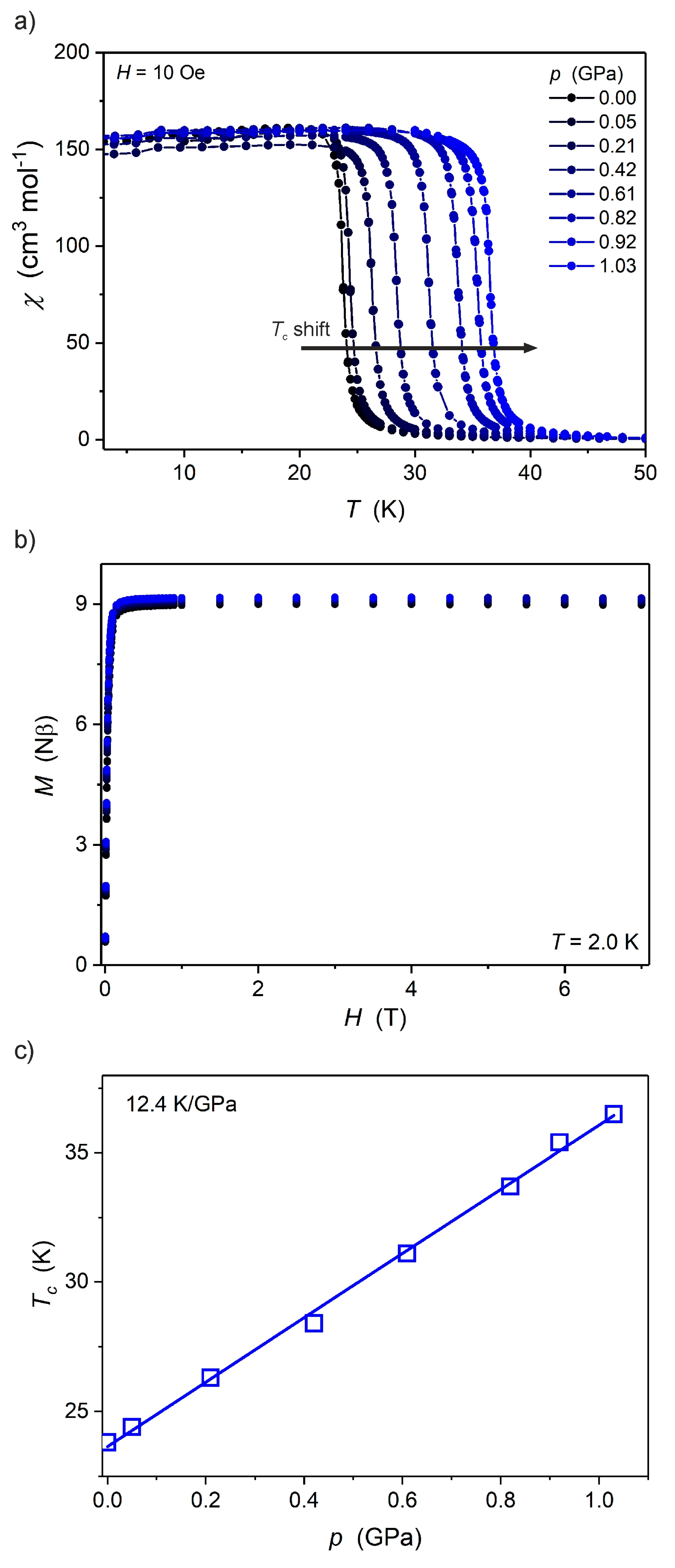
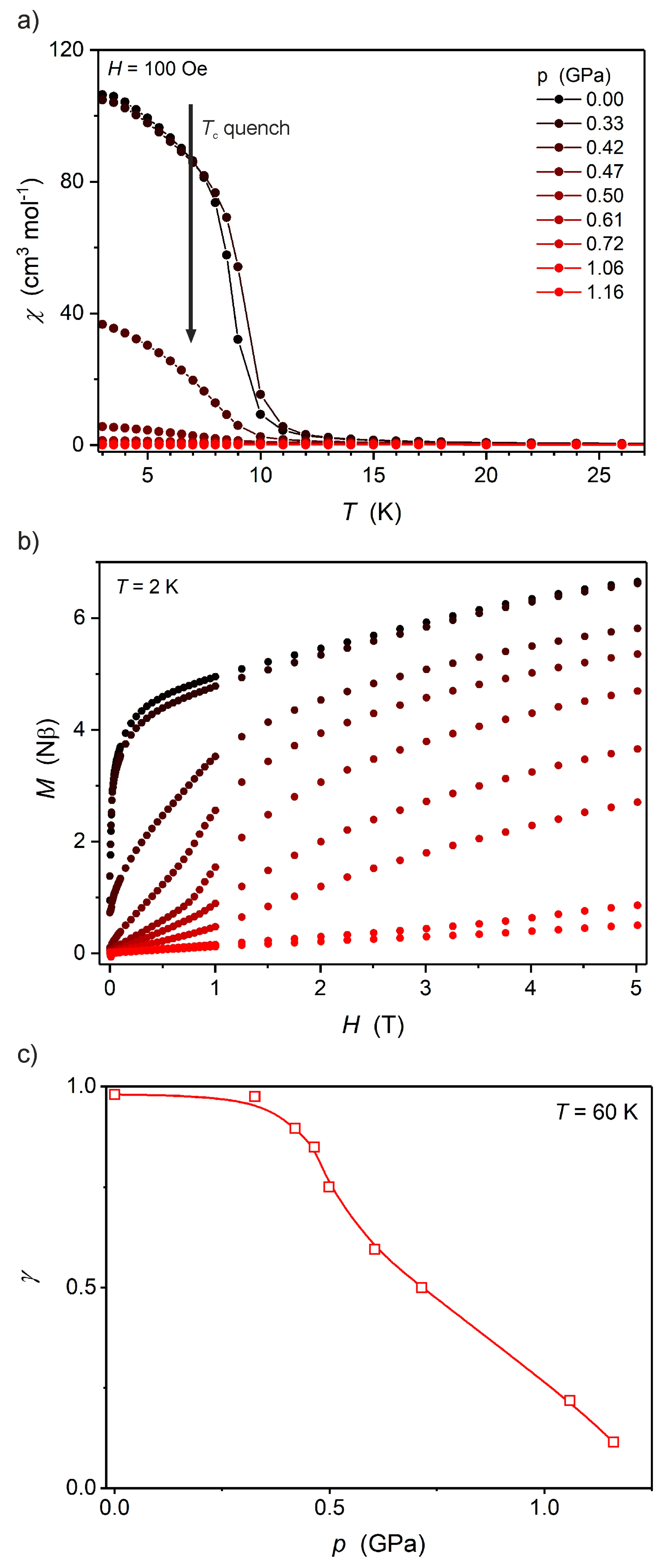
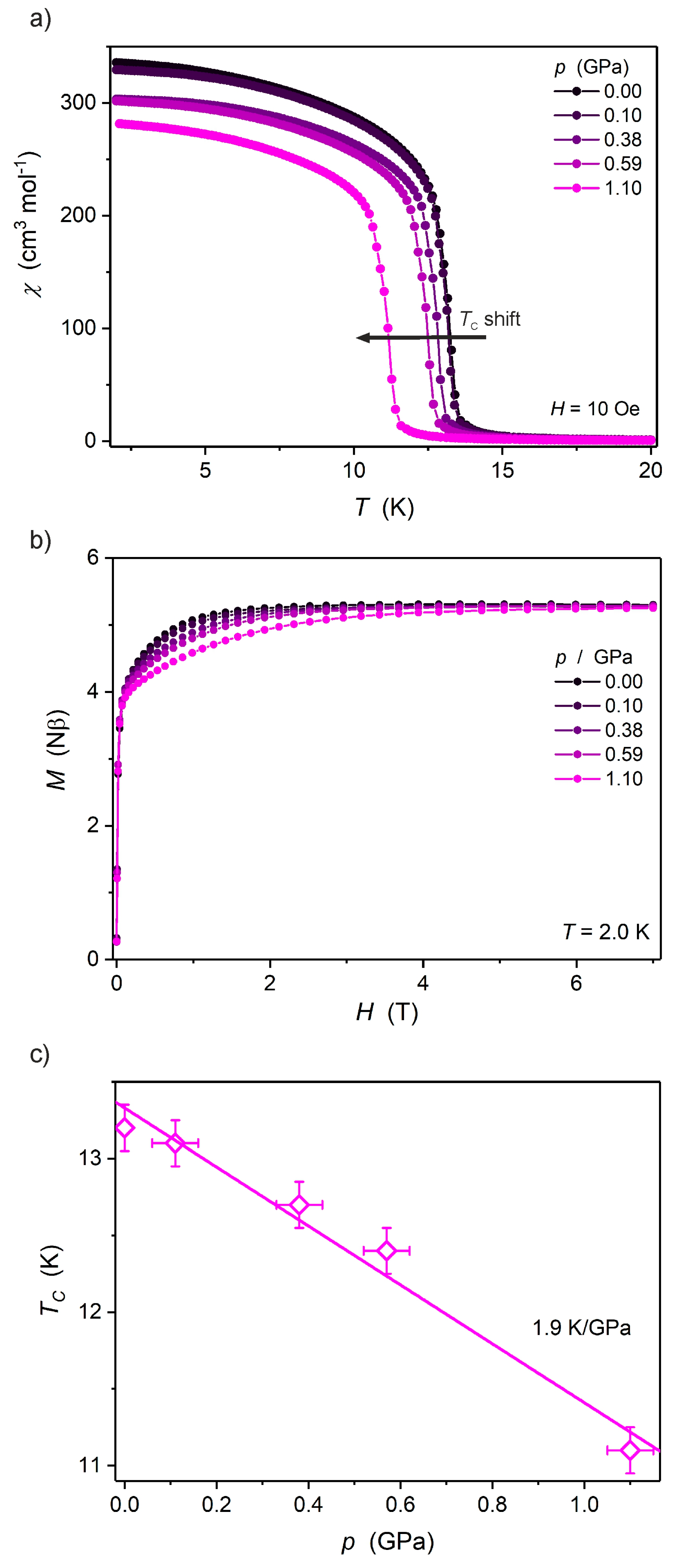
2.2. Magnetic Properties under High Pressure
3. Materials and Methods
3.1. Materials
3.2. Single-Crystal X-ray Diffraction under Pressure
3.3. Magnetic Measurements under Pressure
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Woodall, C.H.; Craig, G.A.; Prescimone, A.; Misek, M.; Cano, J.; Faus, J.; Probert, M.R.; Parsons, S.; Moggach, S.; Martínez-Lillo, J.; et al. Pressure induced enhancement of the magnetic ordering temperature in rhenium(IV) monomers. Nat. Commun. 2016, 7, 13870. [Google Scholar] [CrossRef] [PubMed]
- Pinkowicz, D.; Kurpiewska, K.; Lewiński, K.; Bałanda, M.; Mihalik, M.; Sieklucka, M.Z.B. High-pressure single-crystal XRD and magnetic study of a octacyanoniobate-based magnetic sponge. CrystEngComm 2012, 14, 5224–5229. [Google Scholar] [CrossRef]
- Coronado, E.; Giménez-López, M.C.; Korzeniak, T.; Levchenko, G.; Romero, F.M.; Segura, A.; Garcia-Baonza, V.; Cezar, J.C.; de Groot, F.M.; Milner, A.; et al. Pressure-Induced Magnetic Switching and Linkage Isomerism in K0.4Fe4[Cr(CN)6]2.8·16H2O: X-ray Absorption and Magnetic Circular Dichroism Studies. J. Am. Chem. Soc. 2008, 130, 15519–15532. [Google Scholar] [CrossRef] [PubMed]
- Ohba, M.; Kaneko, W.; Kitagawa, S.; Maeda, T.; Mito, M. Pressure Response of Three-Dimensional Cyanide-Bridged Bimetallic Magnets. J. Am. Chem. Soc. 2008, 130, 4475–4484. [Google Scholar] [CrossRef] [PubMed]
- Shum, W.W.; Her, J.H.; Stephens, P.W.; Lee, Y.; Miller, J.S. Observation of the Pressure Dependent Reversible Enhancement of Tc and Loss of the Anomalous Constricted Hysteresis for [Ru2(O2CMe)4]3[Cr(CN)6]. Adv. Mater. 2007, 19, 2910–2913. [Google Scholar] [CrossRef]
- Craig, G.A.; Sarkar, A.; Woodall, C.H.; Hay, M.A.; Marriott, K.E.; Kamenev, K.V.; Moggach, S.A.; Brechin, E.K.; Parsons, S.; Rajaraman, G.; et al. Rajaraman and M. Murrie. Probing the origin of the giant magnetic anisotropy in trigonal bipyramidal Ni(ii) under high pressure. Chem. Sci. 2018, 9, 1551–1559. [Google Scholar] [CrossRef]
- Prescimone, A.; Sanchez-Benitez, J.; Kamenev, K.K.; Moggach, S.A.; Warren, J.E.; Lennie, A.R.; Murrie, M.; Parsons, S.; Brechin, E.K. High pressure studies of hydroxo-bridged Cu(ii) dimers. Dalton Trans. 2010, 39, 113–123. [Google Scholar] [CrossRef]
- Pinkowicz, D.; Rams, M.; Mišek, M.; Kamenev, K.V.; Tomkowiak, H.; Katrusiak, A.; Sieklucka, B. Enforcing Multifunctionality: A Pressure-Induced Spin-Crossover Photomagnet. J. Am. Chem. Soc. 2015, 137, 8795–8802. [Google Scholar] [CrossRef]
- Gütlich, P.; Ksenofontov, V.; Gaspar, A.B. Pressure effect studies on spin crossover systems. Coord. Chem. Rev. 2005, 249, 1811–1829. [Google Scholar] [CrossRef]
- Katrusiak, A. High-pressure devices. In International Tables for Crystallography, Volume H, Powder Diffraction; Gilmore, C.J., Kaduk, J.A., Schenk, H., Eds.; John Wiley & Sons: New York, NY, USA, 2018; pp. 156–173. [Google Scholar] [CrossRef]
- Kamarád, J.; Machátová, Z.; Arnold, Z. High pressure cells for magnetic measurements—Destruction and functional tests. Rev. Sci. Instrum. 2004, 75, 5022–5025. [Google Scholar] [CrossRef]
- Awaga, K.; Sekine, T.; Okawa, M.; Fujita, W.; Holmes, S.M.; Girolami, G.S. High-pressure effects on a manganese hexacyanomanganate ferrimagnet with TN = 29K. Chem. Phys. Lett. 1998, 293, 352–356. [Google Scholar] [CrossRef]
- Pinkowicz, D.; Pełka, R.; Drath, O.; Nitek, W.; Bałanda, M.; Majcher, A.M.; Poneti, G.; Sieklucka, B. Nature of Magnetic Interactions in 3D {[MII(pyrazole)4]2[NbIV(CN)8]·4H2O}n (M = Mn, Fe, Co, Ni) Molecular Magnets. Inorg. Chem. 2010, 49, 7565–7576. [Google Scholar] [CrossRef]
- Merrill, L.; Bassett, W.A. Miniature diamond anvil pressure cell for single crystal x-ray diffraction studies. Rev. Sci. Instrum. 1974, 45, 290–294. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. Solid Earth 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Byrne, P.J.; Richardson, P.J.; Chang, J.; Kusmartseva, A.F.; Allan, D.R.; Jones, A.C.; Kamenev, K.V.; Tasker, P.A.; Parsons, S. Piezochromism in Nickel Salicylaldoximato Complexes: Tuning Crystal-Field Splitting with High Pressure. Chem. Eur. J. 2012, 18, 7738–7748. [Google Scholar] [CrossRef] [PubMed]
- Madsen, S.R.; Overgaard, J.; Stalke, D.; Iversen, B.B. High-pressure single crystal X-ray diffraction study of the linear metal chain compound Co3(dpa)4Br2·CH2Cl2. Dalton Trans. 2015, 44, 9038–9043. [Google Scholar] [CrossRef] [PubMed]
- Tabor, D. The bulk modulus of rubber. Polymer 1994, 35, 2759–2763. [Google Scholar] [CrossRef]
- Motokawa, N.; Miyasaka, H.; Yamashita, M. Pressure effect on the three-dimensional charge-transfer ferromagnet [{Ru2(m-FPhCO2)4}2(BTDA-TCNQ)]. Dalton Trans. 2010, 39, 4724–4726. [Google Scholar] [CrossRef] [PubMed]
- Mito, M.; Matsumoto, K.; Komorida, Y.; Deguchi, H.; Takagi, S.; Tajiri, T.; Iwamoto, T.; Kawae, T.; Tokita, M.; Takeda, K. Volume shrinkage dependence of ferromagnetic moment in lanthanide ferromagnets gadolinium, terbium, dysprosium, and holmium. J. Phys. Chem. Solids 2009, 70, 1290–1296. [Google Scholar] [CrossRef]
- Kataev, V.; Golze, C.; Alfonsov, A.; Klingeler, R.; Büchner, B.; Goiran, M.; Broto, J.M.; Rakoto, H.; Mennerich, C.; Klauss, H.H.; et al. Magnetism of a novel tetranuclear nickel(II) cluster in strong magnetic fields. J. Phys. Conf. Ser. 2006, 51, 351–354. [Google Scholar] [CrossRef]
- Handzlik, G.; Magott, M.; Sieklucka, B.; Pinkowicz, D. Alternative Synthetic Route to Potassium Octacyanidoniobate (IV) and Its Molybdenum Congener. Eur. J. Inorg. Chem. 2016, 2016, 4872–4877. [Google Scholar] [CrossRef]
- Katrusiak, A. Shadowing and absorption corrections of single-crystal high-pressure data. Zeitschrift Für Kristallographie Crystalline Materials 2004, 219, 461–467. [Google Scholar] [CrossRef]
- Sheldrick, G. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
| Formula | C32H40N24NbNi2O4 |
| Temperature, K | 296(2) |
| λ, Å | 0.71073 Å |
| Molecular weight, g/mol | 1035.11 |
| Crystallographic system | tetragonal |
| Space group | I41/a |
| 0.0001 GPa | |
| Unit cell, Å | a = 21.4340(4) |
| c = 9.6410(2) | |
| Volume V, Å3 | V = 4429.23(15) |
| 0.25(2) GPa | |
| Unit cell, Å | a = 21.2935(17) |
| c = 9.584(2) | |
| Volume V, Å3 | V = 4345.0(10) |
| 0.61(2) GPa | |
| Unit cell, Å | a = 21.2002(7) |
| c = 9.4404(5) | |
| Volume V, Å3 | V = 4243.0(3) |
| 1.00(2) GPa | |
| Unit cell, Å | a = 21.0921(13) |
| c = 9.3306(11) | |
| Volume V, Å3 | V = 4151.0(6) |
| 1.30(2) GPa | |
| Unit cell, Å | a = 20.9721(8) |
| c = 9.292(2) | |
| Volume V, Å3 | V = 4087.1(1) |
| 1.50(2) GPa | |
| Unit cell, Å | a = 20.8535(18) |
| c = 9.219(7) | |
| Volume V, Å3 | V = 4009(3) |
| 1.88(2) GPa | |
| Unit cell, Å | a = 20.8438(9) |
| c = 9.184(4) | |
| Volume V, Å3 | V = 3990.3(17) |
| 2.15(2) GPa | |
| Unit cell, Å | a = 20.704(10) |
| c = 9.167(7) | |
| Volume V, Å3 | V = 3930(4) |
| 2.48(2) GPa | |
| Unit cell, Å | a = 20.635(16) |
| c = 9.121(6) | |
| Volume V, Å3 | V = 3884(5) |
| Mn2Nb | Fe2Nb | Ni2Nb | |
|---|---|---|---|
| Δ(M-NCN)/Δp (Å GPa−1) | −0.044 | −0.067 | −0.040 |
| Δ(M-Npyrazole)/Δp (Å GPa−1) | −0.003 | −0.020 | −0.007 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Handzlik, G.; Sieklucka, B.; Tomkowiak, H.; Katrusiak, A.; Pinkowicz, D. How to Quench Ferromagnetic Ordering in a CN-Bridged Ni(II)-Nb(IV) Molecular Magnet? A Combined High-Pressure Single-Crystal X-Ray Diffraction and Magnetic Study. Magnetochemistry 2019, 5, 33. https://doi.org/10.3390/magnetochemistry5020033
Handzlik G, Sieklucka B, Tomkowiak H, Katrusiak A, Pinkowicz D. How to Quench Ferromagnetic Ordering in a CN-Bridged Ni(II)-Nb(IV) Molecular Magnet? A Combined High-Pressure Single-Crystal X-Ray Diffraction and Magnetic Study. Magnetochemistry. 2019; 5(2):33. https://doi.org/10.3390/magnetochemistry5020033
Chicago/Turabian StyleHandzlik, Gabriela, Barbara Sieklucka, Hanna Tomkowiak, Andrzej Katrusiak, and Dawid Pinkowicz. 2019. "How to Quench Ferromagnetic Ordering in a CN-Bridged Ni(II)-Nb(IV) Molecular Magnet? A Combined High-Pressure Single-Crystal X-Ray Diffraction and Magnetic Study" Magnetochemistry 5, no. 2: 33. https://doi.org/10.3390/magnetochemistry5020033
APA StyleHandzlik, G., Sieklucka, B., Tomkowiak, H., Katrusiak, A., & Pinkowicz, D. (2019). How to Quench Ferromagnetic Ordering in a CN-Bridged Ni(II)-Nb(IV) Molecular Magnet? A Combined High-Pressure Single-Crystal X-Ray Diffraction and Magnetic Study. Magnetochemistry, 5(2), 33. https://doi.org/10.3390/magnetochemistry5020033