Abstract
The complexes [Ln2(hfac)6(L)]·nC6H14 (Ln = Dy (1) n = 0, Yb (2) n = 1) with the L chiral 3,14-di-(2-pyridyl)-4,13-diaza[6]helicene ligand (hfac− = 1,1,1,5,5,5-hexafluoroacetylacetonate) have been synthesized in their racemic form and structurally and magnetically characterized. Both complexes behave as field-induced single molecule magnets in the crystalline phase. These magnetic properties were rationalized by ab initio calculations.
1. Introduction
The development of nanomaterials for high density data storage, the development of molecular Qubits/Qudits for quantum computing and spintronics is very active in the field of molecular magnetism, and both chemists and physicists communities are working hand-in-hand to make rapid progress in this field [1,2,3,4,5,6,7]. In this context, lanthanide-based complexes are currently intensively studied, especially those displaying Single-Molecule Magnet (SMM) behavior. The interest in such species is due to the intrinsic strong magnetic anisotropy and high magnetic moment of the lanthanides [8,9,10,11,12,13,14,15]. The electronic density distribution leads to two classes of lanthanides i.e., prolate ions (axial distribution) and oblate ions (planar distribution) [16]. The most popular ions for each class are the YbIII and DyIII ions, respectively. The coordination sphere plays a crucial role for tuning adequate electronic distribution and energy splitting of the ground multiplet state leading to the observation of SMM behavior. For the oblate DyIII ion, the association of the β-diketonate anions and bis-chelating nitrogenated ligand (N2O6 coordination sphere) often permits the detection of slow magnetic relaxation, which is not the case for the prolate YbIII ion [17,18,19,20,21,22,23].
In addition, another challenge is to combine one more property to the SMM behavior. In this framework, a hot topic is the design of chiral SMMs [24,25,26]. In our group, special attention is devoted to the use of high optical activity ligands such as the [n]-helicene ligand. By studying the complexes [Dy(hfac)3(bpyhelicene)] and [Dy(tta)3(bpyhelicene)] where bpyhelicene = 3-(2-pyridyl)-4-aza[6]-helicene ligand, some of us demonstrated that the different X-ray structures between the racemic and enantiomerically pure forms could lead to drastic changes of magnetic behavior due to the change of dipolar interaction intensity or nature (ferro versus antiferromagnetic) [27,28].
In the present paper, we proposed to go one step forward by functionalizing the [6]-helicene core with two 2,2-bipyridine moieties. The resulting 3,14-di-(2-pyridyl)-4,13-diaza[6]helicene ligand (L) (Scheme 1) was coordinated to Ln(hfac)3 units (Ln = Dy and Yb) giving rise to the dinuclear complexes of formula [Ln2(hfac)6(L)]·C6H14. The two compounds were structurally characterized by X-ray diffraction and their magnetic properties studied by static and dynamic measurements.
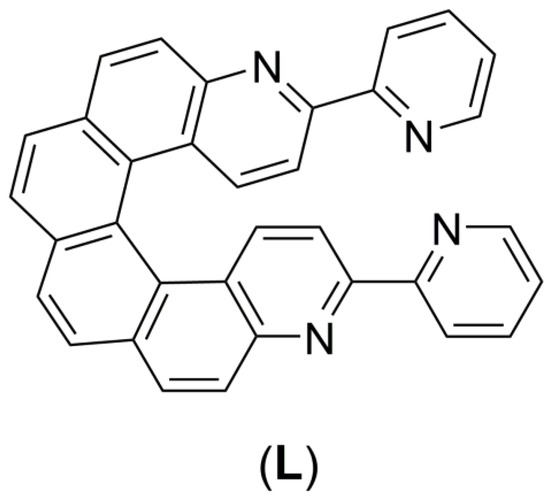
Scheme 1.
Molecular structure of L.
2. Results and Discussion
2.1. X-ray Structures
The coordination reaction of the chiral 3,14-di-(2-pyridyl)-4,13-diaza[6]helicene ligand (L) and tris(1,1,1,5,5,5-hexafluoroaacethylacetonate)bis(aqueous)LnIII in CH2Cl2 led to the formation of both complexes 1 (Ln = Dy) and 2 (Ln = Yb). Both compounds crystallized in the triclinic centrosymmetric space group P-1 (Figure 1 and Figure S1 and Figure S2, Table S1). The asymmetric unit is composed by a [Ln2(hfac)6(L)] dinuclear species and one n-hexane molecule of crystallization for 2. The two 2,2′-bipyridine coordination sites are occupied by a Ln(hfac)3 (hfac− = 1,1,1,5,5,5-hexafluoroacethyacetonate) moiety. Thus each LnIII ion is surrounded by two nitrogen atoms and six oxygen atoms coming from the three hfac− anions and the L ligand. Nevertheless the two resulting N2O6 coordination polyhedrons have distinct symmetries, as shown by the deviations from ideal symmetries determined from the SHAPE program (Table S2) [29]. Since distinct symmetries lead to different electronic distributions, a significant impact on the magnetic properties could be expected (see magnetic section).
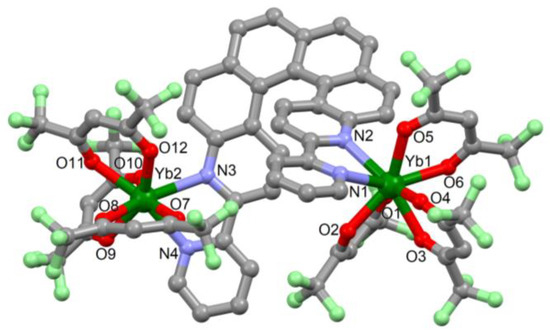
Figure 1.
Molecular structure of 2. Hydrogen atoms and molecules of crystallization are omitted for clarity.
Both enantiomers are present in the cell since the reaction is performed starting from the racemic mixture of L. The two planes represented by the two 2,2′-bipyridine moieties form an angle of 55.3(1)° and 61.0(1)° and the conformation of the ligand leads to an intramolecular Ln–Ln distance of 9.320 Å and 9.890 Å for 1 and 2, respectively.
Remarkably, even if on the molecular level the two compounds are very similar, the two crystal packings are drastically different. For 1, the crystal packing reveals that head-to-tail heterochiral dimers are formed with the presence of π–π interactions between the 2,2-bipyridyl terminal moiety and the helicenic core (Figure 2). An organic network runs along the a axis thanks to π–π interactions between the helicenic cores of neighboring dimers (Figure 2).
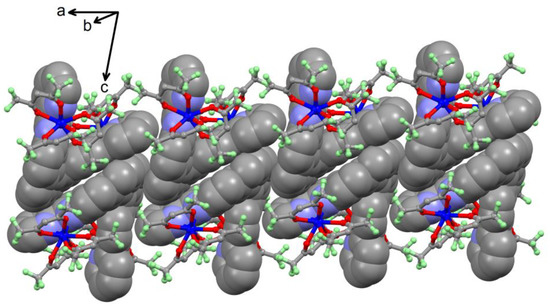
Figure 2.
Crystal packing of 1 along the a axis. “Spacefill” and “ball and sticks” representations are used for the L ligands and organometallic moieties, respectively.
For 2, the crystal packing reveals that the homochiral dinuclear complexes arrange themselves along the a axis while the dinuclear complexes with the other enantiomer of L form the neighboring arrangement (Figure 3), thus yielding alternated arrays of homochiral columns. Surprisingly the organic network is not built through π–π stacking as observed for 1 and for the mononuclear complexes involving the 3-(2-pyridyl)-4-aza[6]-helicene ligand [27] but through CH–π interactions between the 2,2′-bipyridine moieties.
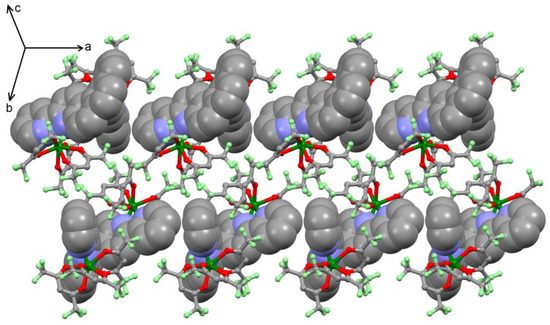
Figure 3.
Crystal packing of 2 along the a axis. “Spacefill” and “ball and sticks” representations are used for L ligands and organometallic moieties, respectively.
The shortest Ln–Ln intermolecular distance is 8.179 Å and 8.956 Å for 1 and 2, respectively, which is similar to the distances measured in the mononuclear complexes involving both Dy(hfac)3 and Dy(tta)3 metallo-precursor [27,28].
2.2. Magnetic Properties
2.2.1. Static magnetic Measurements
The temperature dependence of χMT for the samples 1 and 2 are represented in Figure 4. The room temperature values are 26.82 cm3·K·mol−1 and 5.00 cm3·K·mol−1, respectively, for 1 and 2 which are in good agreement with the expected value of 28.34 cm3·K·mol−1 and 5.14 cm3·K·mol−1 for two isolated DyIII ions (6H15/2 ground state multiplet) and YbIII (2F7/2 ground state multiplet), respectively [30]. Upon cooling, χMT decreases monotonically down to 21.10 cm3·K·mol−1 for 1 and 3.11 cm3·K·mol−1 for 2 due to the thermal depopulation of the MJ states. The field dependence of the magnetization measured at 2.0 K reaches the value of 10.36 µB for 1 and 3.41 µB for 2 under a magnetic field of 50 kOe, which is far from the expected saturated values of 20 µB for 1 and 4 µB for 2 (Figure 4) [30].
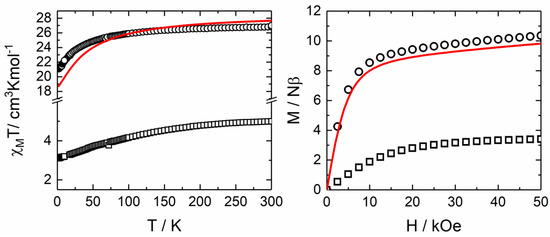
Figure 4.
Temperature dependence of χMT for 1 (circles) and 2 (squares) (left). The field variations of the magnetization at 2 K for 1 (circles) and 2 (squares) (right). Full red lines correspond to the simulated curves from ab initio calculations for 1.
2.2.2. Dynamic Magnetic Measurements
The out-of-phase component of the ac susceptibility (χM”) for both compounds 1 and 2 were measured using immobilized crunched single crystals. For both compounds, no out-of-phase signal was detected in zero magnetic field. In order to suppress the fast magnetic relaxation through quantum tunneling of the magnetization (QTM), the field dependence of the magnetic susceptibility is studied. For both compounds, the application of a small magnetic field led to the appearance of an out-of-phase component of the magnetic susceptibility. Nevertheless for 1, two contributions are observed whatever the value of the magnetic field (Figure S3) and the value of 800 Oe is selected (value at which the fast relaxation contribution is centered at the lowest frequency i.e., 152 Hz at 2 K), while for 2, the maximum of the out-of-phase component remains up to 1000 Hz (Figure S4). Thus the frequency dependence of the magnetic susceptibility for 1 and 2 has been measured up to 10,000 Hz.
Under an applied field of 800 Oe, 1 highlighted a frequency dependence of the out-of-phase signal of the magnetization (Figure 5a and Figure S5). We manually selected the frequency maxima to plot the temperature dependence of the relaxation time (log(τ) vs T for both high (HF, open circles) and low frequency (LF, full circles) contributions (Figure 5b, Table S3). The relaxation time follows the Arrhenius law τ = τ0 exp(Δ/kT) at high temperature with τ0 = 4.6(3) × 10−8 s and Δ = 16.6(1) cm−1 for HF and τ0 = 1.2(2) × 10−7 s and Δ = 37.7(5) cm−1 for LF (Figure 5b), while other magnetic relaxation pathways are observed at lower temperatures such as Raman and Direct processes. The two different relaxation times could be attributed to the two crystallographically independent Dy centers.
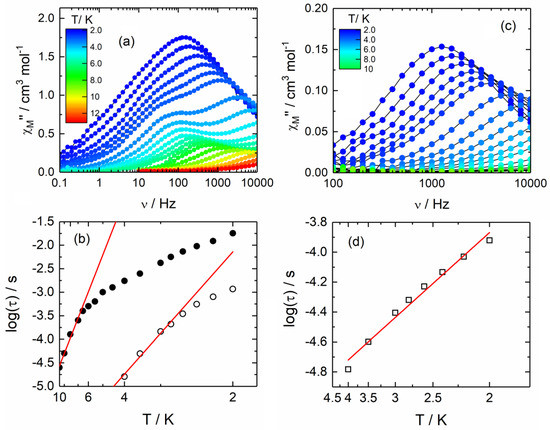
Figure 5.
(a) Frequency dependence of χM” between 2 and 13 K for 1 at 800 Oe and (b) temperature variations of the relaxation times for Dy1 (open circles) and Dy2 (full circles) (attribution based on the computational calculations, see text) for 1 in the temperature range of 2 to 10 K with the best fitted curve (red lines) with the Arrhenius law. (c) Frequency dependence of χM” for 2 at 1000 Oe between 2 and 9 K and (d) temperature variation of the relaxation time for 2 in the temperature range of 2 to 4 K with the best fitted curve with the Arrhenius law (red line).
Under an applied field of 1000 Oe, 2 highlighted a frequency dependence of the out-of-phase signal of the magnetization (Figure 5c and Figure S6) which can be also analyzed in the framework of the extended Debye model [31,32]. The temperature dependence of the relaxation time was extracted and depicted in Figure 5d (Table S3). The relaxation time follows the Arrhenius law τ = τ0 exp(Δ/kT) between 2 and 4 K with τ0 = 2.7(4) × 10−6 s and Δ = 5.5(3) cm−1 (Figure 5d). Even if the magnetic performances of 2 are modest, the observation of a field-induced SMM for an YbIII ion in a N2O6 coordination site has unprecedented example.
2.2.3. Ab Initio Calculations
SA-CASSCF/RASSI-SO calculations were performed for 1 to rationalize the observed magnetic properties (see computational details). The calculated χMT vs T and M vs H (Figure 4) curves fairly well reproduce the experimental curves. Dy1 presents a strongly mixed ground state (30% MJ = |±13/2>, 27% MJ = |±11/2>, 23% MJ = |±15/2>, and 11% MJ = |±7/2>, Table S4) defined by a g-tensor with a main component gZ = 14.94 and exhibiting non-negligible transversal components with gX = 1.34 and gY = 2.01 confirming the low anisotropy character of the ground state (for a pure MJ = |±15/2> ground state, the fully axial, Ising-type, g-tensor expected possess gX = gY = 0.0 and gZ = 20.0). For Dy2, the ground state is calculated to be mainly MJ = |±15/2> (86% MJ = |±15/2> and 11% MJ = |±11/2>, Table S5) with a g-tensor showing a stronger anisotropy character than Dy1, with gZ = 18.97 and lower transversal components (gX = 0.17 and gY = 0.33). At this point the Dy1 and Dy2 magnetic relaxations could be attributed to the HF and LF contributions, respectively. The main component of the ground state g-tensor of each DyIII center is represented in Figure 6. For both magnetic centers, the main magnetic axis appears perpendicular to the plane containing the N atoms from the helicene ligand, as expected for an oblate ion in this coordination sphere [33,34].
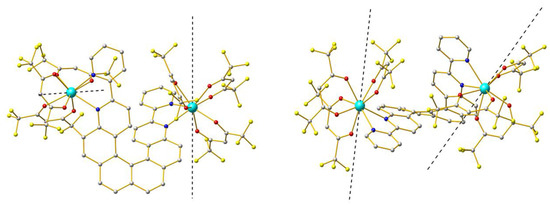
Figure 6.
Orientations of the ground state g-tensor main component (gZ) characterizing the magnetic anisotropy calculated on each Dy center (dark dashed lines) with a top view (left) and a side view (right) of the helicene ligand.
The deviations observed between the two magnetic centers may be related to the differences in the coordination spheres. In fact, it is well-known that to one electronic distribution is associated one magnetic behavior, and consequently when more than one crystallographically lanthanide center is identified in a polynuclear SMM, a multi-magnetic relaxation is expected [35,36,37,38,39,40,41]. In order to give more insights into the relaxation mechanisms observed for the two DyIII centers, we computed the transversal magnetic moments between the Stark levels of each Kramers ion (Figure 7). The two magnetic centers relax slightly differently with probable main relaxation pathways through the 1st excited state. However, the major relaxation for Dy1 seems to proceed with large quantum-tunneling elements (0.558 μB and 2.304 μB for the ground and first excited states, respectively) while Dy2 displays much weaker QTM values. These differences are in the trend of the experimental results with a faster relaxation of the magnetization for Dy1 arising from the large QTM values compared to Dy2 which shows a slower relaxation (small QTM values between the first KDs). The difference between the calculated energy barrier (Δ = 55.9 cm−1 and 96 cm−1) and the experimental barriers (Δ = 16.6 cm−1 and 37.7 cm−1), while the trend is conserved, is common in the literature [42,43,44] and may be explained because the coupling of spin-phonon degrees of freedom in the SMM relaxation is not taken into account in the ab initio model [45,46].
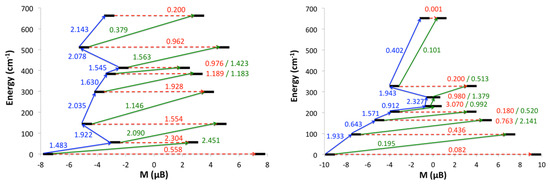
Figure 7.
Computed magnetization blocking barrier in complex 1 for each DyIII ion (Dy1 on the left and Dy2 on the right). Numbers provided on each arrow are the mean absolute values for the corresponding matrix elements of the magnetic transition dipole moment.
A qualitative comparison with the literature highlighted a classic magnetic behavior for the LF Dy magnetic relaxation while the HF Dy magnetic relaxation displayed a faster relaxation of the magnetization than the classical DyIII in N2O6 coordination environment [17,18,19,20,21,22,23]. Such an observation could be due to the specific electronic distribution caused by the bulky 3,14-di-(2-pyridyl)-4,13-diaza[6]helicene ligand.
3. Conclusions
In this article, the [6]-helicene-based lanthanide SMM family was extended starting from the 3,14-di-(2-pyridyl)-4,13-diaza[6]helicene ligand. The latter is composed of two 2,2′-bipyridine coordination sites able to coordinate two Ln(hfac)3 units (hfac− = 1,1,1,5,5,5-hexafluoroacetylacetonate) to give the dinuclear complexes of formula [Ln2(hfac)6(L)]·nC6H14 (Ln = Dy (1) n = 0, Yb (2) n = 1). Both compounds have been characterized by X-ray diffraction and displayed field-induced Single-Molecule Magnet behavior. The magnetic properties of 1 were rationalized by ab initio calculations. It is worth noting that 2 is the first N2O6 YbIII field-induced SMM. These systems are still under investigation by our group to study the optical and magnetic properties of their enantiomerically pure forms.
4. Materials and Methods
4.1. Synthesis General Procedures and Materials
The precursor Dy(hfac)3·2H2O (hfac− = 1,1,1,5,5,5-hexafluoroacetyacetonate anion) was synthesized following previously reported methods [47]. All other reagents were commercially available and used without further purification.
4.2. Synthesis of Complex [Ln2(hfac)6(L)]·nC6H14 (Ln = Dy (1) n = 0, Yb (2) n = 1)
Ln(hfac)3·2H2O (32.8 mg for Ln = Dy and 33.2 mg for Ln = Yb, 0.04 mmol) were dissolved in 5 mL of CH2Cl2 and then added to a solution of 5 mL of CH2Cl2 containing 9.7 mg of L (0.02 mmol). After 20 min of stirring, 30 mL of n-hexane was layered at room temperature in the dark. Slow diffusion following by slow evaporation lead to yellow single crystals that were suitable for X-ray studies. Yield: 17.7 mg (41%) for 1 and 21.4 mg (49%) for 2. Anal. Calcd (%) for C64H26Dy2F36N4O12: C 37.43, H 1.27, N 2.73; found: C 37.39, H 1.33 N, 2.75. Anal. Calcd (%) for C70H40Yb2F36N4O12: C 38.53, H 1.83, N 2.57; found: C 38.47, H 1.99 N, 2.50.
4.3. Crystallography
Single crystals of 1 and 2 were mounted on a APEXIII D8 VENTURE Bruker-AXS diffractometer for data collection (MoKα radiation source, λ = 0.71073 Å), from the Centre de Diffractométrie (CDIFX), Université de Rennes 1, France (Table S1). The structure was solved with a direct method using the SHELXT program [48] and refined with a full matrix least-squares method on F2 using the SHELXL-14/7 program [49]. Complete crystal structure results as a CIF file including bond lengths, angles, and atomic coordinates are deposited as Supporting Information. CCDC number is 1854828 and 1854829 for compounds 1 and 2, respectively.
4.4. Physical Measurements
The elemental analyses of the compounds were performed at the Centre Régional de Mesures Physiques de l’Ouest, Rennes. The dc magnetic susceptibility measurements were performed on solid polycrystalline samples with a Quantum Design MPMS-XL SQUID magnetometer between 2 and 300 K in an applied magnetic field of 0.2 kOe for temperatures of 2–20 K, 2 kOe between 20 and 80 K and 10 kOe above. These measurements were all corrected for the diamagnetic contribution as calculated by Pascal’s constants. The ac magnetic susceptibility measurements were performed on both Quantum Design MPMS-XL SQUID magnetometer and Quantum Design PPMS system equipped with ac/dc probe.
4.5. Computational Details
The atomic positions were extracted from the X-ray diffraction crystal structure of the [Dy2(hfac)6(L)] system (L = 3,14-di-(2-pyridyl)-4,13-diaza[6]helicene). A calculation is performed on each magnetic center while the other DyIII ion is replaced by the diamagnetic YIII ion.
All ab initio calculations were performed using the State-Averaged Complete Active Space Self-Consistent Field approach with the restricted-active-space-state-interaction method (SA-CASSCF/RASSI-SO), as implemented in the MOLCAS quantum-chemistry package (version 8.0) [50]. The relativistic effects are treated in two steps on the basis of the Douglas–Kroll Hamiltonian. The scalar terms were included in the basis-set generation and were used to determine the CASSCF wavefunctions and energies [51]. Spin-orbit coupling was then added within the RASSI-SO method, which mixes the calculated CASSCF wavefunctions [52,53]. The resulting spin-orbit wavefunctions and energies were used to compute the magnetic properties and g-tensors of the ground state multiplet following the pseudospin S = 1/2 formalism, as implemented in the SINGLE-ANISO routine [43,46]. Cholesky decomposition of the bielectronic integrals was employed to save disk space and to speed up the calculations [54].
The active space considered in the calculations consisted of the nine 4f electrons of the Dy(III) ion, spanning the seven 4f orbitals; that is, CAS(9,7)SCF. State-averaged CASSCF calculations were performed for all of the sextets (21 roots), all of the quadruplets (224 roots), and 300 out of the 490 doublets of the DyIII ion. Twenty-one sextets, 128 quadruplets, and 107 doublets were mixed through spin–orbit coupling in RASSI-SO. All atoms were described with ANO-RCC basis sets with the following contractions [8s7p4d3f2g1h] for Dy; [7s6p4d2f] for Y; [4s3p2d] for the O and N atoms; [3s2p1d] for C of the first coordination sphere and [3s2p] for the other C atoms; [2s1p] for F and [2s] for the H atoms [55,56].
Supplementary Materials
The following are available online at http://www.mdpi.com/2312-7481/4/3/39/s1, Figure S1: ORTEP view of 1. Thermal ellipsoids are drawn at 30% probability. Hydrogen atoms and solvent molecules of crystallization are omitted for clarity, Figure S2: ORTEP view of 2. Thermal ellipsoids are drawn at 30% probability. Hydrogen atoms and solvent molecules of crystallization are omitted for clarity, Figure S3: Field dependence of the out-of-phase component of the magnetic susceptibility for 1 at 2 K, Figure S4: Field dependence of the out-of-phase component of the magnetic susceptibility for 2 at 2 K, Figure S5: Frequency dependence of the in-phase component of the magnetic susceptibility for 1, Figure S6: Frequency dependence of the in-phase component of the magnetic susceptibility for 2, Table S1: X-ray crystallographic data of 1 and 2, Table S2: SHAPE analysis for 1 and 2, Table S3: Best fitted parameters (χT, χS, τ, and α) with the extended Debye model for 2 at 1000 Oe in the temperature range 2 to 4 K, Table S4: Computed energy levels (the ground state is set at zero), component values of the Lande factor g, and wavefunction composition for each MJ state of the ground-state multiplet for Dy1 of 1, Table S5: Computed energy levels (the ground state is set at zero), component values of the Lande factor g and wavefunction composition for each MJ state of the ground-state multiplet for Dy2 of 1.
Author Contributions
N.S. performed the organic syntheses; F.P. performed the coordination chemistry, crystallizations, the single crystal X-ray diffraction experiments, and structure refinements; O.C. and J.F.G. performed and analyzed the magnetic measurements, V.M. and B.l.G. performed the ab initio calculations. J.C. and L.O. discussed the idea and the results and commented on the manuscript. F.P., O.C., and B.L.G. conceived and designed the experiments and contributed equally to the writing of the article.
Funding
This work was supported by Région Bretagne, Rennes Métropole, CNRS, Université de Rennes 1, and the European Commission through the ERC-CoG 725184 MULTIPROSMM (project n. 725184). N.S. thanks the ANR (ANR-10-BLAN-724-1-NCPCHEM).
Acknowledgments
B.l.G. and V.M. thank the French GENCI/IDRIS-CINES center for high-performance computing resources.
Conflicts of Interest
The authors declare no conflicts of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| SMM | Single Molecule Magnet |
| QTM | Quantum Tunneling of the Magnetization |
| C6H14 | n-hexane |
| hfac | 1,1,1,5,5,5-hexafluoroacetylacetonate |
| PCM | Polarizable Continuum Model |
| CASSCF | Complete Active Space Self-Consistent Field |
| RASSI-SO | Restricted Active Space State Interaction—Spin-Orbit |
References
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.-A.; Cornia, A.; Gatteschi, D.; et al. Magnetic memory of a single-molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, J.; Gaita-Arino, A.; Coronado, E.; Loss, D. Spin qubits with electrically gated polyoxometalate molecules. Nat. Nanotechnol. 2007, 2, 312–317. [Google Scholar] [CrossRef] [PubMed]
- Ganzhorn, M.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Strong spin-phonon coupling between a single-molecule magnet and a carbon nanotube nanoelectromechanical system. Nat. Nanotechnol. 2013, 8, 165–169. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Ariciu, A.; McAdams, S.; Weihe, H.; Bendix, J.; Tuna, F.; Piligkos, S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. [Google Scholar] [CrossRef] [PubMed]
- Benelli, C.; Gatteschi, D. Magnetism of Lanthanides in Molecular Materials with Transition-Metal Ions and Organic Radicals. Chem. Rev. 2002, 102, 2369–2388. [Google Scholar] [CrossRef] [PubMed]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Pointillart, F.; Cador, O.; Le Guennic, B.; Ouahab, L. Uncommon Lanthanide ions in purely 4f Single Molecule Magnets. Coord. Chem. Rev. 2017, 346, 150–175. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kevlin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.S.; Day benjamin, M.; Chen, Y.C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Liddle, S.T.; van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.K.; Murugavel, R. Enricing Lanthanide single-ion magnetism through symmetry and axiality. Chem. Commun. 2018, 54, 3685–3696. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Li, D.-P.; Wang, T.-W.; Li, C.-H.; Liu, D.-S.; Li, Y.-S.; You, X.-Z. Single-ion magnets based on mononuclear lanthanide complexes with chiral Schiff base ligands [Ln(FTA)3L] (Ln = Sm, Eu, Gd, Tb and Dy). Chem. Commun. 2010, 46, 2929–2931. [Google Scholar] [CrossRef] [PubMed]
- Norel, L.; Bernot, K.; Feng, M.; Roisnel, T.; Caneschi, A.; Sessoli, R.; Rigaut, S. A Carbon-rich ruthenium decorated dysprosium single molecule magnet. Chem. Commun. 2012, 48, 3948–3950. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.-J.; Guo, Y.-N.; Tian, J.-L.; Tang, J.; Gu, W.; Liu, X.; Yan, S.-P.; Cheng, P.; Liao, D.-Z. Enhancing Anisotropy Barriers of Dysprosium(III) Single-Ion Magnets. Chem. Eur. J. 2012, 18, 2484–2487. [Google Scholar] [CrossRef] [PubMed]
- Da Cunha, T.T.; Jung, J.; Boulon, M.-E.; Campo, G.; Pointillart, F.; Pereira, C.; Le Guennic, B.; Cador, O.; Bernot, K.; Pineider, F.; et al. Magnetic Poles Determinations and Robustness of Memory Effect upon Solubilization in a DyIII-Based Single Ion Magnet. J. Am. Chem. Soc. 2013, 135, 16332–16335. [Google Scholar] [CrossRef] [PubMed]
- Pointillart, F.; Jung, J.; Berraud-Pache, R.; Le Guennic, B.; Dorcet, V.; Golhen, S.; Cador, O.; Maury, O.; Guyot, Y.; Decurtins, S.; et al. Luminescence and Single-Molecule Magnet Behavior in Lanthnaide Complexes Involving a Tetrathiafulvalene-Fused Dipyridophenazine Ligand. Inorg. Chem. 2015, 54, 5384–5397. [Google Scholar] [CrossRef] [PubMed]
- Bi, Y.; Guo, Y.-N.; Zhao, L.; Guo, Y.; Lin, S.-Y.; Jiang, S.-D.; Tang, J.; Wang, B.-W.; Gao, S. Capping Ligand Perturbed Slow Magnetic Relaxation in Dysprosium Single-Ion Magnets. Chem. Eur. J. 2011, 17, 12476–12481. [Google Scholar] [CrossRef] [PubMed]
- Cosquer, G.; Pointillart, F.; Golhen, S.; Cador, O.; Ouahab, L. Slow Magnetic Relaxation in Condensed versus Dispersed Dysprosium(III) Mononuclear Complexes. Chem. Eur. J. 2013, 19, 7895–7903. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Rouquette, J.; Thibaud, J.M.; Ferreira, R.A.S.; Carlos, L.D.; Donnadieu, B.; Vieru, V.; Chibotaru, L.F.; Konczewicz, L.; Haines, J.; et al. A High-Temperature Molecular Ferroelectric Zn/Dy Complex Exhibiting Single-Ion-Magnet Behavior and Lanthanide Luminescence. Angew. Chem. Int. Ed. 2015, 54, 2236–2240. [Google Scholar] [CrossRef] [PubMed]
- Inglis, R.; White, F.; Piligkos, S.; Wernsdorfer, W.; Brechin, E.K.; Papaefstathiou, G.S. Chiral single-molecule magnets: A partial Mn(III) supertetrahedron from achiral components. Chem. Commun. 2011, 47, 3090–3092. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.M.; Zhang, D.-Q.; Zhu, D.-B. Field-Induced Single-Ion Magnets Based on Enantiopure Chiral β-Diketonate Ligands. Inorg. Chem. 2013, 52, 8933–8940. [Google Scholar] [CrossRef] [PubMed]
- Ou-Yang, J.-K.; Saleh, N.; Fernandez Garcia, G.; Norel, L.; Pointillart, F.; Guizouarn, T.; Cador, O.; Totti, F.; Ouahab, L.; Crassous, J.; et al. Improved slow magnetic relaxation in optically pure helicene-based DyIII single molecule magnets. Chem. Commun. 2016, 52, 14474–14477. [Google Scholar] [CrossRef] [PubMed]
- Fernandez Garcia, G.; Flores Gonzalez, J.; Ou-Yang, J.-K.; Saleh, N.; Pointillart, F.; Cador, O.; Guizouarn, T.; Totti, F.; Ouahab, L.; Crassous, J.; et al. Slow Magnetic Relaxation in Chiral Helicene-Based Coordination Complex of Dysprosium. Magnetochemistry 2017, 3, 2–14. [Google Scholar] [CrossRef]
- Llunell, M.; Casanova, D.; Cirera, J.; Bofill, J.M.; Alemany, P.; Alvarez, S. SHAPE (v. 2.1); Universitat de Barcelona: Barcelona, Spain, 2013. [Google Scholar]
- Kahn, O. Molecular Magnetism; VCH: Weinhem, Germany, 1993. [Google Scholar]
- Dekker, C.; Arts, A.F.M.; Wijn, H.W.; van Duyneveldt, A.J.; Mydosh, J.A. Activated dynamics in a two-dimensional Ising spin glass: Rb2Cu1−xCoxF4. Phys. Rev. B 1989, 40, 11243–11251. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dipersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Bosson, J.; Gouin, J.; Lacour, J. Cationic triangulenes and helicenes: Synthesis, chemical stability, optical properties and extended applications of these unusual dyes. Chem. Soc. Rev. 2014, 43, 2824–2840. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; da Cunha, T.T.; Le Guennic, B.; Pointillart, F.; Pereira, C.L.M.; Luzon, J.; Golhen, S.; Cador, O.; Maury, O.; Ouahab, L. Magnetic Studies of Redox-Active Tetrathiafulvalene-Based Complexes: Dysprosium vs. Ytterbium Ananlogues. Eur. J. Inorg. Chem. 2014, 24, 3888–3894. [Google Scholar] [CrossRef]
- Guo, Y.-N.; Xu, G.-F.; Gamez, P.; Zhao, L.; Lin, S.-Y.; Deng, R.; Tang, J.; Zhang, H.-J. Two-Step Relaxation in a Linear Tetranuclear Dysprosium(III) Aggregate Showing Single-Molecule Magnet Behavior. J. Am. Chem. Soc. 2010, 132, 8538–8539. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Jung, J.; Zhang, P.; Guo, M.; Zhao, L.; Tang, J.; Le Guennic, B. Site-Resolved Two-Step Relaxation Process in an Asymmetric Dy2 Single-Molecule Magnet. Chem. Eur. J. 2016, 22, 1392–1398. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhang, L.; Tang, J. Lanthanide single molecule magnets: Progress and perspective. Dalton Trans. 2015, 44, 3923–3929. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Guo, M.; Tang, J. Recent Developments in Lanthanide Single-Molecule Magnets. Chem. Asian. J. 2017, 12, 2772–2779. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Guo, M.; Li, X.-L.; Tang, J. Molecular magnetism of lanthanide: Advances and perspectives. Coord. Chem. Rev. 2018. [Google Scholar] [CrossRef]
- Pointillart, F.; Guizouarn, T.; Lefeuvre, B.; Golhen, S.; Cador, O.; Ouahab, L. Rational Design of a Lanthanide-Based Complex Featuring Different Single-Molecule Magnets. Chem. Eur. J. 2015, 21, 16929–16934. [Google Scholar] [CrossRef] [PubMed]
- Feng, M.; Pointillart, F.; Lefeuvre, B.; Dorcet, V.; Golhen, S.; Cador, C.; Ouahab, L. Multiple Single-Molecule Magnet Behaviors in Dysprosium Dinuclear Complexes Involving a Multiple Functionalized Tetrathiafulvalene-Based Ligand. Inorg. Chem. 2015, 54, 4021–4028. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Dreiser, J.; Weihe, H.; Sibille, R.; Johannesen, H.V.; Sorensen, M.A.; Nielsen, B.E.; Sigrist, M.; Mutka, H.; Rols, S.; et al. Design of Single-Molecule Magnets: Insufficiency of the Anisotropy Barrier as the Sole Criterion. Inorg. Chem. 2015, 54, 7600–7606. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L.; Soncini, A. The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment. Angew. Chem. Int. Ed. 2008, 47, 4126–4129. [Google Scholar] [CrossRef] [PubMed]
- Lunghi, A.; Totti, F. The role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer. Inorganics 2016, 4, 28–38. [Google Scholar] [CrossRef]
- Lucaccini, E.; Sorace, L.; Perfetti, M.; Costes, J.-P.; Sessoli, R. Beyond the anisotropy barrier: Slow relaxation of the magnetization in both easy-axis and easy-plane Ln(trensal) complexes. Chem. Commun. 2014, 50, 1648–1651. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef] [PubMed]
- Richardson, M.F.; Wagner, W.F.; Sands, D.E. Rare-earth trishexafluoroacetylacetonates and related compounds. J. Inorg. Nucl. Chem. 1968, 30, 1275–1289. [Google Scholar] [CrossRef]
- Sheldrick, G.L. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.F.; Delcey, M.G.; De Vico, L.; Galván, I.F.; Ferré, N.; Frutos, L.M.; Gagliardi, L.; et al. Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations Across the Periodic Table. J. Comput. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Taylor, P.R.; Siegbahn, P.E.M. A Complete Active Space SCF Method (CASSCF) Using a Density Matrix Formulated Super-CI Approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Malmqvist, P.Å.; Roos, B.O.; Schimmelpfennig, B. The Restricted Active Space (RAS) State Interaction Approach with Spin-Orbit Coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
- Malmqvist, P.-Å.; Roos, B.O. The CASSCF State Interaction Method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Aquilante, F.; Malmqvist, P.-Å.; Pedersen, T.B.; Ghosh, A.; Roos, B.O. Cholesky Decomposition-Based Multiconfiguration Second-Order Perturbation Theory (CD-CASPT2): Application to the Spin-State Energetics of CoIII(diiminato)(NPh). J. Chem. Theory Comput. 2008, 4, 694–702. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.A.; Veryazov, V.; Widmark, P.O. Main Group Atoms and Dimers Studied with A New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.; Veryazov, V.; Widmark, P.O.; Borin, A.C. New Relativistic Atomic Natural Orbital Basis Sets for Lanthanide Atoms with Applications to the Ce Diatom and LuF3. J. Phys. Chem. A 2008, 112, 11431–11435. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).