Mapping the Magnetic Anisotropy inside a Ni4 Cubane Spin Cluster Using Polarized Neutron Diffraction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. Magnetic Measurements
2.3. Simulation of Angular-Resolved Magnetic Measurements
2.4. Neutron Diffraction
2.4.1. Polarized Neutron Diffraction
2.4.2. Unpolarized Neutron Diffraction
3. Results and Discussion
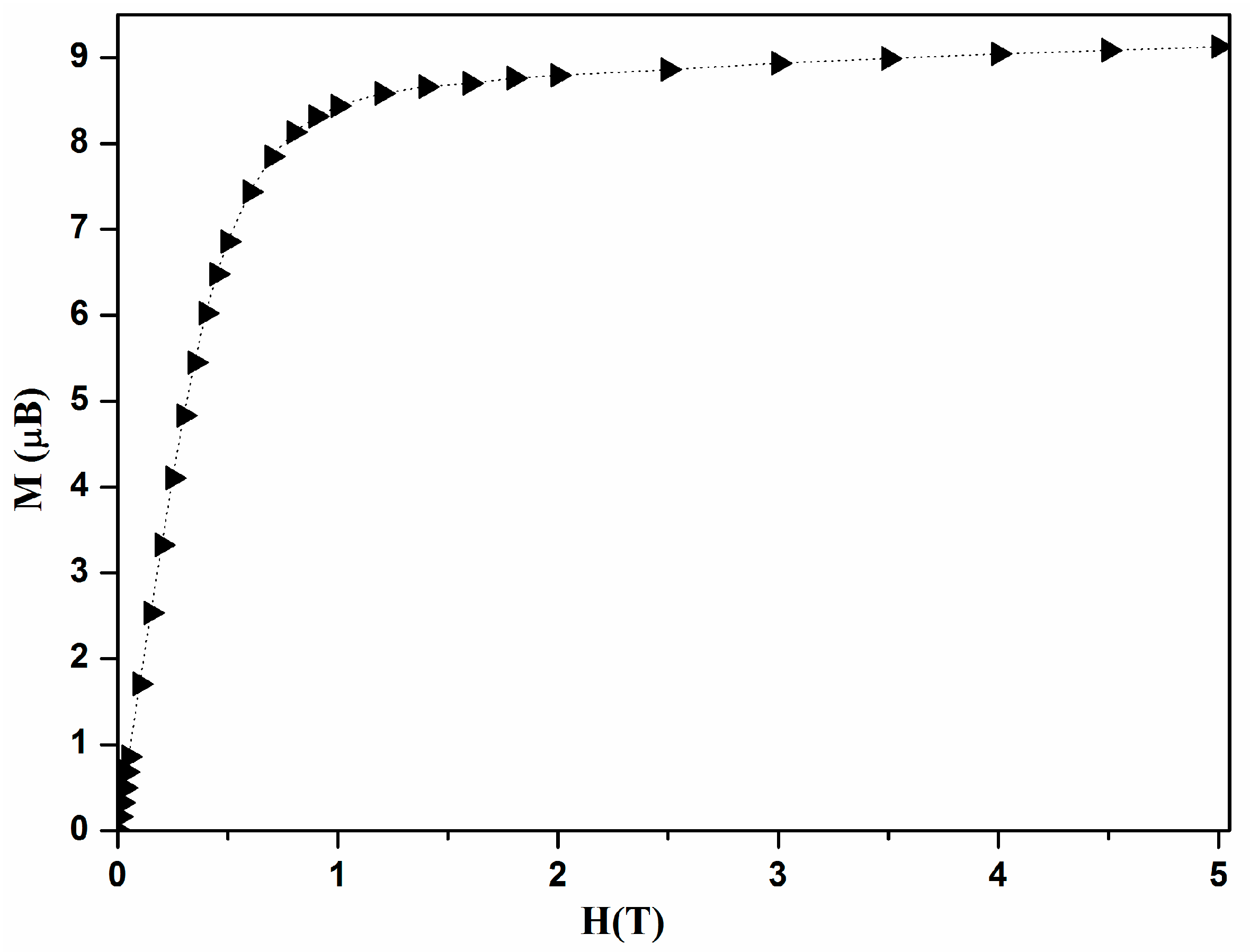
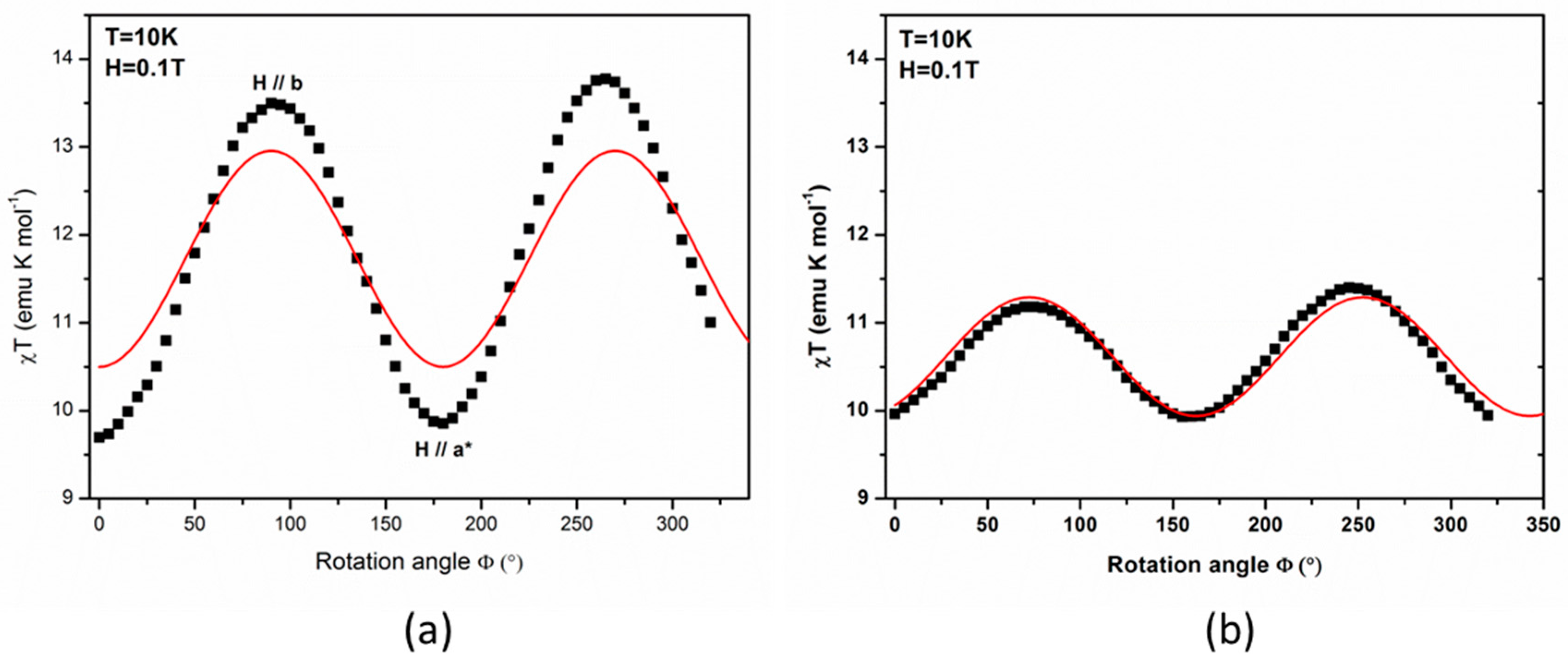
3.1. Bulk Magnetic Anisotropy from Magnetometry
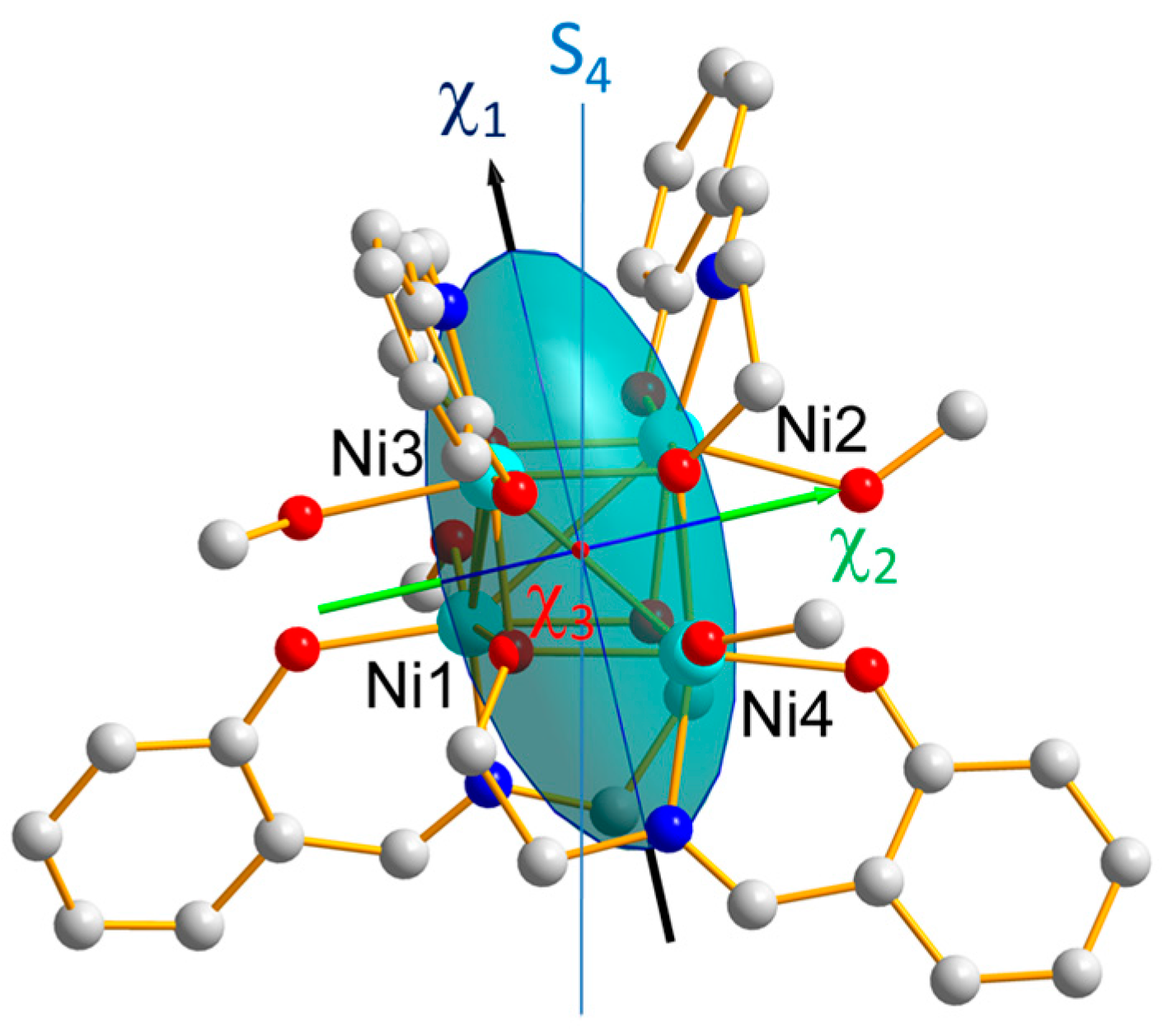
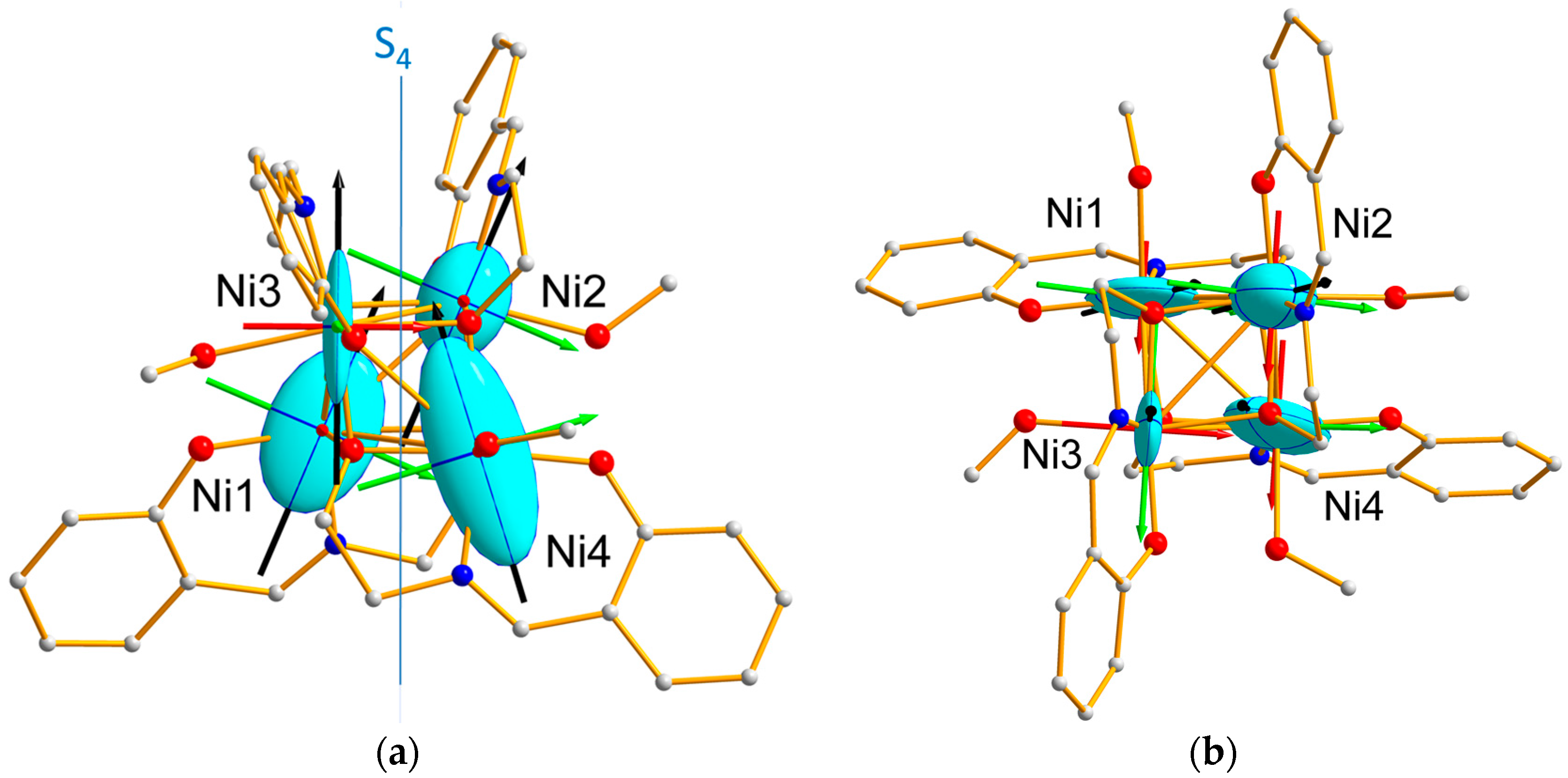
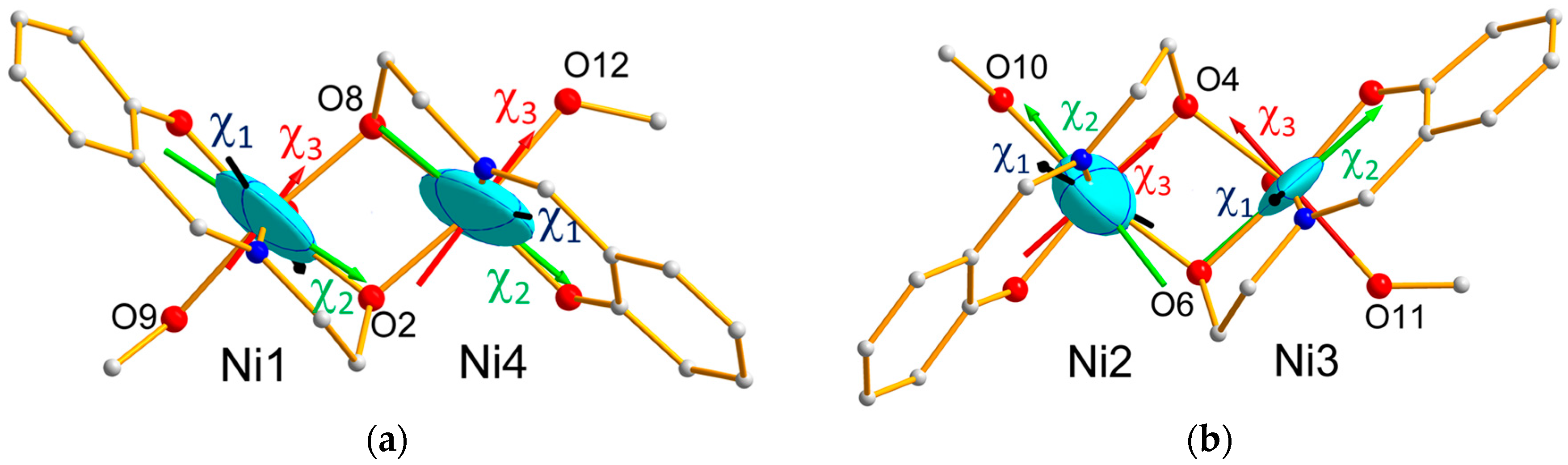
3.2. Local Susceptibility Tensor from PND
3.3. Discussion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Neese, F.; Pantazis, D.A. What is not required to make a single molecule magnet. Faraday Discuss. 2011, 148, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Jung, J.; Cador, O.; Bernot, K.; Pointillart, F.; Luzon, J.; Guennic, B.L. Influence of the supramolecular architecture on the magnetic properties of a DyIII single-molecule magnet: an ab initio investigation. Beilstein. J. Nanotechnol. 2014, 5, 2267–2274. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Jung, J.; Zhang, L.; Tang, J.; Le Guennic, B. Elucidating the magnetic anisotropy and relaxation dynamics of low-coordinate lanthanide compounds. Inorg. Chem. 2016, 55, 1905–1911. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.; Ungur, L.; Aronica, C.; Elmoll, H.; Pilet, G.; Luneau, D. Structure, magnetism, and theoretical study of a mixed-valence CoII3CoIII4 heptanuclear wheel: Lack of SMM behavior despite negative magnetic anisotropy. J. Am. Chem. Soc. 2008, 130, 12445–12455. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Datta, S.; Friend, L.; Cardona-Serra, S.; Gaita-Arino, A.; Coronado, E.; Hill, S. Multi-frequency epr studies of a mononuclear holmium single-molecule magnet based on the polyoxometalate HoIII(W5O18)2]9−. Dalton Trans. 2012, 41, 13697–13704. [Google Scholar] [CrossRef] [PubMed]
- Boulon, M.-E.; Cucinotta, G.; Liu, S.-S.; Jiang, S.-D.; Ungur, L.; Chibotaru, L.F.; Gao, S.; Sessoli, R. Angular-resolved magnetometry beyond triclinic crystals: Out-of-equilibrium studies of Cp*Ercot single-molecule magnet. Chem. Eur. J. 2013, 19, 13726–13731. [Google Scholar] [CrossRef] [PubMed]
- Perfetti, M.; Cucinotta, G.; Boulon, M.-E.; El Hallak, F.; Gao, S.; Sessoli, R. Angular-resolved magnetometry beyond triclinic crystals part II: Torque magnetometry of Cp*Ercot single-molecule magnets. Chem. Eur. J. 2014, 20, 14051–14056. [Google Scholar] [CrossRef] [PubMed]
- Ridier, K.; Mondal, A.; Boilleau, C.; Gillon, B.; Chaboussant, G.; Le Guennic, B.; Costuas, K.; Lescouëzec, R. Polarized neutron diffraction to probe local magnetic anisotropy of a low-spin Fe(III) complex. Angew. Chem. Int. Ed. 2016, 55, 3963–3967. [Google Scholar] [CrossRef] [PubMed]
- Ridier, K.; Gillon, B.; Gukasov, A.; Chaboussant, G.; Cousson, A.; Luneau, D.; Borta, A.; Jacquot, J.-F.; Checa, R.; Chiba, Y.; et al. Polarized neutron diffraction as a tool for mapping the molecular magnetic anisotropy: Local susceptibility tensors in Co2+ complexes. Chem. Eur. J. 2016, 22, 724–735. [Google Scholar] [CrossRef] [PubMed]
- Sieber, A.; Boskovic, C.; Bircher, R.; Waldmann, O.; Ochsenbein, S.T.; Chaboussant, G.; Güdel, H.U.; Kirchner, N.; van Slageren, J.; Wernsdorfer, W.; et al. Synthesis and spectroscopic characterization of a new family of Ni4 spin clusters. Inorg. Chem. 2005, 44, 4315–4325. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, E.; Rodriguez-Fortea, A.; Alemany, P.; Alvarez, S. Density functional study of the exchange coupling in distorted cubane complexes containing the Cu4O4core. Polyhedron 2001, 20, 1323–1327. [Google Scholar] [CrossRef]
- Gukasov, A.; Brown, P.J. Determination of atomic site susceptibility tensors from polarized neutron diffraction data. Phys. Condens. Matter 2002, 14, 8831–8839. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallogr. 2014, 229, 345–352. [Google Scholar]
- Nihei, M.; Hoshino, N.; Ito, T.; Oshio, H. Structures and magnetic properties of metal cubes. Polyhedron 2003, 22, 2359–2362. [Google Scholar] [CrossRef]




| PND Data Collections | ||||
|---|---|---|---|---|
| Instrument | 5c1 (LLB) | |||
| Temperature (K) | 10 | |||
| Field (T) | 2 | |||
| Field components 1 | Hx | −0.7022 | −0.3395 | −0.0256 |
| Hy | 0.1858 | −0.9347 | 0.1361 | |
| Hz | 0.6873 | −0.1054 | 0.9904 | |
| Number of observations | 241 | 258 | 273 | |
| Nobs with |1−R| > 2σ | 47 | 75 | 48 | |
| 4-Circle Neutron Diffraction Data Collection | |
|---|---|
| Instrument | 5c2 (LLB) |
| Temperature (K) | 20 |
| N measured reflections | 225 |
| N merged reflections | 111 |
| N used reflections (I > 3σ) | 91 |
| N refined parameters | 5 |
| R(F) | 0.124 |
| Rw(F) | 0.133 |
| GOF | 5.96 |
| χ11 | χ22 | χ33 | χ23 | χ31 | χ12 | ||
|---|---|---|---|---|---|---|---|
| Cluster 1 | [Ni4] | 1.88(24) | 2.32(12) | 1.04(12) | 0.0 | 0.0 | −0.72(28) |
| Ions 2 | Ni1 | 0.63(18) | 0.68(12) | 0.16(9) | 0.0 | 0.0 | 0.0 |
| Ni2 | 0.42(20) | 0.48(8) | 0.33(6) | 0.0 | 0.0 | 0.0 | |
| Ni3 | 0.23(18) | 0.58(9) | 0.32(7) | 0.0 | 0.0 | −0.18(12) | |
| Ni4 | 0.74(21) | 0.85(11) | 0.20(9) | 0.0 | 0.0 | −0.33(13) | |
| Pairs 3 | Ni1–Ni4 | 1.40(24) | 1.50(14) | 0.36(10) | 0.0 | 0.0 | −0.26(16) |
| Ni2–Ni3 | 0.60(16) | 1.02(10) | 0.66(8) | 0.0 | 0.0 | 0.0 |
| χ1 | χ2 | χ3 | ||
|---|---|---|---|---|
| cluster | [Ni4] | 2.84 | 1.36 | 1.04 |
| ions | Ni1 | 0.68(12) | 0.63(18) | 0.16(9) |
| Ni2 | 0.48(8) | 0.42(20) | 0.33(6) | |
| Ni3 | 0.66 | 0.32 | 0.15 | |
| Ni4 | 1.13 | 0.46 | 0.20 | |
| pairs | Ni1–Ni4 | 1.72 | 1.18 | 0.36 |
| Ni2–Ni3 | 1.02(10) | 0.66(8) | 0.60(16) |
| Central Atom | Axial d(O…O) (Å) | Equatoriald(O…O) (Å) | Equatoriald(N…O) (Å) | |||
|---|---|---|---|---|---|---|
| Ni1 | O8…O9 | 4.246 | O1…O2 | 3.990 | N1…O6 | 4.008 |
| Ni2 | O6…O10 | 4.275 | O3…O4 | 4.007 | N2…O2 | 3.995 |
| Ni3 | O4…O11 | 4.275 | O5…O6 | 3.987 | N3…O8 | 3.977 |
| Ni4 | O2…O12 | 4.254 | O7…O8 | 3.997 | N4…O4 | 4.007 |
| Coupling | Ni…Ni Distance | Ni–O–Ni Angles | Short Ni–O Bond Lengths | Long Ni–O Bond Length | |
|---|---|---|---|---|---|
| ferromagnetic | Ni1–Ni2 | 3.038 | 96.5–96.6 | 2.030, 2.040, 2.051 | 2.116 |
| Ni1–Ni3 | 3.032 | 94.0–96.3 | 2.019, 2.024, 2.051 | 2.121 | |
| Ni2–Ni4 | 3.042 | 91.1–96.3 | 2.033, 2.040, 2.050 | 2.115 | |
| Ni3–Ni4 | 3.039 | 93.1–97.3 | 2.023, 2.024, 2.050 | 2.136 | |
| antiferromagnetic | Ni1–Ni4 | 3.184 | 100.4 | 2.022, 2.030 | 2.115, 2.121 |
| Ni2–Ni3 | 3.195 | 100.1–101.2 | 2.019, 2.033 | 2.116, 2.136 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iasco, O.; Chumakov, Y.; Guégan, F.; Gillon, B.; Lenertz, M.; Bataille, A.; Jacquot, J.-F.; Luneau, D. Mapping the Magnetic Anisotropy inside a Ni4 Cubane Spin Cluster Using Polarized Neutron Diffraction. Magnetochemistry 2017, 3, 25. https://doi.org/10.3390/magnetochemistry3030025
Iasco O, Chumakov Y, Guégan F, Gillon B, Lenertz M, Bataille A, Jacquot J-F, Luneau D. Mapping the Magnetic Anisotropy inside a Ni4 Cubane Spin Cluster Using Polarized Neutron Diffraction. Magnetochemistry. 2017; 3(3):25. https://doi.org/10.3390/magnetochemistry3030025
Chicago/Turabian StyleIasco, Olga, Yuri Chumakov, Frédéric Guégan, Béatrice Gillon, Marc Lenertz, Alexandre Bataille, Jean-François Jacquot, and Dominique Luneau. 2017. "Mapping the Magnetic Anisotropy inside a Ni4 Cubane Spin Cluster Using Polarized Neutron Diffraction" Magnetochemistry 3, no. 3: 25. https://doi.org/10.3390/magnetochemistry3030025
APA StyleIasco, O., Chumakov, Y., Guégan, F., Gillon, B., Lenertz, M., Bataille, A., Jacquot, J.-F., & Luneau, D. (2017). Mapping the Magnetic Anisotropy inside a Ni4 Cubane Spin Cluster Using Polarized Neutron Diffraction. Magnetochemistry, 3(3), 25. https://doi.org/10.3390/magnetochemistry3030025






