The Highly Conducting Spin-Crossover Compound Combining Fe(III) Cation Complex with TCNQ in a Fractional Reduction State. Synthesis, Structure, Electric and Magnetic Properties
Abstract
:1. Introduction
2. Results and Discussion
2.1. Synthesis
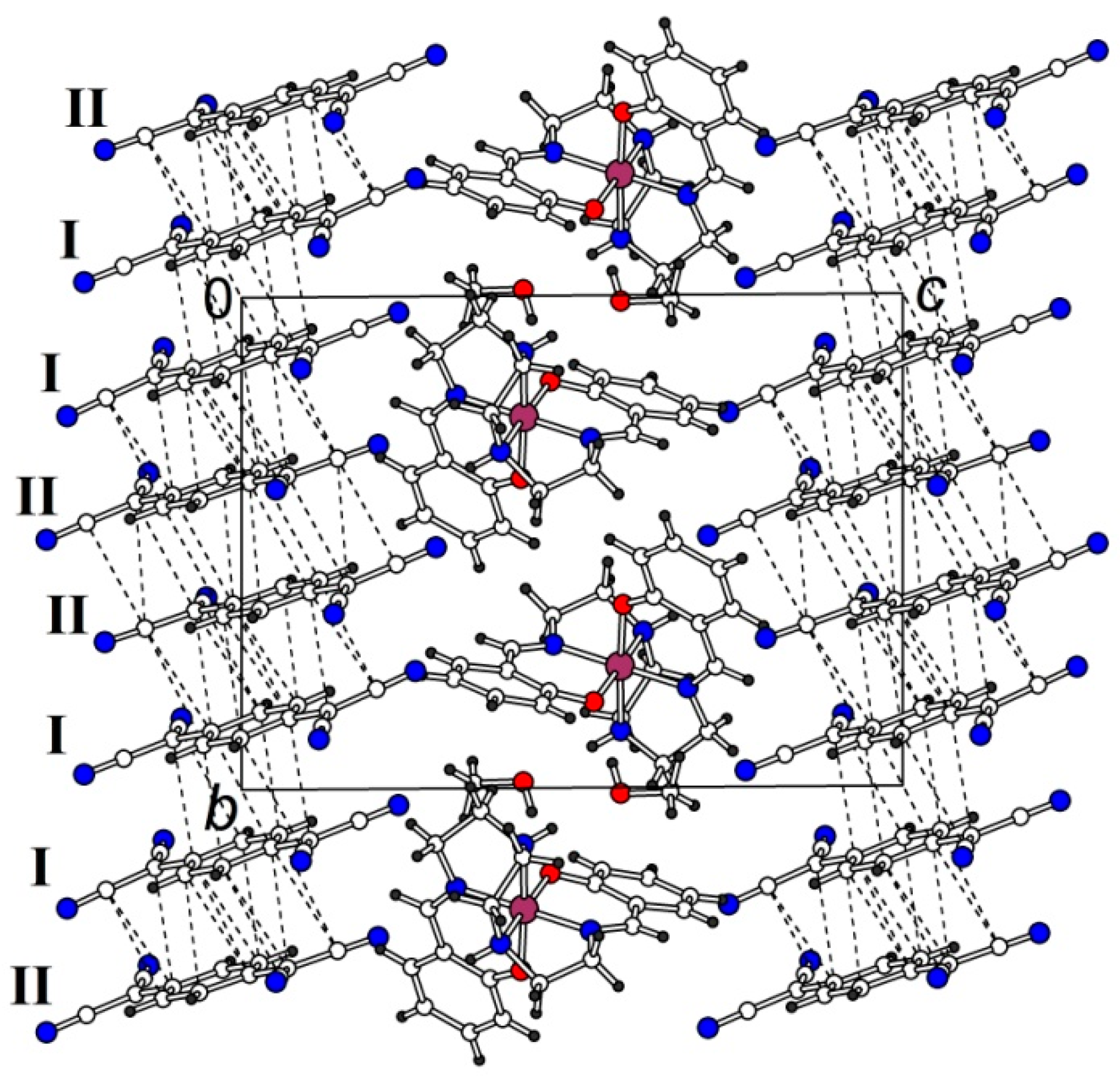
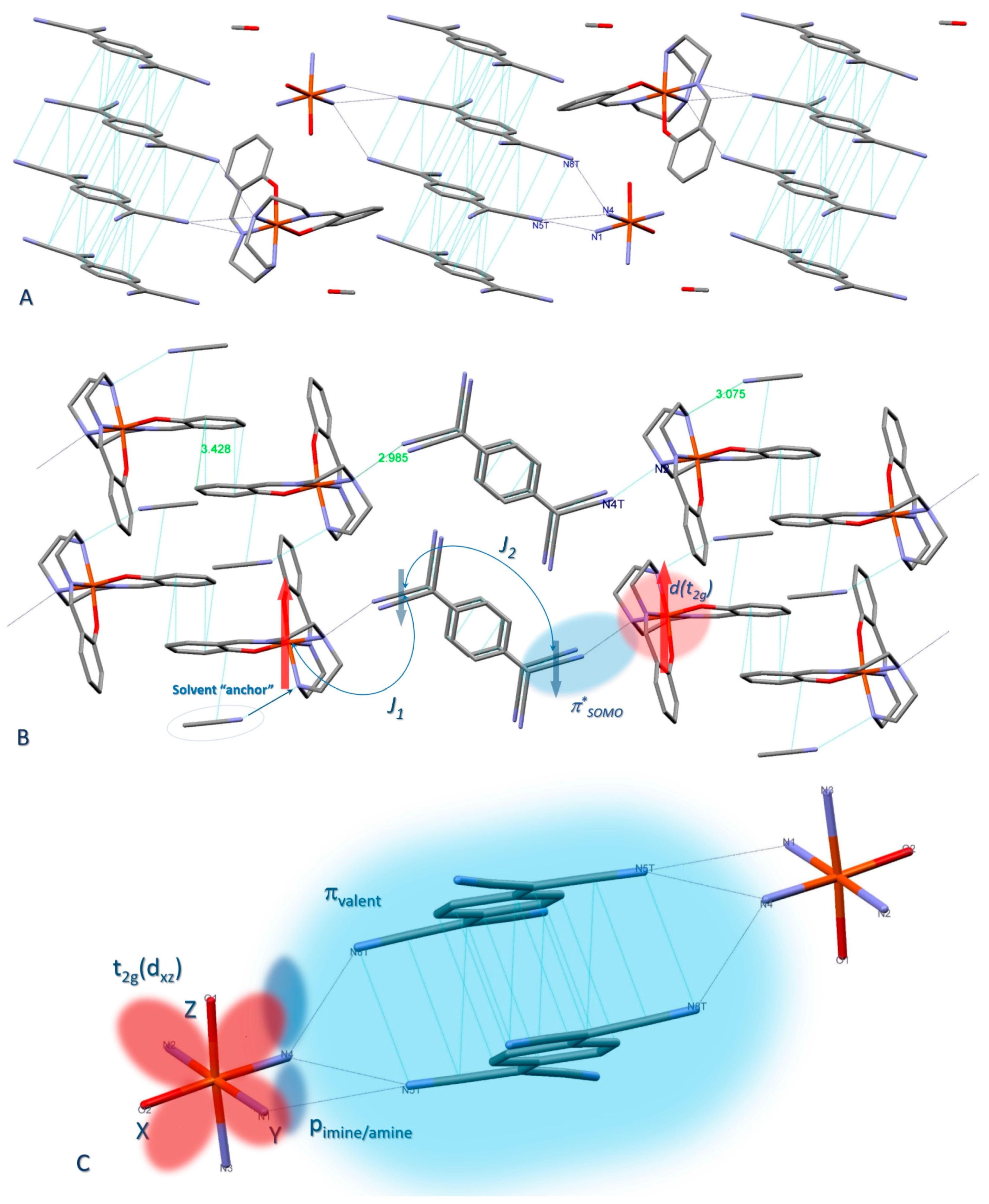
2.2. Crystal Structure
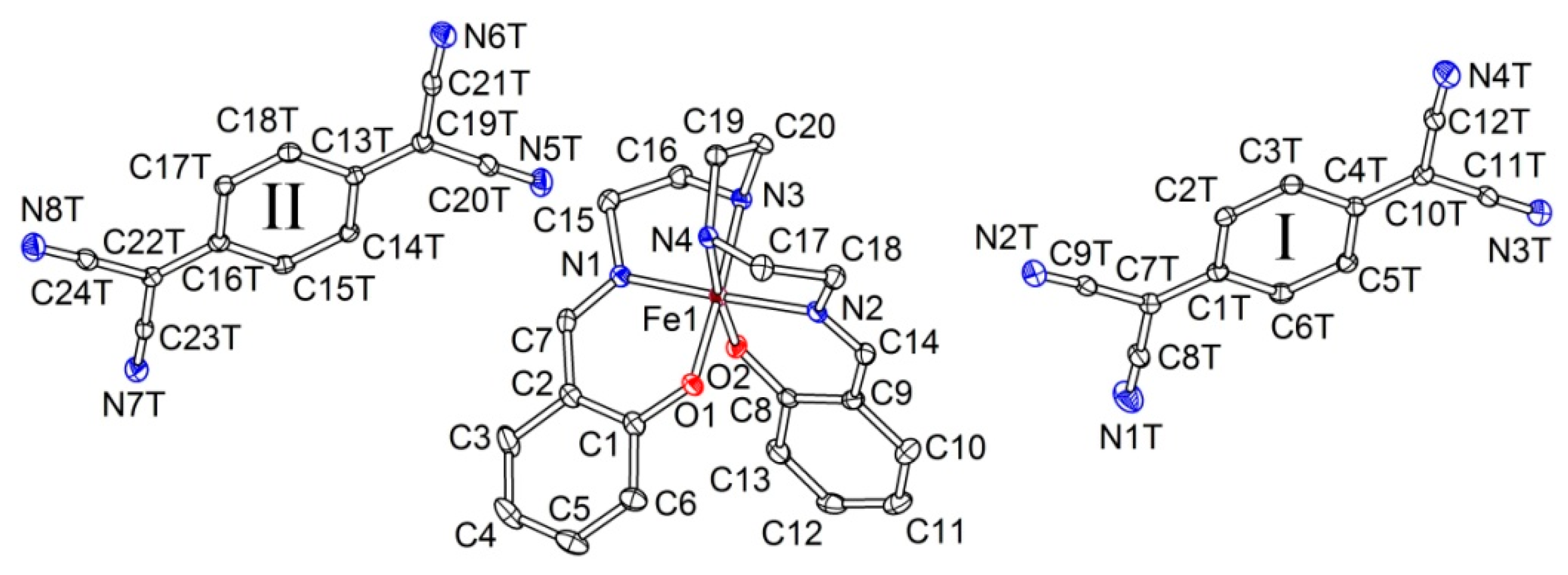
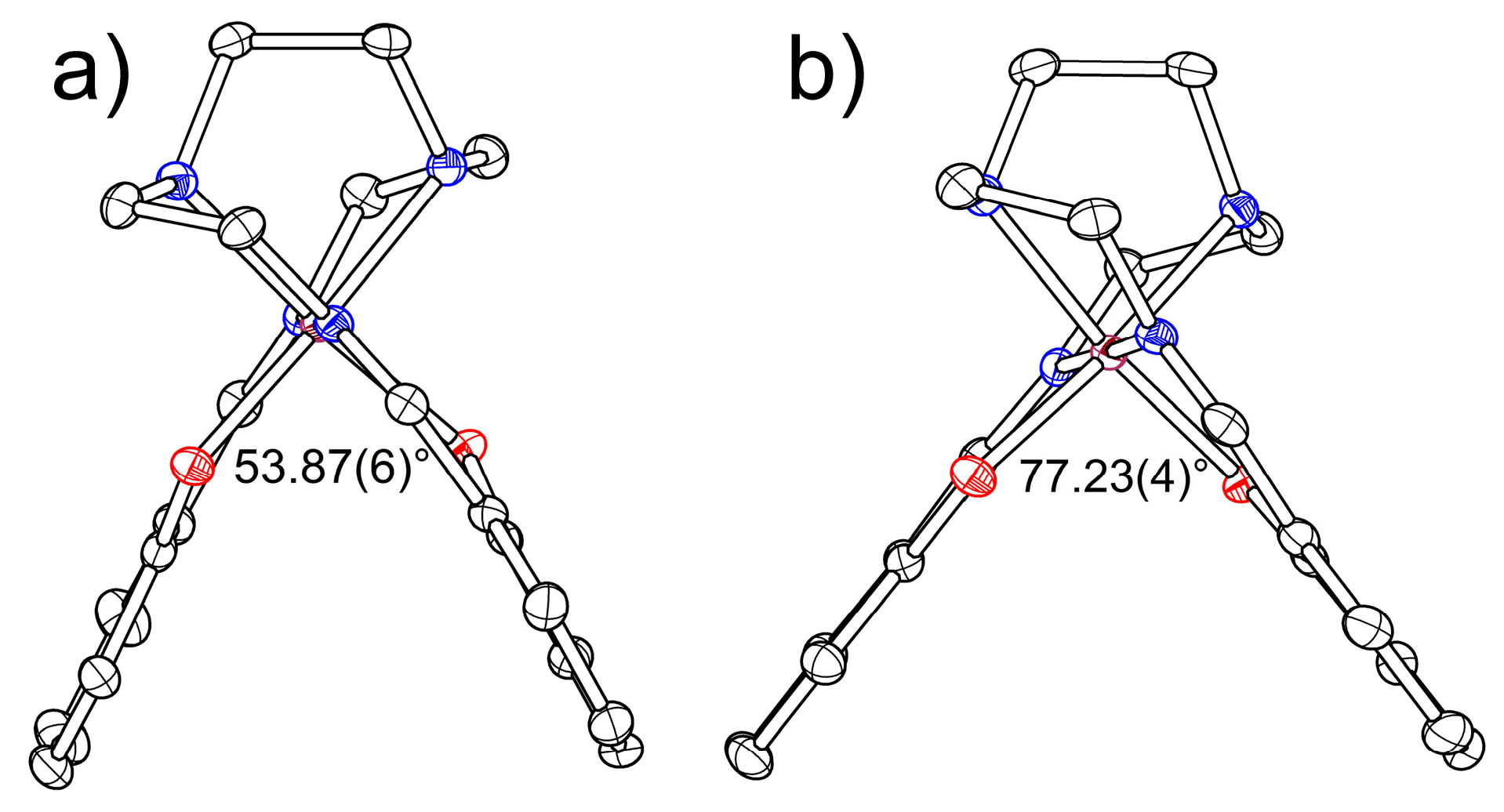
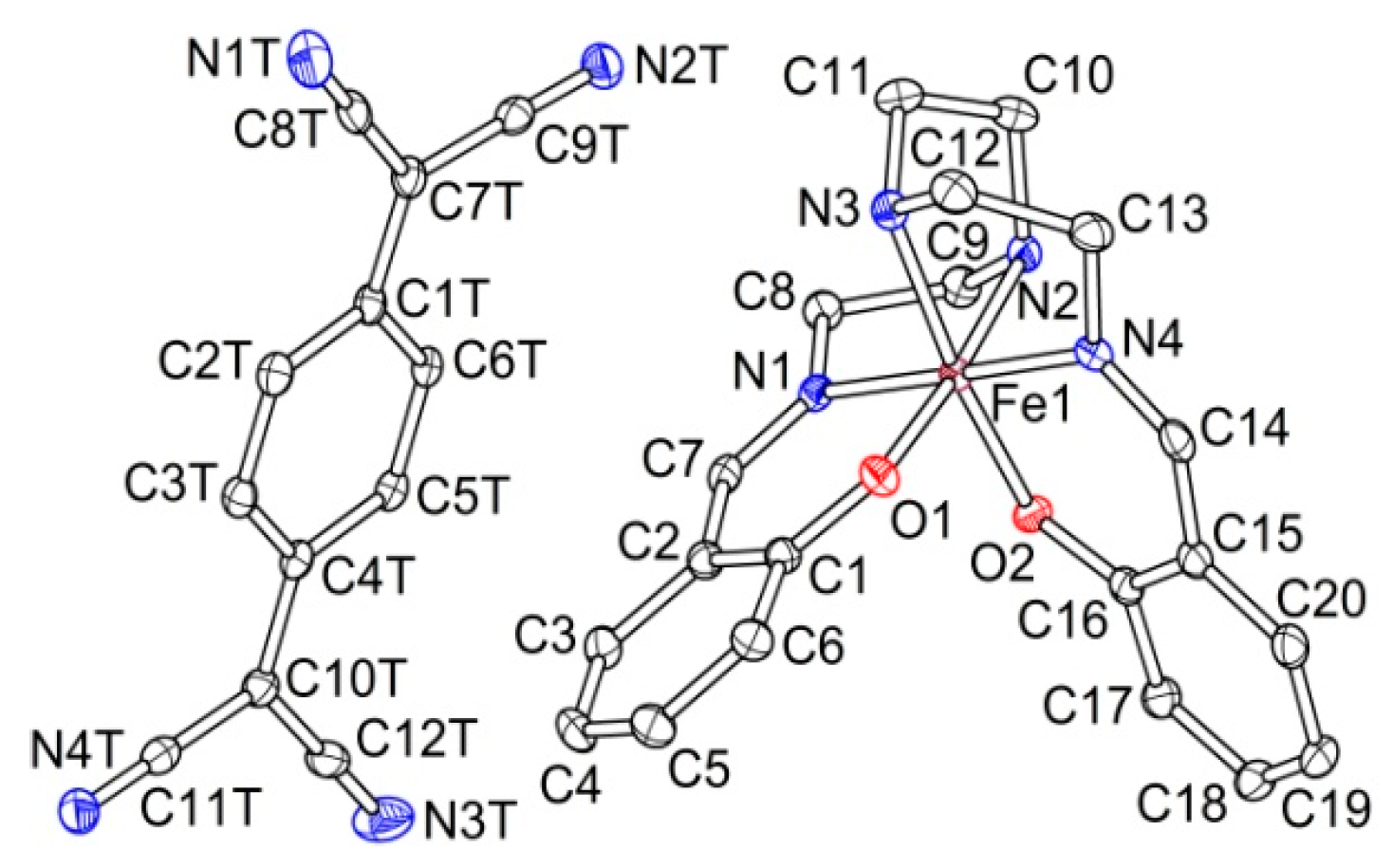
2.2.1. [Fe(III)(sal2-trien)](TCNQ)2·CH3OH (1·MeOH)
2.2.2. [Fe(III)(sal2-trien)](TCNQ)·CH3CN (2)
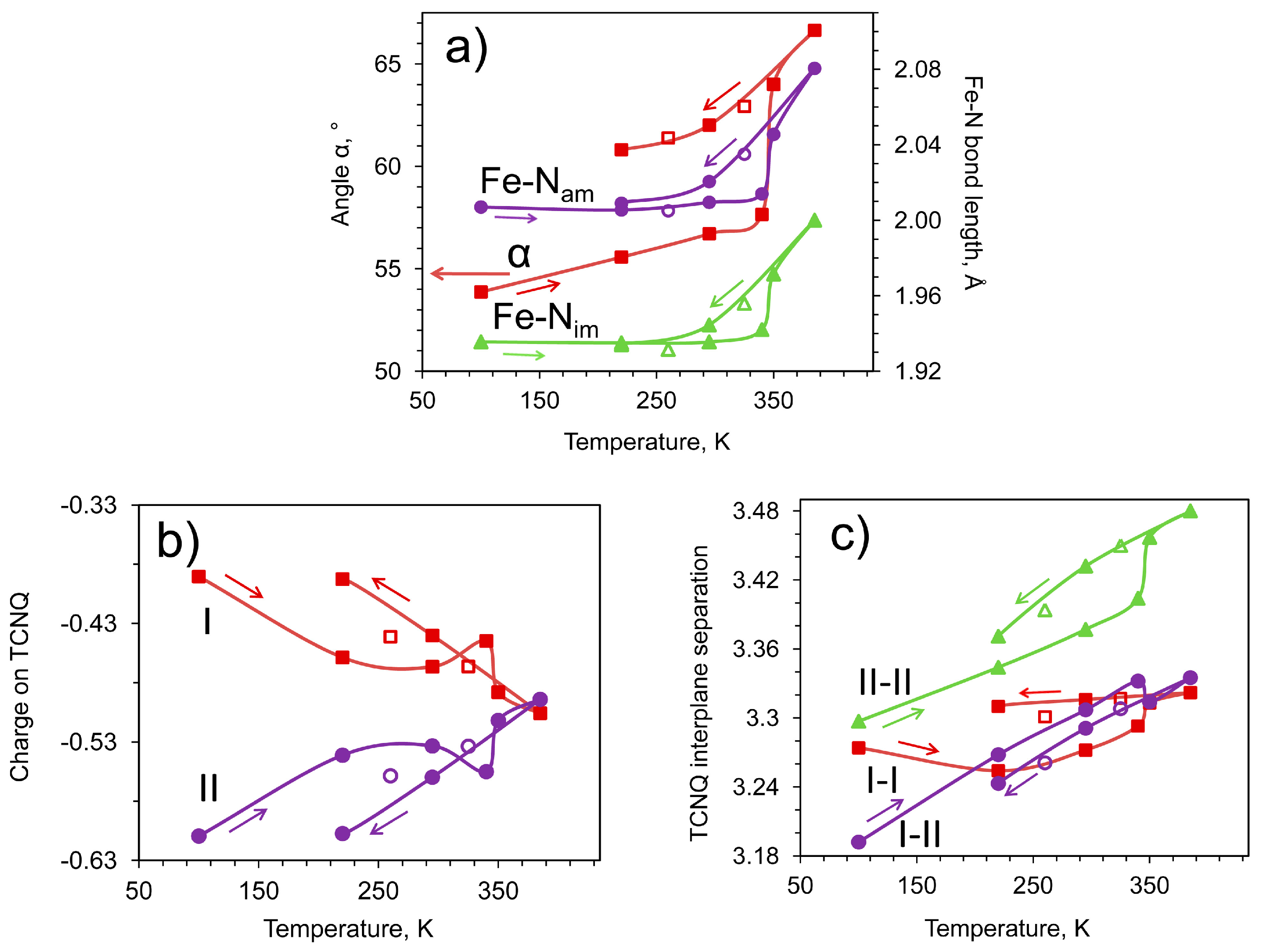
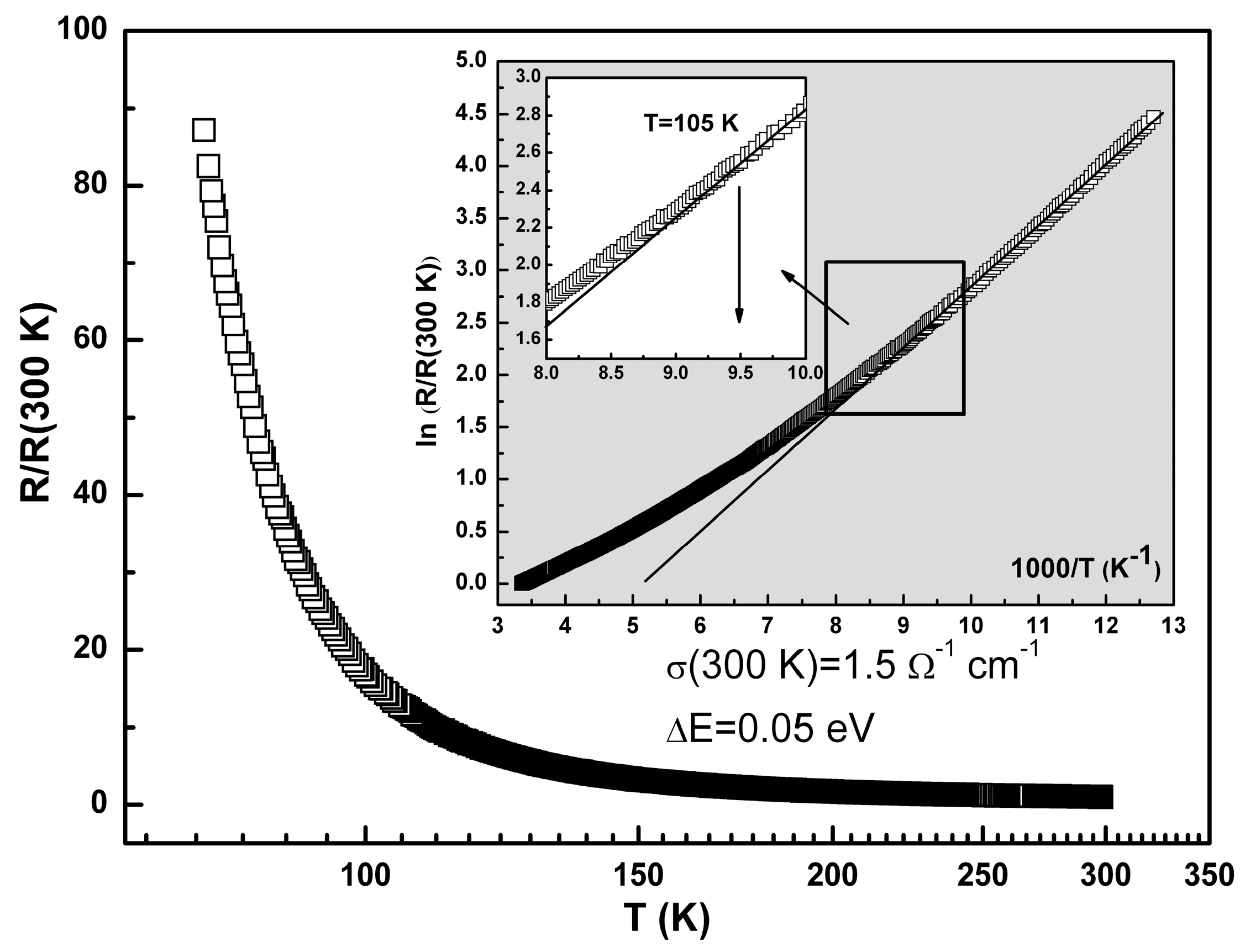
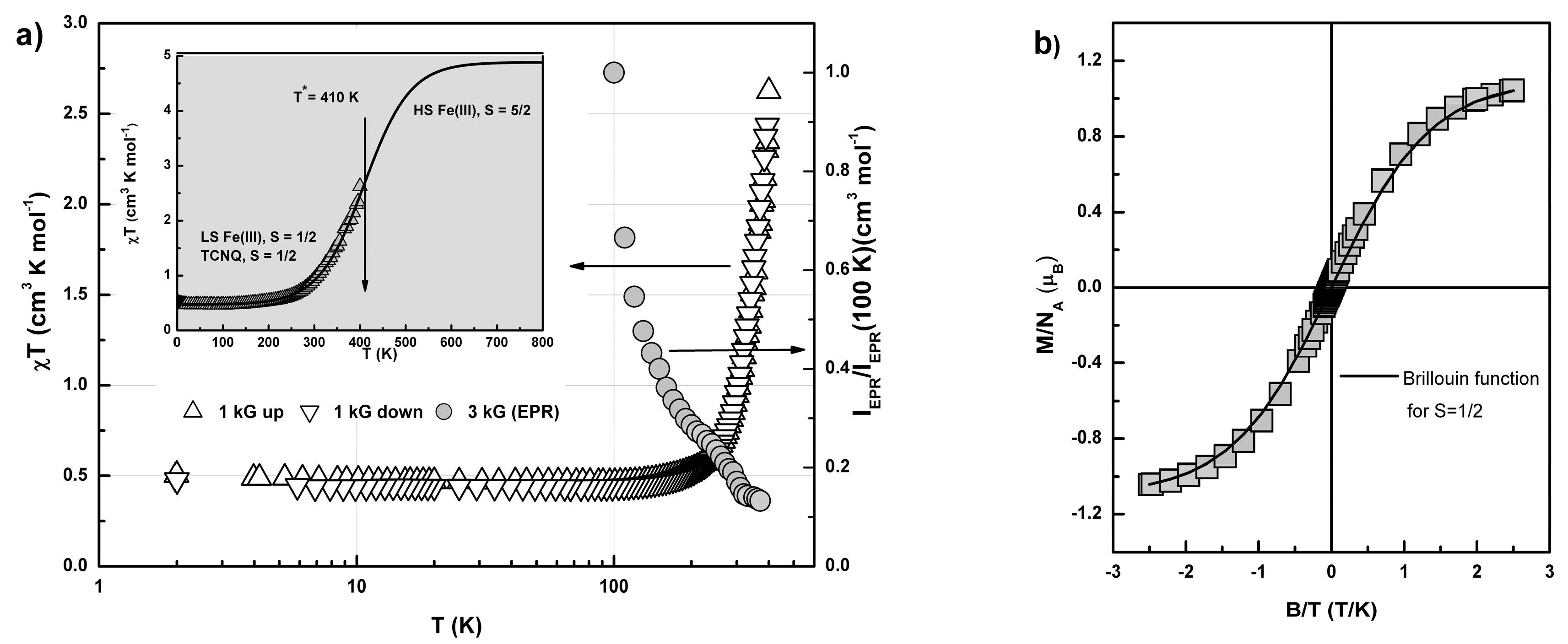
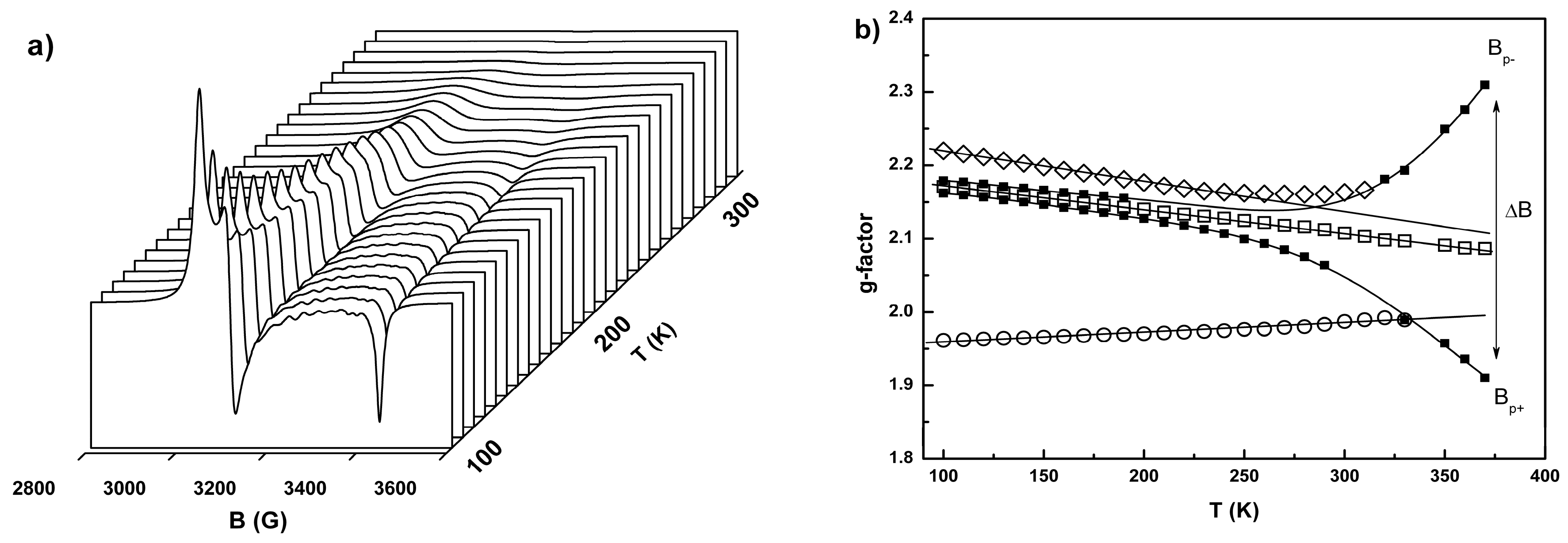
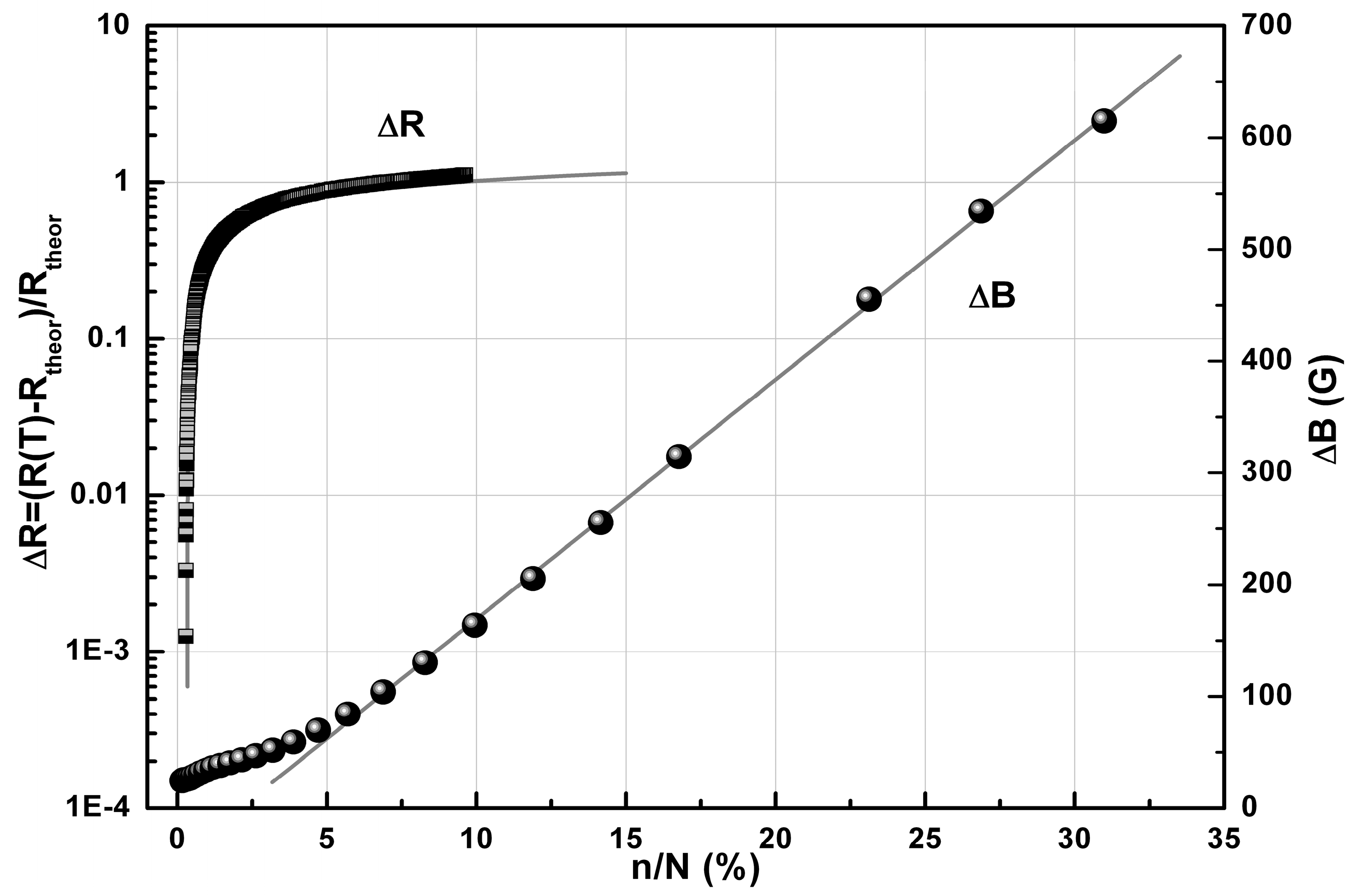
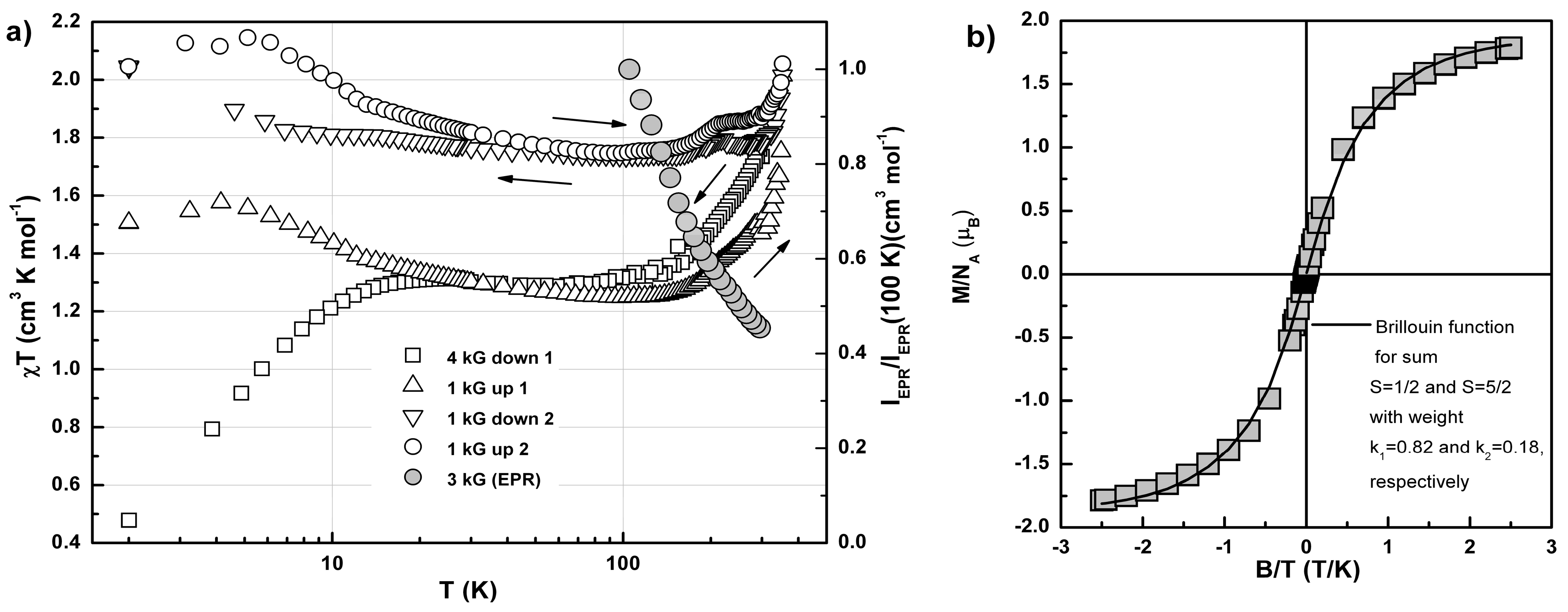
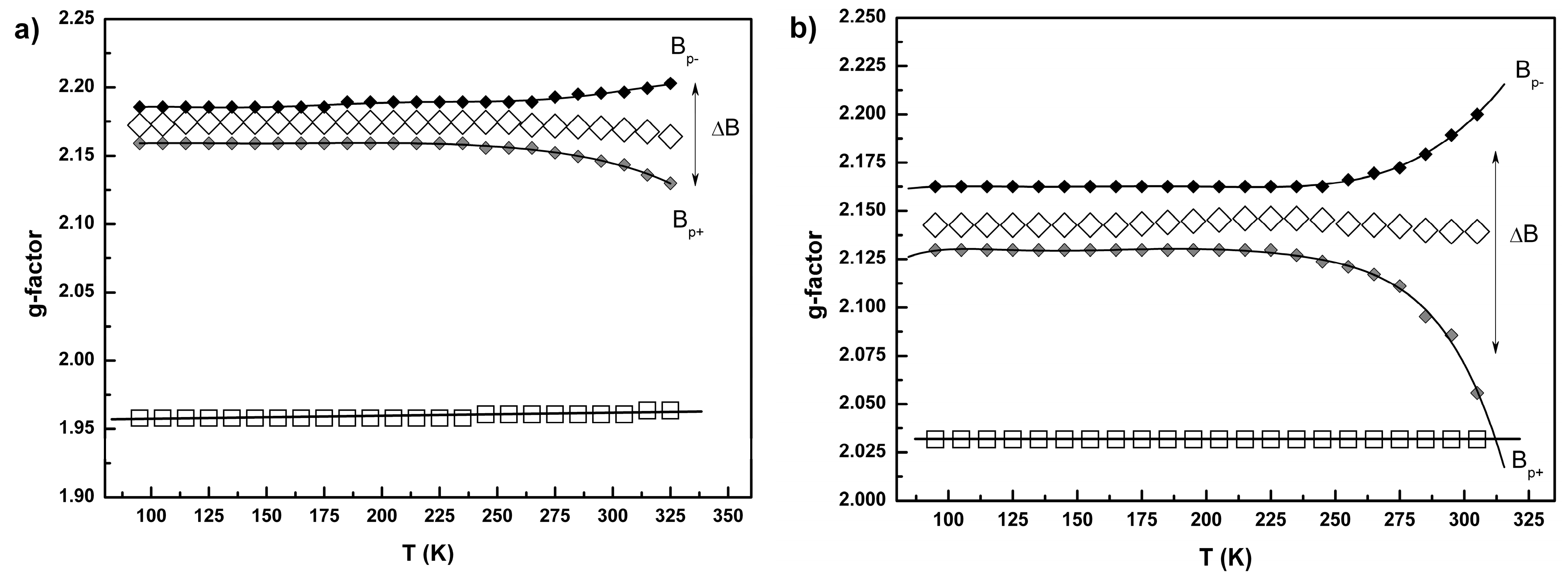
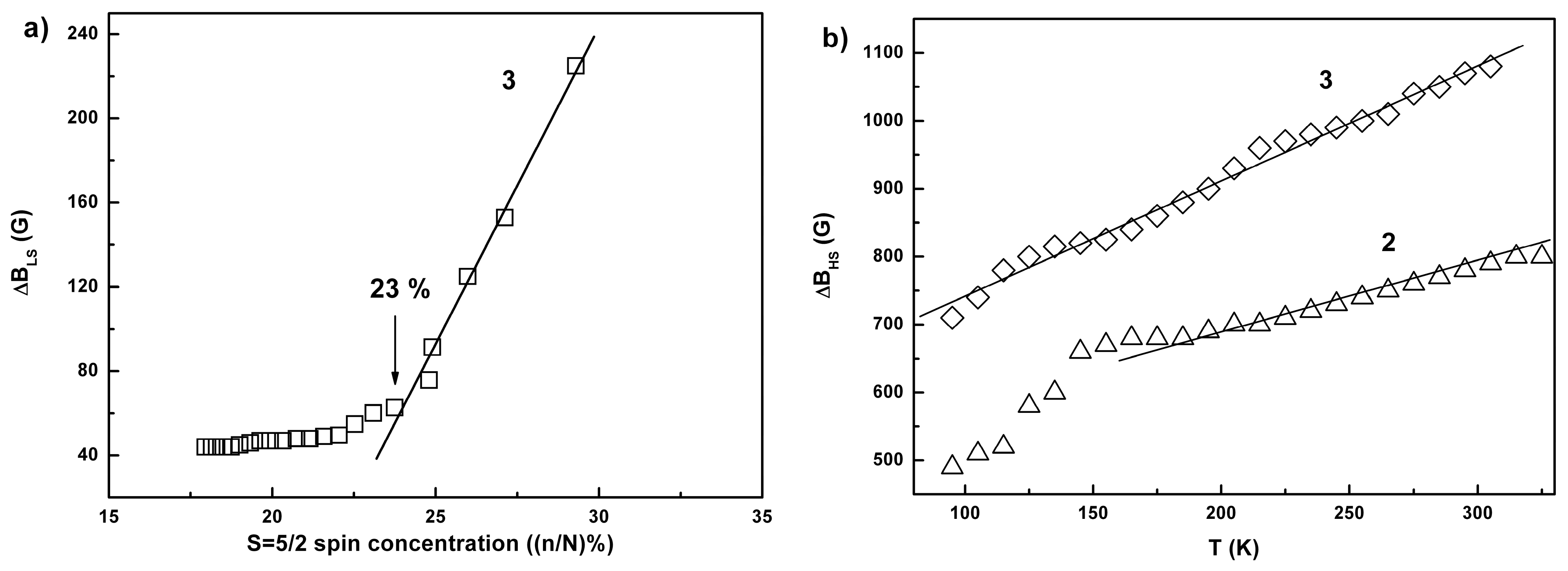
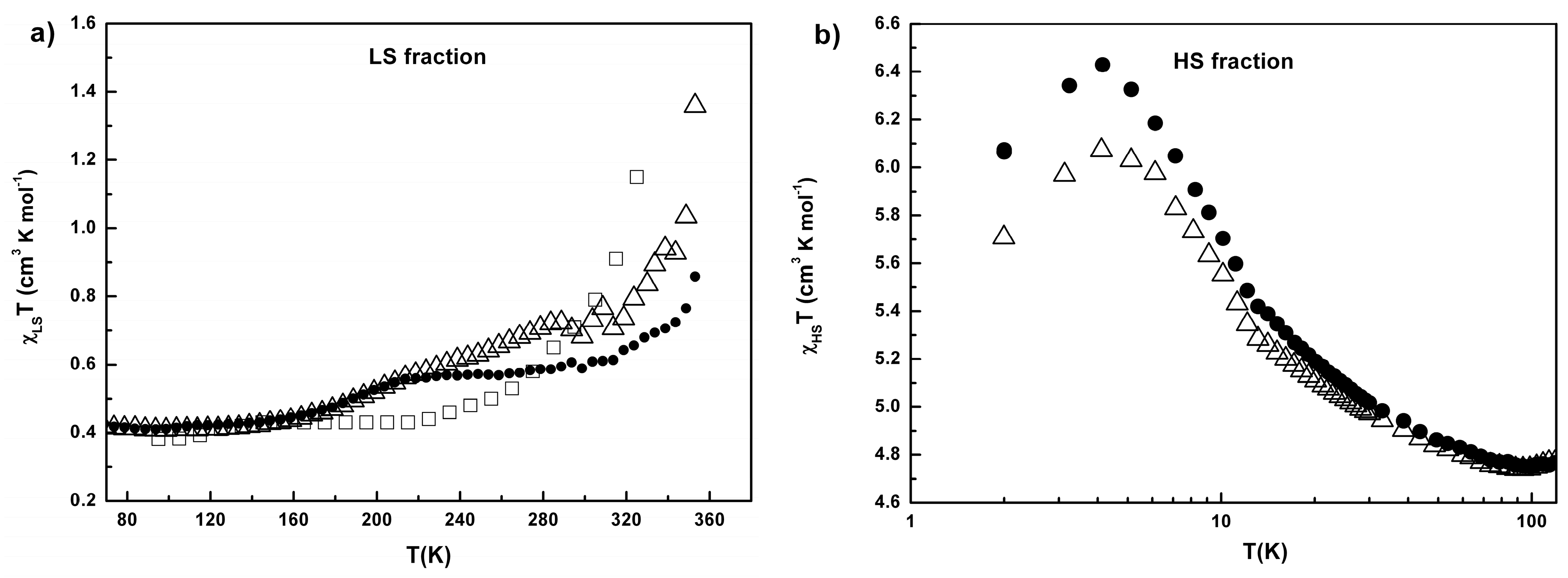
2.3. Conductivity and Magnetic Properties
3. Materials and Methods
3.1. Synthesis
3.2. Thermogravimetric Analysis
3.3. X-ray Crystallography
3.4. Transport and Magnetic Measurements
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sugawara, T. and Miyazaki, A. Magnetism and Conductivity. In Multifunctional Molecular Materials; Ouahab, L., Ed.; Pan Stanford Publishing, Pte. Ltd.: Singapore, 2013; pp. 1–60. [Google Scholar]
- Coronado, E.; Day, P. Magnetic molecular conductors. Chem. Rev. 2004, 104, 5419–5449. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, H.; Cui, H.; Kobayashi, A. Organic Metals and Superconductors Based on BETS (BETS = Bis(ethylenedithio)tetraselenafulvalene). Chem. Rev. 2004, 104, 5265–5288. [Google Scholar] [CrossRef] [PubMed]
- Enoki, T.; Miyazaki, A. Magnetic TTF-based charge-transfer complexes. Chem. Rev. 2004, 104, 5449–5477. [Google Scholar] [CrossRef] [PubMed]
- Kushch, N.D.; Yagubskii, E.B.; Kartsovnik, M.V.; Buravov, L.I.; Dubrovskii, A.D.; Biberacher, W. Pi-donor BETS based bifunctional superconductor with polymeric dicyanamidomanganate(II) anion layer: κ-(BETS)2Mn[N(CN)2]3. J. Am. Chem. Soc. 2008, 130, 7238–7240. [Google Scholar] [CrossRef] [PubMed]
- Vyaselev, O.M.; Kartsovnik, M.V.; Biberacher, W.; Zorina, L.V.; Kushch, N.D.; Yagubskii, E.B. Magnetic transformations in the organic conductor κ-(BETS)2Mn[N(CN)2]3 at the metal-insulator transition. Phys. Rev. B 2011, 83, 094425. [Google Scholar] [CrossRef]
- Kurmoo, M.; Graham, A.W.; Day, P.; Coles, S.J.; Hursthouse, M.B.; Caulfield, J.L.; Singleton, J.; Pratt, F.L.; Hayes, W.; Ducasse, L.; et al. Superconducting and semiconducting magnetic charge-transfer salts: (BEDT-TTF)4AFe(C2O4)3C6H5CN (A = H2O, K, NH4). J. Am. Chem. Soc. 1995, 117, 12209–12217. [Google Scholar] [CrossRef]
- Rashid, S.; Turner, S.S.; Day, P.; Howard, J.A.K.; Guionneau, P.; McInnes, E.J.L.; Mabbs, F.E.; Clark, R.J.H.; Firth, S.; Biggs, T.J. New superconducting charge-transfer salts (BEDT-TTF)4[A·M(C2O4)3]·C6H5NO2 (A = H3O or NH4, M = Cr or Fe, BEDT-TTF = bis(ethylenedithio)tetrathiafulvalene). J. Mater. Chem. 2001, 11, 2095–2101. [Google Scholar] [CrossRef]
- Laukhin, V.N.; Audouard, A.; Fortin, J.-Y.; Vignolles, D.; Prokhorova, T.G.; Yagubskii, E.B.; Canadell, E. Quantum oscillations in coupled orbits networks of (BEDT-TTF) salts with tris(oxalato)metallate anions. Low Temp. Phys. (Fiz. Nizk. Temp.) 2017, 43, 33–40. [Google Scholar] [CrossRef] [Green Version]
- Prokhorova, T.G.; Yagubskii, E.B. Organic conductors and superconductors based on bis(ethylenedithio)tetrathiafulvalene radical cation salts with supramolecular tris(oxalato)metallate anions. Russ. Chem. Rev. 2017, 86, 164–180. [Google Scholar] [CrossRef]
- Otsuka, T.; Kobayashi, A.; Miyamoto, Y.; Kiuchi, J.; Nakamura, S.; Wada, N.; Fujiwara, E.; Fujiwara, H.; Kobayashi, H. Organic antiferromagnetic metals exhibiting superconducting transitions κ-(BETS)2FeX4 (X = Cl, Br): Drastic effect of halogen substitution on the successive phase transitions. J. Solid State Chem. 2001, 159, 407–412. [Google Scholar] [CrossRef]
- Ojima, E.; Fujiwara, H.; Kato, K.; Kobayashi, H.; Tanaka, H.; Kobayashi, A.; Tokumoto, M.; Cassoux, P. Antiferromagnetic organic metal exhibiting superconducting transition, κ-(BETS)2FeBr4 [BETS = bis(ethylenedithio)tetraselenafulvalene]. J. Am. Chem. Soc. 1999, 121, 5581–5582. [Google Scholar] [CrossRef]
- Coronado, E.; Galan-Mascaros, J.R.; Gomez-Garcia, C.J.; Laukhin, V.N. Coexistence of ferromagnetism and metallic conductivity in a molecule-based layered compound. Nature 2000, 408, 447–449. [Google Scholar] [CrossRef] [PubMed]
- Uji, S.; Shinagawa, H.; Terashima, T.; Yakabe, T.; Terai, Y.; Tokumoto, M.; Kobayashi, A.; Tanaka, H.; Kobayashi, H. Magnetic-field-induced superconductivity in a two-dimensional organic conductor. Nature 2001, 410, 908–910. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, H.; Kobayashi, H.; Fujiwara, E.; Kobayashi, A. An indication of magnetic-field-induced superconductivity in a bifunctional layered organic conductor, κ-(BETS)2FeBr4. J. Am. Chem. Soc. 2002, 124, 6816–6817. [Google Scholar] [CrossRef] [PubMed]
- Valade, L.; Malfant, I.; Faulmann, C. Toward bifunctional materials with conducting, photochromic, and spin crossover properties. In Multifunctional Molecular Materials; Ouahab, L., Ed.; Pan Stanford Publishing, Pte. Ltd.: Singapore, 2013; pp. 149–184. [Google Scholar]
- Sato, O.; Li, Z.-Y.; Yao, Z.-S.; Kang, S.; Kanegawa, S. Multifunctional materials combining spin-crossover with conductivity and magnetic ordering. In Spin-Crossover Materials: Properties and Applications; Halcrow, M.A., Ed.; John Wiley & Sons: Oxford, UK, 2013; pp. 304–319. [Google Scholar]
- Kato, R. Conducting Metal Dithiolene Complexes: Structural and Electronic Properties. Chem. Rev. 2004, 104, 5319–5346. [Google Scholar] [CrossRef] [PubMed]
- Melby, L.R.; Harder, R.J.; Hertler, W.R.; Mahler, W.; Benson, R.E.; Mochel, W.E. Substituted Quinodimethans. II. Anion-radical Derivatives and Complexes of 7,7,8,8-Tetracyano-quinodimethan. J. Am. Chem. Soc. 1962, 84, 3374–3387. [Google Scholar] [CrossRef]
- Schegolev, I.F. Electric and magnetic properties of linear conducting chains. Phys. Status Solidi (a) 1972, 12, 9–45. [Google Scholar] [CrossRef]
- Shibaeva, L.; Atovmyan, O. The structure of conducting 7,7,8,8-tetracyanoquinodimethane complexes. J. Struct. Chem. 1972, 13, 514–531. [Google Scholar] [CrossRef]
- Yagubskii, E.B. From quasi-one-dimensional conductors based on TCNQ salts to the first quasi-two-dimensional superconductors at ambient pressure based on BEDT-TTF triiodides. In Organic Conductor, Superconductors and Magnets: From Synthesis to Molecular Electronics; Ouahab, L., Yagubskii, E.B., Eds.; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2003; pp. 45–65. [Google Scholar]
- Herbstein, F.H.; Kapon, M. Classification of closed shell TCNQ salts into structural families and comparison of diffraction and spectroscopic methods of assigning charge states to TCNQ moieties. Crystallogr. Rev. 2008, 14, 3–74. [Google Scholar] [CrossRef]
- Halcrow, M.A. (Ed.) Spin-Crossover Materials: Properties and Applications; John Wiley & Sons: Oxford, UK, 2013.
- Halcrow, M.A. Structure: Function relationships in molecular spin-crossover complexes. Chem. Soc. Rev. 2011, 40, 4119–4142. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Herchel, R.; Šalitroŝ, I.; Trávniček, Z.; MoncoǏ, J.; Fuess, H.; Ruben, M.; Linert, W. Anion driven modulation of magnetic intermolecular interactions and spin crossover properties in an isomorphous series of mononuclear iron(III) complexes with a hexadentate Schiff base ligand. CrystEngComm 2012, 14, 7015–7024. [Google Scholar] [CrossRef]
- Murata, K.; Kagoshima, S.; Yasuzuka, S.; Yoshino, H.; Kondo, R. High-Pressure Research in Organic Conductors. J. Phys. Soc. Jpn. 2006, 75, 051015. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Murata, K. Recent progress in high-pressure studies on organic conductors. Sci. Technol. Adv. Mater. 2009, 10, 024307. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Cui, H.-B.; Okano, Y.; Kobayashi, H.; Einaga, Y.; Sato, O. Electrical Conductivity Modulation Coupled to a High-Spin–Low-Spin Conversion in the Molecular System [FeIII(qsal)2][Ni(dmit)2]3·CH3CN·H2O. Inorg. Chem. 2006, 45, 5739–5741. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Cui, H.-B.; Okano, Y.; Kobayashi, H.; Mori, H.; Tajima, H.; Einaga, Y.; Sato, O. Evidence of the Chemical Uniaxial Strain Effect on Electrical Conductivity in the Spin-Crossover Conducting Molecular System: [FeIII(qnal)2][Pd(dmit)2]5·Acetone. J. Am. Chem. Soc. 2008, 130, 6688–6689. [Google Scholar] [CrossRef] [PubMed]
- Nihei, M.; Takahashi, N.; Nishikawa, H.; Oshio, H. Spin-crossover behavior and electrical conduction property in iron(II) complexes with tetrathiafulvalene moieties. Dalton Trans. 2011, 40, 2154–2156. [Google Scholar] [CrossRef] [PubMed]
- Plan, H.; Benjamin, S.M.; Steven, E.; Brooks, J.S.; Shatruk, M. Photomagnetic Response in Highly Conductive Iron(II) Spin-Crossover Complexes with TCNQ Radicals. Angew. Chem. Int. Ed. 2015, 54, 823–827. [Google Scholar]
- Zhang, X.; Wang, Z.-X.; Xie, H.; Li, M.-X.; Woods, T.J.; Dunbar, K.R. A cobalt(II) spin-crossover compound with partially charged TCNQ radicals and an anomalous conducting behavior. Chem. Sci. 2016, 7, 1569–1574. [Google Scholar] [CrossRef]
- Dorbes, S.; Valade, L.; Real, J.A.; Faulmann, C. [Fe(sal2-trien)][Ni(dmit)2]: Towards switchable spin crossover molecular conductors. Chem. Commun. 2005, 69–71. [Google Scholar] [CrossRef] [PubMed]
- Faulmann, C.; Dorbes, S.; Real, J.A.; Valade, L. Electrical conductivity and spin crossover: Towards the first achievement with a metal bis dithiolene complex. J. Low Temp. Phys. 2006, 142, 261–266. [Google Scholar] [CrossRef]
- Faulmann, C.; Dorbes, S.; Garreau de Bonneval, B.; Molnar, G.; Bousseksou, A.; Gomes-Garcia, C.J.; Coronado, E.; Valade, L. Towards molecular conductors with a spin-crossover phenomenon: Crystal structures, magnetic properties and Mossbauer spectra of [Fe(salten)Mepepy][M(dmit)2] complexes. Eur. J. Inorg. Chem. 2005, 2005, 3261–3270. [Google Scholar] [CrossRef]
- Faulmann, C.; Jacob, K.; Dorbes, S.; Lampert, S.; Malfant, I.; Doublet, M.-L.; Valade, L.; Real, J.A. Electrical conductivity and spin crossover: A new achievement with a metal bis dithiolene complex. Inorg. Chem. 2007, 46, 8548–8559. [Google Scholar] [CrossRef] [PubMed]
- Fukuroi, K.; Takahashi, K.; Mochida, T.; Sakurai, T.; Ohta, H.; Yamamoto, T.; Einada, Y.; Mori, H. Synergistic Spin Transition between Spin Crossover and Spin-Peierls-like Singlet Formation in the Halogen-Bonded Molecular Hybrid System: [Fe(Iqsal)2][Ni(dmit)2]·CH3CN·H2O. Angew. Chem. Int. Ed. 2014, 53, 1983–1986. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Fujita, N.; Matsubayashi, G.E.; Mori, W. Modified chesnut model for spin-crossover semiconductors [Fe(acpa)2](TCNQ)n. Mol. Cryst. Liq. Cryst. 2002, 379, 365–370. [Google Scholar] [CrossRef]
- Shvachko, Y.N.; Starichenko, D.V.; Korolyov, A.V.; Yagubskii, E.B.; Kotov, A.I.; Buravov, L.I.; Lyssenko, K.A.; Zverev, V.N.; Simonov, S.V.; Zorina, L.V.; et al. The Conducting Spin-Crossover Compound Combining Fe(II) Cation Complex with TCNQ in a Fractional Reduction State. Inorg. Chem. 2016, 55, 9121–9130. [Google Scholar] [CrossRef] [PubMed]
- Kistenmacher, T.J.; Emge, T.J.; Bloch, A.N.; Cowan, D.O. Structure of the red, semiconducting form of 4,4′,5,5′-tetramethyl-Δ2,2′-bi-1,3-diselenole-7,7,8,8-tetracyano-p-quinodimethane, TMTSF-TCNQ. Acta Cryst. B 1982, 38, 1193–1199. [Google Scholar] [CrossRef]
- Radváková, A.; Kazheva, O.N.; Chekhlov, A.N.; Dyachenko, O.A.; Kucmin, M.; Kajňaková, M.; Feher, A.; Starodub, V.A. Two-gap magnetic structure of the two-stack anion-radical salt (N-Me-3,5-Di-Me-Py)(TCNQ)2 (Py is pyridine). J. Phys. Chem. Solids 2010, 71, 752–757. [Google Scholar] [CrossRef]
- Pukacki, W.; Graja, A. Electric and magnetic properties of organometallic TCNQ salts. Synth. Met. 1988, 24, 137–143. [Google Scholar] [CrossRef]
- Petersen, R.L.; Symons, M.C.R.; Taiwo, F.A. Application of radiation and ESR spectroscopy to the study of ferryl haemoglobin. J. Chem. Soc. Faraday Trans. 1 1989, 85, 2435–2444. [Google Scholar] [CrossRef]
- Pilbrow, J.R. Transition Ion Electron Paramagnetic Resonance; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Hagen, W.R. Biomolecular EPR Spectroscopy; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Weil, J.A.; Wertz, J.E.; Bolton, J.R. Electron Paramagnetic Resonance: Elementary Theory and Practical Applications; John Wiley: New York, NY, USA, 1994. [Google Scholar]
- Paradis, N.; Le Gac, F.; Guionneau, P.; Largeteau, A.; Yufit, D.S.; Rosa, P.; Létard, J.-F.; Chastanet, G. Effects of Internal and External Pressure on the [Fe(PM-PEA)2(NCS)2] Spin-Crossover Compound (with PM-PEA=N-(21-pyridylmethylene)-4(phenylethynyl)aniline). Magnetochemistry 2016, 2, 15–32. [Google Scholar] [CrossRef]
- Barnes, S.E. Theory of electron spin resonance of magnetic ions in metals. Adv. Phys. 1981, 30, 801–938. [Google Scholar] [CrossRef]
- Kürti, J.; Menczel, G. g-Factor anisotropy and charge transfer in three complex TCNQ salts. Phys. Status Solidi B 1980, 102, 639–645. [Google Scholar] [CrossRef]
- Brooker, S. Spin crossover with thermal hysteresis: Practicalities and lessons learnt. Chem. Soc. Rev. 2014, 44, 2880–2892. [Google Scholar] [CrossRef] [PubMed]
- Benelli, C.; Gatteschi, D. Introduction to Molecular Magnetism: From Transition Metals to Lanthanides; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Létard, J.-F.; Guionneau, P.; Rabardel, L.; Howard, J.A.K.; Goeta, A.E.; Chasseau, D.; Kahn, O. Structural, Magnetic, and Photomagnetic Studies of a Mononuclear Iron(II) Derivative Exhibiting an Exceptionally Abrupt Spin Transition. Light-Induced Thermal Hysteresis Phenomenon. Inorg. Chem. 1998, 37, 4432–4441. [Google Scholar] [CrossRef] [PubMed]
- Day, P.; Underhill, A.E. Metal-organic and Organic Molecular Magnets. Phil. Trans. R. Soc. Lond. A 1999, 357, 2849–3184. [Google Scholar]
- Starodub, V.A.; Starodub, T.N. Radical anion salts and charge transfer complexes based on tetracyanoquinodimethane and other strong π-electron acceptors. Russ. Chem. Rev. 2014, 83, 391–438. [Google Scholar] [CrossRef]
- Zhao, H.; Heintz, R.A.; Ouyang, X.; Grandinetti, G.; Cowen, J.; Dunbar, K.R. Insight into the Behavior of M(TCNQ)n (n = 1, 2) Crystalline Solids and Films: X-ray, Magnetic and Conducting Properties. NATO ASI: Supramolecular Engineering of Synthetic Metallic Materials: Conductors and Magnets; Veciana, J., Ed.; Kluwer: Dordrecht, The Netherlands, 1999; Volume 518, pp. 353–376. [Google Scholar]
- Clerac, R.; O’Kane, S.; Cowen, J.; Ouyang, X.; Heintz, R.A.; Zhao, H.; Bazile, M.J., Jr.; Dunbar, K.R. Glassy Magnets Composed of Metals Coordinated to 7,7,8,8-tetracyanoquinodimethane: M(TCNQ)2 (M = Mn, Fe, Co, Ni). Chem. Mater. 2003, 15, 1840–1850. [Google Scholar] [CrossRef]
- Nweedle, M.F.; Wilson, L.J. Variable spin iron(III) chelates with hexadentate ligands derived from triethylenetetramine and various salicylaldehydes. Synthesis, characterization, and solution state studies of a new 2T ↔ 6A spin equilibrium system. J. Am. Chem. Soc. 1976, 98, 4824–4834. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Cryst. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, H.C. Method for Measuring Electrical Resistivity of Anisotropic Materials. J. Appl. Phys. 1971, 42, 2971. [Google Scholar] [CrossRef]
- Buravov, L.I. Calculation of resistance anisotropy with regard to model ends by conformal-transformation. Zhurnal Tekh. Fiz. 1989, 59, 138–142. [Google Scholar]

| Parameter | 1·MeOH 100 K | 1·MeOH 220 K | 1·MeOH 295 K | 1·MeOH 340 K | 1 350 K | 1 385 K | 1 325 K | 1 295 K | 1 260 K | 1 220 K |
|---|---|---|---|---|---|---|---|---|---|---|
| av. (Fe–Nim), Å | 1.936(8) | 1.935(7) | 1.936(8) | 1.942(9) | 1.97(2) | 2.00(2) | 1.96(2) | 1.945(15) | 1.931(13) | 1.934(9) |
| av. (Fe–Nam), Å | 2.007(2) | 2.006(4) | 2.010(4) | 2.014(2) | 2.05(2) | 2.08(2) | 2.035(17) | 2.021(10) | 2.005(8) | 2.009(6) |
| α, ° | 53.87(6) | 55.57(5) | 56.71(4) | 57.65(8) | 64.00(11) | 66.12(12) | 62.93(9) | 62.01(7) | 61.39(6) | 60.81(5) |
| δ (I) | −0.39 | −0.46 | −0.47 | −0.44 | −0.49 | −0.51 | −0.47 | −0.44 | −0.44 | −0.39 |
| δ (II) | −0.61 | −0.54 | −0.53 | −0.56 | −0.51 | −0.49 | −0.53 | −0.56 | −0.56 | −0.61 |
| I-I, Å | 3.274(4) | 3.254(5) | 3.272(8) | 3.293(9) | 3.313(5) | 3.322(6) | 3.317(7) | 3.316(7) | 3.301(7) | 3.310(9) |
| I-II, Å | 3.19(4) | 3.27(4) | 3.31(4) | 3.33(4) | 3.31(4) | 3.34(4) | 3.31(5) | 3.29(5) | 3.26(5) | 3.24(5) |
| II-II, Å | 3.297(6) | 3.344(6) | 3.377(6) | 3.404(5) | 3.457(8) | 3.480(7) | 3.450(8) | 3.432(10) | 3.394(9) | 3.371(9) |
| Parameter | 2 100 K | 2 220 K | 2 295 K | 2 325 K |
|---|---|---|---|---|
| av. (Fe–Nim), Å | 1.931(3) | 1.927(1) | 1.927(2) | 1.931(7) |
| av. (Fe–Nam), Å | 2.006(1) | 2.003(2) | 2.007(2) | 2.013(3) |
| α, ° | 77.23(4) | 77.85(5) | 78.02(5) | 77.96(6) |
| d, Å | 3.044(4) | 3.071(9) | 3.097(12) | 3.112(13) |
| Parameter | 1·MeOH 100 K | 1·MeOH 220 K | 1·MeOH 295 K | 1·MeOH 340 K | 1 350 K | 1 385 K | 1 325 K |
| Cell setting | triclinic | triclinic | triclinic | triclinic | triclinic | triclinic | triclinic |
| Formula | C45H36FeN12O3 | C45H36FeN12O3 | C45H36FeN12O3 | C45H36FeN12O3 | C44H32FeN12O2 | C44H32FeN12O2 | C44H32FeN12O2 |
| Molecular weight | 848.71 | 848.71 | 848.71 | 848.71 | 816.67 | 816.67 | 816.67 |
| Crystal size (mm) | 0.40 × 0.20 × 0.14 | 0.40 × 0.20 × 0.14 | 0.39 × 0.23 × 0.07 | 0.55 × 0.19 × 0.06 | 0.55 × 0.19 × 0.06 | 0.39 × 0.23 × 0.07 | 0.55 × 0.19 × 0.06 |
| λ(MoKα) (Å) | 0.71073 | 0.71073 | 0.71073 | 0.71073 | 0.71073 | 0.71073 | 0.71073 |
| Space group, Z | P, 2 | P, 2 | P, 2 | P, 2 | P, 2 | P, 2 | P, 2 |
| a (Å) | 8.9571(5) | 8.9675(3) | 8.9616(2) | 8.9838(3) | 8.8932(5) | 8.8948(3) | 8.9218(2) |
| b (Å) | 13.1036(7) | 13.2483(5) | 13.3489(2) | 13.4223(5) | 12.9755(8) | 13.0374(7) | 12.9832(4) |
| c (Å) | 17.4234(9) | 17.4794(7) | 17.5163(3) | 17.5869(5) | 17.6089(5) | 17.7142(7) | 17.6134(4) |
| α (°) | 89.338(1) | 89.1589(8) | 88.976(2) | 88.985(3) | 91.234(4) | 91.106(4) | 91.356(2) |
| β (°) | 85.101(1) | 85.2423(8) | 85.3650(10) | 85.425(3) | 86.922(4) | 87.062(3) | 86.696(2) |
| γ (°) | 78.027(1) | 78.3151(8) | 78.525(2) | 78.782(3) | 82.757(5) | 82.846(4) | 82.570(2) |
| Cell volume (Å3) | 1993.2(2) | 2026.58(13) | 2046.83(7) | 2073.54(12) | 2012.01(18) | 2034.87(15) | 2018.73(9) |
| ρ (g/cm3) | 1.414 | 1.391 | 1.377 | 1.359 | 1.348 | 1.333 | 1.344 |
| μ, cm−1 | 4.38 | 4.31 | 4.26 | 4.21 | 4.29 | 4.24 | 4.28 |
| Refls collected/unique | 24,684/10,591 | 21,590/10,764 | 22,180/10,116 | 20,254/10,910 | 16,091/9254 | 21,019/10,054 | 17,015/9203 |
| Rint | 0.0552 | 0.0371 | 0.0139 | 0.0515 | 0.0217 | 0.0353 | 0.0178 |
| θmax (°) | 29.0 | 29.0 | 28.3 | 31.1 | 28.3 | 28.3 | 28.3 |
| Refls with [I > 2σ(I)] | 7166 | 7057 | 8542 | 7150 | 5480 | 4017 | 6038 |
| Parameters refined | 562 | 562 | 560 | 560 | 538 | 538 | 538 |
| Final R1, wR2 [I > 2σ(I)] | 0.0496, 0.1022 | 0.0426, 0.0920 | 0.0348, 0.0884 | 0.0597, 0.1327 | 0.0613/0.1386 | 0.0699, 0.1311 | 0.0569, 0.1244 |
| Goodness-of-fit | 1.011 | 1.000 | 1.002 | 1.000 | 1.006 | 1.003 | 1.003 |
| Residual el. density (e·Å−3) | 0.502/−0.633 | 0.349/−0.482 | 0.279/−0.219 | 1.109/−0.331 | 0.489/−0.621 | 0.495/−0.349 | 0.559/−0.705 |
| CCDC reference | 1527039 | 1527040 | 1527042 | 1527041 | 1527043 | 1527044 | 1527045 |
| Parameter | 1 295 K | 1 260 K | 1 220 K | 2 100 K | 2 220 K | 2 295 K | 2 325 K |
| Cell setting | triclinic | triclinic | triclinic | triclinic | triclinic | triclinic | triclinic |
| Formula | C44H32FeN12O2 | C44H32FeN12O2 | C44H32FeN12O2 | C34H31FeN9O2 | C34H31FeN9O2 | C34H31FeN9O2 | C34H31FeN9O2 |
| Molecular weight | 816.67 | 816.67 | 816.67 | 653.53 | 653.53 | 653.53 | 653.53 |
| Crystal size (mm) | 0.55 × 0.19 × 0.06 | 0.55 × 0.19 × 0.06 | 0.55 × 0.19 × 0.06 | 0.13 × 0.10 × 0.08 | 0.52 × 0.28 × 0.05 | 0.52 × 0.28 × 0.05 | 0.52 × 0.28 × 0.05 |
| λ(MoKα) (Å) | 0.71073 | 0.71073 | 0.71073 | 0.71073 | 0.71073 | 0.71073 | 0.71073 |
| Space group, Z | P, 2 | P, 2 | P, 2 | P, 2 | P, 2 | P, 2 | P, 2 |
| a (Å) | 8.9230(2) | 8.8950(2) | 8.9120(2) | 7.6085(8) | 7.6695(4) | 7.7072(4) | 7.72945(18) |
| b (Å) | 12.9439(3) | 12.8594(3) | 12.8379(3) | 14.2710(16) | 14.3596(5) | 14.3879(6) | 14.4016(4) |
| c (Å) | 17.5498(3) | 17.4386(3) | 17.4233(4) | 16.0300(18) | 16.0693(5) | 16.1428(6) | 16.1913(6) |
| α (°) | 91.432(2) | 91.464(2) | 91.468(2) | 67.454(2) | 66.939(3) | 66.861(4) | 66.872(3) |
| β (°) | 86.497(2) | 86.312(2) | 86.152(2) | 85.078(2) | 84.870(3) | 84.786(4) | 84.831(3) |
| γ (°) | 82.430(2) | 82.310(2) | 82.220(2) | 76.296(2) | 76.089(4) | 75.980(4) | 75.969(2) |
| Cell volume (Å3) | 2004.44(7) | 1971.49(7) | 1969.41(8) | 1561.7(3) | 1580.51(11) | 1597.03(13) | 1608.02(9) |
| ρ (g/cm3) | 1.353 | 1.376 | 1.377 | 1.390 | 1.373 | 1.359 | 1.350 |
| μ, cm−1 | 4.31 | 4.38 | 4.38 | 5.30 | 5.24 | 5.19 | 5.15 |
| Refls collected/unique | 16,900/9137 | 15,460/8994 | 16,836/9234 | 19,290/8302 | 16,642/8648 | 17,204/8850 | 16,515/8763 |
| Rint | 0.0165 | 0.0177 | 0.0171 | 0.0627 | 0.0179 | 0.0229 | 0.0220 |
| θmax (°) | 28.3 | 28.3 | 29.5 | 29.0 | 28.8 | 29.0 | 28.8 |
| Refls with [I > 2σ(I)] | 6665 | 6990 | 7080 | 6003 | 7172 | 6739 | 6104 |
| Parameters refined | 538 | 538 | 538 | 423 | 426 | 426 | 426 |
| Final R1, wR2 [I > 2σ(I)] | 0.0479, 0.1080 | 0.0427, 0.0924 | 0.0387, 0.0877 | 0.0391, 0.0814 | 0.0348, 0.0776 | 0.0406, 0.0871 | 0.0459, 0.0953 |
| Goodness-of-fit | 1.003 | 1.004 | 1.001 | 1.007 | 1.006 | 1.005 | 1.001 |
| Residual el. density (e·Å−3) | 0.447/−0.652 | 0.387/−0.548 | 0.335/−0.349 | 0.487/−0.448 | 0.310/−0.437 | 0.312/−0.443 | 0.350/−0.202 |
| CCDC reference | 1527046 | 1527047 | 1527048 | 1527049 | 1527050 | 1527051 | 1527052 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shvachko, Y.N.; Starichenko, D.V.; Korolyov, A.V.; Kotov, A.I.; Buravov, L.I.; Zverev, V.N.; Simonov, S.V.; Zorina, L.V.; Yagubskii, E.B. The Highly Conducting Spin-Crossover Compound Combining Fe(III) Cation Complex with TCNQ in a Fractional Reduction State. Synthesis, Structure, Electric and Magnetic Properties. Magnetochemistry 2017, 3, 9. https://doi.org/10.3390/magnetochemistry3010009
Shvachko YN, Starichenko DV, Korolyov AV, Kotov AI, Buravov LI, Zverev VN, Simonov SV, Zorina LV, Yagubskii EB. The Highly Conducting Spin-Crossover Compound Combining Fe(III) Cation Complex with TCNQ in a Fractional Reduction State. Synthesis, Structure, Electric and Magnetic Properties. Magnetochemistry. 2017; 3(1):9. https://doi.org/10.3390/magnetochemistry3010009
Chicago/Turabian StyleShvachko, Yuri N., Denis V. Starichenko, Aleksander V. Korolyov, Alexander I. Kotov, Lev I. Buravov, Vladimir N. Zverev, Sergey V. Simonov, Leokadiya V. Zorina, and Eduard B. Yagubskii. 2017. "The Highly Conducting Spin-Crossover Compound Combining Fe(III) Cation Complex with TCNQ in a Fractional Reduction State. Synthesis, Structure, Electric and Magnetic Properties" Magnetochemistry 3, no. 1: 9. https://doi.org/10.3390/magnetochemistry3010009
APA StyleShvachko, Y. N., Starichenko, D. V., Korolyov, A. V., Kotov, A. I., Buravov, L. I., Zverev, V. N., Simonov, S. V., Zorina, L. V., & Yagubskii, E. B. (2017). The Highly Conducting Spin-Crossover Compound Combining Fe(III) Cation Complex with TCNQ in a Fractional Reduction State. Synthesis, Structure, Electric and Magnetic Properties. Magnetochemistry, 3(1), 9. https://doi.org/10.3390/magnetochemistry3010009







