Magnetocaloric Properties of (MnFeRu)2(PSi) as Magnetic Refrigerants near Room Temperature
Abstract
:1. Introduction
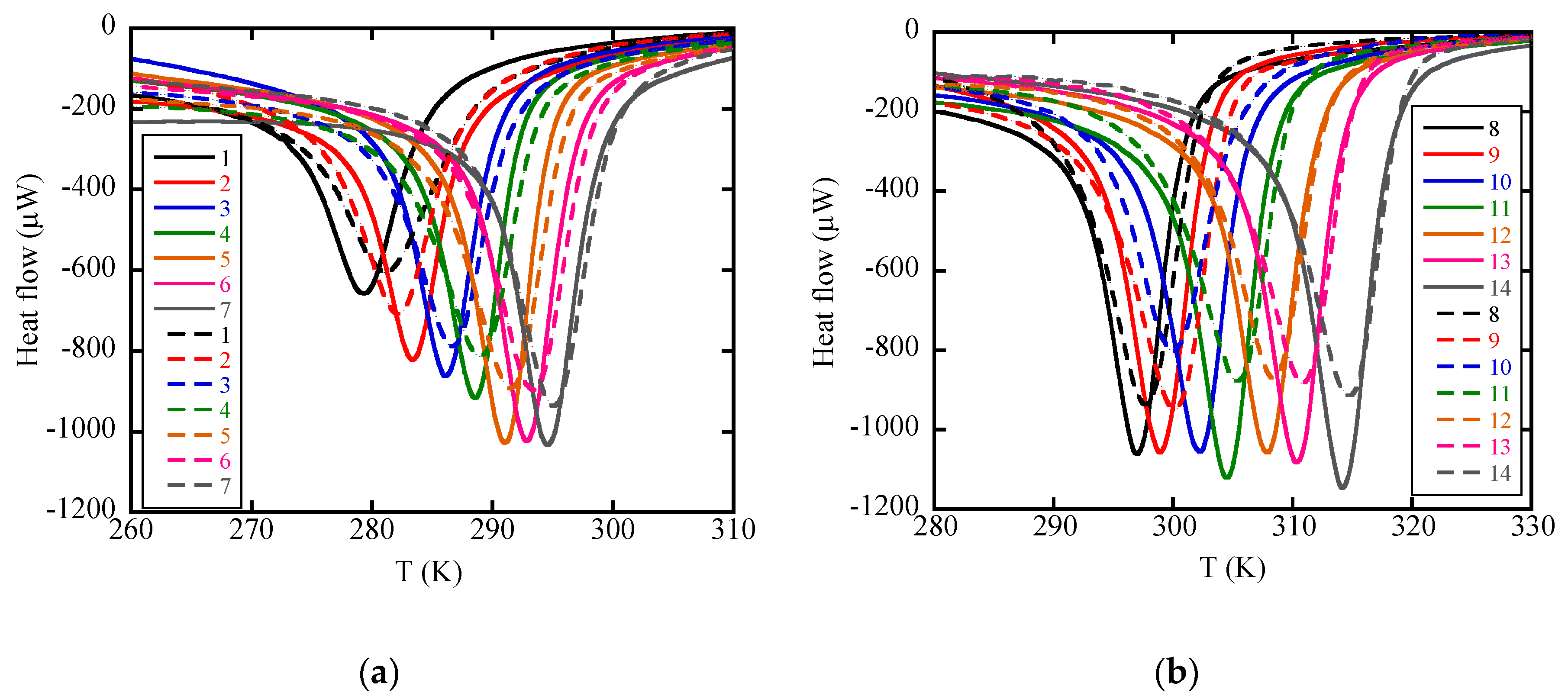
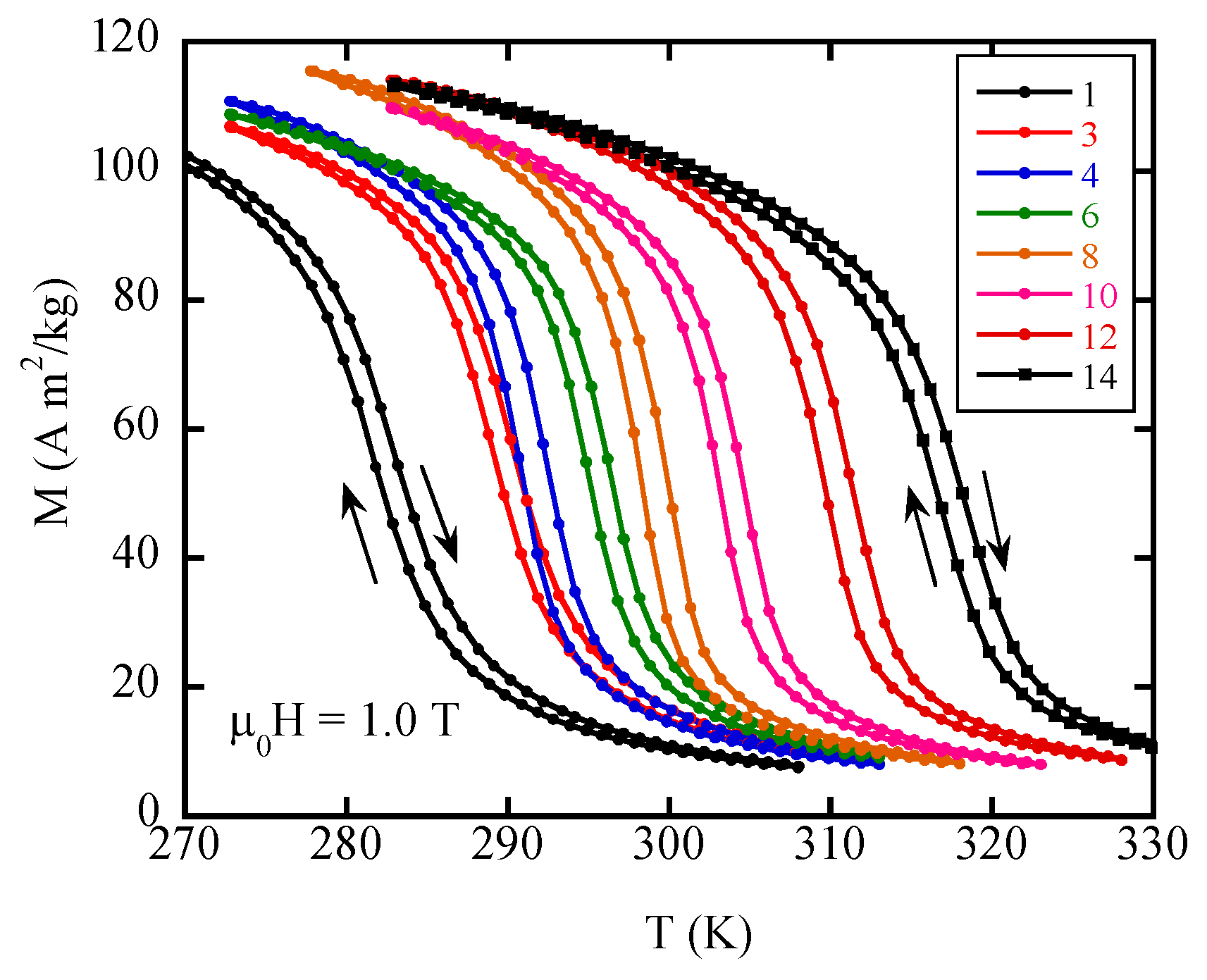
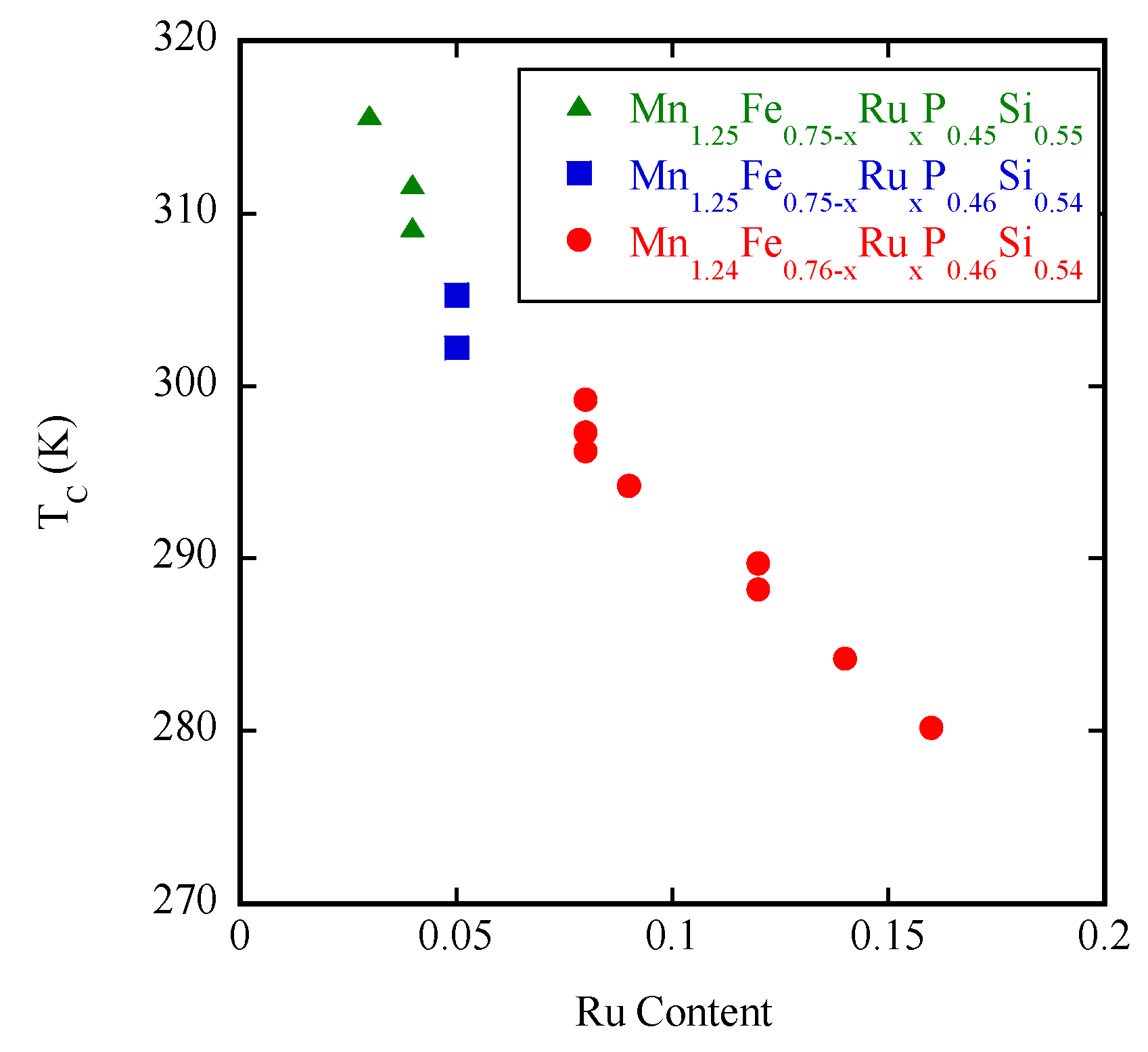
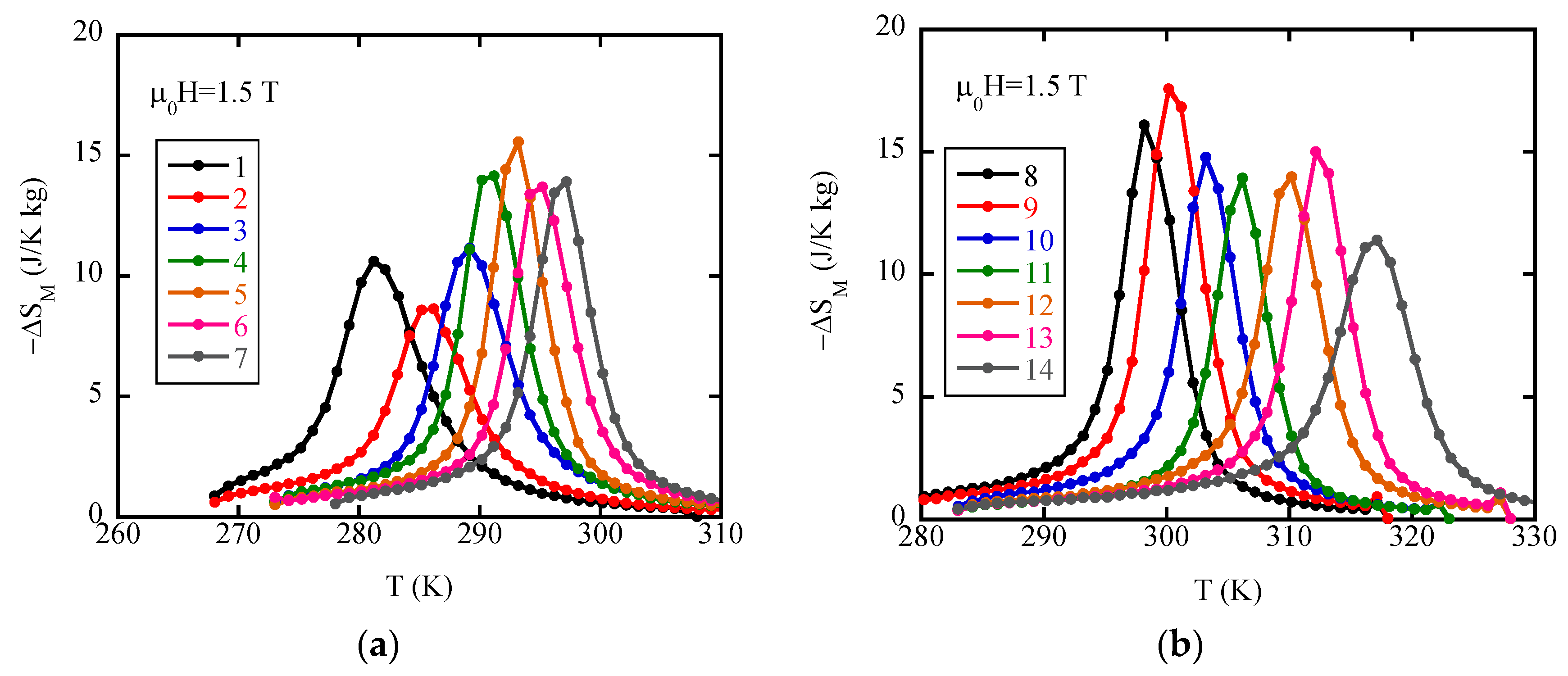
2. Results and Discussion
3. Materials and Methods
4. Conclusions
- (i)
- Repetitive annealing improves the homogeneity of the sample and it makes the magnetic transition sharper.
- (ii)
- We succeeded in the fine control of TC between 275 and 315 K by changing the Ru content and the sintering temperature. Roughly speaking, TC is determined by the Ru content and it is decreased by increasing the Ru content nearly linearly at a rate of 2.5 K/at. % Ru in Mn~1.24Fe~0.76−xRuxP~0.46Si~0.54.
- (iii)
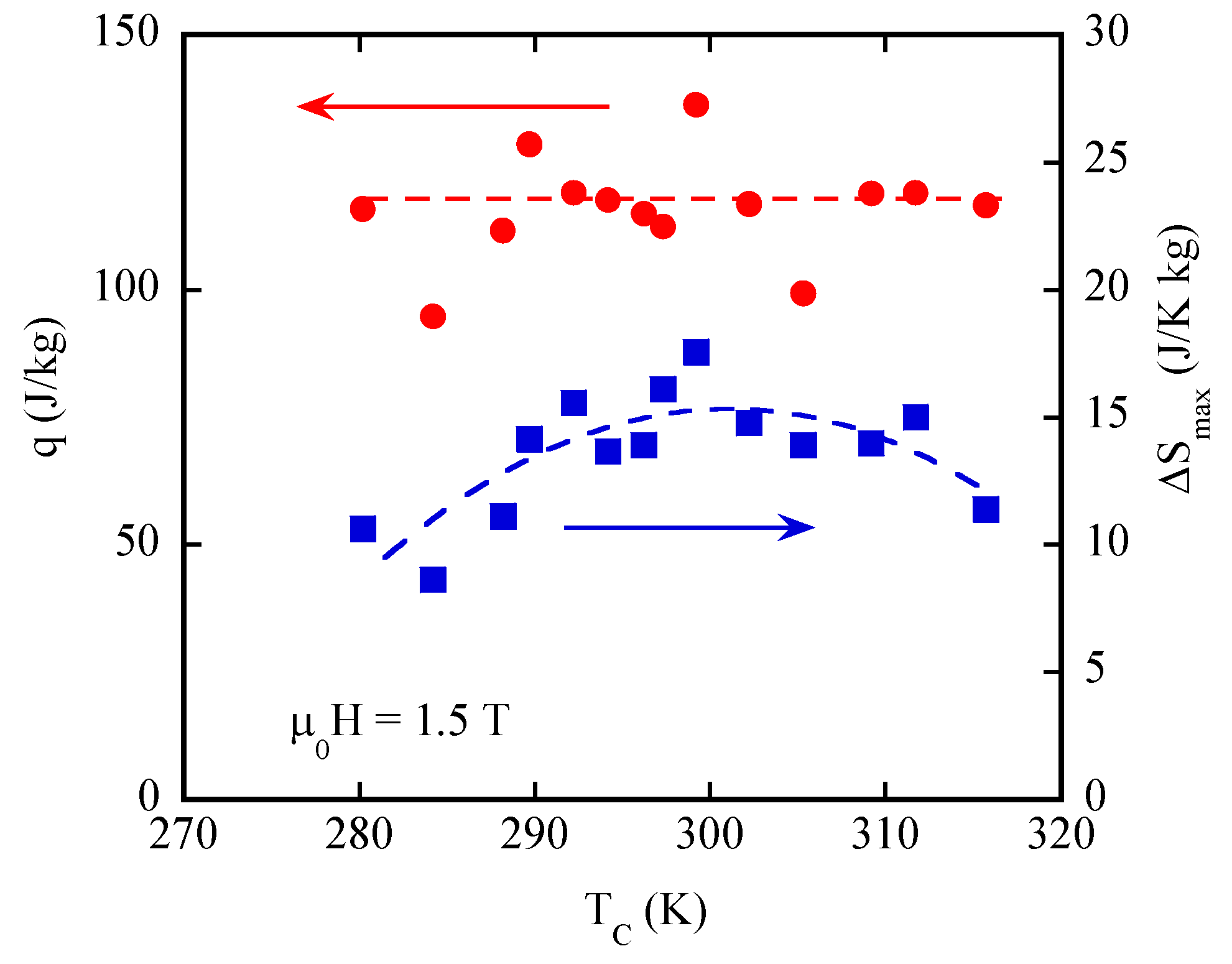
- All the compounds undergo the FOMT and exhibit large MCEs with ∆Thys less than 2 K. It was found that the refrigerant capacity is almost constant in the composition ranges studied.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brown, G.V. Magnetic heat pumping near room temperature. J. Appl. Phys. 1976, 47, 3673–3680. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
- Wada, H.; Tanabe, Y. Giant magnetocaloric effect of MnAs1−xSbx. Appl. Phys. Lett. 2001, 79, 3302–3304. [Google Scholar] [CrossRef]
- Tegus, O.; Brück, E.; Buschow, K.H.J.; de Boer, F.R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef] [PubMed]
- Fujita, A.; Fujieda, S.; Hasegawa, Y.; Fukamichi, K. Itinerant-electron metamagnetic transition and large magnetocaloric effects in La(FexSi1−x)13 compounds and their hydrides. Phys. Rev. B 2003, 67, 104416. [Google Scholar] [CrossRef]
- Krenke, T.; Duman, E.; Acet, M.; Wassermann, E.F.; Moya, X.; Manosa, L.; Planes, A. Inverse magnetocaloric effect in ferromagnetic Ni-Mn-Sn alloys. Nat. Mater. 2005, 4, 450–454. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Yue, M.; Zhang, J.; McQueen, T.M.; Lynn, J.W.; Wang, X.; Chen, Y.; Li, J.; Cava, R.J.; Liu, X.; et al. Origin and tuning of the magnetocaloric effect in the magnetic refrigerant Mn1.1Fe0.9(P0.8Ge0.2). Phys. Rev. B 2009, 79, 014435. [Google Scholar] [CrossRef]
- Cam Thanh, D.T.; Brück, E.; Trung, N.T.; Klaasse, J.C.P.; Buschow, K.H.J.; Ou, Z.Q.; Tegus, O.; Caron, L. Structure, magnetism, and magnetocaloric properties of MnFeP1−xSix compounds. J. Appl. Phys. 2008, 103, 07B318. [Google Scholar] [CrossRef]
- Yue, M.; Li, Z.Q.; Xu, H.; Huang, Q.Z.; Liu, X.B.; Liu, D.M.; Zhang, J.X. Effect of annealing on the structure and magnetic properties of Mn1.1Fe0.9P0.8Ge0.2 compound. J. Appl. Phys. 2010, 107, 09A939. [Google Scholar] [CrossRef]
- Dung, N.H.; Zhang, L.; Ou, Z.Q.; Brück, E. From first-order magneto-elastic to magneto-structural transition in (Mn,Fe)1.95P0.50Si0.50 compounds. Appl. Phys. Lett. 2011, 99, 092511. [Google Scholar] [CrossRef]
- Wada, H.; Nakamura, K.; Katagiri, K.; Ohnishi, T.; Yamashita, K.; Matsushita, A. Tuning the Curie temperature and thermal hysteresis of giant magnetocaloric (MnFe)2PX (X = Ge and Si) compounds by the Ru substitution. Jpn. J. Appl. Phys. 2014, 53, 063001. [Google Scholar] [CrossRef]
- Brück, E.; Trung, N.T.; Ou, Z.Q.; Buschow, K.H.J. Enhanced magnetocaloric effects and tunable thermal hysteresis in transition metal pnictides. Scr. Mater. 2012, 67, 590–593. [Google Scholar] [CrossRef]
- Wada, H.; Takahara, T.; Katagiri, K.; Ohnishi, T.; Soejima, K.; Yamashita, K. Recent progress of magnetocaloric effect and magnetic refrigerant materials of Mn compounds. J. Appl. Phys. 2015, 117, 172606. [Google Scholar] [CrossRef]
- Yu, H.Y.; Zhu, Z.R.; Lai, J.W.; Zheng, Z.G.; Zeng, D.C.; Zhang, J.L. Enhance magnetocaloric effects in Mn1.15Fe0.85P0.52Si0.45B0.03 alloy achieved by copper-mould casting and annealing treatments. J. Alloys Compd. 2015, 649, 1043–1047. [Google Scholar] [CrossRef]
- Höglin, V.; Cedervall, J.; Andersson, M.S.; Sarkar, T.; Hudl, M.; Nordblad, P.; Andersson, Y.; Sahlberg, M. Phase diagram, structures and magnetism of the FeMnP1−xSix-system. RSC Adv. 2015, 5, 8278–8285. [Google Scholar] [CrossRef]
- Ou, Z.Q. Magnetic Structure and Phase Formation of Magnetocaloric Mn-Fe-P-X Compounds. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 10 July 2013. [Google Scholar]
- Balli, M.; Fruchart, D.; Gignoux, D.; Zach, R. The “colossal” magnetocaloric effect in Mn1−xFexAs: What are we really measuring? Appl. Phys. Lett. 2009, 95, 072509. [Google Scholar] [CrossRef]
- Quintana-Nedelcos, A.; Sánchez Llamazares, J.L.; Sánchez-Valdés, C.F.; Álvarez Alonso, P.; Gorria, P.; Shamba, P.; Morley, N.A. On the correct estimation of the magnetic entropy change across the magneto-structural transition from the Maxwell relation: Study of MnCoGeBx alloy ribbons. J. Alloys Compd. 2017, 694, 1189–1195. [Google Scholar] [CrossRef]
- Caron, L.; Ba Doan, N.; Ranno, L. On entropy change measurements around first order phase transitions in caloric materials. J. Phys. Condens. Matter 2017, 29, 075401. [Google Scholar] [CrossRef] [PubMed]
- Wada, H.; Tanabe, Y.; Shiga, M.; Sugawara, H.; Sato, H. Magnetocaloric effects of Laves phase Er(Co1−xNix)2 compounds. J. Alloys. Compd. 2001, 316, 245–249. [Google Scholar] [CrossRef]
- Wada, H.; Matsuo, S.; Mitsuda, A. Pressure dependence of magnetic entropy change and magnetic transition in MnAs1−xSbx. Phys. Rev. B 2009, 79, 092407. [Google Scholar] [CrossRef]
| Sample No. | Nominal Composition | Sintering Temp. (°C) | TC (K) | ∆Thys (K) |
|---|---|---|---|---|
| 1 | Mn1.24Fe0.60Ru0.16P0.46Si0.54 | 1105 | 280.4 | 1.4 |
| 2 | Mn1.24Fe0.62Ru0.14P0.46Si0.54 | 1110 | 284.5 | 1.5 |
| 3 | Mn1.24Fe0.64Ru0.12P0.46Si0.54 | 1105 | 288.1 | 1.4 |
| 4 | Mn1.24Fe0.64Ru0.12P0.46Si0.54 | 1100 | 289.7 | 1.8 |
| 5 | Mn1.23Fe0.65Ru0.12P0.46Si0.54 | 1100 | 292.3 | 1.7 |
| 6 | Mn1.24Fe0.67Ru0.09P0.46Si0.54 | 1100 | 294.3 | 1.5 |
| 7 | Mn1.24Fe0.68Ru0.08P0.46Si0.54 | 1100 | 296.1 | 1.8 |
| 8 | Mn1.24Fe0.68Ru0.08P0.46Si0.54 | 1095 | 297.4 | 1.7 |
| 9 | Mn1.24Fe0.68Ru0.08P0.46Si0.54 | 1090 | 299.7 | 1.5 |
| 10 | Mn1.25Fe0.70Ru0.05P0.46Si0.54 | 1100 | 302.3 | 1.8 |
| 11 | Mn1.25Fe0.70Ru0.05P0.46Si0.54 | 1090 | 305.3 | 1.7 |
| 12 | Mn1.25Fe0.71Ru0.04P0.45Si0.55 | 1085 | 309.0 | 1.8 |
| 13 | Mn1.25Fe0.71Ru0.04P0.45Si0.55 | 1090 | 311.8 | 1.8 |
| 14 | Mn1.25Fe0.72Ru0.03P0.45Si0.55 | 1085 | 315.9 | 1.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohnishi, T.; Soejima, K.; Yamashita, K.; Wada, H. Magnetocaloric Properties of (MnFeRu)2(PSi) as Magnetic Refrigerants near Room Temperature. Magnetochemistry 2017, 3, 6. https://doi.org/10.3390/magnetochemistry3010006
Ohnishi T, Soejima K, Yamashita K, Wada H. Magnetocaloric Properties of (MnFeRu)2(PSi) as Magnetic Refrigerants near Room Temperature. Magnetochemistry. 2017; 3(1):6. https://doi.org/10.3390/magnetochemistry3010006
Chicago/Turabian StyleOhnishi, Takayuki, Kei Soejima, Keiichiro Yamashita, and Hirofumi Wada. 2017. "Magnetocaloric Properties of (MnFeRu)2(PSi) as Magnetic Refrigerants near Room Temperature" Magnetochemistry 3, no. 1: 6. https://doi.org/10.3390/magnetochemistry3010006
APA StyleOhnishi, T., Soejima, K., Yamashita, K., & Wada, H. (2017). Magnetocaloric Properties of (MnFeRu)2(PSi) as Magnetic Refrigerants near Room Temperature. Magnetochemistry, 3(1), 6. https://doi.org/10.3390/magnetochemistry3010006





