Antiferromagnetic Insulating Ground State of Molecular π-d System Λ-(BETS)2FeCl4 (BETS = Bis(ethylenedithio)tetraselenafulvalene): A Theoretical and Experimental Review
Abstract
:1. Introduction
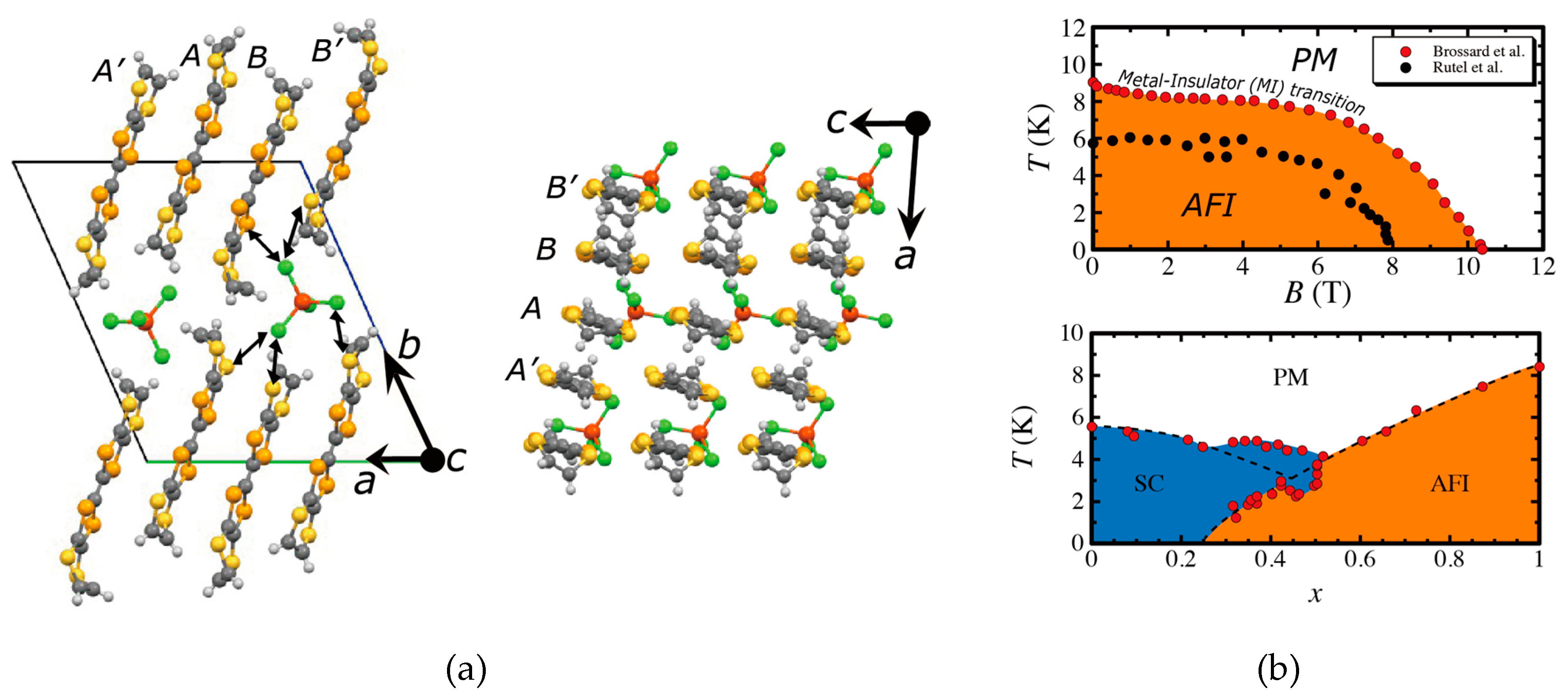
2. Crystal Structure and Phase Diagram
3. Previous Experimental and Theoretical Studies
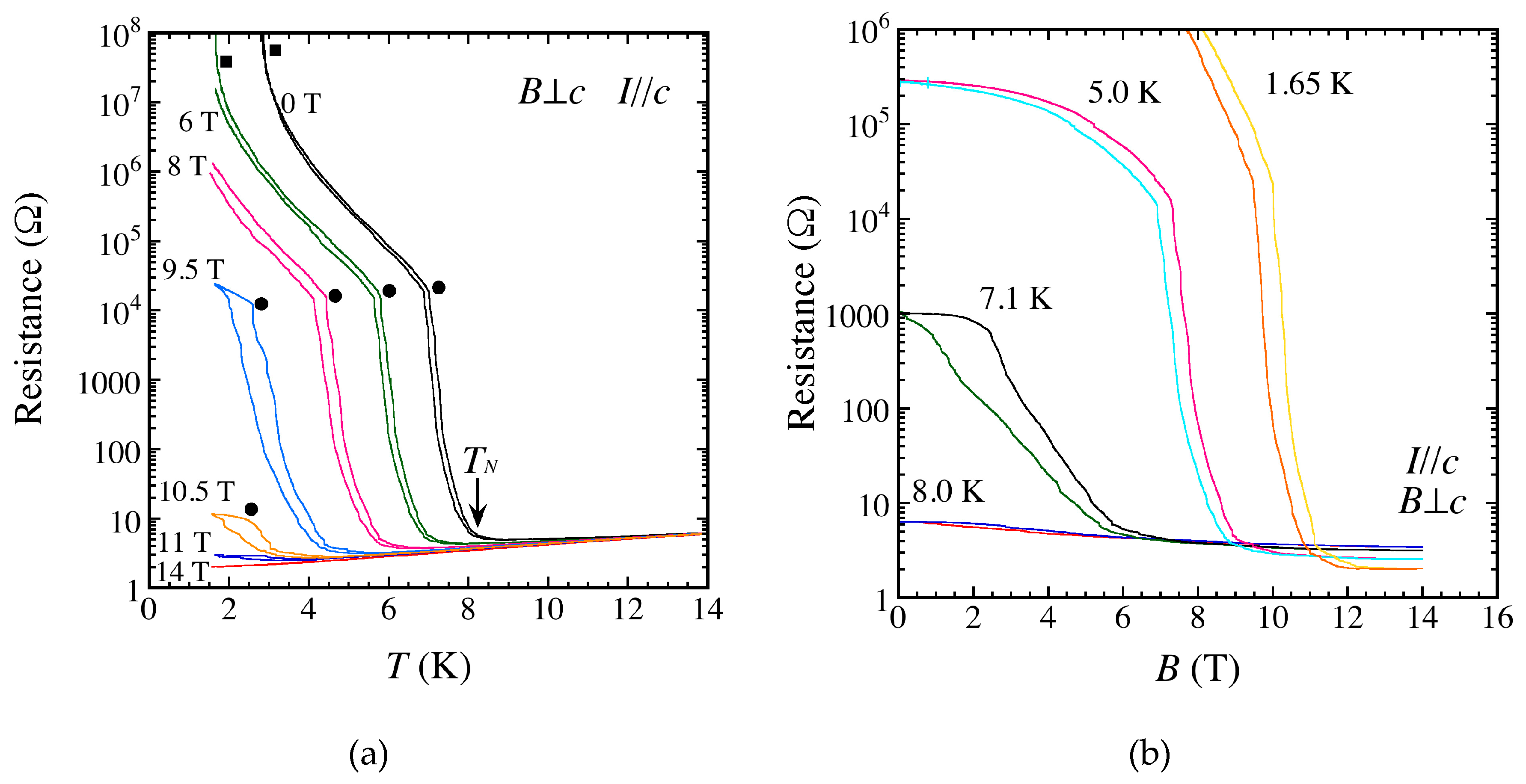
3.1. Transport and Magnetic Properties
3.2. Specific Heat Measurements and the Paramagnetic Fe Model
3.3. Theoretical Studies
3.4. Other Experimental Studies
4. ESR Measurements
4.1. Previous ESR Studies
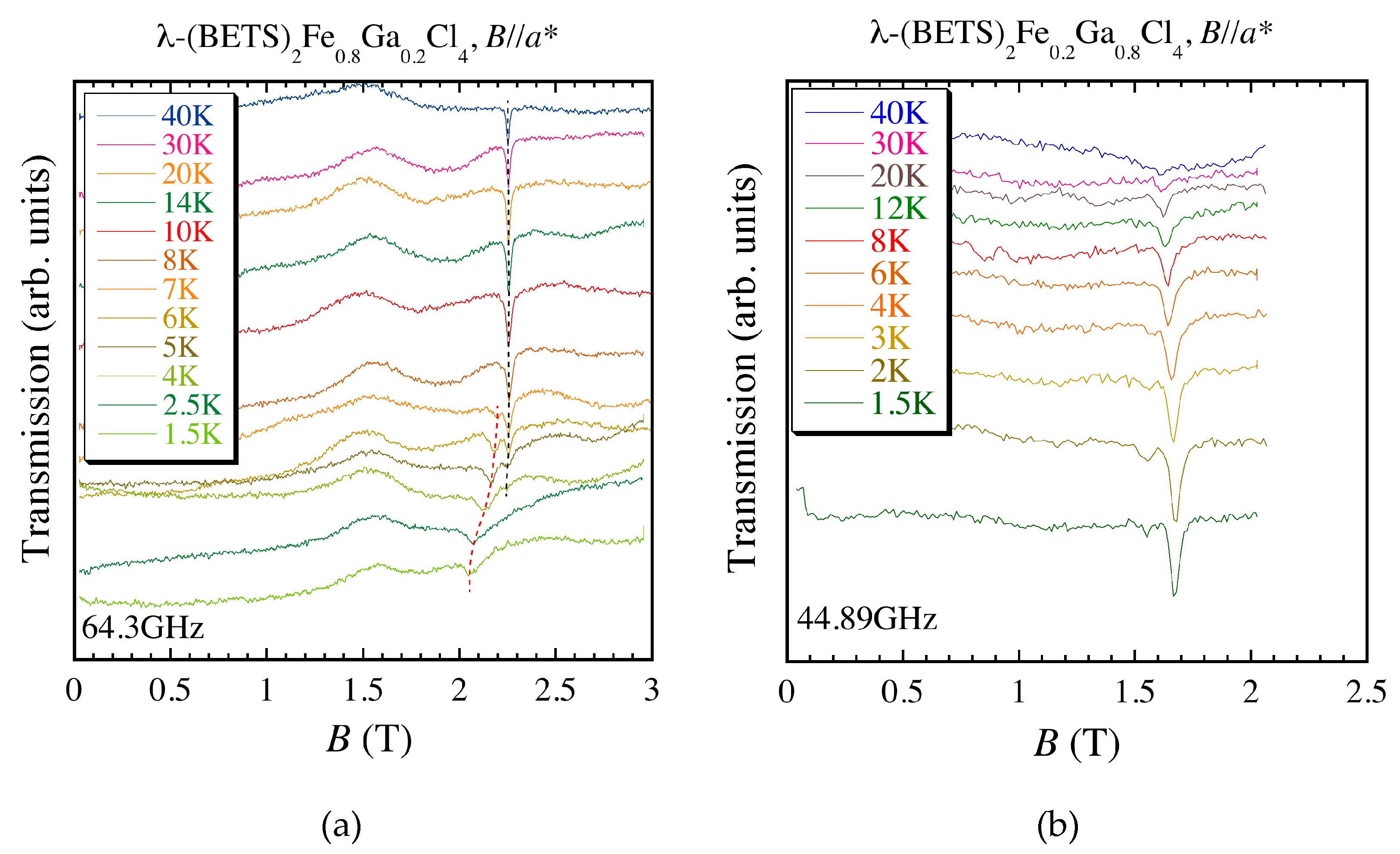
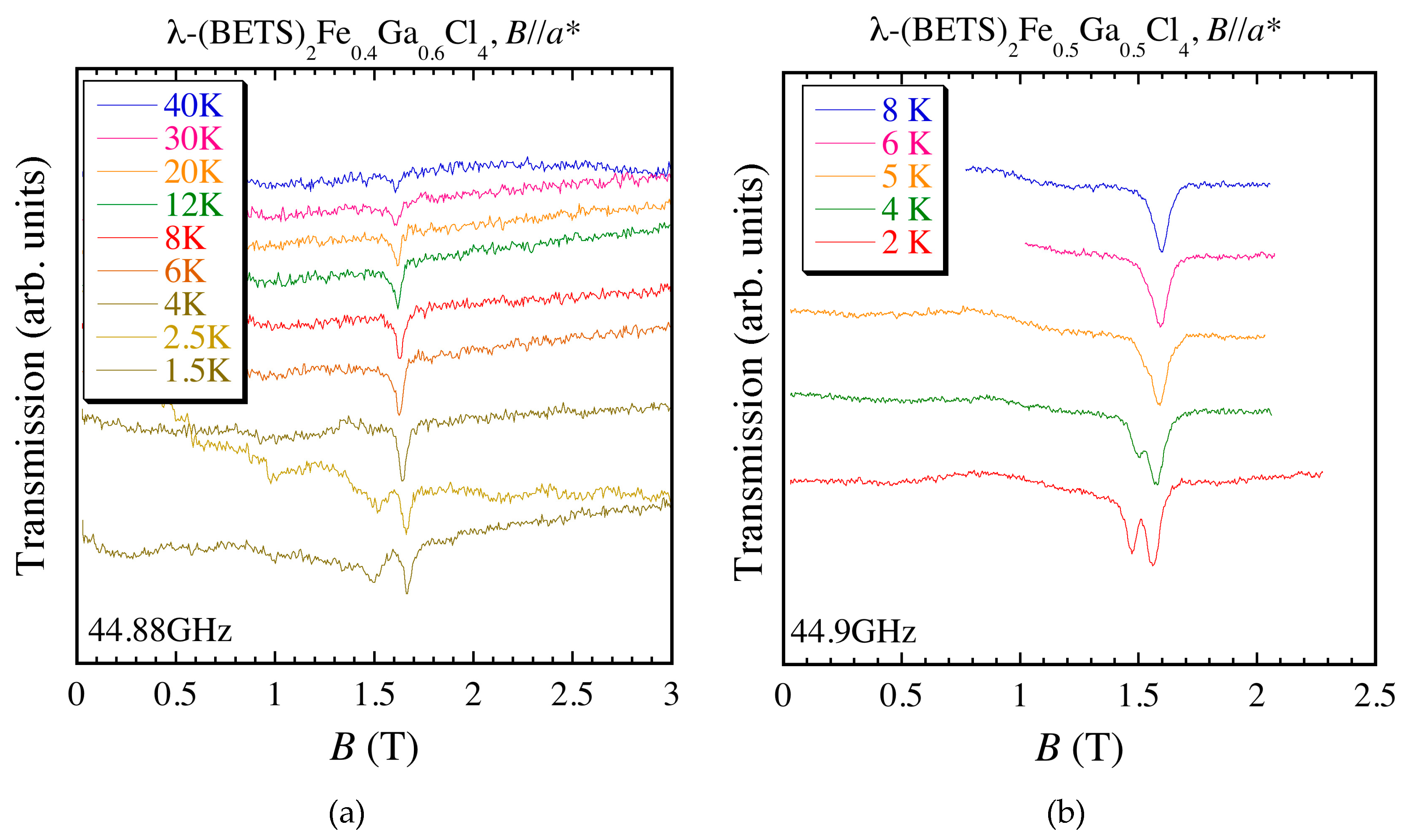
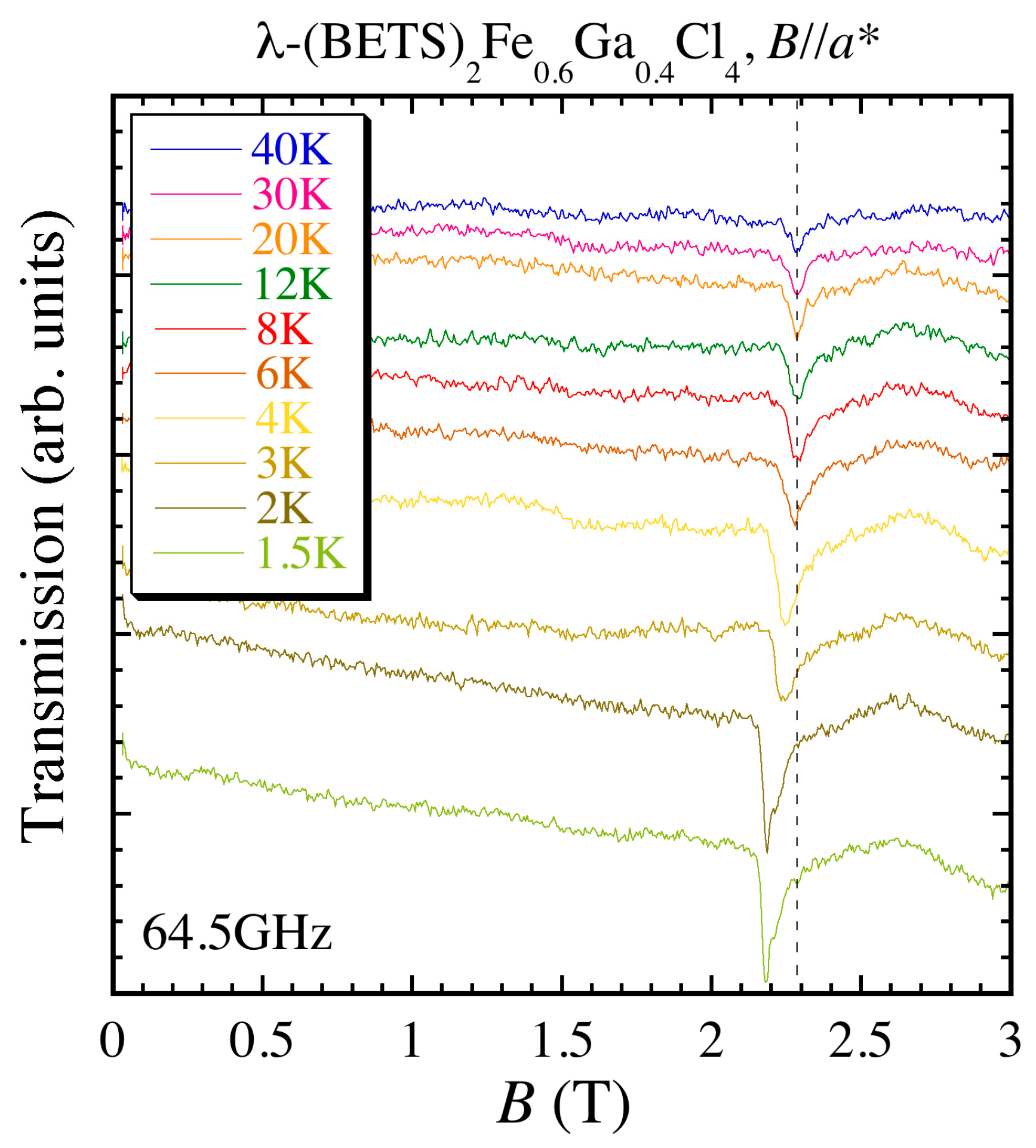
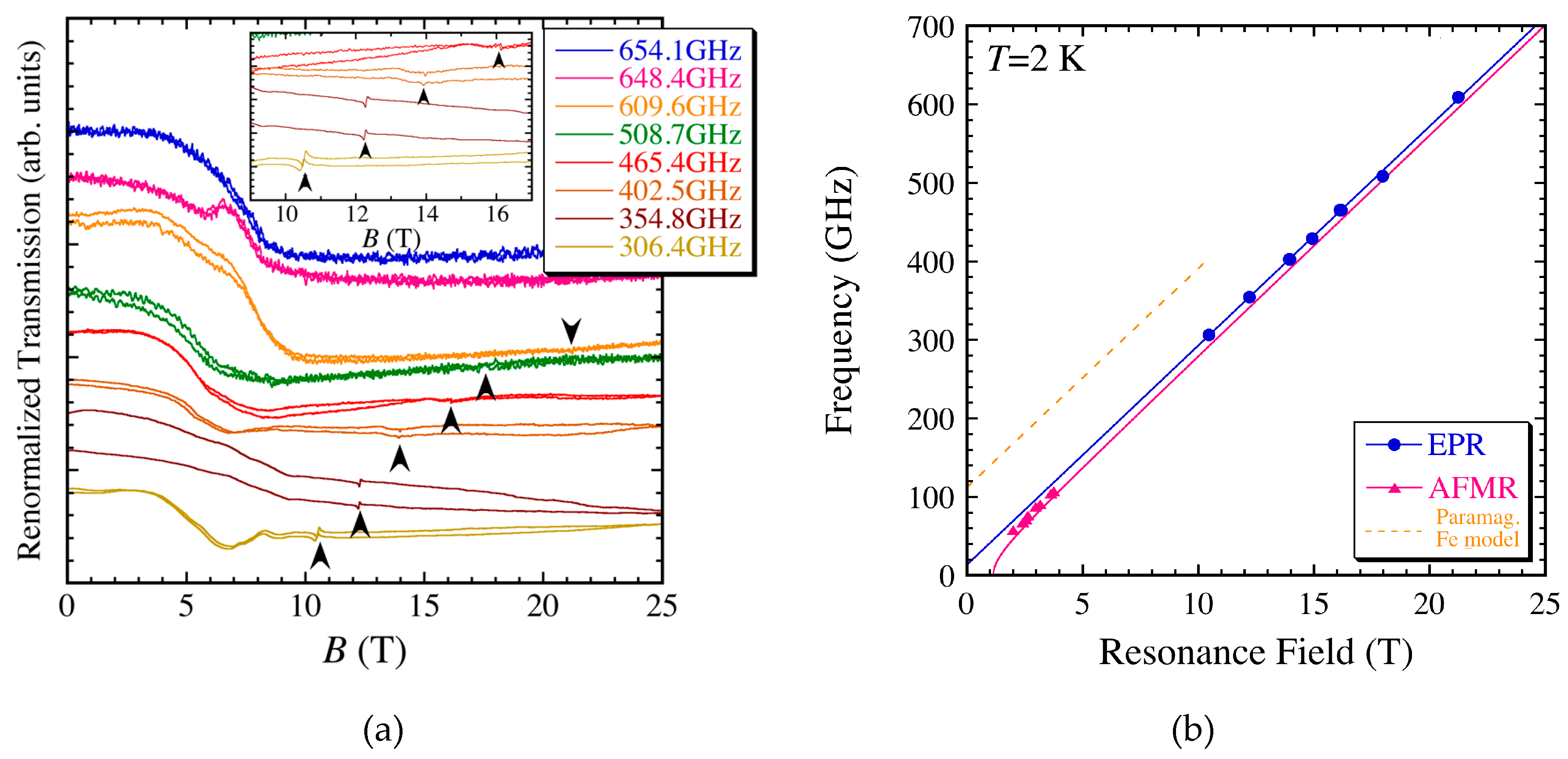
4.2. ESR Results of λ-(BETS)2FexGa1−xCl4 (x = 0.2~1.0)
5. Conclusions and Future Prospects
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Enomoto, K.; Yamaura, J.-I.; Miyazaki, A.; Enoki, T. Electronic and magnetic properties of organic conductors (DMET)2MBr4 (M = Fe, Ga). Bull. Chem. Soc. Jpn. 2003, 76, 945–959. [Google Scholar] [CrossRef]
- Hanasaki, N.; Tajima, H.; Matsuda, M.; Naito, T.; Inabe, T. Giant negative magnetoresistance in quasi-one-dimensional conductor TPP[Fe(Pc)(CN)2]2: Interplay between local moments and one-dimensional conduction electrons. Phys. Rev. B 2000, 62, 5839. [Google Scholar] [CrossRef]
- Uji, S.; Shinagawa, H.; Terashima, T.; Yakabe, T.; Terai, Y.; Tokumoto, M.; Kobayashi, A.; Tanaka, H.; Kobayashi, H. Magnetic0field-induced superconductivity in a two-dimensional organic conductor. Nature 2001, 410, 908–910. [Google Scholar] [CrossRef] [PubMed]
- Balicas, L.; Brooks, J.S.; Storr, K.; Uji, S.; Tokumoto, M.; Tanaka, H.; Kobayashi, H.; Kobayashi, A.; Barzykin, V.; Gor’kov, L.P. Superconductivity in an organic insulator at very high magnetic field. Phys. Rev. Lett. 2001, 87, 067002. [Google Scholar] [CrossRef] [PubMed]
- Uji, S.; Brooks, J.S. Magnetic-field-induced superconductivity in organic conductors. J. Phys. Soc. Jpn. 2006, 75, 051014. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tomita, H.; Naito, T.; Kobayashi, A.; Sakai, F.; Watanabe, T.; Cassoux, P. New BETS Conductors with Magnetic Anions (BETS = bis (ethylenedithio)tetraselenafulvalene). J. Am. Chem. Soc. 1996, 118, 368–377. [Google Scholar] [CrossRef]
- Tokumoto, M.; Naito, T.; Kobayashi, H.; Kobayashi, A.; Laukhin, V.N.; Brossard, L.; Cassoux, P. Magnetic anisotropy of organic conductor λ-(BETS)2FeCl4. Synth. Met. 1997, 86, 2161–2162. [Google Scholar] [CrossRef]
- Brossard, L.; Clerac, R.; Coulon, C.; Tokumoto, M.; Ziman, T.; Petrov, D.K.; Laukhin, V.N.; Naughton, M.J.; Audouard, A.; Goze, F.; et al. Interplay between chains of localised spins and two-dimensional sheets of organic donors in the synthetically built magnetic multilayer. Eur. Phys. J. B 1998, 1, 439–452. [Google Scholar] [CrossRef]
- Hotta, C.; Fukuyama, H. Effects of localized spins in quasi-two dimensional organic conductors. J. Phys. Soc. Jpn. 2000, 69, 2577–2596. [Google Scholar] [CrossRef]
- Cépas, O.; McKenzie, R.H.; Merino, J. Magnetic-field-induced superconductivity in layered organic molecular crystals with localized magnetic moments. Phys. Rev. B 2002, 65, 100502R. [Google Scholar] [CrossRef]
- Akiba, H.; Nakano, S.; Nishio, Y.; Kajita, K.; Zhou, B.; Kobayashi, A.; Kobayashi, H. Mysterious Paramagnetic States of Fe 3d Spin in Antiferromagnetic Insulator of λ-BETS2FeCl4 System. J. Phys. Soc. Jpn. 2009, 78, 033601. [Google Scholar] [CrossRef]
- Rutel, I.; Okubo, S.; Brooks, J.S.; Jobiliong, E.; Kobayashi, H.; Kobayashi, A.; Tanaka, H. Millimeter-wave investigation of the antiferromagnetic phase in λ-(BETS)2FeCl4 in high magnetic fields. Phys. Rev. B 2003, 68, 144435. [Google Scholar] [CrossRef]
- Cui, H.-B.; Kobayashi, H.; Kobayashi, A. Phase diagram and anomalous constant resistivity state of a magnetic organic superconducting alloy, λ-(BETS)2FexGa1−xCl4. J. Mat. Chem. 2007, 17, 45–48. [Google Scholar] [CrossRef]
- Uji, S.; Shinagawa, H.; Terakura, C.; Terashima, T.; Yakabe, T.; Terai, Y.; Tokumoto, M.; Kobayashi, A.; Tanaka, H.; Kobayashi, H. Fermi surface studies in the magnetic-field-induced superconductor λ-(BETS)2FeCl4. Phys. Rev. B 2001, 64, 024531. [Google Scholar] [CrossRef]
- Sato, A.; Ojima, E.; Akutsu, H.; Kobayashi, H.; Kobayashi, A.; Cassoux, P. Temperature-Composition Phase Diagram of the Organic Alloys, λ-BETS2(FexGa1−x)Cl4, with Mixed Magnetic and Non-Magnetic Anions. Chem. Lett. 1998, 27, 673. [Google Scholar] [CrossRef]
- Goze, F.; Laukhin, V.N.; Brossard, L.; Audouard, A.; Ulmet, J.P.; Askenazy, S.; Naito, T.; Kobayashi, H.; Kobayashi, A.; Tokumoto, M.; et al. Magnetotransport Measurements on the λ-Phase of the Organic Conductors (BETS)2MCl4 (M = Ga, Fe). Magnetic-Field-Restored Highly Conducting State in λ-(BETS)2FeCl4. Eur. Phys. Lett. 1994, 28, 427–432, ibid. Physica B 1995, 211, 290–292. [Google Scholar] [CrossRef]
- Akutsu, H.; Kato, K.; Ojima, E.; Kobayashi, H.; Tanaka, H.; Kobayashi, A.; Cassoux, P. Coupling of metal-insulator and antiferromagnetic transitions in the highly correlated organic conductor incorporating magnetic anions, λ-BETS2FeBrxCl4−x [BETS = Bis (ethylenedithio) tetraselenafulvalene]. Phys. Rev. B 1998, 58, 9294–9302. [Google Scholar] [CrossRef]
- Sasaki, T.; Uozaki, H.; Endo, S.; Toyota, N. Magnetic torque of λ-(BETS)2FeCl4. Synth. Met. 2001, 120, 759–760. [Google Scholar] [CrossRef]
- Uji, S.; Terakura, C.; Terashima, T.; Yakabe, T.; Terai, Y.; Tokumoto, M.; Kobayashi, A.; Sakai, F.; Tanaka, H.; Kobayashi, H. Fermi surface and internal magnetic field of the organic conductor λ-(BETS)2FexGa1−xCl4. Phys. Rev. B 2002, 65, 113101. [Google Scholar] [CrossRef]
- Sato, A.; Ojima, E.; Akutsu, H.; Nakazawa, Y.; Kobayashi, H.; Tanaka, H.; Kobayashi, A.; Cassoux, P. Magnetic properties of λ-BETS2(FexGa1−x)Cl4 exhibiting a superconductor-to-insulator transition (0.35 < x < 0.5). Phys. Rev. B 2000, 61, 111–114. [Google Scholar]
- Negishi, E.; Uozaki, H.; Ishizaki, Y.; Tsuchiya, H.; Endo, S.; Abe, Y.; Matsui, H.; Toyota, N. Specific heat studies for λ-(BEDT-TSF)2FeCl4. Synth. Met. 2003, 133–134, 555–556. [Google Scholar] [CrossRef]
- Akiba, H.; Nobori, K.; Shimada, K.; Nishio, Y.; Kajita, K.; Zhou, B.; Kobayahshi, A.; Kobayashi, H. Magnetic and Thermal Properties of λ-(BETS)2FeCl4 System—Fe 3d Spin in Antiferromagnetic Insulating Phase—. J. Phys. Soc. Jpn. 2011, 80, 063601. [Google Scholar] [CrossRef]
- Akiba, H.; Sugawara, H.; Nobori, K.; Shimada, K.; Tajima, N.; Nishio, Y.; Kajita, K.; Zhou, B.; Kobayashi, A.; Kobayashi, H. Paramagnetic Metal—Antiferromagnetic Insulator Transition of λ-BETS2FexGa1−xCl4 System. J. Phys. Soc. Jpn. 2012, 81, 053601. [Google Scholar] [CrossRef]
- Shimada, K.; Akiba, H.; Tajima, N.; Kajita, K.; Nishio, Y.; Kato, R.; Kobayashi, A.; Kobayashi, H. Temperature Dependence of Internal Field by Analysis of Specific Heat on an Organic Conductor λ-BETS2FeCl4. JPS Conf. Proc. 2014, 1, 012110. [Google Scholar]
- Shimada, K.; Tajima, N.; Kajita, K.; Nishio, Y. Effective Field Study of Canted Antiferromagnetic Insulating Phase in Magnetic Organic Conductor λ-(BETS)2FeCl4 through Specific Heat Measurement. J. Phys. Soc. Jpn. 2016, 85, 023601. [Google Scholar] [CrossRef]
- Waerenborgh, J.C.; Rabaça, S.; Almeida, M.; Lopes, E.B.; Kobayashi, A.; Zhou, B.; Brooks, J.S. Mössbauer spectroscopy and magnetic transition of λ-(BETS)2FeCl4. Phys. Rev. B 2010, 81, 060413R. [Google Scholar] [CrossRef]
- Sugiura, S.; Shimada, K.; Tajima, N.; Nishio, Y.; Terashima, T.; Isono, T.; Kobayashi, A.; Zhou, B.; Kato, R.; Uji, S. Charge Transport in Antiferromagnetic Insulating Phase of Two-Dimensional Organic Conductor λ-(BETS)2FeCl4. J. Phys. Soc. Jpn. 2016, 85, 064703. [Google Scholar] [CrossRef]
- Sugiura, S.; Shimada, K.; Tajima, N.; Nishio, Y.; Terashima, T.; Isono, T.; Kato, R.; Uji, S. Magnetic Torque Studies in Two-Dimensional Organic Conductor λ-(BETS)2FeCl4. J. Phys. Soc. Jpn. 2017, 86, 014702. [Google Scholar] [CrossRef]
- Mori, T.; Katsuhara, M. Estimation of πd-Interactions in Organic Conductors Including Magnetic Anions. J. Phys. Soc. Jpn. 2002, 71, 826–844. [Google Scholar] [CrossRef]
- Ito, K.; Shimahara, H. Mean Field Theory of a Coupled Heisenberg Model and Its Application to an Organic Antiferromagnet with Magnetic Anions. J. Phys. Soc. Jpn. 2016, 85, 024704. [Google Scholar] [CrossRef]
- Shimahara, H.; Ito, K. Spin-Flop Transition and a Tilted Canted Spin Structure in a Coupled Antiferromagnet. J. Phys. Soc. Jpn. 2016, 85, 043708. [Google Scholar] [CrossRef]
- Matsui, H.; Tsuchiya, H.; Negishi, E.; Uozaki, H.; Ishizaki, Y.; Abe, Y.; Endo, S.; Toyota, N. Anomalous dielectric response in the π-d correlated metallic state of λ-(BEDT-TSF)2FeCl4. J. Phys. Soc. Jpn. 2001, 70, 2501–2504. [Google Scholar] [CrossRef]
- Kitano, H.; Maeda, A. Comment on “Anomalous dielectric response in the π-d correlated metallic state of λ-(BEDT-TSF)2FeCl4”. J. Phys. Soc. Jpn. 2002, 71, 666–667. [Google Scholar] [CrossRef]
- Matsui, H.; Tsuchiya, H.; Toyota, N. Reply to Comment by H. Kitano and A. Maeda. J. Phys. Soc. Jpn. 2002, 71, 668–669. [Google Scholar] [CrossRef]
- Matsui, H.; Tsuchiya, H.; Suzuki, T.; Negishi, E.; Toyota, N. Relaxor ferroelectric behavior and collective modes in the π-d correlated anomalous metal λ-(BEDT-TSF)2FeCl4. Phys. Rev. B 2003, 68, 155105. [Google Scholar] [CrossRef]
- Watanabe, M.; Komiyama, S.; Kiyanagi, R.; Noda, Y.; Negishi, E.; Toyota, N. Evidence of the First-Order Nature of the Metal–Insulator Phase Transition in λ-(BEDT-TSF)2FeCl4. J. Phys. Soc. Jpn. 2003, 72, 452–453. [Google Scholar] [CrossRef]
- Komiyama, S.; Watanabe, M.; Noda, Y.; Negishi, E.; Toyota, N. Relaxor-like Behavior in λ-(BEDT-TSF)2FeCl4 Studied by SR X-ray Diffraction. J. Phys. Soc. Jpn. 2004, 73, 2385–2388. [Google Scholar] [CrossRef]
- Toyota, N.; Abe, Y.; Matsui, H.; Negishi, E.; Ishizaki, Y.; Tsuchiya, H.; Uozaki, H. Nonlinear electrical transport in λ-(BEDT-TSF)2FeCl4. Phys. Rev. B 2002, 66, 033201. [Google Scholar] [CrossRef]
- Negishi, E.; Kuwabara, T.; Komiyama, S.; Watanabe, M.; Noda, Y.; Mori, T.; Matsui, H.; Toyota, N. Dielectric ordering and colossal magnetodielectricity in the antiferromagnetic insulating state of λ-(BEDT-TSF)2FeCl4. Phys. Rev. B 2005, 71, 012416. [Google Scholar] [CrossRef]
- Oh, J.I.; Naughton, M.J.; Courcet, T.; Malfant, I.; Cassoux, P.; Tokumoto, M.; Akutsu, H.; Kobayashi, H.; Kobayashi, A. Torque anisotropy in λ-(BEDT-TSF)2FeCl4. Synth. Met. 1999, 103, 1861–1864. [Google Scholar] [CrossRef]
- Endo, S.; Goto, T.; Fukase, T.; Matsui, H.; Uozaki, H.; Tsuchiya, H.; Negishi, E.; Ishizaki, Y.; Abe, Y.; Toyota, N. Anomalous Splitting of 1H-NMR Spectra in λ-(BEDT-TSF)2FeCl4. J. Phys. Soc. Jpn. 2002, 71, 732–734. [Google Scholar] [CrossRef]
- Wu, G.; Ranin, P.; Gaidos, G.; Clark, W.G.; Brown, S.E.; Balicas, L.; Montgomery, L.K. 1H-NMR spin-echo measurements of the spin dynamic properties in λ-(BETS)2FeCl4. Phys. Rev. B 2007, 75, 174416. [Google Scholar] [CrossRef]
- Hiraki, K.; Mayaffre, H.; Horvatic, M.; Berthier, C.; Uji, S.; Yamaguchi, T.; Tanaka, H.; Kobayashi, A.; Kobayashi, H.; Takahashi, T. 77Se NMR Evidence for the Jaccarino–Peter Mechanism in the Field Induced Superconductor, λ-(BETS)2FeCl4. J. Phys. Soc. Jpn. 2007, 76, 124708. [Google Scholar] [CrossRef]
- Kawamata, S.; Kizawa, T.; Suzuki, T.; Negishi, E.; Matsui, H.; Toyota, N.; Ishida, T. π-d Correlation in λ-(BEDT-TSF)2Fe1−xGaxCl4 by ESR Measurements. J. Phys. Soc. Jpn. 2006, 75, 104715. [Google Scholar] [CrossRef]
- Oshima, Y.; Jobiliong, E.; Brooks, J.S.; Zvyagin, S.A.; Krzystek, J.; Tanaka, H.; Kobayashi, A.; Cui, H.; Kobayashi, H. EMR Measurements of Field-Induced Superconductor λ-(BEDT-TSF)2Fe1−xGaxCl4. Synth. Met. 2005, 153, 365–368. [Google Scholar] [CrossRef]
- Suzuki, T.; Matsui, H.; Tsuchiya, H.; Negishi, E.; Koyama, K.; Toyota, N. Antiferromagnetic resonance in λ-(BETS)2FeCl4. Phys. Rev. B 2003, 67, 020408R. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oshima, Y.; Cui, H.; Kato, R. Antiferromagnetic Insulating Ground State of Molecular π-d System Λ-(BETS)2FeCl4 (BETS = Bis(ethylenedithio)tetraselenafulvalene): A Theoretical and Experimental Review. Magnetochemistry 2017, 3, 10. https://doi.org/10.3390/magnetochemistry3010010
Oshima Y, Cui H, Kato R. Antiferromagnetic Insulating Ground State of Molecular π-d System Λ-(BETS)2FeCl4 (BETS = Bis(ethylenedithio)tetraselenafulvalene): A Theoretical and Experimental Review. Magnetochemistry. 2017; 3(1):10. https://doi.org/10.3390/magnetochemistry3010010
Chicago/Turabian StyleOshima, Yugo, Heng‐Bo Cui, and Reizo Kato. 2017. "Antiferromagnetic Insulating Ground State of Molecular π-d System Λ-(BETS)2FeCl4 (BETS = Bis(ethylenedithio)tetraselenafulvalene): A Theoretical and Experimental Review" Magnetochemistry 3, no. 1: 10. https://doi.org/10.3390/magnetochemistry3010010
APA StyleOshima, Y., Cui, H., & Kato, R. (2017). Antiferromagnetic Insulating Ground State of Molecular π-d System Λ-(BETS)2FeCl4 (BETS = Bis(ethylenedithio)tetraselenafulvalene): A Theoretical and Experimental Review. Magnetochemistry, 3(1), 10. https://doi.org/10.3390/magnetochemistry3010010





