Perspectives on Neutron Scattering in Lanthanide-Based Single-Molecule Magnets and a Case Study of the Tb2(μ-N2) System
Abstract
:1. Introduction
2. General Challenges in Studying the Magnetism in Ln-Based SMMs
2.1. Experimental Aspects of Ln-Based Clusters
2.2. Challenges of Analysis
2.3. Perspectives of Neutron Scattering Techniques
3. Inelastic Neutron Scattering Study of the Tb2(μ-N2) System
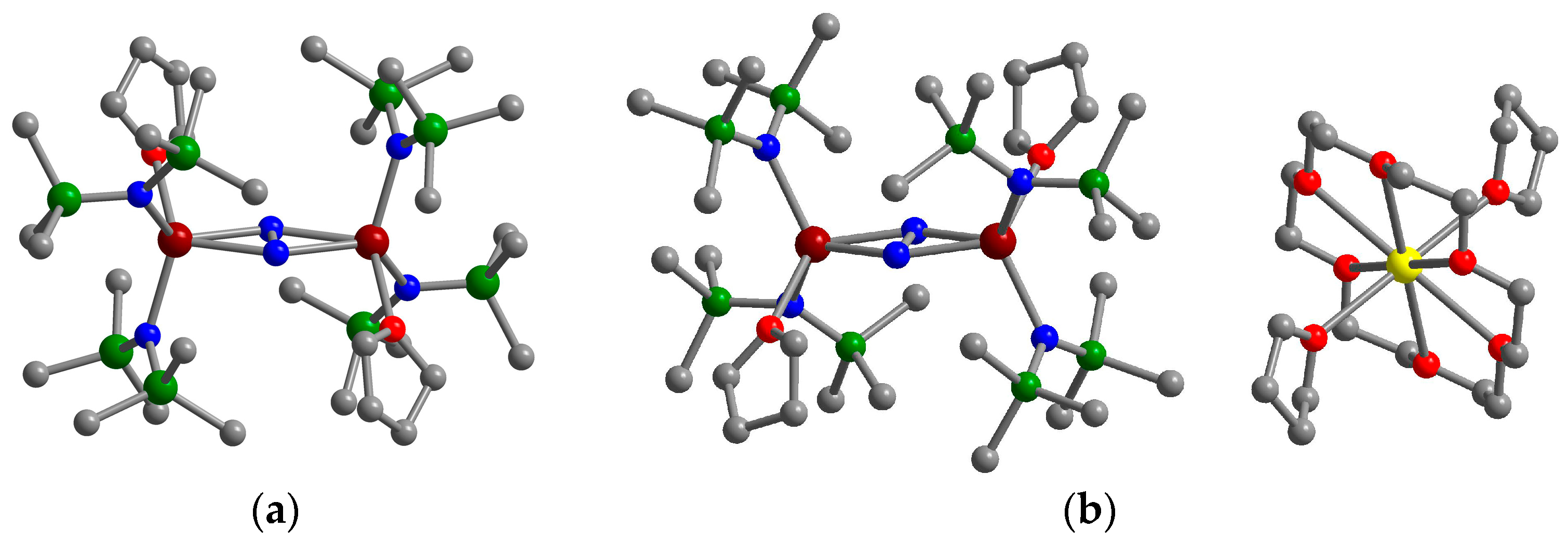
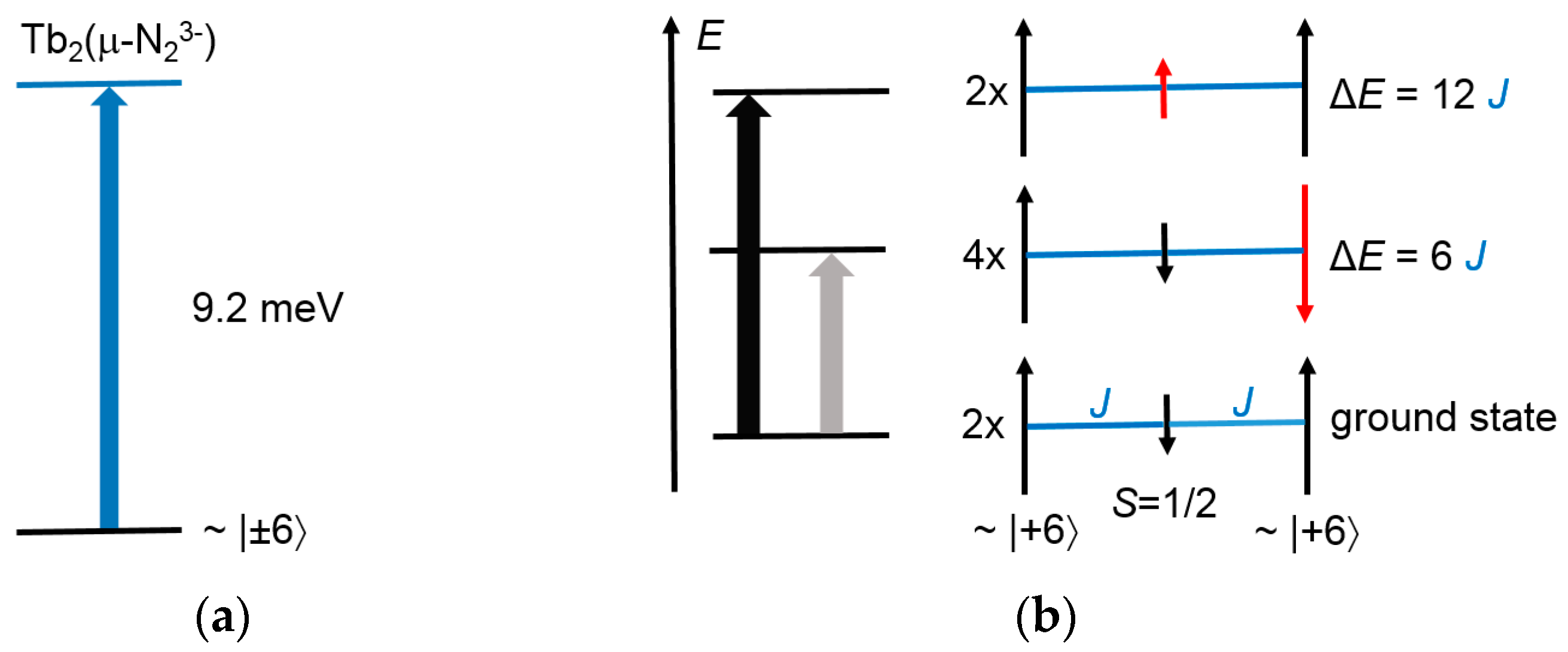
3.1. Introduction to the Tb2(μ-N2) System
3.2. Experimental Details
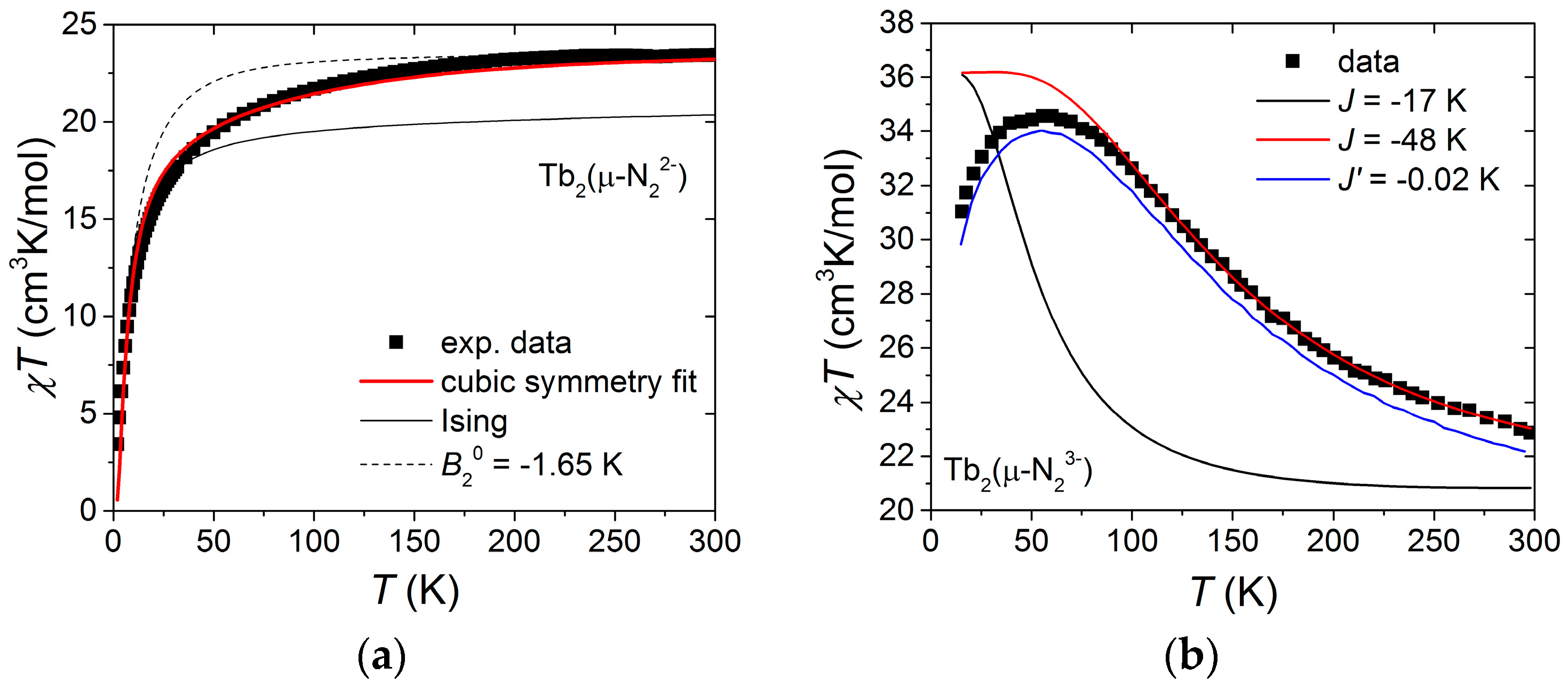
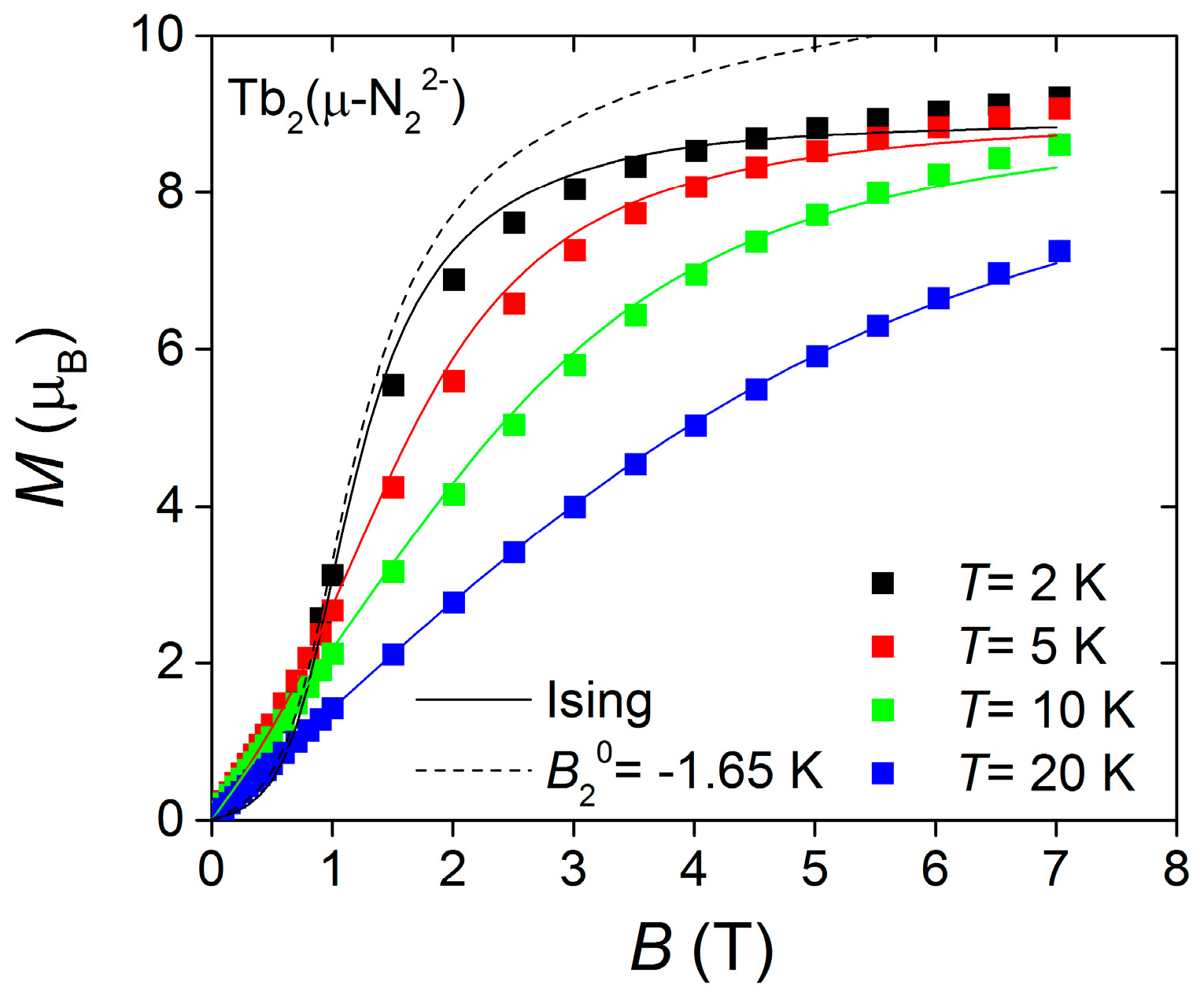
3.3. Magnetization Data for the Parent Compound 1
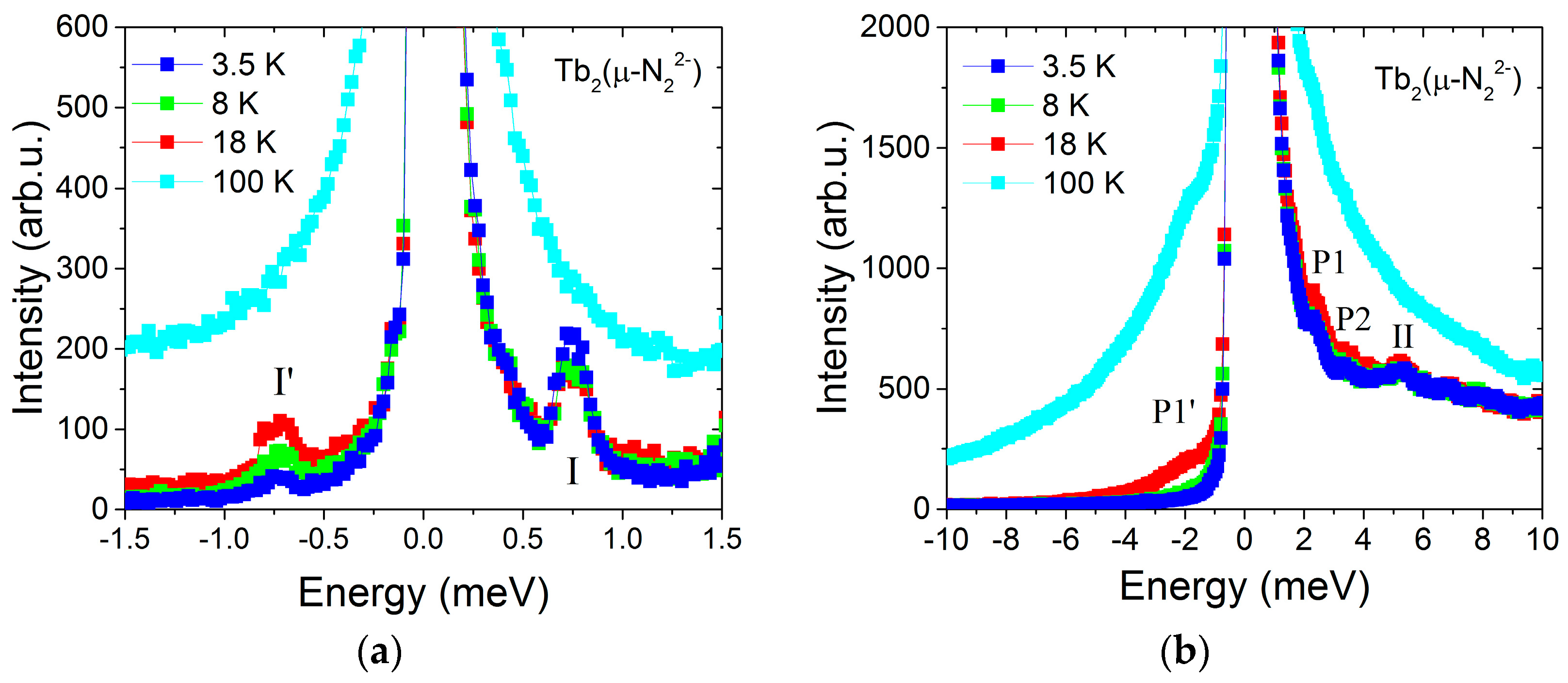
3.4. Inelastic Neutron Scattering Data for the Parent Compound 1
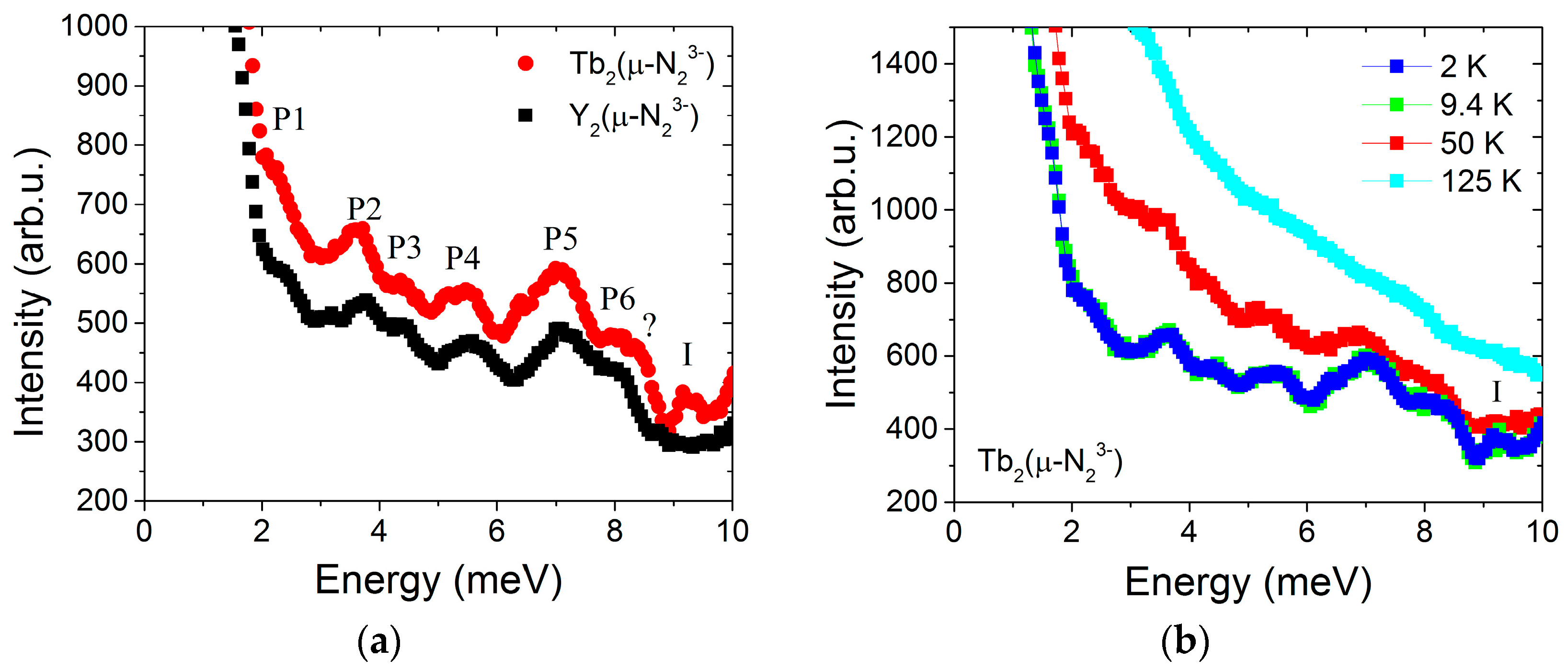
3.5. Inelastic Neutron Scattering Data for the SMM Compound 2 and YIII Analogue 3
4. Discussion
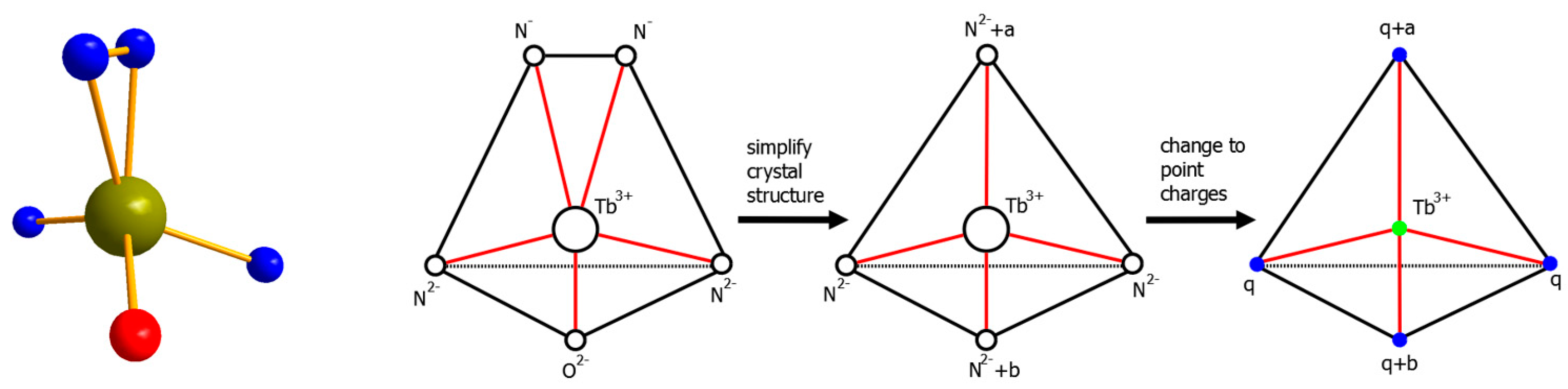
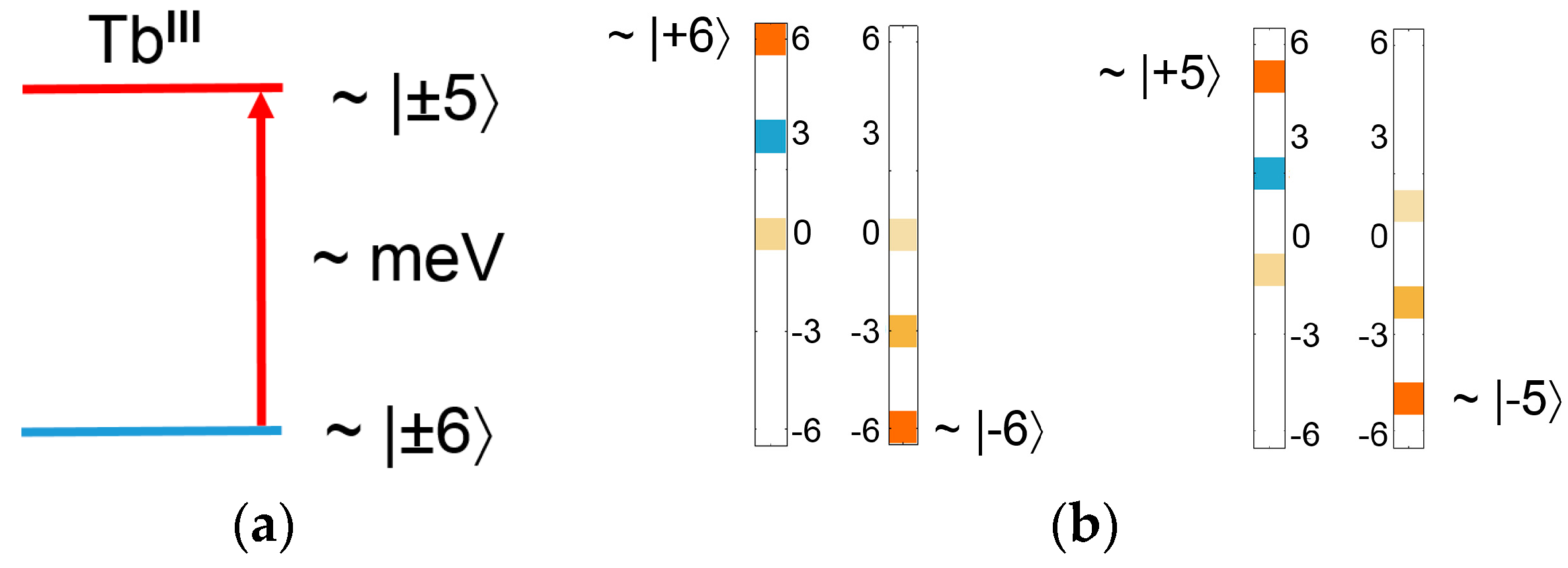
4.1. Insights from the Point Charge Model
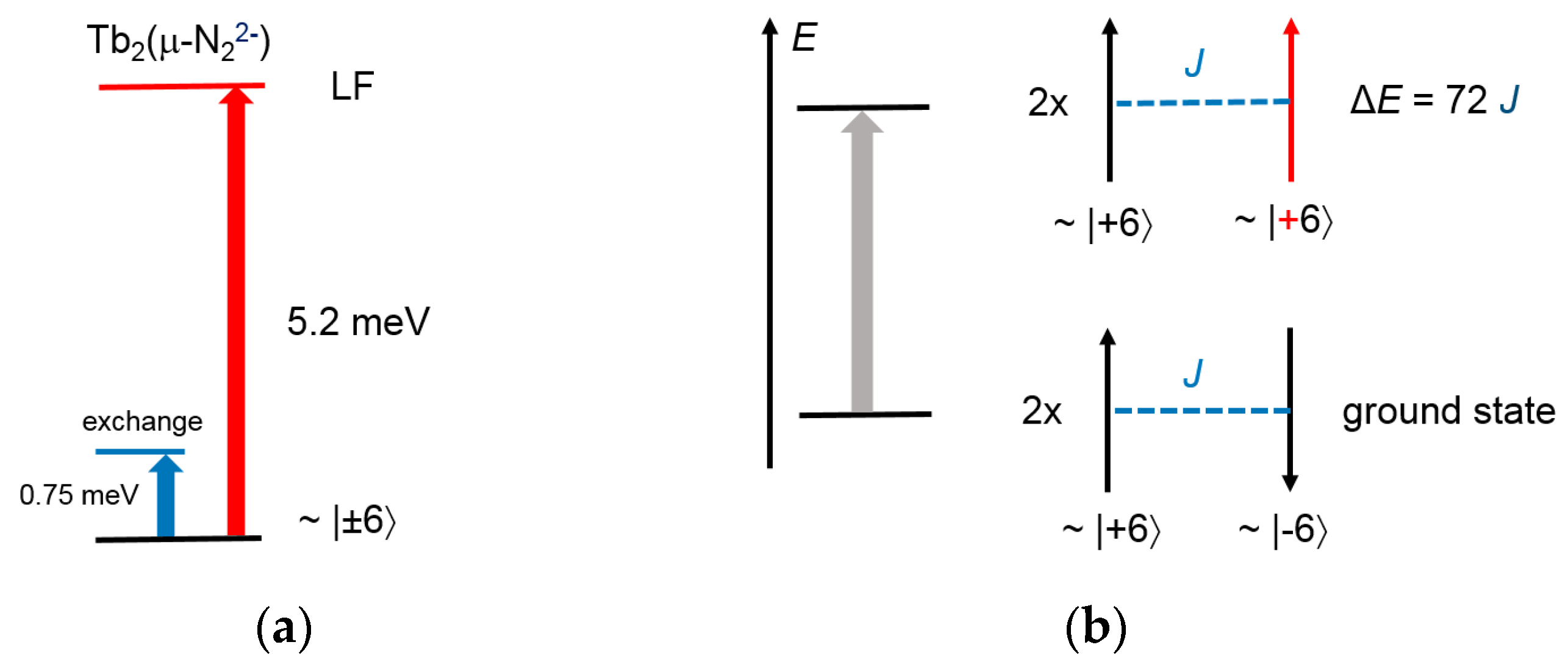
4.2. The Parent Compound 1
4.3. The SMM Compound 2
5. Materials and Methods
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Rinehart, J.D.; Fang, M.; Evans, W.J.; Long, J.R. A N23− Radical-Bridged Terbium Complex Exhibiting Magnetic Hysteresis at 14 K. J. Am. Chem. Soc. 2011, 133, 14236–14239. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Fang, M.; Evans, W.J.; Long, J.R. Strong exchange and magnetic blocking in N23−-radical-bridged lanthanide complexes. Nat. Chem. 2011, 3, 538–542. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-C.; Liu, J.-L.; Ungur, L.; Liu, J.; Li, Q.-W.; Wang, L.-F.; Ni, Z.-P.; Chibotaru, L.F.; Chen, X.-M.; Tong, M.-L. Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets. J. Am. Chem. Soc. 2016, 138, 2829–2837. [Google Scholar] [CrossRef] [PubMed]
- Ungur, L.; Lin, S.-Y.; Tang, J.; Chibotaru, L.F. Single-molecule toroics in Ising-type lanthanide molecular clusters. Chem. Soc. Rev. 2014, 43, 6894–6905. [Google Scholar] [CrossRef] [PubMed]
- Sharples, J.W.; Collison, D.; McInnes, E.J.L.; Schnack, J.; Palacios, E.; Evangelisti, M. Quantum signatures of a molecular nanomagnet in direct magnetocaloric measurements. Nat. Commun. 2014, 5, 5321. [Google Scholar] [CrossRef] [PubMed]
- Shiddiq, M.; Komijani, D.; Duan, Y.; Gaita-Ariño, A.; Coronado, E.; Hill, S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Hewitt, I.; Madhu, N.T.; Chastanet, G.; Wernsdorfer, W.; Anson, C.E.; Benelli, C.; Sessoli, R.; Powell, A.K. Dysprosium Triangles Showing Single-Molecule Magnet Behavior of Thermally Excited Spin States. Angew. Chem. Int. Ed. 2006, 45, 1729–1733. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L.; Soncini, A. The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment. Angew. Chem. Int. Ed. 2008, 47, 4126–4129. [Google Scholar] [CrossRef] [PubMed]
- Luis, F.; Repollés, A.; Martínez-Pérez, M.J.; Aguilà, D.; Roubeau, O.; Zueco, D.; Alonso, P.J.; Evangelisti, M.; Camón, A.; Sesé, J.; et al. Molecular Prototypes for Spin-Based CNOT and SWAP Quantum Gates. Phys. Rev. Lett. 2011, 107, 117203. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Ungur, L.; Chibotaru, L.F. Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets. Inorg. Chem. 2016, 55, 10043–10056. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Zhang, P. Lanthanide Single Molecule Magnets, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Liddle, S.T.; van Slageren, J. Improving f-element single molecule magnets. Chem. Soc. Rev. 2015, 44, 6655–6669. [Google Scholar] [CrossRef] [PubMed]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Jensen, J.; Mackintosh, A.R. Rare Earth Magnetism; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Newman, D.J. Theory of lanthanide crystal fields. Adv. Phys. 1971, 20, 197–256. [Google Scholar] [CrossRef]
- Christou, G.; Gatteschi, D.; Hendrickson, D.N.; Sessoli, R. Single-Molecule Magnets. MRS Bull. 2000, 25, 66–71. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials. Angew. Chem. Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Waldmann, O. A Criterion for the Anisotropy Barrier in Single-Molecule Magnets. Inorg. Chem. 2007, 46, 10035–10037. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Woodruff, D.N.; Bendix, J.; Clérac, R. Experimental Aspects of Lanthanide Single-Molecule Magnet Physics. In Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 125–152. [Google Scholar]
- Furrer, A.; Waldmann, O. Magnetic cluster excitations. Rev. Mod. Phys. 2013, 85, 367–420. [Google Scholar] [CrossRef]
- Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A. Mononuclear Lanthanide Complexes: Use of the Crystal Field Theory to Design Single-Ion Magnets and Spin Qubits. In Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 27–60. [Google Scholar]
- Sorace, L.; Gatteschi, D. Electronic Structure and Magnetic Properties of Lanthanide Molecular Complexes. In Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 1–26. [Google Scholar]
- Klokishner, S.I.; Ostrovsky, S.M.; Reu, O.S.; Palii, A.V.; Tregenna-Piggott, P.L.W.; Brock-Nannestad, T.; Bendix, J.; Mutka, H. Magnetic Anisotropy in the [CuIILTbIII(hfac)2]2 Single Molecule Magnet: Experimental Study and Theoretical Modeling. J. Phys. Chem. C 2009, 113, 8573–8582. [Google Scholar] [CrossRef]
- Magnani, N.; Caciuffo, R.; Colineau, E.; Wastin, F.; Baraldi, A.; Buffagni, E.; Capelletti, R.; Carretta, S.; Mazzera, M.; Adroja, D.T.; et al. Low-energy spectrum of a Tm-based double-decker complex. Phys. Rev. B 2009, 79, 104407. [Google Scholar] [CrossRef]
- Dreiser, J.; Pedersen, K.S.; Piamonteze, C.; Rusponi, S.; Salman, Z.; Ali, M.E.; Schau-Magnussen, M.; Thuesen, C.A.; Piligkos, S.; Weihe, H.; et al. Direct observation of a ferri-to-ferromagnetic transition in a fluoride-bridged 3d-4f molecular cluster. Chem. Sci. 2012, 3, 1024–1032. [Google Scholar] [CrossRef]
- Kofu, M.; Yamamuro, O.; Kajiwara, T.; Yoshimura, Y.; Nakano, M.; Nakajima, K.; Ohira-Kawamura, S.; Kikuchi, T.; Inamura, Y. Hyperfine structure of magnetic excitations in a Tb-based single-molecule magnet studied by high-resolution neutron spectroscopy. Phys. Rev. B 2013, 88, 64405. [Google Scholar] [CrossRef]
- Marx, R.; Moro, F.; Dorfel, M.; Ungur, L.; Waters, M.; Jiang, S.D.; Orlita, M.; Taylor, J.; Frey, W.; Chibotaru, L.F.; et al. Spectroscopic determination of crystal field splittings in lanthanide double deckers. Chem. Sci. 2014, 5, 3287–3293. [Google Scholar] [CrossRef]
- Baker, M.L.; Tanaka, T.; Murakami, R.; Ohira-Kawamura, S.; Nakajima, K.; Ishida, T.; Nojiri, H. Relationship between Torsion and Anisotropic Exchange Coupling in a TbIII-Radical-Based Single-Molecule Magnet. Inorg. Chem. 2015, 54, 5732–5738. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Ungur, L.; Sigrist, M.; Sundt, A.; Schau-Magnussen, M.; Vieru, V.; Mutka, H.; Rols, S.; Weihe, H.; Waldmann, O.; et al. Modifying the properties of 4f single-ion magnets by peripheral ligand functionalisation. Chem. Sci. 2014, 5, 1650–1660. [Google Scholar] [CrossRef]
- Kettles, F.J.; Milway, V.A.; Tuna, F.; Valiente, R.; Thomas, L.H.; Wernsdorfer, W.; Ochsenbein, S.T.; Murrie, M. Exchange Interactions at the Origin of Slow Relaxation of the Magnetization in {TbCu3} and {DyCu3} Single-Molecule Magnets. Inorg. Chem. 2014, 53, 8970–8978. [Google Scholar] [CrossRef] [PubMed]
- Giansiracusa, M.J.; Vonci, M.; Van den Heuvel, W.; Gable, R.W.; Moubaraki, B.; Murray, K.S.; Yu, D.; Mole, R.A.; Soncini, A.; Boskovic, C. Carbonate-Bridged Lanthanoid Triangles: Single-Molecule Magnet Behavior, Inelastic Neutron Scattering, and Ab Initio Studies. Inorg. Chem. 2016, 55, 5201–5214. [Google Scholar] [CrossRef] [PubMed]
- Vonci, M.; Giansiracusa, M.J.; Gable, R.W.; Van den Heuvel, W.; Latham, K.; Moubaraki, B.; Murray, K.S.; Yu, D.; Mole, R.A.; Soncini, A.; et al. Ab initio calculations as a quantitative tool in the inelastic neutron scattering study of a single-molecule magnet analogue. Chem. Commun. 2016, 52, 2091–2094. [Google Scholar] [CrossRef] [PubMed]
- Buschow, K.H.J.; de Boer, F.R. Physics of Magnetism and Magnetic Materials, 1st ed.; Kluver Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Blagg, R.J.; Ungur, L.; Tuna, F.; Speak, J.; Comar, P.; Collison, D.; Wernsdorfer, W.; McInnes, E.J.L.; Chibotaru, L.F.; Winpenny, R.E.P. Magnetic relaxation pathways in lanthanide single-molecule magnets. Nat. Chem 2013, 5, 673–678. [Google Scholar] [CrossRef] [PubMed]
- Demir, S.; Jeon, I.-R.; Long, J.R.; Harris, T.D. Radical ligand-containing single-molecule magnets. Coord. Chem. Rev. 2015, 289–290, 149–176. [Google Scholar] [CrossRef]
- Bewley, R.I.; Taylor, J.W.; Bennington, S.M. LET, a cold neutron multi-disk chopper spectrometer at ISIS. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2011, 637, 128–134. [Google Scholar] [CrossRef]
- Konstantatos, A.; Bewley, R.; Barra, A.-L.; Bendix, J.; Piligkos, S.; Weihe, H. In-Depth Magnetic Characterization of a [2 × 2] Mn(III) Square Grid Using SQUID Magnetometry, Inelastic Neutron Scattering, and High-Field Electron Paramagnetic Resonance Spectroscopy. Inorg. Chem. 2016, 55, 10377–10382. [Google Scholar] [CrossRef] [PubMed]
- Woolfson, R.J.; Timco, G.A.; Chiesa, A.; Vitorica-Yrezabal, I.J.; Tuna, F.; Guidi, T.; Pavarini, E.; Santini, P.; Carretta, S.; Winpenny, R.E.P. [CrF(O2CtBu)2]9: Synthesis and Characterization of a Regular Homometallic Ring with an Odd Number of Metal Centers and Electrons. Angew. Chem. Int. Ed. 2016, 55, 8856–8859. [Google Scholar] [CrossRef] [PubMed]
- EPR (and photon-based spectroscopy in general) is subject to the selection rules ΔM = ±1 and ΔS = 0, and INS to the rules ΔM = 0, ±1 and ΔS = 0, ±1. The selection rules of transitions within or between J multiplets are obtained by replacing M → MJ, S → J.
- Moreno Pineda, E.; Chilton, N.F.; Marx, R.; Dörfel, M.; Sells, D.O.; Neugebauer, P.; Jiang, S.-D.; Collison, D.; van Slageren, J.; McInnes, E.J.L.; et al. Direct measurement of dysprosium(III)-dysprosium(III) interactions in a single-molecule magnet. Nat. Commun. 2014, 5, 5243. [Google Scholar] [CrossRef] [PubMed]
- Dreiser, J.; Pedersen, K.S.; Schnegg, A.; Holldack, K.; Nehrkorn, J.; Sigrist, M.; Tregenna-Piggott, P.; Mutka, H.; Weihe, H.; Mironov, V.S.; et al. Three-Axis Anisotropic Exchange Coupling in the Single-Molecule Magnets NEt4[MnIII2(5-Brsalen)2(MeOH)2MIII(CN)6] (M = Ru, Os). Chem. Eur. J. 2013, 19, 3693–3701. [Google Scholar] [CrossRef] [PubMed]
- Koehler, W.C.; Moon, R.M.; Cable, J.W.; Child, H.R. Neutron scattering experiments on gadolinium. J. Phys. Colloq. 1971, 32, C1-296–C1-298. [Google Scholar] [CrossRef]
- Yu, J.; LeClair, P.R.; Mankey, G.J.; Robertson, J.L.; Crow, M.L.; Tian, W. Exploring the magnetic phase diagram of dysprosium with neutron diffraction. Phys. Rev. B 2015, 91, 14404. [Google Scholar] [CrossRef]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Dreiser, J.; Waldmann, O.; Dobe, C.; Carver, G.; Ochsenbein, S.T.; Sieber, A.; Güdel, H.U.; van Duijn, J.; Taylor, J.; Podlesnyak, A. Quantized antiferromagnetic spin waves in the molecular Heisenberg ring CsFe8. Phys. Rev. B 2010, 81, 24408. [Google Scholar] [CrossRef]
- Ungur, L.; Chibotaru, L.F. Computational Modelling of the Magnetic Properties of Lanthanide Compounds. In Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 153–184. [Google Scholar]
- Furrer, A.; Güdel, H.U.; Blank, H.; Heidemann, A. Direct Observation of Exchange Splittings in Cs3Tb2Br9 by Neutron Spectroscopy. Phys. Rev. Lett. 1989, 62, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Furrer, A.; Güdel, H.U.; Krausz, E.R.; Blank, H. Neutron spectroscopic study of anisotropic exchange in the dimer compound Cs3Ho2Br9. Phys. Rev. Lett. 1990, 64, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.-N.; Ungur, L.; Granroth, G.E.; Powell, A.K.; Wu, C.; Nagler, S.E.; Tang, J.; Chibotaru, L.F.; Cui, D. An NCN-pincer ligand dysprosium single-ion magnet showing magnetic relaxation via the second excited state. Sci. Rep. 2014, 4, 5471. [Google Scholar] [CrossRef] [PubMed]
- Hutchings, M.T. Point-Charge Calculations of Energy Levels of Magnetic Ions in Crystalline Electric Fields. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 1964; Volume 16, pp. 227–273. [Google Scholar]
- Baker, M.L.; Guidi, T.; Carretta, S.; Ollivier, J.; Mutka, H.; Gudel, H.U.; Timco, G.A.; McInnes, E.J.L.; Amoretti, G.; Winpenny, R.E.P.; et al. Spin dynamics of molecular nanomagnets unravelled at atomic scale by four-dimensional inelastic neutron scattering. Nat. Phys. 2012, 8, 906–911. [Google Scholar] [CrossRef]
- Guidi, T.; Gillon, B.; Mason, S.A.; Garlatti, E.; Carretta, S.; Santini, P.; Stunault, A.; Caciuffo, R.; van Slageren, J.; Klemke, B.; et al. Direct observation of finite size effects in chains of antiferromagnetically coupled spins. Nat. Commun. 2015, 6, 7061. [Google Scholar] [CrossRef] [PubMed]
- Waldmann, O.; Bircher, R.; Carver, G.; Sieber, A.; Güdel, H.U.; Mutka, H. Exchange-coupling constants, spin density map, and Q dependence of the inelastic neutron scattering intensity in single-molecule magnets. Phys. Rev. B 2007, 75, 174438. [Google Scholar] [CrossRef]
- Borta, A.; Gillon, B.; Gukasov, A.; Cousson, A.; Luneau, D.; Jeanneau, E.; Ciumacov, I.; Sakiyama, H.; Tone, K.; Mikuriya, M. Local magnetic moments in a dinuclear Co2+ complex as seen by polarized neutron diffraction: Beyond the effective spin-1/2 model. Phys. Rev. B 2011, 83, 184429. [Google Scholar] [CrossRef]
- Zaharko, O.; Pregelj, M.; Zorko, A.; Podgajny, R.; Gukasov, A.; van Tol, J.; Klokishner, S.I.; Ostrovsky, S.; Delley, B. Source of magnetic anisotropy in quasi-two-dimensional XY {Cu4(tetrenH5)W(CN)8]4·7.2 H2O}n bilayer molecular magnet. Phys. Rev. B 2013, 87, 24406. [Google Scholar] [CrossRef]
- Ridier, K.; Gillon, B.; Gukasov, A.; Chaboussant, G.; Cousson, A.; Luneau, D.; Borta, A.; Jacquot, J.-F.; Checa, R.; Chiba, Y.; et al. Polarized Neutron Diffraction as a Tool for Mapping Molecular Magnetic Anisotropy: Local Susceptibility Tensors in CoII Complexes. Chem. Eur. J. 2016, 22, 724–735. [Google Scholar] [CrossRef] [PubMed]
- Ridier, K.; Mondal, A.; Boilleau, C.; Cador, O.; Gillon, B.; Chaboussant, G.; Le Guennic, B.; Costuas, K.; Lescouëzec, R. Polarized Neutron Diffraction to Probe Local Magnetic Anisotropy of a Low-Spin Fe(III) Complex. Angew. Chem. Int. Ed. 2016, 55, 3963–3967. [Google Scholar] [CrossRef] [PubMed]
- Evans, W.J.; Lee, D.S.; Rego, D.B.; Perotti, J.M.; Kozimor, S.A.; Moore, E.K.; Ziller, J.W. Expanding Dinitrogen Reduction Chemistry to Trivalent Lanthanides via the LnZ3/Alkali Metal Reduction System: Evaluation of the Generality of Forming Ln2(μ-η2:η2-N2) Complexes via LnZ3/K. J. Am. Chem. Soc. 2004, 126, 14574–14582. [Google Scholar] [CrossRef] [PubMed]
- Schnack, J. Influence of intermolecular interactions on magnetic observables. Phys. Rev. B 2016, 93, 54421. [Google Scholar] [CrossRef]
- Albuquerque, A.F.; Alet, F.; Corboz, P.; Dayal, P.; Feiguin, A.; Fuchs, S.; Gamper, L.; Gull, E.; Gürtler, S.; Honecker, A.; et al. The ALPS project release 1.3: Open-source software for strongly correlated systems. J. Magn. Magn. Mater. 2007, 310, 1187–1193. [Google Scholar] [CrossRef]
- Bauer, B.; Carr, L.D.; Evertz, L.D.; Feiguin, A.; Freire, J.; Fuchs, S.; Gamper, L.; Gukelberger, J.; Gull, E.; Guertler, S.; et al. The ALPS project release 2.0: Open source software for strongly correlated systems. J. Stat. Mech. Theory Exp. 2011, 2011, P05001. [Google Scholar] [CrossRef]
- Bain, G.A.; Berry, J.F. Diamagnetic Corrections and Pascal’s Constants. J. Chem. Educ. 2008, 85, 532. [Google Scholar] [CrossRef]

| H | Cr | Mn | Fe | Y | La | Nd | Sm | Gd | Tb | Dy | Ho | Er | Yb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.33 | 13.3 | 2.6 | 3.1 | 1.3 | 9 | 50 | 5922 | 49,700 | 23 | 994 | 65 | 159 | 35 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prša, K.; Nehrkorn, J.; Corbey, J.F.; Evans, W.J.; Demir, S.; Long, J.R.; Guidi, T.; Waldmann, O. Perspectives on Neutron Scattering in Lanthanide-Based Single-Molecule Magnets and a Case Study of the Tb2(μ-N2) System. Magnetochemistry 2016, 2, 45. https://doi.org/10.3390/magnetochemistry2040045
Prša K, Nehrkorn J, Corbey JF, Evans WJ, Demir S, Long JR, Guidi T, Waldmann O. Perspectives on Neutron Scattering in Lanthanide-Based Single-Molecule Magnets and a Case Study of the Tb2(μ-N2) System. Magnetochemistry. 2016; 2(4):45. https://doi.org/10.3390/magnetochemistry2040045
Chicago/Turabian StylePrša, Krunoslav, Joscha Nehrkorn, Jordan F. Corbey, William J. Evans, Selvan Demir, Jeffrey R. Long, Tatiana Guidi, and Oliver Waldmann. 2016. "Perspectives on Neutron Scattering in Lanthanide-Based Single-Molecule Magnets and a Case Study of the Tb2(μ-N2) System" Magnetochemistry 2, no. 4: 45. https://doi.org/10.3390/magnetochemistry2040045
APA StylePrša, K., Nehrkorn, J., Corbey, J. F., Evans, W. J., Demir, S., Long, J. R., Guidi, T., & Waldmann, O. (2016). Perspectives on Neutron Scattering in Lanthanide-Based Single-Molecule Magnets and a Case Study of the Tb2(μ-N2) System. Magnetochemistry, 2(4), 45. https://doi.org/10.3390/magnetochemistry2040045







