Evidence of Slow Magnetic Relaxation in Co(AcO)2(py)2(H2O)2
Abstract
:1. Introduction
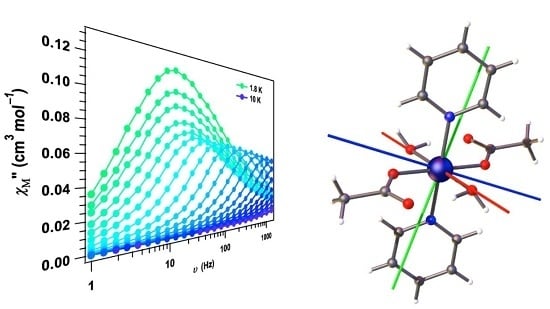
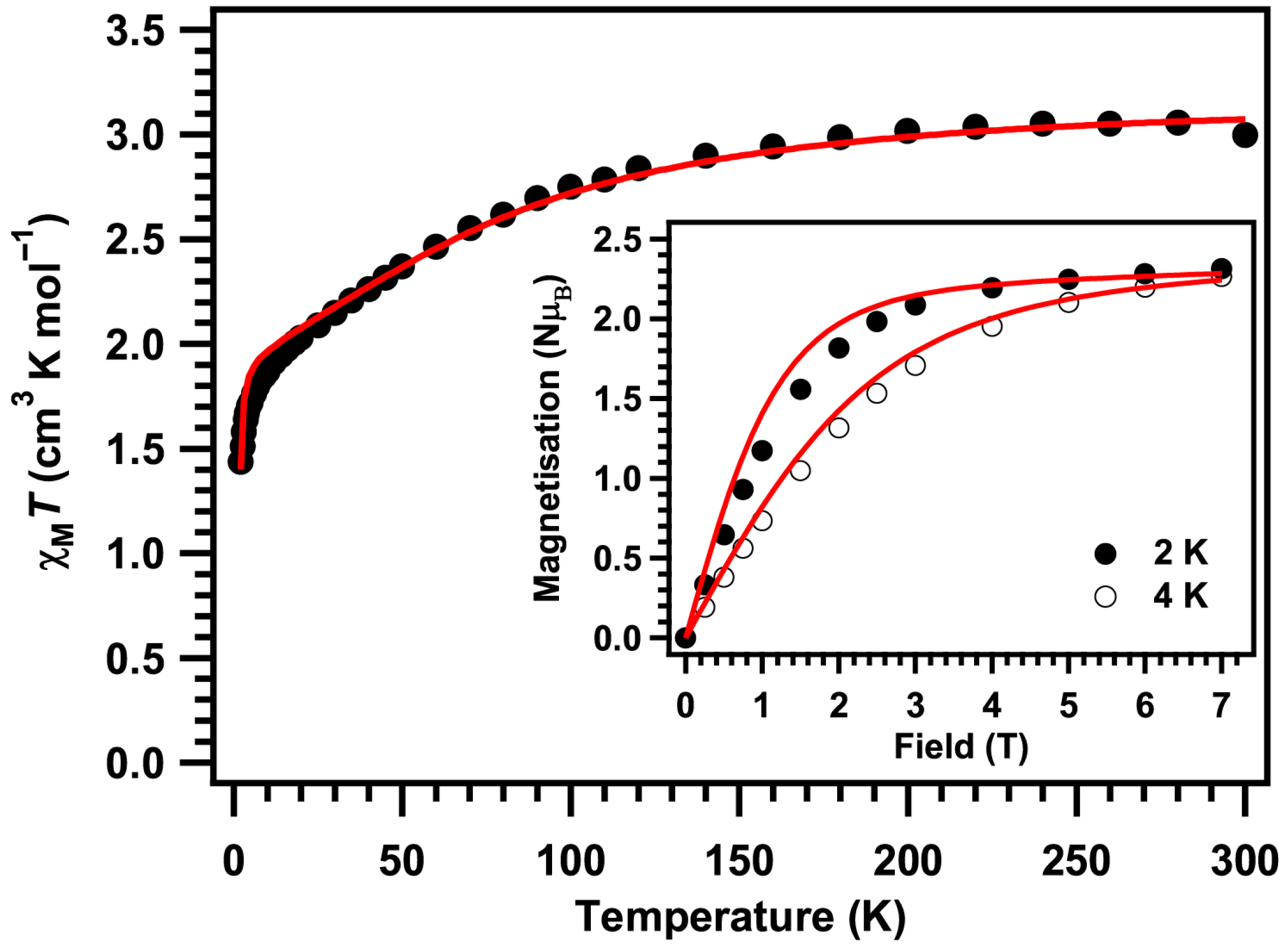
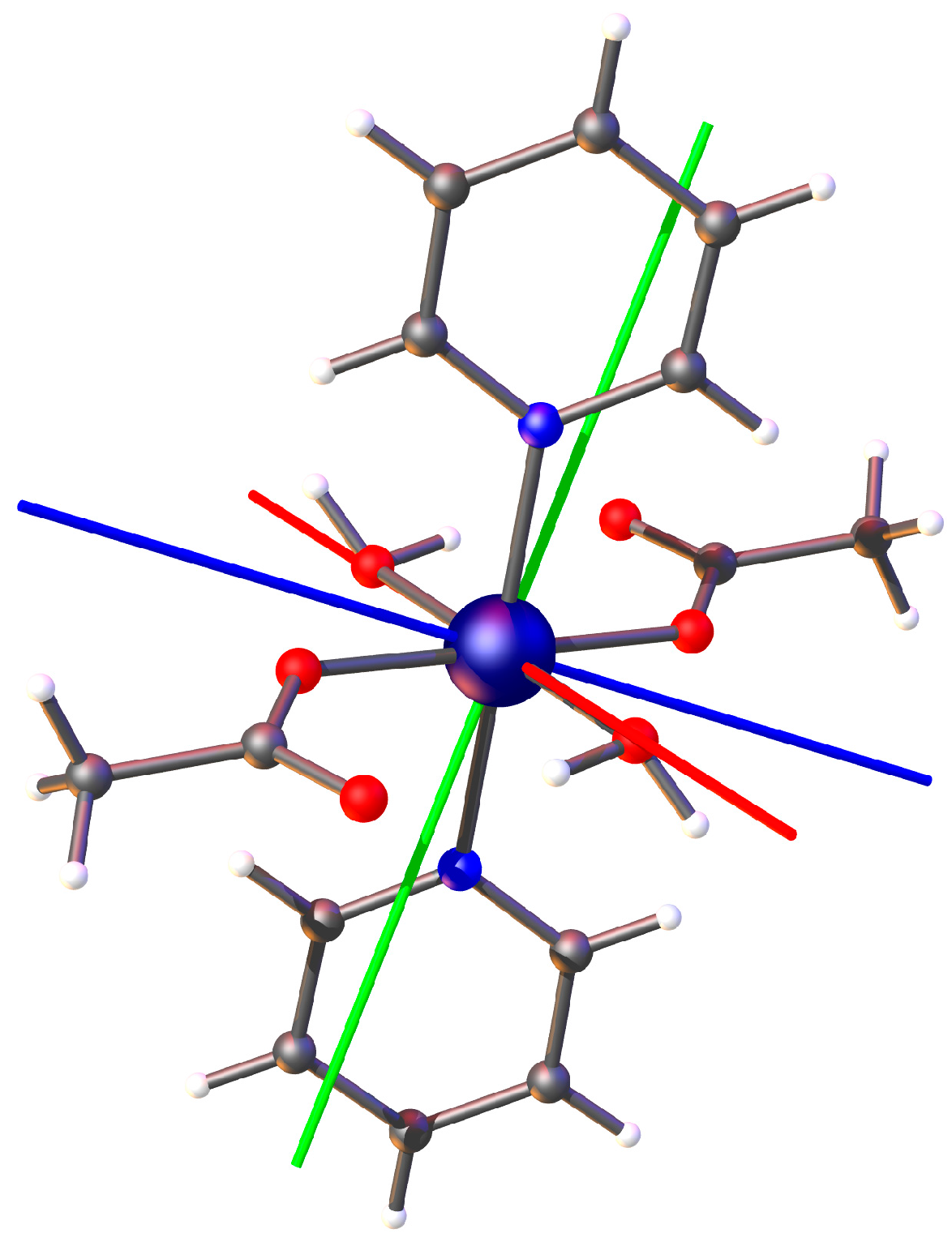
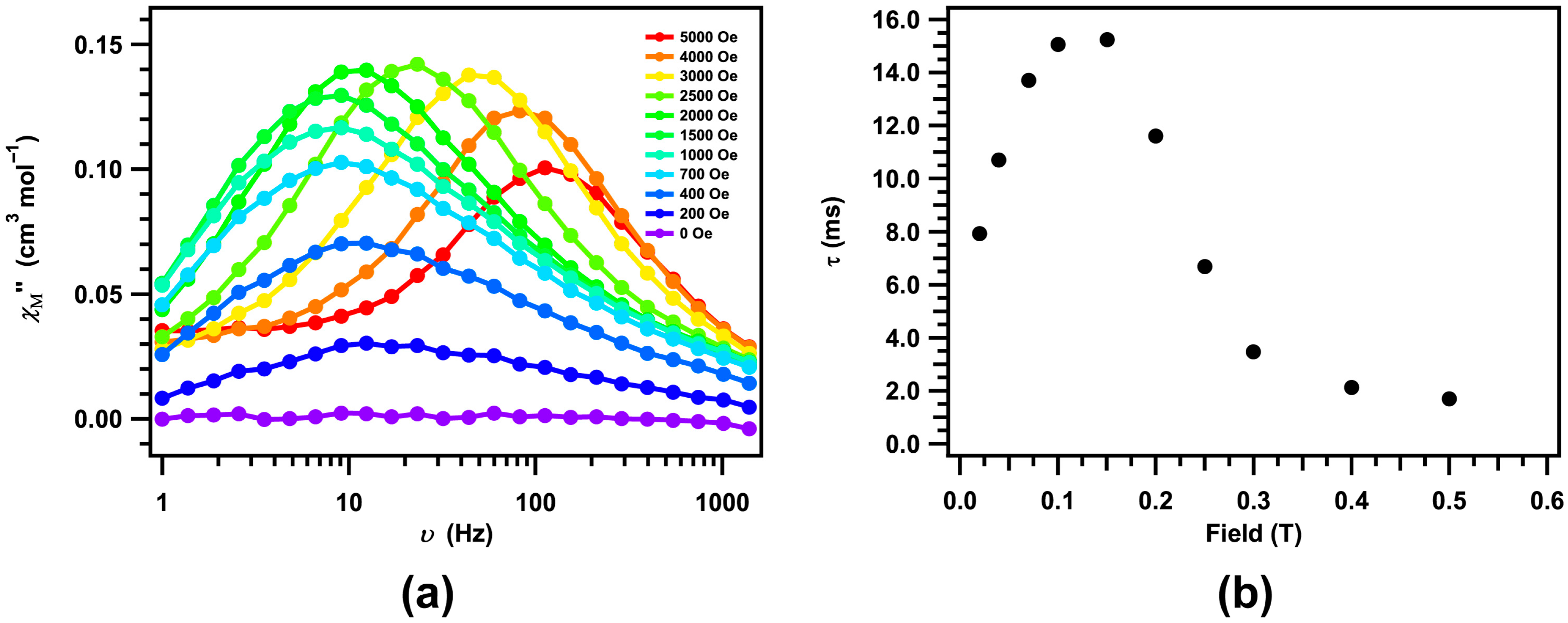
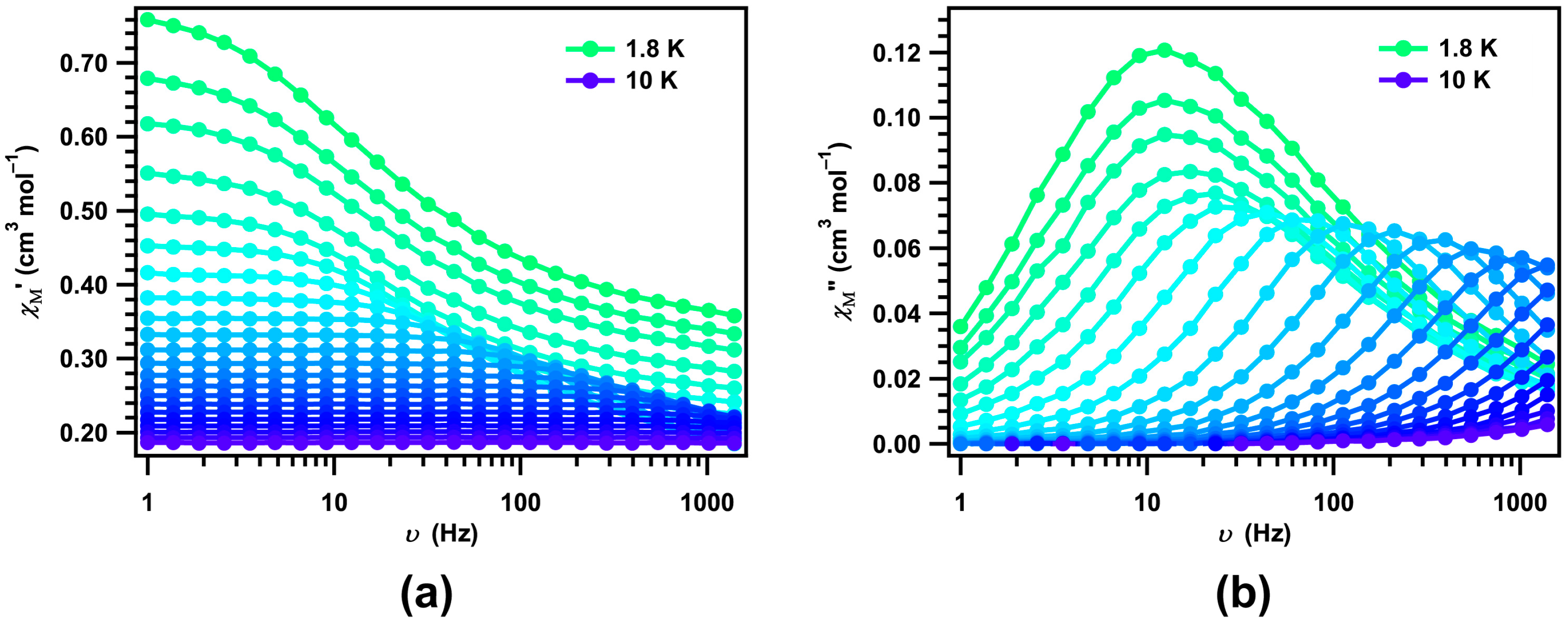
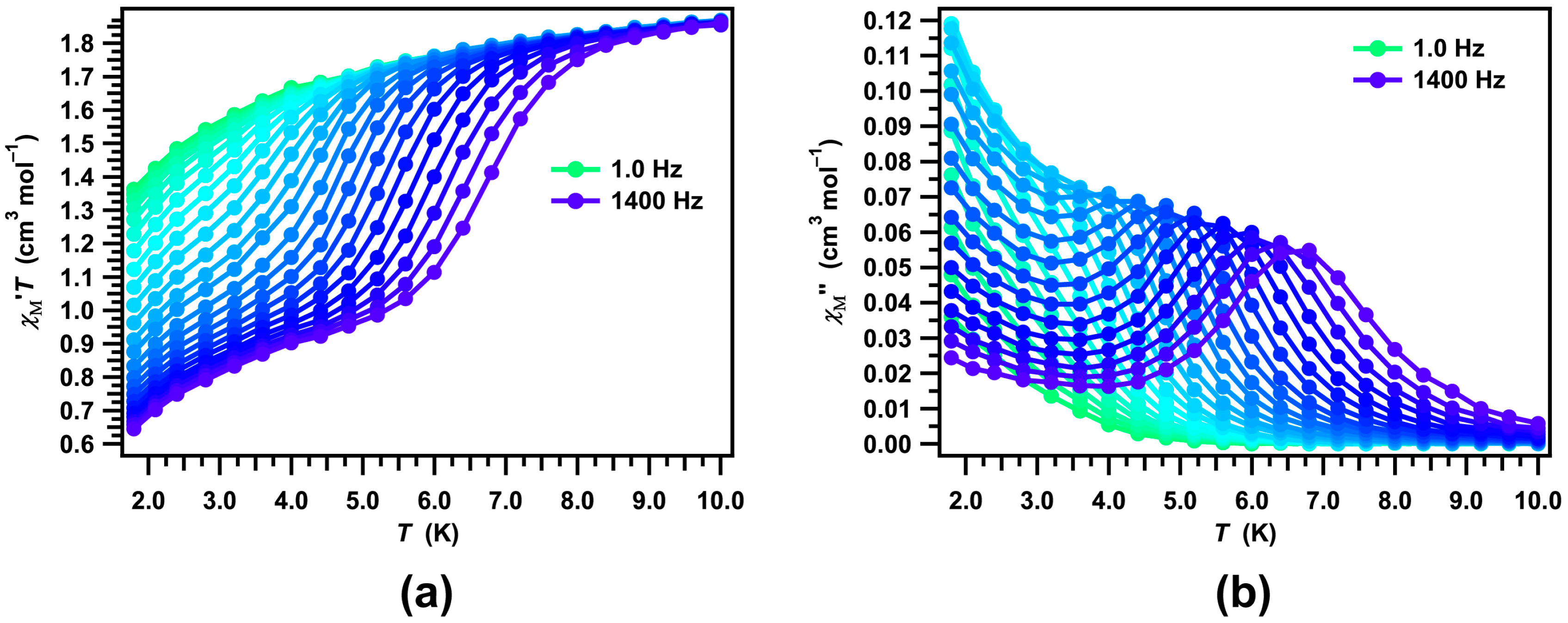
2. Results and Discussion
3. Materials and Methods
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SMM | Single-molecule magnet |
| ZFS | Zero-field splitting |
| EPR | Electron paramagnetic resonance |
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Lanthanide double-decker complexes functioning as magnets at the single-molecular level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Gregson, M.; Chilton, N.F.; Ariciu, A.-M.; Tuna, F.; Crowe, I.F.; Lewis, W.; Blake, A.J.; Collison, D.; McInnes, E.J.L.; Winpenny, R.E.P.; et al. A monometallic lanthanide bis (methanediimide) single molecule magnet with a large energy barrier and complex spin relaxation behavior. Chem. Sci. 2016, 7, 155–165. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic blocking in a linear iron(I) complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.J.; Chang, C.J.; Long, J.R. Slow-relaxation in a high-spin iron(II) complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef] [PubMed]
- Bar, A.K.; Pichon, C.; Gogoi, N.; Duhayon, C.; Ramasesha, S.; Sutter, J.-P. Single ion behaviour of heptacoordinated Fe(II) complexes: on the importance of supramolecular organization. Chem. Commun. 2015, 51, 3616–3619. [Google Scholar] [CrossRef] [PubMed]
- Craig, G.A.; Murrie, M. 3d single ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef] [PubMed]
- Kahn, O. Molecular Magnetism; Wiley-Blackwell: New York, NY, USA, 1993. [Google Scholar]
- Rechkemmer, Y.; Breitgoff, F.D.; van der Meer, M.; Atanasov, M.; Hake, M.; Orlita, M.; Neugetsauer, P.; Neese, F.; Sarkar, B.; van Slageren, J. A four-coordinate cobalt(II) single-ion magnet with coercivity and very high energy barrier. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef] [PubMed]
- Titos-Padilla, S.; Ruiz, J.; Herrera, J.M.; Brechin, E.K.; Wernsdorfer, W.; Lloret, F.; Colacio, E. New relativistic ANO basis sets for transition metal atoms. Inorg. Chem. 2013, 52, 9620–9626. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Long, J.R. Slow magnetic relaxation at zero field in the tetrahedral complex [Co(SPh)4]2-. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef] [PubMed]
- Buchholz, A.; Eseola, A.O.; Plass, W. Slow magnetic relaxation in mononuclear tetrahedral cobalt(II) complexes with 2-(1H-imidazol-2-yl)phenol based ligands. Comptes Rendus Chim. 2012, 15, 929–936. [Google Scholar] [CrossRef]
- Zhu, Y.-Y.; Cui, C.; Zhang, Y.-Q.; Jia, J.-H.; Guo, X.; Gao, C.; Qian, K.; Jiang, S.-D.; Wang, B.-W.; Wang, Z.-M.; et al. Zero-field slow magnetic relaxation from single Co(II) ion: a transition metal single-molecule magnet with high anisotropy barrier. Chem. Sci. 2013, 4, 1802–1806. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Telser, J.; Long, J.R. Slow magnetic relaxation in the tertrahedral cobalt(II) complexes [Co(EPh)4]2- (E=O, S, Se). Polyhedron 2013, 64, 209–217. [Google Scholar] [CrossRef]
- Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.E.; Varzatskii, O.A.; Voloschin, Y.Z.; Winpenny, R.E.P. A trigonal prismatic mononuclear cobalt(II) complex showing single-molecule magnet behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef] [PubMed]
- Boča, R.; Miklovič, J.; Titiš, J. Simple mononuclear cobalt(II) complex: A single-molecule magnet showing two slow relaxation processes. Inorg. Chem. 2014, 53, 2367–2369. [Google Scholar] [CrossRef] [PubMed]
- Saber, M.R.; Dunbar, K.R. Ligands effects on the magnetic anisotropy of tetrahedral cobalt complexes. Chem. Commun. 2014, 50, 12266–12269. [Google Scholar] [CrossRef] [PubMed]
- Fataftah, M.S.; Zadrozny, J.M.; Rogers, D.M.; Freedman, D.E. A mononuclear transition metal single-molecule magnet in a nuclear spin-free ligand environment. Inorg. Chem. 2014, 53, 10716–10721. [Google Scholar] [CrossRef] [PubMed]
- Cucos, P.; Tuna, F.; Sorace, L.; Matei, I.; Maxim, C.; Shova, S.; Gheorghe, R.; Caneschi, A.; Hillebrand, M.; Andruh, M. Magnetic and luminescent binuclear double-stranded helicates. Inorg. Chem. 2014, 53, 7738–7747. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Liu, J.; Piro, N.A.; Chang, C.J.; Hill, S.; Long, J.R. Slow magnetic relaxation in a pseudotetrahedral cobalt(II) complex with easy-plane anisotropy. Chem. Commun. 2012, 48, 3927–3929. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Liu, T.; Wu, D.; Cheng, J.; Ouyang, Z.W.; Duan, C. Field-induced slow-relaxation of magnetization in a tetrahedral Co(II) complex with easy plane anisotropy. Dalton Trans. 2013, 42, 15326–15331. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, S.; Upadhyay, A.; Singh, S.K.; Langley, S.K.; Walsh, J.P.S.; Murray, K.S.; Rajaraman, G.; Shanmugam, M. A synthetic strategy for switching the single ion anisotropy in tetrahedral cobalt(II) complexes. Chem. Commun. 2014, 51, 3739–3742. [Google Scholar] [CrossRef] [PubMed]
- Colacio, E.; Ruiz, J.; Cremades, E.; Krzystek, J.; Carretta, S.; Cano, J.; Guidi, T.; Wernsdorfer, W.; Brechin, E.K. Slow magnetic relaxation in a CoII–YIII single-ion magnet with positive axial zero-field splitting. Angew. Chem. Int. Ed. 2013, 52, 9130–9134. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coca, S.; Urtizberea, A.; Cremades, E.; Alonso, P.J.; Camón, A.; Ruiz, E.; Luis, F. Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, K.S.; Dreiser, J.; Weihe, H.; Sibille, R.; Johannesen, H.V.; Sørensen, M.A.; Nielsen, B.E.; Sigrist, M.; Mutka, H.; Rols, S.; et al. Design of single-molecule magnets: Insufficiency of the anisotropy barrier as the sole criterion. Inorg. Chem. 2015, 54, 7600–7606. [Google Scholar] [CrossRef] [PubMed]
- Bailey, A.; Griffith, W.P.; Leung, D.W.C.; White, A.J.P.; Williams, D.J. Ozonolysis for the preparation of high-oxidation state transition metal complexes, and the X-ray crystal structure of Co(py)2(OAc)2(H2O)2. Polyhedron 2004, 23, 2631–2636. [Google Scholar] [CrossRef]
- Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.F.; Delcey, M.G.; de Vico, L.; Fdez Galván, I.; Ferré, N.; Frutos, L.M.; Gagliardi, L.; et al. MOLCAS 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table. Comp. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef] [PubMed]
- Figgis, B.N.; Hitchman, M.A. Ligand Field Theory and Its Applications, 1st ed.; Wiley-VCH: New York, NY, USA, 2000. [Google Scholar]
- Lloret, F.; Julve, M.; Cano, J.; Ruiz-García, R.; Pardo, E. Magnetic properties of six-coordinated high-spin cobalt(II) complexes: Theoretical background and its application. Inorg. Chim. Acta 2008, 361, 3432–3445. [Google Scholar] [CrossRef]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comp. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Oxford University Press: Oxford, UK, 1970. [Google Scholar]
- Pointillart, F.; Golhen, S.; le Guennic, B.; Guizouarn, T.; Ouahab, L.; Cador, O. Magnetic memory in an isotopically enriched and magnetically isolated mononuclear dysprosium complex. Angew. Chem. Int. Ed. Engl. 2015, 54, 1504–1507. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.O. Main group atoms and dimers studied with a new relativistic ANO basis set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.O. New relativistic ANO basis sets for transition metal atoms. J. Phys. Chem. A 2005, 109, 6575–6579. [Google Scholar] [CrossRef] [PubMed]
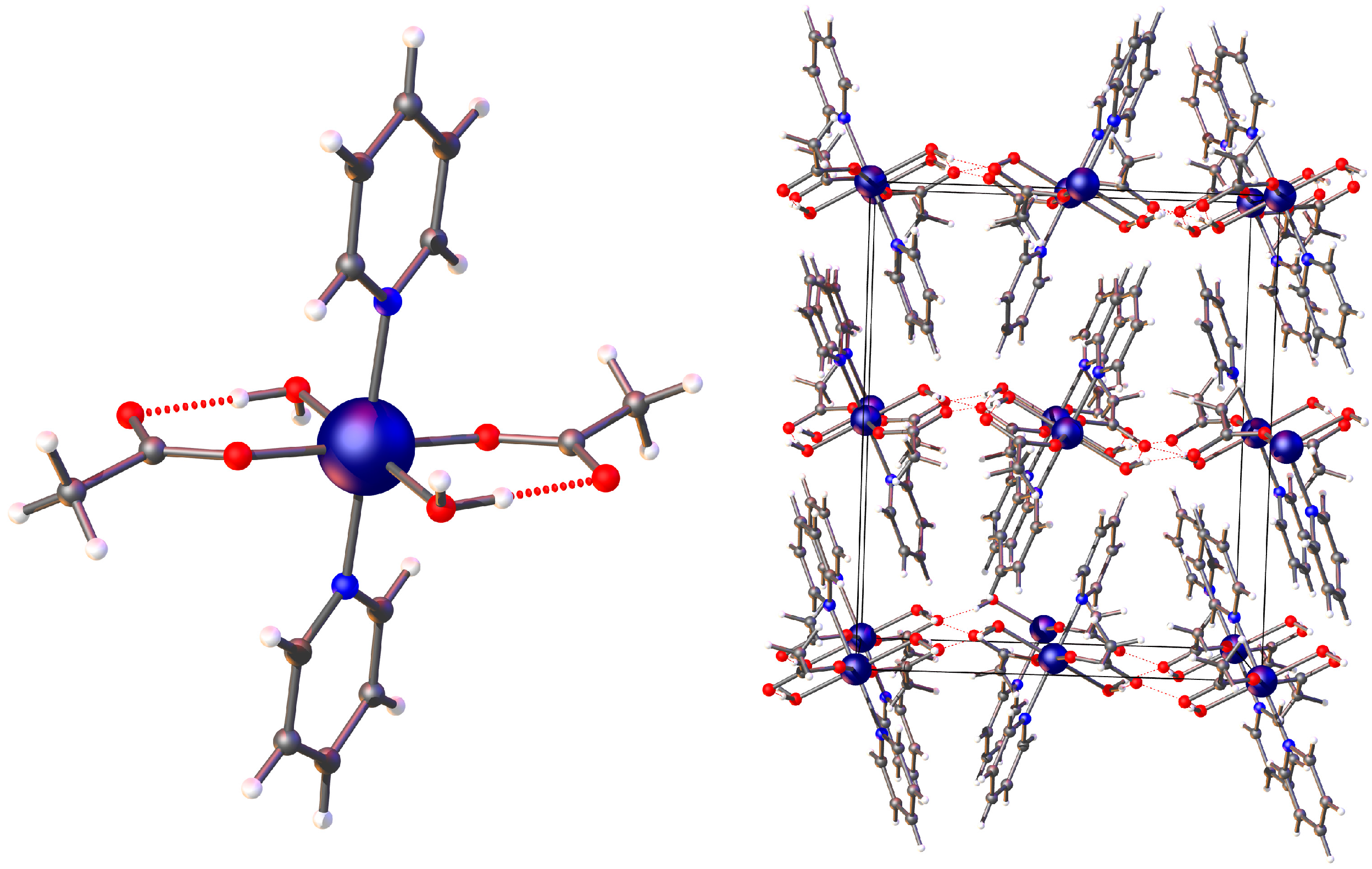

| Bond Length (Å) | Angle (°) | ||
|---|---|---|---|
| Co1–O1 | 2.076 (2) | O1–Co1–O2 | 88.78 (8) |
| Co1–O3 | 2.121 (2) | O1–Co1–N1 | 90.54 (10) |
| Co1–N1 | 2.159 (3) | O2–Co1–N1 | 92.69 (10) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walsh, J.P.S.; Bowling, G.; Ariciu, A.-M.; Jailani, N.F.M.; Chilton, N.F.; Waddell, P.G.; Collison, D.; Tuna, F.; Higham, L.J. Evidence of Slow Magnetic Relaxation in Co(AcO)2(py)2(H2O)2. Magnetochemistry 2016, 2, 23. https://doi.org/10.3390/magnetochemistry2020023
Walsh JPS, Bowling G, Ariciu A-M, Jailani NFM, Chilton NF, Waddell PG, Collison D, Tuna F, Higham LJ. Evidence of Slow Magnetic Relaxation in Co(AcO)2(py)2(H2O)2. Magnetochemistry. 2016; 2(2):23. https://doi.org/10.3390/magnetochemistry2020023
Chicago/Turabian StyleWalsh, James P. S., Graeme Bowling, Ana-Maria Ariciu, Nur F. M. Jailani, Nicholas F. Chilton, Paul G. Waddell, David Collison, Floriana Tuna, and Lee J. Higham. 2016. "Evidence of Slow Magnetic Relaxation in Co(AcO)2(py)2(H2O)2" Magnetochemistry 2, no. 2: 23. https://doi.org/10.3390/magnetochemistry2020023
APA StyleWalsh, J. P. S., Bowling, G., Ariciu, A.-M., Jailani, N. F. M., Chilton, N. F., Waddell, P. G., Collison, D., Tuna, F., & Higham, L. J. (2016). Evidence of Slow Magnetic Relaxation in Co(AcO)2(py)2(H2O)2. Magnetochemistry, 2(2), 23. https://doi.org/10.3390/magnetochemistry2020023