The Advancing Understanding of Magnetorheological Fluids and Elastomers: A Comparative Review Analyzing Mechanical and Viscoelastic Properties
Abstract
1. Introduction
2. Magneto-Mechanical Characterizations
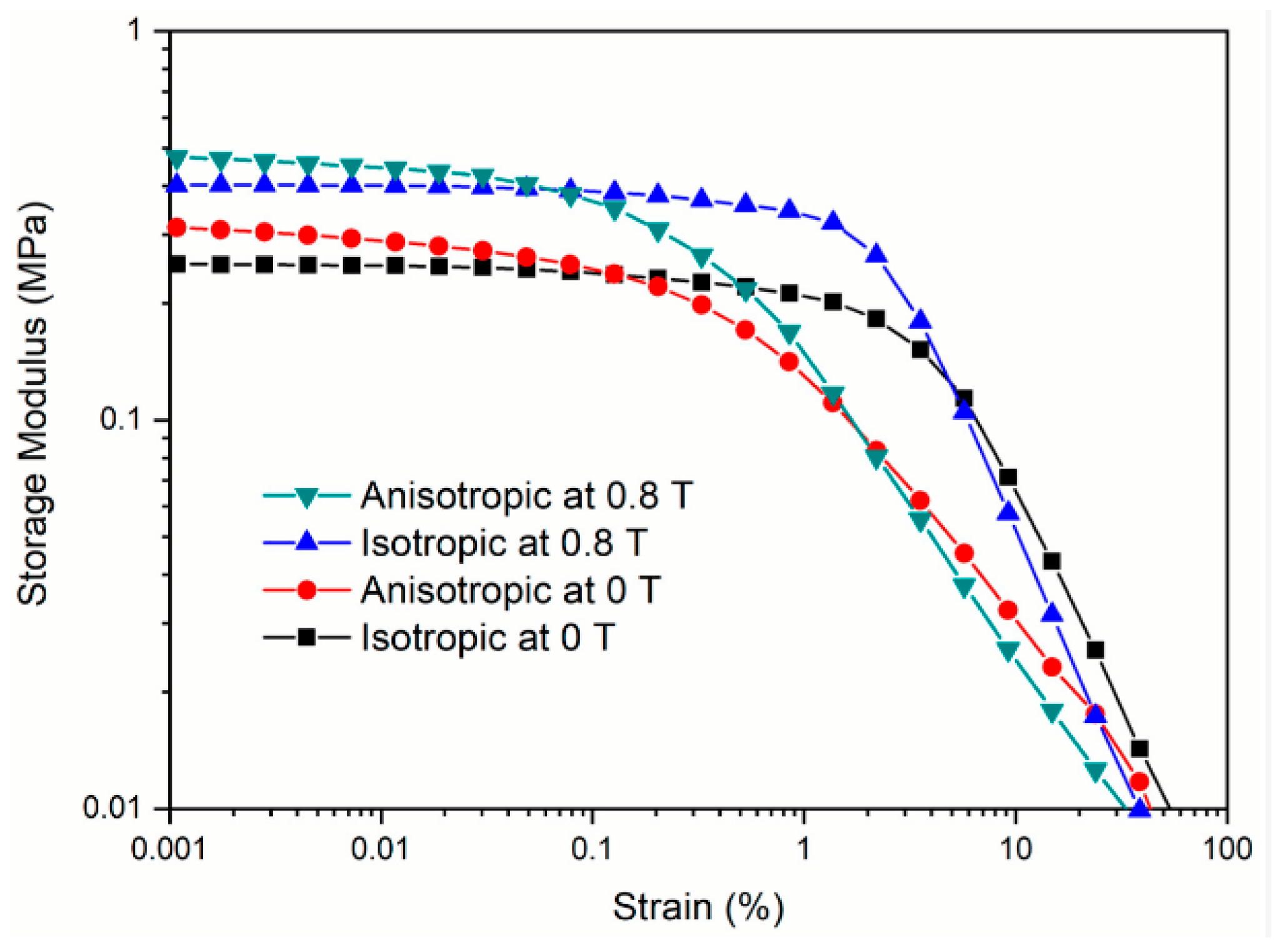
2.1. Strain Amplitude Effect
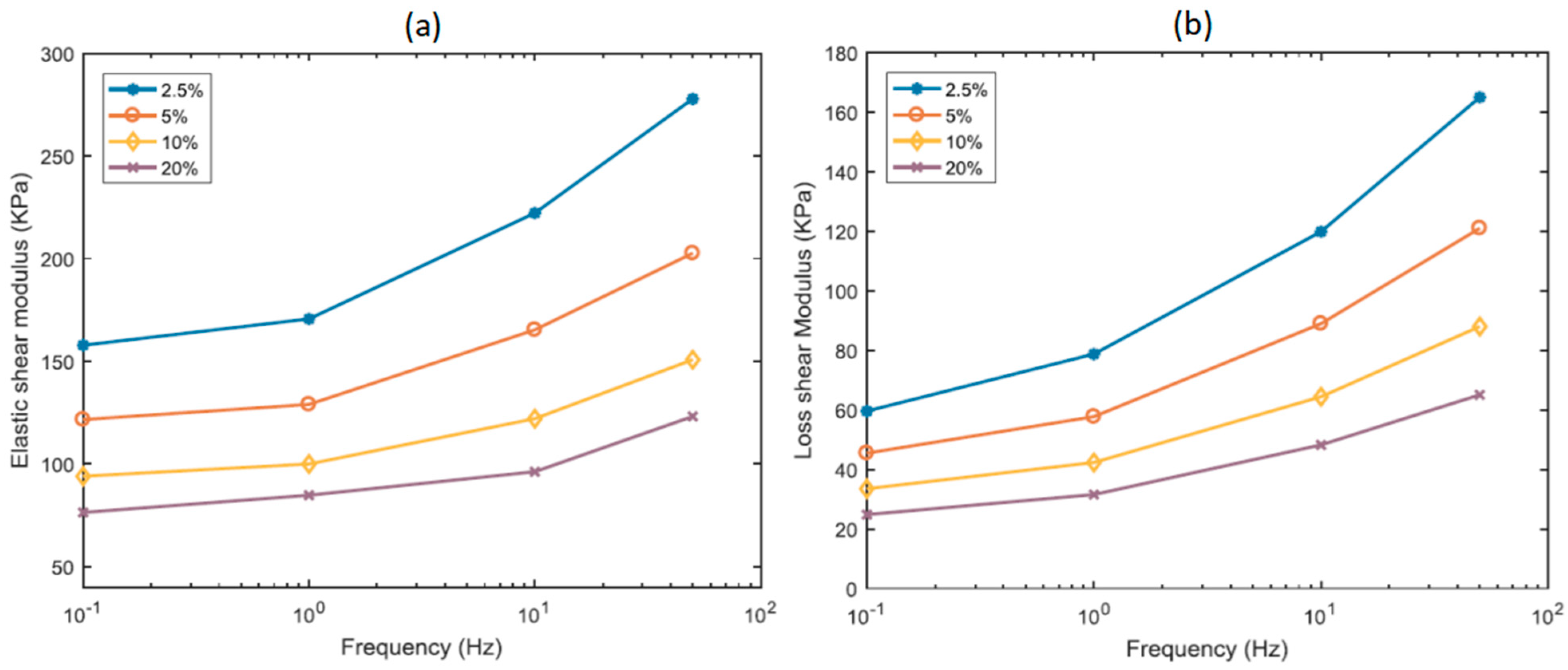
2.2. Frequency Effect
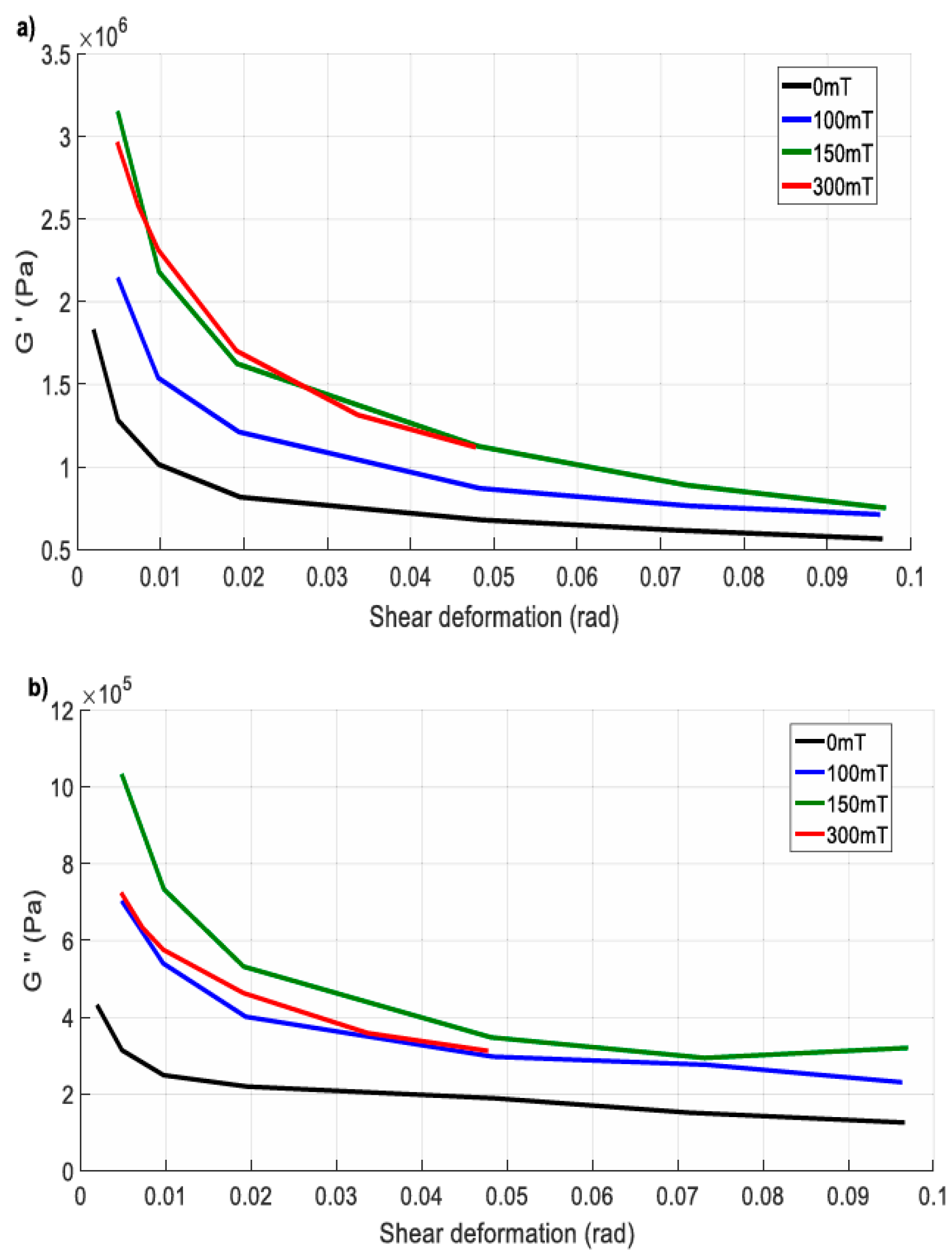
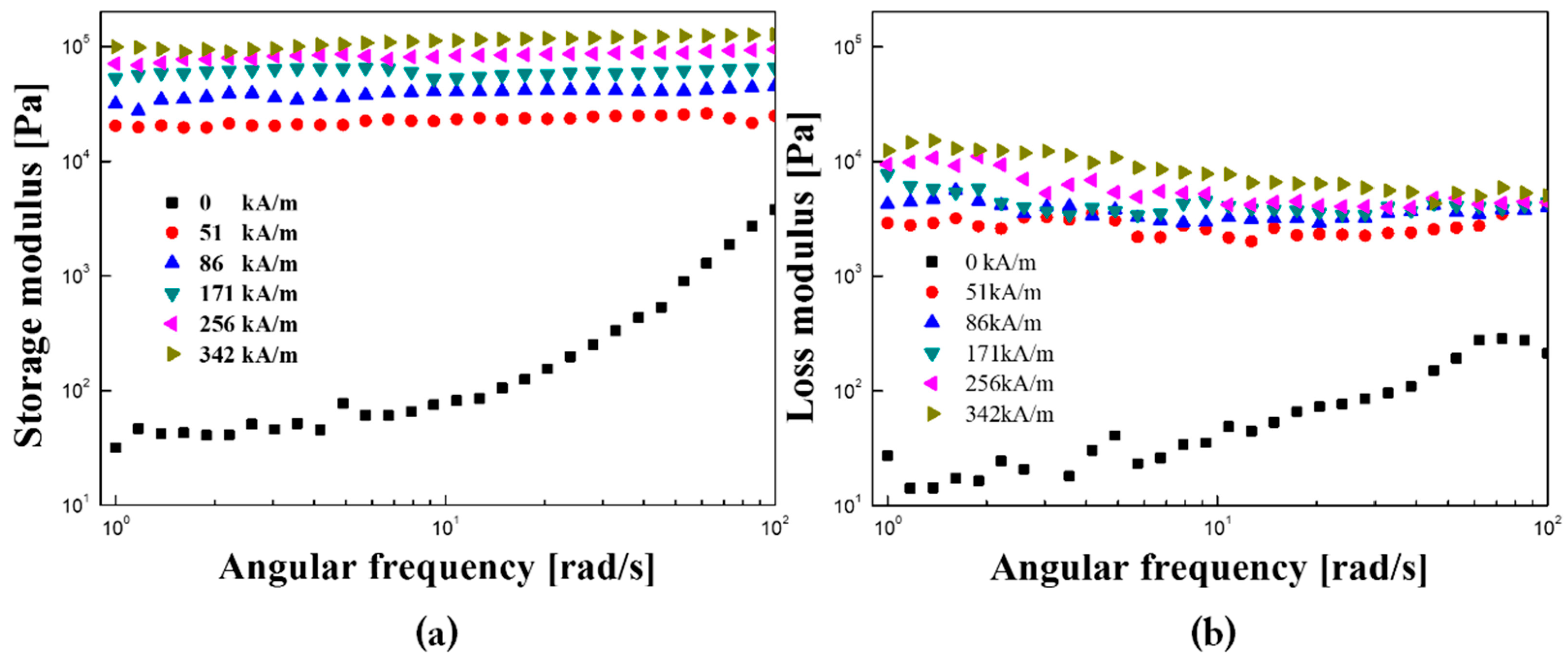
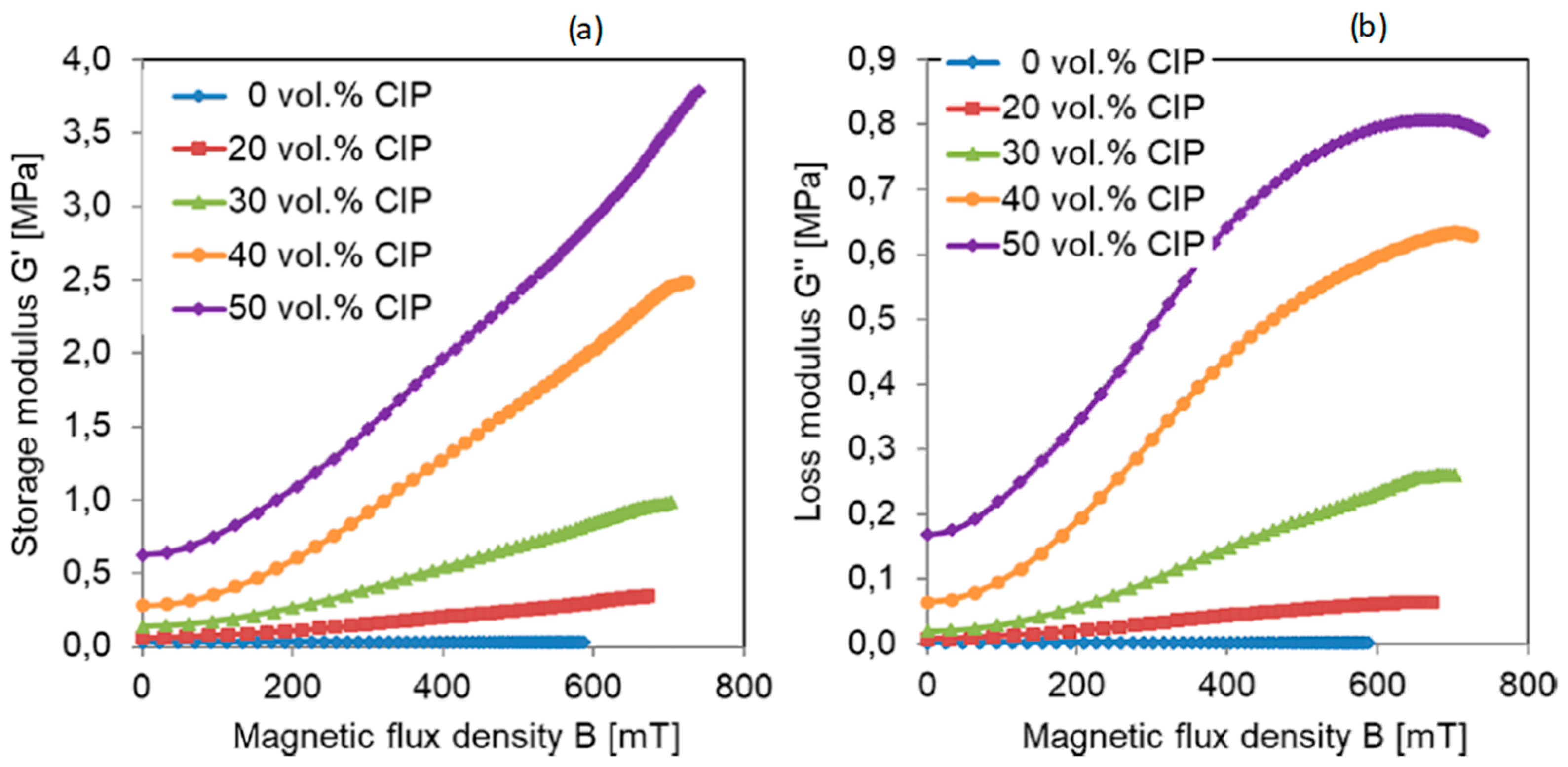
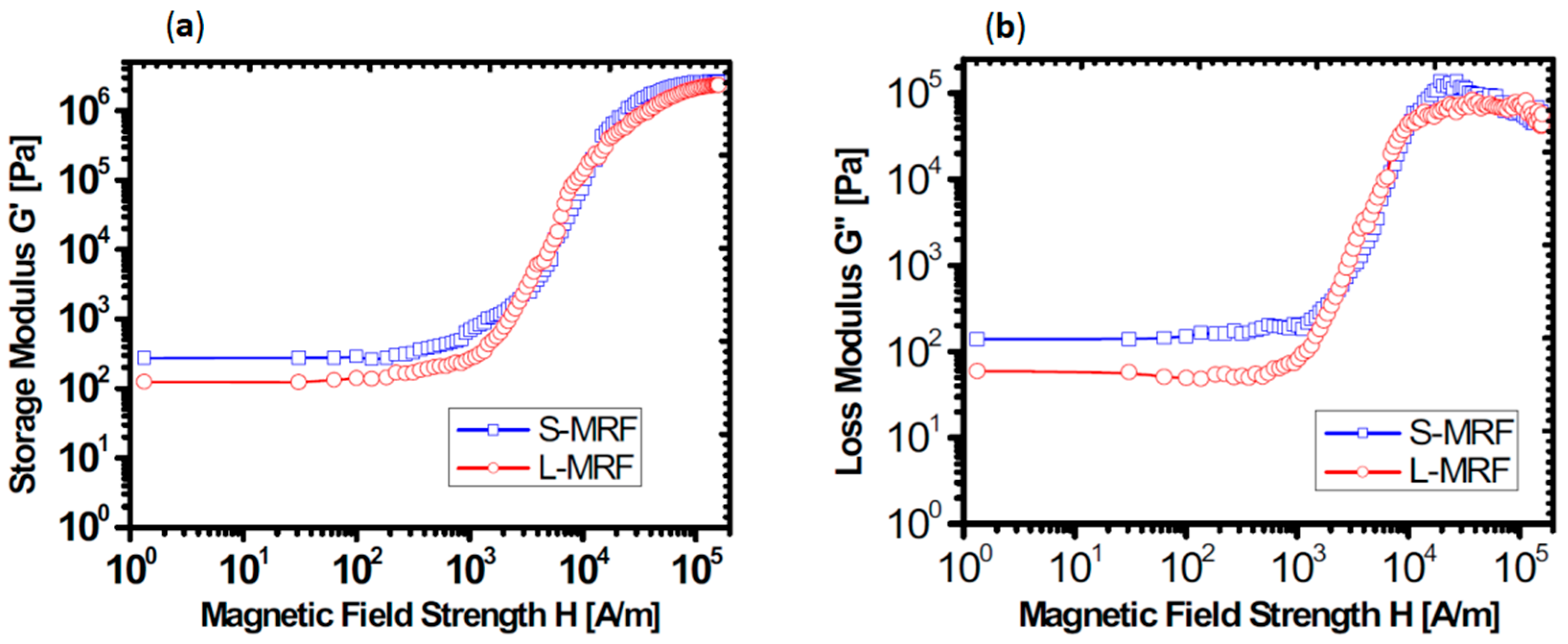
2.3. Magnetic Flux Density Effect
2.4. Temperature Effect
3. MR Elastomers’ Major Advantages
3.1. A Solution Without Sediments and Deposits
3.2. A Solution Without Sealing Requirements
3.3. Rapid Response Time of MR Elastomers
3.4. Improved Durability
3.5. Relatively Low Weight
3.6. Reduced Energy Consumption
3.7. Enhanced Response in Stiffness Control
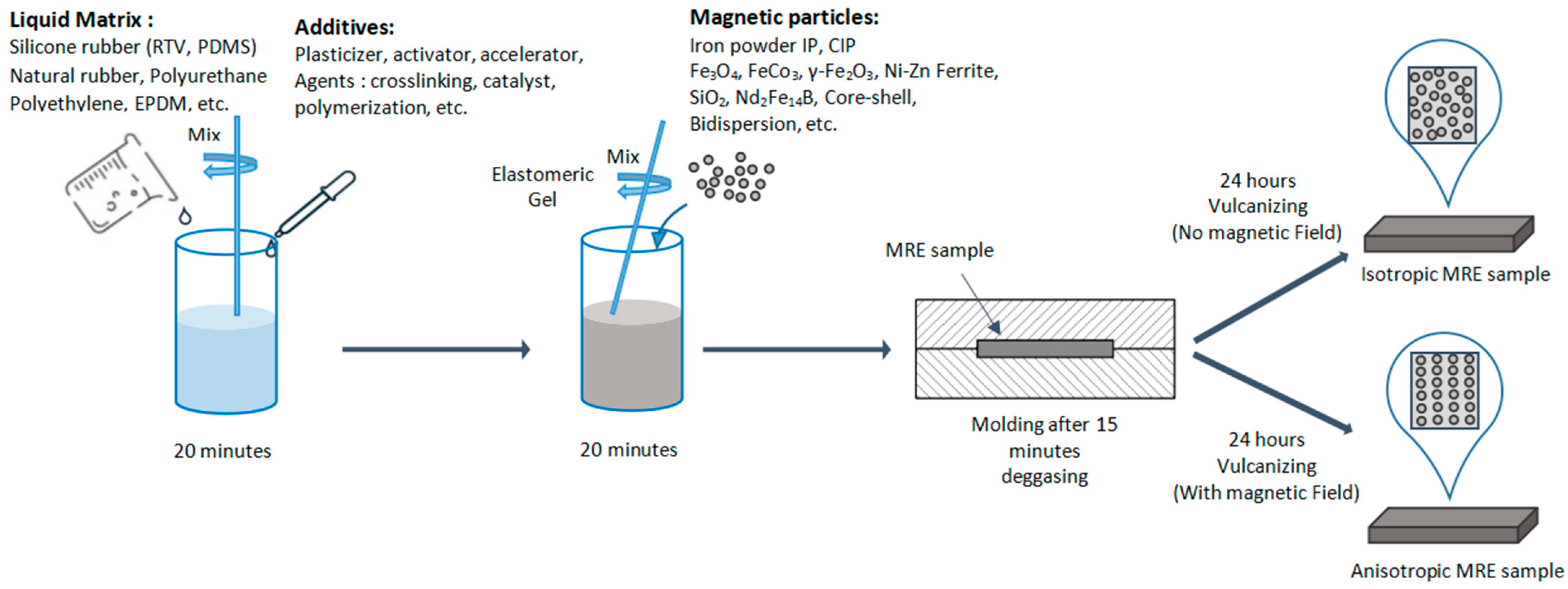
3.8. Anisotropic Structure
3.9. MR Effect of MR Elastomers
3.10. Magnetostrictive Effect
4. MR Elastomers’ Limitations
4.1. Incompatibility Between Magnetic Particles and Elastomer Matrices
4.2. Deterioration Sensitivity: Another MR Elastomer Obstacle
4.3. Oxidation Issues in Elastomers
5. MR Fluids’ Major Positive Characteristics
5.1. Viscosity Control
5.2. MR Fluids Rapid Response Time
5.3. MR Effect of MRFs: A Key Characteristic
5.4. Wide Operating Temperature Range
6. MR Fluids’ Limitations
6.1. Sedimentation Issue
6.2. Agglomeration Effect
6.3. Sealing Issues and Environmental Contamination
6.4. Thickening Phenomenon
6.5. High Density
6.6. High Cost
6.7. Particle Oxidation/Corrosion Issue
- Loss of magnetic properties: Iron oxides exhibit a significantly lower-saturation magnetization (MS) compared to ferromagnetic component-based particles such as CIP particles.
- Decrease in mechanical performance and MR effect due to the reduced magnetic properties of the particles.
- Reduction in yield stress induced by the magnetic field, which decreases as the degree of oxidation increases.
- Increase in friction and leakage in a zero magnetic field.
- Increase in fluid viscosity without a magnetic field.
- Changes in particle surface from very smooth to very rough have also been observed.
- Increase in the mass of magnetic particles due to the presence of oxides.
- Formation of a stabilized oxidation film on the particle surface.
- The type of dispersing liquid influences the level of particle oxidation.
7. Other Comparative Elements
7.1. Structure and Composition
7.2. Pre-Elasticity and Post-Elasticity Regimes
7.3. MR Effect
7.4. Response Time
7.5. Supported Stress Levels
7.6. Application Areas and Opportunities
8. Other MR Behavior Mechanisms
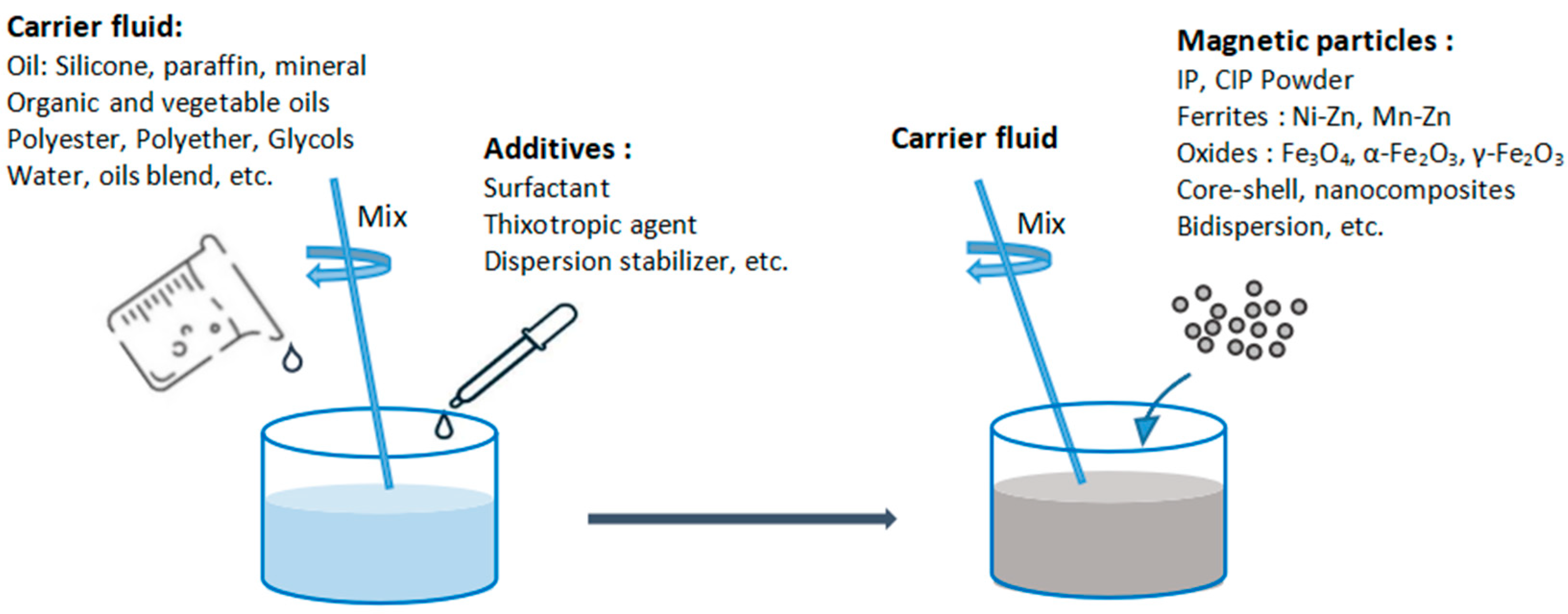
8.1. Matrix MRE and Carrier Fluid
8.2. Charged Particles and Dispersed Phases
- Low residual magnetization, which represents the remaining magnetic effect on ferromagnetic materials after the magnetic field is removed.
- High permeability, which measures the material’s magnetization relative to an applied magnetic field.
- High saturation magnetization, which corresponds to the maximum magnetization achievable by the material.
8.3. Spherical Carbonyl Iron: Ideal Selection for MR Materials
8.4. Performance Optimization Through Additives
- Opening up application possibilities based on MREs, offering sensing and actuation capabilities such as changes in resistance and capacitance [4].
9. Conclusions
- The various types of carrier fluids, magnetic particles, and additives and their influence on the properties of these materials have been discussed.
- An outline is given of common magneto-mechanical characterizations of MREs and MRFs, including dynamic tests, particularly shear, compression, and tension tests, conducted with and without a magnetic field.
- Among the reported studies, various experimental methods, such as rotational rheometry, double-lap shear tests, and dynamic mechanical analysis (DMA), were used. However, hysteresis characteristics, whether in stress–strain or force–displacement, were less frequently reported in the reviewed studies.
- A detailed account was given of the influence of operating conditions, such as strain amplitude and excitation frequency. Furthermore, a wide range of magnetic field intensities (magnetic sweep) and operating temperatures has been explored.
- The results discussed in these studies have generally been reported in terms of storage modulus, loss modulus, and loss factor Tan δ. Additionally, the constant shear magnetorheological properties of MRFs have been evaluated through yield stress and shear viscosity.
- A synthesis was presented in the form of a comparative analysis between MRFs and MREs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rabinow, J. The Magnetic Fluid Clutch. Electr. Eng. 1948, 67, 1308–1315. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C. A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 1996, 5607–5614. [Google Scholar]
- Carlson, J.D.; Jolly, M.R. MR fluid, foam and elastomer devices. Mechatronics 2000, 10, 555–569. [Google Scholar] [CrossRef]
- Bastola, A.K.; Hossain, M. A review on magneto-mechanical characterizations of magnetorheological elastomers. Compos. Part B 2020, 200, 108348. [Google Scholar] [CrossRef]
- Carlson, J.D.; Catanzarite, D.M.; Clair, K.A.S. Commercial magneto-rheological fluid devices. Int. J. Mod. Phys. B 1996, 10, 2857–2865. [Google Scholar] [CrossRef]
- Phulé, P.P. Synthesis of Novel Magnetorheological Fluids. MRS Bull. 1998, 23, 23–25. [Google Scholar] [CrossRef]
- Jolly, M.R.; Bender, J.W.; Carlson, J.D. Properties and Applications of Commercial Magnetorheological Fluids. J. Intell. Mater. Syst. Struct. 1999, 10, 5–13. [Google Scholar] [CrossRef]
- Rinaldi, C.; Chaves, A.; Elborai, S.; He, X.T.; Zahn, M. Magnetic fluid rheology and flows. Curr. Opin. Colloid Interface Sci. 2005, 10, 141–157. [Google Scholar] [CrossRef]
- Bell, R.C.; Miller, E.D.; Karli, J.O.; Vavreck, A.N.; Zimmerman, D.T. Influence of particle shape on the properties of Magnetorheological fluids. Int. J. Mod. Phys. B 2007, 21, 5018–5025. [Google Scholar] [CrossRef]
- De Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological fluids: A review. Soft Matter 2011, 7, 3701. [Google Scholar] [CrossRef]
- Rigbi, Z.; Jilken, L. The response of an elastomer filled with soft ferrite to mechanical and magnetic influences. J. Magn. Magn. Mater. 1983, 37, 267–276. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Li, W.; Du, H. A state-of-the-art review on magnetorheological elastomer devices. Smart Mater. Struct. 2014, 23, 123001. [Google Scholar] [CrossRef]
- Morillas, J.R.; de Vicente, J. Magnetorheology: A review. Soft Matter 2020, 16, 9614. [Google Scholar] [CrossRef] [PubMed]
- Kallio, M. The Elastic and Damping Properties of Magnetorheological Elastomers; VTT: Espoo, Finland, 2005; Volume 3, p. 87. [Google Scholar]
- Moreno, M.A.; Gonzalez-Rico, J.; Lopez-Donaire, M.L.; Arias, A.; Garcia-Gonzalez, D. New experimental insights into magneto-mechanical rate dependences of magnetorheological elastomers. Compos. Part B 2021, 224, 109148. [Google Scholar] [CrossRef]
- Bellan, C.; Bossis, G. Field dependence of viscoelastic properties of MR elastomers. Int. J. Mod. Phys. B 2002, 16, 2447–2453. [Google Scholar] [CrossRef]
- Zhou, G.Y. Shear properties of a magnetorheological elastomer. Smart Mater. Struct. 2003, 12, 139. [Google Scholar] [CrossRef]
- Gong, X.L.; Zhang, X.Z.; Zhang, P.Q. Fabrication and characterization of isotropic magnetorheological elastomers. Polym. Test. 2005, 24, 669–676. [Google Scholar] [CrossRef]
- Coquelle, E.; Bossis, G.; Szabo, D.; Giulieri, F. Micromechanical analysis of an elastomer filled with particles organized in chain-like structure. J. Mater. Sci. 2006, 41, 5941–5953. [Google Scholar] [CrossRef]
- Li, J.; Gong, X.; Xu, Z.B.; Jiang, W. The effect of pre-structure process on magnetorheological elastomer performance. Int. J. Mater. Res. 2008, 99, 1358–1364. [Google Scholar] [CrossRef]
- Agirre-Olabide, I.; Berasategui, J.; Elejabarrieta, M.J.; Bou-Ali, M.M. Characterization of the linear viscoelastic region of magnetorheological elastomers. J. Intell. Mater. Syst. Struct. 2014, 25, 2074–2081. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Y.; Li, J.; Gu, X. A hysteresis model for dynamic behaviour of magnetorheological elastomer base isolator. Smart Mater. Struct. 2016, 25, 055029. [Google Scholar] [CrossRef]
- Sapouna, K.; Xiong, Y.P.; Shenoi, R.A. Dynamic mechanical properties of isotropic/anisotropic silicon magnetorheological elastomer composites. Smart Mater. Struct. 2017, 26, 115010. [Google Scholar] [CrossRef]
- Perales-Martínez, I.A.; Palacios-Pineda, L.M. Enhancement of a magnetorheological PDMS elastomer with CIP particles. Polym. Test. 2017, 57, 78–86. [Google Scholar] [CrossRef]
- Khanouki, M.A.; Sedaghati, R.; Hemmatian, M. Experimental characterization and microscale modeling of isotropic and anisotropic magnetorheological elastomers. Compos. Part B 2019, 176, 107311. [Google Scholar] [CrossRef]
- Bastola, A.K.; Li, L. A new type of vibration isolator based on magnetorheological elastomer. Mater. Des. 2018, 157, 431–436. [Google Scholar] [CrossRef]
- Bellelli, A.; Spaggiari, A. Magneto-mechanical characterization of magnetorheological elastomers. J. Intell. Mater. Syst. Struct. 2019, 30, 2534–2543. [Google Scholar] [CrossRef]
- Dargahi, A.; Sedaghati, R.; Rakheja, S. On the properties of magnetorheological elastomers in shear mode: Design, fabrication and characterization. Compos. Part B 2019, 159, 269–283. [Google Scholar] [CrossRef]
- Nam, T.H.; Petrikova, I.; Marvalova, B. Experimental characterization and viscoelastic modeling of isotropic and anisotropic magnetorheological elastomers. Polym. Test. 2020, 81, 106272. [Google Scholar] [CrossRef]
- Vatandoost, H.; Hemmatian, M.; Sedaghati, R.; Rakheja, S. Dynamic characterization of isotropic and anisotropic magnetorheological elastomers in the oscillatory squeeze mode superimposed on large static pre-strain. Compos. Part B 2020, 182, 107648. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhang, J.; Zhang, M.; Liu, L.; Zhai, P. A magnetic field- and frequency-dependent dynamic shear modulus model for isotropic silicone rubber-based magnetorheological elastomers. Compos. Sci. Technol. 2021, 204, 108637. [Google Scholar] [CrossRef]
- Jung, H.-J.; Lee, S.-J.; Jang, D.-D.; Kim, I.-H.; Koo, J.-H.; Khan, F. Dynamic Characterization of Magneto-Rheological Elastomers in Shear Mode. IEEE Trans. Magn. 2009, 45, 3930–3933. [Google Scholar] [CrossRef]
- Samal, S.; Vlach, J.; Kavan, P. Improved mechanical properties of magneto rheological elastomeric composite with isotropic iron filler distribution. Ciência Tecnol. Dos Mater. 2016, 28, 155–161. [Google Scholar] [CrossRef]
- De Souza Eloy, F.; Gomes, G.F.; Ancelotti, A.C., Jr.; da Cunha, S.S., Jr.; Bombard, A.J.F.; Junqueira, D.M. Experimental dynamic analysis of composite sandwich beams with magnetorheological honeycomb core. Eng. Struct. 2018, 176, 231–242. [Google Scholar] [CrossRef]
- Wan, Y.; Xiong, Y.; Zhang, S. Temperature dependent dynamic mechanical properties of Magnetorheological elastomers: Experiment and modeling. Compos. Struct. 2018, 202, 768–773. [Google Scholar] [CrossRef]
- Rouabah, S.; Aguib, S.; Hadji, M.; Kobzili, L. Experimental Characterization of Microcomposite Magnetorheological Elastomer. Manuf. Technol. 2021, 21, 231–240. [Google Scholar] [CrossRef]
- Abramchuk, S.S.; Grishin, D.A.; Kramarenko, E.Y.; Stepanov, G.V.; Khokhlov, A.R. Effect of a homogeneous magnetic field on the mechanical behavior of soft magnetic elastomers under compression. Polym. Sci. Ser. A 2006, 48, 138–145. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Chertovich, A.V.; Kramarenko, E.Y. Magnetorheological and deformation properties of magnetically controlled elastomers with hard magnetic filler. J. Magn. Magn. Mater. 2012, 324, 3448–3451. [Google Scholar] [CrossRef]
- Hapipi, N.; Aziz, S.A.A.; Mazlan, S.A.; Choi, S.B.; Mohamad, N.; Khairi, M.H.A.; Fatah, A.Y.A. The field-dependent rheological properties of plate-like carbonyl iron particle-based magnetorheological elastomers. Results Phys. 2019, 12, 2146–2154. [Google Scholar] [CrossRef]
- Ginder, J.M.; Nichols, M.E.; Elie, L.D.; Tardiff, I.L. Magnetorheological Elastomers: Properties and Applications. In Smart Structures and Materials 1999, Smart Materials Technologies; SPIE: Bellingham, WA, USA, 1999; Volume 3675. [Google Scholar]
- Jung, H.S.; Kwon, S.H.; Choi, H.J.; Jung, J.H.; Kim, Y.G. Magnetic carbonyl iron/natural rubber composite elastomer and its magnetorheology. Compos. Struct. 2016, 136, 106–112. [Google Scholar] [CrossRef]
- Lokander, M.; Reitberger, T.; Stenberg, B. Oxidation of natural rubber-based magnetorheological elastomers. Polym. Degrad. Stab. 2004, 86, 467–471. [Google Scholar] [CrossRef]
- Payne, A.R. The dynamic properties of carbon black loaded natural rubber vulcanizates. Part II. J. Appl. Polym. Sci. 1962, 6, 368–372. [Google Scholar] [CrossRef]
- Raa, K.S.; Pickering, K.L. The effect of silane coupling agent on the dynamic mechanical properties of iron sand/ natural rubber magnetorheological elastomers. Compos. Part B 2016, 90, 115–125. [Google Scholar]
- Kwon, S.H.; Lee, C.J.; Choi, H.J.; Chung, K.H.; Jung, J.H. Viscoelastic and mechanical behaviors of magneto-rheological carbonyl iron/natural rubber composites with magnetic iron oxide nanoparticle. Smart Mater. Struct. 2019, 28, 045012. [Google Scholar] [CrossRef]
- Moksin, N.; Shuib, R.K.; Ismail, H.; Harun, M.K. Frequency and Amplitude Dependence of Magnetorheological Elastomers Composites. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- Boczkowska, A.; Awietjan, S.F. Smart composites of urethane elastomers with carbonyl iron. J. Mater. Sci. 2009, 44, 4104–4111. [Google Scholar] [CrossRef]
- Ju, B.; Tang, R.; Zhang, D.; Yang, B.; Yu, M.; Liao, C.; Yuan, X.; Zhang, L.; Liu, J. Dynamic mechanical properties of magnetorheological elastomers based on polyurethane matrix. Polym. Compos. 2016, 37, 1587–1595. [Google Scholar] [CrossRef]
- Kukla, M.; Górecki, J.; Malujda, I.; Talaśka, K.; Tarkowski, P. The determination of mechanical properties of magnetorheological elastomers (MREs). Procedia Eng. 2017, 177, 324–330. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Averis, L.M.E.; Kwon, S.H.; Choi, H.J. Magnetostrictive and viscoelastic characteristics of polyurethane-based magnetorheological elastomer. J. Ind. Eng. Chem. 2019, 73, 128–133. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Chung, K.; Liu, C.; Choi, S.B.; Choi, H.J. Formation of core–shell structured complex microparticles during fabrication of magnetorheological elastomers and their magnetorheological behavior. Smart Mater. Struct. 2016, 25, 115028. [Google Scholar] [CrossRef]
- Burgaz, E.; Goksuzoglu, M. Effects of magnetic particles and carbon black on structure and properties of magnetorheological elastomers. Polym. Test. 2020, 81, 106233. [Google Scholar] [CrossRef]
- Su, J.; Zhang, J. Improvement of mechanical and dielectrical properties of ethylene propylene diene monomer (EPDM)/barium titanate (BaTiO3) by layered mica and graphite flakes. Compos. Part B 2017, 112, 148–157. [Google Scholar] [CrossRef]
- Kaleta, J.; Królewicz, M.; Lewandowski, D. Magnetomechanical properties of anisotropic and isotropic magnetorheological compositeswith thermoplastic elastomer matrices. Smart Mater. Struct. 2011, 20, 085006. [Google Scholar] [CrossRef]
- Shibulal, G.S.; Naskar, K. RFL coated aramid short fiber reinforced thermoplastic elastomer: Mechanical, rheological and morphological characteristics. J. Polym. Res. 2011, 18, 2295–2306. [Google Scholar] [CrossRef]
- Lu, X.; Qiao, X.; Watanabe, H. Mechanical and structural investigation of isotropic and anisotropic thermoplastic magnetorheological elastomer composites based on poly (styrene-b-ethyleneco-butylene-b-styrene) (SEBS). Rheol Acta 2012, 51, 37–50. [Google Scholar] [CrossRef]
- Ivaneiko, I.; Toshchevikov, V.; Saphiannikova, M.; Stockelhuber, K.W.; Petry, F.; Westermann, S.; Heinrich, G. Modeling of dynamic-mechanical behavior of reinforced elastomers using a multiscale approach. Polymer 2016, 82, 356–365. [Google Scholar] [CrossRef]
- Yoon, B.; Kim, J.Y.; Hong, U.; Oh, M.K.; Kim, M.; Han, S.B.; Nam, J.D.; Suhr, J. Dynamic viscoelasticity of silica-filled styrene-butadiene rubber/polybutadiene rubber (SBR/BR) elastomer composites. Compos. Part B Eng. 2020, 187, 107865. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Y.L.; Gong, X.L.; Gong, X.Q.; Zhang, X.Z.; Jiang, W.Q.; Zhang, P.Q.; Chen, Z.Y. New magnetorheological elastomers based on polyurethane/Si-rubber hybrid. Polym. Test. 2005, 24, 324–329. [Google Scholar] [CrossRef]
- Lapcik, L.; Maňas, D.; Lapcikova, B. Effect of filler particle shape on plastic-elastic mechanical behavior of high density poly(ethylene)/mica and poly (ethylene)/wollastonite composites. Compos. Part B 2018, 141, 92–99. [Google Scholar] [CrossRef]
- Chen, L.; Gong, X.L.; Li, W.H. Effect of carbon black on the mechanical performances of magnetorheological elastomers. Polym. Test. 2008, 27, 340–345. [Google Scholar] [CrossRef]
- Wang, X.; Ge, H.Y.; Liu, H.S. Study on epoxy based magnetorheological elastomers. Adv. Mater. Res. 2011, 306, 852–856. [Google Scholar] [CrossRef]
- Qin, Y.; Li, Y.; Yang, K.; Huang, Z.X.; Chen, J. Study on Damping Properties of Fe12O19Sr/NBR Composite. Adv. Mater. Res. 2014, 1046, 3–7. [Google Scholar] [CrossRef]
- Xu, Z.D.; Suo, S.; Zhu, J.T.; Guo, Y.Q. Performance tests and modeling on high damping magnetorheological elastomers based on bromobutyl rubber. J. Intell. Mater. Syst. Struct. 2018, 29, 1025–1037. [Google Scholar] [CrossRef]
- Gao, T.; Xie, R.; Chung, K. Microstructure and dynamic mechanical properties of magnetorheological elastomer based on ethylene/acrylic elastomer prepared using different manufacturing methods. Micro Nano Lett. 2018, 13, 1026–1030. [Google Scholar] [CrossRef]
- Wang, F.; Ma, Y.; Zhang, H.; Gu, J.; Yin, J.; Jia, X.; Zhang, H.; Wang, Y.; Fu, X.; Yu, R.; et al. Rheological properties and sedimentation stability of magnetorheological fluid based on multi-walled carbon nanotubes/cobalt ferrite nanocomposites. J. Mol. Liq. 2021, 324, 115103. [Google Scholar] [CrossRef]
- Gao, C.Y.; Baek, E.; You, C.Y.; Choi, H.J. Magnetic-stimuli rheological response of soft-magnetic manganese ferrite nanoparticle suspension. Colloid Polym. Sci. 2021, 299, 865–872. [Google Scholar] [CrossRef]
- Zhu, W.; Dong, X.; Huang, H.; Qi, M. Iron nanoparticles-based magnetorheological fluids: A balance between MR effect and sedimentation stability. J. Magn. Magn. Mater. 2019, 491, 165556. [Google Scholar] [CrossRef]
- Tong, Y.; Dong, X.; Qi, M. High performance magnetorheological fluids with flower-like cobalt particles. Smart Mater. Struct. 2017, 26, 025023. [Google Scholar] [CrossRef]
- Bae, D.H.; Han, W.J.; Gao, C.Y.; Dong, Y.Z.; Choi, H.J. Preparation and Magnetorheological Response of Triangular-Shaped Single-Crystalline Magnetite Particle-Based Magnetic Fluid. IEEE Trans. Magn. 2018, 54, 2001504. [Google Scholar] [CrossRef]
- Jahan, N.; Pathak, S.; Jain, K.; Pant, R.P. Enhancement in viscoelastic properties of flake-shaped iron based magnetorheological fluid using ferrofluide. Colloids Surf. A 2017, 529, 88–94. [Google Scholar] [CrossRef]
- Lee, J.H.; Lu, Q.; Lee, J.Y.; Choi, H.J. Polymer-Magnetic Composite Particles of Fe3O4/Poly (o-anisidine) and Their Suspension Characteristics under Applied Magnetic Fields. Polymers 2019, 11, 219. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.Y.; Kim, M.W.; Bae, D.H.; Dong, Y.Z.; Piao, S.H.; Choi, H.J. Fe3O4 nanoparticle-embedded polystyrene composite particles fabricated via a Shirasu porous glass membrane technique and their magnetorheology. Polymer 2017, 125, 21–29. [Google Scholar] [CrossRef]
- Han, S.; Choi, J.; Han, H.N.; Kim, S.; Seo, Y. Effect of Particle Shape Anisotropy on the Performance and Stability of Magnetorheological Fluids. ACS Appl. Electron. Mater. 2021, 3, 2526–2533. [Google Scholar] [CrossRef]
- Kwon, S.H.; Na, S.M.; Flatau, A.B.; Choi, H.J. Fe–Ga alloy based magnetorheological fluid and its viscoelastic characteristics. J. Ind. Eng. Chem. 2020, 82, 433–438. [Google Scholar] [CrossRef]
- Min, T.H.; Choi, H.J.; Kim, N.-H.; Park, K.; You, C.-Y. Effects of surface treatment on magnetic carbonyl iron/polyaniline microspheres and their magnetorheological study. Colloids Surf. A 2017, 531, 48–55. [Google Scholar] [CrossRef]
- Kwon, S.H.; Sim, B.; Choi, H.J. Magnetorheological Characteristics of Nano-Sized Iron Oxide Coated Polyaniline Composites. IEEE Trans. Magn. 2016, 52, 9401404. [Google Scholar] [CrossRef]
- Dong, X.; Tong, Y.; Ma, N.; Qi, M.; Ou, J. Properties of cobalt nanofibers-based magnetorheological fluids. RSC Adv. 2015, 5, 13958–13963. [Google Scholar] [CrossRef]
- Hong, C.H.; Liu, Y.D.; Choi, H.J. Carbonyl iron suspension with halloysite additive and its magnetorheology. Appl. Clay Sci. 2013, 80–81, 366–371. [Google Scholar] [CrossRef]
- Kim, M.W.; Han, W.J.; Kim, Y.H.; Choi, H.J. Effect of a hard magnetic particle additive on rheological characteristics of microspherical carbonyl iron-based magnetorheological fluid. Colloids Surf. A Physicochem. Eng. Asp. 2016, 506, 812–820. [Google Scholar] [CrossRef]
- Guo, C.; Gong, X.; Xuan, S.; Zong, L.; Peng, C. Normal forces of magnetorheological luids under oscillatory shear. J. Magn. Magn. Mater. 2012, 324, 1218–1224. [Google Scholar] [CrossRef]
- Arief, I.; Mukhopadhyay, P.K. Dynamic and rate-dependent yielding behavior of Co0.9Ni0.1 microcluster based magnetorheological fluids. J. Magn. Magn. Mater. 2016, 397, 57–63. [Google Scholar] [CrossRef]
- Felicia, L.J.; John, R.; Philip, J. Rheological Properties of Magnetorheological Fluid with Silica Nanoparticles Stabilizers—A Comparison with Ferrofluid. J. Nanofluids 2013, 2, 75–84. [Google Scholar] [CrossRef]
- Upadhyay, R.V.; Laherisheth, Z.; Shah, K. Rheological properties of soft magnetic flake shaped iron particle based magnetorheological fluid in dynamic mode. Smart Mater. Struct. 2014, 23, 015002. [Google Scholar] [CrossRef]
- Shah, K.; Choi, S.-B. The field-dependent rheological properties of magnetorheological fluids featuring plate-like iron particles. Front. Mater. 2014, 1, 21. [Google Scholar] [CrossRef]
- Peng, G.R.; Li, W.H.; Tian, T.F.; Ding, J.; Nakano, M. Experimental and modeling study of viscoelastic behaviors of magneto-rheological shear thickening fluids. Korea-Aust. Rheol. J. 2014, 26, 149–158. [Google Scholar] [CrossRef]
- Kim, M.S.; Liu, Y.D.; Park, B.J.; You, C.-Y.; Choi, H.J. Carbonyl iron particles dispersed in a polymer solution and their rheological characteristics under applied magnetic field. J. Ind. Eng. Chem. 2012, 18, 664–667. [Google Scholar] [CrossRef]
- Hato, M.J.; Choi, H.J.; Sim, H.H.; Park, B.O.; Ray, S.S. Magnetic carbonyl iron suspension with organoclay additive and its magnetorheological properties. Colloids Surf. A Physicochem. Eng. Asp. 2011, 377, 103–109. [Google Scholar] [CrossRef]
- Felicia, L.J.; Vinod, S.; Philip, J. Recent Advances in Magnetorheology of Ferrofluids (Magnetic Nanofluids)—A Critical Review. J. Nanofluids 2016, 5, 1–22. [Google Scholar] [CrossRef]
- Kim, J.E.; Choi, H.J. Magnetic Carbonyl Iron Particle Dispersed in Viscoelastic Fluid and Its Magnetorheological Property. IEEE Trans. Magn. 2011, 47, 3173–3176. [Google Scholar] [CrossRef]
- Jinaga, R.; Jagadeesha, T.; Kolekar, S.; Choi, S.B. The synthesis of organic oils blended magnetorheological fluids with the field-dependent material characterization. Int. J. Mol. Sci. 2019, 20, 5766. [Google Scholar] [CrossRef] [PubMed]
- Wollny, K.; Siegfried, L.J.H. Magneto Sweep—A new method for characterizing the viscoelastic behavior of magneto-rheological fluids. Appl. Rheol. 2002, 12, 25–31. [Google Scholar] [CrossRef]
- Shetty, B.G.; Prasad, P.S.S. Rheological Properties of a Honge Oil-based Magnetorheological Fluid used as Carrier Liquid. Def. Sci. J. 2011, 61, 583–589. [Google Scholar] [CrossRef]
- Gómez-Ramírez, A.; López-López, M.T.; González-Caballero, F.; Durán, J.D.G. Stability of magnetorheological fluids in ionic liquids. Smart Mater. Struct. 2011, 20, 045001. [Google Scholar] [CrossRef]
- Iglesias, G.R.; López-López, M.T.; Durán, J.D.G.; González-Caballero, F.; Delgado, A.V. Dynamic characterization of extremely bidisperse magnetorheological fluids. J. Colloid Interface Sci. 2012, 377, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.E.; Ko, J.-D.; Liu, Y.D.; Kim, I.G.; Choi, H.J. Effect of Medium Oil on Magnetorheology of Soft Carbonyl Iron Particles. IEEE Trans. Magn. 2012, 48, 3442–3445. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Ecker, E.; Stepanov, G.V.; Shamonin, M. Experimental study of the magnetic field enhanced Payne effect in magnetorheological elastomers. Soft Matter 2014, 10, 8765. [Google Scholar] [CrossRef] [PubMed]
- Molchanov, V.S.; Stepanov, G.V.; Vasiliev, V.G.; Kramarenko, E.Y.; Khokhlov, A.R.; Xu, Z.-D.; Guo, Y.-Q. Viscoelastic Properties of Magnetorheological Elastomers for Damping Applications. Macromol. Mater. Eng. 2014, 299, 1116–1125. [Google Scholar] [CrossRef]
- Nedjar, A.; Aguib, S.; Djedid, T.; Nour, A.; Settet, A.; Tourab, M. Analysis of the dynamic behavior of magnetorheological elastomer composite: Elaboration and identification of rheological properties. Silicon 2019, 11, 1287–1293. [Google Scholar] [CrossRef]
- Zainudin, A.A.; Yunus, N.A.; Mazlan, S.A.; Shabdin, M.K.; Abdul Aziz, S.A.; Nordin, N.A.; Nazmi, N.; Abdul Rahman, M.A. Rheological and resistance properties of magnetorheological elastomer with cobalt for sensor application. Appl. Sci. 2020, 10, 1638. [Google Scholar] [CrossRef]
- An, J.S.; Kwon, S.H.; Choi, H.J.; Jung, J.H.; Kim, Y.G. Modified silane-coated carbonyl iron/natural rubber composite elastomer and its magnetorheological performance. Compos. Struct. 2017, 160, 1020–1026. [Google Scholar] [CrossRef]
- Jaafar, M.F.; Mustapha, F.; Mustapha, M. Review of current research progress related to magnetorheological elastomer material. J. Mater. Res. Technol. 2021, 15, 5010–5045. [Google Scholar] [CrossRef]
- Tong, Y.; Dong, X.; Qi, M. Payne effect and damping properties of flower-like cobalt particles-based magnetorheological elastomers. Compos. Commun. 2019, 15, 120–128. [Google Scholar] [CrossRef]
- Burhannuddin, N.L.; Nordin, N.A.; Mazlan, S.A.; Aziz, S.A.A.; Kuwano, N.; Jamari, S.K.M.; Ubaidillah. Physicochemical characterization and rheological properties of magnetic elastomers containing different shapes of corroded carbonyl iron particles. Sci. Rep. 2021, 11, 868. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Sun, L.Z. Dynamic mechanical behavior of magnetorheological nanocomposites filled with carbon nanotubes. Appl. Phys. Lett. 2011, 99, 131912. [Google Scholar] [CrossRef]
- Li, J.; Gong, X.; Zhu, H.; Jiang, W. Influence of particle coating on dynamic mechanical behaviors of magnetorheological elastomers. Polym. Test. 2009, 28, 331–337. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Stepanov, G.V.; Shamonin, M.; Monkman, G.J.; Khokhlov, A.R.; Kramarenko, E.Y. Hysteresis of the viscoelastic properties and the normal force in magnetically and mechanically soft magnetoactive elastomers: Effects of filler composition, strain amplitude and magnetic field. Polymer 2015, 76, 191–202. [Google Scholar] [CrossRef]
- Li, W.H.; Du, H.; Chen, G.S.; Yeo, H. Viscoelastic properties of MR fluids under oscillatory shear. In Smart Structures and Materials Damping and Isolation; SPIE: Bellingham, WA, USA, 2001; Volume 4331. [Google Scholar]
- Lu, Q.; Choi, K.; Nam, J.D.; Choi, H.J. Review: Magnetic Polymer Composite Particles: Design and Magnetorheology. Polymers 2021, 13, 512. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Li, D.; Sun, B.; Jiang, L.; Zhou, Y.; Wen, S.; Chen, S. Surface modification of carbonyl iron particles using dopamine and silane coupling agent for high-performance magnetorheological elastomers. Polym. Test. 2023, 119, 107935. [Google Scholar] [CrossRef]
- Salem, A.M.H.; Ali, A.; Ramli, R.B.; Muthalif, A.G.A.; Julai, S. Effect of Carbonyl Iron Particle Types on the Structure and Performance of Magnetorheological Elastomers: A Frequency and Strain Dependent Study. Polymers 2022, 14, 4193. [Google Scholar] [CrossRef] [PubMed]
- Cutillas, S.; Liu, J. Particle dynamics of structure formation and disintegration in a model magnetorheological fluid. Int. J. Mod. Phys. B 2002, 16, 2314–2320. [Google Scholar] [CrossRef]
- Böse, H.; Gerlach, T.; Ehrlich, J. Magnetorheological elastomers—An underestimated class of soft actuator materials. J. Intell. Mater. Syst. Struct. 2021, 32, 1550–1564. [Google Scholar] [CrossRef]
- Aguib, S.; Nour, A.; Zahloul, H.; Bossis, G.; Chevalier, Y.; Lançon, P. Dynamic behavior analysis of a magnetorheological elastomer sandwich plate. Int. J. Mech. Sci. 2014, 87, 118–136. [Google Scholar] [CrossRef]
- Boczkowska, A.; Awietjan, S.F. Microstructure and Properties of Magnetorheological Elastomers. In Advanced Elastomers-Technology, Properties and Applications; IntechOpen: London, UK, 2012; Volume 595. [Google Scholar]
- Diez, A.G.; Tubio, C.R.; Gutiérrez, J.G.; Lanceros-Mendez, S. A Review: Magnetorheological Elastomer-Based Materials and Devices: State of the Art and Future Perspectives. Adv. Eng. Mater 2021, 23, 210–240. [Google Scholar] [CrossRef]
- Fan, Y.; Gong, X.; Xuan, S.; Zhang, W.; Zheng, J.; Jiang, W. Interfacial friction damping properties in magnetorheological elastomers. Smart Mater. Struct 2011, 20, 035007. [Google Scholar] [CrossRef]
- Kang, S.S.; Choi, K.; Nam, J.; Choi, H.J. Review: Magnetorheological Elastomers: Fabrication, Characteristics, and Applications. Materials 2020, 13, 4597. [Google Scholar] [CrossRef] [PubMed]
- Arslan Hafeez, M.; Usman, M.; Umer, M.A.; Hanif, A. Recent progress in isotropic magnetorheological elastomers and their properties: A review. Polymers 2020, 12, 3023. [Google Scholar] [CrossRef] [PubMed]
- Fakhree, M.A.M.; Nordin, N.A.; Nazmi, N.; Mazlan, S.A.; Aziz, S.A.A.; Ubaidillah, U.; Choi, S.B. Field-dependent rheological properties of magnetorheological elastomer with fountain-like particle chain alignment. Micromachines 2022, 13, 492. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Fang, F.; Huang, W.; Chen, Y.; Qi, S.; Yu, M. Dynamic mechanical hysteresis of magnetorheological elastomers subjected to the cyclic loading and periodic magnetic field. Front. Mater. 2019, 6, 292. [Google Scholar] [CrossRef]
- Khairi, M.H.A.; Noor, E.E.M.; Ubaidillah, U.; Aziz, S.A.A.; Mazlan, S.A.; Tarmizi, S.M.A.; Nordin, N.A. Enhancement of magneto-induced modulus by the combination of filler and plasticizer additives-based magnetorheological elastomer. Materials 2022, 15, 6396. [Google Scholar] [CrossRef] [PubMed]
- De Vicente, J.; Vereda, F.; Segovia-Gutiérrez, J.P.; Morales, M.P.; Hidalgo-Álvarez, R. Effect of particle shape in magnetorheology. J. Rheol. 2010, 54, 1337. [Google Scholar] [CrossRef]
- Ramos, J.; de Vicente, J.; Hidalgo-Alvarez, R. Small-Amplitude Oscillatory Shear Magnetorheology of Inverse Ferrofluids. Langmuir 2010, 26, 9334–9341. [Google Scholar] [CrossRef] [PubMed]
- Shah, K.; Oh, J.S.; Choi, S.-B.; Upadhyay, R.V. Plate-like iron particles based bidisperse magnetorheological fluid. J. Appl. Phys. 2013, 114, 213904. [Google Scholar] [CrossRef]
- Arief, I.; Mukhopadhyay, P.K. Magnetorheological Payne effect in bidisperse MR fluids containing Fe nanorods and Fe3O4 nanospheres: A dynamic rheological study. J. Alloys Compd. 2017, 696, 1053–1058. [Google Scholar] [CrossRef]
- Wen, Q.; Shen, L.; Li, J.; Xuan, S.; Li, Z.; Fan, X.; Li, B.; Gong, X. Temperature dependent magneto-mechanical properties of magnetorheological elastomers. J. Magn. Magn. Mater. 2020, 497, 165998. [Google Scholar] [CrossRef]
- Ji, J.; Ge, X.; Pang, X.; Liu, R.; Wen, S.; Sun, J.; Liang, W.; Ge, J.; Chen, X. Synthesis and Characterization of Room Temperature Vulcanized Silicone Rubber Using Methoxyl-Capped MQ Silicone Resin as Self-Reinforced Cross-Linker. Polymers 2019, 11, 1142. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Huang, X.; Liu, H.; Shang, S.; Song, Z.; Song, J. Preparation and properties of room temperature vulcanized silicone rubber based on rosin-grafted polydimethylsiloxane. RSC Adv. 2018, 8, 14684. [Google Scholar] [CrossRef] [PubMed]
- Tourab, M.; Khebli, A.; Chikh, N.; Aguib, S.; Abdelkader, N.; Djedid, T.; Nedjar, A. Elaboration and Identification of the Mechanical Properties of Magnetorheological Elastomer in Frequency-temperature Dependence. Mater. Sci. 2024, 30, 253–259. [Google Scholar] [CrossRef]
- Rashid, R.Z.; Yunus, A.; Mazlan, N.A.; Johari, S.A.; Aziz, N.; Nordin, S.A.A.; Johari, N. Temperature dependent on mechanical and rheological properties of EPDM-based magnetorheological elastomers using silica nanoparticles. Materials 2022, 15, 2556. [Google Scholar] [CrossRef] [PubMed]
- Hemmatian, M.; Sedaghati, R.; Rakheja, S. Temperature dependency of magnetorheological fluids’ properties under var-ying strain amplitude and rate. J. Magn. Magn. Mater. 2020, 498, 109–166. [Google Scholar] [CrossRef]
- Kamble, V.G.; Kolekar, S.; Panda, H.S.; Ammourah, S.; Jagadeesha, T. Magneto rheological fluid: Fabrication and characterization of its temperature-dependent properties. Mater. Today Proc. 2021, 45, 4813–4818. [Google Scholar] [CrossRef]
- Sherman, S.G.; Powell, L.A.; Becnel, A.C.; Wereley, N.M. Scaling temperature dependent rheology of magnetorheological fluids. J. Appl. Phys. 2015, 117, 17C751. [Google Scholar] [CrossRef]
- Wang, D.; Zi, B.; Zeng, Y.; Xie, F.; Hou, Y. Measurement of temperature-dependent mechanical properties of magnetorheological fluids using a parallel disk shear stress testing device. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 1725–1737. [Google Scholar] [CrossRef]
- Susan-Resiga, D. A rheological model for magneto-rheological fluids. J. Intell. Mater. Syst. Struct. 2009, 20, 1001–1010. [Google Scholar] [CrossRef]
- Li, W.H.; Chen, G.; Yeo, S.H.; Du, H. Temperature dependence of MR fluids. Int. J. Mod. Phys. B 2002, 16, 2725–2731. [Google Scholar] [CrossRef]
- Weiss, K.D.; Duclos, T.G. Controllable fluids: The temperature dependence of post-yield properties. Int. J. Mod. Phys. B 1994, 8, 3015–3032. [Google Scholar] [CrossRef]
- Aziz, S.A.A.; Aziz, M.S.A.; Shabdin, M.K. Rheological Properties of Mg Substituted Cobalt Nickel Ferrite Nanoparticles as an Additive in Magnetorheological Elastomer. In Proceedings of the 6th International Conference and Exhibition on Sustainable Energy and Advanced Materials, Surakarta, Indonesia, 16–17 October 2019; Lecture Notes in Mechanical Engineering. Springer: Singapore, 2020. [Google Scholar]
- Liu, T.; Xu, Y. Magnetorheological elastomers: Materials and applications. In Smart and Functional Soft Materials; IntechOpen: London, UK, 2019; Volume 5. [Google Scholar]
- Skalski, P.; Kalita, K. Role of magnetorheological fluids and elastomers in today’s world. Acta Mech. Autom. 2017, 11, 4. [Google Scholar] [CrossRef]
- Samal, S.; Škodová, M.; Abate, L.; Blanco, I. Magneto-Rheological Elastomer Composites: A Review. Appl. Sci 2020, 10, 4899. [Google Scholar] [CrossRef]
- Raju, A.; Choi, S.-B.; Ferdaus, M.M. A state of art on magneto-rheological materials and their potential applications. J. Intell. Mater. Syst. Struct. 2018, 29, 2051–2095. [Google Scholar] [CrossRef]
- Alkhalaf, A.; Hooshiar, A.; Dargahi, J. Composite magnetorheological elastomers for tactile displays: Enhanced MR-effect through bi-layer composition. Compos. Part B Eng. 2020, 190, 107888. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Y.; Wang, Y.; Deng, H.; Gong, X.; Zhang, P.; Jiang, W.; Chen, Z. Magnetorheological elastomers based on isobutylene–isoprene rubber. Polym. Eng. Sci. 2006, 46, 264–268. [Google Scholar] [CrossRef]
- Wang, X.; Gordaninejad, F.; Calgar, M.; Liu, Y.; Sutrisno, J.; Fuchs, A. Sensing behavior of magnetorheological elastomers. J. Mech. Des. 2009, 131, 091004. [Google Scholar] [CrossRef]
- Rezaie, E.; Hajalilou, A.; Rezanezhad, A.; Abouzari-Lotf, E.; Arsalani, N. Magnetorheological studies of polymer nanocomposites. In Rheology of Polymer Blends and Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2020; pp. 263–294. [Google Scholar]
- Boczkowska, A.; Awietjan, S.F.; Wroblewski, R. Microstructure–property relationships of urethane magnetorheological elastomers. Smart Mater. Struct. 2007, 16, 1924–1930. [Google Scholar] [CrossRef]
- Li, W.H.; Zhang, X.Z.; Du, H. Magnetorheological Elastomers and Their Applications. In Advances in Elastomers I: Blends and Interpenetrating Networks; Visakh, P., Thomas, S., Chandra, A., Mathew, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 11. [Google Scholar]
- Johari, M.A.F.; Mazlan, S.A.; Aziz, S.A.A.; Nordin, N.A.; Johari, N.; Nazmi, N. An overview of durability evaluations of elastomer-based magnetorheological materials. IEEE Access 2020, 8, 134536–134552. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, X.L.; Jiang, W.Q.; Fan, Y.C. Investigation of the durability of anisotropic magnetorheological elastomers based on mixedrubber. Smart Mater. Struct. 2010, 19, 085008. [Google Scholar] [CrossRef]
- Sohoni, G.B.; Mark, J.E. Anisotropic Reinforcement in Elastomers Containing Magnetic Filler Particles. J. Appl. Polym. Sci. 1987, 34, 2853–2859. [Google Scholar] [CrossRef]
- Dong, X.; Ma, N.; Qi, M.; Li, J.; Guan, X.; Ou, J. Properties of magneto-rheological fluids based on amorphous micro-particles. Trans. Nonferrous Met. Soc. China 2012, 22, 2979–2983. [Google Scholar] [CrossRef]
- Martins, A.; Fereidooni, A.; Suleman, A.; Wickramasinghe, V. Test rig development and characterization of magnetorheological elastomers. In Proceedings of the 25th AIAA/AHS Adaptive Structures Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Mitsumata, T.; Ohori, S.; Honda, A.; Kawai, M. Magnetism and viscoelasticity of magnetic elastomers with wide range modulation of dynamic modulus. Soft Matter 2013, 9, 904–912. [Google Scholar] [CrossRef]
- Ubaidillah; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent Progress on Magnetorheological Solids: Materials, Fabrication, Testing, and Applications. Adv. Eng. Mater. 2015, 17, 563. [Google Scholar] [CrossRef]
- Stolbov, O.V.; Raikher, Y.L.; Stepanov, G.V.; Chertovich, A.V.; Kramarenko, E.Y.; Khokhlov, A.R. Low-frequency rheology of magnetically controlled elastomers with isotropic structure. Polym. Sci. Ser. A 2010, 52, 1344–1354. [Google Scholar] [CrossRef]
- Johnson, N.; Gordaninejad, F.; Wang, X. Dynamic behavior of thick magnetorheological elastomers. J. Intell. Mater. Syst. Struct. 2018, 29, 183–193. [Google Scholar] [CrossRef]
- Lokander, M.; Stenberg, B. Improving the magnetorheological effect in isotropic magnetorheological rubber materials. Polym. Test. 2003, 22, 677–680. [Google Scholar] [CrossRef]
- Kwon, S.H.; Lee, J.H.; Choi, H.J. Review: Magnetic Particle Filled Elastomeric Hybrid Composites and Their Magnetorheological Response. Materials 2018, 11, 1040. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.L.; Gong, X.L.; Jiang, W.Q.; Li, J.F.; Xu, Z.B.; Li, W.H. Study on the damping properties of magnetorheological elastomers based on cis-polybutadiene rubber. Polym. Test. 2008, 27, 520–526. [Google Scholar] [CrossRef]
- Bodelot, L.; Pössinger, T.; Danas, K.; Triantafyllidis, N.; Bolzmacher, C. Magnetorheological Elastomers: Experimental and Modeling Aspects. In Mechanics of Composite and Multi-functional Materials; Springer: Berlin/Heidelberg, Germany, 2016; Volume 7. [Google Scholar]
- Wang, X.; Gordaninejad, F. Study of magnetorheological fluids at high shear rates. Rheol Acta 2006, 45, 899–908. [Google Scholar] [CrossRef]
- Farshad, M.; Le Roux, M. Compression properties of magnetostrictive polymer composite gels. Polym. Test. 2005, 24, 163–168. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Abramchuk, S.S.; Grishin, D.A.; Nikitin, L.V.; Kramarenko, E.Y.; Khokhlov, A.R. Effect of a homogeneous magnetic field on the viscoelastic behavior of magnetic elastomers. Polymer 2007, 48, 488–495. [Google Scholar] [CrossRef]
- Hajalilou, A.; Kianvash, A.; Shameli, K.; Lavvafi, H. Carbonyl iron based magnetorheological effects with silver nanoparticles via green assisted coating. Appl. Phys. Lett. 2017, 110, 261902. [Google Scholar] [CrossRef]
- Ashtiani, M.; Hashemabadi, S.H.; Ghaffari, A. A review on the magnetorheological fluid preparation and stabilization. J. Magn. Magn. Mater. 2015, 374, 716–730. [Google Scholar] [CrossRef]
- Eshgarf, H.; Nadooshan, A.A.; Raisi, A. Review article: An overview on properties and applications of magnetorheological fluids: Dampers, batteries, valves and brakes. J. Energy Storage 2022, 50, 104648. [Google Scholar] [CrossRef]
- Zareie, S.; Zabihollah, A. The recent advances in magnetorheological fluids-based applications. In Emerging Trends in Mechatronics; IntechOpen: London, UK, 2020; p. 129. [Google Scholar]
- Zhu, M.; Yu, M.; Qi, S.; Fu, J. Investigations on response time of magnetorheological elastomer under compression mode. Smart Mater. Struct. 2018, 27, 055017. [Google Scholar] [CrossRef]
- Ginder, J.M.; Nichols, M.E.; Elie, L.D.; Clark, S.M. Controllable-Stiffness Components Based On Magnetorheological Elastomers. In Smart Structures and Materials 2000: Smart Structures and Integrated Systems; SPIE: Bellingham, WA, USA, 2000; Volume 3985. [Google Scholar]
- Thiagarajan, S.; Koh, A.S. Performance and stability of magnetorheological fluids—A detailed review of the state of the art. Adv. Eng. Mater. 2021, 23, 2001458. [Google Scholar] [CrossRef]
- Hajalilou, A.; Mazlan, S.A.; Shila, S.T. Magnetic carbonyl iron suspension with Ni–Zn ferrite additive and its magnetorheological properties. Mater. Lett. 2016, 181, 196–199. [Google Scholar] [CrossRef]
- Gu, X.; Li, Y.; Li, J. Investigations on response time of magnetorheological elastomer isolator for real-time control implementation. Smart Mater. Struct. 2016, 25, 11LT04. [Google Scholar] [CrossRef]
- Koo, J.-H.; Goncalves, F.D.; Ahmadian, M. A comprehensive analysis of the response time of MR dampers. Smart Mater. Struct. 2006, 15, 351–358. [Google Scholar] [CrossRef]
- Morillas, J.R.; de Vicente, J. On the yield stress in magnetorheological fluids: A direct comparison between 3D simulations and experiments. Compos. Part B Eng. 2019, 160, 626–631. [Google Scholar] [CrossRef]
- Vishwakarma, P.N.; Mishra, P.; Sharma, S.K. Characterization of a magnetorheological fluid damper a review. Mater. Today Proc. 2022, 56, 2988–2994. [Google Scholar] [CrossRef]
- Zhu, W.; Dong, X.; Huang, H.; Qi, M. Enhanced magnetorheological effect and sedimentation stability of bimodal magnetorheological fluids doped with iron nanoparticles. J. Intell. Mater. Syst. Struct. 2021, 32, 1271–1277. [Google Scholar] [CrossRef]
- Cvek, M.; Mrlik, M.; Moucka, M.; Sedlacik, M. A systematical study of the overall influence of carbon allotrope additives on performance, stability and redispersibility of magnetorheological fluids. Colloids Surf. A 2018, 543, 83–92. [Google Scholar] [CrossRef]
- Gómez-Ramírez, A.; Lopez-Lopez, M.T.; Duran, J.D.G.; Gonzalez-Caballero, F. Influence of particle shape on the magnetic and magnetorheological properties of nanoparticle suspensions. Soft Matter 2009, 5, 3888–3895. [Google Scholar] [CrossRef]
- Kim, H.M.; Choi, H.J. Enhanced Magnetorheological Response of Carbonyl Iron Suspension with Added ZnFe2O4 Particles. IEEE Trans. Magn. 2021, 58, 1–5. [Google Scholar] [CrossRef]
- Suvarna, N.; Raju, A.; Hegde, S. A review of magneto rheological fluid in suspension and torsional devices. AIP Conf. Proc. 2021, 2317, 050003. [Google Scholar]
- Olabi, A.G.; Grunwald, A. Design and application of magneto-rheological fluid. Mater. Des. 2007, 28, 2658–2664. [Google Scholar] [CrossRef]
- Rabbani, Y.; Ashtiani, M.; Hashemabadi, S.H. An experimental study on the effects of temperature and magnetic field strength on the magnetorheological fluid stability and MR effect. Soft Matter 2015, 11, 4453–4460. [Google Scholar] [CrossRef] [PubMed]
- Ginder, J.M.; Davis, L.C.; Elie, L.D. Rheology of Magnetorheological Fluids: Models and Measurements. Int. J. Mod. Phys. B 1996, 10, 3293–3303. [Google Scholar] [CrossRef]
- Anupama, A.V.; Kumaran, V.; Sahoo, B. Application of monodisperse Fe3O4 submicrospheres in magnetorheological fluids. J. Ind. Eng. Chem. 2018, 67, 347–357. [Google Scholar] [CrossRef]
- Xu, Y.; Liao, G.; Liu, T. Magneto-sensitive smart materials and magnetorheological mechanism. In Nanofluid Flow in Porous Media; IntechOpen: London, UK, 2019. [Google Scholar]
- Bica, I.; Liu, Y.D.; Choi, H.J. Physical characteristics of magnetorheological suspensions and their applications. J. Ind. Eng. Chem. 2013, 19, 394–406. [Google Scholar] [CrossRef]
- Wang, J.; Meng, G. Magnetorheological fluid devices: Principles, characteristics and applications in mechanical engineering. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2001, 215, 165–174. [Google Scholar] [CrossRef]
- Choi, S.-B. Thermal Conductivity and Temperature Dependency of Magnetorheological Fluids and Application Systems—A Chronological Review. Micromachines 2023, 14, 2096. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Sehgal, R.; Wani, M.F.; Sharma, M.D. Stabilization and tribological properties of magnetorheological (MR) fluids: A review. J. Magn. Magn. Mater. 2021, 538, 168295. [Google Scholar] [CrossRef]
- Chen, S.; Huang, J.; Jian, K.; Ding, J. Analysis of influence of temperature on magnetorheological fluid and transmission performance. Adv. Mater. Sci. Eng. 2015, 2015, 583076. [Google Scholar] [CrossRef]
- Maharani, E.T.; Seo, M.-W.; Sohn, J.W.; Oh, J.-S.; Choi, S.-B. The Influence of Current Magnitudes and Profiles on the Sedimentation of Magnetorheological Fluids: An Experimental Work. Magnetochemistry 2024, 10, 18. [Google Scholar] [CrossRef]
- Kumbhar, B.K.; Patil, S.R.; Sawant, S.M. Synthesis and characterization of magneto-rheological (MR) fluids for MR brake application. Eng. Sci. Technol. Int. J. 2015, 18, 432–438. [Google Scholar] [CrossRef]
- Chuah, W.H.; Zhang, W.L.; Choi, H.J.; Seo, Y. Magnetorheology of Core−Shell Structured Carbonyl Iron/Polystyrene Foam Microparticles Suspension with Enhanced Stability. Macromolecules 2015, 48, 7311–7319. [Google Scholar] [CrossRef]
- Jiang, W.; Zhu, H.; Guo, C.; Li, J.; Xue, Q.; Feng, J.; Gong, X. Poly(methyl methacrylate)-coated carbonyl iron particles and their magnetorheological characteristics. Polym. Int. 2010, 59, 879–883. [Google Scholar] [CrossRef]
- Mrlik, M.; Sedlacik, M.; Pavlinek, V.; Peer, P.; Filip, P.; Saha, P. Magnetorheology of carbonyl iron particles coated with polypyrrole ribbons: The steady shear study. J. Phys. Conf. Ser. 2013, 412, 012016. [Google Scholar] [CrossRef]
- Song, K.H.; Park, B.J.; Choi, H.J. Effect of Magnetic Nanoparticle Additive on Characteristics of Magnetorheological Fluid. IEEE Trans. Magn. 2009, 45, 4045. [Google Scholar] [CrossRef]
- Park, B.J.; Kim, M.S.; Choi, H.J. Fabrication and magnetorheological property of core/shell structured magnetic composite particle encapsulated with cross-linked poly (methyl methacrylate). Mater. Lett. 2009, 63, 2178–2180. [Google Scholar] [CrossRef]
- Pu, H.T.; Jiang, F.J.; Yang, Z.; Yan, B.; Liao, X. Effects of Polyvinylpyrrolidone and Carbon Nanotubes on Magnetorheological Properties of Iron-Based Magnetorheological Fluid. J. Appl. Polym. Sci. 2006, 102, 1653–1657. [Google Scholar] [CrossRef]
- Ngatu, G.T.; Wereley, N.M.; Karli, J.O.; Bell, R.C. Dimorphic magnetorheological fluids: Exploiting partial substitution of microspheres by nanowires. Smart Mater. Struct. 2008, 17, 045022. [Google Scholar] [CrossRef]
- Fang, F.F.; Choi, H.J.; Choi, W.S. Two-layer coating with polymer and carbon nanotube on magnetic carbonyl iron particle and its Magnetorheology. Colloid Polym Sci 2010, 288, 359–363. [Google Scholar] [CrossRef]
- Farjoud, A.; Craft, M.; Burke, W.; Ahmadian, M. Experimental Investigation of MR Squeeze Mounts. J. Intell. Mater. Syst. Struct. 2011, 22, 1645–1652. [Google Scholar] [CrossRef]
- Adjerid, K. A study on the dynamic characterization of a tunable magneto-rheological fluid-elastic mount in squeeze mode vibration. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2011. [Google Scholar]
- Wahid, S.A.; Ismail, I.; Aid, S.; Rahim, M.S.A. Magneto-rheological defects and failures: A review. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 114. [Google Scholar]
- Farjoud, A.; Cavey, R.; Ahmadian, M.; Craft, M. Magneto-rheological fluid behavior in squeeze mode. Smart Mater. Struct. 2009, 18, 095001. [Google Scholar] [CrossRef]
- Phu, D.X.; Choi, S.-B. Magnetorheological Fluid Based Devices Reported in 2013–2018: Mini-Review and Comment on Structural Configurations. Mini-Review and Comment on Structural Configurations. Front. Mater. 2019, 6, 19. [Google Scholar] [CrossRef]
- Kumar, J.S.; Paul, P.S.; Raghunathan, G.; Alex, D.G. A review of challenges and solutions in the preparation and use of magnetorheological fluids. Int. J. Mech. Mater. Eng. 2019, 14, 13. [Google Scholar] [CrossRef]
- Claracq, J.; Sarrazin, J.; Montfort, J.P. Viscoelastic properties of magnetorheological fluids. Rheol Acta 2004, 43, 38–49. [Google Scholar] [CrossRef]
- Fang, F.F.; Choi, H.J.; Jhon, M.S. Magnetorheology of soft magnetic carbonyl iron suspension with single-walled carbon nanotube additive and its yield stress scaling function. Colloids Surf. A Physicochem. Eng. Asp. 2009, 351, 46–51. [Google Scholar] [CrossRef]
- Plachy, T.; Kutalkova, E.; Sedlacik, M.; Vesel, A.; Masar, M.; Kuritka, I. Impact of corrosion process of carbonyl iron particles on magnetorheological behavior of their suspensions. J. Ind. Eng. Chem. 2018, 66, 362–369. [Google Scholar] [CrossRef]
- Esmaeilzare, A.; Rezaei, S.M.; Ramezanzadeh, B. Corrosion and Magnetic Properties of Encapsulated Carbonyl Iron Particles in Aqueous Suspension by Inorganic Thin Films for Magnetorheological Finishing Application. Appl. Surf. Sci. 2018, 436, 1200–1212. [Google Scholar] [CrossRef]
- Deng, H.X.; Gong, X.L. Application of magnetorheological elastomer to vibration absorber. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1938–1947. [Google Scholar] [CrossRef]
- Li, W.H.; Zhang, X.; Du, H. Development and simulation evaluation of a magnetorheological elastomer isolator for seat vibration control. J. Intell. Mater. Syst. Struct. 2012, 23, 1041–1048. [Google Scholar] [CrossRef]
- Shahrivar, K.; De Vicente, J. Thermoresponsive polymer-based magneto-rheological (MR) composites as a bridge between MR fluids and MR elastomers. Soft Matter 2013, 9, 11451–11456. [Google Scholar] [CrossRef]
- Spaggiari, A. Properties and applications of Magnetorheological fluids. Fract. Struct. Integr. 2013, 7, 48–61. [Google Scholar] [CrossRef]
- Vatandoost, H.; Norouzi, M.; Alehashem, S.M.S.; Smoukov, S.K. A novel phenomenological model for dynamic behavior of magnetorheological elastomers in tension–compression mode. Smart Mater. Struct. 2017, 26, 065011. [Google Scholar] [CrossRef]
- Venkategowda, T.; Manjunatha, L.H.; Anilkumar, P.R. Dynamic mechanical behavior of natural fibers reinforced polymer matrix composites—A review. Mater. Today Proc. 2022, 54, 395–401. [Google Scholar] [CrossRef]
- Yang, C.Y.; Fu, J.; Yu, M.; Zheng, X.; Ju, B.X. A new magnetorheological elastomer isolator in shear–compression mixed mode. J. Intell. Mater. Syst. Struct. 2015, 26, 1290–1300. [Google Scholar] [CrossRef]
- Imaduddin, F.; Li, Y.; Mazlan, S.A.; Sutrisno, J.; Koga, T.; Yahya, I.; Choi, S.B. A new class of magnetorheological elastomers based on waste tire rubber and the characterization of their properties. Smart Mater. Struct. 2016, 25, 115002. [Google Scholar] [CrossRef]
- Kim, Y.H.; Ahn, W.J.; Choi, H.J.; Seo, Y. Fabrication and magnetic stimuli-response of polydopamine-coated core–shell structured carbonyl iron microspheres. Colloid Polym. Sci. 2016, 294, 329–337. [Google Scholar] [CrossRef]
- Wang, Y.F.; He, L.; Yu, W.X.; Yang, X. Study on the magnetorheological effect of MR elastomer under shear-compression mode. Adv. Mater. Res. 2011, 239, 3018–3023. [Google Scholar] [CrossRef]
- Wang, H.; Bi, C.; Kan, J.; Gao, C.; Xiao, W. The mechanical property of magnetorheological fluid under compression, elongation, and shearing. J. Intell. Mater. Syst. Struct. 2011, 22, 811–816. [Google Scholar] [CrossRef]
- Borin, D.; Stepanov, G.; Dohmen, E. Hybrid magnetoactive elastomer with a soft matrix and mixed powder. Arch. Appl. Mech. 2019, 89, 105–117. [Google Scholar] [CrossRef]
- Du, H.; Li, W.H.; Zhang, N. Semi-active variable stiffness vibration control of vehicle seat suspension using an MR elastomer isolator. Smart Mater. Struct. 2011, 20, 105003. [Google Scholar] [CrossRef]
- Liao, G.J.; Gong, X.L.; Kang, C.J.; Xuan, S.H. The design of an active–adaptive tuned vibration absorber based on magnetorheological elastomer and its vibration attenuation performance. Smart Mater. Struct 2011, 20, 075015. [Google Scholar]
- Puente-Córdova, J.G.; Reyes-Melo, M.E.; Palacios-Pineda, L.M.; Martínez-Perales, I.A.; Martínez-Romero, O.; Elías-Zúñiga, A. Fabrication and characterization of isotropic and anisotropic magnetorheological elastomers based on silicone rubber and carbonyl iron microparticles. Polymers 2018, 10, 1343. [Google Scholar] [CrossRef] [PubMed]
- Berasategi, J.D.; Salazar, A.; Gomez, J.; Gutierrez, M.S.; Sebastián, M.; Bou-Ali, J.M. Barandiaran. Anisotropic behaviour analysis of silicone/carbonyl iron particles magnetorheological elastomers. Rheologica Acta 2020, 59, 469–476. [Google Scholar] [CrossRef]
- Dassisti, M.; Brunetti, G. Introduction to Magnetorheological Fluids. In Reference Module in Materials Science and Materials Engineering; Polytechnic University of Bari: Bari, Italy, 2021. [Google Scholar]
- Von Lockette, P.R.; Lofland, S.E.; Koo, J.H.; Kadlowec, J.; Dermond, M. Dynamic characterization of bimodal particle mixtures in silicone rubber magnetorheological materials. Polym. Test. 2008, 27, 931–935. [Google Scholar] [CrossRef]
- Winger, J.; Schümann, M.; Kupka, A.; Odenbach, S. Influence of the particle size on the magnetorheological effect of magnetorheological elastomers. J. Magn. Magn. Mater. 2019, 481, 176–182. [Google Scholar] [CrossRef]
- Khayam, S.U.; Usman, M.; Umer, M.A.; Rafique, A. Development and characterization of a novel hybrid magnetorheological elastomer incorporating micro and nano size iron fillers. Mater. Des. 2020, 192, 108748. [Google Scholar] [CrossRef]
- Upadhyay, R.V. Steady Shear Rheology and Magnetic Properties of Flake-Shaped Iron Particle-Based MR Fluid: Before and After Tribology Study. Braz. J. Phys. 2019, 49, 820–828. [Google Scholar] [CrossRef]
- Maan, A.; Rai, B.; Tyagi, V.; Kaicker, P.K. Studies on Rheological Properties of Magneto-Rheological Fluid as a Function of Particle Size and Concentration. In Recent Trends in Materials and Devices: Proceedings of ICRTMD 2019; Springer: Singapore, 2020; pp. 233–244. [Google Scholar]
- Pei, P.; Peng, Y. Constitutive modeling of magnetorheological fluids: A review. J. Magn. Magn. Mater. 2022, 550, 169076. [Google Scholar] [CrossRef]
- Muhammad, A.; Yao, X.L.; Deng, Z.C. Review of magnetorheological (MR) fluids and its applications in vibration control. J. Mar. Sci. Appl. 2006, 5, 17–29. [Google Scholar] [CrossRef]
- Segovia-Gutiérrez, J.P.; Berli, C.L.A.; de Vicente, J. Nonlinear viscoelasticity and two-step yielding in magnetorheology: A colloidal gel approach to understand the effect of particle concentration. J. Rheol. 2012, 56, 1429. [Google Scholar] [CrossRef]
- Shokrollahi, H. The effect of the volume fraction and viscosity on the compression and tension behavior of the cobalt-ferrite magneto-rheological fluids. Eng. Sci. Technol. Int. J. 2016, 19, 604–609. [Google Scholar] [CrossRef][Green Version]
- Huimin, S.; Xuli, Z.; Nannan, L.; Jiefeng, M.; Liang, L.; Shixu, L. Effect of different volume fraction magnetorheological fluids on its shear properties. J. Phys. Conf. Ser. 2019, 1187, 032078. [Google Scholar] [CrossRef]
- Anupama, A.V.; Kumaran, V.; Sahoo, B. Effect of magnetic dipolar interactions and size dispersity on the origin of steady state magnetomechanical response in bidisperse Mn–Zn ferrite spherical particle based magnetorheological fluids. New J. Chem. 2019, 43, 9969. [Google Scholar] [CrossRef]
- Acharya, S.; Saini, T.R.S.; Kumar, H. Determination of optimal magnetorheological fluid particle loading and size for shear mode monotube damper. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 392. [Google Scholar] [CrossRef]
- Sun, W.; Yu, J.; Cai, Y. Influence of magnetic field, magnetic particle percentages, and particle diameters on the stiffness of magnetorheological fluids. J. Intell. Mater. Syst. Struct. 2020, 31, 2312–2325. [Google Scholar] [CrossRef]
- Tang, H. Particle size polydispersity of the rheological properties in magnetorheological fluids. Sci. China Phys. Mech. Astron. 2011, 54, 1258–1262. [Google Scholar] [CrossRef]
- Sarkar, C.; Hirani, H. Effect of Particle Size on Shear Stress of Magnetorheological Fluids. Smart Sci. 2015, 3, 65–73. [Google Scholar] [CrossRef]
- Vatandoost, H.; Rakheja, S.; Sedaghati, R. Effects of iron particles volume fraction on compression mode properties of magnetorheological elastomers. J. Magn. Magn. Mater. 2021, 522, 167552. [Google Scholar] [CrossRef]
- Kumar, V.; Lee, D.-J. Iron particle and anisotropic effects on mechanical properties of magneto-sensitive elastomers. J. Magn. Magn. Mater. 2017, 441, 105–112. [Google Scholar] [CrossRef]
- Wu, C.; Cheng, C.; Abd El-Aty, A.; Li, T.; Qin, Y.; Yang, Q.; Hu, S.; Xu, Y.; Guo, X. Influence of particles size and concentration of carbonyl iron powder on magnetorheological properties of silicone rubber-based magnetorheological elastomer. Mater. Res. Express 2020, 7, 086101. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Borin, D.Y.; Bakhtiiarov, A.V.; Storozhenko, P.A. Influence of the size of magnetic filler particles on the properties of hybrid magnetic elastomer with magnetically hard filler. J. Magn. Magn. Mater. 2020, 498, 166071. [Google Scholar] [CrossRef]
- Gao, W.; Wang, X. Experimental and theoretical investigations on magnetoelastic shear behavior of isotropic MR elastomers under gradient magnetic fields. J. Magn. Magn. Mater. 2019, 483, 196–204. [Google Scholar] [CrossRef]
- Borin, D.Y.; Stepanov, G.V.; Odenbach, S. Tuning the tensile modulus of magnetorheological elastomers with magnetically hard powder. J. Phys. Conf. Ser. 2013, 412, 012040. [Google Scholar] [CrossRef]
- Linke, J.M.; Borin, D.Y.; Odenbach, S. First-order reversal curve analysis of magnetoactive elastomers. RSC Adv. 2016, 6, 100407. [Google Scholar] [CrossRef]
- Sanchez, P.A.; Stolbov, O.V.; Kantorovich, S.S.; Raikher, Y.L. Modeling the magnetostriction effect in elastomers with magnetically soft and hard particles. Soft Matter 2019, 15, 7145. [Google Scholar] [CrossRef] [PubMed]
- Bellucci, F.S.; de Almeida, F.C.L.; Nobre, M.A.L.; Rodríguez-Pérez, M.A.; Paschoalini, A.T.; Job, A.E. Magnetic properties of vulcanized natural rubber nanocomposites as a function of the concentration, size and shape of the magnetic fillers. Compos. Part B 2016, 85, 196–206. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kumar, V.; Lee, D.J. Compressive properties of magnetorheological elastomer with different magnetic fields and types of filler. Polym. Adv. Technol. 2019, 30, 1106–1115. [Google Scholar] [CrossRef]
- Kumar, V.; Lee, D.J. Mechanical properties and magnetic effect of new magneto-rheological elastomers filled with multi-wall carbon nanotubes and iron particles. J. Magn. Magn. Mater. 2019, 482, 329–335. [Google Scholar] [CrossRef]
- Tadic, M.; Kralj, S.; Kopanja, L. Synthesis, particle shape characterization, magnetic properties and surface modification of superparamagnetic iron oxide nanochains. Mater. Charact. 2019, 148, 123–133. [Google Scholar] [CrossRef]
- Jung, H.S.; Choi, H.J. Hydrothermal fabrication of octahedral-shaped Fe3O4 nanoparticles and their magnetorheological response. J. Appl. Phys. 2015, 117, 17E708. [Google Scholar] [CrossRef]
- Laherisheth, Z.; Upadhyay, R.V. Influence of particle shape on the magnetic and steady shear magnetorheological properties of nanoparticle based MR fluids. Smart Mater. Struct. 2017, 26, 054008. [Google Scholar] [CrossRef]
- Wu, J.; Pei, L.; Xuan, S.; Yan, Q.; Gong, X. Particle size dependent rheological property in magnetic fluid. J. Magn. Magn. Mater. 2016, 408, 18–25. [Google Scholar] [CrossRef]
- Aloui, S.; Klüppel, M. Magneto-rheological response of elastomer composites with hybrid-magnetic fillers. Smart Mater. Struct. 2014, 24, 025016. [Google Scholar] [CrossRef]
- Kumar, J.S.; Alex, D.G.; Paul, P.S. Synthesis of Magnetorheological fluid Compositions for Valve Mode Operation. Mater. Today Proc. 2020, 22, 1870–1877. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Borin, D.Y.; Kramarenko, E.Y.; Bogdanov, V.V.; Semerenko, D.A.; Storozhenko, P.A. Magnetoactive Elastomer Based on Magnetically Hard Filler: Synthesis and Study of Viscoelastic and Damping Properties. Polym. Sci. Ser. A 2014, 56, 603–613. [Google Scholar] [CrossRef]
- Kalina, K.A.; Brummund, J.; Metsch, P.; Kästner, M.; Borin, D.Y.; Linke, J.M.; Odenbach, S. Modeling of magnetic hystereses in soft MREs filled with NdFeB particles. Smart Mater. Struct. 2017, 26, 105019. [Google Scholar] [CrossRef]
- Ahmad Khairi, M.H.; Mazlan, S.A.; Choi, S.B.; Abdul Aziz, S.A.; Mohamad, N.; Hapipi, N.M.; Nordin, N. Role of Additives in Enhancing the Rheological Properties of Magnetorheological Solids: A Review. Adv. Eng. Mater. 2018, 21, 1800696. [Google Scholar] [CrossRef]
- Chen, D.; Yu, M.; Zhu, M.; Qi, S.; Fu, J. Carbonyl iron powder surface modification of magnetorheological elastomers for vibration absorbing application. Smart Mater. Struct. 2016, 25, 115005. [Google Scholar] [CrossRef]
- Ahmad Khairi, M.H.; Mazlan, S.A.; Ubaidillah; Ku Ahmad, K.Z.; Choi, S.B.; Abdul Aziz, S.A.; Yunus, N.A. The field-dependent complex modulus of magnetorheological elastomers consisting of sucrose acetate isobutyrate ester. J. Intell. Mater. Syst. Struct. 2017, 28, 1993–2004. [Google Scholar] [CrossRef]
- Ge, L.; Gong, X.; Fan, Y.; Xuan, S. Preparation and mechanical properties of the magnetorheological elastomer based on natural rubber/rosin glycerin hybrid matrix. Smart Mater. Struct. 2013, 22, 115029. [Google Scholar] [CrossRef]
- Bira, N.; Dhagat, P.; Davidson, J.R. A review of magnetic elastomers and their role in soft robotics. Front. Robot. AI 2020, 7, 588391. [Google Scholar] [CrossRef] [PubMed]
- Genc, S.; Derin, B. Field Responsive Fluids–A Review. Key Eng. Mater. 2012, 521, 87–99. [Google Scholar] [CrossRef]
- Gopinath, B.; Sathishkumar, G.K.; Karthik, P.; Charles, M.M.; Ashok, K.G.; Ibrahim, M.; Akheel, M.M. A systematic study of the impact of additives on structural and mechanical properties of Magnetorheological fluids. Mater. Today Proc. 2021, 37, 1721–1728. [Google Scholar] [CrossRef]
- Sedlacik, M.; Pavlinek, V.; Lehocky, M.; Mracek, A.; Grulich, O.; Svrcinova, P.; Filip, P.; Vesel, A. Plasma-treated carbonyl iron particles as a dispersed phase in magnetorheological fluids. Colloids Surf. A Physicochem. Eng. Asp. 2011, 387, 99–103. [Google Scholar] [CrossRef]
- López-López, M.T.; De Vicente, J.; González-Caballero, F.; Durán, J.D.G. Stability of magnetizable colloidal suspensions by addition of oleic acid and silica nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2005, 264, 75–81. [Google Scholar] [CrossRef]
- Bae, D.H.; Choi, H.J.; Choi, K.; Do Nam, J.; Islam, M.S.; Kao, N. Microcrystalline cellulose added carbonyl iron suspension and its magnetorheology. Colloids Surf. A Physicochem. Eng. Asp. 2017, 514, 161–167. [Google Scholar] [CrossRef]



| Matrix | Magnetic Particle | MRE Type | Ref. | ||
|---|---|---|---|---|---|
| Type | Size | Content | |||
| Silicone rubber | CIP | 3–4 μm | 10–20–30 vol% | Anisotrop. | [2] |
| 2 μm | 15 vol% | Isotrop./Anisotrop. | [16] | ||
| 3 μm | 27 vol% | Anisotrop. | [17] | ||
| 3 μm | 20 to 70 wt% | – | [18] | ||
| 2–10 μm | 10 vol% | Anisotrop. | [19] | ||
| 3–5 μm | 80 wt% | Isotrop. | [20] | ||
| 1.25 ± 0.55 μm | 0–10–30 vol% | Isotrop./Anisotrop. | [21] | ||
| 3–5 μm | 23 vol% | Anisotropic | [22] | ||
| 4–6 to 220 μm | 30 vol% | Isotrop./Anisotrop. | [23] | ||
| 5–9 μm | 10–40 wt% | Isotrop. | [24] | ||
| 3.9–5 μm | 5 to 40 vol% | Isotrop./Anisotrop. | [25] | ||
| 3–5 μm | 70 wt% | Isotrop. | [26] | ||
| 45 µm | 0:20:80 | Isotrop./Anisotrop. | [27] | ||
| 3.9–5 μm | 12.5 to 40 vol% | Isotrop. | [28] | ||
| 2–5 μm | 27 vol% | Isotrop./Anisotrop. | [29] | ||
| 3.9 to 5 μm | 30 vol% | Isotrop./Anisotrop. | [30] | ||
| 5 μm | 40–50–60 wt% | Isotropic | [31] | ||
| IP | 10 μm | 30 vol% | Isotropic | [32] | |
| 50–150 μm | 30 vol% | Isotrop./Anisotrop. | [33] | ||
| 0 to 250 µm | 30–60 wt% | Anisotrop. | [34] | ||
| 5–9 μm | 30 vol% | Anisotrop. | [35] | ||
| 2.5 μm | 30 vol% | Anisotropic | [36] | ||
| IP/Fe3O4 | 2–3/0.2–0.3 µm | 7–14/22–24–27 vol % | Isotrop. | [37] | |
| CIP/FeNdB | 3/1–100 μm | 35/68 wt% | Anisotrop. | [38] | |
| Bi-disp.: CIP (plates/spherical) | 1–10 μm | 70 wt% | Isotrop./Anisotrop. | [39] | |
| Natural rubber | CIP | 0.5–5 μm | 27 vol% | Isotrop./Anisotrop. | [40] |
| 3–5 μm | 55 wt% | Isotrop./Anisotrop. | [41] | ||
| IP | <60 μm | 0 to 37 vol% | Isotrop. | [42] | |
| Carbon Black | 100 μm | 5.6 to 38.4 vol% | Isotrop. | [43] | |
| Iron Sand | 45–56 μm | 70 wt% | Isotrop./Anisotrop. | [44] | |
| Bi-disp.: CIP/γ-Fe2O3 | 3–5 μm/leng. = 500 nm | 62 wt% | Anisot. | [45] | |
| Ni-Zn Ferrite | 6 μm | 0 to 45 wt% | Isotrop./Anisotrop. | [46] | |
| Polyurethane | CIP | 6–9 μm | 1.5–33 vol% | Anisotrop. | [47] |
| 5–8 μm | 50–60–70 wt% | Isotrop./Anisotrop. | [48] | ||
| 6–9 μm | 33 vol% | Anisotrop. | [49] | ||
| 5 μm | 10–20–40 vol% | Isotrop. | [50] | ||
| EPDM | Core-shell: CIP/CB | 3.8–5.3 μm | 0:10 to 40 vol% | Anisotrop. | [51] |
| Bi-disp.: CIP/BIP | 3.8–5.4/5–16 μm | 1.7 to 14.65 wt% | Isotrop. | [52] | |
| Bi-disp.: BT/Graphite BT/Mica | mica 10 μm/graphite 10 μm | 30/5 to 20 vol% (both) | Isotrop. | [53] | |
| Thermoplastic rubber | IP | 60 µm | 35 vol% | Isotrop./Anisotrop. | [54] |
| Aramid Short Fibers | leng./diam (3 mm/10–12 μm) | 1 to 10 wt% | Isotrop. | [55] | |
| CIP | 3–5 μm | 67 wt% | Isotrop. | [56] | |
| SBR | Silica | 20–50 nm | 30 to 90 wt% | Isotrop. | [57] |
| SBR/BR | Silica | – | 31 vol% | Isotrop. | [58] |
| PU/SR | CIP | 3–5 μm | 63–73 wt% | Isotrop. | [59] |
| Polyethylene | Bi-disp.: Mica/ Wollastonite | 17 μm/49 μm | 5–10–15 wt% | Isotrop. | [60] |
| NR/SR/Chloroprene | IP | 2.5 μm | 60 wt% | Anisotrop. | [61] |
| Epoxy resin | CIP | 4.5 µm | 33.3 to 71.4 wt% | Isotrop. | [62] |
| Acrylonitrile butadiene rubber | Fe12O19Sr | – | 66.7–75–80 wt% | Isotrop. | [63] |
| Bromobutyl rubber | CIP | – | 60–70 wt% | Isotrop./Anisotrop. | [64] |
| Ethylene/Acrylic | CIP | 3–5 μm | 0–10–40 vol% | Isotrop./Anisotrop. | [65] |
| Carrier Fluid | Magnetic Particle | Ref. | ||
|---|---|---|---|---|
| Type | Size | Content | ||
| Silicone oil | MWCNT/CoFe2O4 (Nanocomposite) | fibrous shape | 25 wt% | [66] |
| MnFe2O4 | 20–30 nm | 10 vol% | [67] | |
| Bi-dispersion: CIP(µ)/CIP(Nano) | 2–4 μm/30–50 nm | 40 vol% | [68] | |
| Cobalt(µ)-flower-like Shape | 2–5 μm | 12 vol% | [69] | |
| Fe3O4-triangular-shaped | ~100 nm | 7 vol% | [70] | |
| Bi-dispersion: IP(µ) Flake/Fe3O4 (Nano) | 15–30 μm/~ | 5–10–20 vol% | [71] | |
| Core–shell: Fe3O4POA (Poly O-anisidine) | ~445 nm | 10 vol% | [72] | |
| Core–shell: Fe3O4/(PS) Polystyrene | ~127 nm | 10 vol% | [73] | |
| Core–shell: Fe3O4/(PS) Polystyrene | 50–100 nm | 10 vol% | [74] | |
| Fe-Ga Alloy: Flake Shaped Galfenol | irregular shape | 30 wt% | [75] | |
| Core–shell: CIP/PANI (Polyaniline) | ~3.66 μm | 10 vol% | [76] | |
| Fe3O4/PANI (Polyaniline) | fibrous shape | 2 vol% | [77] | |
| Cobalt Nanofibers | fibrous shape | 12 vol% | [78] | |
| Bi-dispersion: CIP(µ)/Halloysite | 4.25 μm/625 nm | 70/1 wt% | [79] | |
| Bi-dispersion: CIP(µ)/γ-Fe2-O3 | 7 μm | 70/0.5 to 2 wt% | [80] | |
| CIP (µ) | 6 μm | 20–30 vol% | [81] | |
| Castor oil | CoNi-Nanoclusters | 450 nm | 15–20 vol% | [82] |
| Bi-dispersion: CIP(µ)/Silica (Nano) | 10–12 μm/20 nm | 4.5 vol% | [83] | |
| Paraffin oil | IP(µ)—Flake Shaped | 7–8 µm | 10–20 vol% | [84] |
| Bi-dispersion: IP(µ)/IP(µ)—Plate Like | 2 (small)/19 (large) μm | 16 vol% | [85] | |
| Ethylene glycol | Fumed Silica Hydrophile | 14 nm | 25 wt% | [86] |
| Poly(ethylene oxide) | CIP(µ) | 2 μm | 20 vol% | [87] |
| Lubricating oil (Yubase 8) | CIP(µ)/Organic Clay | 4.25 μm | 25/0.5 to 3 wt% | [88] |
| kerosene | Fe3O4 | 13 nm | 11–17 vol% | [89] |
| viscoelastic matrix: Polyisobutylene (PIB)/polybutene (PB) | CIP (µ) | 7 μm | 25 vol% | [90] |
| Blend: silicone oil/Honey/organic oil | IP (µ) | 1–10 µm | 30 wt% | [91] |
| Blend: low + high viscous mineral oils | CIP (µ) | 4–6 µm | 80 wt% | [92] |
| Hong oil | CIP (µ) | 6–9 µm | 20–30–40 vol% | [93] |
| Ionic liquid | Core–shell: Silica/CIP | 0.5–2.5 µm | 10 vol% | [94] |
| Mineral oil | CIP (µ) | 900 ± 300 nm | 1.55 to 7.9 vol% | [95] |
| Grease medium | CIP (µ) | 7 μm | 50 wt% | [96] |
| G′ (Mpa) | G″ (Mpa) | Particles | Content (%) | Matrix | Loading | Mag. Field (mT) | Ref. |
|---|---|---|---|---|---|---|---|
| 0.24 | \ | CIP-PMMA | 30 (wt) | HTV SR | shear | 1000 | [20] |
| 1.1 | 0.5 | CIP | 40 (vol) | SR | shear | 450 | [28] |
| 2.2 | 0.75 | CIP | 27 (vol) | SR | shear | 651 | [29] |
| 3 | 0.9 | CIP | 30 (vol) | RTV SR | shear | 325 | [36] |
| 3 | 1 | CIP | 40 (vol) | RTV SR | shear | 300 | [99] |
| 3.05/1.25 | \ | CIP | 70 (wt) | SR | compression/shear | 500 | [219] |
| 4.6 | \ | CIP | 30 (vol) | SR | compression | 750 | [30] |
| 10 | 3.5 | CIP | 30 (vol) | NR | compression | 60 | [21] |
| 16 | 9 | Fe3O4 | 40 (wt) | waste tires R | shear | 1000 | [220] |
| 20 | 4 | CIP | 30 (vol) | SR | compression | 500 | [23] |
| G′ (Kpa) | G″ (Kpa) | Particles | Content (%) | Fluid | Loading | Mag. Field (mT) | Ref. |
|---|---|---|---|---|---|---|---|
| 12 | 5 | CIP/Silica | 4.5 (vol) | Castor oil | Shear | 200 | [83] |
| 60 | 9 | MWCNT/COFe2O4 | 25 (wt) | Silicone oil | Shear | 250 | [66] |
| 300 | 13 | Co-Ni | 20 (vol) | Castor oil | Shear | 500 | [82] |
| 1000 | 100 | CIP | 20 (vol) | Silicone oil | Shear | 280 | [71] |
| 1000 | 100 | Fe-Ga | 30 (wt) | Silicone oil | Shear | 430 | [75] |
| 1000 | 100 | CIP | 10 (vol) | Silicone oil | Shear | 430 | [76] |
| 1100 | 300 | Co | 12 (vol) | Silicone oil | Shear | 312 | [69] |
| 3000 | 100 | CIP | 20 (vol) | Paraffin oil | Shear | 90 | [84] |
| 3000 | 300 | CIP | 40 (vol) | Silicone oil | Shear | 350 | [68] |
| 4000 | 200 | CIP | 10 (vol) | Silicone oil | Shear | 430 | [74] |
| 10,000 | 200 | Ni | 22 (wt) | Castor oil | Shear | 1000 | [133] |
| 10,000 | 100 | CIP | 20 (vol) | Silicone oil | Shear | 430 | [221] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouabah, S.; Didouche, F.-Y.; Khebli, A.; Aguib, S.; Chikh, N. The Advancing Understanding of Magnetorheological Fluids and Elastomers: A Comparative Review Analyzing Mechanical and Viscoelastic Properties. Magnetochemistry 2025, 11, 62. https://doi.org/10.3390/magnetochemistry11080062
Rouabah S, Didouche F-Y, Khebli A, Aguib S, Chikh N. The Advancing Understanding of Magnetorheological Fluids and Elastomers: A Comparative Review Analyzing Mechanical and Viscoelastic Properties. Magnetochemistry. 2025; 11(8):62. https://doi.org/10.3390/magnetochemistry11080062
Chicago/Turabian StyleRouabah, Salah, Fadila-Yasmina Didouche, Abdelmalek Khebli, Salah Aguib, and Noureddine Chikh. 2025. "The Advancing Understanding of Magnetorheological Fluids and Elastomers: A Comparative Review Analyzing Mechanical and Viscoelastic Properties" Magnetochemistry 11, no. 8: 62. https://doi.org/10.3390/magnetochemistry11080062
APA StyleRouabah, S., Didouche, F.-Y., Khebli, A., Aguib, S., & Chikh, N. (2025). The Advancing Understanding of Magnetorheological Fluids and Elastomers: A Comparative Review Analyzing Mechanical and Viscoelastic Properties. Magnetochemistry, 11(8), 62. https://doi.org/10.3390/magnetochemistry11080062






