Case Study on Homogeneous–Heterogeneous Chemical Reactions in a Magneto Hydrodynamics Darcy–Forchheimer Model with Bioconvection in Inclined Channels

Abstract

This study focuses on understanding the bioconvection in Jeffery–Hamel (JH) flow, which has valuable applications in areas like converging dies, hydrology, and the automotive industry, which make it a topic of practical importance. This research aims to explore Homogeneous–Heterogeneous (HH) chemical reactions in a magnetic Darcy–Forchheimer model with bioconvection in convergent/divergent channels. To analyze the role of porosity, the Darcy–Forchheimer law is applied. The main system of equations is simplified through similarity transformation into ordinary differential equations solved numerically with the help of the NDSolve technique. The results, compared with previous studies for validation, are presented through graphs and tables. The study reveals that in divergent channels, the velocity decreases with higher solid volume fractions, while in convergent channels, it increases. Furthermore, various physical parameters, such as the Eckert number and porosity parameter, increase skin friction in divergent channels but decrease it in convergent channels. These findings suggest that the parameters investigated in this study can effectively enhance homogeneous reactions, providing valuable insights for practical applications.

1. Introduction

Bioconvection discusses the natural movement that occurs when microorganisms, such as bacteria, interact with a base fluid, leading to density-driven instability. This phenomenon is especially visible in dilute fluids where microorganisms tend to migrate, causing variations in density. Bioconvection has significant applications in biological sciences and bio-microsystems research, as well as in practical fields like microbially enhanced oil recovery. In this context, microorganisms and nutrients, such as vitamins and proteins, are introduced into oil-bearing layers to improve permeability and correct material inconsistencies. Understanding bioconvection in conjunction with physical factors is essential for such applications. The study of bioconvection becomes even more interesting and realistic when integrated with non-Newtonian fluid characteristics, slip conditions, induced magnetic fields, and nonlinear thermal radiation. For instance, Maxwell nanofluid flow combined with gyrotactic microorganisms, heat generation, and nonlinear radiative effects has been explored by Chu et al. [1], providing valuable insights into these complex interactions. A study of radiative magnetized nanofluid flow involving microorganisms and chemical reactions was conducted by Ramzan et al. [2], who included motile bacteria in their analysis. Kairi et al. [3] studied the MHD flow of Casson nanofluid past a stretching sheet with gyrotactic microorganisms. Dhlamini et al. [4] analyzed chemically reactive nanofluid flow with activation energy and bioconvection, noting an increase in the microorganism profile with higher Brownian motion parameters. Li et al. [5] explored how increasing the Prandtl number enhanced the density profile of gyrotactic bacteria in the bioconvective flow of Casson hybrid nanofluid. The researchers explored various model such as [6,7,8].

Homogeneous–Heterogeneous (HH) reactions are important in different chemical processes, including biochemical reactions, fermentation, electrochemical catalysis, semiconductor film formation, and iron production in blast furnaces. Regardless of their importance, the effects of (HH) reactions on fluid flow, particularly in microchannels between two cylinders, have been underexplored in existing research. These reactions exhibit distinct conversion rates of reactants on the fluids flow active surfaces. Chaudhary and Merkin [9] constructed a mathematical model to study (HH) reactions near a stagnation point in boundary layer flow, employing isothermal cubic kinetics for Homogeneous reactions and first-order kinetics for Heterogeneous ones. They later expanded their work to reveal the loss of autocatalysts in such systems [10]. Merkin [11] further examined (HH) reactions in boundary layer flow over a flat plate. Abbas and Sheikh [12] examined the influence of uniform suction and slip conditions on (HH) reactions in Casson fluid over an extending/narrowing sheet. Giri et al. [13] examined MHD nanofluid flow using stretchable cylinders, incorporating (HH) reaction mechanisms and advanced heat transfer techniques to gain deeper insights. Due to the importance of chemical reactions, scientists have discussed different models, such as [14,15].

The flow of fluid in convergent/divergent (CD) channels plays an essential role in various scientific and technological fields. It finds applications in chemical, mechanical, industrial, and biological engineering. The flow of blood in veins is due to (CD) channels. Essentially, (CD) channels involve a two-dimensional incompressible flow between convergent/divergent walls intersecting at an angle, originating from a source or sink. These channels are extensively utilized in biomechanical systems, pharmaceutical engineering, aeronautics, and dynamic systems. Moreover, industries such as thermosphere, locomotive fabrication, discarded organization, groundwater cure, power generation, petroleum extraction, permeable coverings, and agriculture also influence (CD) channels. Jeffery and Hamel [16,17] introduced a pioneering model for fluid flow in (CD) channels. Kumar et al. [18] explored tri-hybrid nanofluid flow through a rotating disk. Asghar et al. [19] studied the influence of the Joule effect on heat transfer in expandable (CD) channels using tri-hybrid nanofluids with varying parameters. Ahmad and Farooq [20] scrutinized the double diffusive Jeffrey–Hamel flow of small fluid volume in porous media. Adnan and Ashraf [21] examined how the Joule effect and heat generation/absorption influence heat transfer in tri-hybrid nanofluids within stretchable (CD) channels. Shilpa et al. [22] analyzed the influence of energy on thermophoretic particle deposition in nanomaterial flows through (CD) channels. Numerous researchers have further studied fluid flow in extending or narrowing channels [23,24,25,26,27,28,29], contributing significantly to the understanding of (CD) channel dynamics.

The interaction between magnetic fields and electrically conducting fields is known as Magneto hydrodynamics (MHD). In MHD flows, the existence of a magnetic field induces electric currents within the fluid, resulting in a Lorentz force that alters the fluid’s flow behavior. This interplay is critical for optimizing processes in various industries. Recent advances in MHD research have focused on developing numerical methods and experimental approaches to analyze the complex dynamics of MHD systems. MHD has diverse applications, including power generation, materials processing, and space exploration. For instance, MHD generators in power plants convert thermal energy into electricity, while MHD pumps and mixers are employed to control fluid behavior in materials processing. Similarly, MHD engines are instrumental in satellite motion control for space exploration. Researchers like Makinde et al. [30] have studied the MHD flow of nanofluids over radiatively heated surfaces, and Dehghani, Toghraie, and Mehmandoust [31] explored the impact of MHD on flow behavior in fluted channels. ElShorbagy et al. [32] investigated mixed convective nanofluid flow in trapezoidal channels with porous media, observing that an increase in porous material height affects the Nusselt number. Mohammadi and Nassab [33] examined the effects of magnetic fields in cavities with complex geometries, concluding that stronger magnetic fields reduce flow intensity. Other studies, such as [34,35,36,37,38], have explored MHD effects on various fluids and configurations, demonstrating the vast potential of MHD in diverse scientific and industrial applications. The uses of MHD in fluid flow are very essential, such as [39,40,41].

On the basis of the literature review, it is found that the study of Homogeneous–Heterogeneous chemical reactions in an MHD Darcy–Forchheimer Model with bioconvection in a convergent/divergent Channel is relatively new. The bioconvection model itself is a well-established framework in fluid flow through porous structures. This research provides valuable insights into the behavior and performance of such a bioconvection effect within porous media. As a result, this work paves a new and innovative path in the field, offering numerous practical applications and attracting both academics and industry professionals eager to leverage these groundbreaking findings to foster creativity and efficiency across various manufacturing processes. The widespread application of this model could benefit numerous industries, including automotive, solar thermal systems, microfluidics, medical devices, nuclear reactors, and aerospace.

2. Formulation of the Model

Let us consider a two-dimensional, incompressible, bioconvection Jeffery–Hamel (JH) flow, which is flowing through convergent/divergent and stretching/shrinking channels. The following assumptions are made in this analysis:

• The flow is considered steady and incompressible.
• The influence of thermal energy and viscous dissipation is incorporated into the analysis.
• The flow is affected by non-parallel stretchable channels, which induce variable flow characteristics due to the channel geometry.
• The effects of the magnetic field and the non-Newtonian behavior are also considered, along with heat and mass transfer phenomena.
• The coupled system of equations is solved using suitable mathematical techniques, such as the similarity transformation, to obtain the flow and temperature profiles.
• We use polar coordinates $\left(r,\hspace{0.17em}\theta \right)$ to formulate the mode.
• The energy, continuity, and momentum equations are reduced, such as in [42,43], as follows:

The geometry of the problem is represented in Figure 1.

$${\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial }{\partial r}}\left(ru\right)=0$$

(1)

$$u{\displaystyle \frac{\partial u}{\partial r}}=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial p}{\partial r}}+{\displaystyle \frac{\mu }{\rho }}\left({\displaystyle \frac{{\partial }^{2}u}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^{2}u}{\partial {\theta }^2}}-{\displaystyle \frac{u}{r}}\right)-{\displaystyle \frac{v}{\rho }}{\displaystyle \frac{u}{k}}-F^{*}{u}^2,$$

(2)

$${\displaystyle \frac{2}{r^2}}{\displaystyle \frac{\partial u}{\partial \theta }}{\displaystyle \frac{\mu }{\rho }}-{\displaystyle \frac{1}{r\rho }}{\displaystyle \frac{\partial p}{\partial \theta }}=0,$$

(3)

$$u{\displaystyle \frac{\partial T}{\partial r}}=\alpha \left({\displaystyle \frac{{\partial }^{2}T}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial T}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^{2}T}{\partial {\theta }^2}}\right)-{\displaystyle \frac{Q_0}{\left(\rho c_p\right)r^2}}T+\left({\displaystyle \frac{\partial \Delta h_1}{{\delta }_s}}\right){\displaystyle \frac{K{r}^4}{\left(\rho c_p\right)}}\hspace{0.17em}A{B}^3$$

(4)

$$u{\displaystyle \frac{\partial A}{\partial r}}=D_A\left({\displaystyle \frac{{\partial }^{2}A}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial A}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^{2}A}{\partial {\theta }^2}}\right)\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}K{r}^{4}A{B}^3$$

(5)

$$u{\displaystyle \frac{\partial B}{\partial r}}=D_B\left({\displaystyle \frac{{\partial }^{2}B}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial B}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^{2}B}{\partial {\theta }^2}}\right)\hspace{0.17em}+\hspace{0.17em}K{r}^{4}A{B}^3$$

(6)

$$u{\displaystyle \frac{\partial N}{\partial r}}=D_N\left({\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial N}{\partial r}}+{\displaystyle \frac{{\partial }^{2}N}{\partial r^2}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^{2}N}{\partial {\theta }^2}}\right)\hspace{0.17em}\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{b{W}_C{r}^2}{A_W}}\left(N{\displaystyle \frac{{\partial }^{2}A}{\partial r^2}}+{\displaystyle \frac{\partial N}{\partial r}}{\displaystyle \frac{\partial A}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{\partial N}{\partial \theta }}{\displaystyle \frac{\partial A}{\partial \theta }}\hspace{0.17em}+\hspace{0.17em}{\displaystyle \frac{N}{r^2}}{\displaystyle \frac{{\partial }^{2}A}{\partial {\theta }^2}}\right)\hspace{0.17em}$$

(7)

$$\left.\begin{array}{l}u={\displaystyle \frac{U}{r}},\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{\partial T}{\partial \theta }}=0,\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{\partial u}{\partial \theta }}=0,\hspace{0.17em}{\displaystyle \frac{\partial A}{\partial \theta }}={\displaystyle \frac{k_s}{D_A}}A,\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{\partial B}{\partial \theta }}=\hspace{0.17em}\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{k_s}{D_B}}A,\hspace{0.17em}\hspace{0.17em}{\displaystyle \frac{\partial N}{\partial \theta }}=0\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}\theta =0,\\ u_r=U_w={\displaystyle \frac{s}{r}},\hspace{0.17em}\hspace{0.17em}T={\displaystyle \frac{T_w}{r^2}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}A=A_w,\hspace{0.17em}\hspace{0.17em}B=\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}N=\hspace{0.17em}{N}_w\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}\theta =\alpha .\end{array}\right\}$$

(8)

Here, $U$ designates the frequency moment in a circular way, $U_w$ depicts velocity of the wall, $T_w$ represents temperature, $\mu$ represents dynamic viscosity, $k$ designates the medium’s permeability, $K$ designates thermal conductivity, $\rho$ is used for the density of the fluid, and $c_p$ represents heat capacity.

$$F\left(\theta \right)=\hspace{0.17em}r\hspace{0.17em}u\hspace{0.17em}\left(r,\hspace{0.17em}\theta \right).$$

(9)

The following are the transformations:

$$f\left(\eta \right)={\displaystyle \frac{F\left(\theta \right)}{U}},\hspace{0.17em}\eta ={\displaystyle \frac{\theta }{\alpha }},\hspace{0.17em}\mathrm{\Phi }={\displaystyle \frac{T}{T_w}}{r}^2,\hspace{0.17em}\hspace{0.17em}P\left(\eta \right)={\displaystyle \frac{A}{A_w}}{r}^2,\hspace{0.17em}\hspace{0.17em}H\left(\eta \right)={\displaystyle \frac{B}{A_w}}{r}^2,\hspace{0.17em}X\left(\eta \right)={\displaystyle \frac{N}{N_w}}{r}^2$$

(10)

After applying the transformations, we obtain the governing equations:

$$f^{‴}+2\alpha \mathrm{Re}\left(f{f}^{\prime }\right)+\left(4-K_p\right){\alpha }^2{f}^{\prime }+2{\alpha }^2{F}_r{f^{\prime }}^2=0,$$

(11)

$${\mathrm{\Phi }}^{″}+4{\alpha }^2\mathrm{\Phi }+2\mathrm{Pr}\mathrm{Re}\alpha \hspace{0.17em}\mathrm{\Phi }\hspace{0.17em}f+\hspace{0.17em}Q\hspace{0.17em}{\alpha }^2\mathrm{\Phi }\hspace{0.17em}+\hspace{0.17em}W{\alpha }^{2}P{H}^3=0,$$

(12)

$$P^{″}+\hspace{0.17em}4{\alpha }^{2}P+2S{c}_a\mathrm{Re}\alpha \hspace{0.17em}P\hspace{0.17em}f\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}S{c}_a\mathrm{\Gamma }P{H}^3=0,$$

(13)

$$H^{″}+\hspace{0.17em}4{\alpha }^{2}H+2S{c}_b\mathrm{Re}\alpha \hspace{0.17em}H\hspace{0.17em}f\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}S{c}_b\mathrm{\Gamma }P{H}^3=0,$$

(14)

$$X^{″}+\hspace{0.17em}4{\alpha }^{2}X+2Sb\mathrm{Re}\alpha \hspace{0.17em}X\hspace{0.17em}f-Pe\left(10{\alpha }^{2}XP+X^{\prime }{P}^{\prime }\hspace{0.17em}+\hspace{0.17em}X{P}^{″}\right)=0.$$

(15)

According to the associated conditions

$$\begin{array}{l}f\left(0\right)=\hspace{0.17em}0,\hspace{0.17em}{f}^{\prime }\hspace{0.17em}\left(0\right)=\hspace{0.17em}0,\hspace{0.17em}{\mathrm{\Phi }}^{\prime }\hspace{0.17em}\left(0\right)=\hspace{0.17em}0,\hspace{0.17em}f\left(1\right)=\hspace{0.17em}c,\hspace{0.17em}\mathrm{\Phi }\left(1\right)=\hspace{0.17em}1,\\ P^{\prime }\left(0\right)=\hspace{0.17em}\gamma \hspace{0.17em}\alpha \hspace{0.17em}P\left(0\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}P\left(1\right)=\hspace{0.17em}1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{H}^{\prime }\left(0\right)=\hspace{0.17em}{\displaystyle \frac{\gamma }{\lambda }}P\left(0\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}H\left(1\right)=\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{X}^{\prime }\left(0\right)=\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}X\left(1\right)=\hspace{0.17em}1.\end{array}$$

(16)

Here, $F_r={\displaystyle \frac{c_p}{\sqrt{k}}}$ designates the Darcy–Forchheimer constant, $K_p={\displaystyle \frac{\nu }{kU}}$ depicts the porosity parameter, $\mathrm{Re}={\displaystyle \frac{U\alpha }{\nu }}$ designates the Reynolds number, $Pr={\displaystyle \frac{\left(\rho c_p\right)U}{K}}$ represents the Prandtl number, and $c={\displaystyle \frac{s}{U}}$ represents the stretching parameter. For the convergent channel, we consider $\alpha <0$, and for the divergent channel, we assume $\alpha >0$.

3. Engineering Quantities

$$\mathrm{Re}C={\displaystyle \frac{f^{\prime }\left(1\right)}{f^{‴}+2\alpha \mathrm{Re}}}$$

(17)

$$\alpha Nu={\mathrm{\Phi }}^{\prime }\left(1\right)\left({\displaystyle \frac{1+Rd}{\alpha }}\right)$$

(18)

$$N{n}_X=-{\displaystyle \frac{1}{\alpha }}{X}^{\prime }\left(1\right)$$

(19)

4. Mathematical Technique and Validations

The scheme of Equations (11)–(14) with boundary conditions (15) are resolved by the NDSolve approach. This technique mathematically grabs differential equations. The system of (ODEs) comprises multiple equations denoted as $\left(s_1,s_2,s_3.......s_n\right)$, with $\xi$ as the independent variable and n is the dependent variable $\left(r_1,r_2,r_3,..........r_n\right)$. Furthermore, it contains boundary conditions resolved by the system of the partial differential equations. The NDSolve procedure is [{$\left(s_1,s_2,s_3.......s_n\right)$, BCs}, $\left(r_1,r_2,r_3,..........r_n\right)$, and {ξ, ξ_min, ξ_max}].

The flow chart of the proposed problem is shown in Figure 2.

5. Results and Discussion

In this segment, we examine different parameters like the alpha, porosity parameter, Reynolds number, and Peclet number against $f\left(\eta \right)$, $\mathrm{\Theta }\left(\eta \right)$, and $\varphi \left(\eta \right)$. Here, we analyze the behavior of these physical parameters on both convergent $\left(\alpha <0\right)$ and divergent $\left(\alpha >0\right)$ channels. The ranges of various physical parameters are considered to check their behavior and effects: $\hspace{0.17em}{\displaystyle \frac{\pi }{20}}\le \alpha \le {\displaystyle \frac{\pi }{100}},\hspace{0.17em}0.1\le kp\le 0.5,\hspace{0.17em}0.2\le \mathrm{Re}\le 0.6,\hspace{0.17em}0.1\le Sb\le 0.6,\hspace{0.17em}0.1,\le \hspace{0.17em}Pe\hspace{0.17em}\le \hspace{0.17em}0.5.$

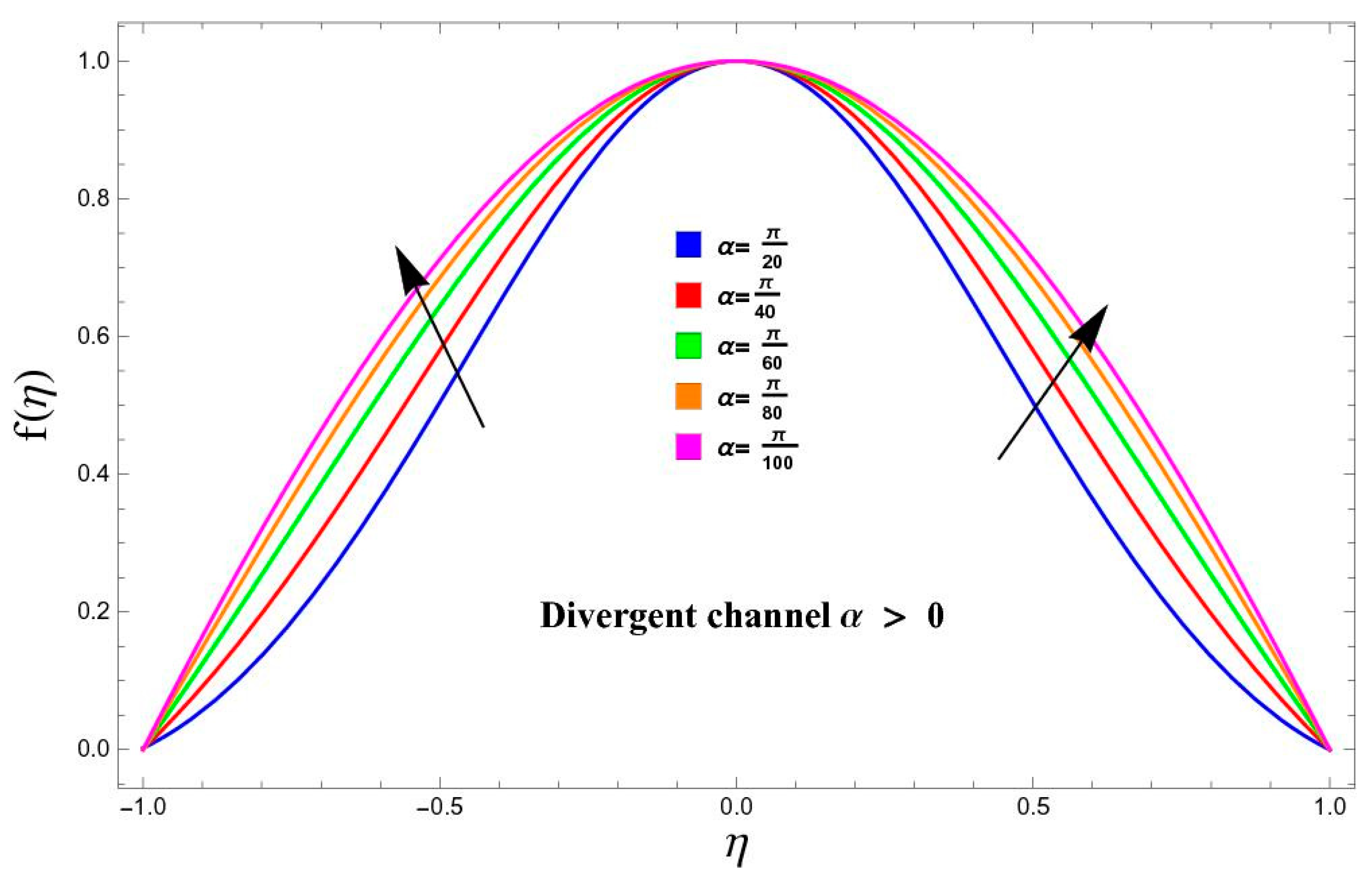
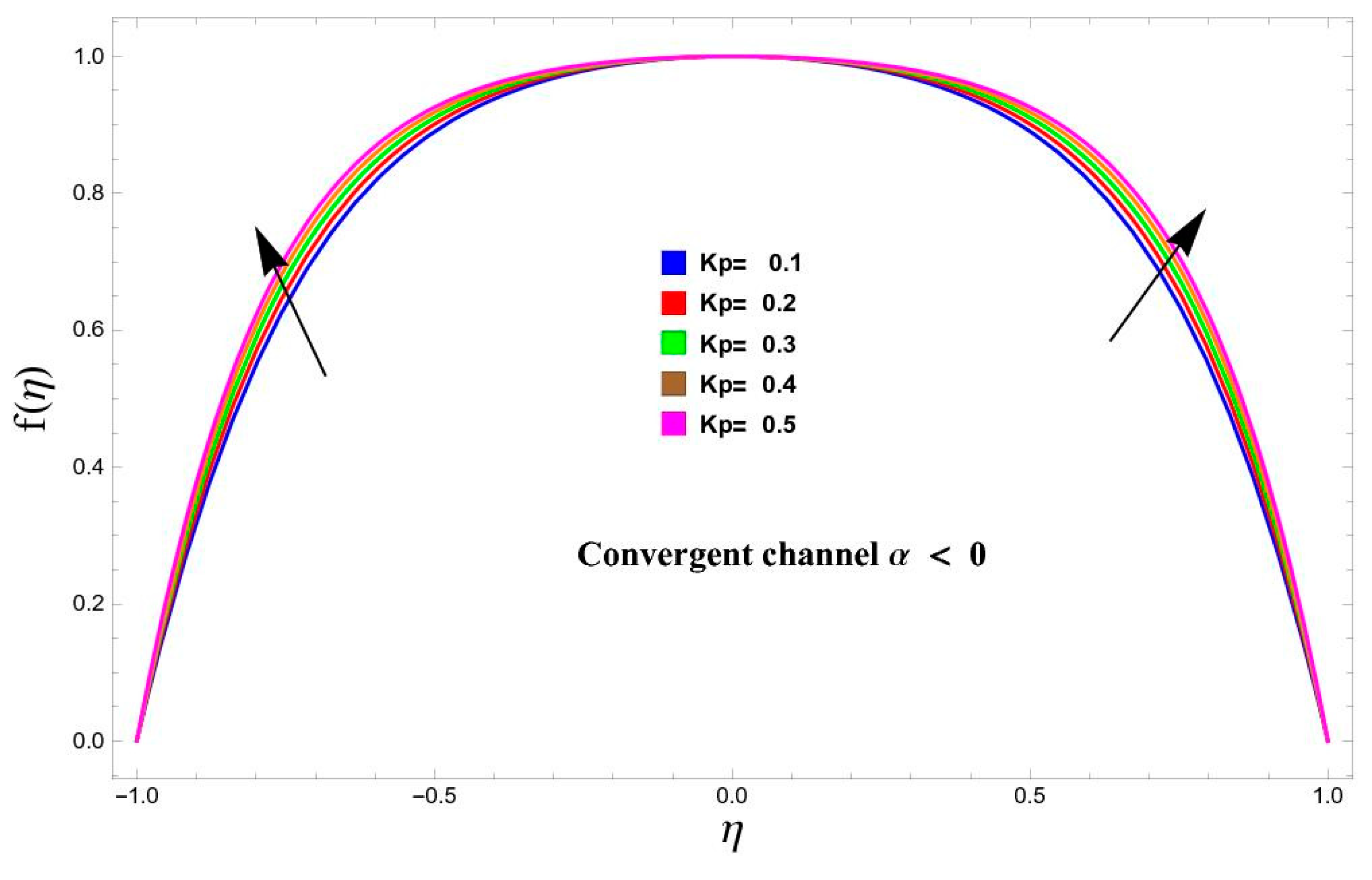
5.1. Variation in Velocity

This section explores the behavior of various parameters like the alpha $\alpha$ and porosity parameter $Kp$ for both convergent $\left(\alpha <0\right)$ and divergent $\left(\alpha >0\right)$ channels versus the velocity $f\left(\eta \right)$ profile. Figure 3 discusses the influence of angle $\alpha$ against velocity for the convergent $\left(\alpha <0\right)$ channel. The velocity behavior in a convergent $\left(\alpha <0\right)$ or divergent $\left(\alpha >0\right)$ channel is influenced by the channel’s geometry. In the convergent case, as $\alpha$ becomes more negative, the channel narrows, increasing flow resistance and reducing velocity. This restriction limits the space available for fluid movement, leading to a decline in velocity. Conversely, in the divergent case (see Figure 4), where $\alpha >0$, the channel expands, reducing resistance and allowing the fluid to accelerate. As a result, velocity increases with higher values of $\alpha$, as the widening geometry provides more space for fluid motion and facilitates smoother flow.

Furthermore, it is clear that velocity decreases in the upper or lower part of the channel while it is at its maximum in the center of the channel region. The logic behind the velocity enhancing with larger channel angle values is that the rising intensity of the inclination angle overcomes the impact of frictional forces and offers a greater reaction with velocity $f\left(\eta \right)$ due to the divergent channel’s strong effects. The influence of the porosity parameter $Kp$ versus velocity for convergent $\left(\alpha <0\right)$ and divergent walls is discussed in Figure 5 and Figure 6. Greater values of the porosity parameter enhance the velocity for both extending/narrowing walls $\left(\alpha <0,\alpha >0\right)$.

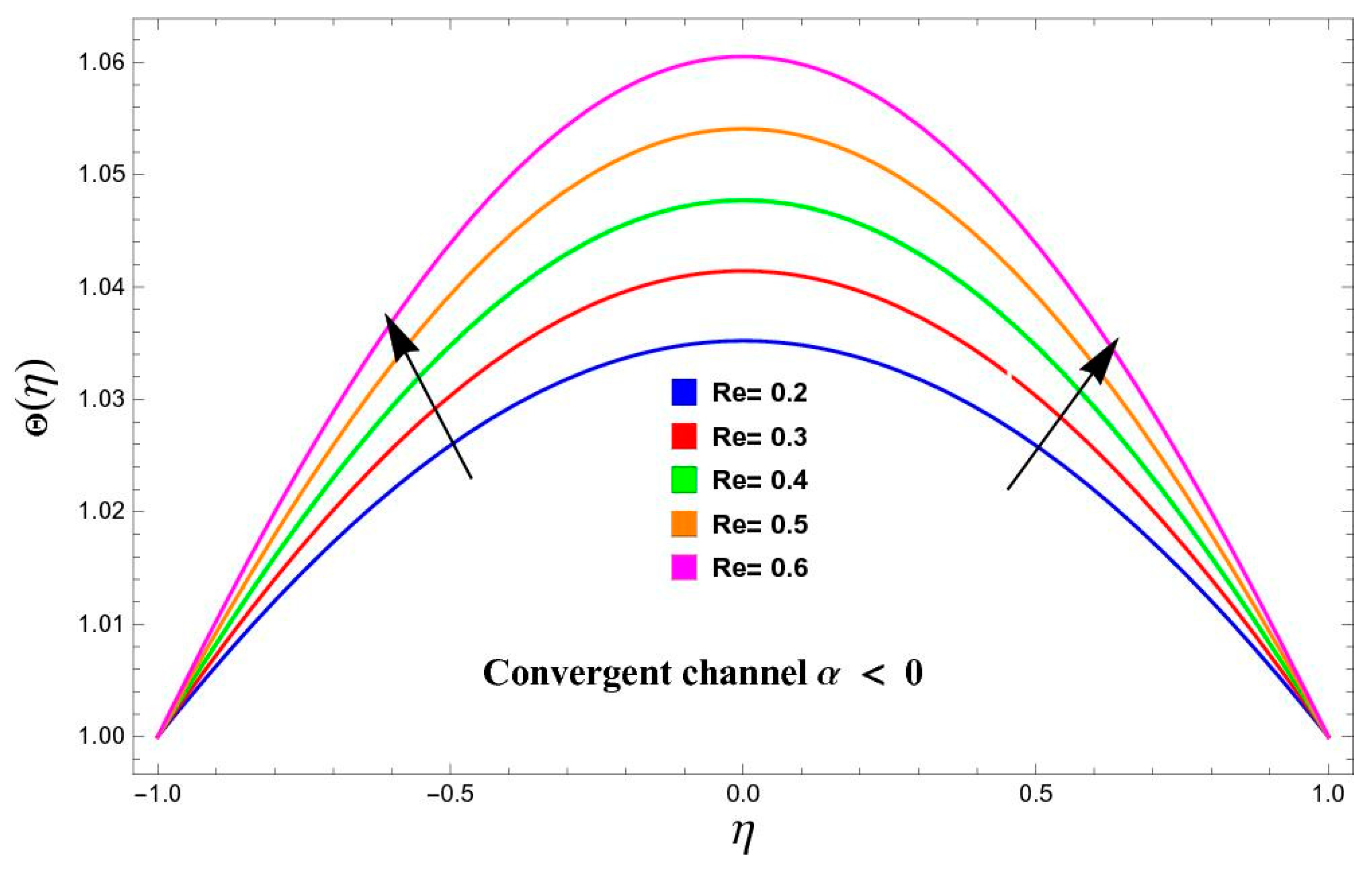
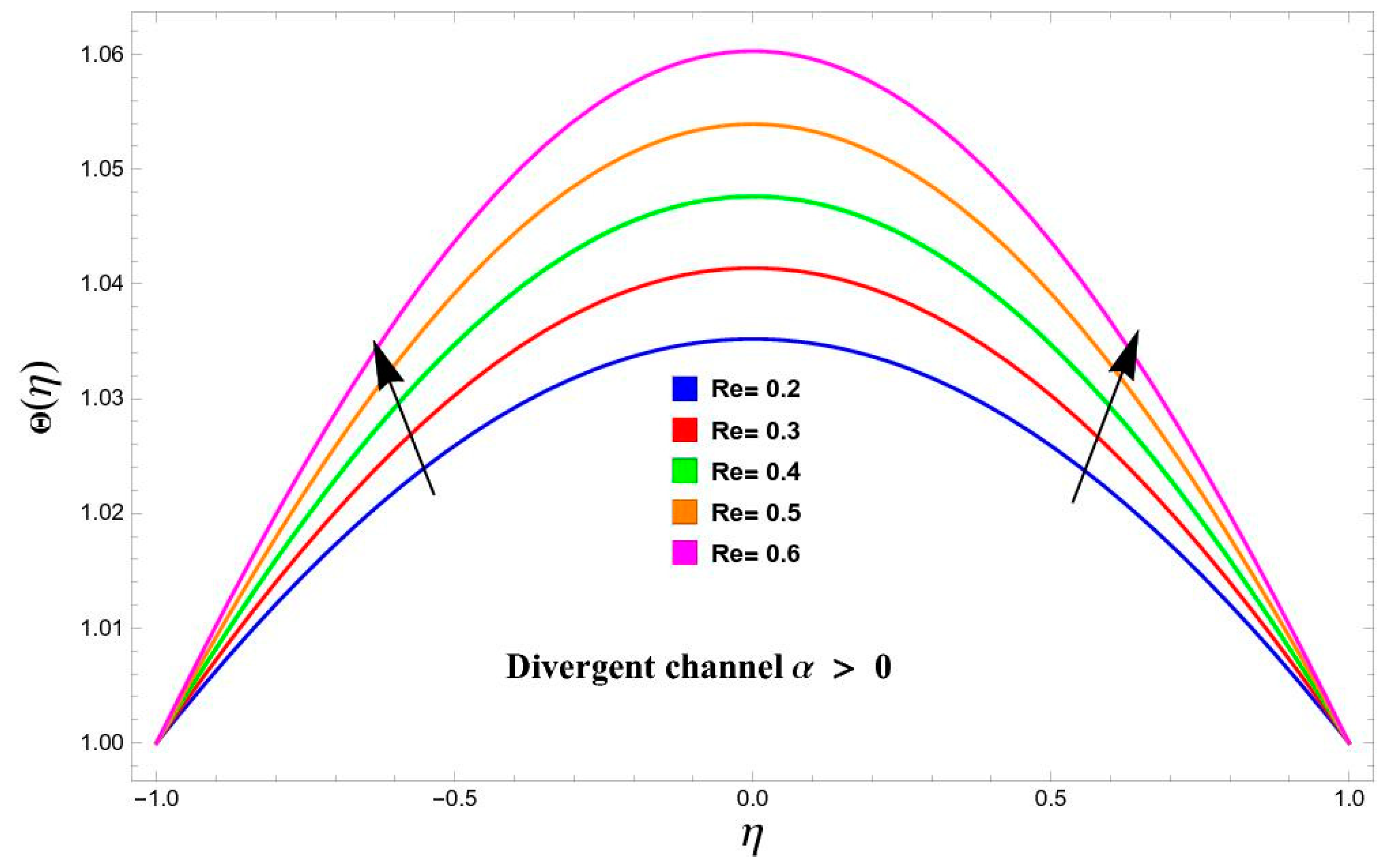
5.2. Variation in Temperature

In this section, from Figure 7, Figure 8, Figure 9 and Figure 10, we analyzed the estimation of the temperature profile $\mathrm{\Theta }\left(\eta \right)$ against different physical parameters such as heat source $Q$ and Reynolds number $\mathrm{Re}$ for both convergent/divergent $\left(\alpha <0,\alpha >0\right)$ channels. Figure 7 and Figure 8 investigate the temperature $\mathrm{\Theta }\left(\eta \right)$ against $Q$ for both extending/narrowing walls. The temperature $\mathrm{\Theta }\left(\eta \right)$ enhances, owing to the greater values of $Q$ for both convergent/divergent channels. In this scenario, a higher coefficient of the heat source corresponds to a reduction in thermal energy for a given heat source variable. Additionally, it is noteworthy that temperature variations occur more rapidly in the divergent case compared to the convergent case. The influence of temperature $\mathrm{\Theta }\left(\eta \right)$ versus Reynolds number $\mathrm{Re}$ is investigated for both extending/narrowing $\left(\alpha <0,\alpha >0\right)$ walls in Figure 9 and Figure 10. The temperature $\mathrm{\Theta }\left(\eta \right)$ characteristics for both divergent/convergent $\left(\alpha <0,\alpha >0\right)$ for the altered estimation of the Reynolds number $\mathrm{Re}$ is same. A greater Reynolds number $\mathrm{Re}$ increases the temperature. Higher values of the Reynolds number $\mathrm{Re}$ can cause flow separation near the channel walls. Since the Reynolds number $\mathrm{Re}$ represents the ratio of momentum forces to viscous forces, an increase in the Reynolds number $\mathrm{Re}$ indicates stronger momentum forces. This results in greater heat generation, leading to an enhancement in the nanofluid’s temperature.

5.3. Concentration Profile

In this section we analyze different physical parameters such as the Reynolds number and Peclet number against the homogeneous reaction for both extending/narrowing walls. Figure 11 and Figure 12 investigate the estimation of the homogenous reaction versus the Reynolds number for both convergent/divergent channels. It is clear that there is an identical variation in the homogenous reaction against the Reynolds number for both extending/narrowing walls. The density of microorganisms in the divergent channel rises as a result of mass buildup driven by the decreased fluid flow velocity in the diverging channel at boosted Reynolds numbers. The number of microorganisms also rises as the divergent channel increases.

5.4. Variation in Homogenous Reactions

This is the last subsection in the discussion. In this section we analyze different physical parameters such as the Reynolds number and Peclet number against a homogeneous reaction for both extending/narrowing walls. Figure 13 and Figure 14 investigate the estimation of a homogenous reaction versus the Reynolds number for both convergent/divergent channels. It is clear that there is an identical variation in homogenous reactions against the Reynolds number for both extending/narrowing walls. The density of microorganisms in the divergent channel rises as a result of mass buildup driven on by the decreased fluid flow velocity in the diverging channel at boosted Reynolds numbers. The number of microorganisms also rises as the divergent channel increases. The greatest cell swimming speed divided by the diffusivity is known as the Peclet number. As the Peclet number rises, the swimming speed of the microorganisms increases and, consequently, the density of the microorganisms declines. Similarly, the Sb and Peclet number are elaborated upon in Figure 15, Figure 16, Figure 17 and Figure 18 against homogeneous reactions for both convergent/divergent $\left(\alpha <0,\alpha >0\right)$ channels. A greater Peclet number enhances the homogeneous reaction for both extending/narrowing $\left(\alpha <0,\alpha >0\right)$ walls.

Figure 19 shows that as the divergence angle $\alpha$ increases, the skin friction coefficient $Cf$ also increases for all values of $\eta$. This indicates that a more divergent channel leads to higher wall shear stress due to the stronger velocity gradients near the wall. The effect becomes more pronounced as $\eta$ increases, highlighting the significant role of channel geometry in flow behavior. Figure 20 shows that in a divergent channel, the Nusselt number (Nu) increases with the dimensionless parameter $\eta$ for all alpha angles ($\alpha$). Smaller $\alpha$ values (e.g., π/20) yield higher Nu, indicating better heat transfer, while larger α values (e.g., π/3) result in lower Nu. This suggests that smaller divergence angles enhance heat transfer efficiency, likely due to improved flow patterns, which is useful for designing thermal systems like heat exchangers. Figure 21 shows that the mass transfer of gyrotactic microorganisms initially increases with η for all α values, peaking around η = 0.4, then decreases as η approaches 1.0. Smaller α values (e.g., π/20) result in higher Nu peaks (around 0.15), indicating better mass transfer, while larger α values (e.g., π/100) yield lower Nu peaks (around 0.05). This suggests that a smaller divergence angle enhances the mass transfer of gyrotactic microorganisms, likely due to improved flow dynamics and reduced separation. These findings are useful for optimizing microfluidic systems involving microorganisms, though further studies on other parameters like flow rate or channel geometry could provide more insights.

6. Final Remarks

We have studied a numerical model of the Jeffery–Hamel flow of non-Newtonian fluid through a non-parallel inclined channel with thermal radiation and homogeneous–heterogeneous reactions in convergent/divergent channels. From this research work, we concluded a number of important points which are listed below:

• Solutions obtained with the help of the NDSolve method used in Mathematica tool give good results.
• The alpha against velocity profile $f(\eta )$ exhibits opposite behavior; that is, velocity decreases in the convergent $\left(\alpha <0\right)$ channel while increasing in the divergent $\left(\alpha >0\right)$ channel.
• The behavior of velocity $f(\eta )$ against porosity $Kp$ is the same in both cases of the convergent/divergent $\left(\alpha <0,\hspace{0.17em}\alpha >0\right)$ channels.
• The influence of temperature $\mathrm{\Theta }(\eta )$ versus various parameters such as $Q$ and $\mathrm{Re}$ increases in both cases of convergent and divergent $\left(\alpha <0,\hspace{0.17em}\alpha >0\right)$ walls.
• The concentration $\varphi (\eta )$ rises for both convergent/divergent $\left(\alpha <0,\hspace{0.17em}\alpha >0\right)$ channels due to higher Reynolds number values.