Skyrmion Pair Racetrack Utilizing Hall Motion
Abstract
1. Introduction
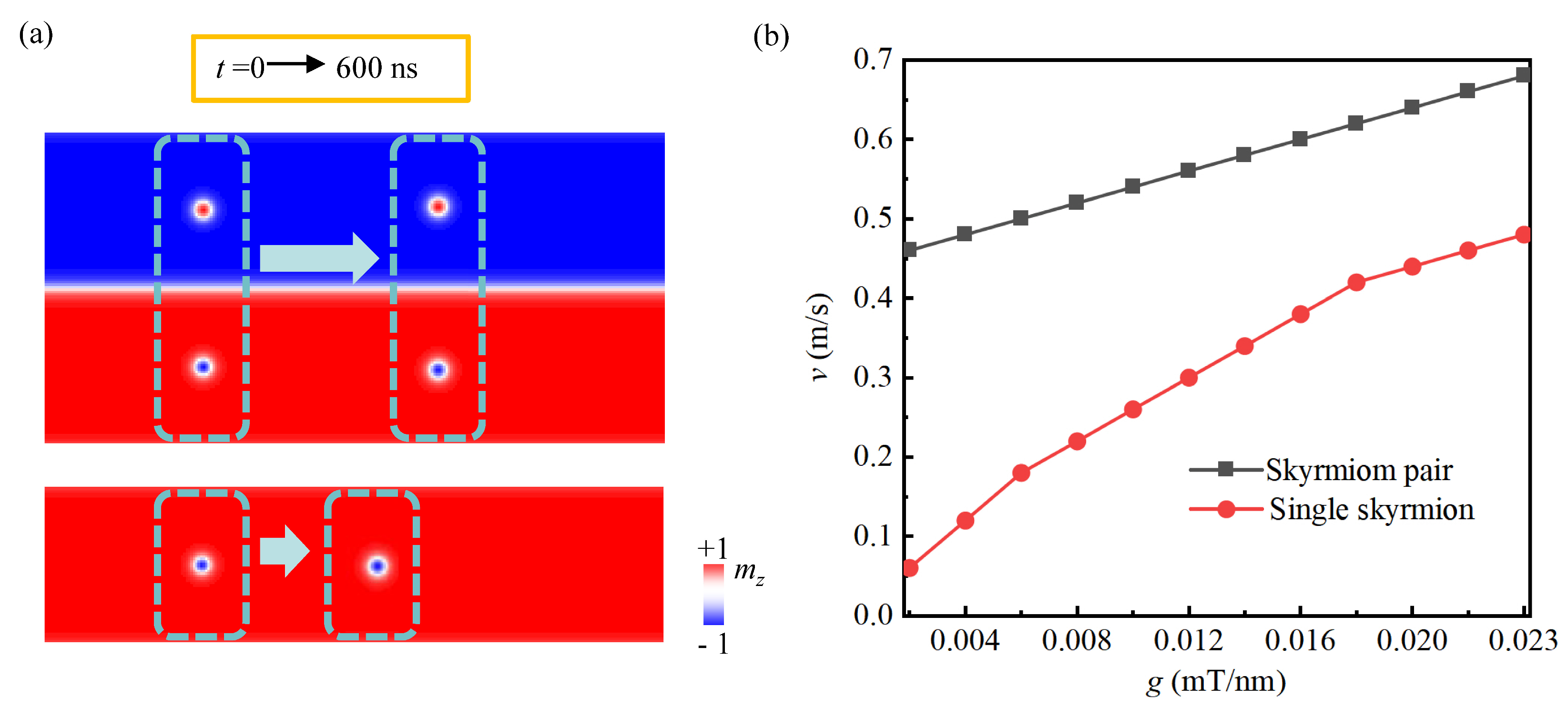
2. Results and Discussions
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Tonomura, A.; Yu, X.Z.; Yanagisawa, K.; Matsuda, T.; Onose, Y.; Kanazawa, N. Real-Space Observation of Skyrmion Lattice in Helimagnet MnSi Thin Samples. Nano Lett. 2012, 12, 1673–1677. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.J.; Chen, G.; Liu, K.; Zang, J.D.; te Velthuis, S.G.E.; Hoffmann, A. Skyrmions in magnetic multilayers. Phys. Rep. Rev. Sect. Phys. Lett. 2017, 704, 1–49. [Google Scholar] [CrossRef]
- Deng, Z.; Shi, T.; Krasnok, A.; Li, X.P.; Alù, A. Observation of localized magnetic plasmon skyrmions. Nat. Commun. 2022, 13, 1. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.W.; Song, D.S.; Wei, W.S.; Nan, P.F.; Zhang, S.L.; Ge, B.H. Electrical manipulation of skyrmions in a chiral magnet. Nat. Commun. 2022, 13, 1593. [Google Scholar] [CrossRef] [PubMed]
- Fert, A.; Reyren, N.; Cros, V. Magnetic skyrmions: Advances in physics and potential applications. Nat. Rev. Mater. 2017, 2, 7. [Google Scholar] [CrossRef]
- Ullah, A.; Balasubramanian, B.; Tiwari, B.; Giri, B.; Sellmyer, D.J.; Skomski, R.; Xu, X.S. Topological spin textures and topological Hall effect in centrosymmetric magnetic nanoparticles. Phys. Rev. B 2023, 108, 184432. [Google Scholar] [CrossRef]
- Ullah, A.; Balamurugan, B.; Zhang, W.; Valloppilly, S.; Li, X.Z.; Pahari, R.; Yue, L.P.; Sokolov, A.; Sellmyer, D.J.; Skomski, R. Crystal Structure and Dzyaloshinski-Moriya Micromagnetics. IEEE Trans. Magn. 2019, 55, 7100305. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Zhang, X.C.; Ezawa, M.; Zhou, Y. Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 2015, 5, 9400. [Google Scholar] [CrossRef]
- Song, K.M.; Jeong, J.S.; Pan, B.; Zhang, X.C.; Xia, J.; Cha, S. Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 2020, 3, 148–155. [Google Scholar] [CrossRef]
- Zhang, X.C.; Zhou, Y.; Song, K.M.; Park, T.E.; Xia, J.; Ezawa, M. Skyrmion-electronics: Writing, deleting, reading and processing magnetic skyrmions toward spintronic applications. J. Phys. Condens. Matter 2020, 32, 14. [Google Scholar] [CrossRef]
- Mishra, K.K.; Lone, A.H.; Srinivasan, S.; Fariborzi, H.; Setti, G. Magnetic skyrmion: From fundamental physics to pioneering applications. Appl. Phys. Rev. 2025, 12, 011315. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Jonietz, F.; Mühlbauer, S.; Pfleiderer, C.; Neubauer, A.; Münzer, W.; Bauer, A. Spin Transfer Torques in MnSi at Ultralow Current Densities. Science 2010, 330, 1648–1651. [Google Scholar] [CrossRef] [PubMed]
- Lepadatu, S.; Saarikoski, H.; Beacham, R.; Benitez, M.J.; Moores, T.A.; Burnell, G. Synthetic ferrimagnet nanowires with very low critical current density for coupled domain wall motion. Sci. Rep. 2017, 7, 1640. [Google Scholar] [CrossRef] [PubMed]
- Koyama, T.; Chiba, D.; Ueda, K.; Kondou, K.; Tanigawa, H.; Fukami, S. Observation of the intrinsic pinning of a magnetic domain wall in a ferromagnetic nanowire. Nat. Mater. 2011, 10, 194–197. [Google Scholar] [CrossRef]
- Lai, P.; Zhao, G.P.; Morvan, F.J.; Wu, S.Q.; Ran, N. Motion of Skyrmions in Well-Separated Two-Lane Racetracks. Spin 2017, 7, 1. [Google Scholar] [CrossRef]
- Song, C.K.; Jin, C.D.; Wang, J.S.; Xia, H.Y.; Wang, J.B.; Liu, Q.F. Skyrmion-based multi-channel racetrack. Appl. Phys. Lett. 2017, 111, 192413. [Google Scholar] [CrossRef]
- Göbel, B.; Mertig, I. Skyrmion ratchet propagation: Utilizing the skyrmion Hall effect in AC racetrack storage devices. Sci. Rep. 2021, 11, 3020. [Google Scholar] [CrossRef]
- Jiang, W.J.; Zhang, X.C.; Yu, G.Q.; Zhang, W.; Wang, X.; Jungfleisch, M.B. Direct observation of the skyrmion Hall effect. Nat. Phys. 2017, 13, 162–169. [Google Scholar] [CrossRef]
- Han, S.U.; Kim, W.; Kim, S.K.; Je, S.G. Tunable domain-wall skyrmion Hall effect driven by a current and a magnetic field. Phys. Rev. B 2024, 109, 014404. [Google Scholar] [CrossRef]
- Zeissler, K.; Finizio, S.; Barton, C.; Huxtable, A.J.; Massey, J.; Raabe, J. Diameter-independent skyrmion Hall angle observed in chiral magnetic multilayers. Nat. Commun. 2020, 11, 428. [Google Scholar] [CrossRef]
- Zhang, X.C.; Zhou, Y.; Ezawa, M. Antiferromagnetic Skyrmion: Stability, Creation and Manipulation. Sci. Rep. 2016, 6, 24795. [Google Scholar] [CrossRef] [PubMed]
- Barker, J.; Tretiakov, O.A. Static and Dynamical Properties of Antiferromagnetic Skyrmions in the Presence of Applied Current and Temperature. Phys. Rev. Lett. 2016, 116, 147203. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.D.; Song, C.K.; Wang, J.B.; Liu, Q.F. Dynamics of antiferromagnetic skyrmion driven by the spin Hall effect. Appl. Phys. Lett. 2016, 109, 182404. [Google Scholar] [CrossRef]
- Pham, V.; Sisodia, N.; Di Manici, I.; Urrestarazu-Larrañaga, J.; Bairagi, K.; Pelloux-Prayer, J.; Guedas, R.; Buda-Prejbeanu, L.D.; Auffret, S.; Locatelli, A.; et al. Fast current-induced skyrmion motion in synthetic antiferromagnets. Science 2024, 384, 307–312. [Google Scholar] [CrossRef]
- Dohi, T.; DuttaGupta, S.; Fukami, S.; Ohno, H. Formation and current-induced motion of synthetic antiferromagnetic skyrmion bubbles. Nat. Commun. 2019, 10, 5153. [Google Scholar] [CrossRef]
- Legrand, W.; Maccariello, D.; Ajejas, F.; Collin, S.; Vecchiola, A.; Bouzehouane, K.; Reyren, N.; Cros, V.; Fert, A. Room-temperature stabilization of antiferromagnetic skyrmions in synthetic antiferromagnets. Nat. Mater. 2020, 19, 34–42. [Google Scholar] [CrossRef]
- Qiu, S.; Liu, J.H.; Chen, Y.B.; Qi, X.L.; Fang, L. Writing skyrmion at a specific position in synthetic antiferromagnetic racetrack by voltage. J. Magn. Magn. Mater. 2022, 554, 169144. [Google Scholar] [CrossRef]
- Gao, S.; Rosales, H.D.; Albarracín, F.G.A.; Tsurkan, V.; Kaur, G.; Fennell, T. Fractional antiferromagnetic skyrmion lattice induced by anisotropic couplings. Nature 2020, 586, 7827. [Google Scholar] [CrossRef]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I. Antiferromagnetic skyrmion crystals: Generation, topological Hall, and topological spin Hall effect. Phys. Rev. B 2017, 96, 060406. [Google Scholar] [CrossRef]
- Lau, M.; Häusler, W.; Thorwart, M. Moving skyrmions in antiferromagnets by sublattice displacements. Phys. Rev. B 2025, 111, 144411. [Google Scholar] [CrossRef]
- Kim, S.K.; Lee, K.J.; Tserkovnyak, Y. Self-focusing skyrmion racetracks in ferrimagnets. Phys. Rev. B 2017, 95, 140404. [Google Scholar] [CrossRef]
- Hirata, Y.; Kim, D.H.; Kim, S.K.; Lee, D.K.; Oh, S.H.; Kim, D.Y.; Nishimura, T.; Okuno, T.; Futakawa, Y.; Yoshikawa, H.; et al. Vanishing skyrmion Hall effect at the angular momentum compensation temperature of a ferrimagnet. Nat. Nanotechnol. 2019, 14, 232–236. [Google Scholar] [CrossRef]
- Xu, H.; Yang, Q.Q.; Liu, Y.; Tian, G.; Qiu, L.; Qin, M.H.; Hou, Z.P. Skyrmion Motion in Ferrimagnets Driven by Magnetic Anisotropy Gradient. Phys. Status Solidi-Rapid Res. Lett. 2024, 18, 5. [Google Scholar] [CrossRef]
- Vélez, S.; Ruiz-Gómez, S.; Schaab, J.; Gradauskaite, E.; Wörnle, M.S.; Welter, P.; Jacot, B.J.; Degen, C.L.; Trassin, M.; Fiebig, M.; et al. Current-driven dynamics and ratchet effect of skyrmion bubbles in a ferrimagnetic insulator. Nat. Nanotechnol. 2022, 17, 834–841. [Google Scholar] [CrossRef]
- Kolesnikov, A.G.; Stebliy, M.E.; Samardak, A.S.; Ognev, A.V. Skyrmionium—High velocity without the skyrmion Hall effect. Sci. Rep. 2018, 8, 1. [Google Scholar] [CrossRef]
- Yang, S.; Zhao, Y.L.; Wu, K.; Chu, Z.Q.; Xu, X.H.; Li, X.G. Reversible conversion between skyrmions and skyrmioniums. Nat. Commun. 2023, 14, 3405. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.L.; Kronast, F.; van der Laan, G.; Hesjedal, T. Real-Space Observation of Skyrmionium in a Ferromagnet-Magnetic Topological Insulator Heterostructure. Nano Lett. 2018, 18, 1057–1063. [Google Scholar] [CrossRef]
- Wang, C.J.; Xiao, D.; Chen, X.; Zhou, Y.; Liu, Y.W. Manipulating and trapping skyrmions by magnetic field gradients. New J. Phys. 2017, 19, 083008. [Google Scholar] [CrossRef]
- Cho, J.; Tamura, E.; Liu, C.Z.; Miki, S.; You, C.Y.; Kim, J.S. Manipulating 1-dimensional skyrmion motion by the external magnetic field gradient. New J. Phys. 2020, 22, 103053. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, C.J.; Zheng, C.X.; Liu, Y.W. Manipulating skyrmions in synthetic antiferromagnetic nanowires by magnetic field gradients. J. Magn. Magn. Mater. 2020, 493, 165740. [Google Scholar] [CrossRef]
- Brearton, R.; Turnbull, L.A.; Verezhak, J.A.T.; Balakrishnan, G.; Hatton, P.D.; van der Laan, G.; Hesjedal, T. Deriving the skyrmion Hall angle from skyrmion lattice dynamics. Nat. Commun. 2021, 12, 2723. [Google Scholar]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 10. [Google Scholar] [CrossRef]
- Liu, J.; Song, C.; Zhao, L.; Cai, L.; Feng, H.; Zhao, B.; Zhao, M.; Zhou, Y.; Fang, L.; Jiang, W. Manipulation of skyrmion by magnetic field gradients: A Stern–Gerlach-like experiment. Nano Lett. 2023, 23, 4931–4937. [Google Scholar] [CrossRef]
- Thiele, A.A. Steady-State Motion of Magnetic Domains. Phys. Rev. Lett. 1973, 30, 230–233. [Google Scholar] [CrossRef]
- Zhang, S.L.; Wang, W.W.; Burn, D.M.; Peng, H.; Berger, H.; Bauer, A. Manipulation of skyrmion motion by magnetic field gradients. Nat. Commun. 2018, 9, 2115. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.J.; Yu, J.H.; Chen, J.; Qin, M.H.; Zeng, M.; Lu, X.B. Magnetic field gradient driven dynamics of isolated skyrmions and antiskyrmions in frustrated magnets. New J. Phys. 2018, 20, 053037. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, S.; Zhang, T.; Han, X.; Liu, J.; Fang, L.; Cheng, Y. Skyrmion Pair Racetrack Utilizing Hall Motion. Magnetochemistry 2025, 11, 90. https://doi.org/10.3390/magnetochemistry11100090
Qiu S, Zhang T, Han X, Liu J, Fang L, Cheng Y. Skyrmion Pair Racetrack Utilizing Hall Motion. Magnetochemistry. 2025; 11(10):90. https://doi.org/10.3390/magnetochemistry11100090
Chicago/Turabian StyleQiu, Shan, Tianle Zhang, Xiaotong Han, Jiahao Liu, Liang Fang, and Yun Cheng. 2025. "Skyrmion Pair Racetrack Utilizing Hall Motion" Magnetochemistry 11, no. 10: 90. https://doi.org/10.3390/magnetochemistry11100090
APA StyleQiu, S., Zhang, T., Han, X., Liu, J., Fang, L., & Cheng, Y. (2025). Skyrmion Pair Racetrack Utilizing Hall Motion. Magnetochemistry, 11(10), 90. https://doi.org/10.3390/magnetochemistry11100090





