Band Structure Calculations, Magnetic Properties and Magnetocaloric Effect of GdCo1.8M0.2 Compounds with M = Fe, Mn, Cu, Al
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
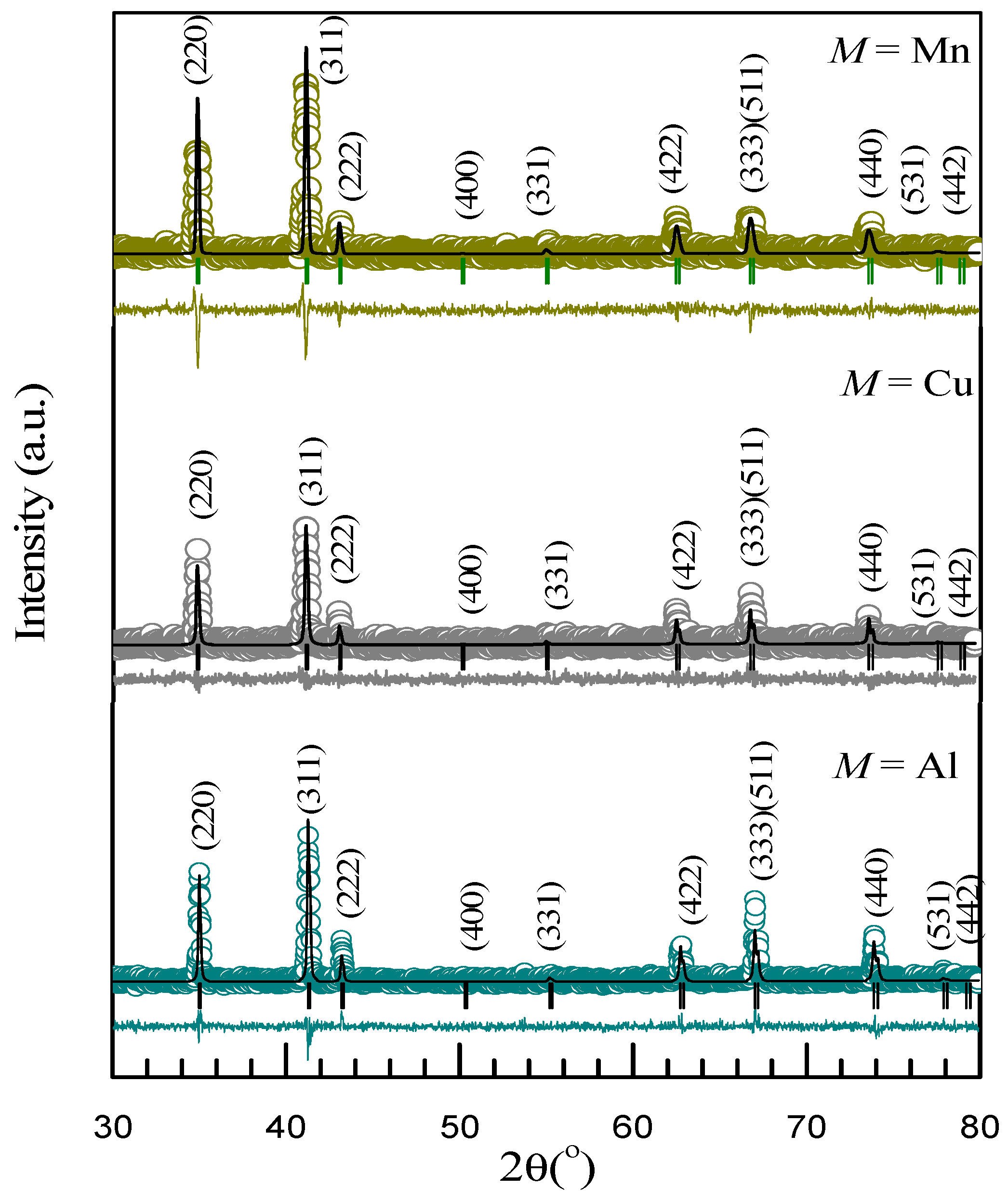
3.1. X-ray Diffraction
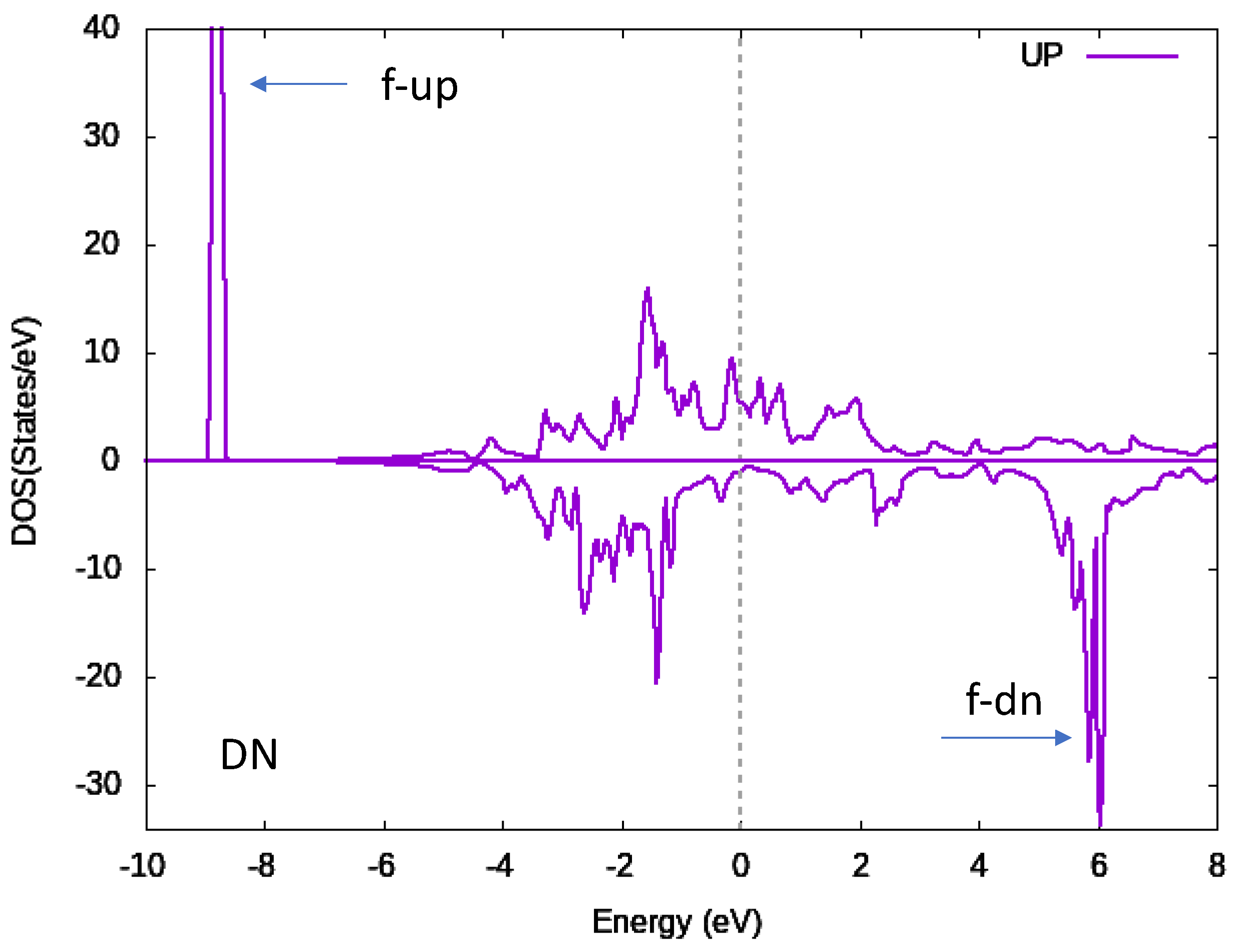
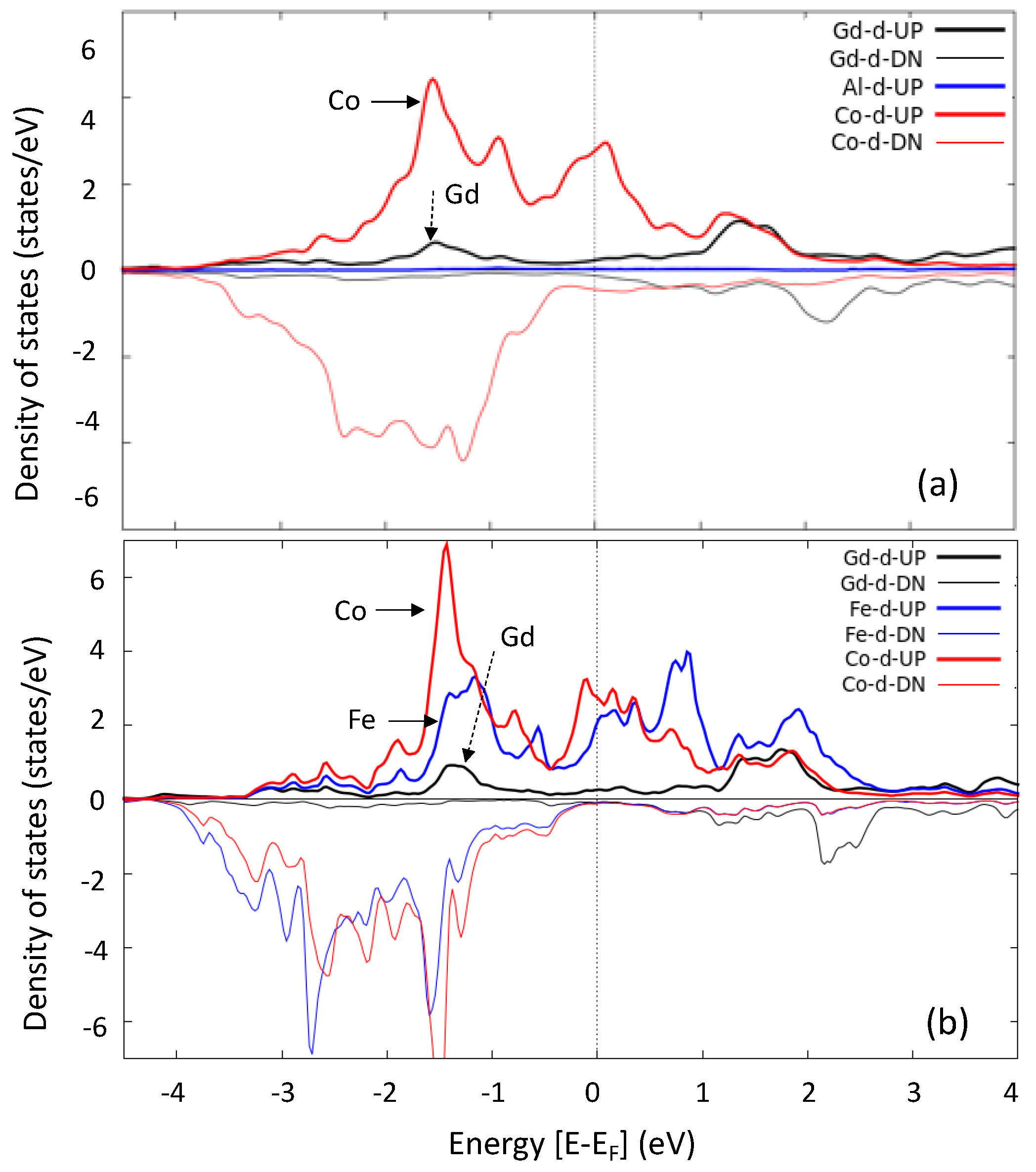
3.2. Band Structure Calculations
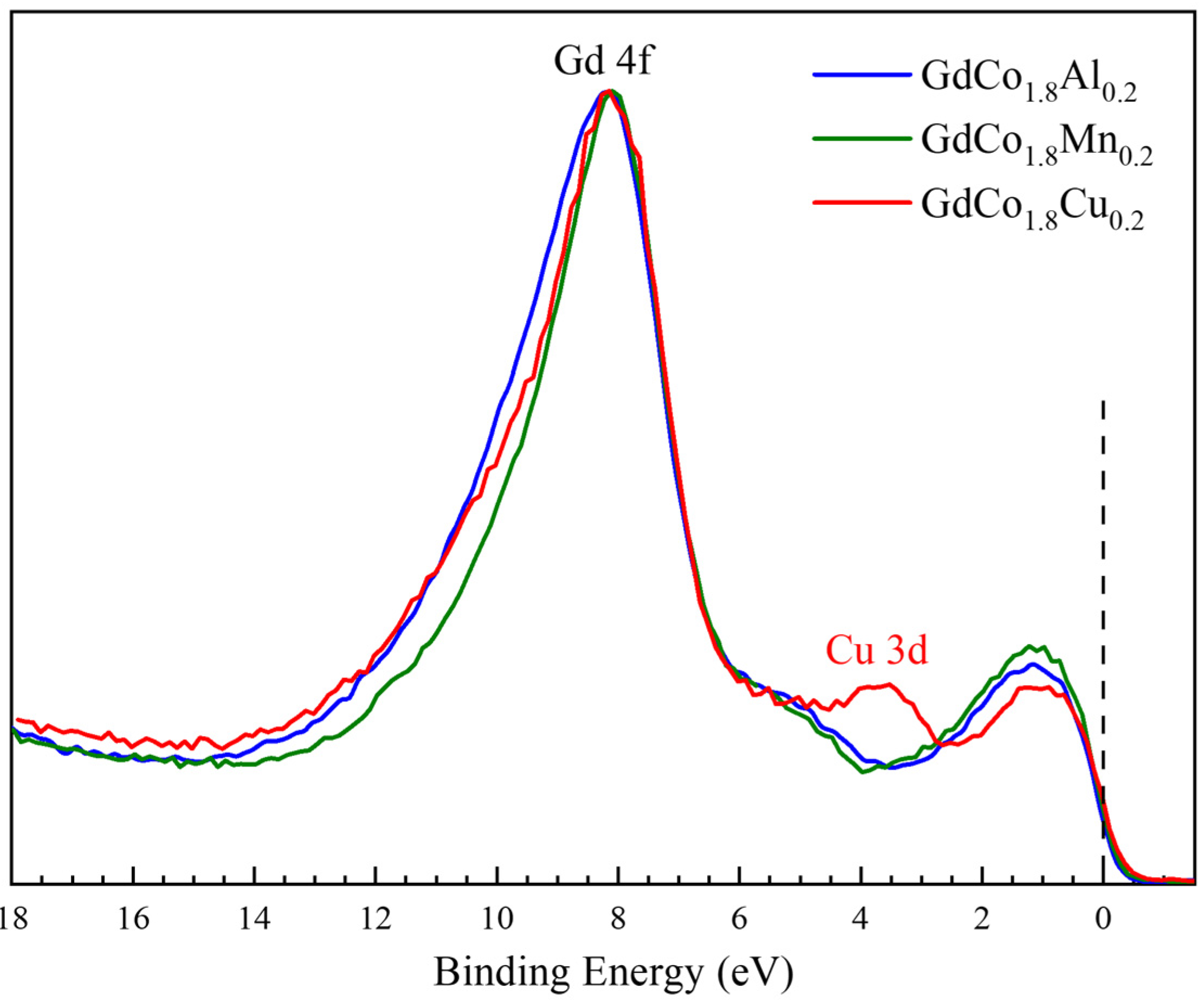
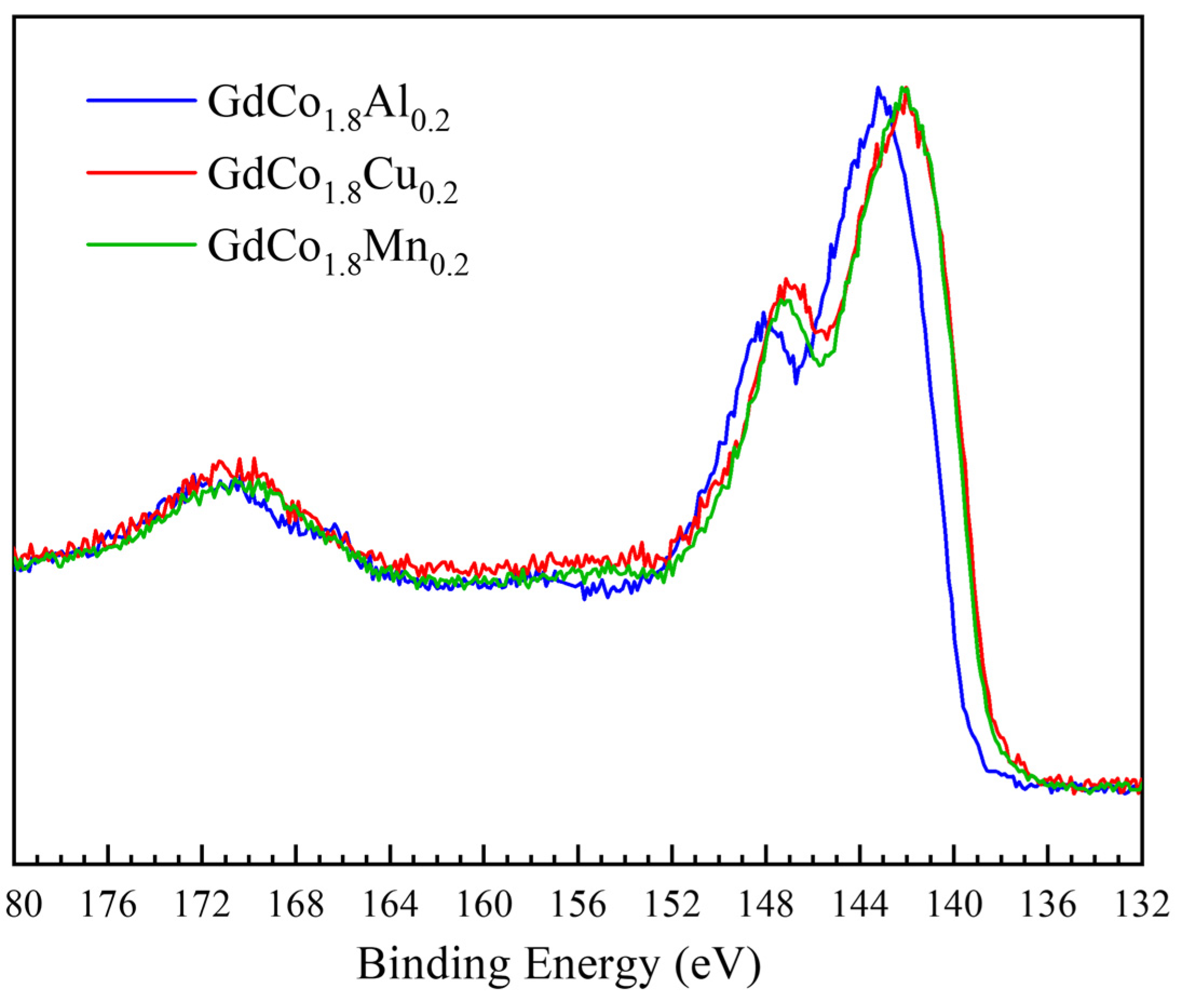
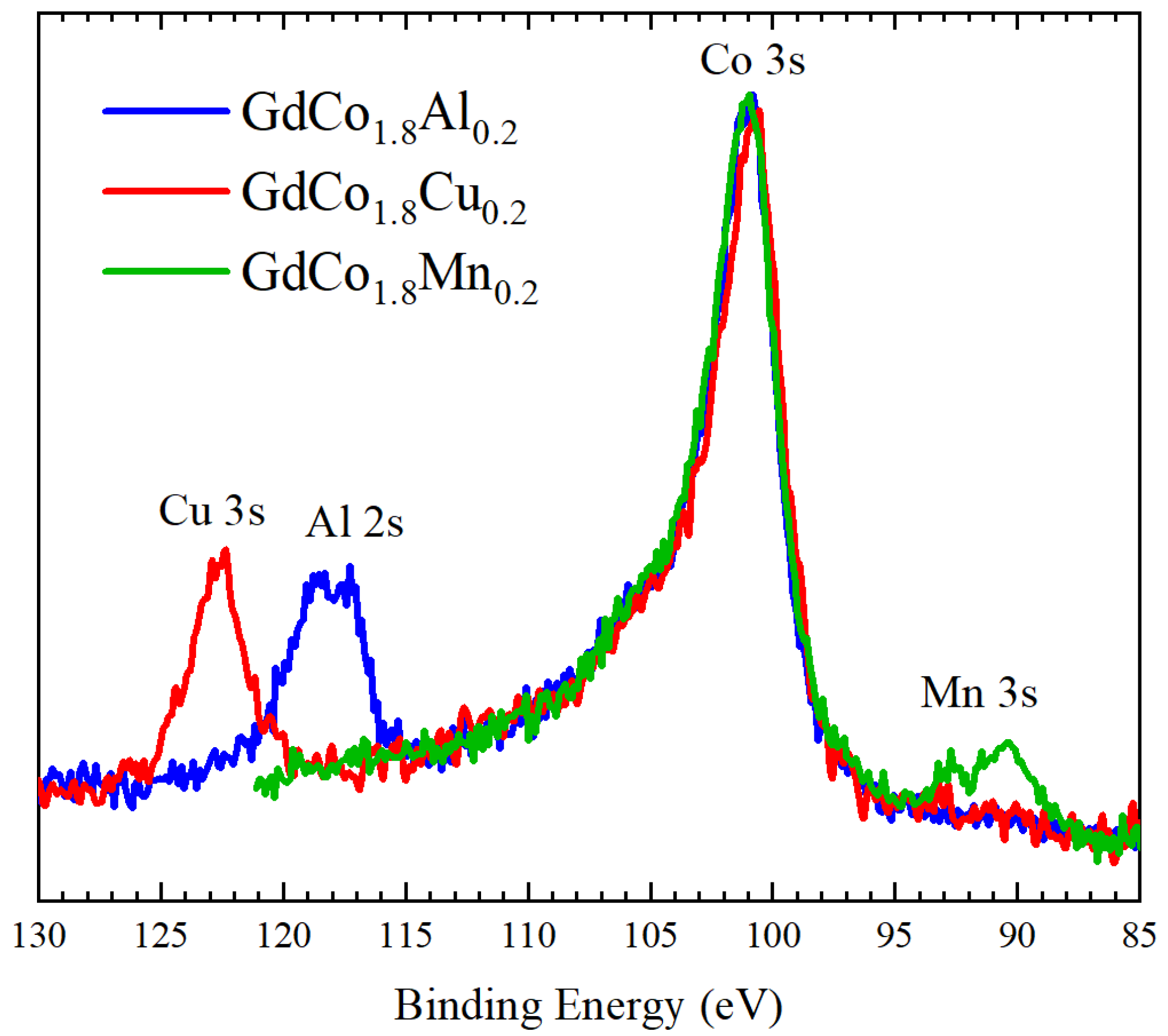
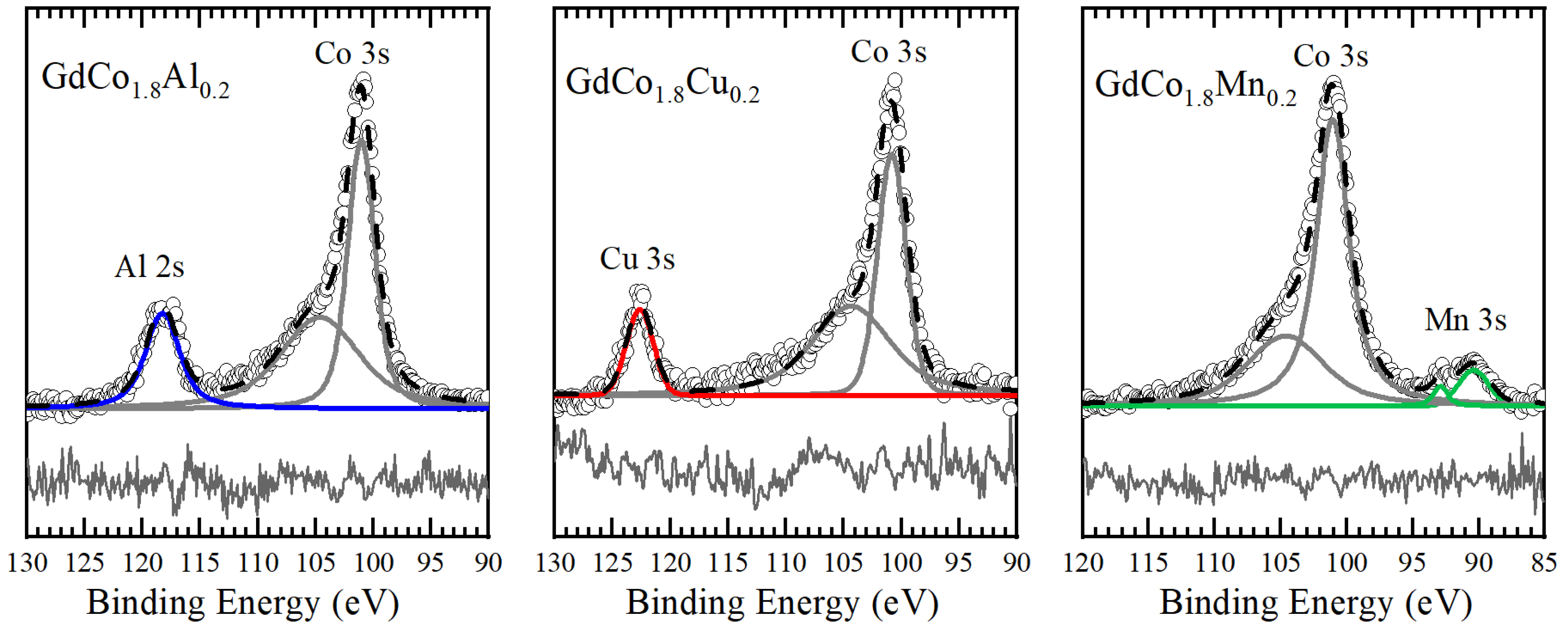
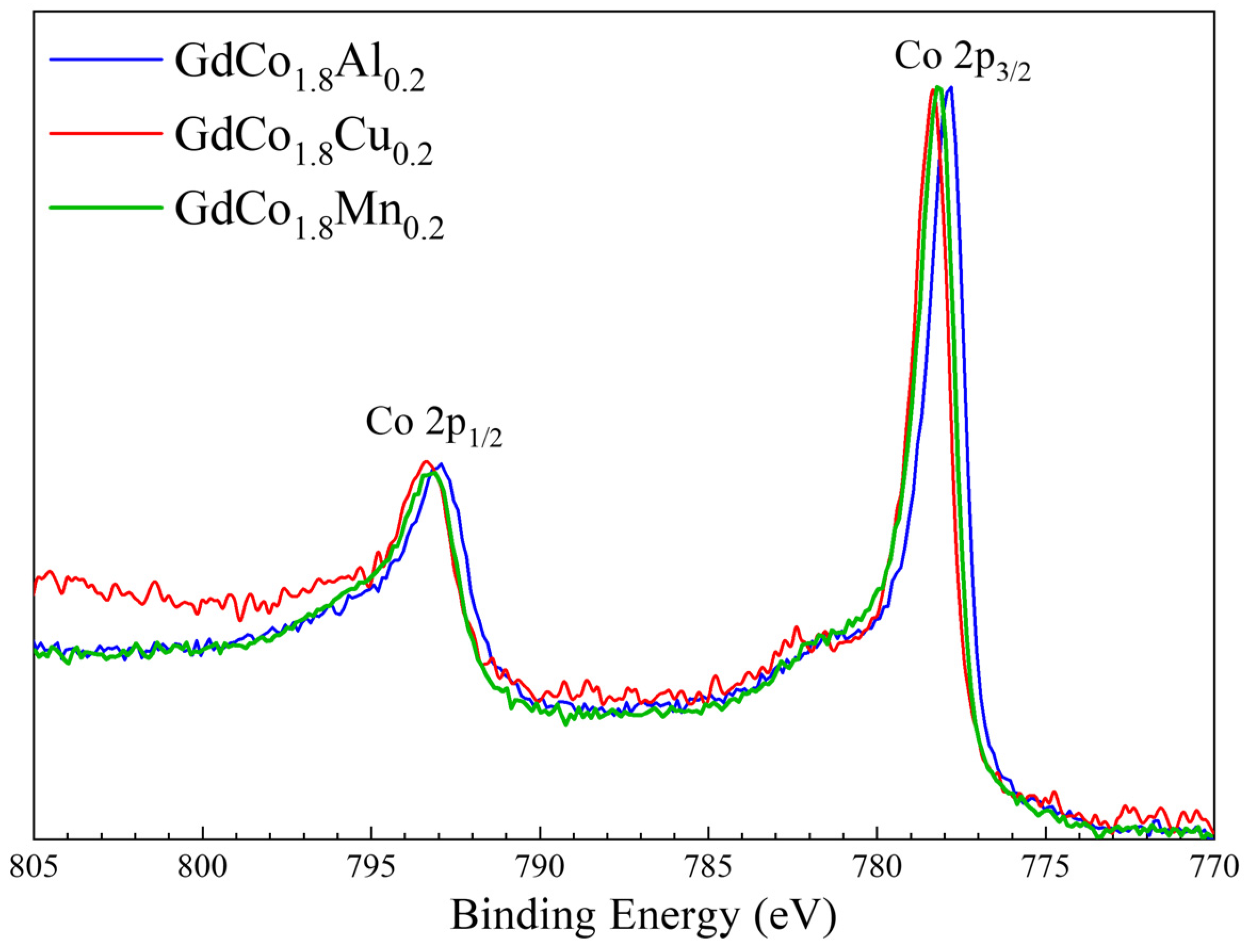
3.3. XPS Spectra of GdCo1.8M0.2 Intermetallic Compounds
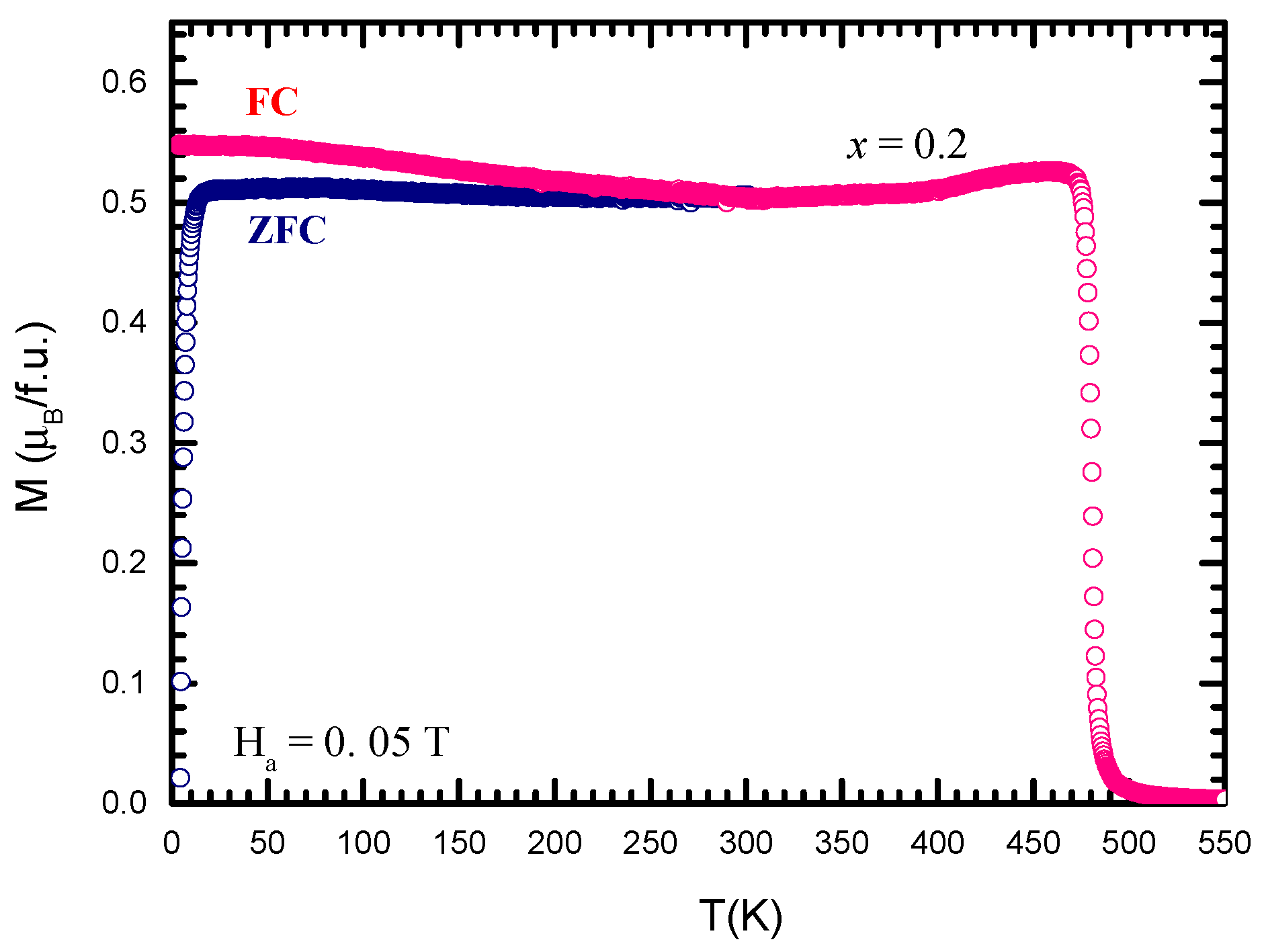
3.4. Magnetic Properties of GdCo2−xMnx Intermetallic Compounds
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burzo, E.; Chelkowski, L.; Kirchmayr, H.R. Compounds between Rare Earth Elements and 3d, 4d, or 5d Elements, Landolt Börnstein Handbuch; Springer: Berlin, Germany, 1990; Volume 19. [Google Scholar] [CrossRef]
- Buschow, K.H.J. Intermetallic compounds of rare earth elements and Ni, Co, or Fe. Phys. Status Solidi A 1971, 7, 199. [Google Scholar] [CrossRef]
- Wallace, W.E.; Swearingen, J.T. Magnetic Characteristics of LaCo5-ThCo5 Pseudobinary System. J. Solid State Chem. 1973, 8, 37. [Google Scholar] [CrossRef]
- González, J.A.; Andrés, J.P.; López Antón, R. Applied Trends in Magnetic Rare Earth/Transition Metal Alloys and Multilayers. Sensors 2021, 21, 5615. [Google Scholar] [CrossRef] [PubMed]
- Bessais, L. Structure and Magnetic Properties of Intermetallic Rare-Earth-Transition-Metal Compounds: A Review. Materials 2022, 15, 201. [Google Scholar] [CrossRef] [PubMed]
- Gschneidner, K.A.; Eyring, L. Handbook on the Physics and Chemistry of Rare Earths; Elsevier: Amsterdam, The Netherlands, 2000; pp. 1–413. [Google Scholar]
- Gschneidner, K.A.; Pecharsky, V.K. Binary rare earth Laves phases—An overview. Z. Krist.-Cryst. Mater. 2006, 221, 375–381. [Google Scholar] [CrossRef]
- Wiesinger, G.; Hilscher, G. Magnetism of hydrides. In Handbook on Magnetic Materials; Buschow, K.-H.-J., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; Chapter 5; pp. 293–456. [Google Scholar] [CrossRef]
- Buschow, K.H.J. Intermetallic compounds of rare-earth and 3d transition metals. Rep. Prog. Phys. 1977, 40, 1179–1256. [Google Scholar] [CrossRef]
- Stein, F.; Leineweber, A. Laves phases: A review of their functional and structural applications and an improved fundamental understanding of stability and properties. J. Mater. Sci. 2021, 56, 5321–5427. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Willard, M.A.; Brück, E.; Chen, C.H.; Sankar, S.G.; Liu, J.P. Magnetic materials and devices for the 21st century: Stronger, lighter, and more energy efficient. Adv. Mater. 2011, 23, 821–842. [Google Scholar] [CrossRef]
- Tishin, A.M.M.; Spichkin, Y.I.I. The Magnetocaloric Effect and Its Applications; series in condensed matter physics; CRC Press: Boca Raton, FL, USA, 2003; Volume 6, pp. 1–475. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge Univerity Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Taylor, K.N.R. Transition metal moment collapse in Gd(Co1−xNix)2. Phys. Lett. 1969, 29, 372–373. [Google Scholar] [CrossRef]
- Bloch, D.; Lemaire, R. Metallic alloys and exchange-enhanced paramagnetism. Application to rare-earths-cobalt alloys. Phys. Rev. B 1970, 2, 2648–2650. [Google Scholar] [CrossRef]
- Campbell, I.A. Indirect exchange for rare earths in metals. J. Phys. F Met. Phys. 1972, 2, 3–7. [Google Scholar] [CrossRef]
- Moriya, T. Recent progress in the theory of itinerant electron magnetism. J. Magn. Magn. Mater. 1979, 14, 1–46. [Google Scholar] [CrossRef]
- Beal-Monod, M.T. Field effects in strongly enhanced paramagnets. Phys. B 1982, 1837, 109–110. [Google Scholar] [CrossRef]
- Yamada, H.; Inoue, J.; Shimizu, M. Electronic structure and magnetic properties of the cubic Laves phase compounds ACo2 (A = Sc, Ti, Zr, Lu and Hf) and ScNi2. J. Phys. F 1985, 15, 169. [Google Scholar] [CrossRef]
- Kuentzler, R.; Tari, A. Electronic properties and the appearance of magnetism in the (Tb1−xYx)Co2 compounds. J. Magn. Magn. Mater. 1986, 61, 29–38. [Google Scholar] [CrossRef]
- Burzo, E.; Lemaire, R. On the magnetic behaviour of RCo2 compounds where R is yttrium or a rare-earth. Solid State Commun. 1992, 84, 1145. [Google Scholar] [CrossRef]
- Moriya, T. Theory of itinerant electron magnetism. J. Magn. Magn. Mater. 1991, 100, 261–271. [Google Scholar] [CrossRef]
- Burzo, E.; Chioncel, L.; Tetean, R.; Isnard, O. On the R 5d band polarization in rare-earth-transition metal compounds. J. Phys. Condens. Matter. 2011, 23, 02601. [Google Scholar] [CrossRef]
- Lemaire, R. Magnetic properties of intermetallic compounds of Co with rare earth metals or Y. [PART I.]. Cobalt 1966, 32, 132–140. [Google Scholar]
- Lemaire, R. Magnetic properties of intermetallic compounds of Co with rare earth metals or Y. PART II. Cobalt 1966, 33, 201–211. [Google Scholar]
- Cyrot, M.; Lavagna, M. Density of states and magnetic properties of the rare-earth compounds RFe2, RCO2 and RNi2. J. Phys. 1979, 40, 763–771. [Google Scholar] [CrossRef]
- Baily, L.J.; Richter, E. Proceeding of the 2nd Intern Workshop on Rare Earth Permanent Magnets and their Applications; Strnat, K.J., Ed.; University of Dayton: Dayton, OH, USA, 1976; p. 235. [Google Scholar]
- Kirchmayer, H.R. Handbook on the Physics and Chemistry of Rare Earths; Gschneidner, K.A., Ed.; Elsevier: Amsterdam, The Netherlands; New York, NY, USA; Oxford, UK, 1979; Chapter 14. [Google Scholar]
- Burzo, E.; Tetean, R.; Sarkozi Zs Chioncel, L.; Neuman, M. Magnetic properties and electronic structures of RCo2−xSix, (R = Gd, Y) compounds. J. Alloys Compd. 2001, 323–324, 490–493. [Google Scholar] [CrossRef]
- Tetean, R.; Burzo, E.; Chioncel, L.; Crainic, T. On the magnetic behaviour of GdCo2–xCux compounds. Phys. Stat. Sol. (A) 2003, 196, 301–304. [Google Scholar] [CrossRef]
- Souca, G.; Dudric, R.; Cotop, R.; Küpper, K.; Tiusan, C.; Tetean, R. Electronic structure, magnetic properties and magnetocaloric effect of GdCo2−xNix. J. Alloys Compd. 2022, 923, 166116. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Magnetocaloric effect and magnetic refrigeration. J. Magn. Magn. Matter. 1999, 200, 44–56. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric Effect. Encycl. Condens. Matter Phys. 2005, 236–244. [Google Scholar] [CrossRef]
- Brück, E. Developments in magnetocaloric refrigeration. J. Phys. D Appl. Phys. 2005, 38, R381–R391. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. Thirty years of near room temperature magnetic cooling: Where we are today and future prospects. Int. J. Refrig. 2008, 31, 945. [Google Scholar] [CrossRef]
- Smith, A.; Bahl, C.R.H.; Bjørk, R.; Engelbrecht, K.; Nielsen, K.K.; Pryds, N. Materials Challenges for High Performance Magnetocaloric Refrigeration Devices. Adv. Energy Mater. 2012, 2, 1288. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Saini, S.M.; Singh, N.; Nautiyal, T.; Auluck, S. Comparative study of optical and magneto-optical properties of GdFe2 and GdCo2. J. Phys. Condens. Matter 2007, 19, 176203. [Google Scholar] [CrossRef]
- Harmon, B.N.; Antropov, V.P.; Liechtenstein, A.I.; Solovyev, I.V.; Anisimov, V. Calculation of magneto-optical properties for 4f systems: LSDA + Hubbard U results. J. Phys. Chem. Solids 1995, 56, 1521. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Wei, S.-H.; Ferreira, L.G. Bernard James E, and Zunger Alex, Electronic properties of random alloys: Special quasirandom structures. Phys. Rev. B 1990, 42, 9622. [Google Scholar] [CrossRef]
- Zunger Alex Wei, S.-H.; Ferreira, L.G.; Bernard James, E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353. [Google Scholar] [CrossRef] [PubMed]
- Szade, J.; Neumann, M.; Karla, I.; Schneider, B.; Fangmeyer, F.; Matteucci, M. Photon energy dependence of the Gd 4d photoemission. Solid State Commun. 2000, 113, 709–712. [Google Scholar] [CrossRef]
- Shirley, D.A. High-Resolution X-ray Photoemission Spectrum of the Valence Bands of Gold. Phys. Rev. B 1972, 5, 4709. [Google Scholar] [CrossRef]
- Rednic, V.; Coldea, M.; Mendiratta, S.K.; Valente, M.; Pop, V.; Neumann, M.; Rednic, L. X-ray photoelectron spectroscopy and magnetism of Mn1−xAlxNi alloys. J. Magn. Magn. Mater. 2009, 321, 3415–3421. [Google Scholar] [CrossRef]
- Givord, D.; Lemaire, R. Magnetic transition and anomalous thermal expansion in R2Fe17 compounds. IEEE Trans. Magn. 1974, 10, 109–113. [Google Scholar] [CrossRef]
- Ćwik, J. Magnetism and magnetocaloric effect in multicomponent Laves-phase compounds: Study and comparative analysis. J. Solid State Chem. 2014, 209, 13–22. [Google Scholar] [CrossRef]
- Gu, Z.; Zhou, B.; Li, J.; Ao, W.; Cheng, G.; Zhao, J. Magnetocaloric effect of GdCo2−xAlx compounds. Solid State Commun. 2007, 141, 548–550. [Google Scholar] [CrossRef]
- Anikin, M.; Tarasov, E.; Kudrevatykh, N.; Zinin, A. Magnetocaloric properties of Gd(Co1−xFex)2 compounds, with x ≤ 0.60. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 185, p. 05009. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.Y.; Luo, J.; Li, J.B.; Liang, J.K.; Wang, Y.C.; Ji, L.N.; Liu, Y.H.; Rao, G.H. Magnetocaloric effect of Gd(Co1−xMnx)2 compounds. Solid State Commun. 2007, 143, 541–544. [Google Scholar] [CrossRef]
- Annaorazov, M.P.; Asatryan, K.A.; Myalikgulyev, G.; Nikitin, S.A.; Tishin, A.M.; Tyurin, A.L. Alloys of the Fe-Rh system as a new class of working material for magnetic refrigerators. Cryogenics 1992, 32, 867–872. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Conde, A. Field dependence of the magnetocaloric effect in materials with a second order phase transition: A master curve for the magnetic entropy change. Appl. Phys. Lett. 2006, 89, 222512. [Google Scholar] [CrossRef]


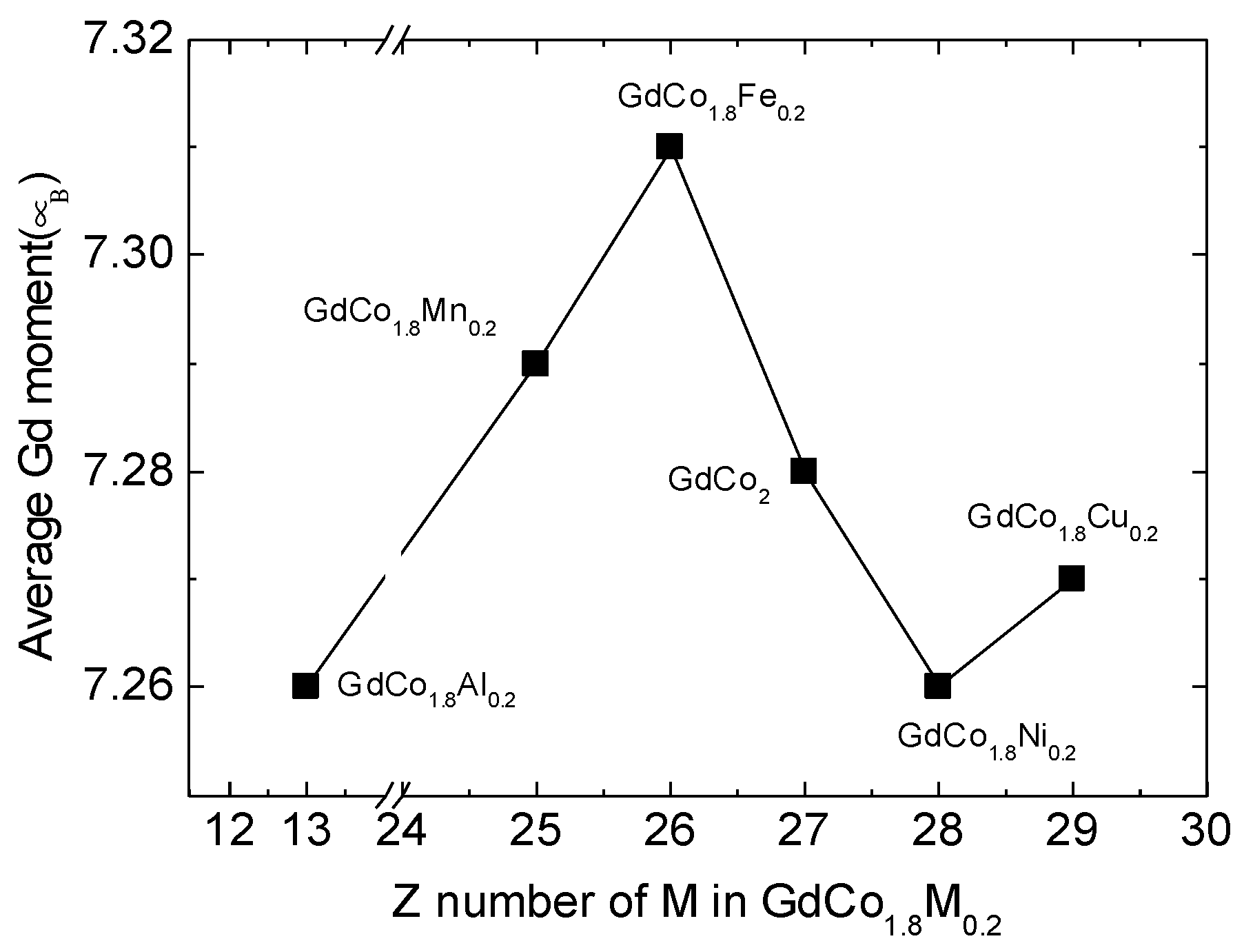

| GdCo1.8M0.2 | Substitutional Element M | Mn | Fe | Co | Ni | Cu | Al |
|---|---|---|---|---|---|---|---|
| ATOM | Position | Spin Moment [μB] | Spin Moment [μB] | Spin Moment [μB] | Spin Moment [μB] | Spin Moment [μB] | Spin Moment [μB] |
| Gd1 | (1/8, 1/8, 1/8) | 7.27 | 7.30 | 7.27 | 7.26 | 7.27 | 7.26 |
| Gd2 | (7/8, 7/8, 7/8) | 7.28 | 7.31 | 7.28 | 7.26 | 7.26 | 7.24 |
| Gd3 | (5/8, 5/8, 1/8) | 7.29 | 7.31 | 7.27 | 7.25 | 7.27 | 7.25 |
| Gd4 | (3/8, 3/8, 7/8) | 7.29 | 7.31 | 7.27 | 7.25 | 7.27 | 7.25 |
| Gd5 | (5/8, 1/8, 5/8) | 7.29 | 7.31 | 7.27 | 7.25 | 7.27 | 7.25 |
| Gd6 | (3/8, 7/8, 3/8) | 7.29 | 7.31 | 7.27 | 7.25 | 7.27 | 7.25 |
| Gd7 | (1/8, 5/8, 5/8) | 7.28 | 7.31 | 7.27 | 7.26 | 7.26 | 7.24 |
| Gd8 | (7/8, 3/8, 3/8) | 7.27 | 7.30 | 7.27 | 7.26 | 7.27 | 7.26 |
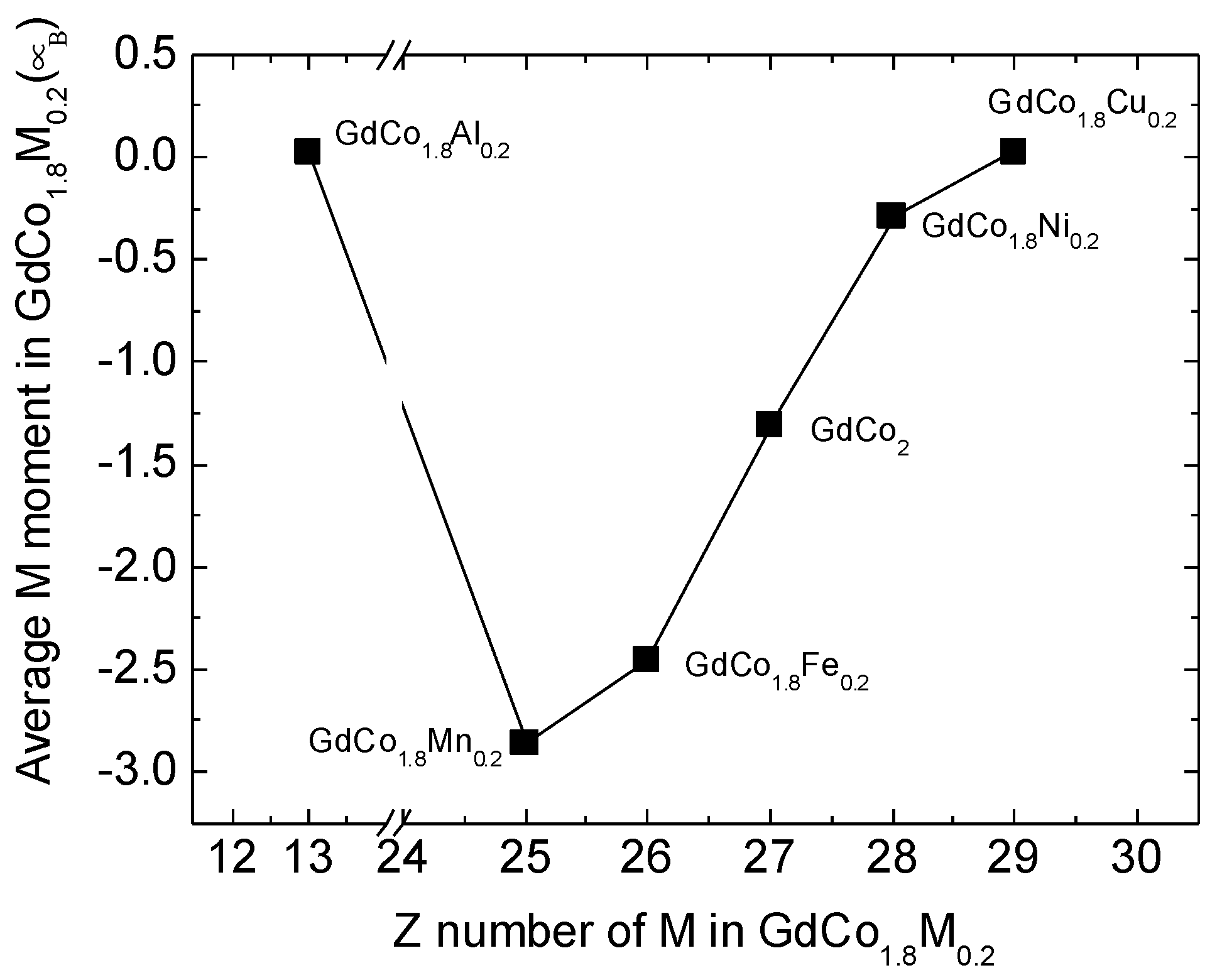
| M1 | (1/2, 1/2, 1/2) | −2.88 | −2.46 | −1.31 | −0.29 | 0.02 | 0.02 |
| M2 | (1/2, 3/4, 3/4) | −2.81 | −2.45 | −1.31 | −0.29 | 0.03 | 0.02 |
| Co3 | (3/4, 3/4, 1/2) | −1.34 | −1.39 | −1.31 | −1.26 | −1.15 | −0.89 |
| Co4 | (3/4, 1/2, 3/4) | −1.34 | −1.39 | −1.31 | −1.26 | −1.15 | −0.89 |
| Co5 | (0, 0, 1/2) | −1.40 | −1.40 | −1.31 | −1.28 | −1.19 | −1.17 |
| Co6 | (0, 1/4, 3/4) | −1.40 | −1.39 | −1.31 | −1.33 | −1.28 | −1.17 |
| Co7 | (1/4, 1/4, 1/2) | −1.36 | −1.38 | −1.31 | −1.31 | −1.24 | −1.08 |
| Co8 | (1/4, 0, 3/4) | −1.34 | −1.39 | −1.31 | −1.26 | −1.15 | −0.89 |
| Co9 | (0, 1/2, 0) | −1.40 | −1.40 | −1.31 | −1.28 | −1.19 | −1.17 |
| Co10 | (0, 3/4, 1/4) | −1.40 | −1.39 | −1.31 | −1.33 | −1.28 | −1.17 |
| Co11 | (1/4, 3/4, 0) | −1.34 | −1.39 | −1.31 | −1.26 | −1.15 | −0.89 |
| Co12 | (1/4, 1/2, 1/4) | −1.36 | −1.38 | −1.31 | −1.31 | −1.24 | −1.08 |
| M3 | (1/2, 0, 0) | −2.88 | −2.46 | −1.31 | −0.29 | 0.02 | 0.02 |
| Co14 | (1/2, 1/4, 1/4) | −1.38 | −1.36 | −1.31 | −1.26 | −1.22 | −1.01 |
| Co15 | (3/4, 1/4, 0) | −1.36 | −1.38 | −1.31 | −1.31 | −1.24 | −1.08 |
| Co16 | (3/4, 0, 1/4) | −1.36 | −1.38 | −1.31 | −1.31 | −1.24 | −1.08 |
| interstitial | 3.84 | 4.73 | 4.09 | 3.80 | 3.93 | 3.78 | |
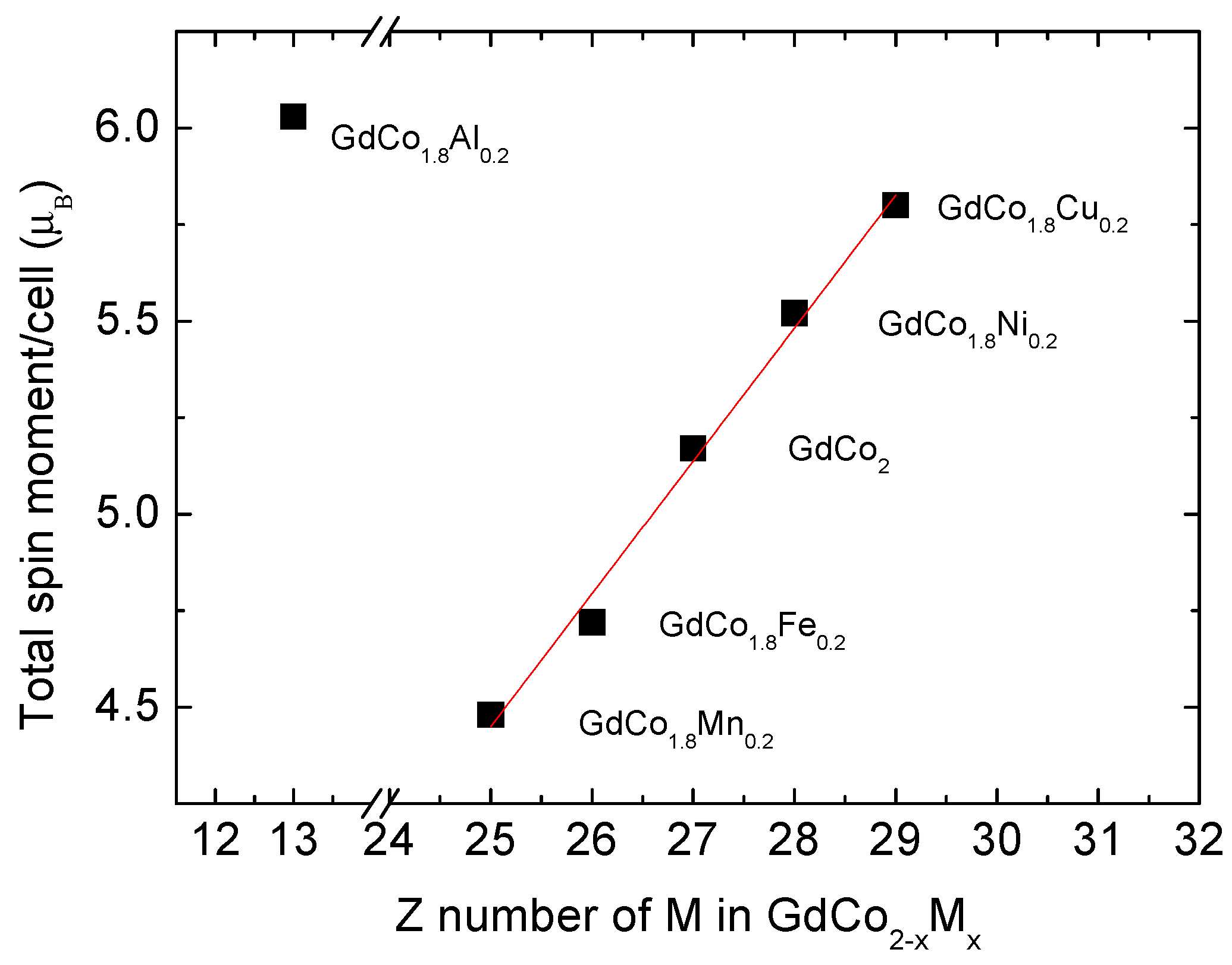
| TOTAL | 35.73 | 37.81 | 41.35 | 44.20 | 46.39 | 48.27 | |
| Moment /elementary cell | 4.47 | 4.73 | 5.17 | 5.52 | 5.80 | 6.03 |
| M | S − 1/2 Binding Energy (eV) | S + 1/2 Binding Energy (eV) | ΔEex (eV) |
|---|---|---|---|
| Al | 101.08 | 104.62 | 3.54 |
| Cu | 100.82 | 104.33 | 3.51 |
| Mn | 101.07 | 104.59 | 3.52 |
| M | Tc (K) | M0 (µB/f.u.) | MGd (µB/atom) | MM (µB/atom) | MCo (µB/atom) |
|---|---|---|---|---|---|
| Al | 382 | 5.78 | 7.26 | −0.03 | 0.82 |
| Cu | 378 | 5.75 | 7.27 | −0.02 | 0.84 |
| Mn | 453 | 4.52 | 7.30 | −2.86 | 1.23 |
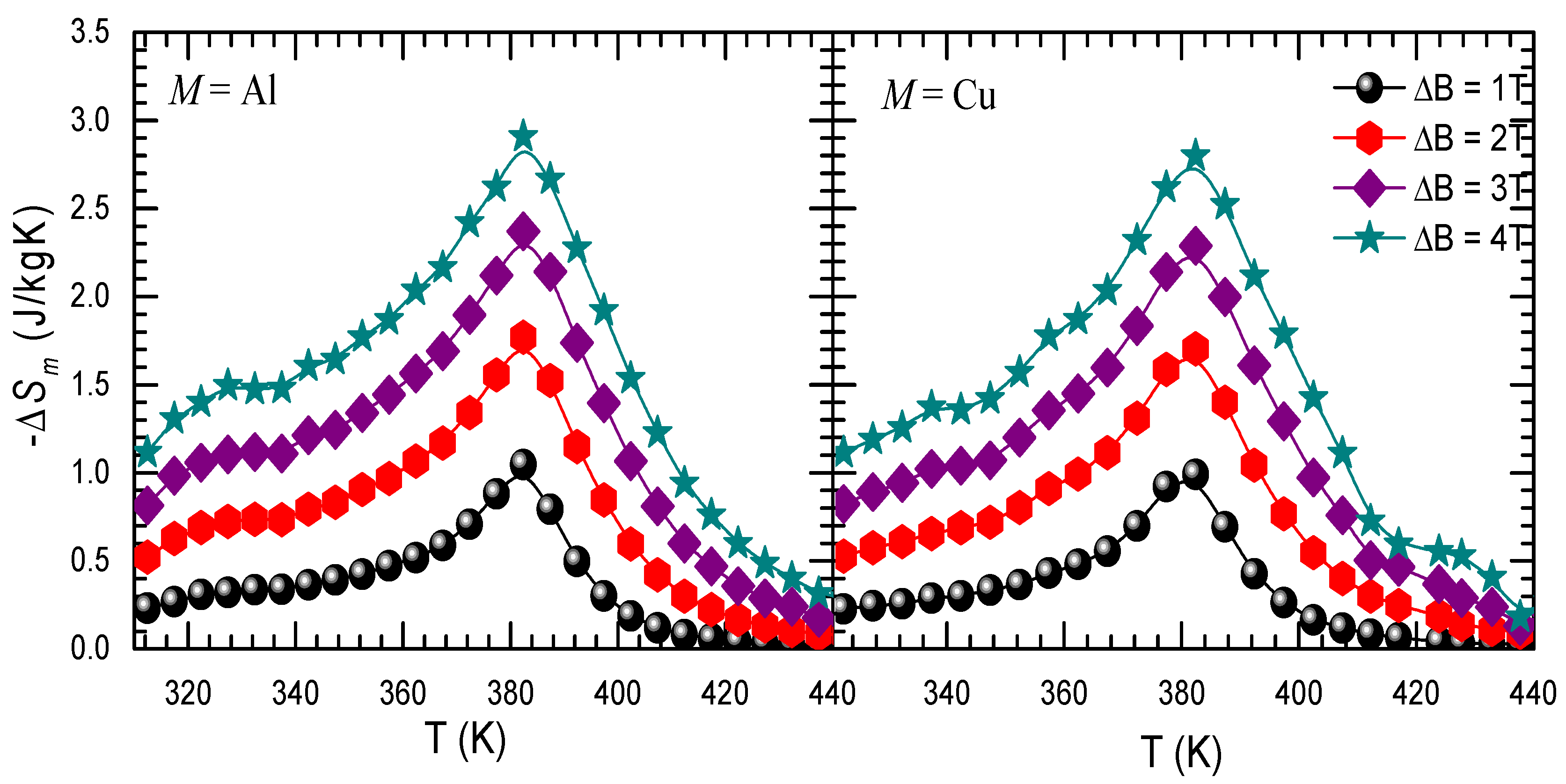
| M | Tmax (K) | |ΔSM| (J/KgK) | δTFWHM (K) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔB = 1 T | ΔB = 2 T | ΔB = 3 T | ΔB = 4 T | ΔB = 1 T | ΔB = 2 T | ΔB = 3 T | ΔB = 4 T | ||
| Cu | 381 | 0.93 | 1.64 | 2.21 | 2.71 | 30 | 45 | 54 | 66 |
| Al | 382 | 1.04 | 1.76 | 2.36 | 2.89 | 31 | 48 | 61 | 82 |
| M | RCP(S) (J/kg) | RCP(S)/ΔB (J/kgT) | ||||||
|---|---|---|---|---|---|---|---|---|
| ΔB = 1 T | ΔB = 2 T | ΔB = 3 T | ΔB = 4 T | ΔB = 1 T | ΔB = 2 T | ΔB = 3 T | ΔB = 4 T | |
| Cu | 27.9 | 73.8 | 119.34 | 178.86 | 27.9 | 36.9 | 39.78 | 44.71 |
| Al | 32.24 | 84.48 | 143.96 | 236.98 | 32.24 | 42.24 | 47.98 | 59.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souca, G.; Dudric, R.; Küpper, K.; Tiusan, C.; Tetean, R. Band Structure Calculations, Magnetic Properties and Magnetocaloric Effect of GdCo1.8M0.2 Compounds with M = Fe, Mn, Cu, Al. Magnetochemistry 2024, 10, 53. https://doi.org/10.3390/magnetochemistry10080053
Souca G, Dudric R, Küpper K, Tiusan C, Tetean R. Band Structure Calculations, Magnetic Properties and Magnetocaloric Effect of GdCo1.8M0.2 Compounds with M = Fe, Mn, Cu, Al. Magnetochemistry. 2024; 10(8):53. https://doi.org/10.3390/magnetochemistry10080053
Chicago/Turabian StyleSouca, Gabriela, Roxana Dudric, Karsten Küpper, Coriolan Tiusan, and Romulus Tetean. 2024. "Band Structure Calculations, Magnetic Properties and Magnetocaloric Effect of GdCo1.8M0.2 Compounds with M = Fe, Mn, Cu, Al" Magnetochemistry 10, no. 8: 53. https://doi.org/10.3390/magnetochemistry10080053
APA StyleSouca, G., Dudric, R., Küpper, K., Tiusan, C., & Tetean, R. (2024). Band Structure Calculations, Magnetic Properties and Magnetocaloric Effect of GdCo1.8M0.2 Compounds with M = Fe, Mn, Cu, Al. Magnetochemistry, 10(8), 53. https://doi.org/10.3390/magnetochemistry10080053





