Nonequivalent Antiferromagnetically Coupled Sublattices Induce Two-Step Spin-Crossover Transitions: Equilibrium and Nonequilibrium Aspects
Abstract
1. Introduction
2. Description of the Model and Derivations of Static and Dynamic Equations
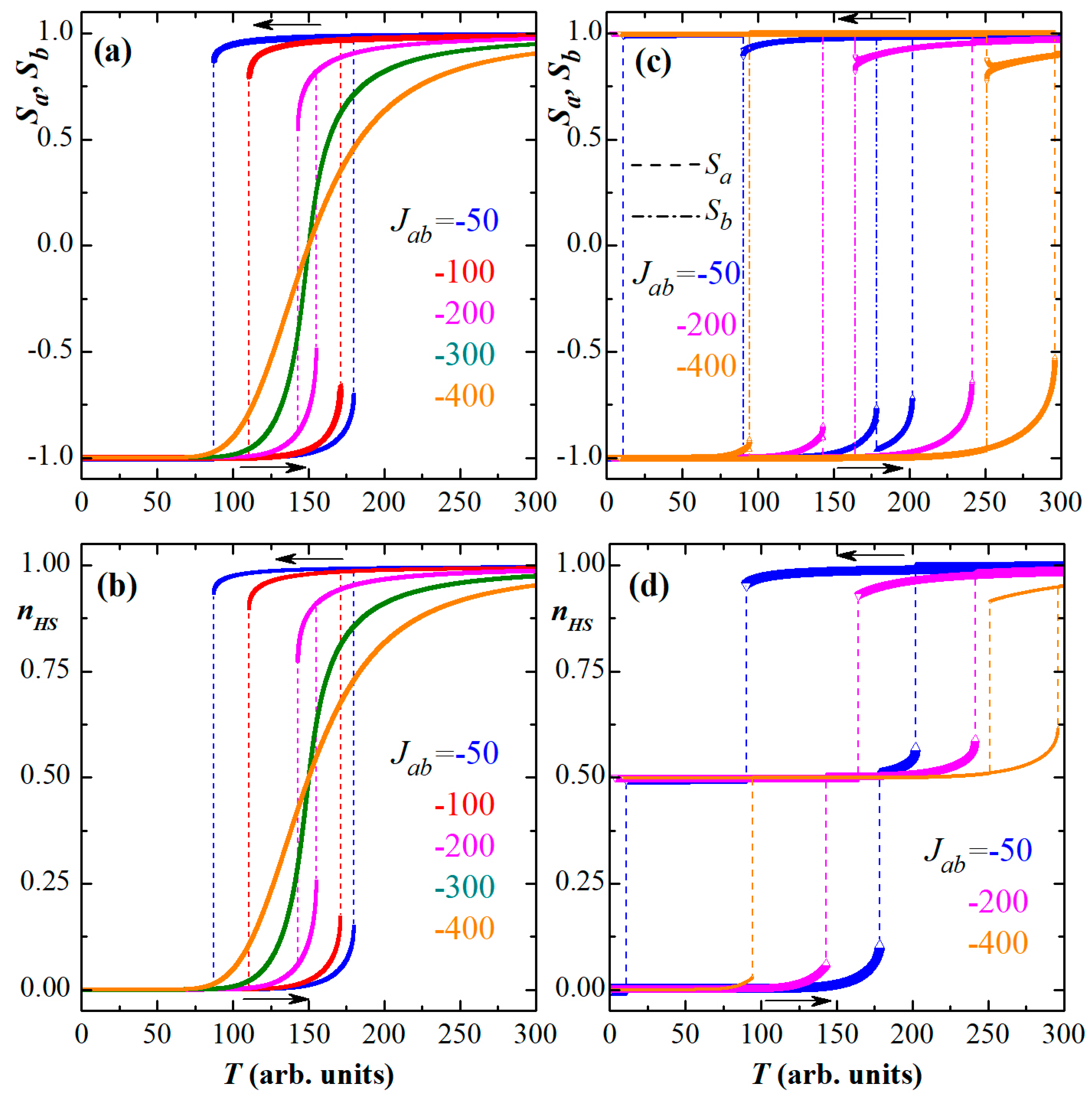
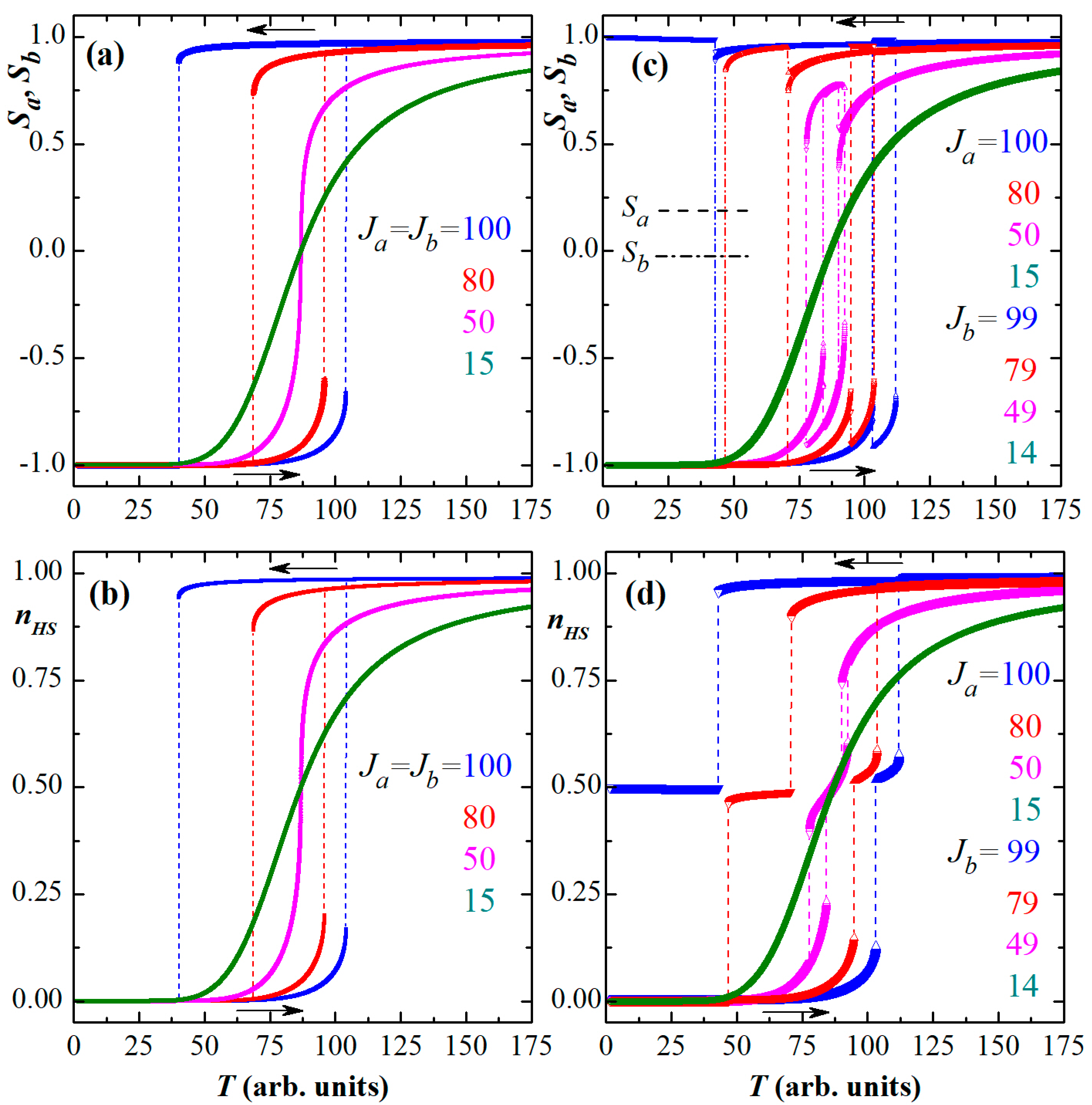
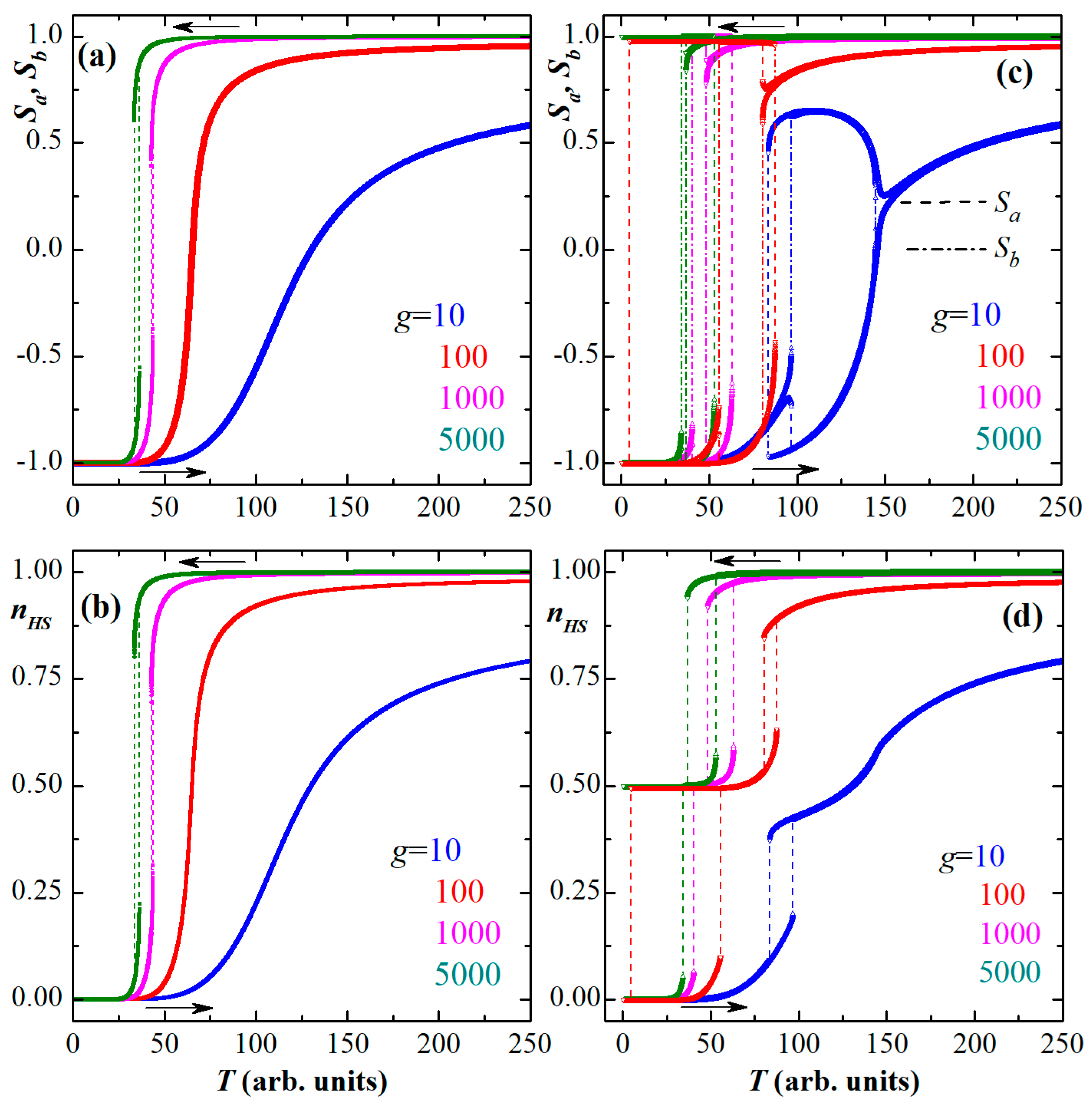
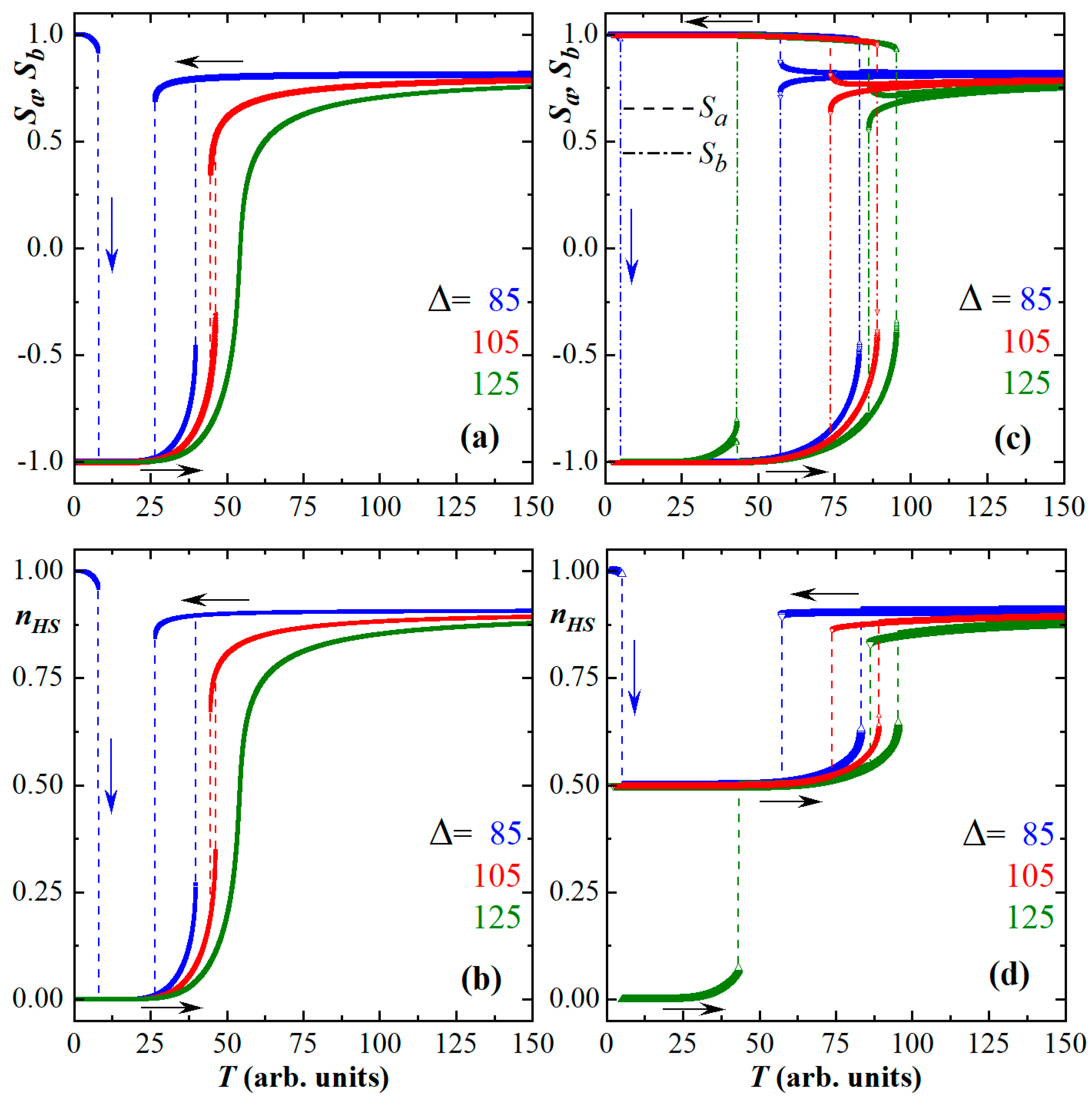
3. Results and Discussion
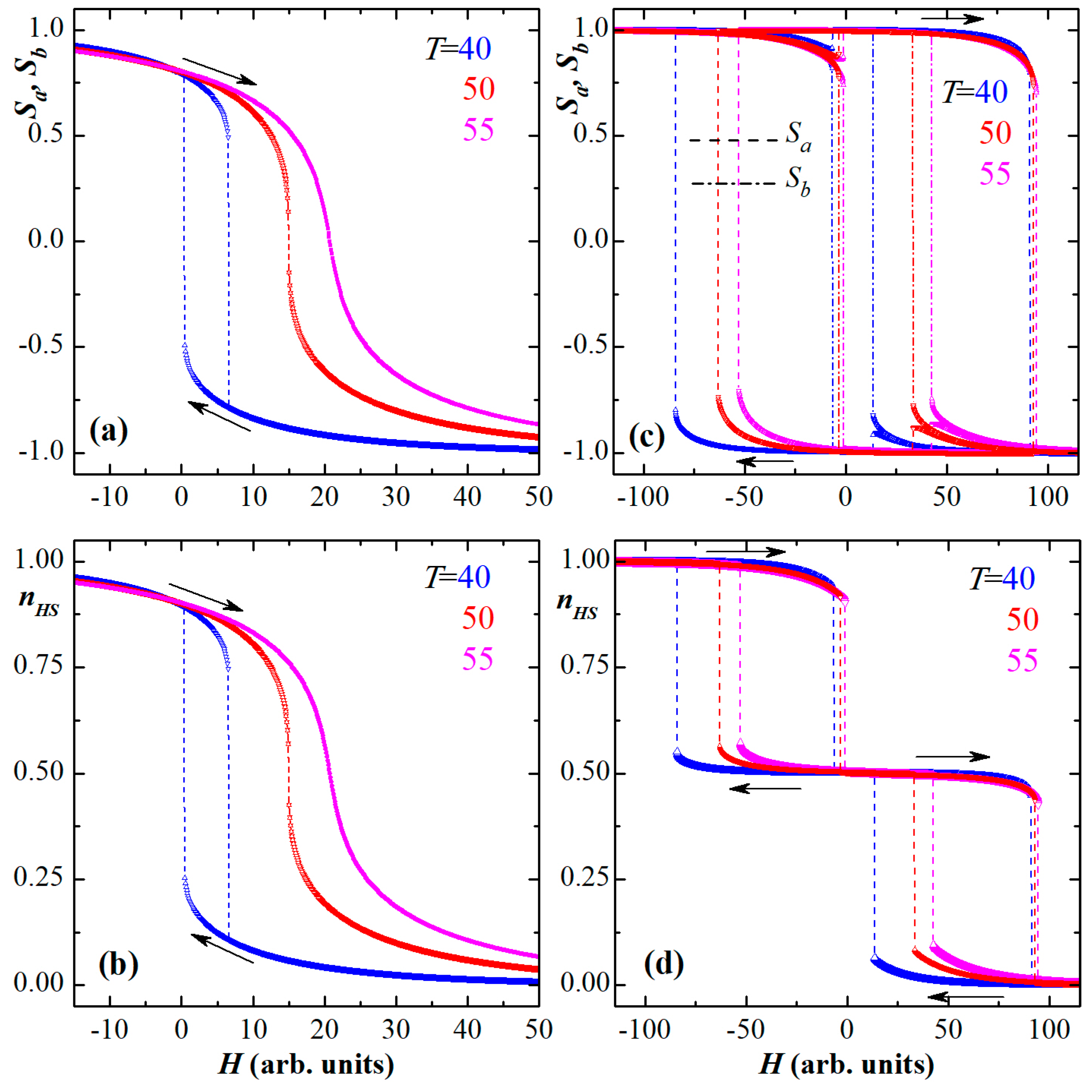
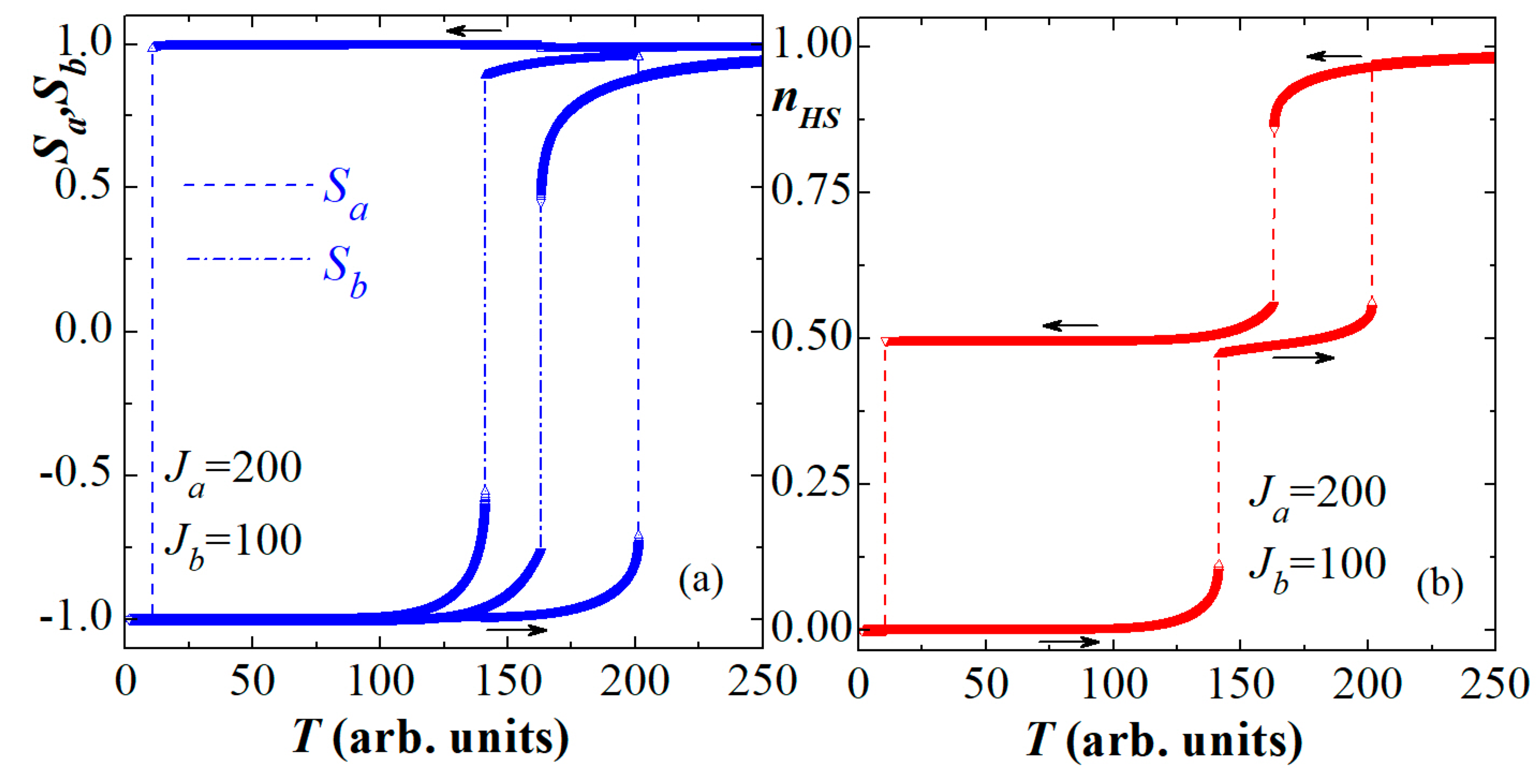
3.1. Static Behaviors
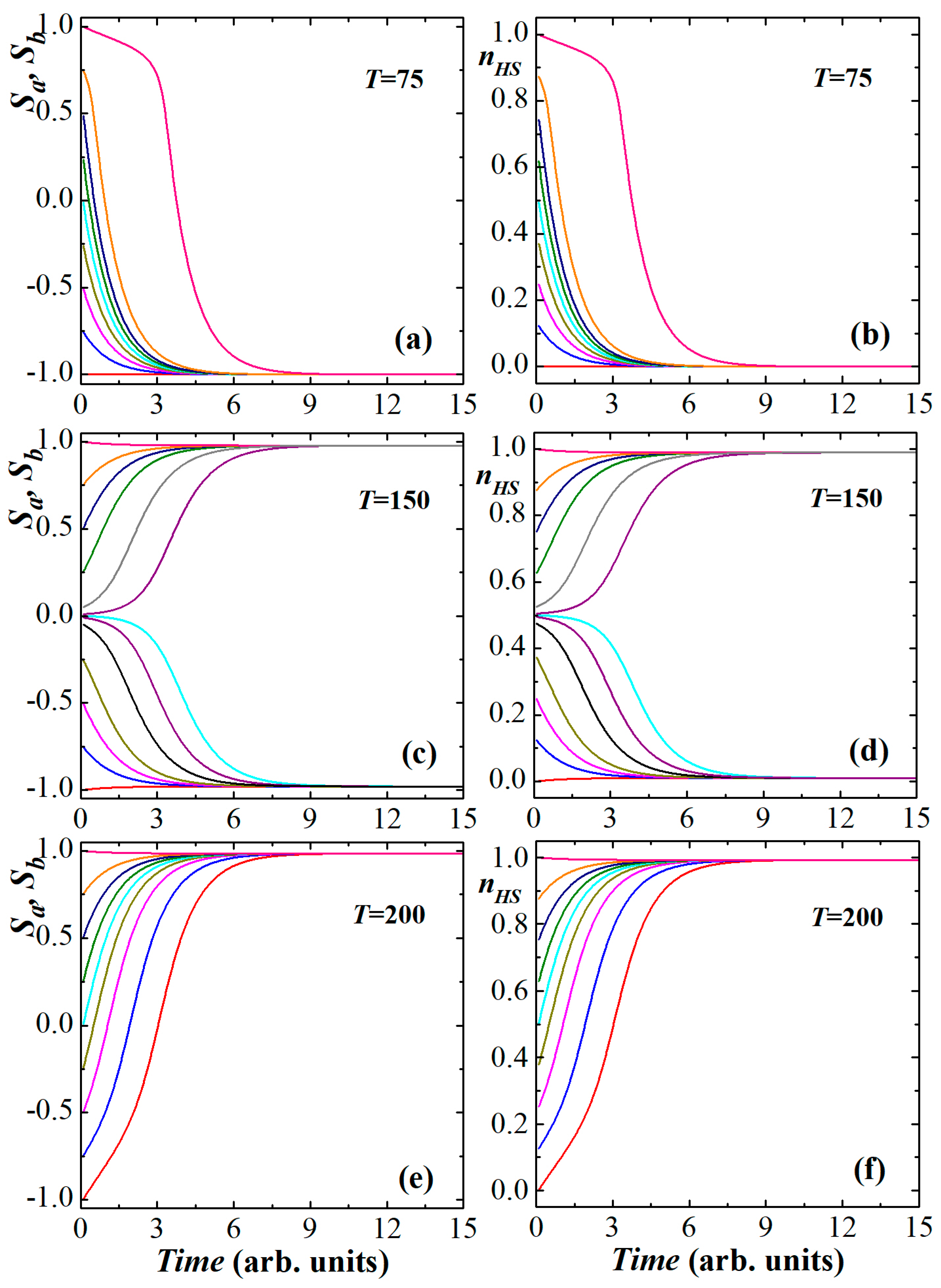
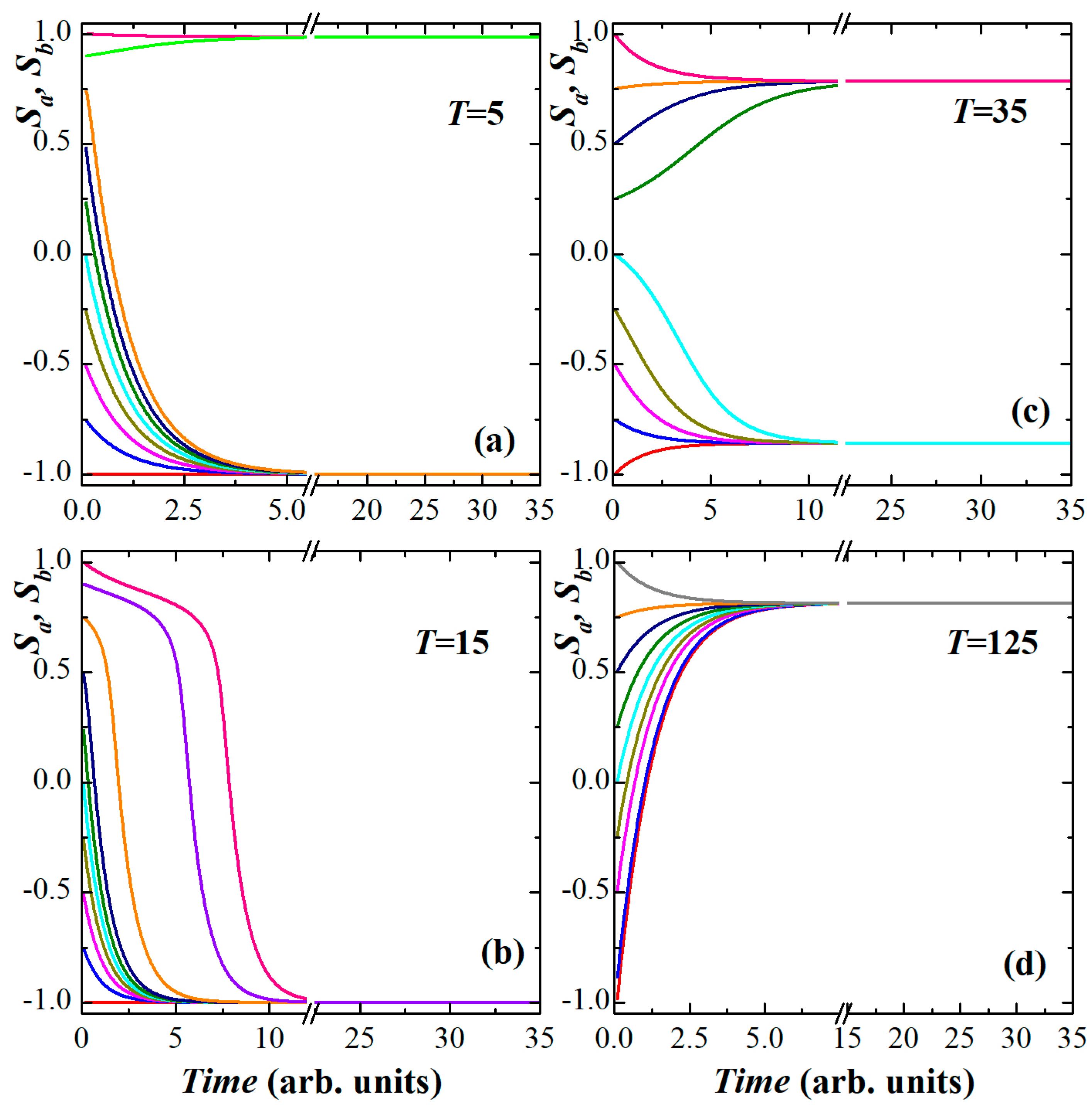
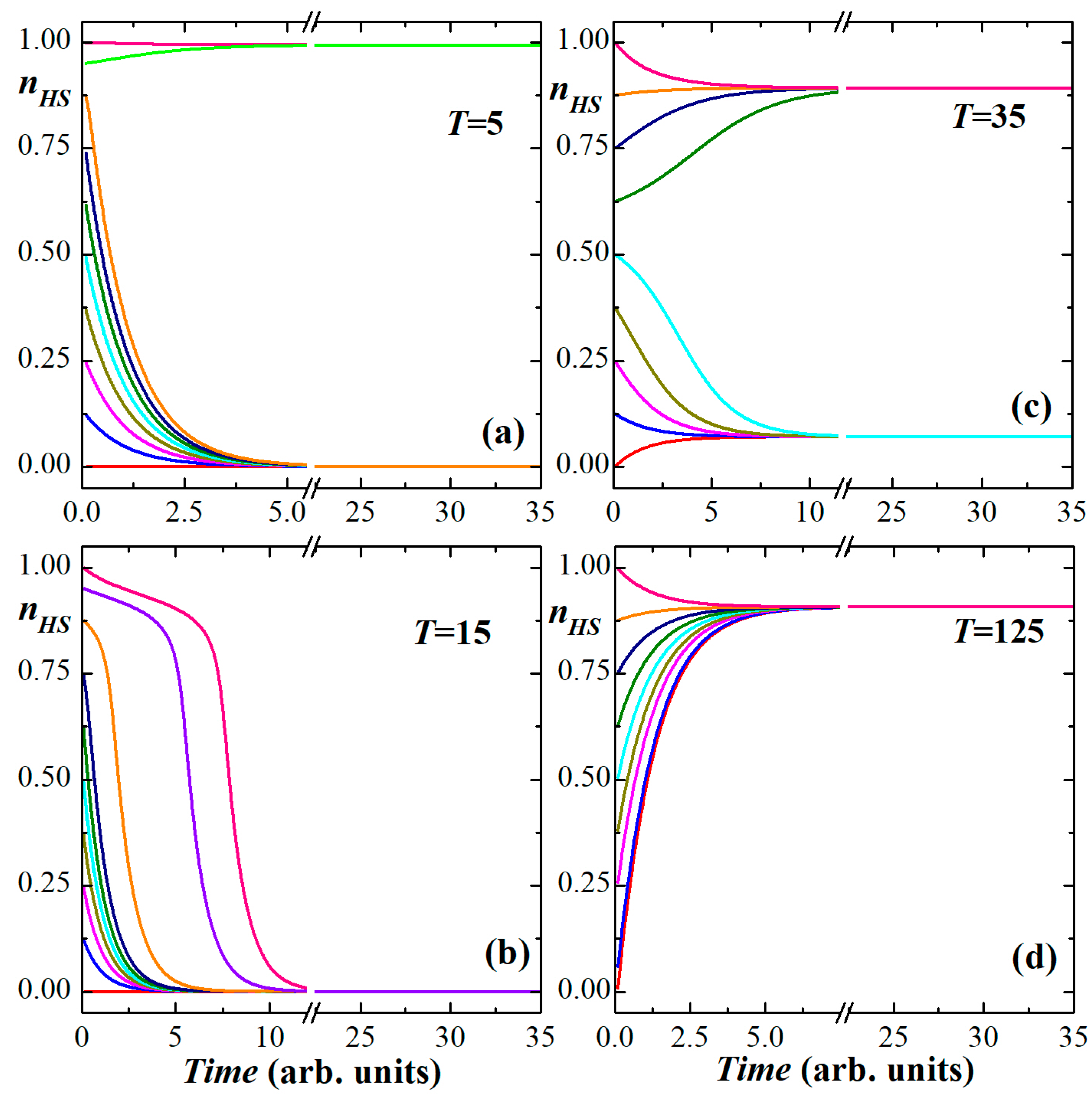
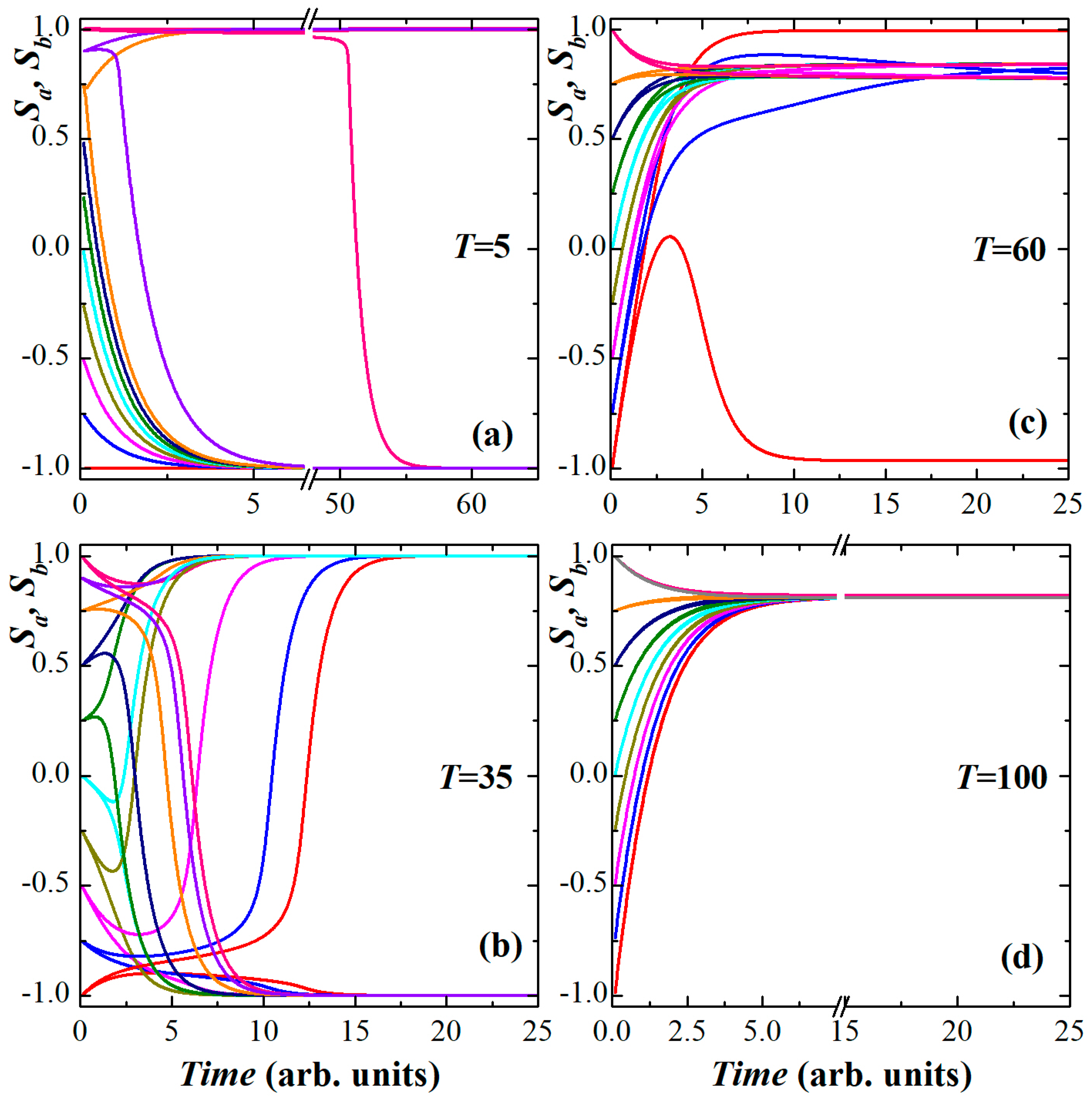
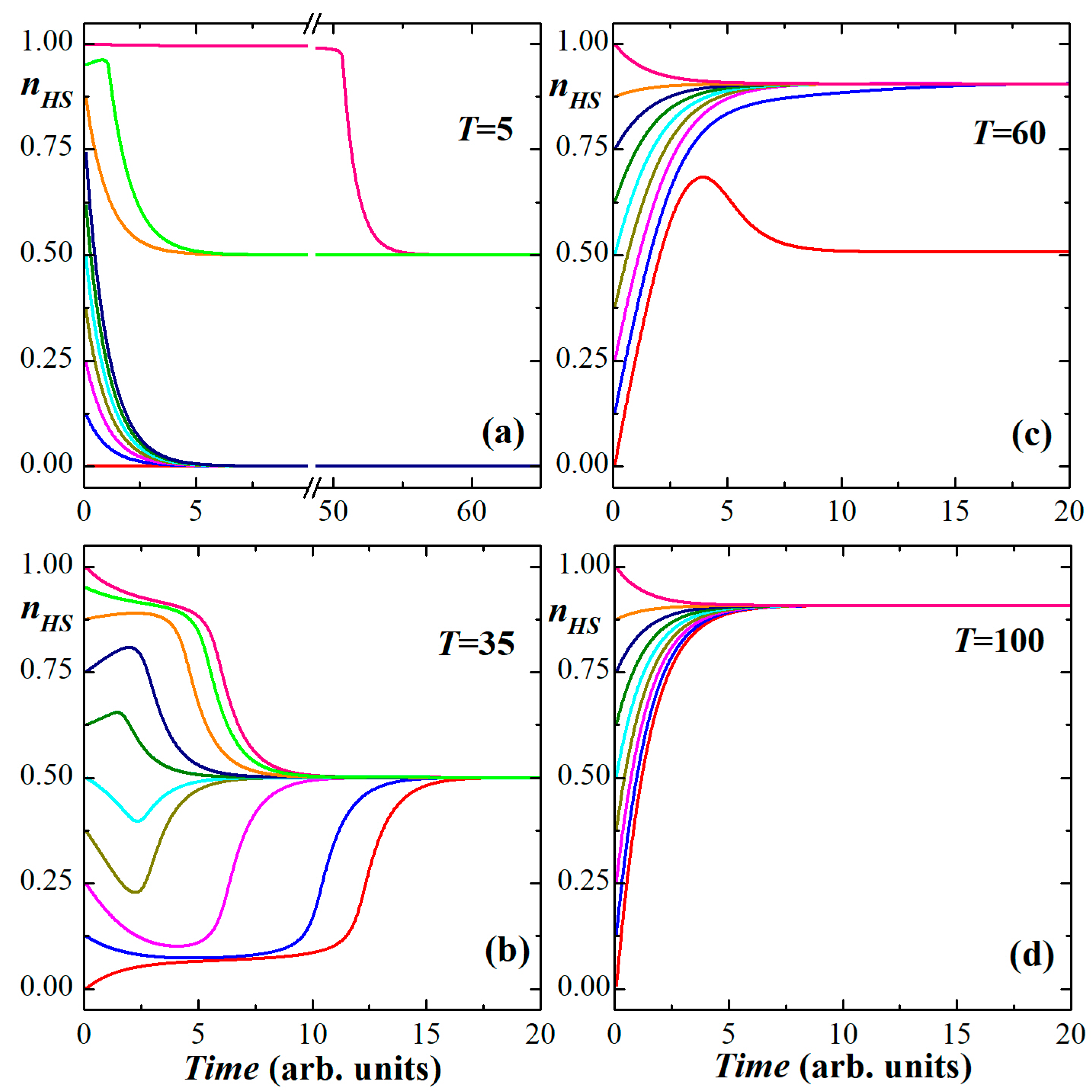
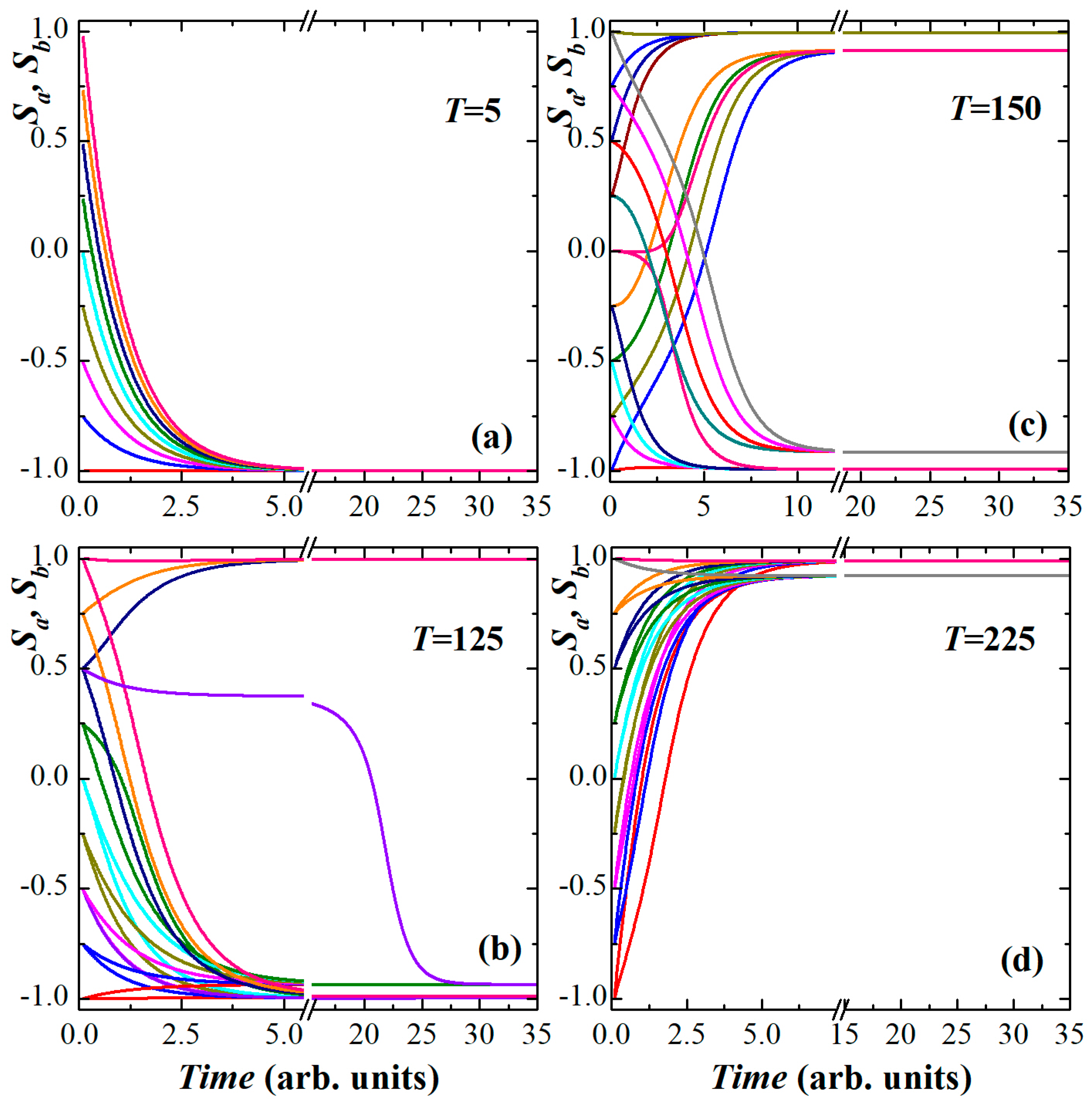
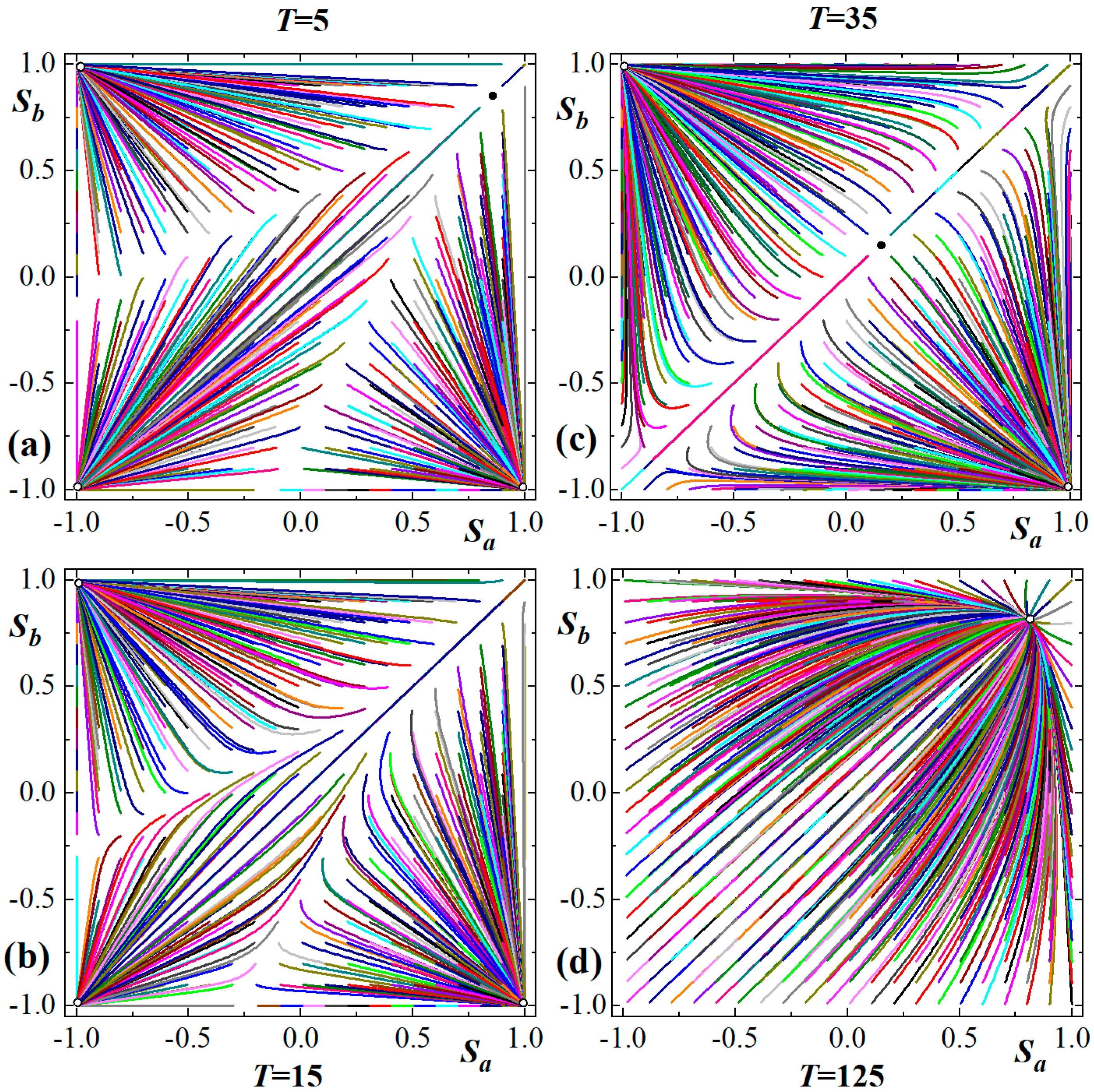
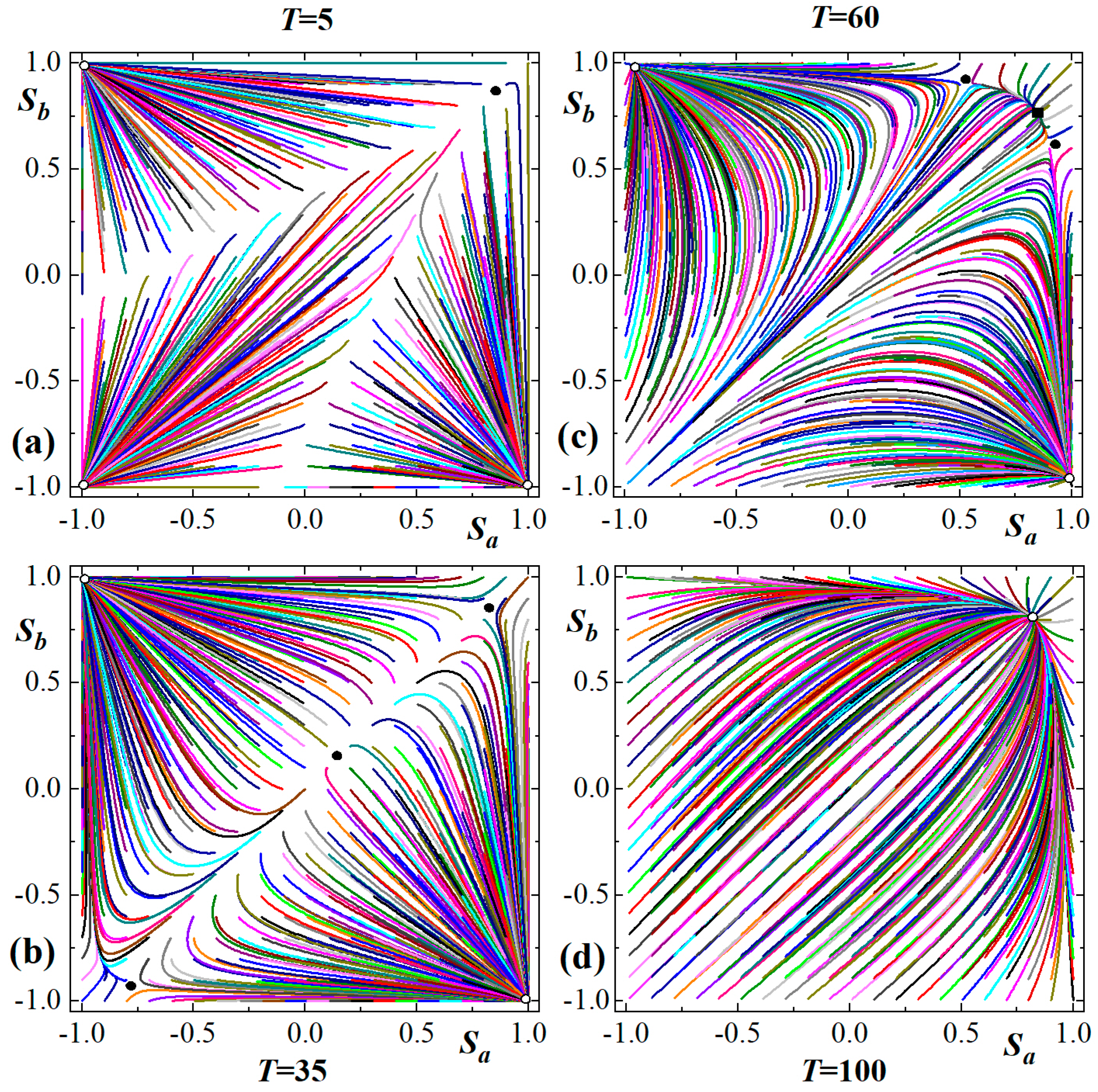
3.2. Time-Dependent Behaviors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gütlich, P.; Gaspar, A.B.; Garcia, Y. Spin state switching in iron coordination compounds. Beilstein J. Org. Chem. 2013, 9, 342–391. [Google Scholar] [CrossRef]
- Bousseksou, A.; Molnár, G.; Salmon, L.; Nicolazzi, W. Molecular spin crossover phenomenon: Recent achievements and prospects. Chem. Soc. Rev. 2011, 40, 3313–3335. [Google Scholar] [CrossRef]
- Lefter, C.; Tan, R.; Tricard, S.; Dugay, J.; Molnár, G.; Salmon, L.; Carrey, J.; Rotaru, A.; Bousseksou, A. On the stability of spin crossover materials: From bulk samples to electronic devices. Polyhedron 2015, 102, 434–440. [Google Scholar] [CrossRef]
- Kahn, O.; Martinez, C.J. Spin-Transition Polymers: From Molecular Materials Toward Memory Devices. Science 1998, 279, 44–48. [Google Scholar] [CrossRef]
- Von Ranke, P.; Alho, B.; Ribeiro, P. First indirect experimental evidence and theoretical discussion of giant refrigeration capacity through the reversible pressure induced spin-crossover phase transition. J. Alloys Compd. 2018, 749, 556–560. [Google Scholar] [CrossRef]
- Gaspar, A.B.; Molnár, G.; Rotaru, A.; Shepherd, H.J. Pressure effect investigations on spin-crossover coordination compounds. Comptes Rendus Chim. 2018, 21, 1095–1120. [Google Scholar] [CrossRef]
- Babilotte, K.; Boukheddaden, K. Theoretical investigations on the pressure effects in spin-crossover materials: Reentrant phase transitions and other behavior. Phys. Rev. B 2020, 101, 174113. [Google Scholar] [CrossRef]
- Muñoz, M.C.; Real, J.A. Thermo-, piezo-, photo- and chemo-switchable spin crossover iron(II)-metallocyanate based coordination polymers. Coord. Chem. Rev. 2011, 255, 2068–2093. [Google Scholar] [CrossRef]
- Bonnet, S.; Molnár, G.; Costa, J.S.; Siegler, M.A.; Spek, A.L.; Bousseksou, A.; Fu, W.-T.; Gamez, P.; Reedijk, J. Influence of Sample Preparation, Temperature, Light, and Pressure on the Two-Step Spin Crossover Mononuclear Compound [Fe(bapbpy)(NCS)2]. Chem. Mater. 2009, 21, 1123–1136. [Google Scholar] [CrossRef]
- Her, J.L.; Matsuda, Y.H.; Nakano, M.; Niwa, Y.; Inada, Y. Magnetic field-induced spin-crossover transition in [MnIII(taa)] studied by X-ray absorption spectroscopy. J. Appl. Phys. 2012, 111, 053921. [Google Scholar] [CrossRef]
- Kimura, S.; Narumi, Y.; Kindo, K.; Nakano, M.; Matsubayashi, G.-E. Field-induced spin-crossover transition of [MnIII(taa)] studied under pulsed magnetic fields. Phys. Rev. B 2005, 72, 064448. [Google Scholar] [CrossRef]
- Mahfoud, T.; Molnár, G.; Bonhommeau, S.; Cobo, S.; Salmon, L.; Demont, P.; Tokoro, H.; Ohkoshi, S.-I.; Boukheddaden, K.; Bousseksou, A. Electric-Field-Induced Charge-Transfer Phase Transition: A Promising Approach Toward Electrically Switchable Devices. J. Am. Chem. Soc. 2009, 131, 15049–15054. [Google Scholar] [CrossRef]
- Lefter, C.; Tan, R.; Dugay, J.; Tricard, S.; Molnár, G.; Salmon, L.; Carrey, J.; Nicolazzi, W.; Rotaru, A.; Bousseksou, A. Unidirectional electric field-induced spin-state switching in spin crossover based microelectronic devices. Chem. Phys. Lett. 2016, 644, 138–141. [Google Scholar] [CrossRef]
- Bonhommeau, S.; Molnár, G.; Goiran, M.; Boukheddaden, K.; Bousseksou, A. Unified dynamical description of pulsed magnetic field and pressure effects on the spin crossover phenomenon. Phys. Rev. B 2006, 74, 064424. [Google Scholar] [CrossRef]
- Desaix, A.; Roubeau, O.; Jeftic, J.; Haasnoot, J.; Boukheddaden, K.; Codjovi, E.; Linarès, J.; Noguès, M.; Varret, F. Light-induced bistability in spin transition solids leading to thermal and optical hysteresis. Eur. Phys. J. B 1998, 6, 183–193. [Google Scholar] [CrossRef]
- Stoleriu, L.; Chakraborty, P.; Hauser, A.; Stancu, A.; Enachescu, C. Thermal hysteresis in spin-crossover compounds studied within the mechanoelastic model and its potential application to nanoparticles. Phys. Rev. B 2011, 84, 134102. [Google Scholar] [CrossRef]
- Paez-Espejo, M.; Sy, M.; Boukheddaden, K. Unprecedented Bistability in Spin-Crossover Solids Based on the Retroaction of the High Spin Low-Spin Interface with the Crystal Bending. J. Am. Chem. Soc. 2018, 140, 11954–11964. [Google Scholar] [CrossRef]
- Gütlich, P. Spin crossover in iron(II)-complexes. Struct. Bond. 1981, 44, 83–195. [Google Scholar] [CrossRef]
- König, E. Nature and dynamics of the spin-state interconversion in metal complexes. Struct. Bond. 1991, 76, 51–152. [Google Scholar] [CrossRef]
- Kahn, O. Spin-crossover molecular materials. Curr. Opin. Solid State Mater. Sci. 1996, 1, 547–554. [Google Scholar] [CrossRef]
- Gütlich, P.; Hauser, A.; Spiering, H. Thermal and Optical Switching of Iron(II) Complexes. Angew. Chem. Int. Ed. 1994, 33, 2024–2054. [Google Scholar] [CrossRef]
- Decurtins, S.; Gütlich, P.; Köhler, C.; Spiering, H.; Hauser, A. Light-induced excited spin state trapping in a transition-metal complex: The hexa-1-propyltetrazole-iron (II) tetrafluoroborate spin-crossover system. Chem. Phys. Lett. 1984, 105, 1–4. [Google Scholar] [CrossRef]
- Renz, F.; Spiering, H.; Goodwin, H.; Gütlich, P. Light-perturbed hysteresis in an iron(II) spin-crossover compound observed by the Mössbauer effect. Hyperfine Interact. 2000, 126, 155–158. [Google Scholar] [CrossRef]
- Tayagaki, T.; Tanaka, K. Photoinduced Phase Transition to a New Macroscopic Spin-Crossover-Complex Phase. Phys. Rev. Lett. 2001, 86, 2886–2889. [Google Scholar] [CrossRef]
- Freysz, E.; Montant, S.; Létard, S.; Létard, J.-F. Single laser pulse induces spin state transition within the hysteresis loop of an Iron compound. Chem. Phys. Lett. 2004, 394, 318–323. [Google Scholar] [CrossRef]
- Bonhommeau, S.; Molnár, G.; Galet, A.; Zwick, A.; Real, J.; McGarvey, J.J.; Bousseksou, A. One Shot Laser Pulse Induced Reversible Spin Transition in the Spin-Crossover Complex [Fe(C4H4N2){Pt(CN)4}] at Room Temperature. Angew. Chem. 2005, 117, 4137–4141. [Google Scholar] [CrossRef]
- Gudyma, I.; Maksymov, A.; Dimian, M. Stochastic kinetics of photoinduced phase transitions in spin-crossover solids. Phys. Rev. E 2013, 88, 042111. [Google Scholar] [CrossRef]
- Milin, E.; Patinec, V.; Triki, S.; Bendeif, E.-E.; Pillet, S.; Marchivie, M.; Chastanet, G.; Boukheddaden, K. Elastic Frustration Triggering Photoinduced Hidden Hysteresis and Multistability in a Two-Dimensional Photoswitchable Hofmann-Like Spin-Crossover Metal–Organic Framework. Inorg. Chem. 2016, 55, 11652–11661. [Google Scholar] [CrossRef]
- Kambara, T. Theory of Pressure-Induced High-Spin ⇄ Low-Spin Transition in Compounds of Iron. J. Phys. Soc. Jpn. 1981, 50, 2257–2264. [Google Scholar] [CrossRef]
- Konishi, Y.; Tokoro, H.; Nishino, M.; Miyashita, S. Monte Carlo Simulation of Pressure-Induced Phase Transitions in Spin-Crossover Materials. Phys. Rev. Lett. 2008, 100, 067206. [Google Scholar] [CrossRef]
- Shepherd, H.J.; Rosa, P.; Vendier, L.; Casati, N.; Létard, J.-F.; Bousseksou, A.; Guionneau, P.; Molnár, G. High-pressure spin-crossover in a dinuclear Fe(ii) complex. Phys. Chem. Chem. Phys. 2012, 14, 5265–5271. [Google Scholar] [CrossRef]
- Bousseksou, A.; Nasser, J.; Linares, J.; Boukheddaden, K.; Varret, F. Ising-like model for the two-step spin-crossover. J. Phys. I 1992, 2, 1381–1403. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Linares, J.; Codjovi, E.; Varret, F.; Niel, V.; Real, J.A. Dynamical Ising-like model for the two-step spin-crossover systems. J. Appl. Phys. 2003, 93, 7103–7105. [Google Scholar] [CrossRef]
- Bousseksou, A.; Varret, F.; Nasser, J. Ising-like model for the two step spin-crossover of binuclear molecules. J. Phys. I 1993, 3, 1463–1473. [Google Scholar] [CrossRef]
- Hôo, B.; Boukheddaden, K.; Varret, F. Two-variable macroscopic model for spin-crossover solids: Static and dynamic effects of the correlations. Eur. Phys. J. B 2000, 17, 449–457. [Google Scholar] [CrossRef]
- Nishino, M.; Miyashita, S. Dynamical process for switching between the metastable ordered magnetic state and the nonmagnetic ground state in a photoinduced phase transition. Phys. Rev. B 2001, 63, 174404. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Linares, J.; Spiering, H.; Varret, F. One-dimensional Ising-like systems: An analytical investigation of the static and dynamic properties, applied to spin-crossover relaxation. Eur. Phys. J. B 2000, 15, 317–326. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Varret, F.; Salunke, S.; Linares, J.; Codjovi, E. Non-linear Relaxation of the Photo-induced High Spin State in Spin-Crossover Solids: Effect of Correlations. Phase Transit. 2002, 75, 733–741. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Nishino, M.; Miyashita, S.; Varret, F. Unified theoretical description of the thermodynamical properties of spin crossover with magnetic interactions. Phys. Rev. B 2005, 72, 014467. [Google Scholar] [CrossRef]
- Nasser, J. First order high-spin/low-spin phase transition induced by acoustic-phonons. Eur. Phys. J. B 2001, 21, 3–10. [Google Scholar] [CrossRef]
- Mouri, S.; Tanaka, K.; Bonhommeau, S.; Moussa, N.O.; Molnár, G.; Bousseksou, A. Relaxation process from photoinduced states of double-step spin-crossover systems using a kinetic two-sublattice Ising-like model including intra-site coupling. Phys. Rev. B 2008, 78, 174308. [Google Scholar] [CrossRef]
- Bousseksou, A.; Constant-Machado, H.; Varret, F. A Simple Ising-Like Model for Spin Conversion Including Molecular Vibrations. J. Phys. I 1995, 5, 747–760. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Shteto, I.; Hôo, B.; Varret, F. Dynamical model for spin-crossover solids. I. Relaxation effects in the mean-field approach. Phys. Rev. B 2000, 62, 14796–14805. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Shteto, I.; Hôo, B.; Varret, F. Dynamical model for spin-crossover solids. II. Static and dynamic effects of light in the mean-field approach. Phys. Rev. B 2000, 62, 14806–14817. [Google Scholar] [CrossRef]
- Nishino, M.; Boukheddaden, K.; Miyashita, S.; Varret, F. Dynamical properties of photoinduced magnetism and spin-crossover phenomena in Prussian blue analogs. J. Phys. Conf. Ser. 2005, 21, 61–66. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Linares, J.; Tanasa, R.; Chong, C. Theoretical investigations on an axial next nearest neighbour Ising-like model for spin crossover solids: One- and two-step spin transitions. J. Phys. Condens. Matter 2007, 19, 106201. [Google Scholar] [CrossRef]
- Nishino, M.; Yamaguchi, K.; Miyashita, S. Switching dynamics between the metastable ordered magnetic state and a nonmagnetic ground state: A possible mechanism for photoinduced ferromagnetism. Phys. Rev. B 1998, 58, 9303–9311. [Google Scholar] [CrossRef]
- Bousseksou, A.; Nasser, J.; Varret, F. Specific heat of two-step spin conversions. J. Magn. Magn. Mater. 1995, 140–144, 1511–1512. [Google Scholar] [CrossRef]
- Yalçın, O.; Veliu, V.; Özüm, S.; Erdem, R. Static and dynamic properties of two-sublattice spin-crossover systems. Phys. B Condens. Matter 2022, 645, 414230. [Google Scholar] [CrossRef]
- Kikuchi, R. A Theory of Cooperative Phenomena. Phys. Rev. B 1951, 81, 988–1003. [Google Scholar] [CrossRef]
- Kikuchi, R. The Path Probability Method. Prog. Theor. Phys. Suppl. 1966, 35, 1–64. [Google Scholar] [CrossRef]
- Nishino, M.; Boukheddaden, K.; Miyashita, S.; Varret, F. Relaxation dynamics of two-step spin-crossover. Polyhedron 2005, 24, 2852–2856. [Google Scholar] [CrossRef]
- Boča, R.; Linert, W. Is There a Need for New Models of the Spin Crossover? In Molecular Magnets Recent Highlights; Springer: Vienna, Austria, 2002; pp. 83–100. [Google Scholar] [CrossRef]
- Boinnard, D.; Bousseksou, A.; Dworkin, A.; Savariault, J.M.; Varret, F.; Tuchagues, J.P. Two-step spin conversion of [FeII(5-NO2-sal-N(1,4,7,10))]: 292, 153, and 103 K X-ray crystal and molecular structure, infrared, magnetic, Moessbauer, calorimetric, and theoretical studies. Inorg. Chem. 1994, 33, 271–281. [Google Scholar] [CrossRef]
- Nishino, M.; Boukheddaden, K.; Miyashita, S.; Varret, F. Arrhenius Monte Carlo study of two-step spin crossover: Equilibrium and relaxation paths. Phys. Rev. B 2003, 68, 224402. [Google Scholar] [CrossRef]
- Miyashita, S.; Konishi, Y.; Tokoro, H.; Nishino, M.; Boukheddaden, K.; Varret, F. Structures of Metastable States in Phase Transitions with a High-Spin Low-Spin Degree of Freedom. Prog. Theor. Phys. 2005, 114, 719–735. [Google Scholar] [CrossRef]
- Tokoro, H.; Miyashita, S.; Hashimoto, K.; Ohkoshi, S.-I. Huge thermal hysteresis loop and a hidden stable phase in a charge-transfer phase transition of Rb0.64Mn[Fe(CN)6]0.88∙1.7H2O. Phys. Rev. B 2006, 73, 172415. [Google Scholar] [CrossRef]
- Konishi, Y.; Tokoro, H.; Nishino, M.; Miyashita, S. Magnetic Properties and Metastable States in Spin-Crossover Transition of Co–Fe Prussian Blue Analogues. J. Phys. Soc. Jpn. 2006, 75, 114603. [Google Scholar] [CrossRef]
- Gindulescu, A.; Rotaru, A.; Linares, J.; Dimian, M.; Nasser, J. Excited metastables electronic spin states in spin crossover compounds studies by atom-phonon coupling model: Gradual and two-step transition cases. J. Appl. Phys. 2010, 107, 09A959. [Google Scholar] [CrossRef]
- Ndiaye, M.M.; Pillet, S.; Bendeif, E.; Marchivie, M.; Chastanet, G.; Boukheddaden, K.; Triki, S. Hidden Hysteretic Behavior of a Paramagnetic Iron(II) Network Revealed by Light Irradiation. Eur. J. Inorg. Chem. 2017, 2018, 305–313. [Google Scholar] [CrossRef]
- Boonprab, T.; Lee, S.J.; Telfer, S.G.; Murray, K.S.; Phonsri, W.; Chastanet, G.; Collet, E.; Trzop, E.; Jameson, G.N.L.; Harding, P.; et al. The First Observation of Hidden Hysteresis in an Iron(III) Spin-Crossover Complex. Angew. Chem. Int. Ed. 2019, 58, 11811–11815. [Google Scholar] [CrossRef] [PubMed]
- Fourati, H.; Bouchez, G.; Paez-Espejo, M.; Triki, S.; Boukheddaden, K. Spatio-temporal Investigations of the Incomplete Spin Transition in a Single Crystal of [Fe(2-pytrz)2{Pt(CN)4}]·3H2O: Experiment and Theory. Crystals 2019, 9, 46. [Google Scholar] [CrossRef]
- Gutlich, P.; Ksenofontov, V.; Gaspar, A. Pressure effect studies on spin crossover systems. Coord. Chem. Rev. 2005, 249, 1811–1829. [Google Scholar] [CrossRef]
- Oke, T.D.; Ndiaye, M.; Hontinfinde, F.; Boukheddaden, K. Magnetic-field induced multi-step transitions in ferromagnetic spin-crossover solids within the BEG model. Eur. Phys. J. B 2021, 94, 38. [Google Scholar] [CrossRef]
- Ogou, S.B.; Oke, D.T.; Karimou, M.; Félix, H.; Boukheddaden, K. BEG spin-1 model with random exchange magnetic interactions for spin-crossover solids. J. Phys. Condens. Matter 2023, 35, 455704. [Google Scholar] [CrossRef] [PubMed]
- Sotnikov, A.; Kuneš, J. Field-induced exciton condensation in LaCoO3. Sci. Rep. 2016, 6, 30510. [Google Scholar] [CrossRef] [PubMed]
- Enachescu, C.; Stoleriu, L.; Stancu, A.; Hauser, A. Competition between photoexcitation and relaxation in spin-crossover complexes in the frame of a mechanoelastic model. Phys. Rev. B 2010, 82, 104114. [Google Scholar] [CrossRef]
- Enachescu, C.; Oetliker, U.; Hauser, A. Photoexcitation in the Spin-Crossover Compound [Fe(pic)3]Cl2·EtOH (pic = 2-Picolylamine). J. Phys. Chem. B 2002, 106, 9540–9545. [Google Scholar] [CrossRef]
- Chakraborty, P.; Enachescu, C.; Hauser, A. Analysis of the Experimental Data for Pure and Diluted [FexZn1–x(bbtr)3](ClO4)2 Spin-Crossover Solids in the Framework of a Mechanoelastic Model. Eur. J. Inorg. Chem. 2013, 2013, 770–780. [Google Scholar] [CrossRef]
- Varret, F.; Boukheddaden, K.; Codjovi, E.; Enachescu, C.; Linarès, J. On the Competition Between Relaxation and Photoexcitations in Spin Crossover Solids under Continuous Irradiation. In Spin Crossover in Transition Metal Compounds II; Springer: Berlin/Heidelberg, Germany, 2004; Volume 234, pp. 199–229. [Google Scholar] [CrossRef]
- Atitoaie, A.; Tanasa, R.; Enachescu, C. Size dependent thermal hysteresis in spin crossover nanoparticles reflected within a Monte Carlo based Ising-like model. J. Magn. Magn. Mater. 2012, 324, 1596–1600. [Google Scholar] [CrossRef]
- Hauser, A.; Gütlich, P.; Hinek, R.; Spiering, H.; Schollmeyer, D. The [Fe(etz)6](BF4)2 Spin-Crossover System—Part One: High-Spin ⇌ Low-Spin Transition in Two Lattice Sites. Chem. A Eur. J. 1996, 2, 1427–1434. [Google Scholar] [CrossRef]
- Hauser, A.; Hinek, R.; Spiering, H.; Gütlich, P. The [Fe(etz)6](BF4)2 Spin-Crossover System—Part Two: Hysteresis in the LIESST Regime. Chem. Eur. J. 1996, 2, 1435–1439. [Google Scholar] [CrossRef]
- Varret, F.; Boukheddaden, K.; Chong, C.; Goujon, A.; Gillon, B.; Jeftic, J.; Hauser, A. Light-induced phase separation in the [Fe(ptz)6] (BF4)2spin-crossover single crystal. EPL 2007, 77, 30007. [Google Scholar] [CrossRef]
- Gudyma, I.; Maksymov, A. The cooperativity in 3D spin-crossover nanocrystals with ferromagnetic and antiferromagnetic surface. Appl. Surf. Sci. 2019, 483, 779–784. [Google Scholar] [CrossRef]
- Erdem, R. Geometrical description of the state space in spin crossover solids with high-spin low-spin degree of freedom. Phys. A 2022, 598, 127335. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veliu, V.; Yalçın, O.; Özüm, S.; Erdem, R. Nonequivalent Antiferromagnetically Coupled Sublattices Induce Two-Step Spin-Crossover Transitions: Equilibrium and Nonequilibrium Aspects. Magnetochemistry 2024, 10, 42. https://doi.org/10.3390/magnetochemistry10060042
Veliu V, Yalçın O, Özüm S, Erdem R. Nonequivalent Antiferromagnetically Coupled Sublattices Induce Two-Step Spin-Crossover Transitions: Equilibrium and Nonequilibrium Aspects. Magnetochemistry. 2024; 10(6):42. https://doi.org/10.3390/magnetochemistry10060042
Chicago/Turabian StyleVeliu, Valon, Orhan Yalçın, Songül Özüm, and Rıza Erdem. 2024. "Nonequivalent Antiferromagnetically Coupled Sublattices Induce Two-Step Spin-Crossover Transitions: Equilibrium and Nonequilibrium Aspects" Magnetochemistry 10, no. 6: 42. https://doi.org/10.3390/magnetochemistry10060042
APA StyleVeliu, V., Yalçın, O., Özüm, S., & Erdem, R. (2024). Nonequivalent Antiferromagnetically Coupled Sublattices Induce Two-Step Spin-Crossover Transitions: Equilibrium and Nonequilibrium Aspects. Magnetochemistry, 10(6), 42. https://doi.org/10.3390/magnetochemistry10060042





