Using the Equivalent Static Pressure Method to Assess Free Fall Damage of the Korla Fragrant Pear
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Materials
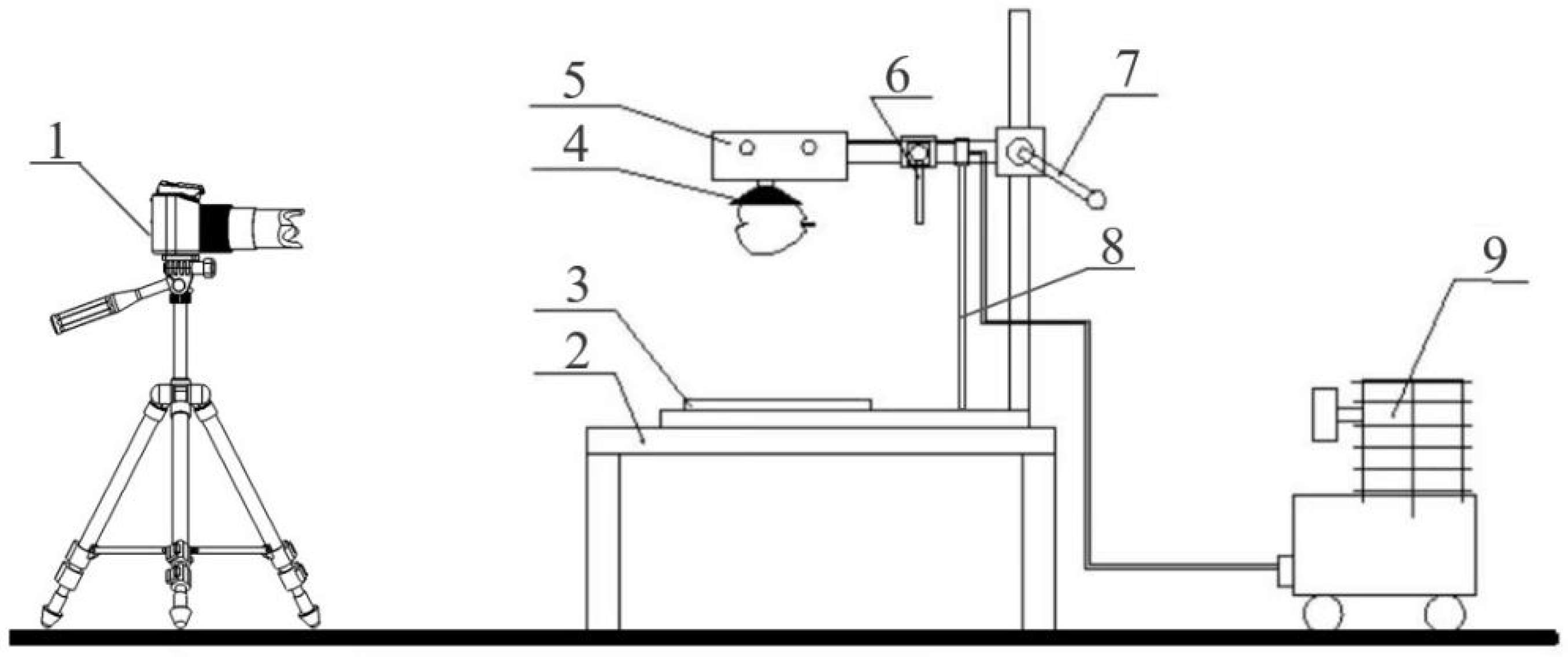
2.2. Impact Test on the Korla Fragrant Pear
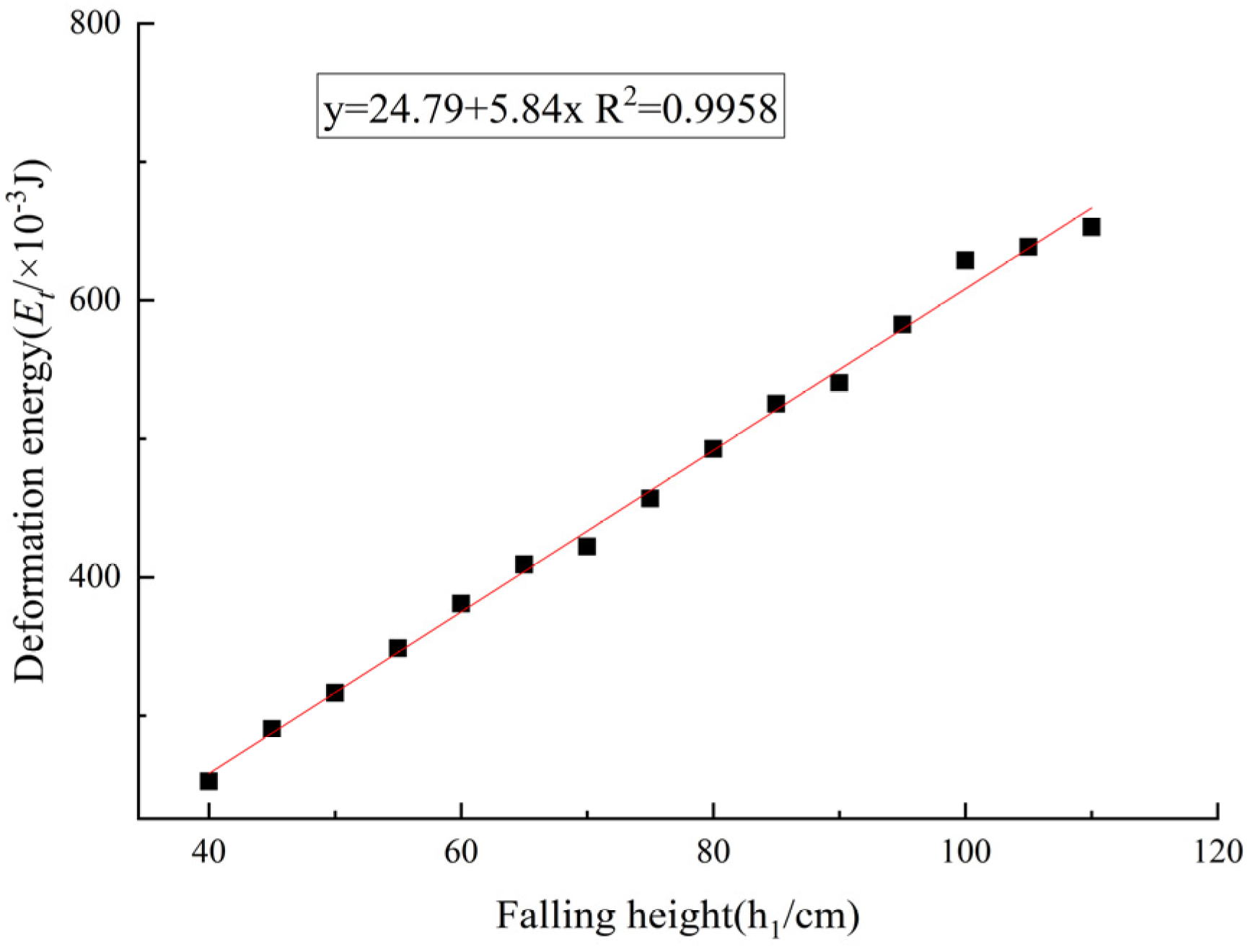
2.3. Calculation of Impact Deformation Energy of the Korla Fragrant Pear
2.4. Compression Test on the Korla Fragrant Pear
2.5. Calculation of Compression Deformation Energy of the Korla Fragrant Pear
2.6. Scanning Electron Microscope Test of the Korla Fragrant Pear
3. Results and Analysis
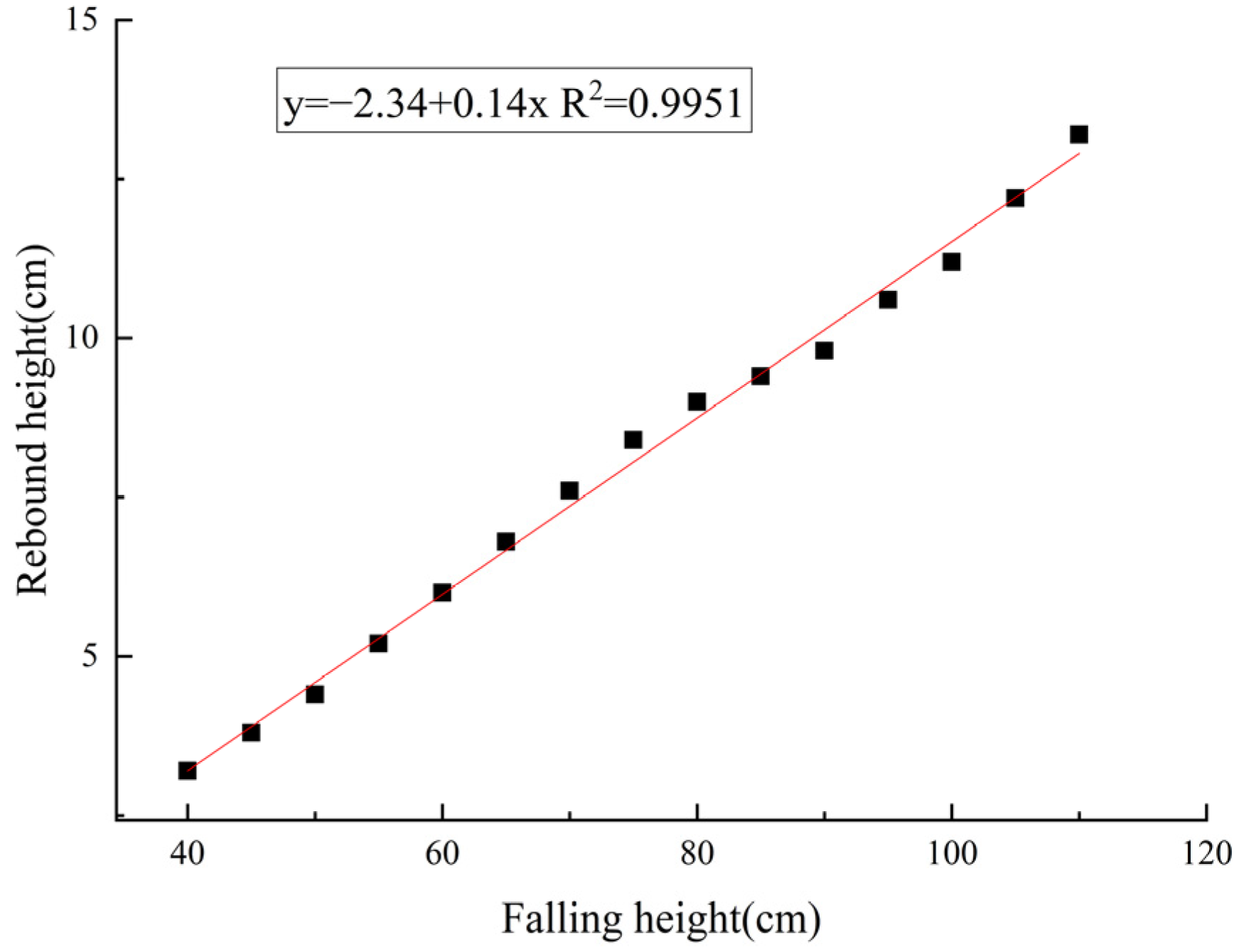
3.1. Calculation of the Equivalent Height of Impact Damage of the Korla Fragrant Pear
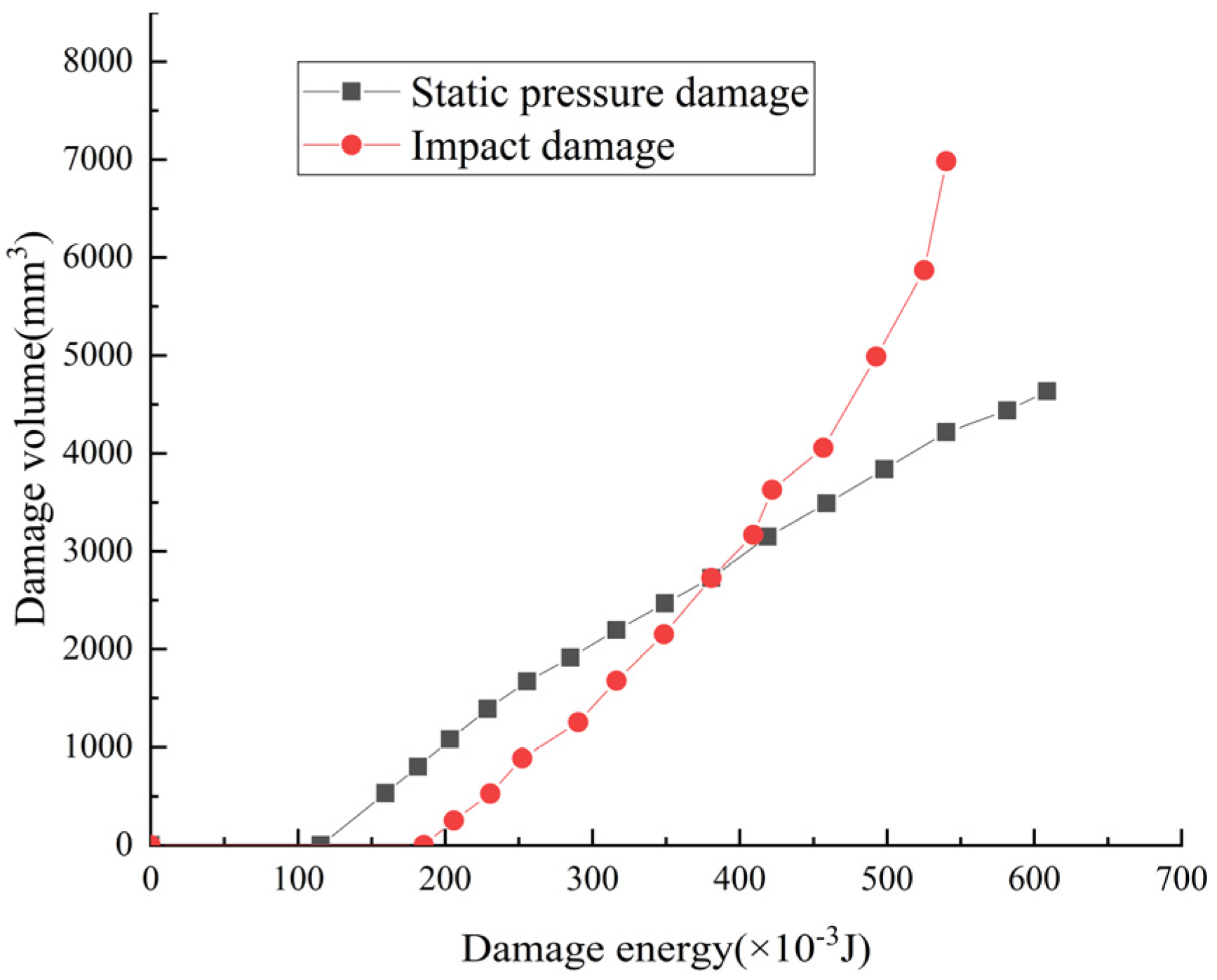
3.2. Calculation of the Damage Volume of the Korla Fragrant Pear
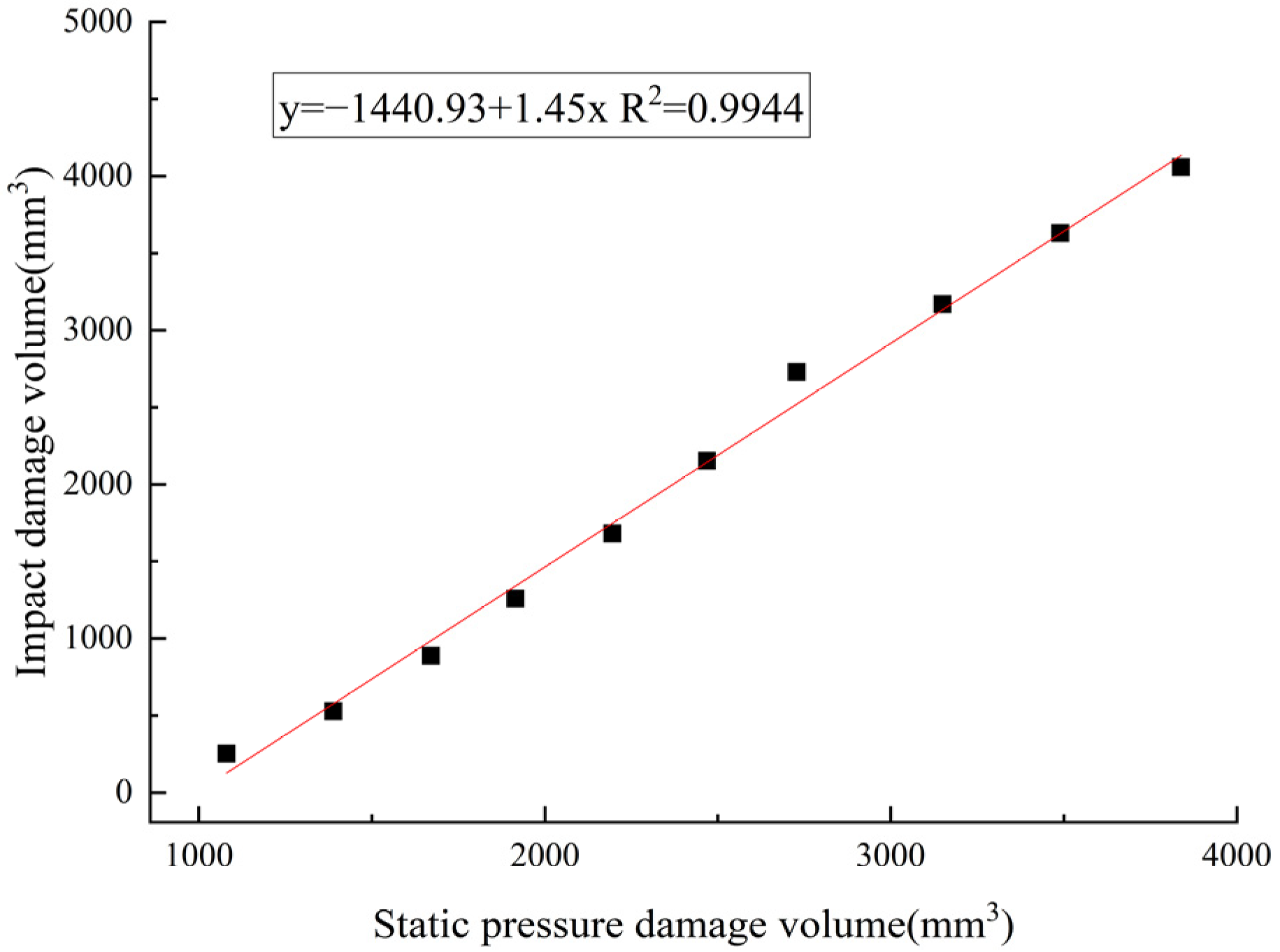
3.3. Verification of the Damage Volume in the Korla Fragrant Pear Impact Test
3.4. Microstructure Analysis of Korla Fragrant Pear Samples Using a Scanning Electron Microscope
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Tang, Y.; Jin, X.; Liu, Y.; Zhang, H.; Niu, H.; Lan, H. Comprehensive evaluation of Korla fragrant pears and optimization of plucking time during the harvest period. Int. J. Agr. Biol. Eng. 2022, 3, 242–250. [Google Scholar]
- Wang, Z.; Tang, Y.; Liu, Y.; Zhang, H.; Zhang, Y.; Lan, H. Inhibitory effect of CaCl2 and carboxymethyl chitosan coating on the after-ripening of Korla fragrant pears in cold storage. Food Sci. Tech-Brazi. 2021, 56, 6777–6790. [Google Scholar]
- Lan, H.; Wang, Z.; Niu, H.; Zhang, H.; Zhang, Y.; Tang, Y.; Liu, Y. A nondestructive testing method for soluble solid content in korla fragrant pears based on electrical properties and artificial neural. Food Sci. Nutr. 2020, 8, 5172–5181. [Google Scholar] [PubMed]
- He, X.; Huang, Z.; Zhang, W.; Chen, B.; Zhou, Y.; Chai, Z. Effects of nitrogen application level on photosynthate distribution of Korla fragrant pear trees. J. Appl. Ecol. 2020, 31, 2637–2643. [Google Scholar]
- Yu, S.; Lan, H.; Li, X.; Zhang, H.; Zeng, Y.; Niu, H.; Niu, X.; Xiao, A.; Liu, Y. Prediction method of shelf life of damaged Korla fragrant pears. J. Food Process Eng. 2021, 44, e13902. [Google Scholar]
- Feng, Z.; Wu, J.; Sun, H.; Li, F. Measurement analysis of contact pressure distribution of apple under compression. Mod. Food Sci. Technol. 2014, 30, 76–81. [Google Scholar]
- Scheffler, O.C.; Coetzee, C.J.; Opara, U.L. A discrete element model (DEM) for predicting apple damage during handling. Bio. Eng. 2018, 172, 29–48. [Google Scholar]
- Li, D.; Meng, X.; Xu, M.; Che, F.; Pan, Y.; Zhao, D. Research on identification Features of Quality Classification of Korla Fragrant Pear. Sto Pro. 2018, 18, 5–15. [Google Scholar]
- He, T.; Li, X.; Wu, Y.; Zhang, F.; Li, S.; Li, J. Investgation on Commodity Differentiation and Price Formation of Kuerle Fragrant Pear. Xinjiang Agr. Sci. 2010, 47, 461–465. [Google Scholar]
- Wu, J.; Li, F.; Ge, Y.; Hu, R. Static pressure contact stress measurement and damage prediction Korla Fragrant Pear. Tran. Chin. Soc. Agr. Eng. 2013, 29, 261–266+299. [Google Scholar]
- Fen, Z.; Wu, J. Study on contact pressure and mechanical damage of apple under compression using pressure-sensitive film. Food Mach. 2015, 31, 186–189. [Google Scholar]
- Sun, H.; Wu, J.; Fen, Z. Measurement of contact pressure distribution and bruise estimation for drop impact of Korla pear. Food Mach. 2013, 29, 183–186. [Google Scholar]
- Yang, Y.; Yu, S.; Li, X.; Zhang, H.; Xiao, A.; Liu, Y.; Su, G. Study on the effect of different picking periods on static pressure damage of Korla fragrant pear. Packag. Food Mach. 2021, 39, 6–11. [Google Scholar]
- Wang, R.; Jiao, Q.; Wei, D.; Gao, Y. Mechanical characteristics and the finite element analysis of grapes. Tran. Chin. Soc. Agr. Eng. 2005, 21, 7–10. [Google Scholar]
- Wu, J. Study on Dynamic Viscoelastic Property and Impact Bruise of Korla Pear. Doctor’s Thesis, Northwest A&F University, Yangling, China, 2011. [Google Scholar]
- Ahmadi, E.; Barikloo, H.; Kashfi, M. Viscoelastic finite element analysis of the dynamic behavior of apple under impact loading with regard to its different layers. Comput. Electron. Agr. 2016, 121, 1–11. [Google Scholar]
- Zeebroeck, M.V.; Linden, V.V.; Darius, P.; Ketelaere, B.D.; Ramon, H.; Tijskens, E. The effect of fruit properties on the bruise susceptibility of tomatoes. Postharvest Biol. Technol. 2007, 45, 168–175. [Google Scholar]
- Xu, R.; Takeda, F.; Krewer, G.; Li, C. Measure of mechanical impacts in commercial bluebery packing lines and potential damage to blueberry fruit. Postharvest Biol. Technol. 2015, 110, 103–113. [Google Scholar]
- Lewis, R.; Yoxall, A.; Canty, L.A.; Romo, R. Development of engineering design tools to help reduce apple bruising. J. Food Eng. 2007, 83, 356–365. [Google Scholar]
- An, X.; Li, Z.; Zude-Sasse, M.; Tchuenbou-Magaia, F.; Yang, Y. Characterization of textural failure mechanics of strawberry fruit. J. Food Eng. 2020, 282, 110016. [Google Scholar]
- Blahovec, J.; Paprštein, F. Susceptibility of pear varieties to bruising. Postharvest Biol. Technol. 2005, 38, 231–238. [Google Scholar] [CrossRef]
- Hung, Y.; Prussia, S.E. Effect of maturity and storage time on the bruise susceptibility of peaches (cv. Red Globe). Trans. Asabe. 1989, 32, 1377–1382. [Google Scholar]
- Unuigbe, O.M.; Onuoha, S.N. Technical note assessment of impact damage to apple fruits. Niger. J. Technol. 2013, 32, 137–140. [Google Scholar]
- Stopa, R.; Szyjewicz, D.; Komarnicki, P.; Kuta, L. Determining the resistance to mechanical damage of apples under impact loads. Postharvest Biol. Technol. 2018, 146, 79–89. [Google Scholar] [CrossRef]
- Yu, W.; Hidayat, L.; Sidebang, B. Study of impact of fresh fruit bunch (FFB) of palm fruits on different surfaces. J. Tek. Ind. Pert Vol. 2011, 21, 94–101. [Google Scholar]
- Zhang, F.; Li, B.; Hai, Y.; Zou, J.; Ouyang, A. Study on the Quantitative Assessment of Impact Damage of Yellow Peaches Using the Combined Hyperspectral Technology and Mechanical Parameters. J. Spectrosc. 2022, 2022, 7526826. [Google Scholar]
- Komarnicki, P.; Stopa, R.; Szyjewicz, D.; Mlotek, M. Evaluation of bruise resistance of pears to impact load. Postharvest Biol. Technol. 2016, 114, 36–44. [Google Scholar]
- Bao, Y.; Yang, C.; Zhao, Y.; Liu, X.; Guo, Y. Impact damage assessment of mechanically harvested blueberry fruit based on impact deformation energy. Tran. Chin. Soc. Agr. Eng. 2017, 33, 283–292. [Google Scholar]
- He, Y.; He, J.; Fang, D.; Du, X. Collision Injury Assessment of Mechanical Harvesting Cerasus humilis Fruit Based on Deformation Energy. Tran. Chin. Soc. Agr. Eng. 2019, 9, 67–72. [Google Scholar]
- He, X.; Zhu, D.; Zhu, J.; Xue, K.; Yu, C.; Liu, J. Study on the influencing factors of collision damage in postharvest processing of apple. J. Chin. Agr. Mech. 2021, 42, 101–108. [Google Scholar]
- Mahdi, R.; Abbas, A.; Rouzbeh, A.; Davoud, K.; Ali, J. Measurement bruise volume of olive during impact test using FEM and quality evaluation of extracted olive oil. Food Sci. Nutr. 2021, 9, 5493–5508. [Google Scholar]
- Chen, C.; Wang, J.; Zhang, J.; Li, J.; Wang, P.; LV, L. Experimental study on the impact of buffering device on falling apple. J. Chin. Agr. Uni. 2022, 27, 149–159. [Google Scholar]





| Types of Management | Management Methods |
|---|---|
| Soil management | This is the use of a base fertiliser in autumn for deep turning, before the winter for flood irrigation. |
| Water supplement | Reasonable irrigation according to the need of fruit trees and soil conditions. |
| Flower and fruit management | Fine pruning, artificial pollination, and bee release in pear orchard; flower and fruit thinning to control the load of single plant; when there are few flowers and fruits, pay attention to protecting the flowers and fruits. |
| Pest control | Pay attention to the protection and utilisation of natural enemies, maintain the ecological balance of farmland, and reduce environmental pollution. |
| Deformation (mm) | Damage Energy E/(×10−3 J) | Static Damage Volume (cm3) | Predicted Impact Damage Volume (cm3) | Equivalent Falling Height (cm) | Actual Impact Damage Volume (cm3) | Deviation (%) |
|---|---|---|---|---|---|---|
| 4.5 | 203.4 | 1080.39 | 125.64 | 30.58 | 120.82 | 4.0 |
| 5 | 255.69 | 1670.88 | 546.85 | 39.54 | 532.17 | 2.8 |
| 5.5 | 316.38 | 2195.43 | 1742.44 | 49.93 | 1713.46 | 1.7 |
| 6 | 380.88 | 2728.54 | 2515.45 | 60.97 | 2483.25 | 1.3 |
| 6.5 | 458.97 | 3489.91 | 3619.44 | 73.97 | 3715.20 | 2.6 |
| 7 | 498.23 | 3838.42 | 4124.78 | 81.07 | 4315.76 | 4.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Li, Z.; Wang, X.; Li, W.; Lan, H.; Liu, Y.; Xu, X.; Tang, Y. Using the Equivalent Static Pressure Method to Assess Free Fall Damage of the Korla Fragrant Pear. Horticulturae 2023, 9, 993. https://doi.org/10.3390/horticulturae9090993
Li C, Li Z, Wang X, Li W, Lan H, Liu Y, Xu X, Tang Y. Using the Equivalent Static Pressure Method to Assess Free Fall Damage of the Korla Fragrant Pear. Horticulturae. 2023; 9(9):993. https://doi.org/10.3390/horticulturae9090993
Chicago/Turabian StyleLi, Cui, Zhanbiao Li, Xingyu Wang, Wen Li, Haipeng Lan, Yang Liu, Xueliang Xu, and Yurong Tang. 2023. "Using the Equivalent Static Pressure Method to Assess Free Fall Damage of the Korla Fragrant Pear" Horticulturae 9, no. 9: 993. https://doi.org/10.3390/horticulturae9090993
APA StyleLi, C., Li, Z., Wang, X., Li, W., Lan, H., Liu, Y., Xu, X., & Tang, Y. (2023). Using the Equivalent Static Pressure Method to Assess Free Fall Damage of the Korla Fragrant Pear. Horticulturae, 9(9), 993. https://doi.org/10.3390/horticulturae9090993






