Estimating Nitrogen Release from Organic Fertilizers for Soilless Production by Analysis of C and N Pools

Abstract

The use of organic fertilizers in soilless pot plant production has sharply increased in recent years. However, there is still a lack of methods for characterizing the N release from organic fertilizers. This bears the risk of an inadequate nutrient supply and, thus, a waste of resources. Therefore, the current research analyzed fourteen commercial organic fertilizers for various C and N pools by extraction in cold and hot water, acid hydrolysis, and thermal fractionation. Furthermore, we conducted an incubation test using a growing medium (80 vol% peat plus 20 vol% green waste compost) and fitted the nitrogen release to different kinetic models. Finally, we calculated the correlations among the best-suited kinetic model parameters and the C and N pools. The C and N pools soluble in water and weak hydrochloride acid varied significantly among the fourteen fertilizers but were closely correlated with each other. The N release from most organic fertilizers could be described very well using the Gompertz function (R² > 0.9), and the parameters of the Gompertz function showed significant correlations with the C and N pools. Hydrolyzable C and N pools provided valuable information about the N release characteristics of organic fertilizers.

1. Introduction

In the last two decades, organic greenhouse production has rapidly grown, mainly focusing on producing fruits and vegetables in soil. However, consumers’ demand for soilless products, such as vegetables, herbs, and ornamentals, is also increasing [1,2,3,4]. A survey by Burnett and Stack [5] revealed fertilization as a significant issue in the organic cultivation of bedding plants. This is particularly true for nitrogen (N) supply, as N applied with organic fertilizers must be mineralized first, and thus, it becomes plant-available only with a delay. To ensure an adequate N supply, growers need reliable information about the time course of the N release from the applied fertilizer [6].

The decomposition pattern of organic residue has been extensively characterized in the literature using various mathematical models. These models include simple first and second-order rate equations [7,8,9], consecutive reaction models that combine multiple first-order rate equations [10,11,12], and flexible sigmoid-shaped functions, such as the Richards, Gompertz, and Weibull functions [13,14,15,16,17,18]. However, simple first-order rate models, which assume N mineralization as a simple function of the substrate N concentration, and consecutive models, which assume two or more pools with different rate coefficients (e.g., labile and refractory fractions), regularly overestimate N release at the beginning [10,11,15,17]. This initial lag phase, which might be due to inhibitory compounds, such as polyphenols [11,19], or by the initial acclimation and regrouping of microbial biomass [14], is quite well-modeled by the unitless and scale-independent shape factor in flexible functions [18]. Subsequently, kinetic parameters can be correlated to the biochemical characteristics of the material [19].

The importance of biochemical characteristics for predicting mineralization rates has been shown in various studies for crop residues and other organic input materials, such as manure [9,20,21,22,23,24,25,26] and, to a lesser extent, for commercial organic fertilizers [27,28,29,30,31]. In addition, countless studies have examined the correlations between the biochemical properties of soil organic matter (SOM) and nitrogen turnover in soils [32]. In all cases—for crop residues and organic fertilizers, as well as for SOM—the most common parameters were the total nitrogen (TN), as well as the total organic carbon (TOC) or total carbon (TC) and the resulting C/N ratios. However, these parameters only show a rough correlation to the nitrogen release of organic fertilizers [27]. A more suitable approach seems to be the characterization of individual nitrogen and carbon pools either by extraction procedures with both hot and cold water, saline, acidic, or alkaline solutions or by thermal analytical techniques, such as thermogravimetry, analysis of evolved gas, or Rock-Eval pyrolysis. Von Lützow et al. [33] gave a detailed overview of the mentioned techniques. De Neve and Hofman [9] used the sequential procedure proposed by Stevenson [34] to characterize the N and C pools of vegetable crop residues whose N mineralization was fitted to a first-order rate equation. The potentially mineralizable nitrogen (N_P) was closely correlated to the C/N ratio of the lignin, lignin content, and water-soluble N. Furthermore, Jensen et al. [24] reported close correlations between water-soluble N and early N mineralization. In addition, the N_P was well described by amounts of various N fractions, whereas the correlations of the N_P to the C/N ratio of the lignin and lignin content were relatively poor. However, they did not describe the N mineralization by kinetic models but correlated the N mineralization at defined dates to analyze the C and N pools. Moreover, De Neve and Hofman [9] and Jensen et al. [24] have reported close correlations between N mineralization and the total N content, and the rate constant was significantly correlated to the percentage of organic N. This is likely attributed to the common practice of applying residues on a dry matter basis, resulting in an increased application of nitrogen (N) as the percentage of organic N increases.

As outlined by Jensen et al. [24], the physiochemical and biochemical properties of the soil used for incubation can significantly affect mineralization patterns. Thus, the results of the listed studies with different mineral soils are hardly comparable and cannot be transferred to growing media for soilless cultivation as their physiochemical and biochemical properties are quite different from those of mineral soils. Therefore, the current research aimed to characterize the N release of various commercial organic fertilizers in a peat-based growing medium by a single kinetic model, and subsequently, to describe the kinetic parameters of C and N pools analyzed by several extraction procedures and evolved gas analysis under pyrolytic conditions.

2. Materials and Methods

2.1. Commercial Organic Fertilizers

Fourteen solid organic fertilizers were purchased from various companies. Six were unprocessed raw materials, three were of animal origin, and three were coarsely ground legumes. Four fertilizers were made of processed plant material, e.g., from the production of starch adhesives. No detailed information about the origin was available for the remaining four fertilizers. In the following section, the fertilizers and their analyzed N, P, K, Mg, and S contents (in brackets), suppliers, raw materials, and pre-processing methods—as far as they are available—are summarized.

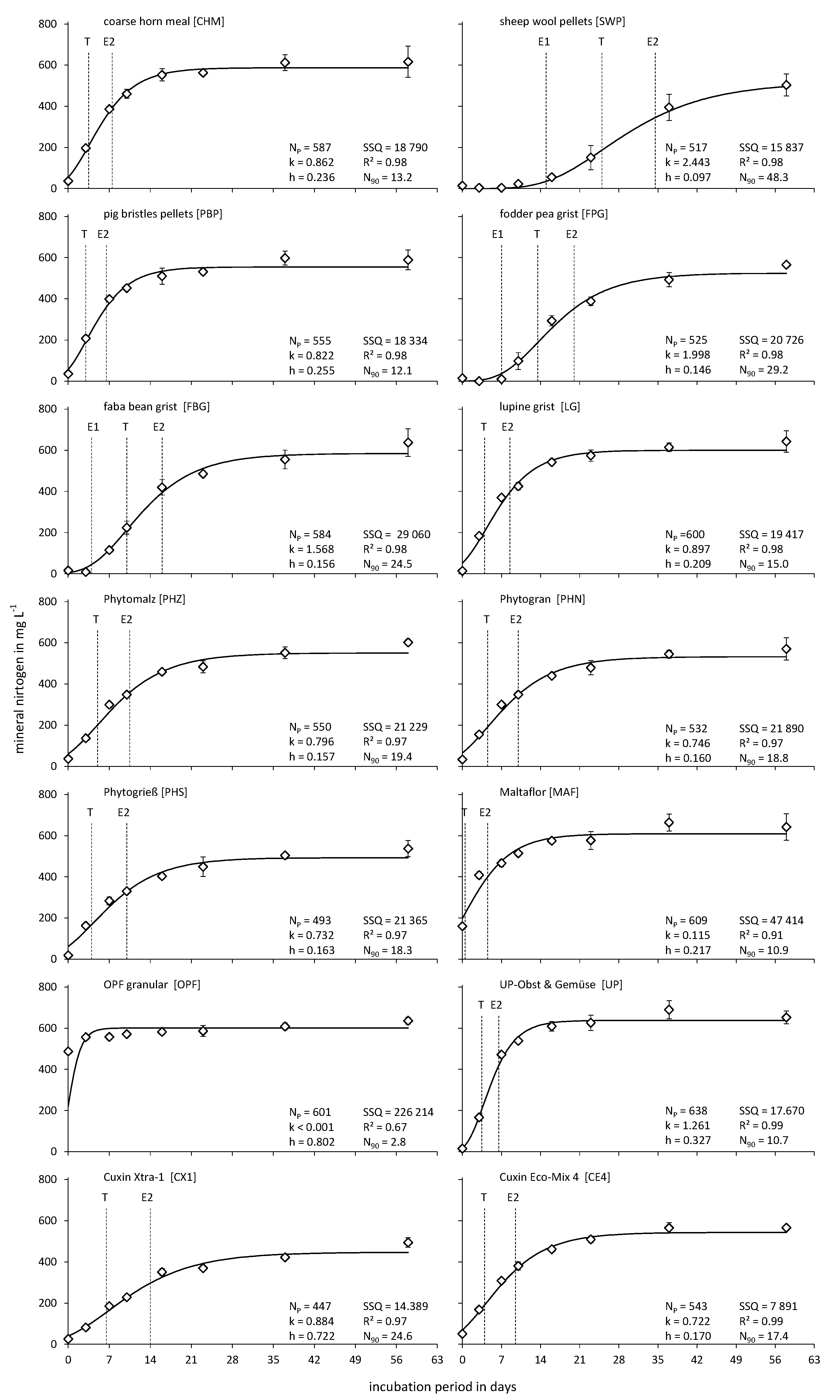
• Coarse horn meal (CHM; 13.8 + 0.6 + 0.0 + 0.1 + 2.0): CHM is made of the horns and hooves of slaughtered ungulates, mainly cattle, with minor adhesions of fur, meat, bones, blood, and manure. According to the regulations of the European Union, hygienization by heating or treatment with propionic acid is mandatory [35]. The main component of horns and hooves is keratin, a group of fibrous proteins [36]. The CHM was purchased from Beckmann & Brehm GmbH (Beckeln/Germany).
• Sheep wool pellets (SWPs; 9.7 + 0.1 + 3.5 + 0.1 + 2.1): SWPs were obtained from Düngepellet Produkt und Vertriebs GmbH (Lauchammer/Germany). Raw and uncleaned wool is a waste product from sheep husbandry and it is pelletized by a thermal–mechanical process. The primary N source of SWPs is keratin. However, the usually unwashed wool contains many waxes, dirt, and feces [37].
• Pig bristle pellets (PBPs; 13.9 + 0.1 + 0.1 + 0 + 2.1): PBPs, also named hair meal pellets, are slaughterhouse waste. The bristles are removed from slaughtered carcasses and typically pasteurized, dried, ground, and pelletized [35]. As with CHM and SWPs, keratin is the primary N source of PBPs. However, pig bristles are less soiled than CHM and SWPs, respectively. The pig bristles were purchased from Beckmann & Brehm GmbH (Beckeln/Germany).
• Fodder pea grist (FPG; 4.3 + 0.3 + 1 + 0.1 + 0.1): The seeds of fodder peas were crushed by us in a malt mill, as this is the current practice for legumes used as fertilizers in organic agriculture [35].
• Faba bean grist (FBG; 3.2 + 0.2 + 0.8 + 0.1 + 0.1): Similar to the seeds of fodder peas, faba bean seeds were also crushed by us.
• Lupine grist (LG; 5.2 + 0.2 + 0.7 + 0.2 + 0.3): Similar to the fodder pea and faba bean seeds, lupine seeds were crushed by us.
• Phytomalz (PHZ; 5.8 + 0.7 + 1.1 + 0.2 + 0.6): Provita^® Phytomalz (Beckmann & Brehm, Beckeln/Germany) is made from protein-rich residues from the food-processing industry. The principal components are malt culms and corn, which are pressed into small pellets, with the addition of vinasse.
• Phytogran (PHN; 5.3 + 0.5 + 1.7 + 0.5 + 0.5): Provita^® Phytogran (Beckmann & Brehm, Beckeln/Germany) is a granulate with a particle size of 2–5 mm. The raw material (residues from the food-processing industry) is dissolved in water, steam-sterilized, and fermented by yeasts. Afterwards, the fermented biomass is dried at about 100 °C, mixed with molasses, and granulated.
• Phytogrieß (PHS; 6.2 + 0.8 + 0.8 + 0.2 + 1.1): Provita^® Phytogrieß (Beckmann & Brehm, Beckeln/Germany) is derived from the fermented residues and glucose of corn gluten production. The granules have a particle size between 0.2 and 2 mm.
• Maltaflor (MAF; 4.9 + 0.6 + 1.2 + 0.4 + 0.7): Maltaflor^® (Maltaflor EUROPA GmbH, Boppard/Germany) is made of malt culms from breweries, vinasse, and vinasse–potassium, as well as grain hulls. After the malting process, the culms are dried, pelletized, and mixed with the vinasse [35].
• OPF granular (OPF; 7.0 + 1.2 + 8.8 + 0.2 + 7): According to the supplier (Plant Health Cure B.V., Oisterwijk/Netherlands), OPF is made of various herbal substances, e.g., fermented sugar beets, and is adjusted to promote the growth of beneficial soil bacteria and mycorrhizal fungi. Most of the nitrogen is amino-derived. The British Soil Association tests all raw materials.
• UP—fruit and vegetables (UP; 8.3 + 1 + 4.6 + 0.2 + 3.8): UP was purchased from Umweltpionier GmbH (Perg/Austria). Similar to OPF, no specific information about the raw materials and processing was available. However, according to the supplier, the fertilizer is a mixture of plant material, clay minerals, and microorganisms. A unique feature of UP is its classification as a foodstuff.
• Cuxin Xtra-1 (CX1; 10.7 + 0.1 + 3.3 + 0.7 + 4.8): DCM ECO-XTRA^® 1 (Deutsche CUXIN Marketing GmbH, Telgte/Germany) is a mixture of animal residues (slaughterhouse waste according to EU ordinance No. 1069/2009), residues of the food, beverage, and feed industry, and tannins from forestry. CX1 is formulated as fine granules, with a particle size between 0.8 and 2.5 mm.
• Cuxin Eco-Mix 4 (CE4; 6.3 + 0.1 + 0.3 + 0.2 + 0.6): DCM Öko-Mix^® 4 (Deutsche CUXIN Marketing GmbH, Telgte/Germany), similar to CX1, is a mixture of animal residues (slaughterhouse waste according to EU ordinance No. 1069/2009), residues of the food, beverage, and feed industry, and cocoa shells or vinasse. The particle size of CE4 is similar to that of CX1.

2.2. Characterization of Carbon and Nitrogen Pools

The total nitrogen (TN) was measured by the Dumas method (TrueSpec N, LECO Cooperation, Moenchengladbach/Germany; according to the VDLUFA Methods Book II.1, No. 3.5.2.7; [38]). The total organic and total carbon (TOC and TC) were measured by combustion under oxygen at 550 and 1000 °C, respectively, and by evolved gas analysis (VDLUFA Methods Book I; No. A 4.1.3.2 and No. A 4.1.3.1; [39]) using an RC 612 elemental analyzer (LECO Cooperation, Moenchengladbach/Germany). Furthermore, the nitrogen was extracted in cold and hot water (CW_N and HW_N) according to the analysis of slow-release urea fertilizers (VDLUFA Methods Book II.1, No. 3.10; [38]). Additionally, nitrogen and carbon hydrolyzable in 0.005 M and 1 M hydrochloric acid (0.005 HA_N/HA_C and 1 HA_N/HA_C) were analyzed [40].

For all extracts, the total soluble nitrogen was measured spectrophotometrically as nitrate after UV-assisted digestion [41] on an AA3 continuous flow analyzer (Bran+Lübbe, Norderstedt/Germany). Furthermore, we analyzed the mineral nitrogen (MN) as a sum of ammonium- and nitrate-N in the cold water extract using the same AA3 continuous flow analyzer. Finally, the soluble organic N (ON) was calculated in all extracts as the difference between the total soluble N in the respective extract and the cold-water-soluble MN.

The determination of the organic carbon hydrolyzable in hydrochloric acid was carried out by ICP-OES (iCAP 6300 Duo, Thermo Scientific, Dreieich/Germany) at 193 nm after strong acidification with nitric acid and purging with high-purity argon [42]. Additionally, the organic carbon pools were characterized by stepwise combustion under pyrolytic conditions at 250, 300, 350, 400, 450, 500, 600, and 1000 °C and subsequent analysis of the evolved CO₂ (Py-TA-EGA; [43]) using a modified RC 612 elemental analyzer (LECO Cooperation, Moenchengladbach/Germany).

The TN, TOC, and TC analyses, Py-TA-EGA, and cold and hot water extractions were conducted in duplicate. Hydrolysis in hydrochloric acid, on the other hand, was performed in triplicate. Control samples (e.g., standard materials) were included in each analytical run to ensure the quality of the analysis and to maintain analytical precision.

2.3. Incubation Experiment

The incubation experiment was conducted according to the procedure proposed by the association of German agricultural analysis and research institutes (VDLUFA) for testing the N dynamics of organic growing media constituents (VDLUFA Methods Book I; No. A 13.5.1; [39]). The organic fertilizers were added on the basis of 1000 mg total N per liter of growing medium consisting of 80% peat (H3-H5 [44]) and 20% green waste compost by volume. The compost successfully fulfilled the growing media compost type II requirements of the German Federal Compost Quality Association [45]. The growing medium was limed to a pH of 5.5 (determined in a CaCl₂ suspension according to the VDLUFA Methods Book I, No. A 5.1.1; [39]). Due to the compost amendment, no other fertilizers except commercial organic fertilizers were added. All fertilizers were incubated in two ways to assess the influence of the particle size. Firstly, the fertilizers were used as received, and only large particles (especially the sheep wool pellets) were carefully crushed by hand to ensure their homogeneous addition to the incubation vessels. Secondly, the fertilizers were chopped in a cutting mill using a 0.5 mm bottom sieve (ZM 1, Retsch, Haan/Germany). This allowed for the evaluation of the effects of the particle size on the nitrogen release.

The Incubation ran for 58 days at 25 °C and 90% relative humidity in the dark. First, the growing medium was moistened with deionized water to 60% of the maximum water capacity (determined according to the VDLUFA Methods Book I, No. A 13.6; [39]), which is assumed to be well suited for microbial activity. Then, the water loss of the growing medium was compensated three times a week during the entire incubation period. On eight dates (days 0, 3, 7, 10, 16, 23, 37, and 58), three incubation vessels per treatment were taken from the incubator and analyzed for CaCl₂/DTPA-soluble ammonium- and nitrate-N photometrically (VDLUFA Methods Book I, No. A 6.1.4.1; [39]). As a basis for the N release calculation, the controls without fertilizer and those with 500 mg N per liter as ammonium nitrate were treated similarly.

On each analysis day, the net mineralization of the fertilizers was calculated as the difference between the ammonium- and nitrate-N contents in the treatments with and without the respective fertilizers. Furthermore, the data from the control fertilized with ammonium nitrate were used to estimate the N turnover (mobilization and immobilization) in the growing media, as the results of the incubation experiment might be less reliable at high nitrogen turnover rates.

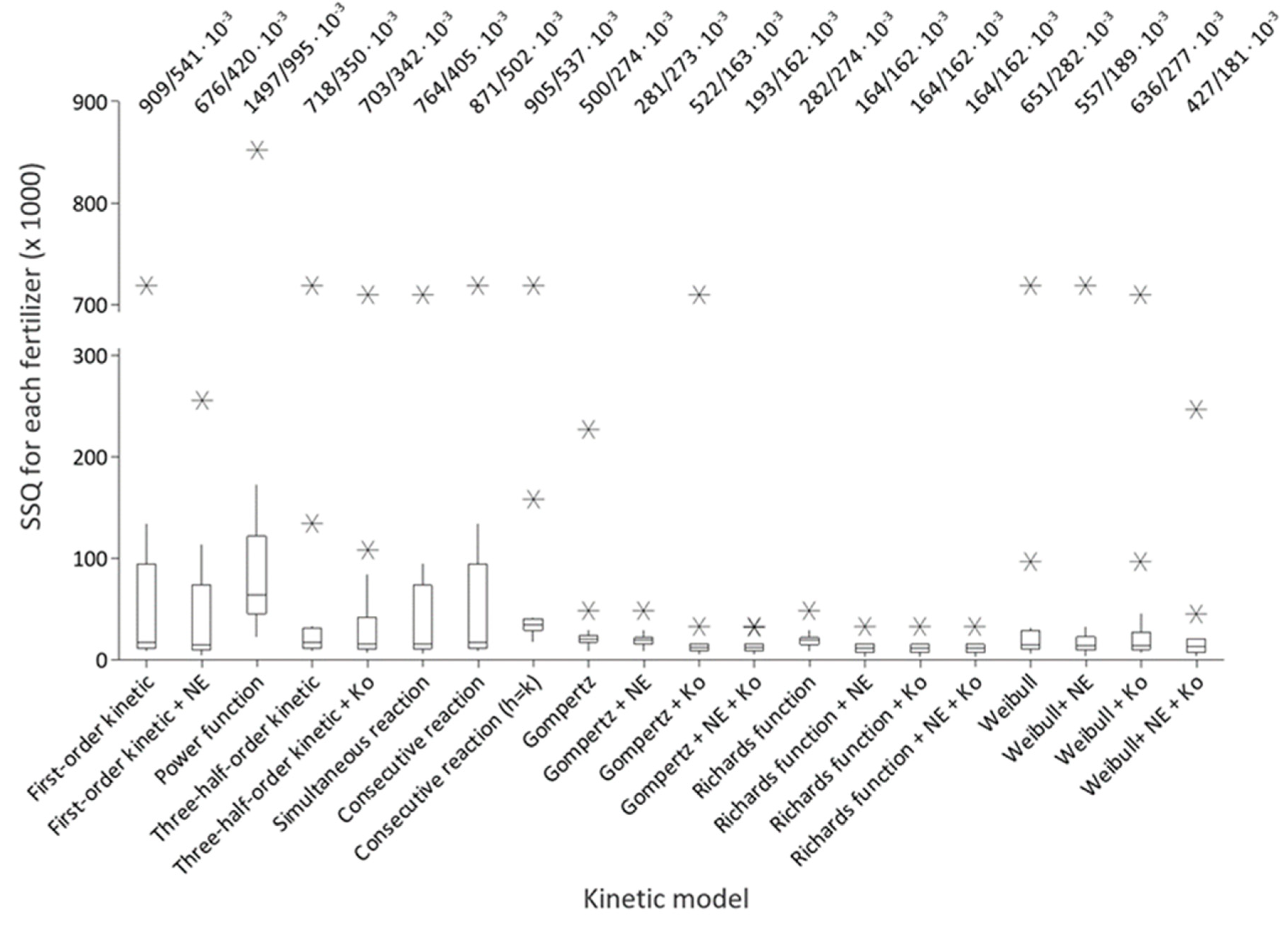
2.4. Calculations and Statistical Analyses

First, various kinetic models used in the literature to describe the decomposition of organic residues in mineral soils (Table 1) were fitted to the N release pattern of the fourteen commercial organic fertilizers. Fitting was performed by an iterative non-linear approach using the generalized reduced gradient algorithm of Microsoft’s SOLVER [46,47]. The starting conditions were set by hand identically for each fertilizer, and the first fitting was calculated. The results obtained were taken as the starting conditions for a new run in the next step. This procedure was repeated four times. As the fitness-of-purpose criterion of the models, the total sum of squares (TSSQ) of the fourteen fertilizers was used.

Furthermore, fitting the fertilizer-specific equations to the N mineralization data was visually rated, and the coefficient of determination (R²) was calculated for each fertilizer. Additionally, the parameters of the most suitable model and some selected points characterizing the time course of the N mineralization were computed by calculating the first and second derivations: (i) the turning point (T) of the original function, which defines the maximum mineralization rate, and (ii) the turning points of the first derivation, indicating the start (E₁) and the end (E₂) of the phase with the maximum mineralization rate. Furthermore, the time until the release of 90% of the potentially mineralizable nitrogen (N₉₀) was calculated. Finally, correlations of the analyzed N and C pools and the C/N ratios to the parameters of the model that best describe the course of N mineralization were computed to identify the pools that were well suited for characterizing the N release of the organic fertilizers. Thereby, correlations were calculated for the entire dataset and after removing the outliers determined by Cook’s distance, with 4/n as the cut-off point [48]. The fitting and visualization of the kinetic models were carried out with MS Excel 2016 (version 16.0, Microsoft Corporation, Redmond, WA, USA). The software package Minitab21 (Minitab, LLC, State College, PA, USA) was used to visualize the C and N pools and to calculate the correlations.

Table 1. Kinetic models for characterization of net N release (N_R in mg L⁻¹) from organic fertilizers in relation to incubation period (t) in days; parameters N_P and N_E represent the potentially and mineralizable N (mg L⁻¹), respectively, parameters h, k, and k(1,2) represent the specific rate constants (mg L⁻¹ d⁻¹), k₀ is the zero-order rate constant for recalcitrant N pools (mg L⁻¹ d⁻¹), F is the proportion of N_P with fast turnover in a simultaneous reaction model, and d and c are unitless shape factors in Richards and Weibull functions (for details, refer to the given references).

Kinetic Model (Number of Parameters)	Equation [Reference]
First-order kinetic (2)	$N_R=N_P\ast \left({1-e}^{-kt}\right)$	[7]
First-order kinetic plus readily available N (NE) (3)	$N_R=N_P\ast {(1-e}^{-kt})+N_E$	[49]
Power function (2)	$N_R={ht}^k$	[50]
Three-half-order kinetic model (3)	$N_R=N_P\ast \left(1-e^{-k_{1}t-0.5\left(k_2{t}^2\right)}\right)$	[51]
Three-half-order kinetic model plus zero order rate constant (k0) (4)	$N_R=N_P\ast \left(1-e^{-k_{1}t-0.5\left(k_2{t}^2\right)}\right)+k_0\mathrm{t}$	[51]
Simultaneous reaction model (4)	$N_R=N_P\ast F\ast \left(1-e^{-ht}\right)+N_P\ast \left(1-\mathrm{F}\right)\ast (1-e^{-kt})$	[52]
Consecutive reaction model (3)	$N_R=N_P-N_P\ast \left(\frac{k{e}^{-ht}-h{e}^{-kt}}{k-h}\right)$	[53]
Consecutive reaction model with rate constants h = k (2)	$N_R=N_P-N_P\ast e^{-kt}\ast (kt+1)$	[53]
Gompertz function (3)	$N_R=N_P\ast e^{{-e}^{(h-kt)}}$	[14]
Gompertz function + NE (4)	$N_R=N_P\ast e^{{-e}^{\left(h-kt\right)}}+N_E$	[14]
Gompertz function + k0 (4)	$N_R=N_P\ast e^{{-e}^{\left(h-kt\right)}}+k_{0}t$	[14]
Gompertz function + NE + K0 (5)	$N_R=N_P\ast e^{{-e}^{\left(h-kt\right)}}+N_E{+k}_{0}t$	[14]
Richards function (4)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}}^{}$	[54]
Richards function + NE (5)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}+N_E}^{}$	[54]
Richards function + k0 (5)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}+k_{0}t}^{}$	[54]
Richards function + NE + K0 (6)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}+N_E+k_{0}t}^{}$	[54]
Weibull function (3)	$N_R=N_P\ast (1-e^{-ktc})$	[15]
Weibull function + NE (4)	$N_R=N_P\ast \left(1-e^{-ktc}\right)+N_E$	[15]
Weibull function + k0 (4)	$N_R=N_P\ast \left(1-e^{-ktc}\right)+k_{0}t$	[15]
Weibull function + NE + K0 (5)	$N_R=N_P\ast \left(1-e^{-ktc}\right)+N_E+k_{0}t$	[15]

Table 1. Kinetic models for characterization of net N release (N_R in mg L⁻¹) from organic fertilizers in relation to incubation period (t) in days; parameters N_P and N_E represent the potentially and mineralizable N (mg L⁻¹), respectively, parameters h, k, and k(1,2) represent the specific rate constants (mg L⁻¹ d⁻¹), k₀ is the zero-order rate constant for recalcitrant N pools (mg L⁻¹ d⁻¹), F is the proportion of N_P with fast turnover in a simultaneous reaction model, and d and c are unitless shape factors in Richards and Weibull functions (for details, refer to the given references).

Kinetic Model (Number of Parameters)	Equation [Reference]
First-order kinetic (2)	$N_R=N_P\ast \left({1-e}^{-kt}\right)$	[7]
First-order kinetic plus readily available N (NE) (3)	$N_R=N_P\ast {(1-e}^{-kt})+N_E$	[49]
Power function (2)	$N_R={ht}^k$	[50]
Three-half-order kinetic model (3)	$N_R=N_P\ast \left(1-e^{-k_{1}t-0.5\left(k_2{t}^2\right)}\right)$	[51]
Three-half-order kinetic model plus zero order rate constant (k0) (4)	$N_R=N_P\ast \left(1-e^{-k_{1}t-0.5\left(k_2{t}^2\right)}\right)+k_0\mathrm{t}$	[51]
Simultaneous reaction model (4)	$N_R=N_P\ast F\ast \left(1-e^{-ht}\right)+N_P\ast \left(1-\mathrm{F}\right)\ast (1-e^{-kt})$	[52]
Consecutive reaction model (3)	$N_R=N_P-N_P\ast \left(\frac{k{e}^{-ht}-h{e}^{-kt}}{k-h}\right)$	[53]
Consecutive reaction model with rate constants h = k (2)	$N_R=N_P-N_P\ast e^{-kt}\ast (kt+1)$	[53]
Gompertz function (3)	$N_R=N_P\ast e^{{-e}^{(h-kt)}}$	[14]
Gompertz function + NE (4)	$N_R=N_P\ast e^{{-e}^{\left(h-kt\right)}}+N_E$	[14]
Gompertz function + k0 (4)	$N_R=N_P\ast e^{{-e}^{\left(h-kt\right)}}+k_{0}t$	[14]
Gompertz function + NE + K0 (5)	$N_R=N_P\ast e^{{-e}^{\left(h-kt\right)}}+N_E{+k}_{0}t$	[14]
Richards function (4)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}}^{}$	[54]
Richards function + NE (5)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}+N_E}^{}$	[54]
Richards function + k0 (5)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}+k_{0}t}^{}$	[54]
Richards function + NE + K0 (6)	$N_R=N_P\ast {{(1+de}^{-k(h-t)}{)}^{(-\frac{1}{d})}+N_E+k_{0}t}^{}$	[54]
Weibull function (3)	$N_R=N_P\ast (1-e^{-ktc})$	[15]
Weibull function + NE (4)	$N_R=N_P\ast \left(1-e^{-ktc}\right)+N_E$	[15]
Weibull function + k0 (4)	$N_R=N_P\ast \left(1-e^{-ktc}\right)+k_{0}t$	[15]
Weibull function + NE + K0 (5)	$N_R=N_P\ast \left(1-e^{-ktc}\right)+N_E+k_{0}t$	[15]

3. Results and Discussion

3.1. Characterization of Nitrogen and Carbon Pools

As fertilizers were added to the incubation experiment on the basis of the TN, the nitrogen and carbon pools were also related to the TN. As shown in Figure 1, most of the fertilizers contained nearly no mineral nitrogen (<50 mg N per g TN), whereas very high amounts of ammonium-N (419 mg N per g TN) were found in the OPF and, to a lesser extent (138 mg N per g TN), in the MAF. Except for 1 HA_ON, the soluble organic N pools differed considerably among the fertilizers. Their proportions of TN ranged from 3.8% to 38% for CW_ON and from 5.3% to 48% for HW_ON, comparable to the values reported by Rubins and Bear [55] for various raw and processed plant (7.0% to 47.5%) and animal (0.2% to 39.3%) products. Using 0.005 M hydrochloric acid gave slightly higher (7.9% to 66%) values and 1 M hydrochloric acid gave remarkably higher (42% to 94%) values, whereas the lowest values were found for the OPF (42%) and MAF (77%) due to their high contents of mineral N.

Due to the low amount of mineral nitrogen in most fertilizers, the percentages of the total soluble N of the TN were equivalent to those of the soluble organic N of the TN. In addition to their similar ranges, the cold water-, hot water-, and 0.005 hydrochloric acid-soluble N pools were highly correlated with each other but not with the 1 M_HA pool (

Table 2. Correlations between total soluble and organic N pools for the fourteen organic fertilizers (Pearson’s correlation coefficient, numbers in brackets indicate significance levels).

	Total N Soluble in			Organic N Soluble in
	Cold Water	Hot Water	0.005 M HCl	Cold Water	Hot Water	0.005 M HCl
Hot water	0.98 (<0.01)			0.95 (<0.01)
0.005 M HCl	0.94 (<0.01)	0.94 (<0.01)		0.92 (<0.01)	0.91 (<0.01)
1 M HCl	0.01 (0.99)	−0.10 (0.75)	0.09 (0.76)	−0.09 (0.77)	−0.20 (0.48)	0.03 (0.91)

).

The variation in the organic C pools hydrolyzable in HA, and the TOC and organic carbon analyzed by Py-TA-EGA (POC), are summarized in Figure 2. The absolute values of TOC ranged between 2523 mg per g TN for the OPF and 11,514 mg per g TN for the FPG. Also, the amounts among the other organic C pools varied considerably from 19% to 88%, 57% to 96%, and 51% to 88% of TOC for 0.005 HA_C, 1 HA_C, and POC, respectively (Figure 2). Most organic carbon pools, whether analyzed by acid hydrolysis or by Py-TA-EGA, were positively correlated with each other (r ≥ 0.87, p < 0.01). This indicates that Py-TA-EGA provided no more information about the organic carbon quality than acid hydrolysis.

With the exception of the TOC/TN ratio, for the calculation of the C/N ratios, only the organic N pools (CW_ON, HW_ON, 0.005 HA_ON, 1 HA_ON, TON)—calculated as the difference between the respective total N and the cold-water-soluble ammonium-N and nitrate-N—were used. The ratios of TOC to TN, TON, and 1 HA_ON, respectively, ranged from 3 to 12 and were quite similar to the values reported by Stadler et al. [30]. With the increasing strength of the extractant (CW < HW < 0.005 M HCl < 1 M HCl), the range of the TOC/ON ratios decreased. This was also true for the ratios of the organic C and organic N pools, both hydrolyzable in 0.005 (0.005 HA_C/ON) and 1 M hydrochloric acid (1 HA_C/ON), respectively (Figure 3).

Due to the described correlations among the different pools of N and C and among several N and C pools whose data are not shown, the ratios of TOC to organic N pools soluble in weak extractants (CW, HW, and 0.005 M HA) were highly correlated with each other (

Table 3. Correlations among C/N ratios calculated from different C and N pools (TOC = total organic carbon, TN = total nitrogen, TON = total organic nitrogen, CW_ON = cold-water-soluble organic nitrogen, HW_ON = hot-water-soluble organic nitrogen, 0.005/1 HA C/ON = organic carbon/organic nitrogen hydrolyzable in 0.005/1 M hydrochloric acid) of the fourteen organic fertilizers (Pearson’s correlation coefficient, numbers in brackets indicate significance levels).

	TOC/ TN	TOC/ TON	TOC/ CW_ON	TOC/ HW_ON	TOC/ 0.005 HA_ON	TOC/ 1 HA_ON	0.005 HA C/ON
TOC/TON	0.98 (<0.01)
TOC/ CW_ON	−0.19 (0.51)	−0.29 (0.31)
TOC/ HW_ON	0.01 (0.99)	−0.08 (0.79)	0.90 (<0.01)
TOC/ 0.005H A_ON	0.04 (0.88)	−0.03 (0.92)	0.77 (<0.01)	0.93 (<0.01)
TOC/ 1 HA_ON	0.95 (<0.01)	0.99 (<0.01)	−0.34 (0.24)	−0.13 (0.67)	0.08 (0.80)
0.005 HA_C/ ON	0.76 (<0.01)	0.71 (<0.01)	0.33 (0.25)	0.54 (0.04)	0.46 (0.10)	0.66 (0.01)
1 HA_C/ON	0.98 (<0.01)	0.98 (<0.01)	−0.25 (0.39)	−0.04 (0.96)	−0.01 (0.96)	0.96 (<0.01)	0.77 (<0.01)

). Furthermore, the TOC to organic N hydrolyzable ratio in 1 M hydrochloric acid (1 HA_ON) was correlated to the TOC/TN and TOC/TON ratios, respectively, which were also closely correlated. A comparably high correlation was found for the ratios of 1 HA_C/ON to TOC/TN, TOC/TON, and TOC/1 HA_ON, respectively. Additionally, a significant correlation existed between the ratios of C/ON analyzed in 0.005 and 1 M HA. This indicates that all tested weak extractants (cold water, hot water, and 0.005 M hydrochloric acid) provided more or less the same information about the organic N and C pools of the organic fertilizers and that in 1 M hydrochloric acid, the hydrolyzable organic C and N are more related to the total content than to the specific pools. This is quite different from other findings on the characterization of soil organic matter [56] but might be explainable by the higher proportion of readily degradable nitrogen-containing compounds in the organic fertilizers compared to soil organic matter. In contrast to soils, where approximately one-third of the organic nitrogen (N) remained non-hydrolyzable even after treatment with 6 M hydrochloric acid [57], the organic fertilizers contained a significantly higher proportion of hydrolyzable N (88 ± 1.5% using 1 M hydrochloric acid).

3.2. Nitrogen Release

Overall, the nitrogen turnover in the control treatments without fertilizer and with 500 mg N per liter as ammonium nitrate was negligible, respectively. In the unfertilized control, the mineral N increased slightly from 14 ± 0.5 at the beginning up to 35 ± 12.0 mg L⁻¹ after 58 days. Nevertheless, the N release from organic fertilizers was corrected for the mineral N in the unfertilized control at each date. No clear trend was observed in the control fertilized with ammonium nitrate. The mineral N oscillated at each date closely (484 ± 17.4 mg L⁻¹) around the target value of 500 mg N per liter. Furthermore, differences in the N release patterns between the chopped and unchopped fertilizers were rather small, and no systematic effect of particle size was found. This result was confirmed in a more detailed subsequent examination using horn shavings milled to defined grain sizes (<1 mm, 1–2 mm, and 2–4 mm). Only in the first two weeks was a slightly faster N release from finer materials observed. In the following four weeks, no differences were apparent [58]. Due to the slightly better reproducibility, only the N release from the chopped fertilizers was considered in the following.

The N release from organic fertilizers is described best by flexible sigmoid-shaped functions, in particular by the Richards and Gompertz functions. As found by Rahn and Lillywhite [59] and Nendel and Reuter [11], for brassica leaves and grape stalks, some fertilizers have shown a lag of mineralization within the first several days of incubation experiments. This was most pronounced for the SWPs, where no mineral N was found within the first seven days. Following the results of Simard and N’dayegamiye [16] for meadows, and of Hara [54] for coated urea fertilizers, this lag phase could not be described by first- or second-order rate equations or by consecutive reaction models but by flexible sigmoid Gompertz and Richards functions. As the parameter d in the Richards function was zero for most fertilizers—except for the OPF and SWPs—the Richards function is almost identical to the Gompertz function [54].

Furthermore, the TSSQ, more than twofold higher for the Gompertz compared to the Richards function (Figure 4), is nearly exclusively due to the relatively poor fitting of the Gompertz function to the N release from OPF. In this case, the SSQ for the OPF (226·10⁻³) contributed nearly half of the TSSQ (500·10⁻³). However, due to the significant proportion of cold-water-soluble ammonium-N discussed in the previous section, it appears that OPF functioned more as a mineral rather than as an organic nitrogen fertilizer. This observation aligns with the fact that 500 out of the 1000 mg TN L⁻¹ added was already present as CAT-soluble mineral N at the start of the 58-day incubation experiment. Despite this, the N mineralization only amounted to approximately 150 mg L⁻¹ by the end of the experiment. Consequently, the subsequent paragraphs only minimally address the OPF.

As shown in Figure 4, adding a term for the easily mineralizable N pool (N_E) did not remarkably reduce the TSSQ for the remaining 13 fertilizers for the Gompertz function (274·10⁻³ to 273·10⁻³) but did for the Richards function (274·10⁻³ to 162·10⁻³). However, as described before, parameter d of the Richards function remained near zero for most fertilizers. This was also true when a zero-order rate constant (k₀) for less degradable N pools was added, which reduced the TSSQ remarkably for both the Gompertz and Richards functions. Finally, as the Richards function is nearly identically to the Gompertz function and the fitting was already very good for the simpler Gompertz function using only the three parameters N_P, h, and k (R² > 0.91, with an exception for OPF: R² = 0.67), this function was selected as the most suitable one. In addition, Gompertz’s function also has a biological justification: The application of easily degradable organic carbon to soils triggers a rapid increase in microbial biomass [60,61,62]. As a result, especially the growth rate of bacteria is significantly enhanced [62]. Concurrently, the Gompertz function has been demonstrated as a reliable model for bacterial growth. The parameters of this function have physiological significance as they can be traced back to the three phases of bacterial growth: the initial lag phase (parameter h), the phase of the maximum growth rate (parameter k), and the stationary phase in which the maximum population density (parameter N_P) is reached [63,64].

Figure 5 shows the fitting of the Gompertz function to the N release from the 14 organic fertilizers. The turning point (T) indicates the day when the maximum mineralization rate was reached, as well as the beginning (E₁) and end (E₂) of the nearly linear N release phase. Additionally, the goodness of fit (SSQ and R²) and the period until a 90% release of N_P (N₉₀) are listed. The percentage of mineralizable organic nitrogen was around 55% of the total added N; it was the lowest for CX1, with 45%, and the highest for UP, with 63%. The same range has been reported for various commercial organic fertilizers by Prasad et al. [65] and Dion et al. [66], using peat-based growing media for incubation experiments, as well as by Müller and von Fragstein und Niemsdorff [28] and Stadler et al. [30], who conducted incubation experiments in mineral soils. Furthermore, Koch et al. [67] and Heuberger et al. [27] calculated only a slightly higher N efficiency (between 40% and 60% of the total added N) for organic fertilizer in pot experiments with pelargonium and basil, respectively. Thus, to ensure a sufficient nitrogen supply, growers have to fertilize on a total N basis, which is about twice the demand of the plants. Except for the SWPs and, to a lesser extent, the FPG and FBG, the fertilizers did not have a lag phase (indicated by parameter k), so linear mineralization started directly after adding the fertilizers (E₁ < 1). The maximum daily N mineralization rate (indicated by parameter h) was lowest for the SWPs, with 16, and highest for UP, with 65 mg L⁻¹ d⁻¹. For the SWPs, due to the already mentioned lag phase of nearly two weeks and the low daily mineralization rate, it took nearly five weeks until two-thirds of the total mineralized nitrogen was released. For the FPG and FBG, which had a lag phase of several days and also a relatively low daily N mineralization rate (<30 mg L⁻¹ d⁻¹), and for CX1, which had no remarkable lag phase but a similar low daily N mineralization rate (18 mg L⁻¹ d⁻¹) to the SWPs, this point was reached within 14 to 20 days. All other fertilizers passed the 66% level within ten days. The CHM, PBPs, MAF, and UP exceeded 90% within 14 days. In addition to the relatively poor nitrogen efficiency, most organic fertilizers’ high velocity of N release might be problematic for growers. For instance, in the cultivation of potted basil, if the entire N demand of about 1000 mg total N per liter [27] is applied at the date of sowing, two weeks later, the mineral N in the growing medium will be between 250 and 500 mg L⁻¹. However, by this date, the seedlings will have just emerged and might be harmed, in particular due to osmotic stress. Thus, complete stockpiling, as recommended by Heuberger et al. [27], is quite risky. Furthermore, in the case of missing nitrification, ammonium-N will accumulate, damaging plants [68]. However, in the current research—except for the OPF—nitrification already started within the first week of incubation. This was probably mainly due to the addition of compost. A similar enhancement of nitrification by compost amendment has been found, e.g., by Delics et al. [58] and Frerichs et al. [68]. However, in contrast to nitrification, neither reported a clear effect of compost amendment on the height or time course of the N mineralization. This might have been due to the fact that none of the composts used in these experiments contained remarkable amounts of mineral N [69].

3.3. Relative Importance of N and C Pools

As mentioned before, OPF is a mineral rather than an organic fertilizer. Thus, we excluded it from the following evaluation of the importance of N and C pools for N release from organic fertilizers. The level of N release to the total applied N (indicated by parameter N_P of the Gompertz function) was closely correlated to the easily soluble N pools (cold water, hot water, and 0.005 M hydrochloric acid) for most fertilizers. The only exception was UP, which had a very high N release in relation to the soluble N pool compared to all other fertilizers. As Cook’s D for UP exceeded the cut-off point more than twice, correlations between the N release and the soluble N pools were calculated with and without the consideration of UP. When all fertilizers were included, the amount of mineralizable nitrogen (N_P) was not significantly correlated to the soluble N pools (r ≤ 0.48; p ≥ 0.08). However, omitting the UP resulted in highly significant correlations for the three named N pools (r ≥ 0.69; p < 0.01), of which the relationship was closest for the total cold-water-soluble N (Figure 6a). A positive relationship between the easily soluble N pools and the mineralization potential was also shown by Iratani and Arnold [20], who found water-soluble N to be twice as influential as water-insoluble N in affecting the N release from various crop residues. Rubins and Bear [55] also emphasized a positive correlation between water-soluble N and N release. Furthermore, they reported decreasing net mineralization with an increasing C/N ratio of the non-lignin fraction. Even immobilization was observed if the C/N ratio was above 20. Coincidentally, a positive correlation between the ratios of the C and N pools hydrolyzable in weak hydrochloric acid and the lag phase of mineralization (described by parameter k) was found (Figure 6b). The hypothesis that the ratio of hydrolyzable C and N pools might be a reliable indicator for short-term net mineralization is supported by the results of Jensen et al. [24], Bushong et al. [70], and Ahn et al. [71]. All authors have reported positive relationships of soluble N and C pools with the short-term mineralization of organic matter. Thus, in products such as FBG, UP, and FPG, with higher ratios of C and N pools in the readily decomposable pools, even the net immobilization might occur within the first days, whereas for products with a lower ratio, the net N mineralization was found right from the beginning. However, the exceptionally high value of k for the SWPs (2.44 mg L⁻¹ d⁻¹) and, thus, the lag phase of nearly 14 days, could not be solely attributed to the ratio of carbon and nitrogen in the easily decomposable pools. The discrepancy between the SWPs and all other fertilizers was confirmed by a Cook’s D > 4/n for the SWPs. One possible reason might be the high amount of wool wax—mainly lanolin—in sheep wool. As the percentages of lanolin and total N are similar in raw sheep wool [72], the amount of added lanolin in the incubation experiment was about 1 g L⁻¹. According to Arunkumar et al. [73], only certain groups of bacteria effectively degrade such wax-rich agricultural residues. Studies on wood fibers have shown that waxes can additionally act as physical and bio-chemical protection against microbial breakdown [72,74,75]. The extended lag phase of the SWPs might be related to the time needed to develop such a wax-degrading bacterial population. Furthermore, keratins—the fibrous proteins forming sheep wool—are highly resistant to hydrolysis by common proteolytic enzymes [76]. This seems, at first sight, contradictory to the fact that hooves (CHM) and pig bristles (PBPs), which also mainly consist of keratins, had no lag phase, and their daily N mineralization rates (45 and 47 mg L⁻¹ d⁻¹) were among the highest of all fertilizers. However, the degradability of keratin-rich residues is closely related to the percentage of different keratin groups (α-, β-, and γ-keratins), the amino acid composition, and the amount of sulfur [76,77,78], which all differ among hooves, hairs, and feathers [37,77,78]. As a coincidence, the amount of easily (0.005 M hydrochloric acid) hydrolyzable organic nitrogen was about five times higher in the CHM and PBPs than in the SWPs. In contrast, the amount of organic nitrogen soluble in 1 M hydrochloric acid was the same for all three fertilizers. Moreover, as for the N_P mentioned before, the maximum daily N mineralization rate (indicated by parameter h of the Gompertz function) of easily hydrolyzable organic N pools was significantly higher for the UP than for the remaining twelve fertilizers. However, for the remaining fertilizers, quickly hydrolyzable organic N pools were only a rough indicator of the maximum daily N mineralization rate (Figure 6c). Thus, the results present here are useful as indicators of the N release from organic fertilizers but cannot be used for a precise prediction thereof.

Before transferring the results to the greenhouse, the influence of plants should be considered as an additional factor. Plant exudate and the microbiology within the rootzone can contribute to this effect [79]. For instance, the study by Gruda and Schnitzler [80] indicated that immobilized nitrogen levels were higher in experiments with plants than those without plants. In addition, root exudates affect the root and shoot growth of plants by attracting beneficial microbiota, chelating nutrients in the rootzone, modulating rootzone pH, and enhancing the availability of specific nutrient elements [79,81]. Furthermore, Helal and Sauerbeck [82] demonstrated that the activation of microorganisms, especially in proximity to the roots, might enhance carbon mobilization from the organic matter. Consequently, the demand for nitrogen increases to support the proliferation of microorganisms. Furthermore, the ongoing substitution of peat in growing media to other organic materials will make the topic more complex, as not only the N release from organic fertilizers but also N immobilization by growing media constituents, such as wood fiber, and the interaction between both processes are of increasing importance [69]. This should be addressed in detail in future research, in which the role of microbial activity and the structure of the microbial community have to be considered.

4. Conclusions

Water-soluble and easily hydrolyzable N and C pools of organic fertilizers are valuable indicators for the potentially mineralizable N and the time course of N release, which can be estimated very well by flexible-shaped sigmoid growth functions—mainly the Gompertz function. This makes organic fertilizers more comparable and can help match the N supply and demand better, thus increasing the efficiency and sustainability of organic pot plant production. In contrast to chemical composition, the particle size was less important for the time course of N release under the test conditions. Furthermore, the presented data highlight the two main challenges growers face when applying organic N fertilizers. First, growers must consider that the N release is only about half of the total applied N; thus, they must double the N supply compared to the N demand. Secondly, N release is relatively fast, which might cause salt damage and make the complete application of nitrogen before planting impossible.