Novel Approach for Statistical Interpretation: A Case Study from Long-Term Crop Production Experiments (Hungary)
Abstract
:1. Introduction
2. Materials and Methods
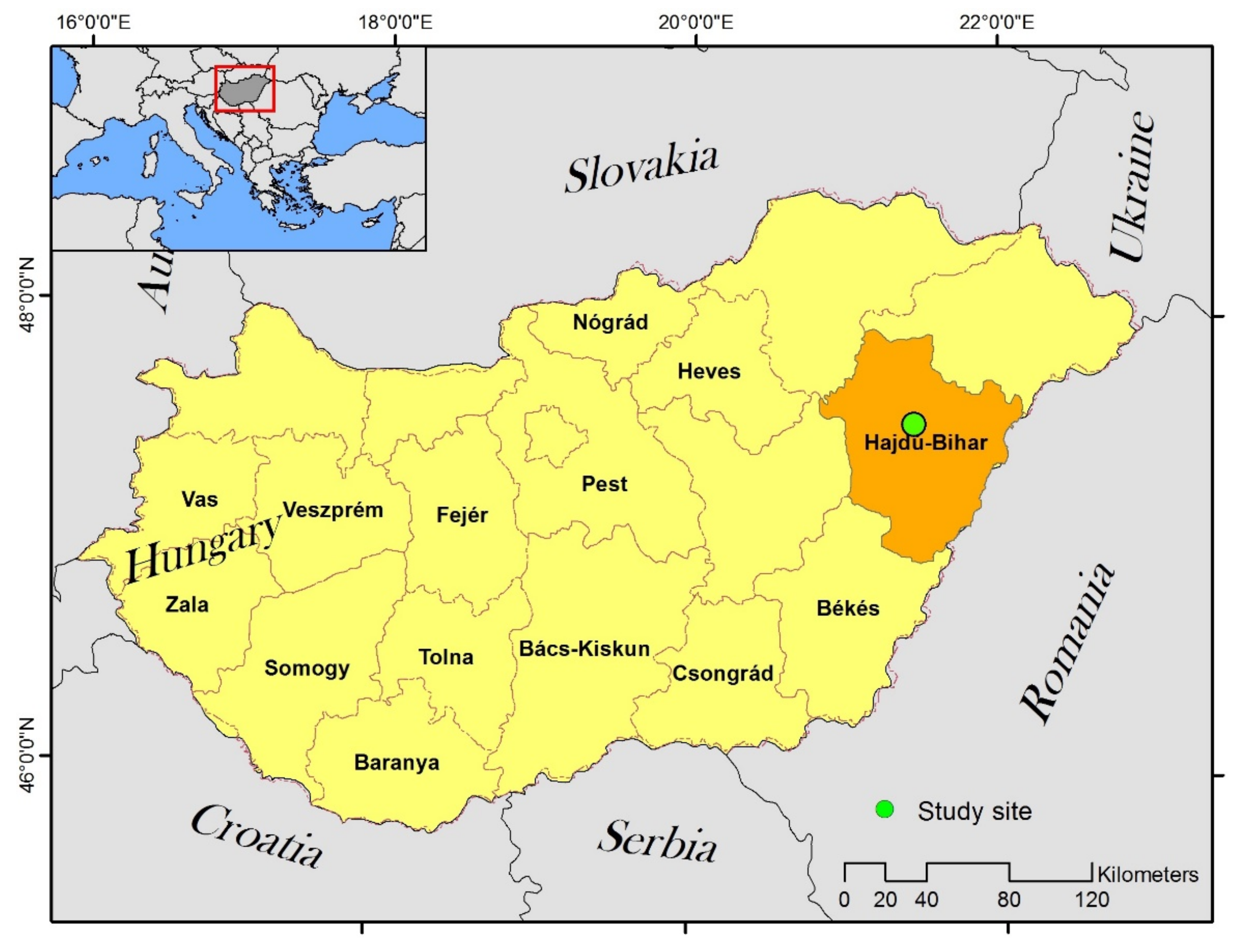
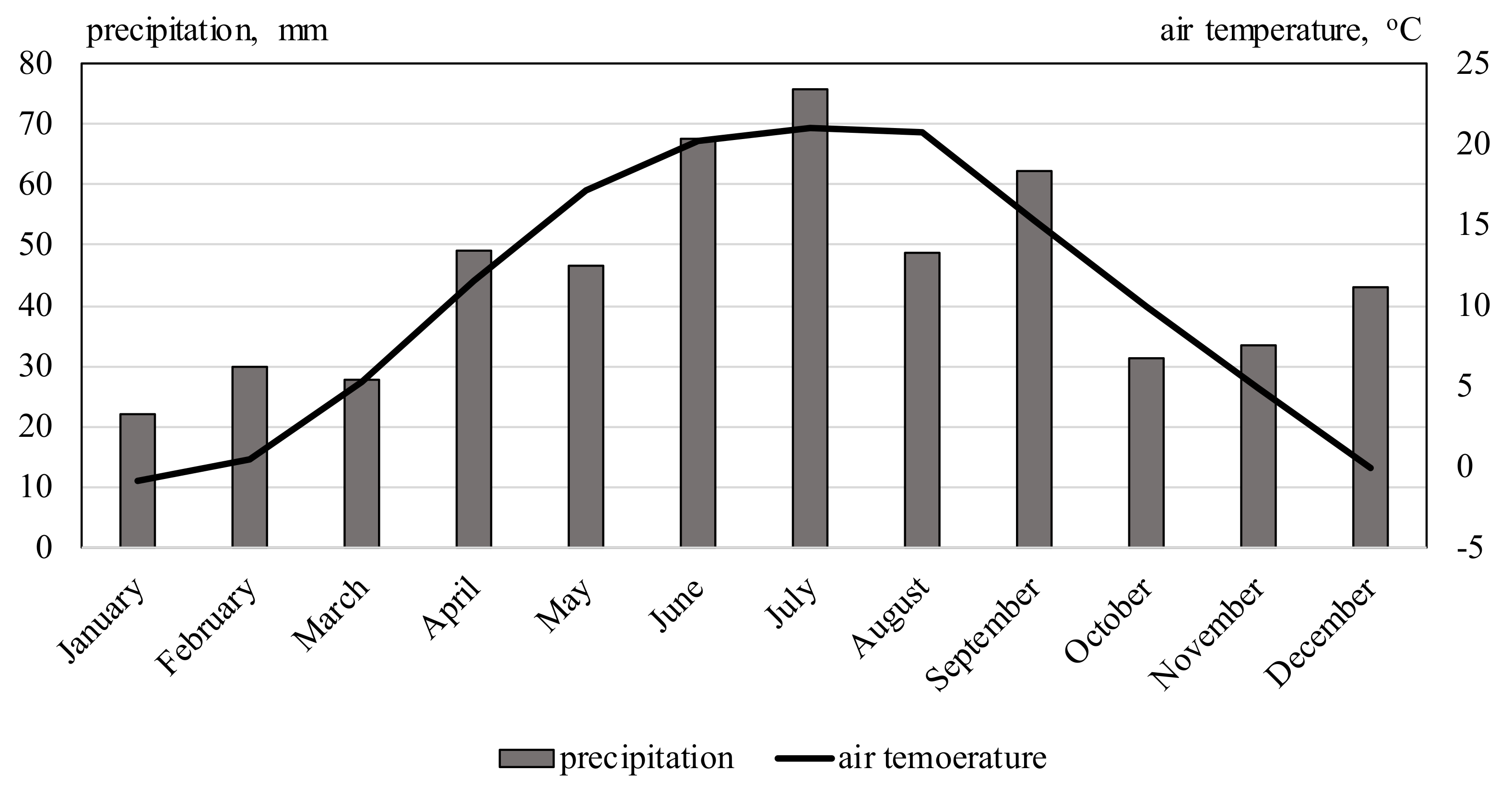
2.1. Site Description and Experiment Design for Data Collection
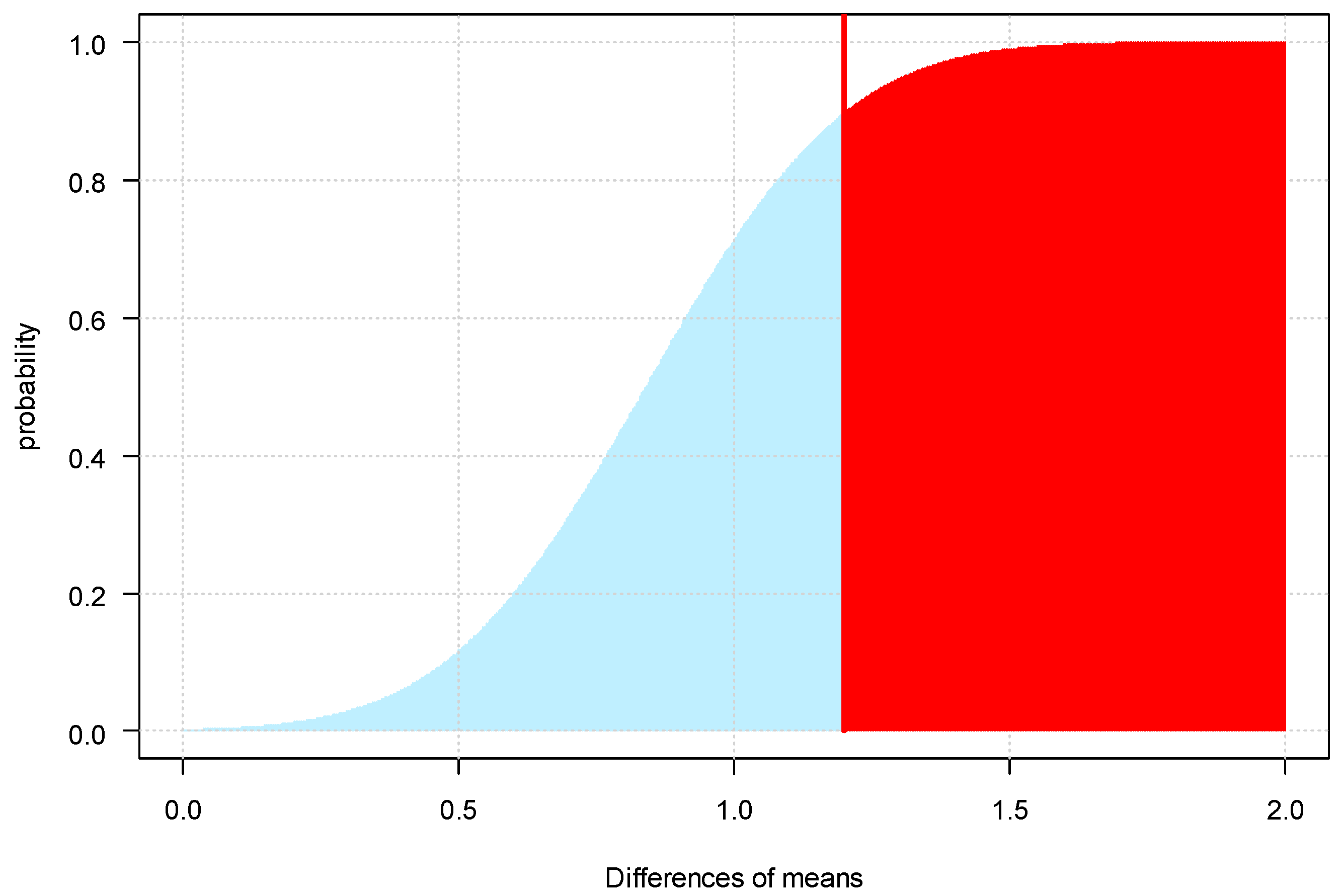
2.2. Steps for Building Professional Statistical Approach (Suggested Approach)
c(“N60-controll ≤ 0.84”,
“N120-N60 ≤ 0.84”,
“N180-N120 ≤ 0.84”,
“N240-N180 ≤ 0.84”,
“N300-N240 ≤ 0.84”)))
2.3. Statistical Analysis Performance
3. Results
3.1. Compression between Traditional and Professional Method
3.2. Application of Professional Hypotheses on Collected Experimental Data
“N60-N30 ≤ 0.323”,
“N90-N60 ≤ 0.34”,
“N120-N90 ≤ 0.326”,
“N150-N120 ≤ 0.353”)
>glht(model, linfct = mcp(npk = K))
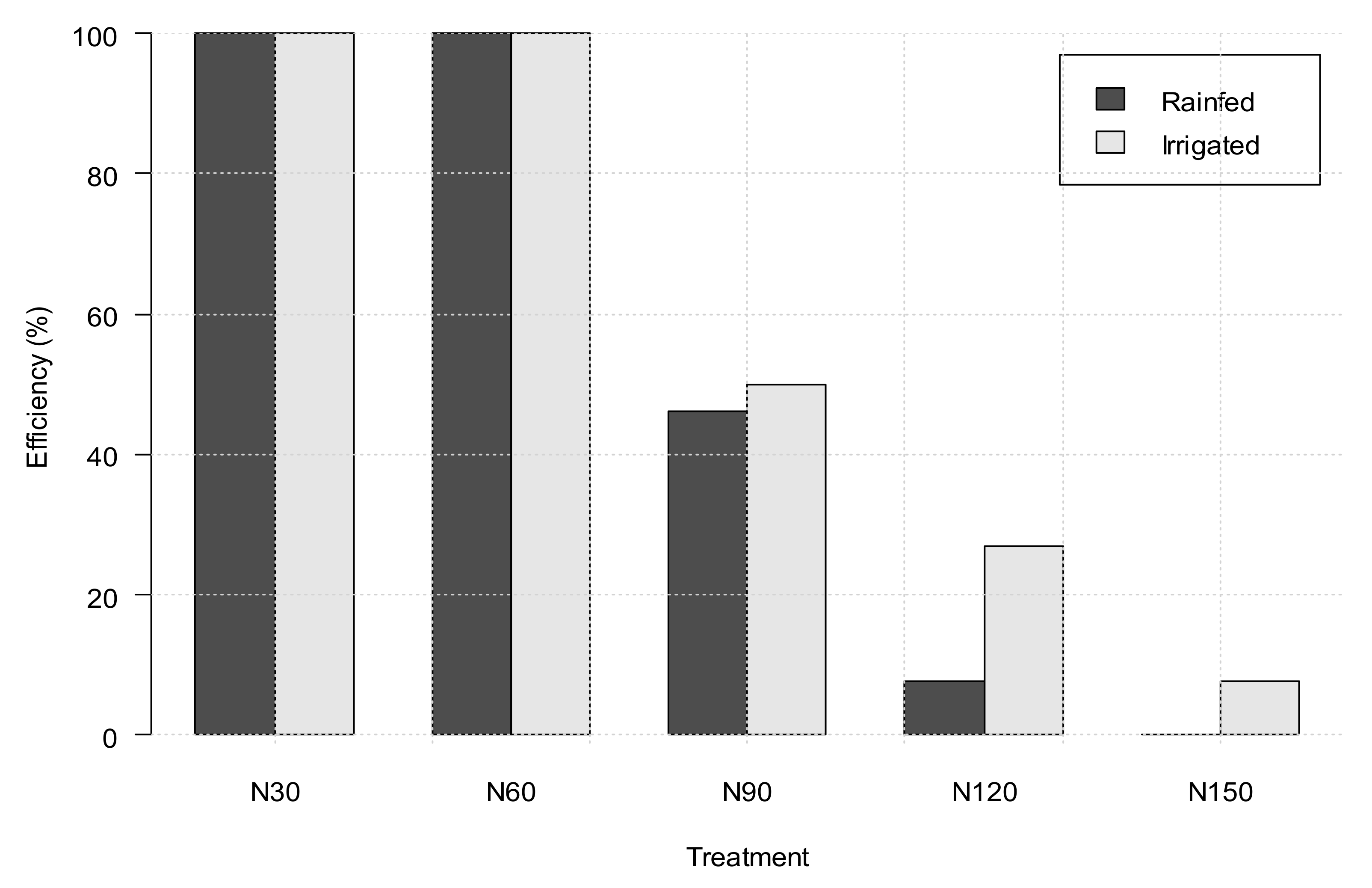
3.2.1. Results of the Non-Irrigated Treatments
3.2.2. Results of the Irrigated Treatments
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Notenbaert, A.; Pfeifer, C.; Silvestri, S.; Herrero, M. Targeting, out-scaling and prioritising climate-smart interventions in agricultural systems: Lessons from applying a generic framework to the livestock sector in sub-Saharan Africa. Agric. Syst. 2017, 1, 153–162. [Google Scholar] [CrossRef]
- Takács, I.; Amiri, M.; Károly, K.; Mohammed, S. Assessing soil quality changes after 10 years of agricultural activities in eastern Hungary. Irrig. Drain. 2021, 70, 1116–1128. [Google Scholar] [CrossRef]
- Mohammed, S.; Al-Ebraheem, A.; Holb, I.J.; Alsafadi, K.; Dikkeh, M.; Pham, Q.B.; Linh, N.T.; Szabo, S. Soil management effects on soil water erosion and runoff in central Syria—A comparative evaluation of general linear model and random forest regression. Water 2020, 12, 2529. [Google Scholar] [CrossRef]
- Kogo, B.K.; Kumar, L.; Koech, R. Climate change and variability in Kenya: A review of impacts on agriculture and food security. Environ. Dev. Sustain. 2021, 23, 23–43. [Google Scholar] [CrossRef]
- Vogel, E.; Donat, M.G.; Alexander, L.V.; Meinshausen, M.; Ray, D.K.; Karoly, D.; Meinshausen, N.; Frieler, K. The effects of climate extremes on global agricultural yields. Environ. Res. Lett. 2019, 14, 054010. [Google Scholar] [CrossRef]
- Chakraborty, S.; Tiedemann, A.V.; Teng, P.S. Climate change: Potential impact on plant diseases. Environ. Pollut. 2000, 108, 317–326. [Google Scholar] [CrossRef]
- Béné, C.; Barange, M.; Subasinghe, R.; Pinstrup-Andersen, P.; Merino, G.; Hemre, G.I.; Williams, M. Feeding 9 billion by 2050–Putting fish back on the menu. Food Secur. 2015, 7, 261–274. [Google Scholar] [CrossRef] [Green Version]
- Bahar, N.H.; Lo, M.; Sanjaya, M.; Van Vianen, J.; Alexander, P.; Ickowitz, A.; Sunderland, T. Meeting the food security challenge for nine billion people in 2050: What impact on forests. Glob. Environ. Chang. 2020, 62, 102056. [Google Scholar] [CrossRef]
- Mohammed, S.; Gill, A.R.; Alsafadi, K.; Hijazi, O.; Yadav, K.K.; Khan, A.H.; Islam, S.; Cabral-Pinto, M.M.; Harsanyi, E. An overview of greenhouse gases emissions in Hungary. J. Clean. Prod. 2021, 127865. [Google Scholar] [CrossRef]
- Mohammed, S.; Alsafadi, K.; Hennawi, S.; Mousavi, S.M.; Kamal-Eddin, F.; Harsanyie, E. Effects of long-term agricultural activities on the availability of heavy metals in Syrian soil: A case study in southern Syria. J. Saudi Soc. Agric. Sci. 2021. [Google Scholar] [CrossRef]
- Onofri, A.; Carbonell, E.A.; Piepho, H.P.; Mortimer, A.M.; Cousens, R.D. Current statistical issues in Weed Research. Weed Res. 2010, 50, 5–24. [Google Scholar] [CrossRef]
- Singh, A.S.; Masuku, M.B. An insight in statistical techniques and design in agricultural and applied research. World J. Agric. Sci. 2012, 8, 568–584. [Google Scholar]
- Rudolph, S.; Wongleecharoen, C.; Lark, R.M.; Marchant, B.P.; Garré, S.; Herbst, M.; Vereecken, H.; Weihermüller, L. Soil apparent conductivity measurements for planning and analysis of agricultural experiments: A case study from Western-Thailand. Geoderma 2016, 267, 220–229. [Google Scholar] [CrossRef]
- Anderson, D.R.; Burnham, K.P.; Thompson, W.L. Null hypothesis testing: Problems, prevalence, and an alternative. J. Wildl. Manag. 2000, 64, 912–923. [Google Scholar] [CrossRef]
- Hobbs, N.T.; Hilborn, R. Alternatives to statistical hypothesis testing in ecology: A guide to self teaching. Ecol. Appl. 2006, 16, 5–19. [Google Scholar] [CrossRef] [Green Version]
- Tavares, L.D.; Carvalho, A.M.; Machado, L.G. An evaluation of the use of statistical procedures in soil science. Rev. Bras. De Ciência Do Solo 2016, 29, 40. [Google Scholar] [CrossRef] [Green Version]
- Raudonius, S. Application of statistics in plant and crop research: Important issues. Zemdirb.-Agric. 2017, 104, 377–382. [Google Scholar] [CrossRef] [Green Version]
- Kramer, M.H.; Paparozzi, E.T.; Stroup, W.W. Statistics in a Horticultural Journal: Problems and solutions. J. Am. Soc. Hortic. Sci. 2016, 141, 400–406. [Google Scholar] [CrossRef]
- Lykken, D.T. Statistical significance in psychological research. Psychol. Bull. 1968, 70, 151–159. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. The earth is round (p <0.05). Am. Psychol. 1994, 49, 997. [Google Scholar]
- Harlow, L.L.; Mulaik, S.A.; Steiger, J.H. (Eds.) Multivariate Applications Book Series. What If There Were No Significance Tests? Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 1997. [Google Scholar] [CrossRef]
- Gigerenzer, G. Mindless statistics. J. Socio-Econ. 2004, 33, 587–606. [Google Scholar] [CrossRef]
- Rinella, M.J.; James, J.J. Invasive plant researchers should calculate effect sizes, not P-values. Invasive Plant Sci. Management. 2010, 3, 106–112. [Google Scholar] [CrossRef]
- Cumming, G. The new statistics: Why and how. Psychol. Sci. 2014, 25, 7–29. [Google Scholar] [CrossRef]
- Robinson, D.H.; Wainer, H. On The Past and Future of Null Hypothesis Significance Testing 1. ETS Res. Rep. Ser. 2001, 2001, i–20. [Google Scholar] [CrossRef]
- Mogie, M. In support of null hypothesis significance testing. Proceedings of the Royal Society of London. Ser. B Biol. Sci. 2004, 271 (Suppl. S3), S82–S84. [Google Scholar] [CrossRef]
- Stephens, P.A.; Buskirk, S.W.; del Rio, C.M. Inference in ecology and evolution. Trends Ecol. Evol. 2007, 22, 192–197. [Google Scholar] [CrossRef]
- Mudge, J.F.; Baker, L.F.; Edge, C.B.; Houlahan, J.E. Setting an optimal α that minimizes errors in null hypothesis significance tests. PLoS ONE 2012, 7, e32734. [Google Scholar] [CrossRef]
- Fisher, R.A. The Design of Experiments; Oliver and Boyd: Edinburgh, UK, 1935. [Google Scholar] [CrossRef]
- Duncan, D.B. Multiple range and multiple F tests. Biometrics 1955, 11, 1–42. [Google Scholar] [CrossRef]
- Dunnett, C.W. A multiple comparison procedure for comparing several treatments with a control. J. Am. Stat. Assoc. 1955, 50, 1096–1121. [Google Scholar] [CrossRef]
- Scheffe, H. The Analysis of Variance; Wiley: New York, NY, USA, 1959. [Google Scholar] [CrossRef]
- Meehl, P.E. Theoretical risks and tabular asterisks: Sir Karl, Sir Ronald, and the slow progress of soft psychology. J. Consult. Clin. Psychol. 1978, 46, 806–834. [Google Scholar] [CrossRef]
- Mohammed, S.; Mirzaei, M.; Pappné Törő, Á.; Anari, M.G.; Moghiseh, E.; Asadi, H.; Szabó, S.; Kakuszi-Széles, A.; Harsányi, E. Soil carbon dioxide emissions from maize (Zea mays L.) fields as influenced by tillage management and climate. Irrig. Drain. 2021. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org (accessed on 5 September 2021).
- Hothorn, T.; Bretz, F.; Westfall, P.; Heiberger, R.M. Multcomp: Simultaneous Inference for General Linear Hypotheses. R package version. 2012, pp. 1–2. Available online: http://CRAN.R-project.org/package=multcomp (accessed on 5 September 2021).
- Mendiburu, F. Agricolae: Statistical Procedures for Agricultural Research. R Package Version 1.3-1. 2019. Available online: https://CRAN.R-project.org/package=agricolae (accessed on 5 September 2021).
- Pawlak, K.; Kołodziejczak, M. The role of agriculture in ensuring food security in developing countries: Considerations in the context of the problem of sustainable food production. Sustainability 2020, 12, 5488. [Google Scholar] [CrossRef]
- Qaim, M. Role of new plant breeding technologies for food security and sustainable agricultural development. Appl. Econ. Perspect. Policy 2020, 42, 129–150. [Google Scholar] [CrossRef]
- Dhankher, O.P.; Foyer, C.H. Climate resilient crops for improving global food security and safety. Plant Cell Environ. 2018, 41, 877–884. [Google Scholar] [CrossRef]
- Ray, D.K.; Mueller, N.D.; West, P.C.; Foley, J.A. Yield trends are insufficient to double global crop production by 2050. PLoS ONE 2013, 8, e66428. [Google Scholar] [CrossRef] [Green Version]
- Zou, H.; Fan, J.; Zhang, F.; Xiang, Y.; Wu, L.; Yan, S. Optimization of drip irrigation and fertilization regimes for high grain yield, crop water productivity and economic benefits of spring maize in Northwest China. Agric. Water Manag. 2020, 230, 105986. [Google Scholar] [CrossRef]
| Fertilization Code | Fertilization Levels |
|---|---|
| N30 | 30 kg N, 23 kg P2O5, 27 kg K2O ha−1 |
| N60 | 60 kg N, 45 kg P2O5, 53 kg K2O ha−1 |
| N90 | 90 kg N, 68 kg P2O5, 80 kg K2O ha−1 |
| N120 | 120 kg N, 90 kg P2O5, 106 kg K2O ha−1 |
| N150 | 150 kg N, 113 kg P2O5, 133 kg K2O ha−1 |
| Control | NA |
| Traditional Approach | ||||
|---|---|---|---|---|
| Statistical Hypotheses | Estimate (t/ha) | Error (t/ha) | t Value | Pr(>|t|) |
| N60 − control = 0 | 2.0286 | 0.2848 | 7.123 | <1 × 10−9 *** |
| N120 − control = 0 | 2.5429 | 0.2848 | 8.928 | <1 × 10−9 *** |
| N180 − control = 0 | 2.6620 | 0.2848 | 9.346 | <1 × 10−9 *** |
| N240 − control = 0 | 2.7477 | 0.2848 | 9.647 | <1 × 10−9 *** |
| N300 − control = 0 | 2.5690 | 0.2848 | 9.020 | <1 × 10−9 *** |
| Professional Hypotheses | ||||
| N60 − control ≤ 0.84 | 2.02862 | 0.28482 | 4.173 | 0.000153 *** |
| N120 − N60 ≤ 0.84 | 0.51429 | 0.28482 | −1.144 | 1.000000 |
| N180 − N120 ≤ 0.84 | 0.11912 | 0.28482 | −2.531 | 1.000000 |
| N240 − N180 ≤ 0.84 | 0.08563 | 0.28482 | −2.649 | 1.000000 |
| N300 − N240 ≤ 0.84 | −0.17862 | 0.28482 | −3.576 | 1.000000 |
| Treatment | N Fertilizer (kg ha−1) | P2O5 Fertilizer (kg ha−1) | K2O Fertilizer (kg ha−1) | Yield Increase (t ha−1) |
|---|---|---|---|---|
| N30 | 30 | 23 | 27 | 0.594 |
| N60 | 60 | 45 | 53 | 0.323 |
| N90 | 90 | 68 | 80 | 0.340 |
| N120 | 120 | 90 | 106 | 0.326 |
| N150 | 150 | 113 | 133 | 0.353 |
| Professional Hypotheses, 1996 | Estimate Std. | Error | t Value | Pr(>|t|) |
| N30 − control ≤ 0.594 | 3.2798 | 0.1229 | 21.857 | <2 × 10−16 *** |
| N60 − N30 ≤ 0.323 | 1.6137 | 0.1229 | 10.503 | <2 × 10−16 *** |
| N90 − N60 ≤ 0.34 | −0.2321 | 0.1229 | −4.656 | 1 |
| N120 − N90 ≤ 0.326 | −0.6147 | 0.1229 | −7.655 | 1 |
| N150 − N120 ≤ 0.353 | −0.5119 | 0.1229 | −7.039 | 1 |
| Professional Hypotheses, 1999 | Estimate Std. | Error | t Value | Pr(>|t|) |
| N30 − control ≤ 0.594 | 2.5532 | 0.1457 | 13.443 | <1 × 10−4 *** |
| N60 − N30 ≤ 0.323 | 1.1310 | 0.1457 | 5.544 | <1 × 10−4 *** |
| N90 − N60 ≤ 0.34 | 0.9199 | 0.1457 | 3.979 | 0.000186 *** |
| N120 − N90 ≤ 0.326 | 0.8425 | 0.1457 | 3.544 | 0.001029 ** |
| N150 − N120 ≤ 0.353 | 0.1466 | 0.1457 | −1.416 | 1.000000 |
| Professional Hypotheses, 1997. | Estimate Std. | Error | t Value | Pr(>|t|) |
| N30 − control ≤ 0.594 | 3.8675385 | 0.1187231 | 27.573 | <0.001 *** |
| N60 − N30 ≤ 0.323 | 0.9151250 | 0.1187231 | 4.987 | <0.001 *** |
| N90 − N60 ≤ 0.34 | 0.4571250 | 0.1187231 | 0.987 | 0.645 |
| N120 − N90 ≤ 0.326 | 0.0004519 | 0.1187231 | −2.742 | 1.000 |
| N150 − N120 ≤ 0.353 | −0.7445673 | 0.1187231 | −9.245 | 1.000 |
| Professional Hypotheses, 2004 | Estimate Std. | Error | t Value | Pr(>|t|) |
| N30 − control ≤ 0.594 | 1.9980 | 0.1592 | 8.817 | <0.001 *** |
| N60 − N30 ≤ 0.323 | 1.1301 | 0.1592 | 5.069 | <0.001 *** |
| N90 − N60 ≤ 0.34 | 0.8407 | 0.1592 | 3.145 | 0.00451 ** |
| N120 − N90 ≤ 0.326 | 1.0774 | 0.1592 | 4.719 | <0.001 *** |
| N150 − N120 ≤ 0.353 | 0.7194 | 0.1592 | 2.301 | 0.05341 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huzsvai, L.; Mohammed, S.; Harsányi, E.; Széles, A. Novel Approach for Statistical Interpretation: A Case Study from Long-Term Crop Production Experiments (Hungary). Horticulturae 2022, 8, 48. https://doi.org/10.3390/horticulturae8010048
Huzsvai L, Mohammed S, Harsányi E, Széles A. Novel Approach for Statistical Interpretation: A Case Study from Long-Term Crop Production Experiments (Hungary). Horticulturae. 2022; 8(1):48. https://doi.org/10.3390/horticulturae8010048
Chicago/Turabian StyleHuzsvai, László, Safwan Mohammed, Endre Harsányi, and Adrienn Széles. 2022. "Novel Approach for Statistical Interpretation: A Case Study from Long-Term Crop Production Experiments (Hungary)" Horticulturae 8, no. 1: 48. https://doi.org/10.3390/horticulturae8010048
APA StyleHuzsvai, L., Mohammed, S., Harsányi, E., & Széles, A. (2022). Novel Approach for Statistical Interpretation: A Case Study from Long-Term Crop Production Experiments (Hungary). Horticulturae, 8(1), 48. https://doi.org/10.3390/horticulturae8010048








