Abstract
The relationship between the size and shape of diaspores was investigated in angiosperms and gymnosperms including determining if being a seed or fruit was a factor. Size was expressed as volume and shape as the departure from a perfect idealized sphere. Departure from sphericity in seeds was found to be independent from volume. Conversely, an inverse relationship was found between departure from sphericity and volume in fruits. Therefore, whether a diaspore is a seed or a fruit should be considered and included in analyses when ecological, functional or evolutionary correlates of diaspore morphology are under investigation.
1. Introduction
In their classic review on “The shapes and sizes of seeds” Harper et al. [1] concluded that the variation of seed size involves some type of compromise with seed number, with the advantage of the large reserves of large seeds opposed by their disadvantages in water relations, dispersion and risk of predation, while seed shapes represented various trade-offs among the forms that maximize the efficiency of packing, dispersal, landing and seedling establishment. Despite the impressive amount of evidence gathered in that review supporting the hypothesis that changes in size and shape of seeds, even very small ones, may affect almost every aspect of seed germination and plant establishment, a number of questions were left unaddressed.
First of all, seed size quantification was performed by weighing seeds not only in the review cited, but overwhelmingly in studies of ecological and functional correlates of seed size. However, seed weight is not a measure of seed size but of seed mass. This would not pose a problem if the density of seeds was similar across species and remained essentially constant under different conditions and during the ageing process, which is not necessarily the case. In fact, moderate to extended ranges of density have been reported in diaspores of scorzonera [2], subterranean clover [3], and color morphs of red clover [4]. The trade-off between seed size and seed number has also been disputed [5,6,7]. Nevertheless, seed size (weight) as a correlate in ecological, functional, and evolutionary studies has been widely used and its significance is firmly established [8,9].
In contrast, seed shape has been much less investigated as a possible ecological, functional, and evolutionary correlate. Among possible reasons for this, the difficulty of accurately defining and quantifying seed shape has certainly played a major role. More often than not, the shape of seeds has been defined by their resemblance with familiar objects like kidneys, lens, letters like Cs or Ds, daggers, or with well-defined geometric figures like ellipses, circles or triangles. All of these descriptions can be found in one taxonomy manual [10] primarily aimed at helping identify the species to which seeds belong. Not surprisingly, a number of descriptions were highly detailed; an extreme case was the description of seeds of Cirsium arvense as “Elongated; broadest above the middle gradually tapered to a narrow, truncate, frequently oblique base and upward to an oblique, slightly depressed, truncate apex. Oval in cross section, sometimes becoming four-angled near the base”. The description of Lithospermum arvense seeds is also worth mentioning for its details such as, “Shaped like a hood or ‘night cap with erect point’, broadest near the middle, gradually tapered to a wide, oval, truncate base and sharply to a pointed apex.” Useful as these descriptions might be to identify the species to which seeds belong, the result was 164 different descriptions for 193 species, almost one per species, which is hardly useful for investigating the ecological, functional, or evolutionary relevance of seed shape.
More recently, an alternative and quantifiable method based upon the similarity between seed shape and a variety of well-defined geometrical forms like the cardioid or the ellipse has been investigated [11]. In this method a J-index ranging from 0 to 100 was generated allowing a description and quantification of seed shape which is independent of size [12].
However, this method used the outline of seeds disregarding their three-dimensional organization, which might play an important role in the ecology of seeds. Therefore, in certain cases, it might be preferable to adopt an alternative but quantifiable and size-independent approach to seed shape, encompassing simultaneously length, width and thickness. This can easily be done by determining the variance of these three dimensions and using the variance as a measure of how much the seed departs from a perfect sphere [13,14].
Thus we investigated whether or not there IS a relationship between seed size, expressed as volume, and seed shape, expressed as departure from perfect sphericity. Because some evidence exists that differences between seeds and fruits might play a role in ecological responses of diaspores, mostly in the framework of persistence in soil [13,15,16] we also investigated the relevance of being a seed or a fruit to the relationship between size and shape of diaspores.
2. Materials and Methods
Diaspore size expressed as volume, and diaspores length, width and thickness were obtained from the third update of the Seed Volume Dataset which can be accessed as a non-proprietary comma-separated (CSV) format file either at https://www.mdpi.com/2306-5729/4/2/61 or at http://home.uevora.pt/~lsdias/SVDS_03plus.csv. A detailed description of the dataset can be found in Ganhão and Dias [17]. The rationale and methods used to determine the volume of diaspores can be found in [18,19].
Diaspores were identified as seeds or as fruits by checking the document used as source of length, width and thickness. Whenever the unit of dispersion is the fruit, but linear dimensions of the seed were available and were abstracted in the dataset, the latter were used and we classified the diaspore as a seed (e.g., Sidastrum paniculatum in [20]). A complete list of the entries, species, families and diaspore classification used in this report can be found as a non-proprietary comma-separated (CSV) format file in Supplementary Table S1.
Departure from sphericity (DS) of diaspores was determined as the population variance of their linear dimensions scaled to length as unity by dividing length (L), width (W) and thickness (T) by length [14]. In a perfectly spherical diaspore (L = W = T), departure from sphericity equals zero, its value increasing as the diaspore, assumed to be an ellipsoid, deviates from a perfect sphere. For perspective, the fruit of Myriophyllum spicatum with a volume of 8.182 mm3 has DS = 0, while the highly elongated fruit of Scorzonera hispanica [2] with a slightly larger volume of 8.362 mm3 can reach DS = 0.195. Illustrative drawings of diaspores of the former species can be found in [21], and of the latter in [22].
Most entries in the Seed Volume Dataset had only values for length and width, the value of thickness being unknown. The same occurred in entries in which the identification of the diaspore as seed or fruit was possible. Therefore, to calculate the departure from sphericity of diaspores the value of T had to be estimated. To do so we rearranged the equation of the volume of an ellipsoid as:
where T’ is the estimated value of T of an ellipsoid with volume VOLLW, L is length, W is width, VOLLW is calculated from L and W, as described in [17,19]. Whenever T’ > L, all linear dimensions (L, W and the newly estimated T’) were divided by T’ instead of by L.
T’ = 6 VOLLW/π L W,
The relationship between departure from sphericity determined from L, W and T (Section 3.1), or from L, W and T’ (Section 3.2), and seed or fruit size was investigated by least squares forward stepwise multiple linear regression with replication and a comparison-wise type I error rate of 0.05 for coefficients. Coefficients of determination (R2) are always presented as proportion of the maximum R2 possible [23]. The complete candidate polynomial included up to the third degree for seed or fruit size, qualitative variables for seed and fruit binary coded as 0 or 1, and all interactions between diaspore size and the qualitative variables.
Volume is a variable resulting from the exponentiation of a linear dimension to the third power, in this case the lineal dimension being the geometric mean of length, width and thickness (multiplied by the constant π/6). Similarly, departure from sphericity, being a population variance, can be viewed as the exponentiation of a linear dimension squared, which is called standard deviation in statistics. Therefore, the two variables can be brought to linear dimensions keeping their original meaning of size and shape. Thus, their relationship can be much better quantified using linear regression in the sense that the variation of one-dimensional diaspore size statistically explains much better the variation of one-dimensional diaspore shape than the original three-dimensional volume and two-dimensional departure from sphericity (not shown here).
Equations were fitted to diaspores with known length, width and thickness, and separately to those in which thickness had to be estimated using Equation (1). Data are presented as mean ± standard error (SE). Regression analyses were performed using Statgraphics Plus for Windows 4.0 (STCS, Inc., Rockville, MD, USA), all other statistical analyses using Microsoft Excel® 2010.
3. Results
Synonym entries apart, 13,899 valid entries (91% of the total) could be classified as seed or fruit and were used to investigate the relationship between size and shape of diaspores. Seeds represented 57% percent of valid entries, 78% of valid entries with known length, width and thickness, and 55% of those lacking thickness. Summary statistics are presented in Table 1.

Table 1.
Range, mean ± SE, median, coefficient of variation (CV), and sample size (n) of volume (VOL, in mm3) and departure from sphericity (DS) of seeds, fruits, and of seeds and fruits combined.
3.1. Diaspores with Known Length, Width and Thickness
Overall, seeds were larger, and departed less from sphericity than fruits. They also had larger values of coefficient of variation than fruits, more by volume than by departure from sphericity, meaning that the values of the two variables were more dispersed in seeds than in fruits.
The regression of departure from sphericity (square root transformed) on volume (cubic root transformed) was highly significant (p < 5 × 10−5; R2 = 0.889). After solving the three-term equation fitted for the values of the qualitative variables that coded for being seed or fruit, two significantly different equations resulted. For seeds the equation was:
DSs’LWT = 0.21830,
DSs’LWT being the square root of the departure from sphericity of seeds with known length, width and thickness, while for fruits the equation was:
DSf’LWT = 0.28240 − 0.00926 VOLf’,
DSf’LWT and VOLf’ being the square root of the departure from sphericity and the cubic root of the volume, respectively, of fruits with known length, width and thickness (Figure 1).
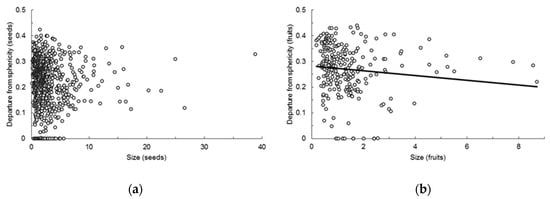
Figure 1.
Observed and estimated relationship between departure from sphericity (square root transformed) and size (volume cubic root transformed) of: (a) Seeds; (b) fruits. All diaspores had known length, width, and thickness.
3.2. Diaspores with Known Length, Width and Estimated Thickness
Overall, seeds were again larger, and departed less from sphericity than fruits. They also had larger values of coefficient of variation than fruits by volume but less by departure from sphericity, meaning that the values of the former variable were more dispersed in seeds than in fruits, the reverse in the latter.
The regression of departure from sphericity (square root transformed) on volume (cubic root transformed) was highly significant (p < 5 × 10−5; R2 = 0.967). After solving the three-term equation fitted for the values of the qualitative variables that coded for being seed or fruit, two significantly different equations resulted. For seeds the equation was:
DSs’LW = 0.26481,
DSs’LW being the square root of the departure from sphericity of seeds with known length and width, and thickness estimated by Equation (1), while for fruits the equation was:
DSf’LW = 0.30982 − 0.00018 VOLf’2,
DSf’LW and VOLf’ being the square root of the departure from sphericity and the cubic root of the volume, respectively, of fruits with known length and width, and thickness estimated by Equation (1) (Figure 2).
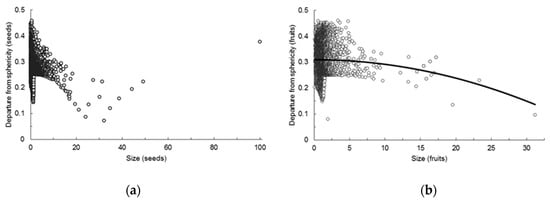
Figure 2.
Observed and estimated relationship between departure from sphericity (square root transformed) and size (volume cubic root transformed) of: (a) Seeds; (b) fruits. All diaspores with known length and width, thickness estimated by Equation (1).
4. Conclusions
The shape of diaspores may be characterized in different ways, which are not necessarily conflicting, depending upon the objectives and questions involved. Here we opted for expressing the shape as the departure from an ideal sphere assuming simultaneously that the volume of diaspores can be equated to the volume of an ellipsoid whose perpendicular axes equal the length, width and thickness of the diaspore in question.
The results reported here made clear three major features. First, there was a relationship between size and shape of diaspores with the variation of the former significantly explaining the variation of the latter. Second, this relationship only existed when diaspores were fruits but not when diaspores were seeds. Third, an inverse relationship existed between the size and shape of fruits, with fruits departing less from a sphere with the increase of their volume.
The results supported these conclusions either when complete information existed and departure from sphericity was calculated from measured values of length, width and thickness of seeds and fruits (Section 3.1), or when thickness data was missing and departure from sphericity had to be calculated using thickness values estimated from the volume, length and width of diaspores (Section 3.2). The latter allowed us to examine and analyze a much wider range of volumes but predictably failed to produce departures from sphericity DS = 0 equated to a perfect sphere. Nevertheless, conclusions based upon complete or incomplete information were essentially the same suggesting that estimated values of departure from sphericity can be also used to investigate ecological, functional or evolutionary correlates.
It is premature to further elaborate on the meaning and implications of differences of seeds and fruits in the relationship between volume and departure from sphericity, but it is clear that the distinction between the two types of plant diaspores should be kept in mind and taken into account in future investigations.
Supplementary Materials
The following are available online at https://www.mdpi.com/2311-7524/5/3/65/s1, Table S1: Seed or fruit classification of diaspores.
Author Contributions
Conceptualization, A.S.D. and L.S.D.; formal analysis, L.S.D.; writing—original draft preparation, L.S.D.; writing—review and editing, A.S.D. and L.S.D.
Funding
This research received no external funding.
Acknowledgments
We thank Emilio Cervantes (Institute of Natural Resources and Agronomy—Consejo Superior de Investigaciones Científicas, Spain) for suggestions done to a previous version of this report.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Harper, J.L.; Lovell, P.H.; Moore, K.G. The shapes and sizes of seeds. Annu. Rev. Ecol. Syst. 1970, 1, 327–356. [Google Scholar] [CrossRef]
- Pereira, I.P.; Dias, A.S.; Dias, L.S. Responses of germination and early growth of scorzonera (Scorzonera hispanica L.) to pH, mineral deficiencies and growth substrates. Bulg. J. Agric. Sci. 2014, 20, 1195–1201. [Google Scholar]
- Costa, A.; Dias, A.S.; Grenho, M.G.; Dias, L.S. Effects of dark or of red, blue or white light on germination of subterranean clover seeds. Emir. J. Food Agric. 2016, 28, 853–864. [Google Scholar] [CrossRef]
- Costa, A.S.; Dias, L.S.; Dias, A.S. Imbibition, germination, and early seedling growth responses of light purple and yellow seeds of red clover to distilled water, sodium chloride, and nutrient solution. Sci 2019, 1, 51. [Google Scholar] [CrossRef]
- Salisbury, E.J. The Reproductive Capacity of Plants; G. Bell and Sons: London, UK, 1942. [Google Scholar]
- Michaels, H.J.; Benner, B.; Hartgerink, A.P.; Lee, T.D.; Rice, S.; Willson, M.F.; Bertin, R.I. Seed size variation: Magnitude, distribution, and ecological correlates. Evol. Ecol. 1988, 2, 157–166. [Google Scholar] [CrossRef]
- Shipley, B.; Dion, J. The allometry of seed production in herbaceous angiosperms. Am. Nat. 1992, 139, 467–483. [Google Scholar] [CrossRef]
- Leishman, M.R.; Wright, I.J.; Moles, A.T.; Westoby, M. The Evolutionary Ecology of Seed Size. In Seeds: The Ecology of Regeneration in Plant Communities, 2nd ed.; Fenner, M., Ed.; CABI Publishing: Wallingford, UK, 2000; pp. 31–57. [Google Scholar]
- Thompson, K. The Functional Ecology of Soil Seed Banks. In Seeds: The Ecology of Regeneration in Plant Communities, 2nd ed.; Fenner, M., Ed.; CABI Publishing: Wallingford, UK, 2000; pp. 215–235. [Google Scholar]
- Delorit, R.J. An Illustrated Taxonomy Manual of Weed Seeds; Agronomy Publications: River Falls, WI, USA, 1970. [Google Scholar]
- Cervantes, E.; Martín, J.J.; Saadaoui, E. Updated methods for seed shape analysis. Scientifica 2016, 2016, 5691825. [Google Scholar] [CrossRef] [PubMed]
- Martín-Gómez, J.J.; Rewicz, A.; Goriewa-Duba, K.; Wiwar, M.; Tocino, Á.; Cervantes, E. Morphological description and classification of wheat kernels based on geometric models. Agronomy 2019, 9, 339. [Google Scholar] [CrossRef]
- Thompson, K.; Band, S.R.; Hodgson, J.G. Seed size and shape predict persistence in soil. Funct. Ecol. 1993, 7, 236–241. [Google Scholar] [CrossRef]
- Bakker, J.P.; Poschlod, P.; Strykstra, R.J.; Bekker, R.M.; Thompson, K. Seed banks and seed dispersal: Important topics in restoration ecology. Acta Bot. Neerl. 1996, 45, 461–490. [Google Scholar] [CrossRef]
- Leishman, M.R.; Westoby, M. Seed size and shape are not related to persistence in soil in Australia in the same way as in Britain. Funct. Ecol. 1998, 12, 480–485. [Google Scholar] [CrossRef]
- Moles, A.T.; Hodson, D.W.; Webb, C.J. Seed size and shape and persistence in soil in New Zealand flora. Oikos 2000, 89, 541–545. [Google Scholar] [CrossRef]
- Ganhão, E.; Dias, L.S. Seed volume dataset—An ongoing inventory of seed size expressed by volume. Data 2019, 4, 61. [Google Scholar] [CrossRef]
- Casco, H.; Dias, L.S. Estimating seed mass and volume from linear dimensions of seeds. Seed Sci. Technol. 2008, 36, 230–236. [Google Scholar] [CrossRef]
- Dias, L.S.; Ganhão, E. Extending the range for accurate estimation of seed volume from incomplete linear dimension data. Seed Sci. Technol. 2012, 40, 129–133. [Google Scholar] [CrossRef]
- Kissmann, K.G.; Groth, D. Plantas Infestantes e Nocivas. Tomo III. Plantas Dicotiledôneas por Ordem Alfabética de Famílias: Geraniaceae a Verbenaceae, 2nd ed.; BASF: São Paulo, Brazil, 2000. [Google Scholar]
- ARSUSDA. Common Weeds of the United States; Dover Publications: New York, NY, USA, 1971. [Google Scholar]
- Guardia, C.D.; Blanca, G. Revisión del género Scorzonera, L. (Compositae, Lactuceae) en la Península Ibérica. An. Jard. Bot. Madr. 1987, 43, 271–354. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley: New York, NY, USA, 1998. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).