Prediction of Selected Minerals in Beef-Type Tomatoes Using Machine Learning for Digital Agriculture

Abstract

Tomato is one of the most important vegetables due to its high production and nutritional value. With the development of digital agriculture, the tomato breeding and processing industries have seen a rapid increase in the need for simple, low-labor, and inexpensive methods for analyzing tomato composition. This study proposes a digital method to predict four minerals (calcium, potassium, phosphorus, and magnesium) in beef-type tomato using machine learning models, including k-nearest neighbors (kNN), artificial neural networks (ANNs), and Support Vector Regression (SVR). The models were discriminated using the coefficient of determination (R²), root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE). The kNN model showed the best performance for estimation of quantity of calcium, potassium, phosphorus, and magnesium. The results demonstrate that kNN consistently outperforms ANNs and SVR across all target nutrients, achieving the highest R² and the lowest error metrics (RMSE, MAE, and MAPE). Notably, kNN achieved an exceptional R² of 0.8723 and a remarkably low MAPE of 3.95% in predicting phosphorus. This study highlights how machine learning can provide a versatile, accurate, and efficient solution for tomato mineral analysis in digital agriculture.

1. Introduction

The tomato originates from the western coast of South America as well as the high Andes Mountains, stretching from the center of Ecuador to northern Chile and the Galápagos Islands [1]. Tomatoes are one of the most popular vegetables worldwide, valued for their taste, nutrition, and consumer preference. According to the Food and Agriculture Organization (FAO), approximately 189 million tons of tomatoes are produced worldwide, with China accounting for 67.5 million tons, followed by India and Turkey with 21.1 million tons and 13 million tons, respectively [2]. Tomatoes contain carbohydrates, organic acids, amino acids, vitamins, pigments, various mineral, and phenolic compounds that are beneficial for human health [3]. Minerals such as calcium (Ca), potassium (K), sodium (Na), phosphorus (P), magnesium (Mg), sulfur (S), and chlorine (Cl) are crucial for human health. These minerals need to be present within the human body at levels of more than 50 mg/day [4]. Minerals such as calcium, magnesium, potassium, phosphorus, and sodium, while comprising a small fraction of a vegetable’s dry matter, are critical to its nutritional value and quality [1,2,3]. Their presence highlights the importance of analyzing and optimizing mineral content in crops for human consumption, which is vital for improving crop quality [5].

The analysis of macro- and micro-elements that play a crucial role in human health and nutrition is an important aspect for studies related to cultivation, processing, and breeding. These elements are quantified through a series of laboratory analyses, which demand significant time, manpower, energy, and high cost. Furthermore, there is a growing challenge in processing and interpreting the vast amount of data acquired through analysis. This highlights the need for alternative, efficient, and cost-effective approaches. In this context, the present study aims to explore the potential of machine learning techniques for predicting the mineral content of tomato (Solanum lycopersicum L.) fruits. The specific research objective is to develop predictive models that can estimate macro- and micro-element concentrations based on spectral and image data, thus reducing reliance on conventional laboratory procedures. The study also addresses the problem of limited existing research on using machine learning for mineral prediction in tomatoes, compared to the relatively well-studied parameters such as color, size, or phytochemical content. In recent years, significant research has been carried out on the use of machine learning and advanced analytical methods in studies on tomato (Solanum lycopersicum L.) quality and nutrient content prediction. For example, spectrophotometric analyses and multiple regression models have been successfully applied to determine chlorophyll and carotenoid dynamics during the development of tomato fruit [6]. Similarly, the prediction of phytochemicals such as lycopene and β-carotene with artificial neural networks and portable spectroscopic devices demonstrated the potential of these techniques in nutrient profile analysis [7,8]. In addition, methods such as machine vision and deep learning have provided effective results in the assessment of physical properties and disease status of tomatoes [9,10]. These studies prove that machine learning offers a wide range of applications in the prediction of tomato quality parameters and also holds promise for the analysis of less studied parameters such as mineral content. However, a significant research gap exists in the application of machine learning techniques to predict the mineral element composition of tomatoes. This is an underexplored area with significant potential to advance both agricultural practices and nutritional assessment. Therefore, this study aims to develop and validate machine learning models for accurately predicting the macro- and micro-element content in tomatoes, thereby addressing the current limitations of traditional analytical approaches and providing a foundation for more efficient quality assessment methods.

The effects of environmental and postharvest factors on the nutritional components of tomatoes play a critical role in the development of prediction models. In a study conducted on this subject, the lycopene content of tomatoes stored at different temperatures and times was estimated by multiple regression analysis. Hydroponically grown tomatoes were stored at 10, 15, 20, 25, and 30 °C for 7 d after harvest, and the a* and b* values were calculated by measuring the color changes before and after storage with a chromometer. The lycopene content was modeled using color, temperature, and time variables before storage, and it was determined that the lycopene content increased when the tomatoes were stored at 20 °C and above (R² = 0.76) [11]. In another study, the sensitivity of tomatoes to mechanical impacts was evaluated and bruise prediction models were developed [12]. Within the scope of the study, the impact forces that the tomatoes were exposed to during transportation and processing were measured with acceleration sensors, and it was determined that the highest impact levels occurred during placement in and removal from harvest crates. Models were developed using multivariate analysis methods such as linear regression, artificial neural networks, and logistic regression for rot prediction. The findings showed that high temperature (>20 °C) and low relative humidity increased rot formation, and the probability of rot increased as the impact force increased [12]. On the other hand, the effects of storage temperature and duration on rot formation and quality deterioration in tomatoes were investigated by the same study. In the experiments, steel balls with a certain mass were dropped on tomatoes from different heights (20, 40, and 60 cm) in order to determine the rot formation threshold, and then the samples were stored at 10 and 22 °C for 10 d, and physical, chemical, and nutritional changes were analyzed every 2 d. Six different regression models were created to predict rot area and quality changes, and it was determined that factors such as storage time, rot area, weight loss, color changes, total soluble solids, and pigment content changed significantly (p < 0.05) as the impact level and temperature increased. The findings showed that firmness, brightness, and color saturation decreased significantly at 22 °C and at high impact levels. Regression models with R² values ranging from 0.76 to 0.95 showed strong performance in predicting rot formation and quality losses [13]. In addition to these studies, a Decision Support System (DSS) was developed to determine the ideal harvest time by estimating the total soluble solids (°Brix) content in industrial tomato cultivation. Within the scope of the study, a data set consisting of 33 input variables was created, including quality data (pH, Bostwick, L, a/b, average weight, °Brix), hybrid type used, weather conditions, and soil data for six different growing periods in the northwestern Peloponnese region of Greece. Thirteen different machine learning algorithms were tested, and the k-nearest neighbor (kNN) algorithm was selected as the fastest and most effective method. It was determined that the estimated °Brix values showed a similar pattern to the real °Brix values. This DSS, which uses real-time weather data as an input, is considered an important tool to help farmers determine the ideal time to harvest the best-quality tomatoes [14]. Finally, a study was conducted to determine the yield gap, analyze production constraints, and increase yield in greenhouse tomato cultivation [15]. A total of 110 greenhouse tomato cultivations in the southern region of Uruguay were studied during the 2014/15 and 2015/16 seasons, and the yields were compared with the potential and achievable yields. The potential yield was calculated with a simulation model based on photosynthetic active radiation (PAR) and light use efficiency, and the assimilation distribution and fruit yield were estimated using the TOMSIM model. The yield gap was determined as 44% or 10.7 kg/m² compared to the potential yield. The study showed that yield can be increased by reducing leaf pruning and increasing plant density in long summer and short spring/summer cultivation, while higher yields can be achieved in autumn cultivation by early planting, reducing leaf pruning, and increasing greenhouse light transmittance [15]. A similar approach is suggested for the estimation of selected minerals in beef-type tomatoes and the integration of data related to both agronomic conditions and postharvest processes into machine learning algorithms. However, studies focusing on the estimation of the mineral content of tomatoes are limited in the current literature. In particular, the rapid analysis of minerals such as potassium, calcium, and magnesium is of great importance in terms of agricultural productivity and human nutrition. This study addresses the gap in the existing literature regarding the lack of robust, non-destructive techniques for the estimation of the mineral content in tomatoes, with a particular focus on potassium, calcium, and magnesium. Inspired by previous methods such as vis–NIR spectroscopy and multivariate analysis [16,17], the current study aimed to present an optimized machine learning model for the estimation of the mineral content in beef-type tomatoes. The findings obtained will provide an innovative contribution both for mineral optimization of producers and for consumer health.

In line with this objective, the nutritional elements of a beef-type tomato variety were predicted using machine learning methods. Three supervised machine learning techniques were used: k-nearest neighbors (kNN), artificial neural networks (ANNs), and Support Vector Regression (SVR). The prediction performance of the models was evaluated using various metrics, including mean absolute percentage error (MAPE), mean absolute error (MAE), root mean square error (RMSE), mean square error (MSE), and R-squared (R²). Additionally, box plots and scatter plots were used to visually represent the model performances.

2. Materials and Methods

2.1. Handling of Raw Materials

A variety of beef-type tomato (AKT-1270) developed by the Vocational School Organic Agriculture at the Akdeniz University Manavgat, Türkiye, was used to predict the mineral content (Figure 1).

The tomatoes utilized in the trials were harvested in June 2023 at a red ripeness stage based on the USDA color chart [12]. A total of 310 tomato samples were randomly selected from 500 harvested tomatoes. Tomatoes were washed under water for 2 min, disinfected with 0.1% sodium hypochlorite, then rinsed with distilled water, dried with paper towels, and stored in a refrigerator (754140 MB, Vestel, Manisa, Türkiye) at 4 °C until analysis. Cleaned tomato samples formed the primary data set used for machine learning model development. All samples were labeled and tracked to ensure traceability throughout the analysis. Before being used in model training, the data from these samples was organized into structured data sets, cleaned for anomalies or missing values, and normalized to ensure compatibility with the algorithms’ input requirements.

2.2. Physicochemical Analysis

Tomato samples were analyzed for total soluble solids (TSS), titratable acidity (TA) and pH, and total dry matter (TDM) and ash contents, according to the methodology reported elsewhere [13]. TSS, expressed in Brix, were determined by a digital refractometer (HHR-2N, ATAGO, Tokyo, Japan), and the results are given as percentage. TA of the tomato was determined by a titration method: tomato juice of about 10 mL was titrated against 0.1 N NaOH. The results are given in percentage of citric acid. The pH was measured by a pH meter (PH 50 Violab, XS Instruments, Carpi, Italy). All tomato samples were dried at 70 °C using a laboratory oven (ELF 11/6B, Carbolite, Hope Valley, Derbyshire, UK). Ash content is expressed in percentage was determined from the total ash, where the samples were dried at 100 °C and burned in an oven at 525 °C. Afterward, the dried samples were weighed.

2.3. Firmness

Tomato firmness was measured using a penetrometer (PCE-PTR 200, PCE Instruments, Southampton, UK) with a 6 mm diameter probe at two diagonally opposite points on the equatorial region of each fruit. Measurements were performed on a total of 30 tomatoes, with each tomato being measured twice. The penetration depth was standardized to 8 mm for all measurements, and the maximum force required for penetration was recorded in Newtons (N). The average of two measurements per tomato was calculated and used for subsequent analysis [14].

2.4. Analytical Determinations

Fructose and glucose

To determine the sugar composition of all samples, 10 g of each sample was weighed into a 50 mL Erlenmeyer flask. The sample was blended using a T25 digital Ultra-Turrax laboratory blender (IKA, Staufen, Germany) at maximum speed (13,500 rpm) for 2 min to ensure complete homogenization. After blending, 20 mL of double-distilled water was added to the homogenized sample, and the mixture was then centrifuged (Universal 320 R Hettich, Hettich, Kirchlengern, Germany) at 6000 rpm at 20 °C for 30 min. From the clear supernatant, 10 mL was taken, mixed with an additional 10 mL of distilled water, and filtered through Whatman No. 1 filter paper. Next, 2 mL of the filtrate was combined with 6 mL of acetonitrile filtered through a membrane filter and analyzed using HPLC. [15] Ultra-pure water (18.2 MΩ·cm resistivity) was used as the mobile phase to ensure optimal separation of polar compounds. A CARBOSep CHO820 CA column (300 mm × 7.8 mm, 8 µm particle size), specifically designed for carbohydrate analysis, was employed under isocratic conditions. The temperature of the column was maintained at 30 °C, and the mobile phase flow rate was set to 0.5 mL/min to achieve precise resolution of sugar analytes.

Lycopene content

The lycopene content in tomatoes was determined using a spectrophotometer system (UV-1800, Shimadzu Manufacturing, Tokyo, Japan). The fruit puree was prepared by blending 100 g of tomatoes using a blender (MSM4B610, Bosch, Gunzenhausen-Schlungenhof, Germany) at high speed for 2 min, followed by sieving through a 1 mm mesh to remove seeds and skins. Then, a 0.5 g sample of the puree was weighed and placed into a 50 mL Erlenmeyer flask containing 5 mL of 95% ethanol and 10 mL of hexane. The lycopene was extracted on an orbital shaker (SH30, Finepcr, Beongil, Republic of Korea) at 180 rpm for 15 min on ice. After shaking, 3 mL of deionized water was added to each vial, and the samples were shaken for an additional 5 min on ice. The vials were then left at room temperature for 5 min to allow for phase separation. The absorbance of the upper fraction, the hexane layer, was measured in a 1 cm path length quartz cuvette at 503 nm using a spectrophotometer, with hexane serving as the blank. The lycopene content of each sample was estimated based on the absorbance at 503 nm and the sample weight [16].

Vitamin C

Ascorbic acid was extracted from tomatoes according to the method described by Karhan et al. [17] with modifications. The samples were weighed at 5 g, and 5 mL of 6% metaphosphoric acid was added. The samples were then centrifuged (Universal 320 R Hettich, Hettich, Kirchlengern, Germany) at 6500 rpm for 10 min at 4 °C. The supernatant was collected, and 0.5 mL of 6% metaphosphoric acid was added and completed into a 10 mL volumetric flask. This extract was filtered through 0.45 µm membrane filter and analyzed by HPLC. The results are expressed as mg ascorbic acid per 100 g fresh weight of tomato.

Mineral content

The concentrations of calcium (Ca), potassium (K), magnesium (Mg), phosphorus (P), and manganese (Mn) were determined as described elsewhere [18]. Briefly, samples were placed in porcelain crucibles and heated in an oven (ELF 11/6B, Carbolite, Derbyshire, UK) at 550 °C for 4 h, and the resulting clear solution was washed with hot water before being transferred to a 100 mL volumetric flask. The solution was then diluted to the mark and filtered through ash-free filter paper (Whatman 42). Finally, the concentrations of Ca, K, Mg, Mn, and P in the samples were analyzed using an inductively coupled plasma optical emission spectrometer (ICP-OES, model 5110, Agilent Technologies, Santa Clara, CA, USA).

2.5. Machine Learning

Descriptive statistics (mean, standard deviation, minimum, and maximum values) were first conducted using IBM SPSS Statistics version 25.0 (IBM Corporation, Armonk, NY, USA) for the experimental data. Missing data were identified using Microsoft Excel (version 2021) by applying the =COUNTBLANK() function to detect empty cells across all variables, followed by manual verification with =ISBLANK() for individual entries. Observations containing missing values were excluded from subsequent analyses to maintain data integrity. By performing extreme value analysis using the generalized extreme value (GEV) distribution method with a threshold-based peak-over-threshold (POT) approach, the presence of outliers in the data set was investigated [19,20]. Specifically, a threshold value was selected based on the empirical 95th percentile of the data. All values exceeding this threshold were considered peaks and modeled using the generalized Pareto distribution, a special case linked to the GEV family. The parameters of the GPD were estimated using maximum likelihood estimation, and diagnostic quantile–quantile plots were examined to assess the suitability of the threshold and the distribution fit. Observations that exhibited extremely low probability were classified as statistical outliers. After this, a total of 294 observations remained for analysis. The min–max normalization method was used in the normalization of data. In the next stage, forward and backward feature selection methods were used. This is a method used to prevent unnecessary variables from being taken into the model. All variables were effective in explaining target variables. After all these procedures, the data set was ready for analysis. In the data set partitioning processes (training and test data set respectively), 80–20%, 75–25%, 70–30%, and 65–35% ratios were performed, and models were established. The best results were obtained when the data set was divided into 70% training and 30% testing. In the modeling phase, three machine learning methods—artificial neural networks (ANNs), Support Vector Regression (SVR), and k-nearest neighbors (kNN)—were used. R², MAE, MAPE, and RMSE values were calculated with the prediction results obtained from the models, and the model results were interpreted individually and comparatively. The dependent and independent variables used in the model are shown in Figure 2.

The evaluation phase involves selecting appropriate metrics and visualization tools to ensure accurate interpretation of the results. In this study, the target variables are continuous; therefore, this is a regression study. R², MAPE, RMSE, and MAE metrics are frequently used in evaluating regression problems [21]. These metrics were also used in this study. Formulas of the metrics are shown in Equations (1)–(4).

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{m}}{\sum }_{i=1}^m\left|Y_i-{\widehat{Y}}_i\right|$$

(1)

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{m}}{\sum }_{i=1}^m\left|{\displaystyle \frac{Y_i-{\widehat{Y}}_i}{Y_i}}\right|$$

(2)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{m}}{\sum }_{i=1}^m{\left(Y_i-{\widehat{Y}}_i\right)}^2}$$

(3)

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^m{\left(Y_i-{\widehat{Y}}_i\right)}^2}{\sum _{i=1}^m{\left(Y_i-\overline{Y}\right)}^2}}$$

(4)

2.6. Artificial Neural Networks (ANNs)

ANNs, which receive information from the environment, store the information received, and use it when necessary, are systems that try to imitate the way the human brain processes and stores information and works by creating connections between mathematical processing units called neurons [22,23]. ANNs, which can process continuous, nominal, sequential, and binary data, are also preferred because they have noisy data tolerance (robust), can classify patterns for which they have not been trained, and can be used even when there is little information about the relationships between attributes and classes [24]. Artificial neural networks acquire knowledge by adjusting the connection weights between their neurons, and this training was performed using the backpropagation algorithm [25,26].

2.7. Support Vector Regression (SVR)

SVR is a computational learning method based on statistical learning theory. Classical learning approaches such as neural networks are designed to minimize errors in the training data set, and this is called empirical risk minimization. SVR is based on the structural risk minimization principle, which provides better generalization ability [27]. Support Vector Regression is divided into two parts: linear and non-linear. SVR, which was developed to solve non-linear regression problems, carries the training data in the input space to a higher dimensional space with the help of a non-linear function and applies linear regression in this space. In non-linear regression models, kernel functions are used to transform the input space into a higher-dimensional feature space [28]. Commonly used kernel functions are linear, sigmoid, rbf (radial basis function), and polynomial.

2.8. K-Nearest Neighbor (kNN)

The kNN method has been used effectively for many complex data classification and regression tasks [29]. kNN is a preferred machine learning model because it is easy to implement, robust, and provides strong analytical results regarding their performance [30]. A distinguishing aspect of kNN compared to other machine learning algorithms is its capacity to handle missing observations and noisy data [31]. It has some disadvantages such as slow work, problems in choosing the number k and distance criteria, and memory problems [32,33]. In regression problems, the kNN algorithm calculates the output value of a test point as the interpolated value of the test point’s nearest neighbors. kNN regressors have the ability to predict an output value by taking a weighted average of data points with similar input characteristics. The number of neighbors to interpolate, k, is determined by the user [34]. The success of kNN depends on calculating distance values and determining the nearest neighbors (k) for a given data point. Euclid, Manhattan, and Minkowski distance measurement functions are generally used to calculate distance values [35].

The Python 3.13.5 programming language was used to establish machine learning (ML) models, in the analysis, to create graphics, and to make descriptive statistics. Grid search was used to find the optimal hyperparameter values for each model in the machine learning approaches used. The parameter settings in the ANN model were as follows: ANN type: feed-forward, hidden_layer_sizes: (128, 256, 128), activation: relu, solver: adam, alpha: 0.0001, learning_rate: adaptive, learning_rate_init: 0.001, power_t: 0.5, max_iter: 3000; activation function: “relu”, solver: “adam”, and maximum number of iterations: 2000. The parameter settings in the kNN model were as follows: n_neighbors: 3, weights: uniform, algorithm: ball_tree, leaf_size: 50, p: 2. The parameter settings in the SVR model were as follows: kernel: poly, degree: 2, gamma: scale, coef0: 0.05, tol: 0.001, C: 5.0, epsilon: 0.005.

3. Results and Discussion

The statistical results obtained as a result of the quality analyses performed on the tomatoes used in the experiments are shown in

Table 1. Descriptive statistics of the variables.

Variables	Mean	Std. Dev.	Min	Max	Var	Kurtosis	Variables	Mean	Std. Dev.	Min	Max	Var	Kurtosis
Brix	4.32	0.76	2.90	6.82	0.57	1.21	Lycopene	51.32	15.72	20.08	105.23	246.10	2.12
TKM	5.72	0.84	4.14	9.15	0.70	3.79	Vitamin C	20.45	3.69	12.98	29.54	13.58	−0.68
Ash	0.50	0.09	0.30	0.75	0.00	−0.24	Manganese	1.13	0.22	0.69	1.76	0.05	−0.32
pH	4.25	0.10	4.03	4.46	0.01	−0.49	Sodium	32.35	4.95	22.68	42.85	24.47	−0.90
Acidity	0.38	0.06	0.27	0.54	0.00	−0.32	Calcium *	360.62	87.62	206.56	583.91	7641.61	−0.57
Hardness	1.07	0.26	0.55	1.70	0.06	−0.67	Potassium *	2305.29	365.29	1305.35	2936.53	132832.67	−0.35
Fructose	1.24	0.29	0.51	2.18	0.09	0.51	Magnesium *	115.41	23.58	78.32	171.63	553.16	−0.41
Glycose	1.10	0.31	0.48	2.05	0.09	0.07	Phosphorus *	169.65	38.16	99.39	325.63	1450.32	3.67

Number of observations: 294, * target variables.

. All variables used in the study take continuous values.

The mean concentration of calcium is 360.62 mg/100 g, with a moderate standard deviation (87.62), indicating moderate variability. The negative kurtosis (−0.57) suggests a platykurtic distribution—flatter than normal—with fewer outliers and a relatively uniform spread. Potassium exhibits the highest mean (2305.29 mg/100 g) and variance (132,832.67), reflecting substantial variation across samples. A kurtosis of −0.35 indicates a slightly platykurtic, well-distributed data set without extreme tails. Magnesium displays a stable distribution with a mean of 115.41 mg/100 g and low variability (SD = 23.58). Kurtosis (−0.41) implies a near-normal, symmetric distribution. The most notable feature for phosphorous is its high kurtosis (3.67), indicating a leptokurtic distribution—data is heavily concentrated around the mean with relatively thin tails. This suggests that P levels are generally consistent.

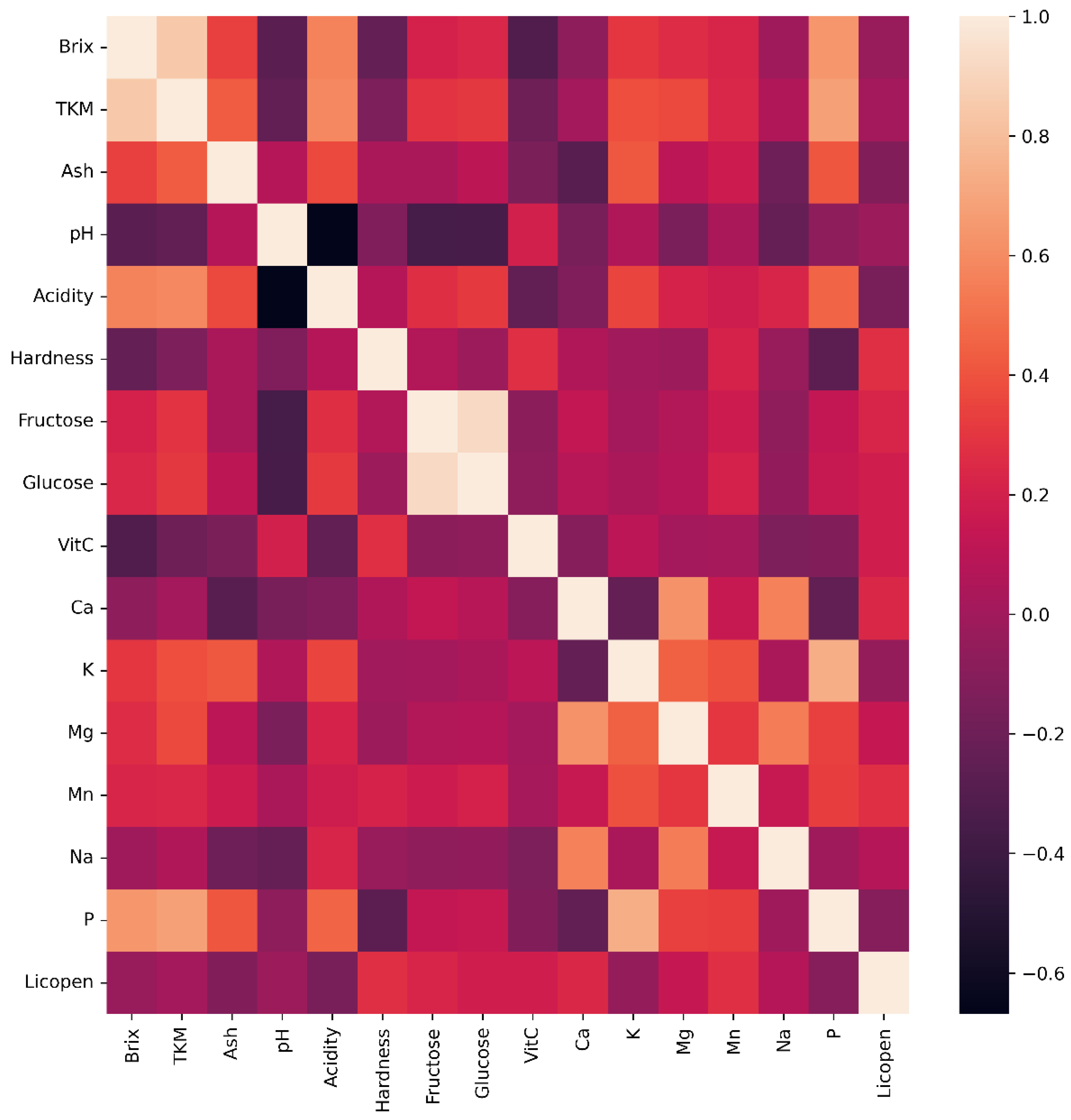
The heat map (Figure 3) shows the correlations of the variables used. Feature selection means eliminating unnecessary or ineffective independent variables when predicting the target variable. Using forward and backward feature selection methods, unnecessary variables were not included in the analysis. As a result of both feature selection methods, the color-related variables L (lightness coordinate in CIE Lab* color space), a (green-red color component), b (blue-yellow color component), c (chroma saturation), and h (hue angle) and vitamin C were not included in the model.

In this study, which focused on estimating the nutritional content of tomatoes, all samples were obtained under consistent growing conditions to minimize the influence of external environmental factors such as temperature and humidity. This controlled approach allowed for a more accurate assessment of the ability of machine learning models to predict mineral content based solely on the internal properties of tomatoes. Three different machine learning methods were used in this context: artificial neural networks, Support Vector Regression, and k-nearest neighbor. The performance of the models was analyzed using evaluation metrics results and is presented in

Table 2. Table of significance between models.

Nutrient Elements	Comparison Models	Paired t-Test	Wilcoxon’s Signed-Rank Test	Significant
Potassium	kNN vs. SVR	0.0012	0.0021	+
	kNN vs. ANN	0.0038	0.0064	+
	SVR vs. ANN	0.0780	0.0890	−
	kNN vs. PLS	0.0012	0.0034	+
Phosphorus	kNN vs. SVR	0.0007	0.0013	+
	kNN vs. ANN	0.0005	0.0010	+
	SVR vs. ANN	0.6820	0.7120	−
	kNN vs. PLS	0.0005	0.0010	+
Magnesium	kNN vs. SVR	0.0089	0.0123	+
	kNN vs. ANN	0.0214	0.0321	+
	SVR vs. ANN	0.3870	0.4120	−
	kNN vs. PLS	0.0021	0.0039	+
Calcium	kNN vs. SVR	0.0016	0.0034	+
	kNN vs. ANN	0.0102	0.0187	+
	SVR vs. ANN	0.1020	0.1240	−
	kNN vs. PLS	0.0008	0.0016	+

.

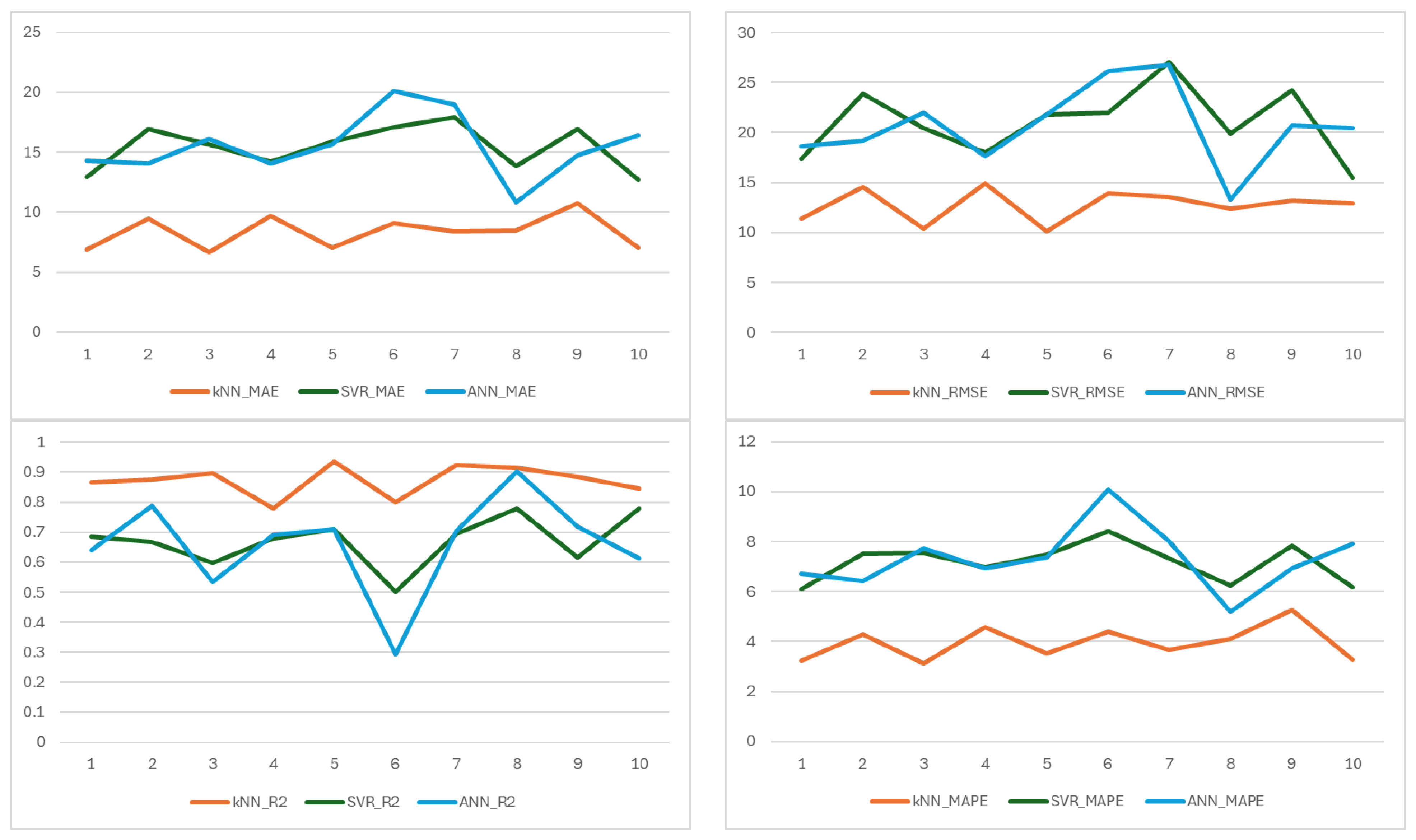
On a fold basis, the metric results of each ML model established to estimate the amount of potassium element are shown in Figure 4. kNN consistently achieved the highest R² values across all 10 folds. This consistency highlights kNN’s strong generalization ability and its effectiveness in capturing non-linear relationships in the data. The SVR model performed poorly in several folds (e.g., folds 6, 9, and 10), suggesting inadequate model fit and a tendency toward underfitting. ANN demonstrated high R² in fold 4, which suggests that the data in this partition may follow a predominantly linear pattern, which ANN can effectively model. However, the lower values in other folds reveal its limitation in capturing non-linear interactions, a common constraint of linear models.

kNN achieved the lowest RMSE values in 8 out of 10 folds. The low RMSE in folds 5, 8, and 10 reflects high predictive accuracy in those subsets. SVR recorded the highest RMSE values across most folds. The exceptionally high error in fold 6 (RMSE = 312.48) suggests a significant prediction failure, possibly due to poor handling of outliers or non-linear patterns. ANN showed intermediate performance. While ANN outperformed kNN in fold 4, it generally exhibited higher errors in other folds, indicating inconsistent performance.

MAE provides a robust measure of average prediction error, and it is less sensitive to extreme values than RMSE. kNN again demonstrated superior performance. The consistently low MAE across folds underscores kNN’s ability to minimize average prediction deviation. SVR had the highest MAE in all folds except fold 2. This indicates that SVR’s predictions deviate substantially from actual values on average. ANN performed better than SVR but worse than kNN.

MAPE expresses prediction error as a percentage of actual values, enabling scale-independent comparison. kNN achieved the lowest MAPE values in all folds. SVR exhibited the highest MAPE. Values exceeding 10% in fold 6 suggest unacceptably high relative errors in certain data partitions. ANN showed best performance in fold 4 (4.63%). While acceptable, it consistently underperformed compared to kNN.

The metric results of each ML model established to estimate the amount of phosphorus element are shown in Figure 5 on a fold basis. The kNN model demonstrates the most consistent and lowest MAE values across 10 folds. In contrast, the SVR model exhibits higher errors, yielding an average MAE of around 15.30. The ANN model shows intermediate performance. Notably, ANN’s performance deteriorates significantly in fold 6, indicating potential instability or sensitivity to data partitioning.

The kNN model again demonstrates the most favorable performance. SVR shows higher RMSE values, fluctuating between 15.50 (fold 10) and 27.07 (fold 7), with a mean RMSE of about 20.69. The ANN model exhibits the highest variability. The notably high RMSE values for both SVR and ANN in folds 6 and 7 suggest that these models struggle with certain data subsets, possibly due to overfitting, inadequate generalization, or sensitivity to outlier instances within those folds.

The kNN model achieves the lowest MAPE values with a mean MAPE of approximately 4.04%. This indicates that, on average, kNN’s predictions deviate from actual values by less than 5%, reflecting high relative accuracy. In contrast, the ANN and SVR models show even greater variability. The exceptionally high MAPE in fold 6 for ANN (over 10%) highlights a significant failure in relative prediction accuracy in that partition, further underscoring its instability.

The kNN model consistently achieves high R² values. This indicates that kNN explains a substantial portion of the target variance across all folds. SVR performs moderately, with a mean of approximately 0.681. The ANN model displays the widest variation in R². The extremely low R² in fold 6 suggests a near-complete failure of ANN to capture the underlying data structure in that fold, likely due to poor convergence, overfitting, or suboptimal hyperparameter settings.

The metric results of each ML model established to estimate the amount of magnesium element are shown in Figure 6 on a fold basis. Analysis of MAPE values reveals that the kNN model achieved the lowest average MAPE of 4.77% across all folds, outperforming both SVR (6.05%) and ANN (5.48%). kNN demonstrated highly accurate percentage-wise predictions and consistent performance across folds. In contrast, the SVR model exhibited notably high MAPE values in certain folds—such as 7.91% in fold 9—suggesting poor generalization and instability in prediction accuracy under specific data splits.

With respect to RMSE, the kNN model demonstrated the best average performance, achieving particularly low RMSE values in folds 4 and 5. The SVR model showed high RMSE values, especially in fold 9 (14.26), indicating the presence of significant prediction errors and inconsistent model behavior. Although the ANN model performed comparably to kNN in some folds, it exhibited higher variability, with elevated RMSE values in folds 3 and 9 (11.98 and 12.76), reflecting less stable predictive accuracy.

In terms of R², the kNN model achieved the highest average coefficient of determination (0.838), surpassing SVR (0.770) and ANN (0.802). kNN consistently explained a high proportion of variance, with R² values exceeding 0.85 in folds 1, 4, 5, and 7. The SVR model, on the other hand, showed a notably lower average R², indicating limited explanatory power. While the ANN model performed moderately, it generally underperformed compared to kNN across most folds, except in fold 5, where it achieved the highest R² (0.920).

Overall, among the three models evaluated, kNN consistently demonstrated superior performance across all evaluation metrics—MAPE, RMSE, and R²—indicating robustness, accuracy, and reliability. SVR exhibited the weakest average performance with high variance across folds, while ANN showed moderate but less stable results.

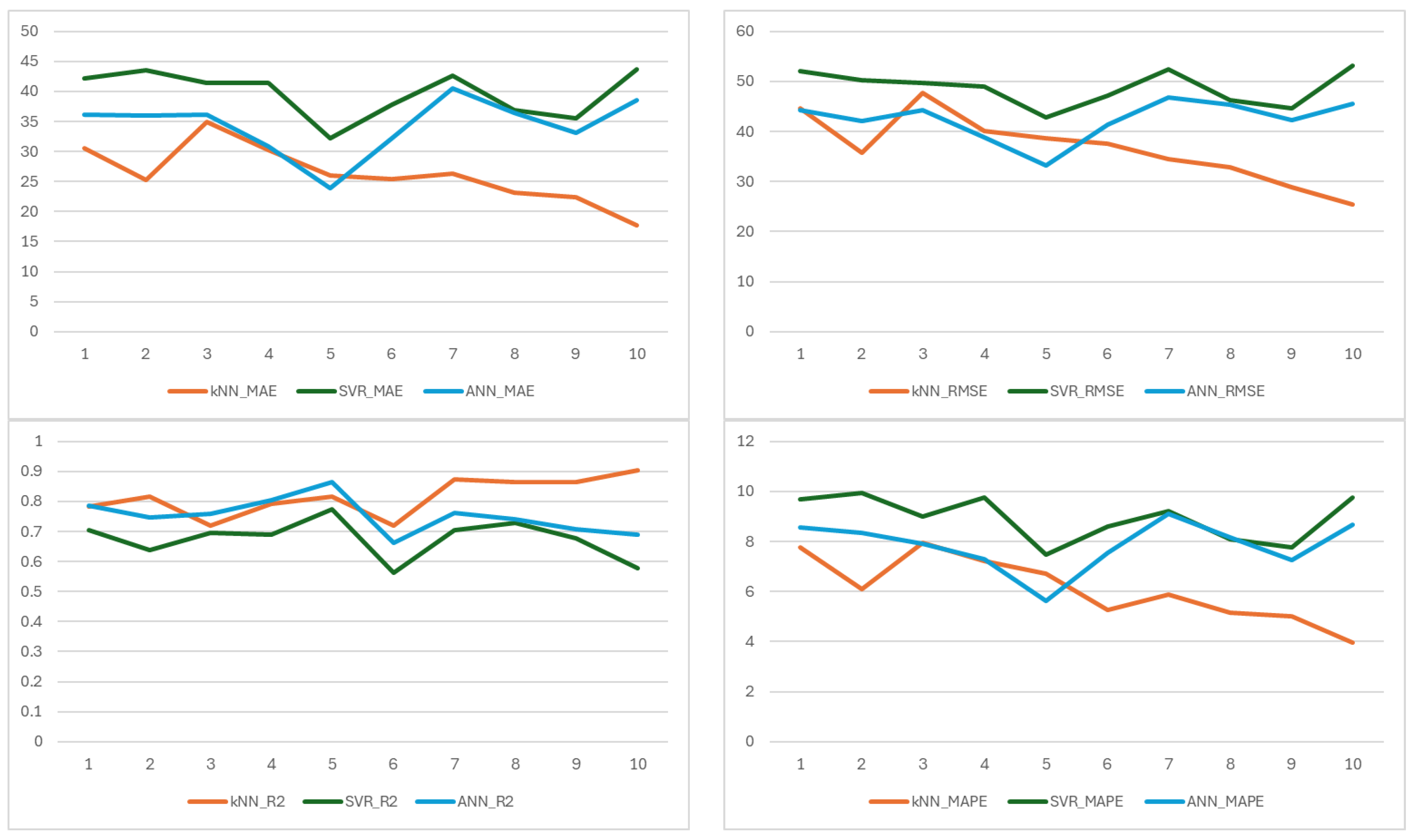
The metric results of each ML model established to estimate the amount of calcium element are shown in Figure 7 on a fold basis. In terms of MAE, the kNN model consistently achieved the lowest error values across all folds. The ANN model achieved a relatively low MAE of 23.87 in fold 5 but generally performed worse than kNN and comparably to or slightly better than SVR in other folds.

Regarding MAPE, kNN achieved an average value of 6.20%, significantly outperforming SVR (8.83%) and ANN (7.54%). In contrast, SVR exhibited consistently high MAPE values. ANN showed moderate performance in MAPE, surpassing SVR but remaining less accurate than kNN.

For RMSE, the average values were 36.51 for kNN, 47.84 for SVR, and 42.05 for ANN. kNN achieved a notably low RMSE in folds 9 and 10 (28.89 and 25.41), demonstrating robustness in minimizing large errors. SVR, however, showed a high RMSE across all folds, indicating instability and sensitivity to outliers. Although ANN achieved the lowest RMSE (33.19) in fold 5, it generally underperformed compared to kNN in the remaining folds.

The R² results revealed that kNN explained an average of 81.8% of the variance in the target variable, significantly higher than SVR (68.7%) and ANN (75.7%). kNN achieved R² values above 0.75 in 8 out of 10 folds, indicating strong and consistent explanatory power. SVR, by contrast, remained below 0.60 in folds 6, 9, and 10 and only exceeded 0.70 in two folds, reflecting poor generalization. ANN achieved the highest R² (0.865) in fold 5 but exhibited higher variability and lower overall consistency compared to kNN.

Paired t-tests and Wilcoxon’s signed-rank tests were performed using MAPE values in 10 folds for each nutrient element. These tests were used to evaluate whether the differences in performance between models were statistically significant. The results are presented in Table 2. The ML models were compared with each other. However, since the best model among the ML models was the one created with kNN, the model created with PLS was only compared with the model created with kNN.

Potassium: kNN achieved a lower MAPE than SVR in 9 out of 10 folds, and it was lower than ANN in 8 out of 10 folds. The mean MAPE difference is 3.18 percentage points (kNN vs. SVR) and 1.65 points (kNN vs. ANN). Both parametric (t-test) and non-parametric (Wilcoxon') tests confirm that kNN significantly outperforms both SVR and ANN in predicting potassium. Phosphorus: kNN achieved a lower MAPE than both SVR and ANN in all 10 folds. The average MAPE reduction is 3.21 points (vs. SVR) and 3.38 points (vs. ANN), which is highly significant in practical terms. Both statistical tests strongly support the superiority of kNN. Magnesium: kNN achieved a lower MAPE than SVR in 9 out of 10 folds, and it was lower than ANN in 8 out of 10 folds. Calcium: The MAPE advantage is consistent and statistically significant. kNN outperformed SVR in 9 out of 10 folds, and ANN in 8 out of 10 folds. The average MAPE difference is 2.83 points (vs. SVR) and 1.74 points (vs. ANN), both statistically significant.

Finally, the kNN model consistently outperforms both ANN and SVR across all four nutrients. The performance advantage of kNN is statistically significant (p < 0.05) in all pairwise comparisons against ANN and SVR. The most dramatic improvement is observed for phosphorus (P), where kNN reduces MAPE from ~7.2% to 3.95%, nearly halving the prediction error. No significant difference was found between SVR and ANN for any nutrient.

Table 3. Metric mean results of ANN, SVR and kNN models.

Nutrient Elements	Method	Evaluation Criteria
		R2	RMSE	MAE	MAPE
Ca	ANN	0.7521	42.41	34.37	7.84
	SVR	0.6749	48.72	39.72	8.93
	kNN	0.8150	36.59	26.17	6.10
	PLS	0.7980	38.21	29.54	6.78
K	ANN	0.6929	195.11	156.38	6.13
	SVR	0.5573	238.23	186.28	7.66
	kNN	0.7818	164.53	113.13	4.48
	PLS Regression	0.7760	197.80	149.2	5.81
Mg	ANN	0.8142	9.73	7.76	5.58
	SVR	0.7781	10.63	8.18	5.84
	kNN	0.8349	9.19	6.43	4.76
	PLS Regression	0.8280	9.41	6.88	5.02
P	ANN	0.6596	20.66	15.53	7.33
	SVR	0.6709	21.04	15.40	7.16
	kNN	0.8723	12.75	8.35	3.95
	PLS Regression	0.8610	13.21	9.44	4.32

Ca: calcium, K: potassium, Mg: magnesium, P: phosphorus.

summarizes the performance of the three machine learning algorithms (ANN, SVR, and kNN) and traditional statistical methods (Partial Least Squares Regression (PLS)) for predicting each nutrient element using R², RMSE, MAE, and MAPE metrics.

Machine Learning Models Results

Calcium: The best performance was achieved by kNN (R² = 0.8150, RMSE = 36.59, MAE = 26.17, MAPE = 6.10%), followed by ANN (R² = 0.7521) and SVR (R² = 0.6749). The R² value of 0.815 indicates that kNN explains over 81% of the variance in Ca content. A low MAPE (6.10%) confirms high predictive accuracy. Ca has a relatively normal, platykurtic distribution. kNN benefits from local similarity in feature space, making it effective when data points cluster naturally. Although SVR is powerful, especially for non-linear structures, kernel selection or hyperparameter tuning may be insufficient here. Similarly, ANN may not have fully utilized its potential due to hyperparameter tuning errors.

Potassium: Similarly, kNN is again the best model (R² = 0.7818, RMSE = 164.53, MAE = 113.13, MAPE = 4.48%), outperforming ANN (R² = 0.6929) and SVR (R² = 0.5573). MAPE indicates very good prediction accuracy at 4.48%. ANN is in second place. SVR, on the other hand, is quite weak. Potassium’s broad distribution (variance: 132,832.67) and high mean may have amplified the difficulty for SVR and may create generalization difficulties in margin-based models such as SVR. kNN may have made more accurate predictions by properly evaluating the neighborhood of high-value examples. Although ANN’s RMSE is high, its low MAPE indicates that while the absolute error is high for large values, the proportional error is low.

Magnesium: For Mg, all models performed relatively well, reflecting the variable’s narrow distribution and lower variance (553.16). kNN again achieved the best performance (R² = 0.8349, RMSE = 9.19, MAE = 6.43, MAPE = 4.76%), slightly outperforming ANN (R² = 0.8142) and SVR (R² = 0.7781). Stable target variables such as Mg are easier to predict, and kNN excels particularly in cases of low error tolerance.

Phosphorus: For P, kNN also provided the best results (R² = 0.8723, RMSE = 12.75, MAE = 8.35, MAPE = 3.95%), while ANN and SVR showed lower but comparable performance (R² = 0.6596 and R² = 0.6709, respectively). kNN dramatically outperforms ANN and SVR. R² = 0.8723 is exceptional, explaining nearly 87% of P’s variability. MAPE of 3.95% indicates very high practical accuracy. P’s leptokurtic distribution (kurtosis = 3.67) means that values are tightly clustered around the mean. kNN excels in such dense regions by leveraging proximity. ANN underperformed, possibly due to limited model complexity or insufficient hyperparameter optimization.

Overall, kNN consistently outperformed both ANN and SVR across all nutrient elements. This indicates that the relationships between explanatory variables and nutrient elements may be highly local and non-linear, conditions under which kNN performs well. ANN generally ranked second, where it performed moderately well, particularly on Mg and K, suggesting its potential for capturing non-linear interactions, albeit with a limited data size. SVR exhibited the weakest performance, likely due to suboptimal kernel and parameter selection, especially for high-variance targets such as Ca and K.

Traditional Statistical Model Results

Calcium: The PLS model performs strongly (R² = 0.798, MAPE = 6.78%), outperforming ANN and SVR, which confirms its status as a robust baseline for spectral data. However, the kNN model still achieves statistically significant improvements over PLS in all metrics (p < 0.05 via paired t-test on MAPE). This demonstrates that kNN effectively captures both linear and non-linear relationships in the data.

Potassium: PLS performs very strongly, achieving R² = 0.776 and MAPE = 5.81%, outperforming ANN and SVR. However, kNN still achieves better performance in all metrics, especially in MAPE (4.48% vs. 5.81%). According to the paired t-test results, kNN vs. PLS (p = 0.0043) on per-fold MAPE is statistically significant.

Magnesium: PLS is the best traditional model (R² = 0.828), slightly better than ANN and SVR. kNN marginally outperforms PLS in all metrics. According to the paired t-test results, kNN vs. PLS (MAPE, p = 0.0021) is significant at α = 0.05.

Phosphorus: PLS is highly effective (R² = 0.861, MAPE = 4.32%), close to kNN, but kNN still outperforms PLS in all metrics. According to the paired t-test results, kNN vs. PLS (MAPE, p = 0.0005) is significant.

kNN consistently outperforms PLS in all metrics. The performance advantage of kNN is statistically significant (p < 0.05) in all cases. SVR performs poorly compared to PLS and kNN.

Abdipour et al. [36] made predictions with a value of R² = 0.861, RMSE = 0.563, and MAE = 0.432 with the ANN model. In another study, Guo et al. [37] made predictions with a value of R² = 0.871 and RMSE = 1.474 with the Support Vector Machine model. Huang et al. [5] made predictions with a value of R² = 0.856, RMSE = 0.1020, and MAE = 0.0793 with the ANN model. Lan et al. [38] made predictions with a value of R² = 0.974 and RMSE = 0.258 with the ANN model. Torkashvand et al. [39] made predictions with a value of R² = 0.850 and RMSE = 0.539 with the ANN model. In this study, the best R² = 0.8150, RMSE = 36.59, MAE = 26.17, and MAPE = 6.10% for calcium was obtained using the model established with the kNN method. The best R² = 0.7818, RMSE = 164.53, MAE = 113.13, and MAPE = 4.48% for potassium was obtained using the model established with the kNN method. The best R² = 0.8349, RMSE = 9.19, MAE = 6.43, and MAPE = 4.76% for magnesium was obtained using the model established with the kNN method. The best R² = 0.8723, RMSE = 12.75, MAE = 8.35, and MAPE = 3.95% for phosphorous was obtained using the model established with the kNN method.

Many ML methods are used to solve problems in the field of agriculture [40,41,42]. In this study, three methods with different working principles, namely SVR, ANN, and kNN, were preferred, predictions were made, and comparisons were made between the results. The kNN method was more successful than all the models established. Kumar et al. (2024) highlighted the success of the kNN algorithm in creating recommendation systems for precision agriculture [43].

While the study focuses on the application of machine learning techniques, especially kNN, ANN, and SVR, comparing these approaches with traditional chemical analysis methods is very useful in terms of the importance of the research. Traditional methods for nutrient analysis, such as inductively coupled plasma (ICP) and atomic absorption spectroscopy (AAS), are quite accurate but suffer from significant disadvantages, including high costs, time consumption, and the need for sample destruction [44]. In contrast, machine-learning-based approaches, as shown in this study, offer a faster and scalable solution for nutrient prediction [37]. Several recent studies have explored the integration of machine learning with spectroscopic methods such as near-infrared (NIR) and hyperspectral imaging for nutrient prediction and have demonstrated their potential to offer comparable or superior accuracy while being significantly more efficient [45,46]. Furthermore, our study highlights the advantages of machine learning models in addressing the limitations of simpler statistical approaches. For example, compared to linear regression, machine learning models such as ANN and kNN are better equipped to process complex, high-dimensional data sets and can decipher non-linear relationships between features that traditional methods might miss [47,48]. This flexibility and robustness make machine learning an increasingly popular choice for agricultural data analysis, as it allows for the inclusion of various variables without making strong assumptions about the data structure.

According to the results of the models established for the prediction of nutrient elements, the training and test phase values are extremely close to each other. In this case, it can be said that there is no overlearning problem during the training phase. It can also be considered as an indication that the established models can make consistent predictions for nutrient elements in tomatoes. The ability to predict nutrient levels in tomatoes in a non-destructive way using machine learning has important practical implications, especially in precision agriculture. These models can be integrated into automated systems for real-time nutrient analysis and provide agricultural enterprises with accurate and immediate data to optimize fertilization applications, increase crop yield, and improve quality control [39,49]. In addition, the models can be adapted to evaluate various other crops, facilitating their use in large-scale agricultural and greenhouse operations, which are increasingly adopting digital agricultural tools for monitoring and decision-making [37,47]. In addition, such models can support sustainability goals by reducing resource wastage and minimizing the need for chemical testing, which is both costly and time-consuming [46,50].

Compared to conventional analytical methods widely used for mineral content determination, such as atomic absorption spectroscopy (AAS) and inductively coupled plasma–optical emission spectroscopy (ICP-OES) [51], the machine-learning-based approach proposed in this study offers several practical advantages. While conventional methods provide highly accurate and reliable quantitative results, they require complex sample preparation processes and are time-consuming, destructive, and costly. In contrast, the integration of machine learning with non-destructive measurements (e.g., vis–NIR spectroscopy or image-based features) provides rapid and relatively low-cost predictions suitable for in situ or real-time applications. Several previous studies have successfully applied regression models or artificial neural networks to predict chemical or physical properties in tomatoes; however, limited attention has been paid to the prediction of specific mineral elements. The current study addresses this gap by focusing on the prediction of essential minerals such as potassium, calcium, and magnesium and demonstrates that the proposed models can achieve promising predictive performance with minimal preprocessing. This approach may be particularly useful for large-scale agricultural monitoring and decision-making processes where efficiency and non-destructiveness are critical [48]. Therefore, the practical applications of this research are very important not only to improve agricultural practices but also to advance the transition to more efficient and environmentally friendly agricultural practices.

4. Conclusions

This study presents a comprehensive evaluation of three machine learning models (artificial neural networks, Support Vector Regression, and k-nearest neighbors, as well as Partial Least Squares Regression) for the prediction of key nutrient elements (calcium, potassium, magnesium, and phosphorus) in beef tomato samples using physicochemical properties. The results demonstrate that kNN consistently outperforms ANN, SVR, and PLS across all target nutrients, achieving the highest coefficient of determination (R²) and the lowest error metrics (RMSE, MAE, and MAPE). Notably, kNN achieved an exceptional R² of 0.8723 and a remarkably low MAPE of 3.95% in predicting phosphorus, a nutrient characterized by a leptokurtic distribution with high central density.

The superior performance of kNN can be attributed to its non-parametric, instance-based learning mechanism, which effectively captures local patterns in densely clustered data. This is particularly advantageous for variables like phosphorus and calcium, where observations are concentrated around the mean with moderate dispersion. ANN generally ranked second, while SVR exhibited the weakest performance. The primary reasons for these differences include the high variance observed in certain target variables (especially calcium and potassium), the relatively limited sample size, and the absence of extensive hyperparameter optimization.

These findings emphasize that the choice of machine learning model depends not only on the power of the algorithm but also on the statistical properties of the data set. In particular, for leptokurtic (peaked) distributions and high-local-density or moderately variable data sets, it can be concluded that non-parametric and sample-based models (e.g., kNN) may be more effective. However, the underperformance of SVR and ANN also highlights the necessity of rigorous preprocessing (e.g., standardization, outlier handling) and hyperparameter tuning to unlock their full potential.

These findings have significant implications for agricultural science and practice, as they provide a reliable tool for the rapid and non-destructive assessment of nutrient content in tomatoes. The success of these models, particularly the kNN approach, presents a promising framework for developing practical applications in assessing and managing crop quality. Future research could be centered on the adaptation of these models to other crops and the inclusion of more environmental and physiological parameters in order to attain an even greater level of accuracy in prediction. These results also testify to the potential of machine learning techniques in the agricultural context; hence, they are very useful for growers and agricultural scientists interested in improving nutrient management practices. Once implemented, these predictive models will assist stakeholders in making informed decisions that can enhance both the quality and yield of crops.

The developed machine learning models are designed for seamless integration into existing digital agriculture platforms via standardized APIs and cloud-based processing and feature computational efficiency optimized for real-time field applications using lightweight algorithms that can run on standard mobile devices and portable spectroscopic equipment. Future work will focus on developing a comprehensive application framework that includes user-friendly interfaces, automated data pipeline management, and field-tested deployment protocols to ensure practical applicability in a variety of agricultural environments.

The study has some limitations. The data used was obtained from beef-type tomatoes, and several important factors were not included in the analysis, such as the season in which the tomatoes were harvested, the duration of sunlight exposure, and the growing environment (greenhouse or field). These factors—temperature, seasonal variations, and fertilizer usage—may significantly impact the data collected on tomatoes. To enhance the predictive power of the study, it is advisable to incorporate additional features, such as soil type, irrigation techniques, and the timing of harvesting. This information could provide valuable insights into the factors influencing the concentration of components in tomatoes. Therefore, it is suggested that future research should test a model using tomato data from various regions or climatic zones. Future research should explore ensemble methods (e.g., stacking kNN with tree-based models), deep learning architectures, and external validation on diverse cultivars and growing conditions to enhance generalizability. Furthermore, integrating spectral or imaging data could improve the accuracy of non-destructive nutrient prediction. This study provides a valuable framework for selecting and optimizing machine learning models in food science and nutrition research, emphasizing that model efficacy is not solely algorithm-dependent but deeply intertwined with the statistical nature of the data. This approach could contribute to increasing the overall robustness of the model. The findings obtained from the studies can be combined with IoT-based systems to perform different precision agriculture applications.