Mechanical Properties of Korla Fragrant Pear Fruiting Branches and Pedicels: Implications for Non-Destructive Harvesting

Abstract

The Korla fragrant pear is a highly valued economic fruit in China’s Xinjiang region. However, biomechanical data on the fruit-bearing branches and pedicels of this species remain incomplete, which to some extent hinders the advancement of harvesting equipment and techniques. Therefore, refining these data is of great significance for the development of efficient and non-destructive harvesting strategies. This study aims to elucidate the mechanical properties of the fruiting branches and peduncles of Korla fragrant pears, thereby establishing a theoretical foundation for the future development of intelligent harvesting technology for this variety. The research utilized axial and radial compression tests, along with three-point bending test methods, to quantitatively analyze the elastic modulus and shear modulus of the branches and peduncles. The test results reveal that the elastic modulus of the fruiting branches under axial compression is 263.51 ± 76.51 MPa, while under radial compression, it measures 135.53 ± 73.73 MPa (where ± represents the standard deviation). In comparison, the elastic modulus of the peduncles is recorded at 152.96 ± 119.95 MPa. Additionally, the three-point bending test yielded a shear modulus of 75.48 ± 32.84 MPa for the branches and 30.23 ± 8.50 MPa for the peduncles. Using finite element static structural analysis, the simulation results aligned closely with the experimental data, falling within an acceptable error range, thus validating the reliability of the testing methods and outcomes. The mechanical parameters obtained in this study are critical for modeling the stress and deformation behaviors of pear-bearing structures during mechanical harvesting. These findings provide valuable theoretical support for the optimization of harvesting device design and operational strategies, with the aim of reducing fruit damage and improving harvesting efficiency in pear orchards.

1. Introduction

Korla fragrant pear, a regional specialty fruit from Xinjiang, China, is renowned for its sweet taste, rich nutritional profile, and excellent storage longevity. Over the years, it has gained widespread recognition both domestically and internationally, consistently ranking as the most valuable brand among pear varieties, with an annual production value exceeding 10 billion Chinese yuan [1]. Despite its economic significance, the harvesting of Korla fragrant pears remains manual, which impedes the industry’s progress towards full industrialization [2]. The development of intelligent harvesting technology is a critical future direction, with the mechanical properties of fruit-bearing branches and pedicels playing a pivotal role in the growth and fruit quality [3]. Consequently, research into the mechanical properties of Korla fragrant pear branches and pedicels is of great significance [2,4]. Understanding the distinct mechanical attributes of the branches and pedicels, and revealing their response mechanisms under external forces, is crucial for optimizing fruit load control during harvesting operations. This knowledge provides essential theoretical support for the advancement of intelligent harvesting technologies. Branches and peduncles are crucial structures that support fruit, and their mechanical properties directly influence the stability of fruit throughout its growth cycle [5]. Particularly after the fruit is suspended, the peduncles and branches must withstand forces arising from the weight of the fruit as well as external environmental factors such as wind and precipitation. These mechanical stresses can lead to bending or breaking of the branches, thereby impacting fruit harvest [6]. Therefore, comprehensive research on the mechanical properties of branches and peduncles is essential for understanding the structural stability of fruits after they are hung and for providing a foundation for subsequent picking technologies.

In recent years, researchers have investigated the mechanical properties of branches and peduncles across various crops. Kang, F. et al. investigated the shear mechanical characteristics of apple branches to provide data support for the research and development of apple pruning equipment [7]. Gao, J. et al. examined the 3D reconstruction technology of pitaya fruit and branches [8]. Wu, W. analyzed the vibration response characteristics and separation deformation patterns of the apple fruit–branch system, offering insights for the efficient harvesting of vibrating fruit harvesting machinery [9]. Zhang, H. explored the mechanical characteristics of sawing apple branches and investigated the shear force variations in apple branches [10]. Liang, Z. et al. studied the mechanical properties of poplar branches, contributing data support for the optimization design of crushing machinery and related simulation experiments [11]. Nenning, T. et al. conducted quasi-static tests on hardwood branches, including beech, oak, and poplar, to evaluate their density, tensile strength, compressive bending strength, and elastic properties [12]. Namari, S. et al. researched the mechanical properties of wood under compression, stretching, and bending [13]. Li, N. et al. investigated the shear mechanical properties of jujube branches during the winter pruning period and developed and optimized machinery for pruning and crushing these branches [14]. These studies have provided a valuable foundation for the mechanical analysis of fruit branches in various crops. Meanwhile, finite element simulation has been widely employed to predict the mechanical behavior of plant materials under diverse loading conditions. It not only serves as an efficient and non-destructive alternative to traditional destructive testing but also facilitates the optimization of harvesting machinery design [15,16]. In the context of fruit harvesting, finite element analysis effectively reveals the stress distribution and deformation patterns of fruit branches and pedicels under bending and tensile loads, thereby providing essential data to support the development of low-damage harvesting equipment [17,18].

In summary, existing research has predominantly focused on crops such as apples, jujubes, and hardwood trees, while relatively limited attention has been paid to Korla fragrant pears. This fruit exhibits unique morphological and structural characteristics, including a thin and easily damaged skin and retained protruding pedicels. These features present specific biomechanical challenges during harvesting, which have not yet been systematically quantified or modeled. As a result, the current understanding of key biomechanical parameters remains insufficient, thus limiting the development and application of intelligent, non-destructive harvesting technologies for this economically important crop.

To address this, the current study systematically conducted mechanical property tests on the fruit-bearing branches and pedicels of Korla fragrant pears. Axial compression, radial compression, and three-point bending tests were performed to measure key mechanical parameters, including the elastic modulus and shear modulus. Finite element simulations were also employed to validate the experimental results. The data obtained in this study will provide important biomechanical evidence for the design of intelligent harvesting equipment and the optimization of operational strategies, thereby promoting the development and application of efficient, non-destructive harvesting technologies in Korla fragrant pear production.

The innovation of this study primarily lies in its pioneering and systematic characterization of the mechanical properties of Korla fragrant pear branches and pedicels under various loading conditions. This work integrates experimental mechanical testing with finite element simulation to validate and elucidate the underlying mechanical response mechanisms. In contrast to previous studies that have predominantly focused on common fruit trees such as apples and jujubes, the present research proposes an integrated experimental–simulation approach specifically tailored to the unique structural and biomechanical features of Korla fragrant pears. This not only introduces a novel research perspective but also provides a solid theoretical foundation for the development of intelligent, low-damage harvesting technologies for pear fruits.

2. Materials and Methods

2.1. Sample Collection, Phenological Stage, Experimental Design, and Testing Equipment

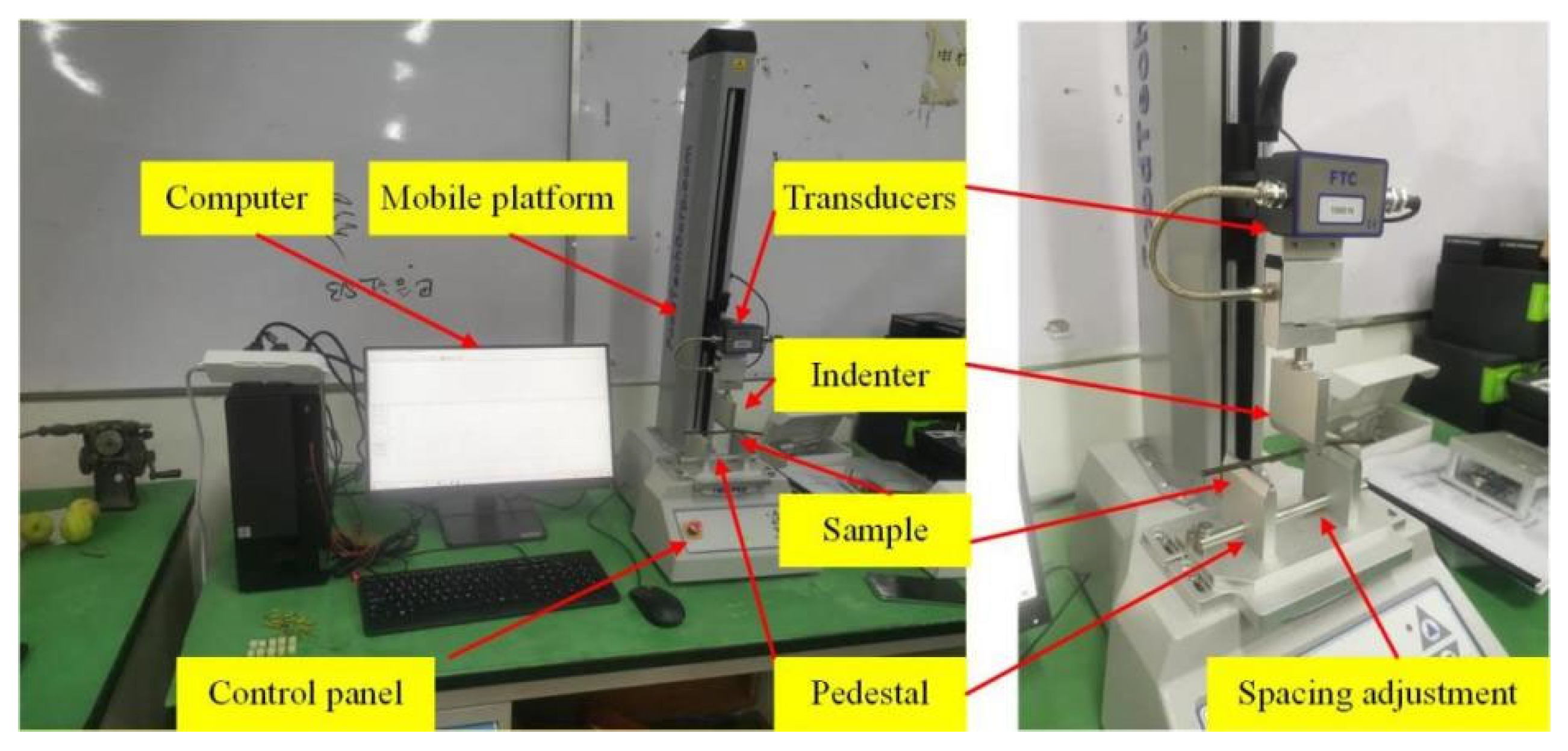
The plant materials used in this study included fruit-bearing branches and pedicels of Korla fragrant pear, collected from a standard demonstration orchard located in the 29th Regiment of Tiemenguan City, Xinjiang. The pear trees were six years old and managed under standardized cultivation practices. Sampling was conducted on 11 September 2024, when the fruits had reached commercial maturity, as determined by local harvesting criteria and schedules. To ensure representativeness and minimize positional bias, a random sampling method was employed, with samples collected from multiple pear trees and various canopy positions (east, west, north, south, upper and lower layers). For each mechanical test type—axial compression, radial compression, and three-point bending—12 fruit-bearing branches and 12 pedicels were collected. Each branch or pedicel was treated as an individual experimental unit, and each test was repeated 10 times to ensure statistical reliability. The branches were sectioned approximately 100 mm above the fruit attachment point, as this region is subjected to the highest mechanical loads during fruit-bearing and is therefore representative of the mechanical behavior relevant to harvesting operations. All mechanical tests were conducted within two days of sample collection to maintain the mechanical integrity of the plant tissues and minimize the effects of post-harvest physiological changes.

The experiments were carried out in the College of Mechanical and Electrical Engineering, Xinjiang Agricultural University. Axial and radial compression tests were performed using a Fengxing series microcomputer-controlled electronic universal testing machine (model WDW-50M, Jinan Yongduo Testing Machine Co., Ltd., Jinan, China), which has a class 1 accuracy rating. The system was equipped with a 2.0 GHz CPU, 1 GB of RAM and a 50 GB hard drive and operated using the Fengxing universal testing machine control software (version 1.2). Prior to testing, the universal testing machine was calibrated in accordance with the manufacturer’s guidelines to ensure measurement accuracy and reliability. This process involved verifying the force measurement system using standard calibration weights and adjusting the equipment to minimize potential errors. Three-point bending tests were conducted using an FTC-TMS-PRO texture analyzer (Beijing YingShengHengTai Technology Co., Ltd., Beijing, China). This instrument features a force measurement range of 0.01 to 1000 N and a force sensor accuracy of ±0.1% of full scale. Prior to the tests, the instrument was calibrated using known loads to ensure the accuracy of the measurements. The FTC-TMS-PRO supports multiple testing modes, including compression, tension, shear, and fracture, and provides comprehensive data analysis capabilities. For data analysis, all mechanical property data were presented as mean ± standard deviation. Statistical analysis was performed using Origin 2022 software.

2.2. Determination of Wet Base Moisture Content of Branches and Fruit Peduncles

The water content of branches and peduncles plays a crucial role in determining their mechanical properties [15,17]. Generally, an increase in moisture content leads to a reduction in stiffness and strength, making the material more susceptible to deformation under stress. Higher moisture content may result in a lower elastic and shear modulus, as water reduces the material’s resistance to deformation. In contrast, lower moisture content typically increases stiffness, but the material becomes more brittle and prone to breakage. Therefore, water content should be considered when analyzing the mechanical properties of branches and peduncles.

When preparing the test sample, we used gardening scissors to cut the branches into 50 mm segments of equal length, ensuring consistency across the samples. The samples were placed in sealed bags to maintain their freshness and minimize changes in mechanical properties prior to testing. 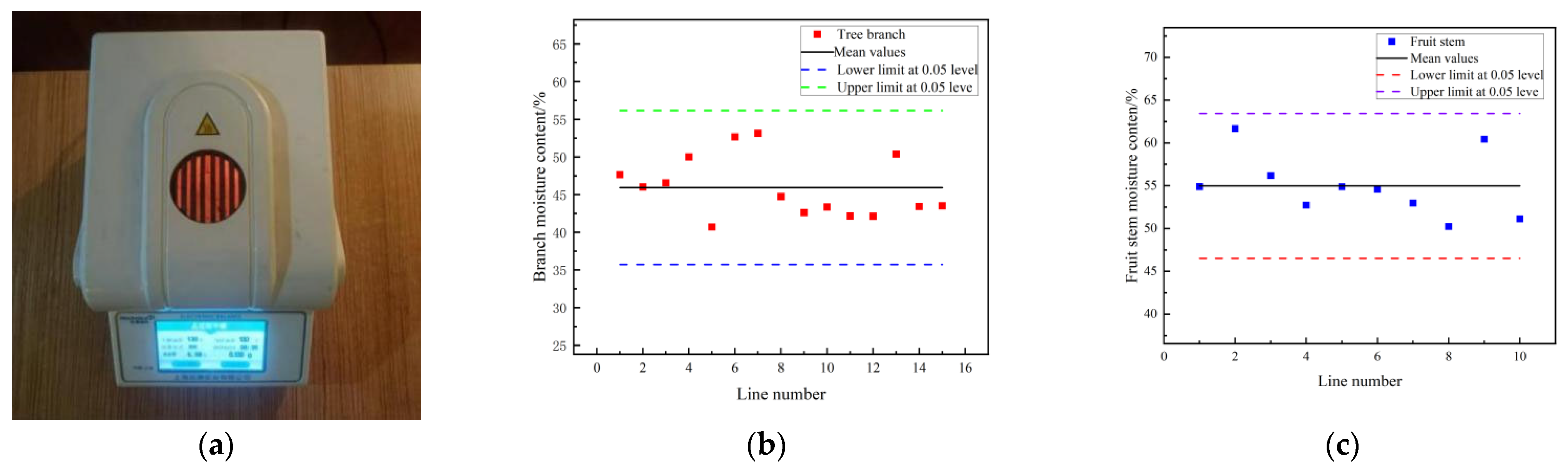The tests were conducted within 24 h of sample collection to ensure the stability of the mechanical properties of the branches [16]. The actual moisture content of each branch segment and stem was measured by using a flower tide rapid water meter. (The apparatus, manufactured by Shanghai Huachao Industrial Company, Shanghai, China, is designed to integrate both heating and drying functions with a weighing mechanism. It facilitates the direct determination of moisture content percentage by comparing the mass of the substance post-desiccation to its wet weight, automatically calculating the moisture value.) During the measurement process, the apparatus underwent precise calibration while controlling environmental conditions, including temperature and humidity, to ensure the consistency of the measurement results and to minimize interference from external factors. We recorded the moisture content data for each twig segment and fruit stalk. To enhance the representativeness of the data and reduce random error, each twig segment and fruit stalk was subjected to 10 replicate measurements, and the average value was taken as the final moisture content.

2.3. Compression Test of Branches and Peduncles

To investigate the mechanical properties of pear tree branches and fruit peduncles, this study conducts both axial and radial compression tests. The elastic modulus is a key physical parameter that characterizes the stiffness of materials and is essential for understanding the mechanical response of branches and fruit peduncles under external forces [15,19,20]. This research examines their mechanical properties by measuring the axial elastic modulus (E_bz) of the branches, the radial elastic modulus (E_br) of the branches, and the radial elastic modulus (E_sr) of the fruit peduncles. These measurements provide critical mechanical data necessary for the design of intelligent harvesting equipment, thereby advancing the development of harvesting technologies that are both efficient and minimize damage.

The axial elastic modulus of branches (E_bz), the radial elastic modulus of branches (E_br), and the radial elastic modulus of pedicels (E_sr) were measured. Ten test samples were prepared for each specimen. Branch samples were fabricated into cylindrical shapes with a length of 10 mm. The average diameter of the axial compression samples of branches was 5.35 ± 1.76 mm, the average diameter of the radial compression samples of branches was 5.33 ± 1.51 mm, and the average diameter of the radial compression samples of pedicels was 3.85 ± 1.19 mm. The experimental procedure is illustrated in Figure 1. The universal testing machine applied load at a rate of 5 mm/min. In the load–displacement test, the force exhibited a linear variation with displacement. The stress, strain, and elastic modulus in the experiments were calculated using the following Equations (1)–(3) [15].

$${\delta }_n={\displaystyle \frac{4F}{{\pi {\mathrm{d}}_s}^2}}$$

(1)

$${\epsilon }_n={\displaystyle \raisebox{1ex}{$\mathrm{\Delta }\mathrm{l}$}\!\left/ \!\raisebox{-1ex}{$l_0$}\right.}$$

(2)

$$E={\displaystyle \frac{{\delta }_n}{{\epsilon }_n}}$$

(3)

In the formula, σ_n—stress, MPa; F—test load, N; d_s—specimen diameter, mm; ε_n—strain; Δl—change in sample length, mm; l₀—length of sample before test, mm; E—modulus of elasticity, MPa.

2.4. Shear Test of Branches and Peduncles

The anisotropic plane bending and shearing modulus of branches and fruit peduncles is typically assessed using the three-point bending test. This test is a simulation method for the risks of bending or breakage that branches and fruit peduncles may experience in their natural environment [15,20]. 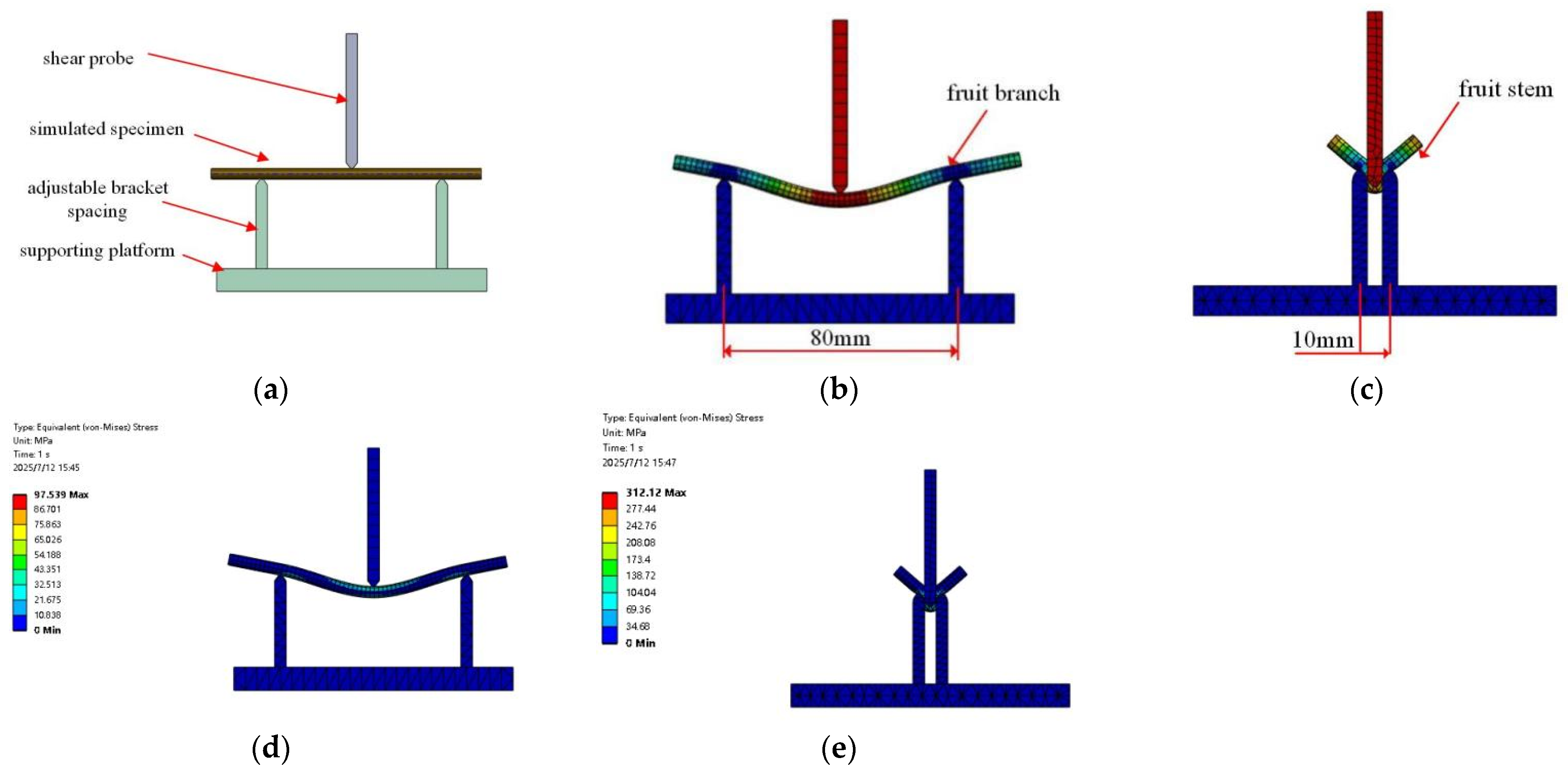Through this testing procedure, the mechanical behavior of branches and fruit peduncles under gradually increasing bending loads can be determined, including the yield point, fracture point, and the energy absorption capacity throughout the entire process [18]. Ten branch samples and ten fruit peduncle samples were prepared for the test. The branch samples were trimmed to equal lengths of 120 mm during fabrication. The test was conducted using an FTC-TMS-PRO texture analyzer, which has a force range of 0–1000 N and is equipped with a shearing test probe and a supporting platform, as illustrated in Figure 2.

The branch specimens should be positioned on the specialized support platform of the texture analyzer, ensuring that the center of each specimen aligns with the midpoint between the two support points, which are separated by a distance of 80 mm. For the fruit peduncle samples, the spacing should be set at 10 mm. During the test, a force is applied vertically downward at the midpoint of the samples to simulate the loads that branches and fruit peduncles may encounter during their natural growth process. The configuration of the samples is illustrated in Figure 3. As the force increases, branches and fruit peduncles will deform until they reach their maximum load-bearing capacity and ultimately fracture. By recording the relationship between force and displacement, the stress–strain curve of the fruit peduncles can be plotted, thereby obtaining the elastic modulus parameters of the branches and fruit peduncles. The prepared branch samples had a diameter of 4.88 ± 0.88 mm, while the fruit peduncle samples had a diameter of 4.10 ± 1.06 mm. The experimental parameters for the texture analyzer were set as follows: an initial force of 20 N, a test speed of 5 mm/min, a return speed of 20 mm/min, and a return distance of 10 mm.

In the load–displacement curve obtained from the test, select the displacement γ_b corresponding to the load F_b, and then calculate the anisotropic plane shear modulus G_r according to the following formula [15,17,21].

$$G_{\mathrm{r}}={\displaystyle \frac{F_{\mathrm{b}}{\delta }^3}{48I{\gamma }_b}}$$

(4)

In the formula, G_r—anisotropic plane bending shear modulus, MPa; F_b—load applied by the indenter, N; $\delta$—support platform spacing, mm; γ_b—displacement of pressure head loading, mm; and I—moment of inertia of the sample, I = πd⁴/64, mm⁴.

The axial torsional shear modulus (G_XY) and the anisotropic plane Poisson’s ratio (μ_r) cannot be directly calculated from the testing machine’s results; therefore, they are estimated using the following formulas.

$$G_{XY}={\displaystyle \frac{E_r}{2(1+{\mu }_{XY})}}$$

(5)

$${\mu }_r\prec {\displaystyle \frac{E_r}{E_Z\sqrt{2{\mu }_{XY}}}}$$

(6)

In the formula, G_XY—axial torsional shear modulus, MPa; E_r—radial elastic modulus, MPa; μ_r—anisotropic Poisson ratio; E_z—axial modulus of elasticity, MPa; and μ_XY—Poisson’s ratio of the same plane.

2.5. Finite Element Simulation of the Three-Point Bending Test

The finite element simulation of the three-point bending test is a computational technique used to predict material behavior under bending loads. This simulation is especially valuable in engineering and materials science, as it enables the analysis of mechanical properties without the need for physical testing [22,23]. To investigate the mechanical characteristics of Korla pear tree branches bearing fruit, a finite element simulation of the three-point bending test was conducted. The objective was to analyze the bending behavior and stress distribution under varying loading conditions by simulating the stress state of the branches during the actual picking process. This approach provides precise mechanical parameters essential for the design of intelligent harvesting machinery, thereby ensuring the reliability and safety of the mechanical operations. The results of the finite element simulation will further our understanding of the structural strength characteristics of Korla pear tree branches. This study holds substantial theoretical value for advancing the intelligent harvesting process in the Korla pear industry [24,25]. Based on the parameters from the three-point bending test conducted on a texture analyzer (as described earlier), with an initial force of 20 N and a test speed of 5 mm/min, the loading conditions were characterized as slow and steady, thereby falling under quasi-static conditions. As a result, static structural analysis is the most appropriate form of finite element analysis for this study. This analysis assumes that the system does not exhibit significant inertial effects or dynamic responses during loading, making it well-suited for simulating structural responses under low-speed, quasi-static loading conditions.

Finite element analysis was performed using the ANSYS Workbench 2022 Static Structural module. The geometries of the branches and pedicels were constructed based on physical measurements, with their diameters and lengths consistent with the experimental samples. The material was assumed to be isotropic and linear elastic in this preliminary simulation, with elastic modulus values derived from experimental tests, a Poisson’s ratio of 0.38 for branches and 0.35 for pedicels, and a density of 750 kg/m³ based on reported values for similar woody tissues [17,21]. A tetrahedral mesh was generated for the finite element models, with an average element size of 3 mm for pedicels and 5 mm for branches, considering their geometric dimensions and mechanical behavior characteristics. A mesh convergence test confirmed that further refinement caused negligible changes (within 5%) in maximum stress and displacement, verifying the stability and reliability of the selected mesh densities. For the boundary conditions, two support points were modeled as fixed constraints, and a vertical displacement load was applied at the midpoint of the upper surface of the specimen. The displacement load replicated the experimental conditions with a loading speed of 5 mm/min, simulating quasi-static loading. The simulation results, including stress distribution and deformation patterns, were compared with the experimental data to validate the model’s accuracy.

3. Results and Discussion

3.1. Analysis of the Water Content in Pear Tree Branches and Fruit Peduncles

In this study, the moisture content of the branches and fruit peduncles was found to be 45.93 ± 4.00% and 54.98 ± 3.69%, respectively. These values were considered when analyzing the mechanical properties of the samples. Experimental conditions, including the maintenance of relatively stable moisture content, were carefully controlled to minimize the influence of water on the mechanical properties during testing. However, future research could further investigate how varying moisture levels affect the mechanical behavior of pear tree branches and fruit peduncles, which would provide deeper insights into their performance under different environmental conditions. Data analysis revealed that the average moisture content (wet basis) of the branches was 45.93 ± 4.00%, while that of the fruit peduncles was 54.98 ± 3.69%. Grubbs’ test was used to identify outliers in the dataset, and the results showed no significant outliers, thereby confirming the consistency and reliability of the data. The measurement tests and subsequent data analysis are presented in Figure 4.

Although this study provides valuable insights into the mechanical behavior of pear tree branches and fruit peduncles, it is important to acknowledge certain limitations. While moisture content was considered in the analysis, the study did not investigate the interaction between moisture content and other mechanical properties, such as shear strength or elasticity, which could provide a more comprehensive understanding of the material’s behavior under stress.

3.2. Analysis of Compression Test Results for Branches and Fruit Peduncles

In the actual stretching experiment, we observed an unexpected phenomenon: despite the increasing tension, the stem and branch samples did not break at the expected failure point, but cracked and slipped at the fixture position, as shown in Figure 5. This phenomenon indicates that traditional tensile tests may not be entirely suitable for these biomass materials, as local stress concentrations at the fixture can result in premature failure. To more accurately measure the axial and radial elastic modulus of stem and branch samples, a universal testing machine was employed to conduct axial and radial compression tests on branch samples. Given the small size and soft characteristics of fragrant pear fruit peduncles, the radial compression test of the fruit stem was utilized as a reference for its performance. This testing method minimizes the influence of the fixture on the sample, thereby providing a more accurate representation of the material’s mechanical behavior.

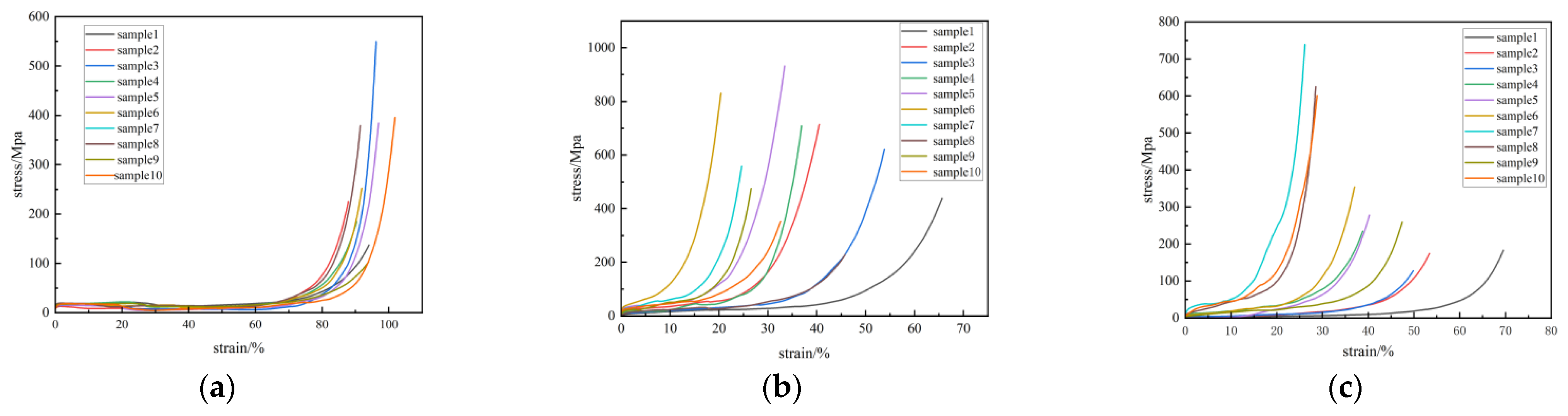
When analyzing the stress–strain curves of the fragrant pear branches and fruit peduncles presented in Figure 6, the following conclusions can be drawn: branches and fruit peduncles exhibit similar mechanical behavior during the compression process. After undergoing a linear elastic phase, the stress increases significantly with the increase in strain, indicating a transition from elastic deformation to plastic deformation. In particular, the axial compression of branches shows a more pronounced yield stage compared to radial compression, which may suggest that the axial fibers are gradually stripped under compression until complete failure occurs at the peak stress.

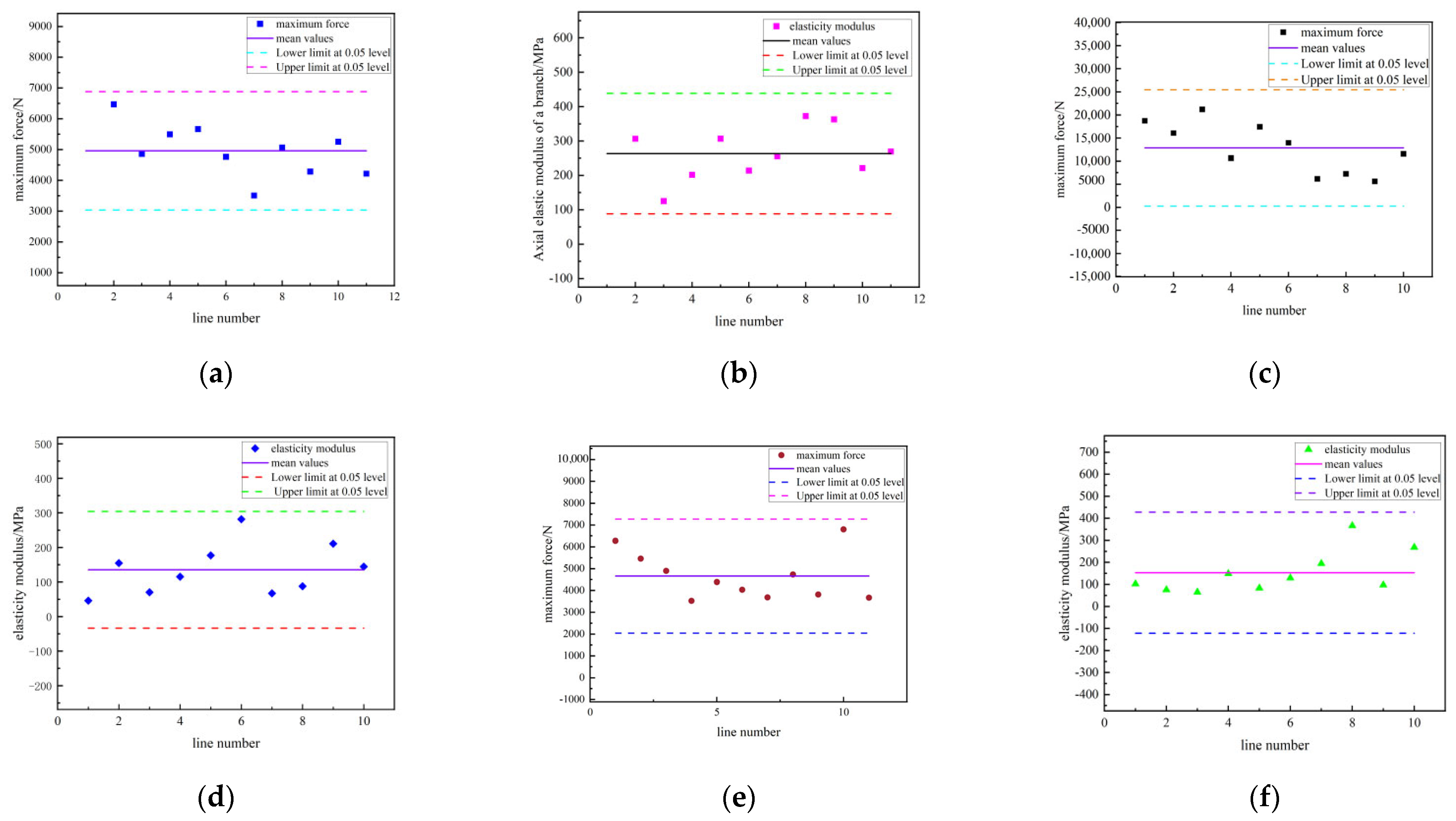
The elastic modulus, as a physical quantity that measures a material’s ability to resist elastic deformation, directly reflects the material’s rigidity. According to the data provided in

Table 1. Maximum force and elastic modulus values for branches and fruit peduncles.

Experimental Values	Branch Axial Compression	Branch Radial Compression	Compression of Fruit Peduncles
Maximum Force/N	4958.75 ± 839.05	12,856.6 ± 5499.62	4659.77 ± 1109.13
Elastic Modulus/MPa	263.51 ± 76.51	135.53 ± 73.73	152.96 ± 119.95

, the elastic modulus for the axial compression of branches is 263.51 MPa, with a standard deviation of 76.51 MPa; the elastic modulus for the radial compression of branches is 135.53 MPa, with a standard deviation of 73.73 MPa; and the elastic modulus for the compression of fruit peduncles is 152.96 MPa, with a standard deviation of 119.95 MPa. These figures indicate that the elastic modulus for the axial compression of branches is the highest, reflecting a greater rigidity compared to radial compression and the compression of fruit peduncles.

Furthermore, the elastic modulus data for the axial and radial compression of branches, the elastic modulus for the compression of fruit peduncles, and the maximum force during compression were subjected to Grubbs’ test for outliers (refer to Figure 7). The test results did not detect any outliers at the significance level of 0.05, thereby confirming the statistical reliability of the dataset obtained. This outcome establishes a robust data foundation for subsequent analyses and comparisons of material properties.

3.3. Analysis of Three-Point Bending Test Results of Branches and Peduncles

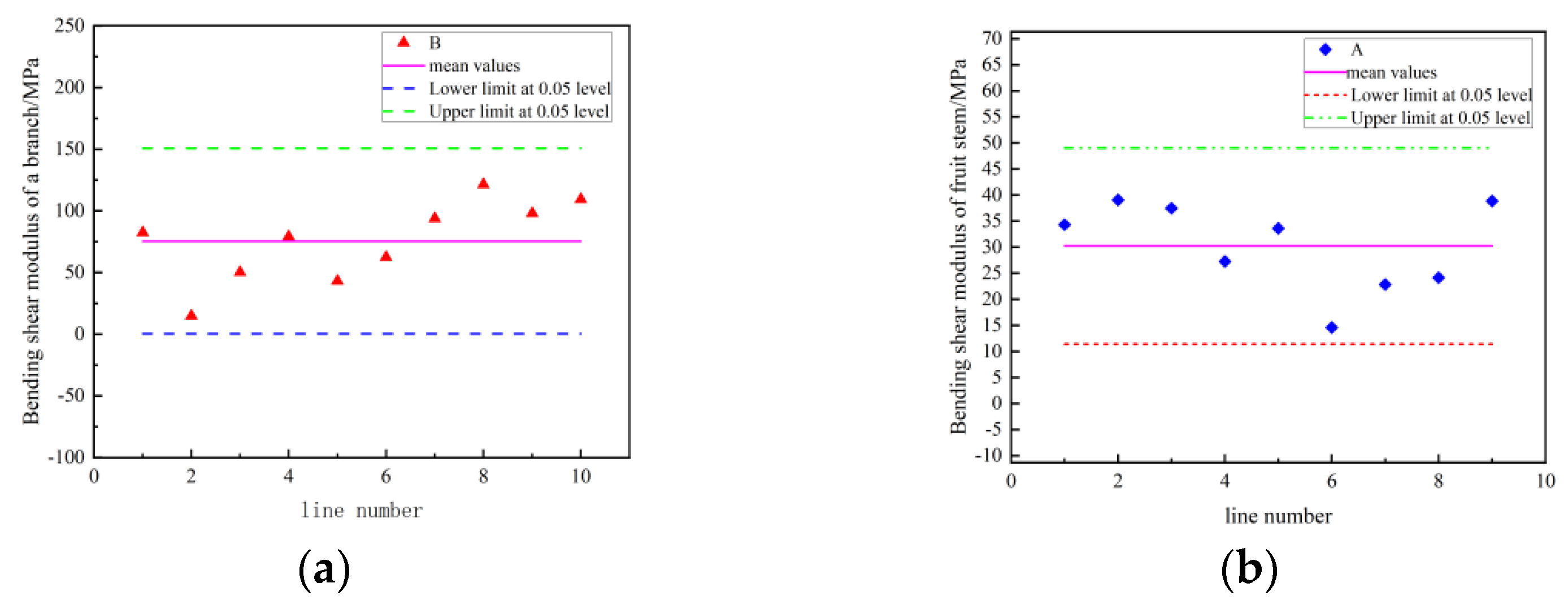
Based on the statistical analysis of the three-point bending tests performed on the branches and peduncles of fragrant pears, the results reveal a significant difference in their mechanical properties. The mean bending shear modulus for the branches was found to be 75.48 MPa, with a standard deviation of 32.84 MPa, indicating a high degree of variability under bending stress. In contrast, the mean bending shear modulus for the peduncles was 30.23 MPa, with a standard deviation of 8.50 MPa, suggesting relatively stable mechanical performance. This discrepancy may be attributed to differences in structural complexity and compositional variation. The Grubbs test applied to the dataset identified no outliers at the 0.05 significance level (as shown in Figure 8), confirming the statistical reliability of the data and providing a solid foundation for subsequent analyses.

In the present study, the selected Poisson’s ratio of 0.38 falls within the range of plane Poisson’s ratios reported for wood in the literature (0.3–0.5), providing a reasonable basis for subsequent mechanical model calculations. By integrating the results of the three-point bending tests with Equations (5) and (6), the axial torsional shear modulus of the fragrant pear branches and peduncles was estimated to be 48.40 MPa and 54.63 MPa, respectively. These values contribute to a deeper understanding of the materials’ mechanical behavior under axial torsion. Additionally, the estimated anisotropic plane Poisson’s ratios for the branches (0.57) and peduncles (0.18) provide insights into the materials’ mechanical behavior under non-isotropic plane conditions. These findings highlight significant differences in the deformation patterns of the two materials under stress. Future research could refine these estimates by employing more sophisticated modeling techniques and further investigating the inherent anisotropy of plant materials.

In summary, this study provides essential mechanical parameters for the optimized design of intelligent harvesting technologies, offering a theoretical foundation to improve harvesting efficiency and minimize fruit damage. Building on this work, further research is needed to explore additional factors that influence the mechanical properties of fragrant pear branches and peduncles, such as the effects of environmental conditions and variations in moisture content. These investigations will contribute to the optimization of harvesting techniques, aiming to reduce damage and enhance harvesting efficiency.

3.4. Finite Element Simulation Result Analysis

The study utilized SolidWorks (2022) to construct three-dimensional models of branches and peduncles, while Ansys Workbench (2022) was employed for finite element simulations to analyze their mechanical responses under various loading conditions. Figure 9 presents the results of the three-dimensional modeling and finite element analysis for both branches and peduncles. The simulation results show strong agreement with the experimental values, validating the reliability of the models. The bending shear modulus of the branches was determined to be 78.42 MPa, corresponding to a relative error of 3.75% compared to the experimentally measured value of 75.48 MPa. For the peduncles, the bending shear modulus was 32.52 MPa, with a relative error of 6.44% compared to the experimental value of 30.23 MPa. Although these errors are acceptable in engineering applications, they suggest that there is room for improvement in the simulation models.

The stress distribution maps (Von Mises stress contours) are presented to visualize the stress concentration and deformation patterns in the branches and pedicels under three-point bending loads. The higher maximum equivalent stress observed in peduncles compared to branches is attributable to their smaller cross-sectional area, lower stiffness, and greater susceptibility to local stress concentration under bending loads, which is consistent with observations in similar fruit-bearing structures reported in previous studies.

This research adopted simplified models, assuming the materials to be isotropic and neglecting the inherent structural differences between branches and peduncles, which may have contributed to the discrepancies between the simulated and experimental values. Furthermore, future studies could investigate the effects of dynamic loading conditions and improve simulation accuracy by incorporating more precise material properties and refined boundary conditions. This would better align the simulations with real-world conditions and provide more accurate data to support the design of intelligent harvesting equipment under varying environmental conditions.

3.5. Discussion

The results of this study provide valuable insights into the mechanical response characteristics of Korla fragrant pear branches and pedicels under various loading conditions. The significantly higher axial elastic modulus of branches compared to the radial modulus and that of pedicels reflects the inherent anisotropic structural properties of woody plant tissues, which are characterized by cellulose microfibrils aligned primarily in the axial direction, thereby effectively resisting tensile and compressive loads. This observation is consistent with findings in apple branches [21], thereby supporting the validity of the mechanical test methods and data obtained in this study. Although microscopic structural observations of branches and pedicels were not conducted in this study, previous research has shown that cellulose microfibrils in woody plant branches and pedicels are primarily aligned axially. The dense arrangement of these axial fibers, combined with a higher degree of lignification, significantly increases axial load-bearing capacity and the elastic modulus [26]. This structural characteristic leads to a higher axial elastic modulus in branches under axial compression. In contrast, during radial compression, the sparser lateral distribution of fibers results in lower stiffness and a higher susceptibility to local buckling deformation [27]. Additionally, the tissue structure of pedicels is relatively more porous than that of branches, with lower cellulose content and degree of lignification, leading to a lower elastic modulus. These considerations provide a plausible explanation for the phenomenon observed in this experiment, where the axial elastic modulus of branches is significantly higher than that in the radial direction and in pedicels.

In the three-point bending tests, the significant differences in shear modulus between branches and pedicels can primarily be attributed to their distinct structural compositions and functional roles. As a perennial load-bearing structure, branches exhibit higher lignification and contain densely and orderly arranged vessels, which contribute to greater rigidity and enhanced resistance to bending. In contrast, pedicels, serving as a temporary link between the fruit and the branch, possess greater flexibility, lower lignification, and relatively weaker mechanical strength. These observations are consistent with previously reported mechanical properties of apple pedicels [21]. Moreover, the high variability and large standard deviation observed in the mechanical parameters of branches in this study may be associated with natural variations in branch diameter and fiber orientation, which can be regarded as inherent structural heterogeneities. Namari et al. have demonstrated that natural defects and tissue heterogeneity in woody plant branches are key factors influencing their mechanical behavior [13]. The shear modulus and Poisson’s ratio obtained in this study further indicate that, under loading conditions, branches exhibit minimal radial contraction, with deformation predominantly occurring in the axial direction—a characteristic typical of lignified plant tissues. In this study, the relatively large standard deviations observed in certain parameters, such as the elastic modulus of fruit peduncles, may be partially attributed to the limited sample size (n = 10). While logistical and equipment constraints restricted the sample size, we recognize that a larger number of replicates would improve the statistical reliability of the results and reduce the influence of outliers. This limitation has been acknowledged in the conclusion, and future studies will expand the sample size to strengthen the robustness and representativeness of the mechanical property data.

The finite element simulation results show good agreement with the experimental data, with the overall error remaining within 6.44%, which is acceptable for engineering applications and confirms the feasibility of using the simplified model for preliminary prediction of the mechanical properties of plant materials. However, the isotropic material assumption employed in the simulation failed to fully capture the inherent anisotropy and tissue-specific differences present in branches and pedicels, which may account for the observed discrepancies between the simulated and experimental results. Previous studies have demonstrated that modeling plant tissues as orthotropic materials can significantly enhance the accuracy of finite element simulations, suggesting that future work should focus on refining the material model in this direction [23,25].

It is worth noting that the moisture content was carefully controlled during the experimental process to minimize its potential influence on the mechanical property measurements. Nevertheless, it is well established that moisture content plays a critical role in determining the mechanical behavior of plant tissues. Previous studies have demonstrated that variations in moisture content can significantly affect the elastic modulus and bending strength of both branches and pedicels [15,17,21]. Therefore, future research should systematically investigate the mechanical response of Korla fragrant pear branches and pedicels under varying moisture conditions, aiming to provide more accurate and reliable input parameters for mechanical modeling and simulation.

This study systematically investigated the mechanical properties of Korla fragrant pear branches and pedicels, thereby significantly enriching the database of mechanical performance data for fruit-bearing branches and pedicels. The findings of this research not only provide a solid theoretical foundation and essential parameter support for the development of intelligent, low-damage harvesting technologies tailored to Korla fragrant pears, but also offer valuable references for the design and optimization of harvesting equipment for other specialty fruit tree species.

4. Conclusions

This study provides novel insights into the mechanical behavior of Korla fragrant pear branches and fruit peduncles under various loading conditions. Through axial and radial compression tests, as well as three-point bending experiments, significant differences in key mechanical parameters—such as the elastic modulus and shear modulus—between branches and fruit peduncles were identified. The results reveal that both components exhibit distinct mechanical responses, which must be carefully considered in the design of intelligent harvesting systems to enhance operational efficiency and minimize fruit damage.

The finite element simulation results showed good agreement with the experimental data, thereby validating the reliability of the modeling approach for analyzing the bending behavior of these plant components. The application of appropriate boundary conditions and refined mesh generation significantly improved the accuracy of the simulations, providing valuable insights into stress distribution and deformation patterns. These findings highlight the potential of finite element modeling as a powerful and effective tool for predicting mechanical behavior and optimizing design parameters in the development of intelligent harvesting technologies.

It should be noted, however, that this study represents a preliminary mechanical characterization focusing primarily on compression and bending properties. The mechanical behavior of plant tissues can be significantly influenced by additional factors such as moisture content, tissue maturity, fiber orientation, tissue density, and natural defects, which were not comprehensively assessed in the present work. Although moisture content was controlled and recorded during testing, future research should systematically investigate the influence of these additional parameters on the mechanical performance of branches and fruit peduncles.

Moreover, for the findings to be fully applicable in the engineering design of intelligent, low-damage harvesting machinery, a more extensive mechanical characterization—including tensile strength, fracture toughness, viscoelastic properties, and dynamic response under impact loading—is necessary. Future investigations should also explore the complex interactions within the integrated “branch–fruit stalk–fruit” system and evaluate the mechanical behavior under varying environmental conditions such as temperature and humidity. Additionally, the development of more advanced finite element models incorporating anisotropic or orthotropic material properties and multi-physics simulations is recommended to enhance prediction accuracy under realistic harvesting scenarios.

Collectively, the mechanical parameters and simulation results reported in this study provide a solid theoretical foundation for intelligent harvesting technology development in Korla fragrant pear orchards and offer valuable reference data for similar specialty fruit tree species.