Using Calibration Transfer Strategy to Update Hyperspectral Model for Quantitating Soluble Solid Content of Blueberry Across Different Batches
Abstract
1. Introduction
2. Materials and Methods
2.1. Collection of Blueberry Samples
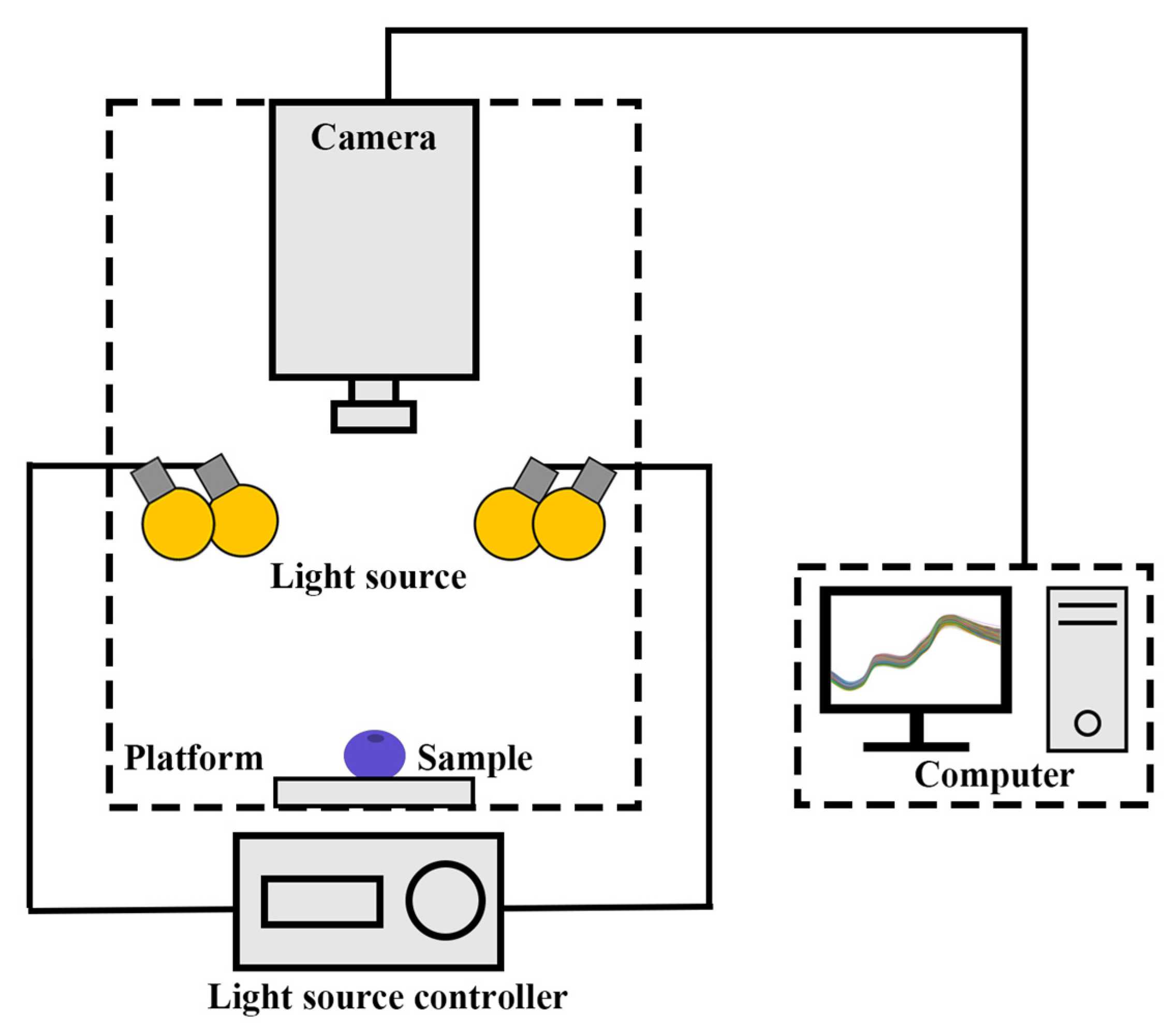
2.2. Hyperspectral Imaging System
2.3. Soluble Solids Content Measurement
2.4. Hyperspectral Image Correction and Spectrums Extraction
2.5. Principal Component Analysis Algorithm
2.6. Data Preprocessing
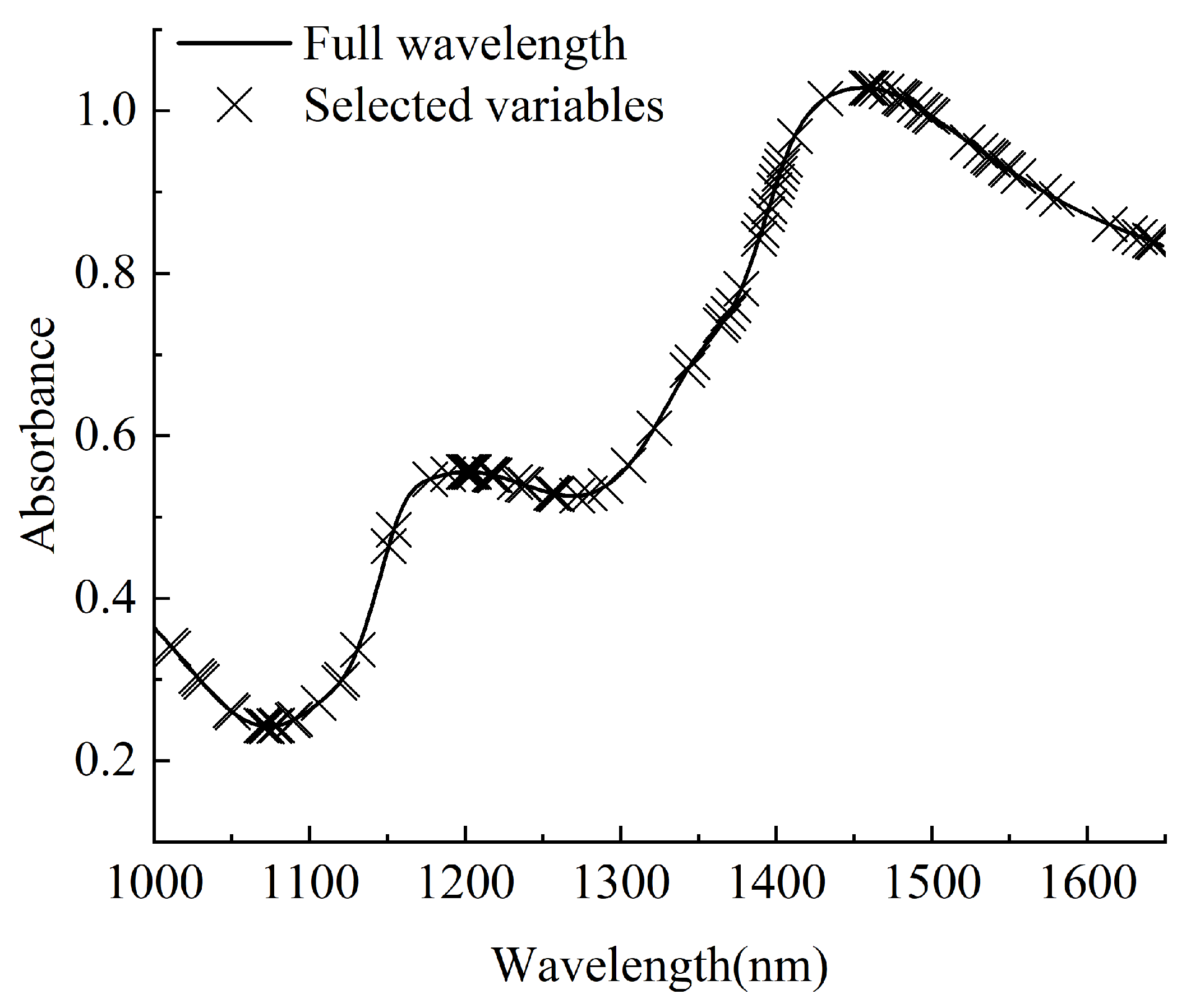
2.7. Feature Wavelength Selection Algorithm
2.8. Modeling Algorithms and Evaluation Criteria
2.9. Calibration Transfer Strategy
3. Results
3.1. Sample Sets Division
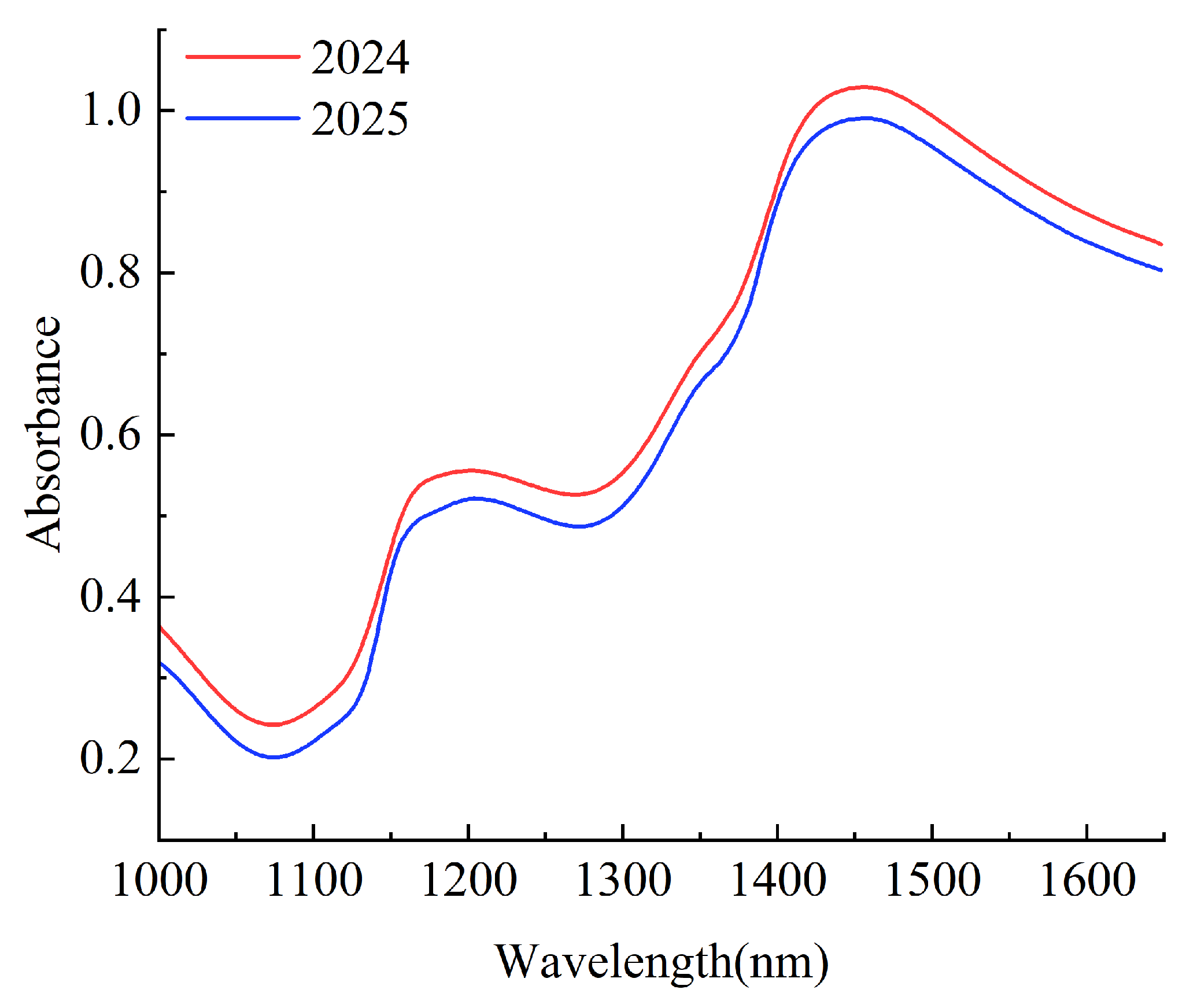
3.2. Spectral Analysis
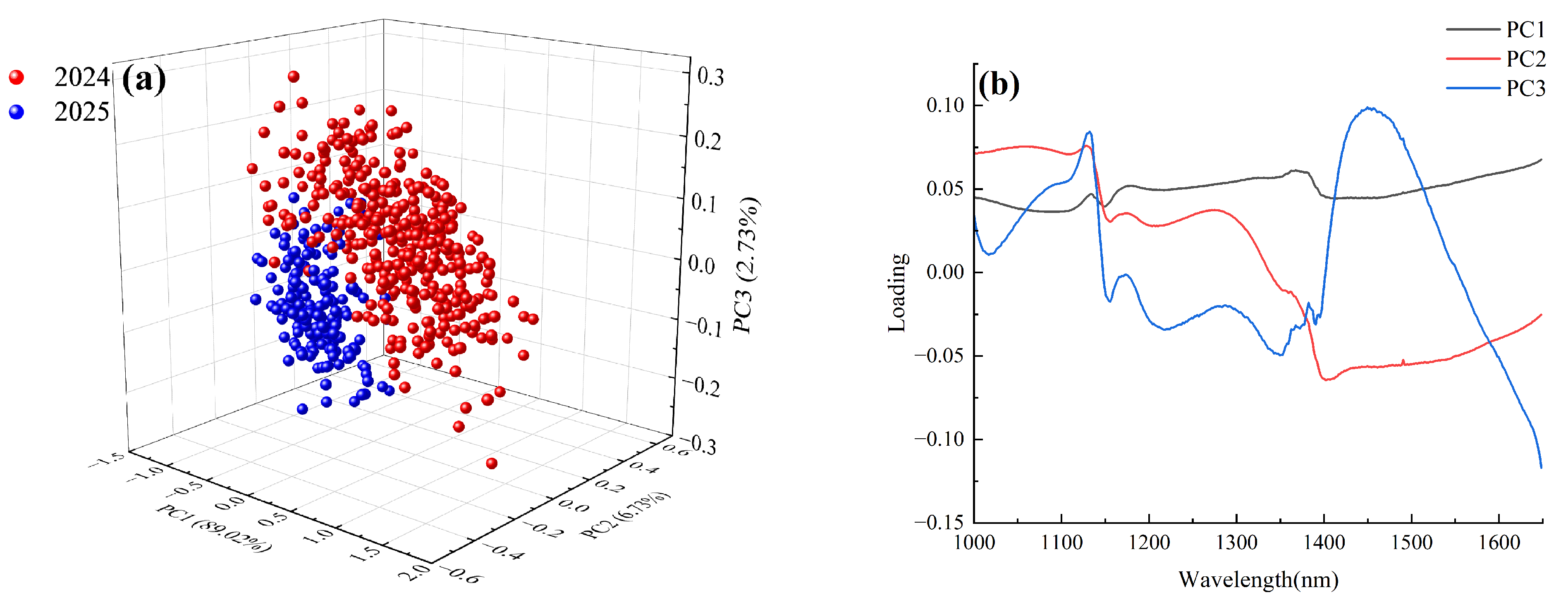
3.3. Principal Component Analysis
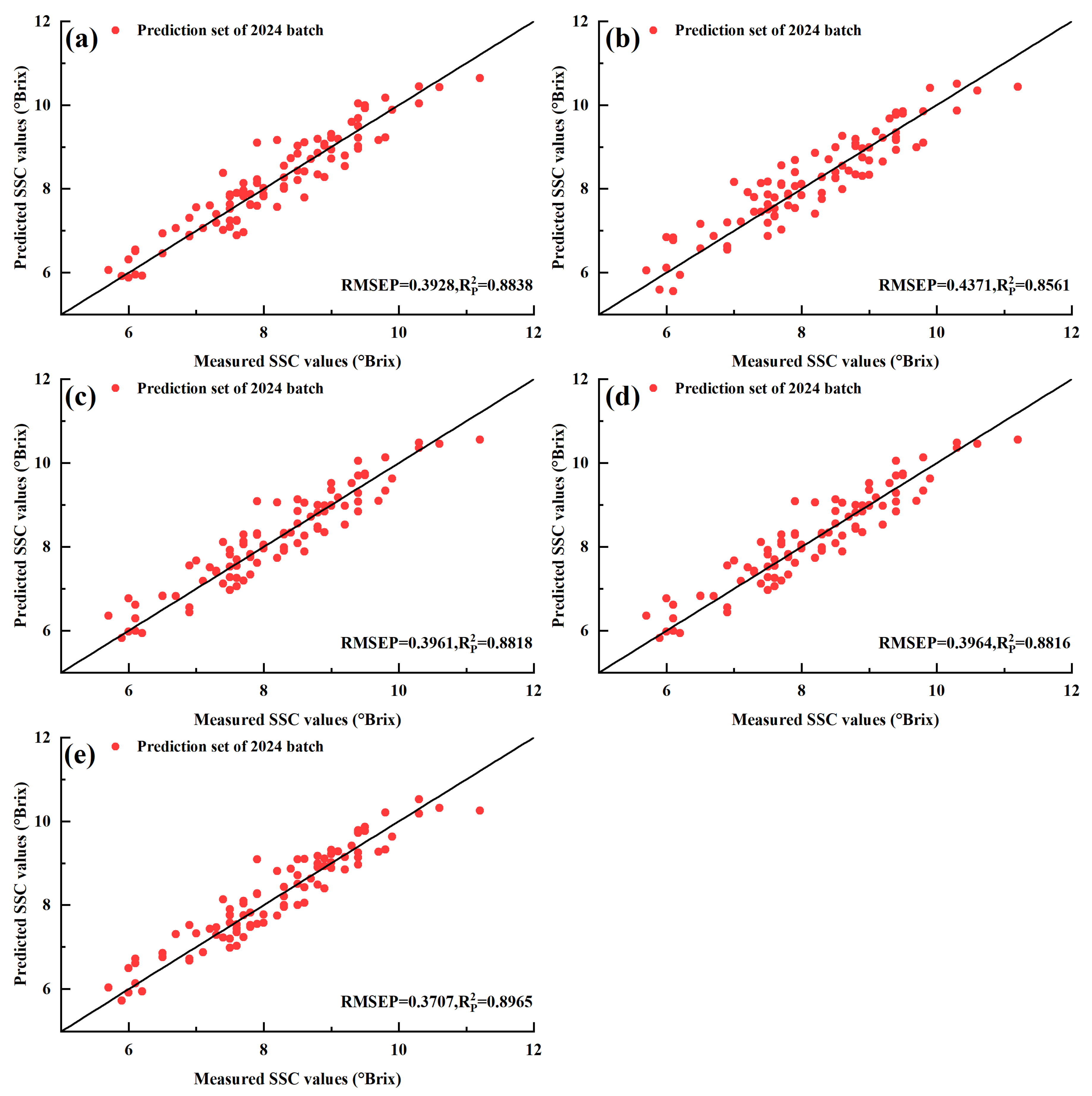
3.4. Spectral Data Preprocessing and PLSR Model Construction
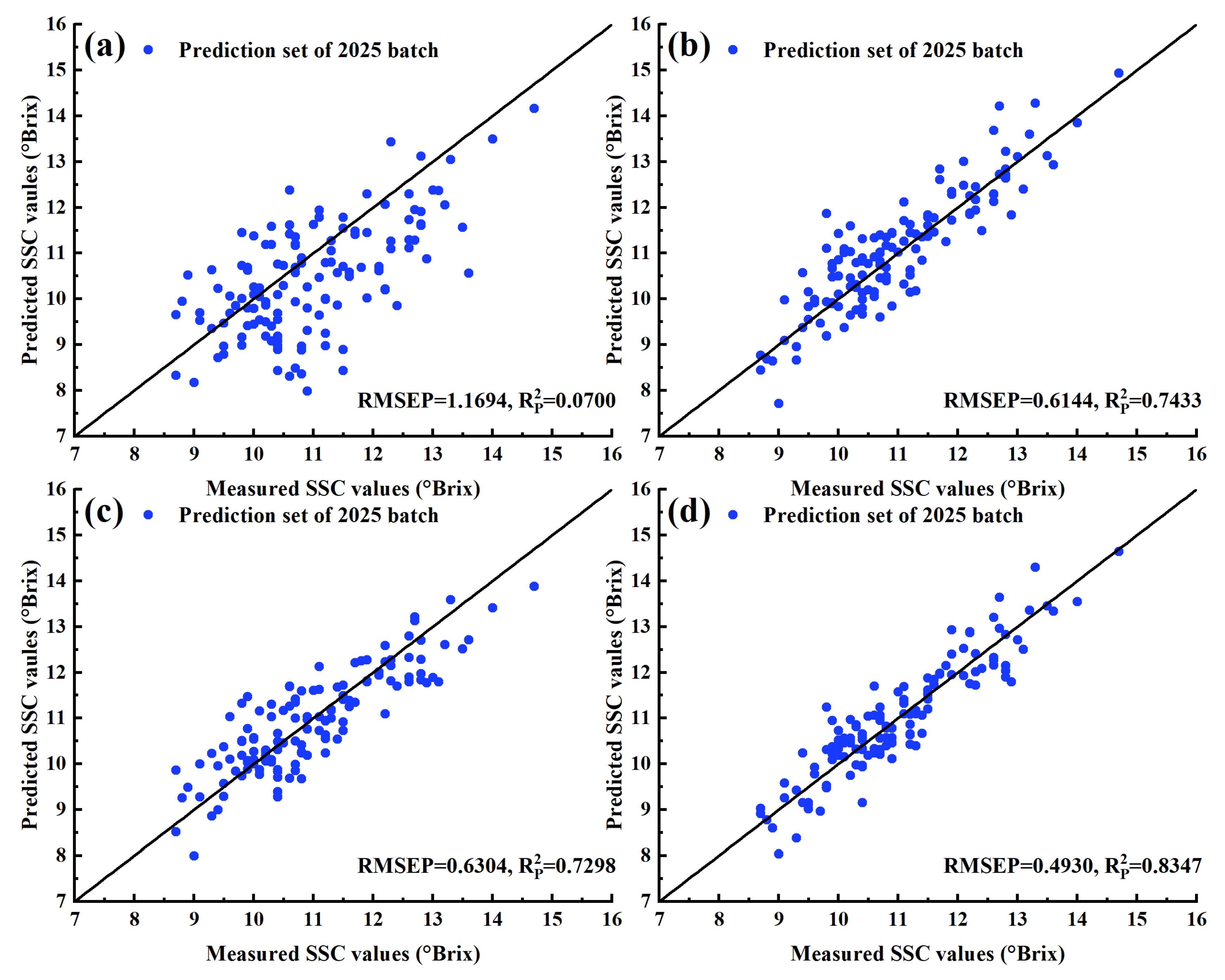
3.5. Models Updated with Calibration Transfer Strategy Using SS-PFCE
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhang, Q.; Cui, M.-Y.; Fu, Y.; Wang, X.-H.; Yang, Q.; Zhu, Y.; Yang, X.-H.; Bi, H.-J.; Gao, X.-L. Aroma enhancement of blueberry wine by postharvest partial dehydration of blueberries. Food Chem. 2023, 426, 136593. [Google Scholar] [CrossRef] [PubMed]
- Stull, A.J.; Cassidy, A.; Djousse, L.; Johnson, S.A.; Krikorian, R.; Lampe, J.W.; Mukamal, K.J.; Nieman, D.C.; Porter Starr, K.N.; Rasmussen, H.; et al. The state of the science on the health benefits of blueberries: A perspective. Front. Nutr. 2024, 11, 1415737. [Google Scholar] [CrossRef] [PubMed]
- Sivapragasam, N.; Neelakandan, N.; Rupasinghe, H.P.V. Potential health benefits of fermented blueberry: A review of current scientific evidence. Trends Food Sci. Technol. 2023, 132, 103–120. [Google Scholar] [CrossRef]
- Rashwan, A.K.; Osman, A.I.; Karim, N.; Mo, J.; Chen, W. Unveiling the Mechanisms of the Development of Blueberries-Based Functional Foods: An Updated and Comprehensive Review. Food Rev. Int. 2023, 40, 1913–1940. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.; Weng, L.; Zou, L.; Jiang, H.; Qiu, J.; Fu, J. Analysis of sucrose addition on the physicochemical properties of blueberry wine in the main fermentation. Front. Nutr. 2023, 9, 1092696. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, J.; Zhu, Y.; Li, T.; Wang, Y.; Gao, X. Intermolecular copigmentation of anthocyanins with phenolic compounds improves color stability in the model and real blueberry fermented beverage. Food Res. Int. 2024, 190, 114632. [Google Scholar] [CrossRef]
- Mishra, G.; Sahni, P.; Pandiselvam, R.; Panda, B.K.; Bhati, D.; Mahanti, N.K.; Kothakota, A.; Kumar, M.; Cozzolino, D. Emerging nondestructive techniques to quantify the textural properties of food: A state-of-art review. J. Texture Stud. 2023, 54, 173–205. [Google Scholar] [CrossRef]
- He, Y.; Xiao, Q.; Bai, X.; Zhou, L.; Liu, F.; Zhang, C. Recent progress of nondestructive techniques for fruits damage inspection: A review. Crit. Rev. Food Sci. Nutr. 2021, 62, 5476–5494. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.; Liu, X.; Gu, Y.; Ren, Z. The Application of Optical Nondestructive Testing for Fresh Berry Fruits. Food Eng. Rev. 2023, 16, 85–115. [Google Scholar] [CrossRef]
- Li, L.; Hu, D.-Y.; Tang, T.-Y.; Tang, Y.-L. Non-destructive detection of the quality attributes of fruits by visible-near infrared spectroscopy. J. Food Meas. Charact. 2022, 17, 1526–1534. [Google Scholar] [CrossRef]
- Cevoli, C.; Iaccheri, E.; Fabbri, A.; Ragni, L. Data fusion of FT-NIR spectroscopy and Vis/NIR hyperspectral imaging to predict quality parameters of yellow flesh “Jintao” kiwifruit. Biosyst. Eng. 2024, 237, 157–169. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, L.; Wang, W.; Zhang, X.; Gu, Q.; Zhu, Y.; Chen, R.; Zhang, C. Visible/near-infrared Spectroscopy and Hyperspectral Imaging Facilitate the Rapid Determination of Soluble Solids Content in Fruits. Food Eng. Rev. 2024, 16, 470–496. [Google Scholar] [CrossRef]
- Rodríguez-Ortega, A.; Aleixos, N.; Blasco, J.; Albert, F.; Munera, S. Study of light penetration depth of a Vis-NIR hyperspectral imaging system for the assessment of fruit quality. A case study in persimmon fruit. J. Food Eng. 2023, 358, 111673. [Google Scholar] [CrossRef]
- Hasanzadeh, B.; Abbaspour-Gilandeh, Y.; Soltani-Nazarloo, A.; Hernández-Hernández, M.; Gallardo-Bernal, I.; Hernández-Hernández, J.L. Non-Destructive Detection of Fruit Quality Parameters Using Hyperspectral Imaging, Multiple Regression Analysis and Artificial Intelligence. Horticulturae 2022, 8, 598. [Google Scholar] [CrossRef]
- Benelli, A.; Cevoli, C.; Ragni, L.; Fabbri, A. In-field and non-destructive monitoring of grapes maturity by hyperspectral imaging. Biosyst. Eng. 2021, 207, 59–67. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Peng, F.; Liu, J.; Han, G. Non-destructive prediction and visualization of anthocyanin content in mulberry fruits using hyperspectral imaging. Front. Plant Sci. 2023, 14, 1137198. [Google Scholar] [CrossRef]
- Wang, B.; Yang, H.; Li, L.; Zhang, S. Non-Destructive Detection of Cerasus Humilis Fruit Quality by Hyperspectral Imaging Combined with Chemometric Method. Horticulturae 2024, 10, 519. [Google Scholar] [CrossRef]
- Chen, G.; Yang, M.; Wang, G.; Dai, J.; Yu, S.; Chen, B.; Liu, D. Exploring a universal model for predicting blueberry soluble solids content based on hyperspectral imaging and transfer learning to address spatial heterogeneity challenge. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 334, 125921. [Google Scholar] [CrossRef]
- K.S., S.; George, S.N.; O.V., A.C.; K.M., J.; P., K.; Francis, J.; George, S. NorBlueNet: Hyperspectral imaging-based hybrid CNN-transformer model for non-destructive SSC analysis in Norwegian wild blueberries. Comput. Electron. Agric. 2025, 235, 110340. [Google Scholar] [CrossRef]
- Qiu, G.; Chen, B.; Lu, H.; Yue, X.; Deng, X.; Ouyang, H.; Li, B.; Wei, X. Nondestructively Determining Soluble Solids Content of Blueberries Using Reflection Hyperspectral Imaging Technique. Agronomy 2024, 14, 2296. [Google Scholar] [CrossRef]
- Meng, L.; Chen, G.; Liu, D.; Tian, N. Universal Modeling for Non-Destructive Testing of Soluble Solids Content in Multi-Variety Blueberries Based on Hyperspectral Imaging Technology. Appl. Sci. 2025, 15, 3888. [Google Scholar] [CrossRef]
- Çetin, N.; Karaman, K.; Kavuncuoğlu, E.; Yıldırım, B.; Jahanbakhshi, A. Using hyperspectral imaging technology and machine learning algorithms for assessing internal quality parameters of apple fruits. Chemom. Intell. Lab. Syst. 2022, 230, 104650. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Pourdarbani, R.; Sabzi, S.; Rohban, M.H.; Arribas, J.I. From Harvest to Market: Non-Destructive Bruise Detection in Kiwifruit Using Convolutional Neural Networks and Hyperspectral Imaging. Horticulturae 2023, 9, 936. [Google Scholar] [CrossRef]
- Cho, B.-H.; Lee, K.-B.; Hong, Y.; Kim, K.-C. Determination of Internal Quality Indices in Oriental Melon Using Snapshot-Type Hyperspectral Image and Machine Learning Model. Agronomy 2022, 12, 2236. [Google Scholar] [CrossRef]
- Kim, M.-J.; Yu, W.-H.; Song, D.-J.; Chun, S.-W.; Kim, M.S.; Lee, A.; Kim, G.; Shin, B.-S.; Mo, C. Prediction of Soluble-Solid Content in Citrus Fruit Using Visible–Near-Infrared Hyperspectral Imaging Based on Effective-Wavelength Selection Algorithm. Sensors 2024, 24, 1512. [Google Scholar] [CrossRef] [PubMed]
- Qiu, G.; Lu, H.; Wang, X.; Wang, C.; Xu, S.; Liang, X.; Fan, C. Nondestructive Detecting Maturity of Pineapples Based on Visible and Near-Infrared Transmittance Spectroscopy Coupled with Machine Learning Methodologies. Horticulturae 2023, 9, 889. [Google Scholar] [CrossRef]
- Wang, Y.; Lysaght, M.J.; Kowalski, B.R. Improvement of multivariate calibration through instrument standardization. Anal. Chem. 1992, 64, 562–564. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.-P.; Zhong, L.-J.; Wang, S.-X.; Yu, R.-Q.; Nordon, A.; Littlejohn, D.; Holden, M. Maintaining the predictive abilities of multivariate calibration models by spectral space transformation. Anal. Chim. Acta 2011, 690, 64–70. [Google Scholar] [CrossRef]
- Liu, Y.; Cai, W.; Shao, X. Linear model correction: A method for transferring a near-infrared multivariate calibration model without standard samples. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2016, 169, 197–201. [Google Scholar] [CrossRef]
- Zhang, J.; Li, B.; Hu, Y.; Zhou, L.; Wang, G.; Guo, G.; Zhang, Q.; Lei, S.; Zhang, A. A parameter-free framework for calibration enhancement of near-infrared spectroscopy based on correlation constraint. Anal. Chim. Acta 2021, 1142, 169–178. [Google Scholar] [CrossRef]
- Mishra, P.; Woltering, E. Handling batch-to-batch variability in portable spectroscopy of fresh fruit with minimal parameter adjustment. Anal. Chim. Acta 2021, 1177, 338771. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Zhang, J.; Cai, W.; Shao, X. Enhancing Transferability of Near-Infrared Spectral Models for Soluble Solids Content Prediction across Different Fruits. Appl. Sci. 2023, 13, 5417. [Google Scholar] [CrossRef]
- Benelli, A.; Cevoli, C.; Fabbri, A.; Ragni, L. Ripeness evaluation of kiwifruit by hyperspectral imaging. Biosyst. Eng. 2022, 223, 42–52. [Google Scholar] [CrossRef]
- Uddin, M.P.; Mamun, M.A.; Hossain, M.A. Effective feature extraction through segmentation-based folded-PCA for hyperspectral image classification. Int. J. Remote Sens. 2019, 40, 7190–7220. [Google Scholar] [CrossRef]
- Nirere, A.; Sun, J.; Kama, R.; Atindana, V.A.; Nikubwimana, F.D.; Dusabe, K.D.; Zhong, Y. Nondestructive detection of adulterated wolfberry (Lycium Chinense) fruits based on hyperspectral imaging technology. J. Food Process Eng. 2023, 46, 14293. [Google Scholar] [CrossRef]
- Abenina, M.I.A.; Maja, J.M.; Cutulle, M.; Melgar, J.C.; Liu, H. Prediction of Potassium in Peach Leaves Using Hyperspectral Imaging and Multivariate Analysis. AgriEngineering 2022, 4, 400–413. [Google Scholar] [CrossRef]
- Haghbin, N.; Bakhshipour, A.; Zareiforoush, H.; Mousanejad, S. Non-destructive pre-symptomatic detection of gray mold infection in kiwifruit using hyperspectral data and chemometrics. Plant Methods 2023, 19, 53. [Google Scholar] [CrossRef]
- Galvao, R.; Araujo, M.; Jose, G.; Pontes, M.; Silva, E.; Saldanha, T. A method for calibration and validation subset partitioning. Talanta 2005, 67, 736–740. [Google Scholar] [CrossRef]
- Faqeerzada, M.A.; Kim, Y.-N.; Kim, H.; Akter, T.; Kim, H.; Park, M.-S.; Kim, M.S.; Baek, I.; Cho, B.-K. Hyperspectral imaging system for pre- and post-harvest defect detection in paprika fruit. Postharvest Biol. Technol. 2024, 218, 113151. [Google Scholar] [CrossRef]
- Khaled, A.Y.; Ekramirad, N.; Donohue, K.D.; Villanueva, R.T.; Adedeji, A.A. Non-Destructive Hyperspectral Imaging and Machine Learning-Based Predictive Models for Physicochemical Quality Attributes of Apples during Storage as Affected by Codling Moth Infestation. Agriculture 2023, 13, 1086. [Google Scholar] [CrossRef]
- Adesokan, M.; Otegbayo, B.; Alamu, E.O.; Olutoyin, M.A.; Maziya-Dixon, B. Evaluating the dry matter content of raw yams using hyperspectral imaging spectroscopy and machine learning. J. Food Compos. Anal. 2024, 135, 106692. [Google Scholar] [CrossRef]
- Jahani, T.; Kashaninejad, M.; Ziaiifar, A.M.; Golzarian, M.; Akbari, N.; Soleimanipour, A. Effect of selected pre-processing methods by PLSR to predict low-fat mozzarella texture measured by hyperspectral imaging. J. Food Meas. Charact. 2024, 18, 5060–5072. [Google Scholar] [CrossRef]
- Ahmed, M.T.; Monjur, O.; Kamruzzaman, M. Deep learning-based hyperspectral image reconstruction for quality assessment of agro-product. J. Food Eng. 2024, 382, 112223. [Google Scholar] [CrossRef]
- Hitchman, S.; Loeffen, M.P.F.; Reis, M.M.; Craigie, C.R. Robustness of hyperspectral imaging and PLSR model predictions of intramuscular fat in lamb M. longissimus lumborum across several flocks and years. Meat Sci. 2021, 179, 108492. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.H.; Tootoonchy, M.; Kämper, W.; Tahmasbian, I.; Farrar, M.B.; Boldingh, H.; Pereira, T.; Jonson, H.; Nichols, J.; Wallace, H.M.; et al. Predicting Carbohydrate Concentrations in Avocado and Macadamia Leaves Using Hyperspectral Imaging with Partial Least Squares Regressions and Artificial Neural Networks. Remote Sens. 2024, 16, 3389. [Google Scholar] [CrossRef]
- Lyu, H.; Grafton, M.; Ramilan, T.; Irwin, M.; Sandoval, E. Hyperspectral Imaging Spectroscopy for Non-Destructive Determination of Grape Berry Total Soluble Solids and Titratable Acidity. Remote Sens. 2024, 16, 1655. [Google Scholar] [CrossRef]
- Lintvedt, T.A.; Andersen, P.V.; Afseth, N.K.; Heia, K.; Lindberg, S.-K.; Wold, J.P. Raman spectroscopy and NIR hyperspectral imaging for in-line estimation of fatty acid features in salmon fillets. Talanta 2023, 254, 124113. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, M.; Zhang, F.; Xiong, Y.; Wang, X.; Ali, S.; Zhang, Y.; Fu, S. Hyperspectral imaging combined with GA-SVM for maize variety identification. Food Sci. Nutr. 2024, 12, 3177–3187. [Google Scholar] [CrossRef]
- Guo, Z.; Zhai, L.; Zou, Y.; Sun, C.; Jayan, H.; El-Seedi, H.R.; Jiang, S.; Cai, J.; Zou, X. Comparative study of Vis/NIR reflectance and transmittance method for on-line detection of strawberry SSC. Comput. Electron. Agric. 2024, 218, 108744. [Google Scholar] [CrossRef]
- Geng, Y.; Ni, H.; Shen, H.; Wang, H.; Wu, J.; Pan, K.; Wu, Y.; Chen, Y.; Luo, Y.; Xu, T.; et al. Feasibility of an NIR spectral calibration transfer algorithm based on optimized feature variables to predict tobacco samples in different states. Anal. Methods 2023, 15, 719–728. [Google Scholar] [CrossRef]
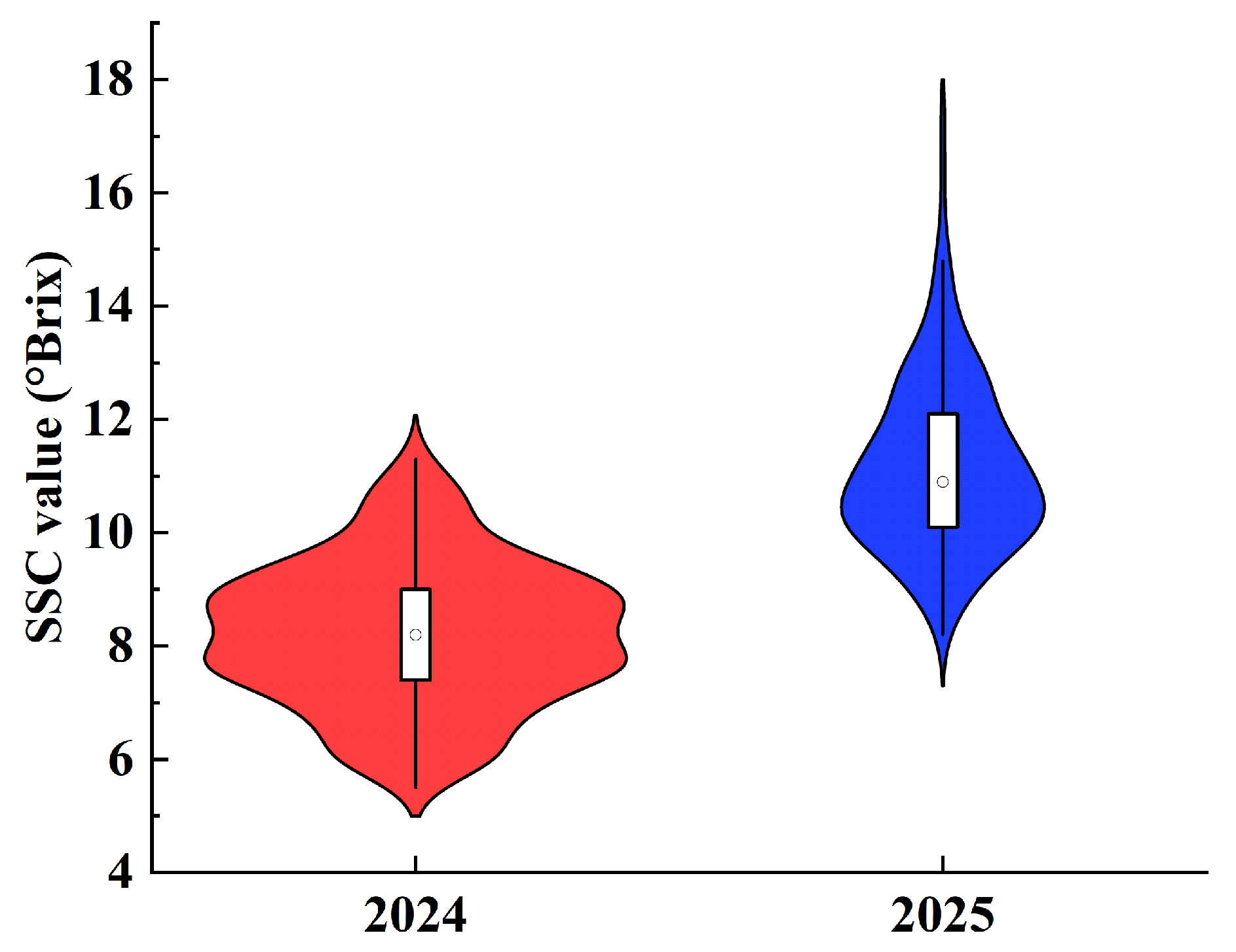
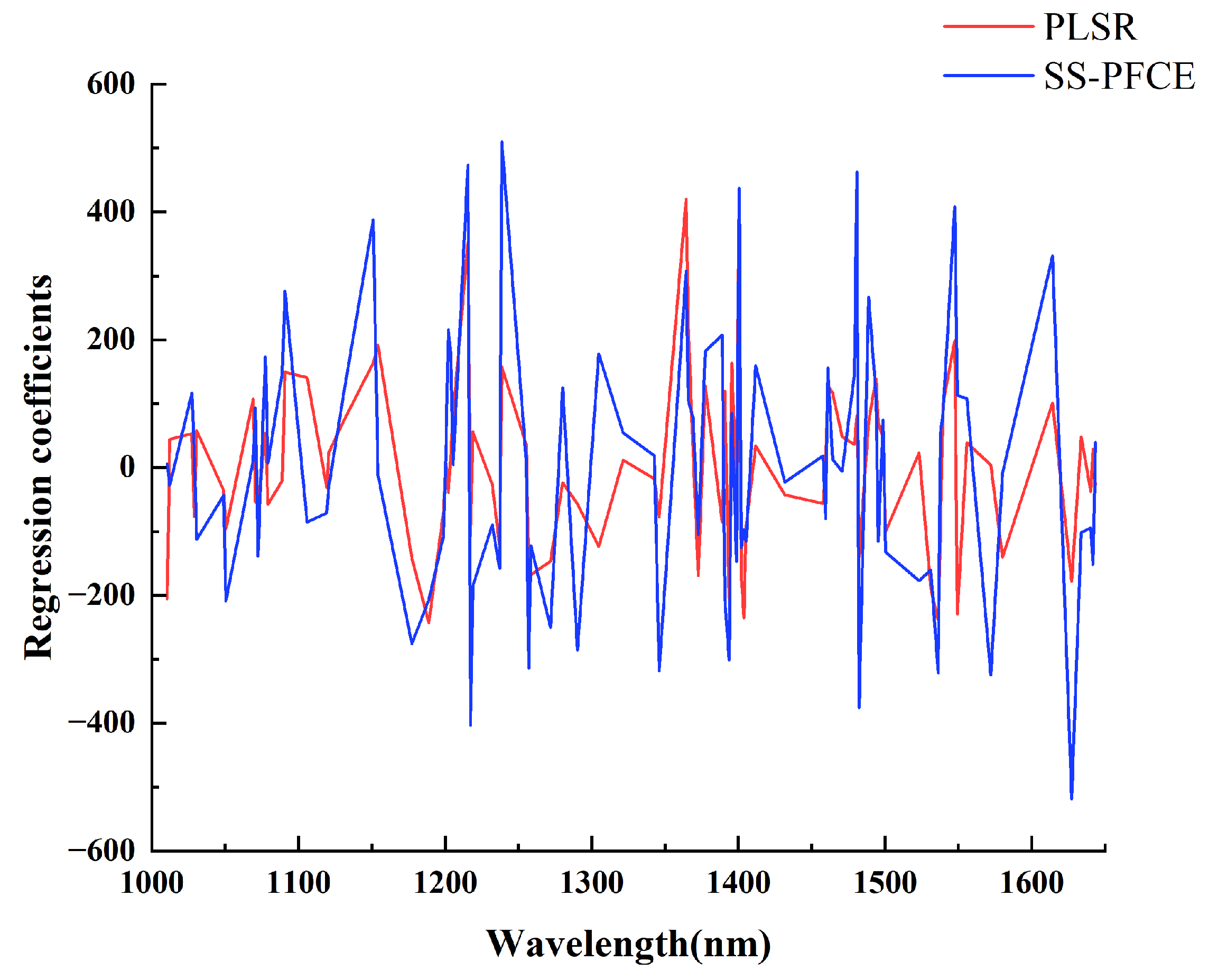
| Year of Sample | Sample Set | Number of Samples | Minimum | Maximum | Average Value | Standard Deviation |
|---|---|---|---|---|---|---|
| 2024 | Calibration Set | 273 | 5.5 | 11.5 | 8.23 | 1.31 |
| Prediction Set | 91 | 5.7 | 11.2 | 8.16 | 1.15 | |
| Total Samples | 364 | 5.5 | 11.5 | 8.21 | 1.27 | |
| 2025 | Calibration Set | 44 | 8.2 | 17.4 | 11.78 | 2.08 |
| Prediction Set | 131 | 8.7 | 14.7 | 10.96 | 1.21 | |
| Total Samples | 175 | 8.2 | 17.4 | 11.17 | 1.52 |
| Preprocessing Methods | Number of Features | LVs | RMSEC | RMSEP | RPD | ||
|---|---|---|---|---|---|---|---|
| RAW | 395 | 31 | 0.3192 | 0.9405 | 0.3928 | 0.8838 | 2.95 |
| SNV | 395 | 27 | 0.3726 | 0.9189 | 0.4371 | 0.8561 | 2.65 |
| SG | 395 | 31 | 0.3295 | 0.9366 | 0.3961 | 0.8818 | 2.93 |
| VN | 395 | 25 | 0.3509 | 0.9281 | 0.3964 | 0.8816 | 2.93 |
| RAW-CARS | 88 | 30 | 0.3191 | 0.9405 | 0.3707 | 0.8965 | 3.13 |
| Model | Calibration Year | Calibration Set Size | RMSEC | RMSEP | RPD | ||
|---|---|---|---|---|---|---|---|
| PLSR | 2024 | 273 | 1.3260 | 0.5919 | 1.1694 | 0.0700 | 1.04 |
| PLSR | 2025 | 44 | 0.1598 | 0.9941 | 0.6144 | 0.7433 | 1.98 |
| PLSR | 2024 + 2025 | 317 | 0.5427 | 0.9176 | 0.6304 | 0.7298 | 1.93 |
| SS-PFCE | 2025 | 44 | 0.3886 | 0.9650 | 0.4930 | 0.8347 | 2.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Huang, X.; Tan, S.; Qiu, G.; Lin, H.; Yue, X.; Chen, J.; Zhong, W.; Li, X.; Zhang, L. Using Calibration Transfer Strategy to Update Hyperspectral Model for Quantitating Soluble Solid Content of Blueberry Across Different Batches. Horticulturae 2025, 11, 830. https://doi.org/10.3390/horticulturae11070830
Chen B, Huang X, Tan S, Qiu G, Lin H, Yue X, Chen J, Zhong W, Li X, Zhang L. Using Calibration Transfer Strategy to Update Hyperspectral Model for Quantitating Soluble Solid Content of Blueberry Across Different Batches. Horticulturae. 2025; 11(7):830. https://doi.org/10.3390/horticulturae11070830
Chicago/Turabian StyleChen, Biao, Xuhuang Huang, Shenwen Tan, Guangjun Qiu, Huaiyin Lin, Xuejun Yue, Junzhi Chen, Wenshan Zhong, Xuantian Li, and Le Zhang. 2025. "Using Calibration Transfer Strategy to Update Hyperspectral Model for Quantitating Soluble Solid Content of Blueberry Across Different Batches" Horticulturae 11, no. 7: 830. https://doi.org/10.3390/horticulturae11070830
APA StyleChen, B., Huang, X., Tan, S., Qiu, G., Lin, H., Yue, X., Chen, J., Zhong, W., Li, X., & Zhang, L. (2025). Using Calibration Transfer Strategy to Update Hyperspectral Model for Quantitating Soluble Solid Content of Blueberry Across Different Batches. Horticulturae, 11(7), 830. https://doi.org/10.3390/horticulturae11070830







