Seed Geometry in Species of the Nepetoideae (Lamiaceae)
Abstract
1. Introduction
2. Materials and Methods
2.1. Seeds
2.2. Photography
2.3. Morphological Measurements
2.4. Quantitative Seed Shape Analysis (J-Index)
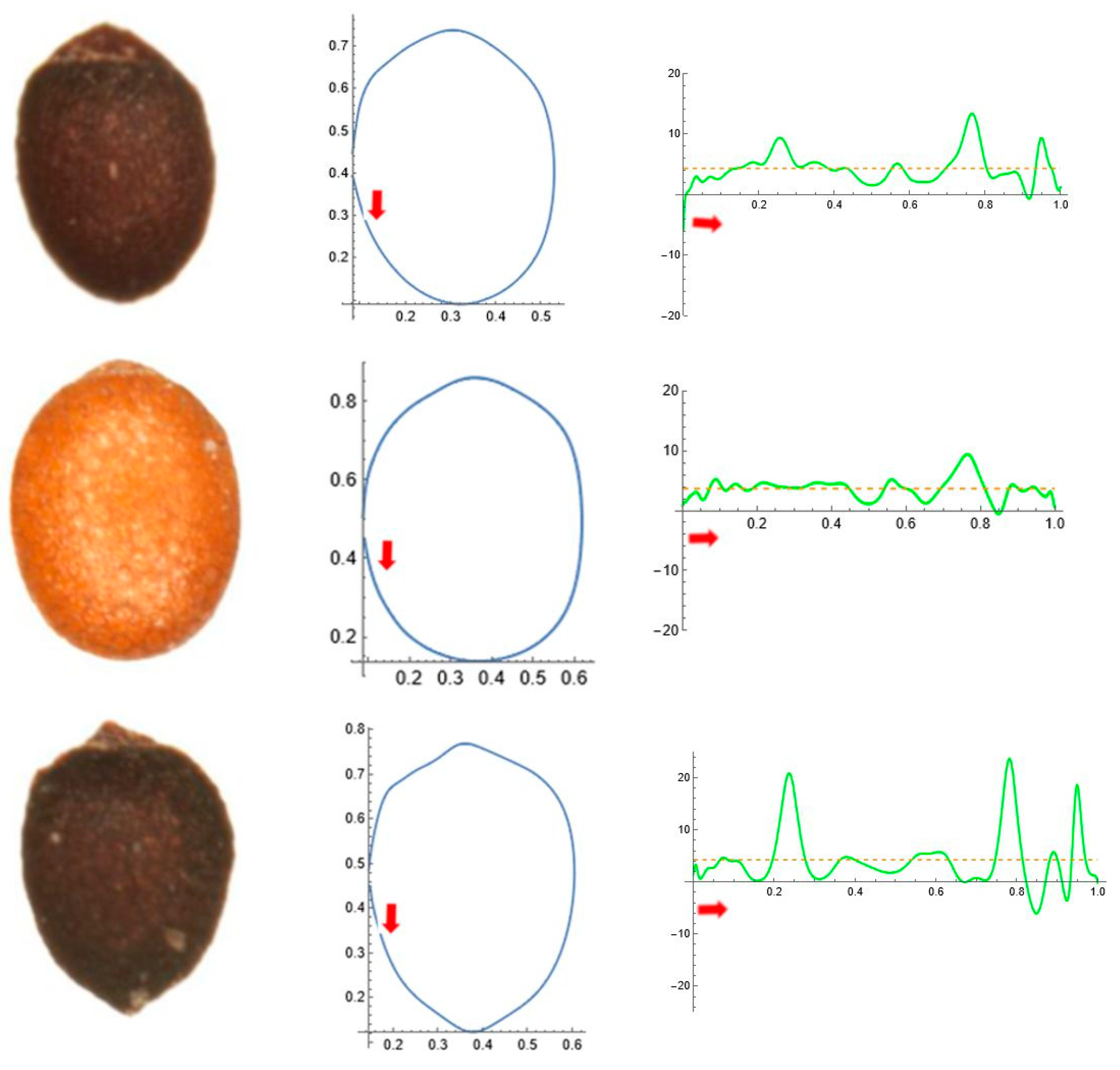
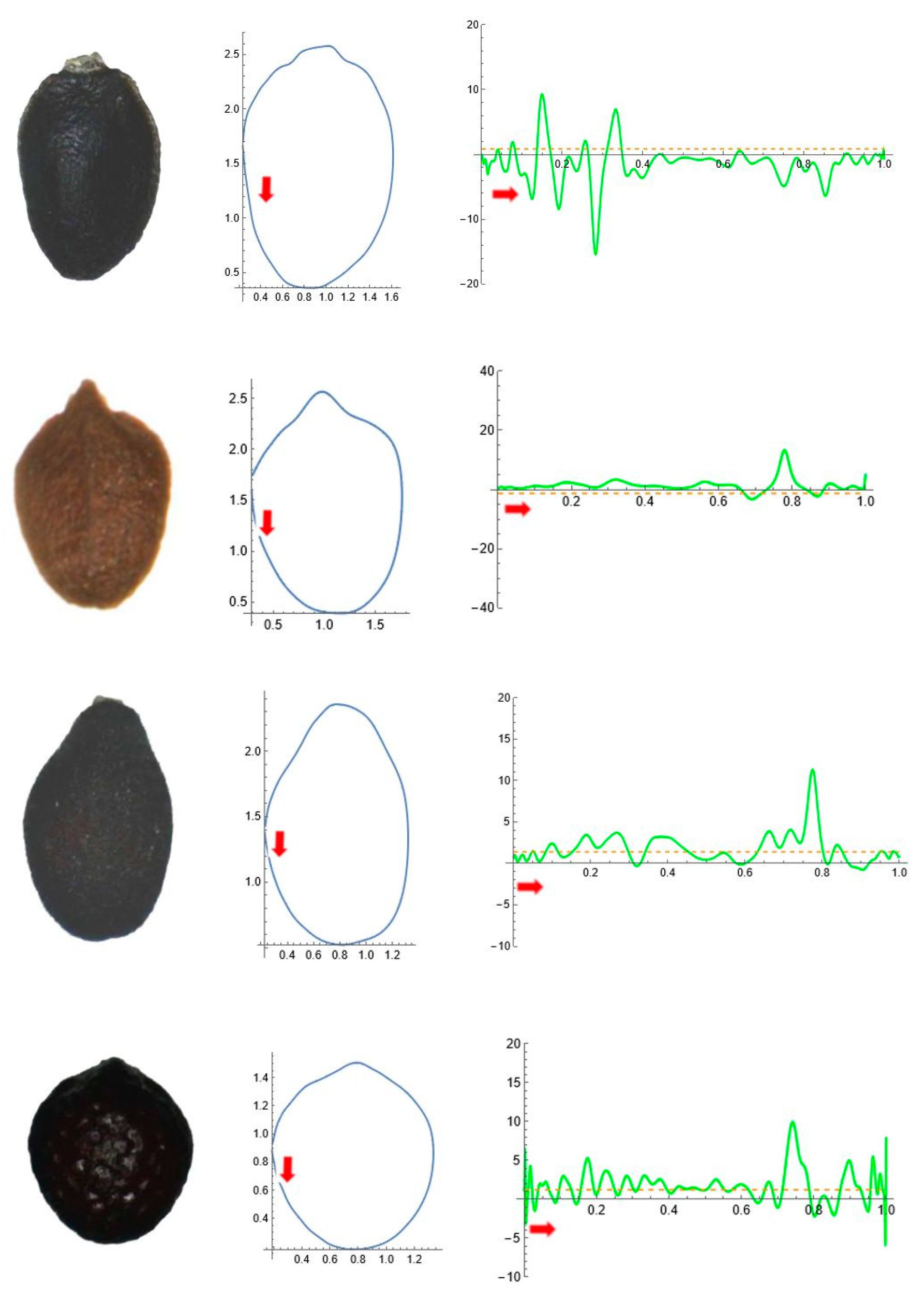
2.5. Curvature Analysis
2.6. Statistical Analysis
3. Results
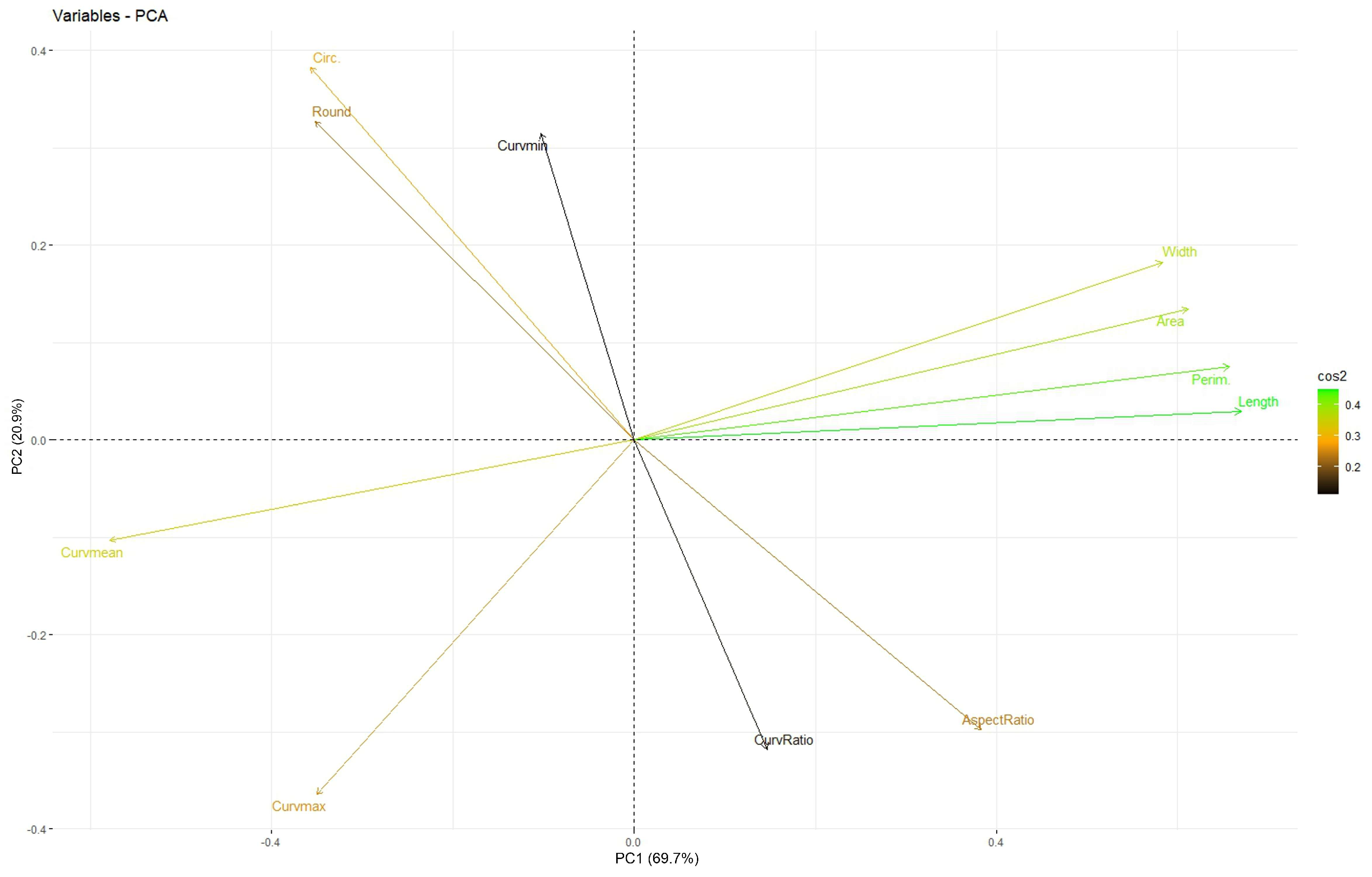
3.1. Factorial Analysis
3.2. Differences Between Tribes and Genera
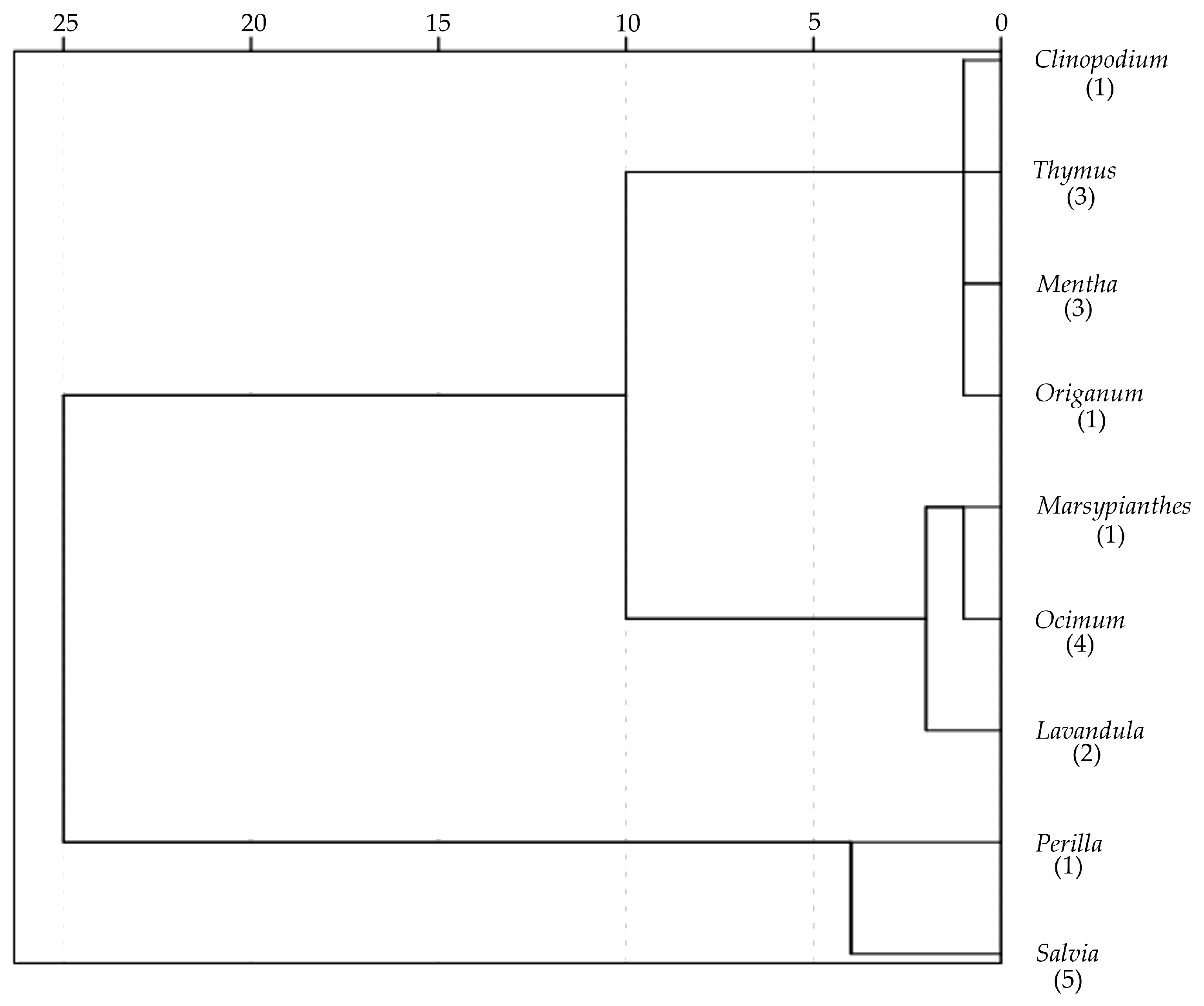
3.3. Hierarchical Clustering
3.4. Average Contours
3.5. Differences in Shape Among the Species of Five Genera
3.5.1. Tribe Mentheae: Mentha
3.5.2. Tribe Mentheae: Salvia
3.5.3. Tribe Mentheae: Thymus
3.5.4. Tribe Ocimeae: Lavandula
3.5.5. Tribe Ocimeae: Ocimum
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Judd, W.S.; Campbell, C.S.; Kellogg, E.A.; Stevens, P.F.; Donoghue, M.J. Plant Systematics: A Phylogenetic Approach; Sinauer Associates, Inc.: Sunderland, MA, USA, 2016. [Google Scholar]
- Berry, P.E. “Lamiales”. Encyclopedia Britannica. Available online: https://www.britannica.com/plant/Lamiales/Main-families (accessed on 20 August 2024).
- Islam, M.; Gottlieb, A.; Maher, M.; Scher, J.; Redford, A. Lamiaceae. Available online: https://www.idtools.org/tools/1060/index.cfm?packageID=2246&entityID=57903 (accessed on 19 November 2024).
- Zhao, F.; Chen, Y.-P.; Salmaki, Y.; Drew, B.T.; Wilson, T.C.; Scheen, A.-C.; Celep, F.; Bräuchler, C.; Bendiksby, M.; Wang, Q.; et al. An updated tribal classification of Lamiaceae based on plastome phylogenomics. BMC Biol. 2021, 19, 2. [Google Scholar] [CrossRef] [PubMed]
- Erdtman, G. Pollen morphology and plant taxonomy. IV. Labiatae, Verbenaceae and Avicenniaceae. Sven. Bot. Tidskr. 1945, 39, 279–285. [Google Scholar]
- Harley, R.M.; Atkins, S.; Budantsev, A.; Cantino, P.D.; Conn, B.J.; Grayer, R.; de Kok, R.; Krestovskaja, T.; Morales, R.; Paton, A.J.; et al. Labiatae. In The Families and Genera of Vascular Plants; Kubitzki, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 7, pp. 167–275. [Google Scholar]
- Stevens, P.F. Angiosperm Phylogeny Website. Version 14, July 2017 [and More or Less Continuously Updated Since].” Will Do. 2001 Onwards. Available online: http://www.mobot.org/MOBOT/research/APweb/ (accessed on 20 December 2024).
- Paton, A.J.; Springate, D.; Suddee, S.; Otieno, D.; Grayer, R.J.; Harley, M.M.; Willis, F.; Simmonds, M.S.; Powell, M.P.; Savolainen, V. Phylogeny and evolution of basils and allies (Ocimeae, Labiatae) based on three plastid DNA regions. Mol. Phylogenet. Evol. 2004, 31, 277–299. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, X.; Chen, Y.; Xu, C.; Wang, Y.; Wang, Q. Phylogenomic analyses revealed widely occurring hybridization events across Elsholtzieae (Lamiaceae). Mol. Phylogenet. Evol. 2024, 198, 108112. [Google Scholar] [CrossRef]
- Marcinek, K.; Krejpcio, Z. Chia seeds (Salvia hispanica): Health promoting properties and therapeutic applications—A review. Rocz. Panstw. Zakl. Hig. 2017, 68, 123–129. [Google Scholar]
- Kulczyński, B.; Kobus-Cisowska, J.; Taczanowski, M.; Kmiecik, D.; Gramza-Michałowska, A. The Chemical Composition and Nutritional Value of Chia Seeds-Current State of Knowledge. Nutrients 2019, 11, 1242. [Google Scholar] [CrossRef]
- Melo, D.; Machado, T.B.; Oliveira, M.B.P.P. Chia seeds: An ancient grain trending in modern human diets. Food Funct. 2019, 10, 3068–3089. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, L.; Hong, X.; Huang, Y.; Lou, G.; Hou, Z.; Abozeid, A.; Wei, Y.; Yang, D. Metabolomic and antioxidant analyses of Salvia miltiorrhiza Bunge and Salvia prattii Hemsl. seeds. Nat. Prod. Res. 2024, 38, 3909–3916. [Google Scholar] [CrossRef]
- Habtemariam, S. Molecular pharmacology of Rosmarinic and Salvianolic acids: Potential seeds for Alzheimer’s and vascular dementia drugs. Int. J. Mol. Sci. 2018, 19, 458. [Google Scholar] [CrossRef]
- Kasem, W.T. Pollen grains and seed-morphology as related to biochemical patterns in five species of genus Ocimum L (Lamiaceae Juss.) of Saudi Arabia. J. Phytol. 2017, 8, 42–48. [Google Scholar] [CrossRef]
- Khali, K.A. Seed morphology and surface microstructure of the genus Plectranthus L. (Lamiaceae) in Arabian Peninsula highlighting on their systematic implications. Aust. J. Crop Sci. 2016, 10, 1222–1231. [Google Scholar] [CrossRef]
- Ozkan, M.; Soy, E. Morphology, Anatomy, Hair and Karyotype Structure of Salvia blepharoclaena Hedge and Hub.-Mor. (Lamiaceae), Endemic to Turkey. Pak. J. Biol. Sci 2007, 10, 893–898. [Google Scholar] [CrossRef]
- Akgül, G.; Ketenoğlu, O.; Pınar, N.M.; Kurt, L. Pollen and seed morphology of the genus Marrubium (Lamiaceae) in Turkey. Ann. Bot. Fenn. 2008, 45, 1–10. [Google Scholar] [CrossRef]
- Sudrarmono Seed Micromorphology of Orthosiphon spp. and Its Relatives (Lamiaceae). In Advances in Biological Sciences Research, Proceedings of the 3rd KOBI Congress, International and National Conferences (KOBICINC 2020), Online, 24–25 November 2020; Atlantis Press: Dordrecht, The Netherlands, 2021; Volume 14, pp. 215–219. [CrossRef]
- Mousavi, S.; Jafari, A.; Najafi, S. Nutlet micromorphological study on Salvia L. (Lamiaceae) from NE Iran. Am. J. Plant Sci. 2013, 4, 1457–1460. [Google Scholar] [CrossRef]
- Kılıç, M.; Mungan Kılıç, F. Nutlet micromorphology of Mardin in Turkey Salvia L. (Lamiaceae) and its systematic implications. Nordic J. Bot. 2021, 39. [Google Scholar] [CrossRef]
- Lane, T.M. Mericarp micromorphology of great plains Scutellaria (Labiatae). Southw. Nat. 1983, 28, 71–79. [Google Scholar] [CrossRef]
- Rodideal, T.; Frunzete, M.E.; Olaru, S.M.; Grigore, M.N.; Zamfirache, M.M.; Ivănescu, L.C. Comparative analysis of seed morphology in genus Scutellaria L. Not. Bot. Horti Agrobot. 2024, 52, 14088. [Google Scholar] [CrossRef]
- Cervantes, E.; Martín, J.J.; Ardanuy, R.; De Diego, J.G.; Tocino, Á. Modeling the Arabidopsis seed shape by a cardioid: Efficacy of the adjustment with a scale change with factor equal to the Golden Ratio and analysis of seed shape in ethylene mutants. J. Plant Physiol. 2010, 167, 408–410. [Google Scholar] [CrossRef]
- Cervantes, E.; Martín, J.J.; Chan, P.K.; Gresshoff, P.M.; Tocino, Á. Seed shape in model legumes: Approximation by a cardioid reveals differences in ethylene insensitive mutants of Lotus japonicus and Medicago truncatula. J. Plant Physiol. 2012, 169, 1359–1365. [Google Scholar] [CrossRef]
- Cervantes, E.; Tocino, A. Geometric analysis of Arabidopsis root apex reveals a new aspect of the ethylene signal transduction pathway in development. J. Plant Physiol. 2005, 162, 1038–1045. [Google Scholar] [CrossRef]
- Noriega, A.; Tocino, A.; Cervantes, E. Hydrogen peroxide treatment results in reduced curvature values in the Arabidopsis root apex. J. Plant Physiol. 2009, 166, 554–558. [Google Scholar] [CrossRef] [PubMed]
- Hedge, I.C. A revision of Salvia in Africa and Arabia. Notes Roy. Bot. Gard. Edinburgh 1974, 33, 1–121. [Google Scholar]
- Drew, B.T.; Sytsma, K.J. Phylogenetics, biogeography, and staminal evolution in the tribe Mentheae (Lamiaceae). Am. J. Bot. 2012, 99, 933–953. [Google Scholar] [CrossRef]
- Walker, J.B.; Sytsma, K.J. Staminal evolution in the genus Salvia (Lamiaceae): Molecular phylogenetic evidence for multiple origins of the staminal lever. Ann. Bot. 2007, 100, 375–391. [Google Scholar] [CrossRef]
- Celep, F.; Kahraman, A.; Atalay, Z.; Doğan, M. Seed morphology of some Salvia species (Lamiaceae) from Turkey and its systematic importance. Plant Syst. Evol. 2014, 300, 1179–1190. [Google Scholar]
- Kriebel, R.; Drew, B.T.; Drummond, C.P.; Gonzalez-Gallegos, J.G.; Celep, F.; Mahdjoub, M.M.; Rose, J.P.; Xiang, C.L.; Hu, G.X.; Walker, J.B.; et al. New World Salvia: Phylogeny, taxonomy, and biogeography. Syst. Bot. 2019, 44, 829–865. [Google Scholar]
- Kahraman, A.; Büyükkartal, H.N.; Doğan, M. Pericarp Ultrastructure of Salvia Section Hemisphace (Mentheae; Nepetoideae; Lamiaceae). Commagene J. Biol. 2018, 2, 1–7. [Google Scholar] [CrossRef]
- Pădure, I.M. Nepeta (Lamiaceae) morphology and anatomy in Romania and their taxonomic significance. In Proceedings of the Plant, Fungal and Habitat Diversity Investigation and Conservation, Proceedings of IV BBC, Sofia, Bulgaria, 20–26 June 2006; pp. 34–38. [Google Scholar]
- Kaya, A.; Dinc, M. Nutlet morphology of six Clinopodium taxa, previously treated as Acinos, in Turkey. Biol. Divers. Conserv. 2015, 7, 119–125. [Google Scholar]
- POWO. Plants of the World Online. Facilitated by the Royal Botanic Gardens, Kew. Published on the Internet. 2024. Available online: https://powo.science.kew.org/ (accessed on 24 December 2024).
- Ferreira, T.; Rasband, W. ImageJ User Guide-Ij1.46r. 2012. 186p. Available online: https://imagej.net/ (accessed on 12 June 2024).
- Cox, E.P. A method of assigning numerical and percentage values to the degree of roundness of sand grains. J. Paleontol. 1927, 1, 179–183. [Google Scholar]
- Riley, N.A. Projection sphericity. J. Sediment. Pet. 1941, 11, 94–97. [Google Scholar]
- Schwartz, H. Two-dimensional feature-shape indexes. Mikroskopie 1980, 37, 64–67. [Google Scholar]
- Cervantes, E.; Martín-Gómez, J.J.; Espinosa-Roldán, F.E.; Muñoz-Organero, G.; Tocino, Á.; Cabello-Sáenz de Santamaría, F. Seed Morphology in Key Spanish Grapevine Cultivars. Agronomy 2021, 11, 734. [Google Scholar] [CrossRef]
- Bézier, P.E. How Renault Uses Numerical Control for Car Body Design and Tooling (Paper 680010 SAE Congress); Society of Automotive Engineers Congress: Detroit, MI, USA, 1968. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing, Version 4.1.2; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org (accessed on 20 November 2024).
- Moein, F.; Jamzad, Z.; Rahiminejad, M.; Landis, J.B.; Mirtadzadini, M.; Soltis, D.E.; Soltis, P.S. Towards a global perspective for Salvia L.: Phylogeny, diversification and floral evolution. J. Evol. Biol. 2023, 36, 589–604. [Google Scholar] [CrossRef] [PubMed]
- Kriebel, R.; Drew, B.T.; Drummond, C.P.; González-Gallegos, J.G.; Celep, F.; Mahdjoub, M.M.; Rose, J.P.; Xiang, C.; Hu, G.; Walker, J.B.; et al. Tracking temporal shifts in area, biomes, and pollinators in the radiation of Salvia (sages) across continents: Leveraging anchored hybrid enrichment and targeted sequence data. Am. J. Bot. 2019, 106, 573–597. [Google Scholar] [CrossRef]
- Martín Gómez, J.J.; Gutiérrez del Pozo, D.; Cervantes, E. Seed shape quantification in the Malvaceae reveals cardioid-shaped seeds predominantly in herbs. Botanica 2019, 25, 21–31. [Google Scholar] [CrossRef]
- Saadaoui, E.; Martín Gómez, J.J.; Tlili, N.; Khaldi, A.; Cervantes, E. Effect of Climate in seed diversity of wild Tunisian Rhus tripartita (Ucria) Grande. J. Adv. Biol. Biotechnol. 2017, 13, 1–10. [Google Scholar] [CrossRef]
- Cervantes, E.; Martín-Gómez, J.J.; del Pozo, D.G.; Tocino, Á. Curvature Analysis of Seed Silhouettes s in the Euphorbiaceae. Seeds 2024, 3, 608–638. [Google Scholar] [CrossRef]
- Katsiotis, A.; Nikoloudakis, N.; Linos, A.; Drossou, A.; Constantinidis, T. Phylogenetic relationships in Origanum spp. based on rDNA sequences and intra-genetic variation of Greek O. vulgare subsp. hirtum revealed by RAPD. Sci. Hortic. 2009, 121, 103–108. [Google Scholar] [CrossRef]
- Bräuchler, C.; Meimberg, H.; Heubl, G. Molecular phylogeny of Menthinae (Lamiaceae, Nepetoideae, Mentheae). Taxonomy, biogeography and conflicts. Mol. Phylogenet. Evol. 2010, 55, 501–523. [Google Scholar] [CrossRef]
- Li, P.; Qi, Z.-C.; Liu, L.-X.; Ohi-Toma, T.; Lee, J.; Hsieh, T.-H.; Fu, C.-X.; Cameron, K.M.; Qiu, Y.-X. Molecular phylogenetics and biogeography of the mint tribe Elsholtzieae (Nepetoideae, Lamiaceae), with an emphasis on its diversification in East Asia. Sci. Rep. 2017, 7, 2057. [Google Scholar] [CrossRef]
- Altindal, D. Determination of genetic diversity of natural sage populations in Mugla region of Turkey. Int. J. Environ. Sci. Technol. 2019, 16, 5219–5226. [Google Scholar] [CrossRef]
- Elmas, S.; Arabaci, O.; Akpinar, E.; Hasancebi, S.; Zeybek, A. Chemical and molecular characterization of Anatolian Sage (Salvia fruticosa mill.) populations distributed naturally in Southwestern Aegean. Appl. Ecol. Environ. Res. 2021, 19, 1407–1421. [Google Scholar] [CrossRef]
- Craft, J.D.; Satyal, P.; Setzer, W.N. The Chemotaxonomy of Common Sage (Salvia officinalis) Based on the Volatile Constituents. Medicines 2017, 4, 47. [Google Scholar] [CrossRef]
- Qian, J.; Song, J.; Gao, H.; Zhu, Y.; Xu, J.; Pang, X.; Yao, H.; Sun, C.; Li, X.; Li, C.; et al. The complete chloroplast genome sequence of the medicinal plant Salvia miltiorrhiza. PLoS ONE 2013, 8, e57607. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, L.; Yang, Y.; Wang, Y.; Yang, L.; Wei, C.; Guo, J.; Yan, K. Complete chloroplast genome sequences of Phlomis fruticose and Phlomoides strigosa and comparative analysis of the genus Phlomis sensu lato (Lamiaceae). Front. Plant Sci. 2022, 13, 1022273. [Google Scholar] [CrossRef]
- Cui, N.; Liao, B.-S.; Liang, C.-L.; Li, S.-F.; Zhang, H.; Xu, J.; Li, X.-W.; Chen, S.-L. Complete chloroplast genome of Salvia plebeia: Organization, specific barcode and phylogenetic analysis. Chin. J. Nat. Med. 2020, 18, 563–572. [Google Scholar] [CrossRef]
- Gao, C.; Wu, C.; Zhang, Q.; Zhao, X.; Wu, M.; Chen, R.; Zhao, Y.; Li, Z. Characterization of chloroplast genomes from two Salvia medicinal plants and gene transfer among their mitochondrial and chloroplast genomes. Front. Genet. 2020, 11, 574962. [Google Scholar] [CrossRef]
- Su, T.; Geng, Y.-F.; Xiang, C.-L.; Zhao, F.; Wang, M.; Gu, L.; Hu, G.-X. Chloroplast genome of Salvia sect: Drymosphace: Comparative and phylogenetic analysis. Diversity 2022, 14, 324. [Google Scholar] [CrossRef]
- Yu, D.; Pei, Y.; Cui, N.; Zhao, G.; Hou, M.; Chen, Y.; Chen, J.; Li, X. Comparative and phylogenetic analysis of complete chloroplast genome sequences of Salvia regarding its worldwide distribution. Sci. Rep. 2023, 13, 14268. [Google Scholar] [CrossRef]
- Bornowski, N.; Hamilton, J.P.; Liao, P.; Wood, J.C.; Dudareva, N.; Buell, C.R. Genome sequencing of four culinary herbs reveals terpenoid genes underlying chemodiversity in the Nepetoideae. DNA Res. 2020, 27, dsaa016. [Google Scholar] [CrossRef]


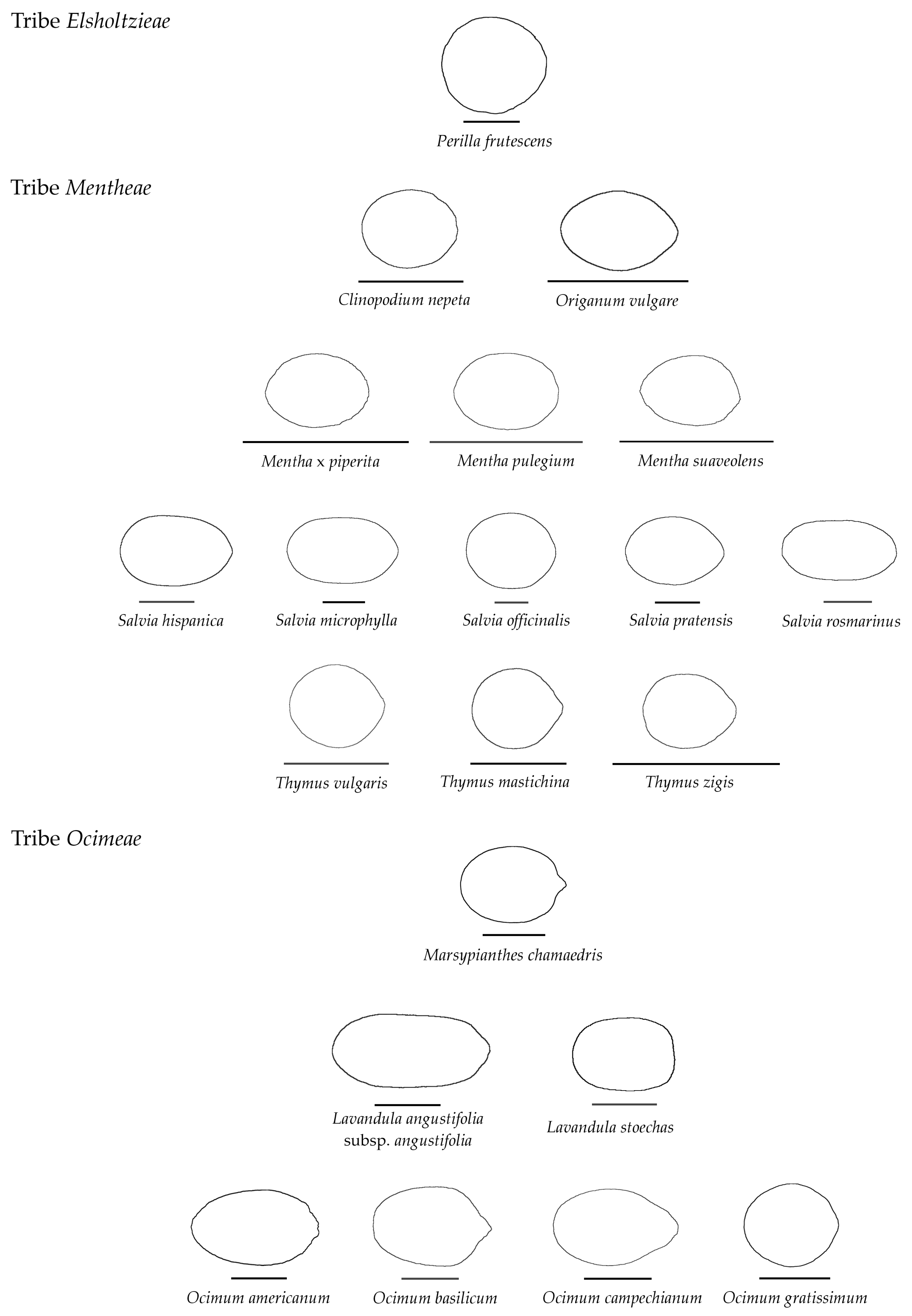
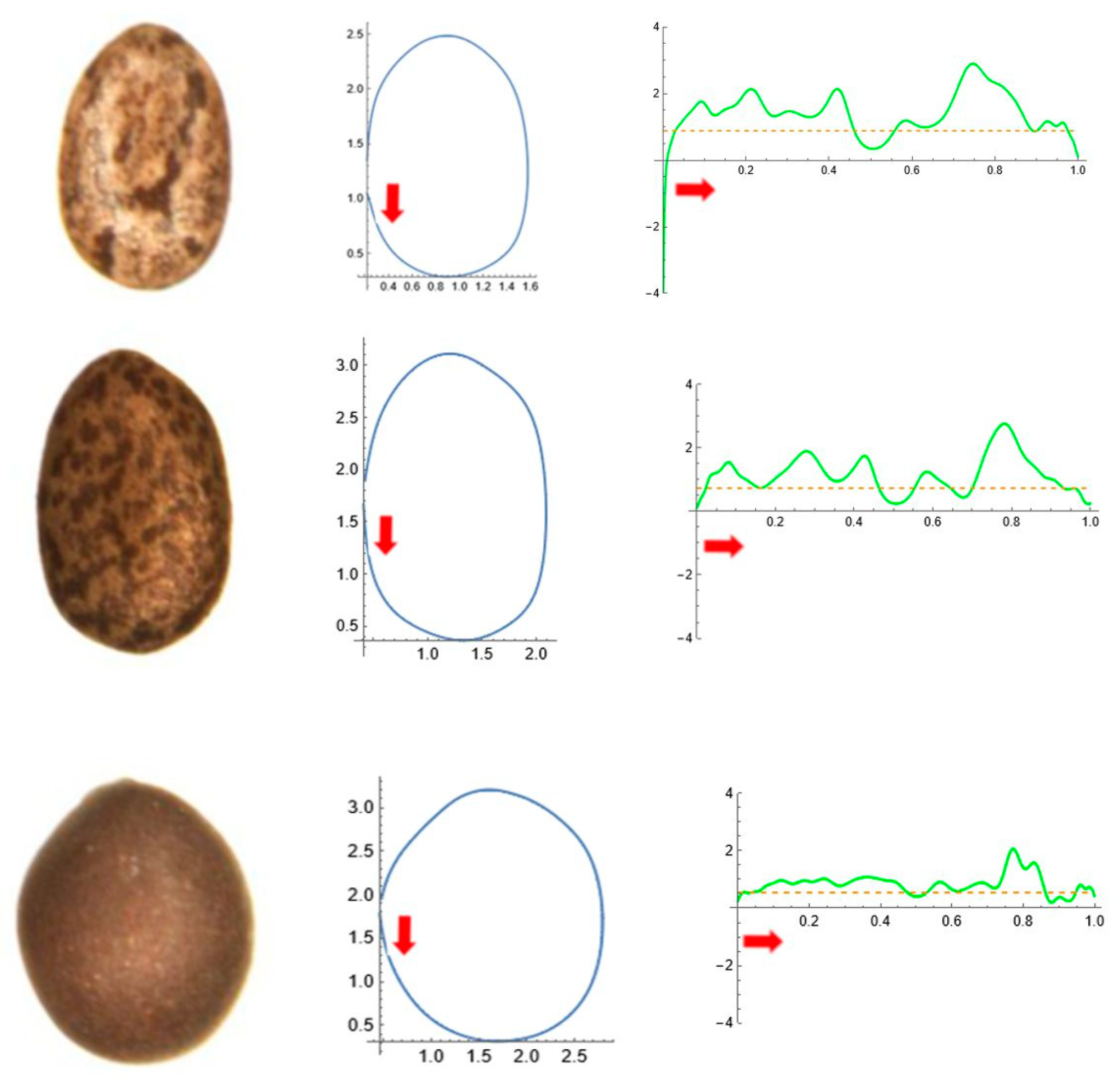
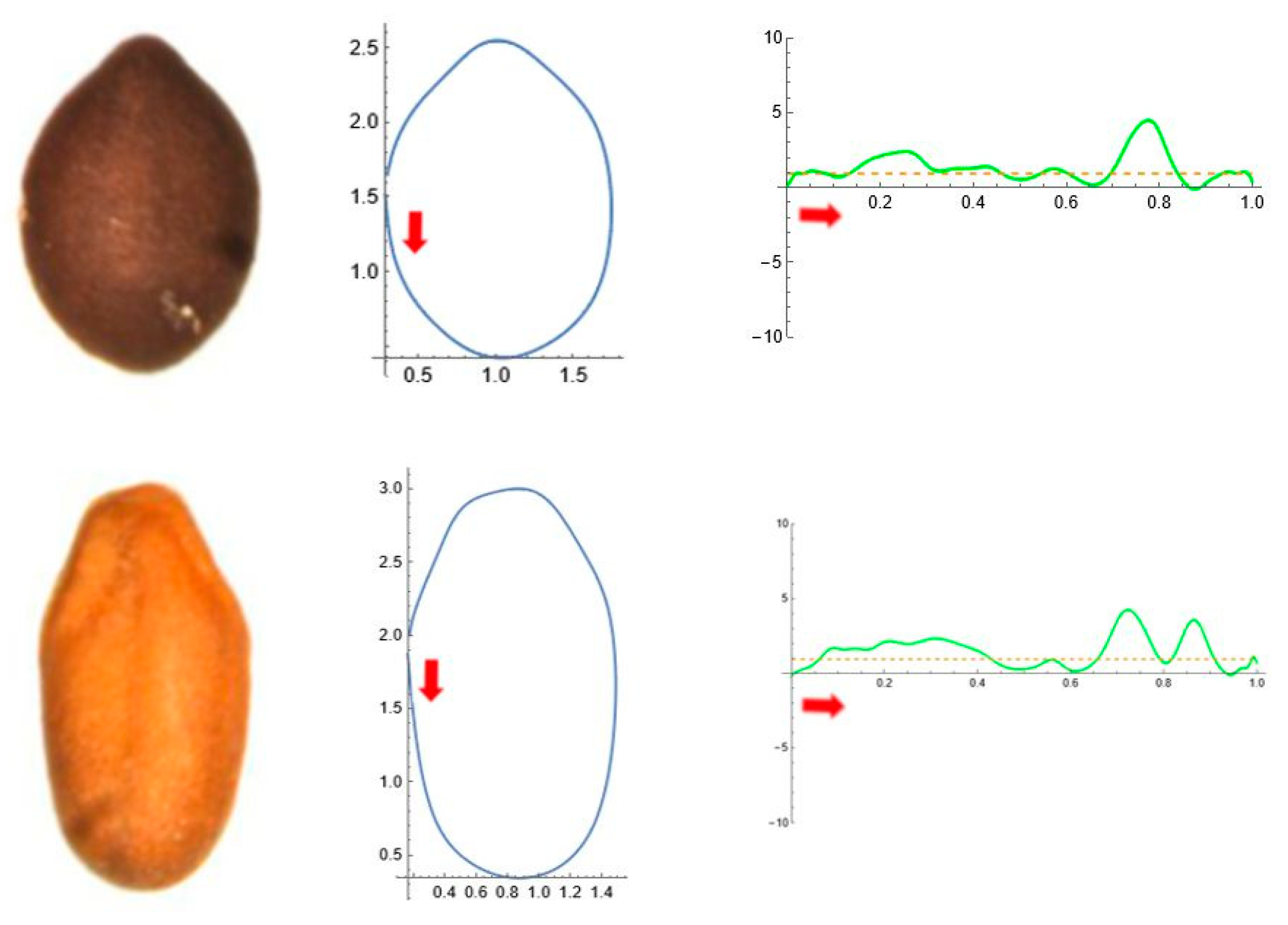
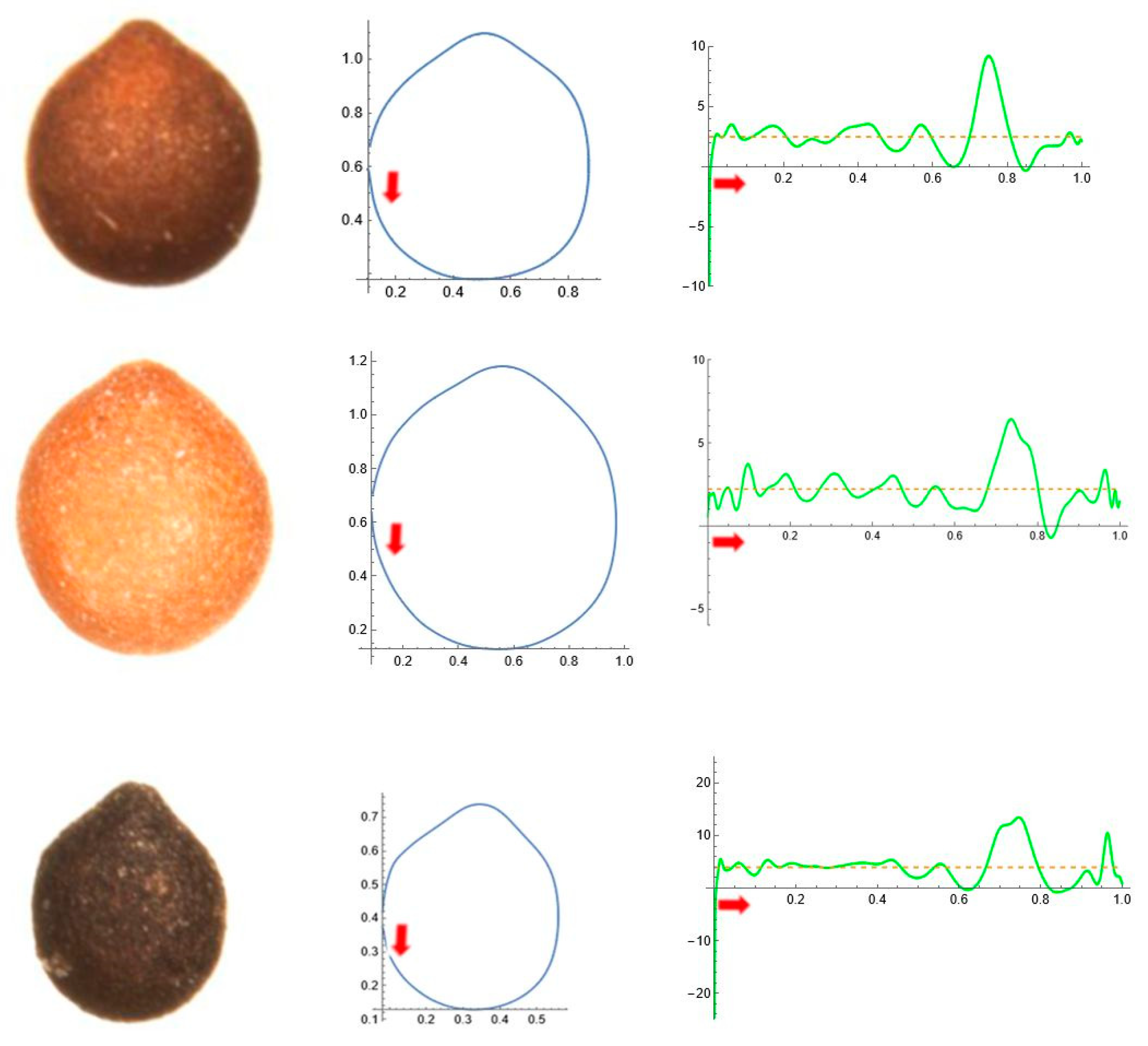
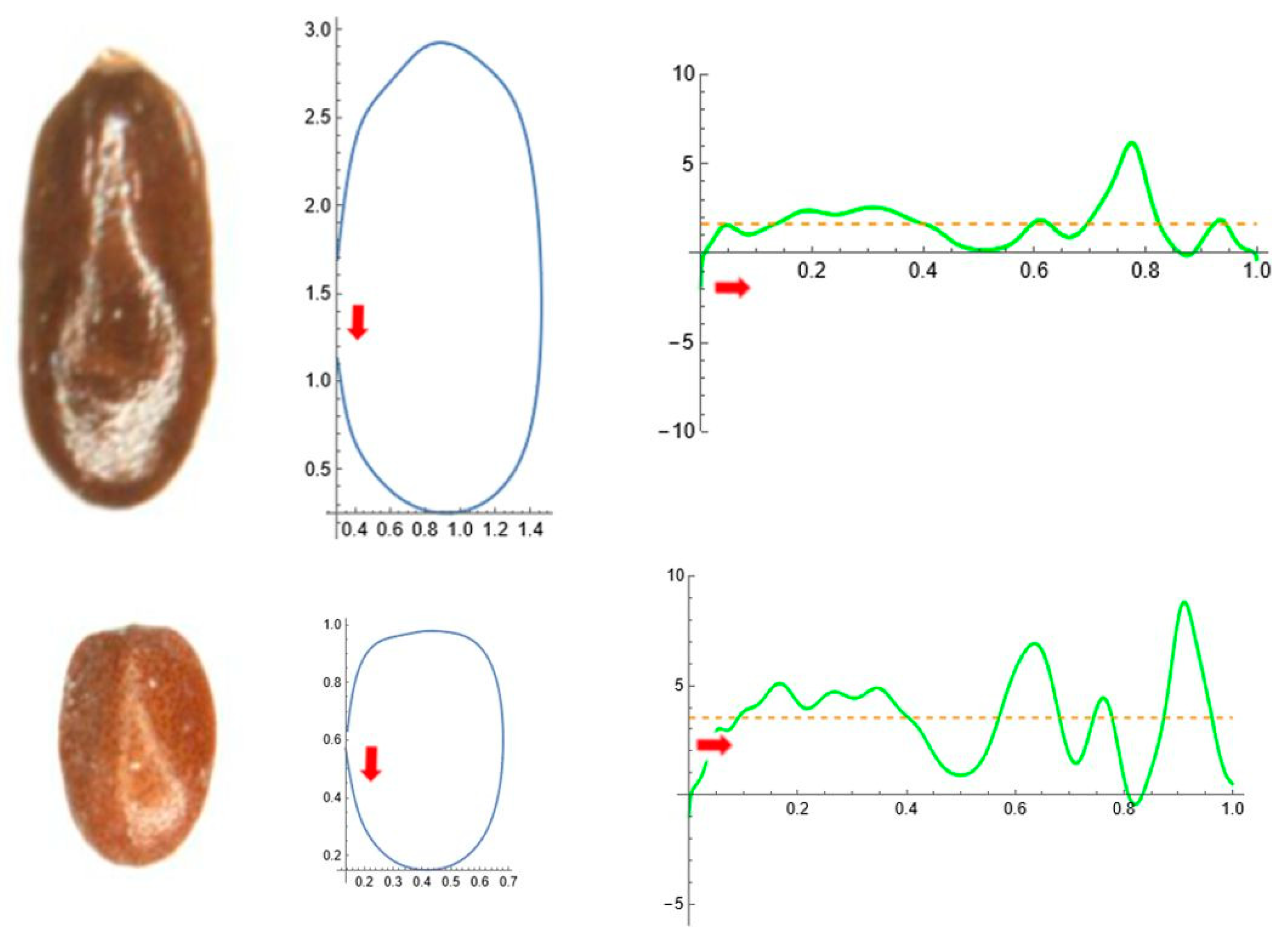
| Tribe/Species | Population (Place of Origin and Date of Collection) | Natural Distribution |
|---|---|---|
| Elsholtzieae | ||
| Perilla frutescens (L.) Britton | Commercial seeds (Dolça Revolució, Barcelona, Spain) | India/China |
| Mentheae | ||
| Clinopodium nepeta (L.) Kuntze | Wild population. Villanueva de Gómez (20 August 2024) | Mediterranean |
| Mentha × piperita L. | Cultivated plants. Villanueva de Gómez (20 August 2024) | European |
| Mentha pulegium L. | Commercial seeds (Eurogarden, Fitó, Barcelona, Spain) | European/Asiatic |
| Mentha suaveolens Ehrh. | Wild population. Villanueva de Gómez (20 August 2024) | European |
| Origanum vulgare L. | Cultivated plants. Salamanca (20 September 2024) | European |
| Salvia hispanica L. | Commercial seeds (Eurogarden, Fitó, Barcelona, Spain) | Mesoamerican |
| Salvia microphylla Sessé & Moc. | Cultivated plants. Villanueva de Gómez (20 July 2024) | Neotropical |
| Salvia officinalis L. | Commercial seeds (Semillas Marcos, Salamanca, Spain) | Mediterranean |
| Salvia pratensis L. | Wild population. Villanueva de Gómez (20 August 2024) | European |
| Salvia rosmarinus Spenn. | Commercial seeds (Eurogarden, Fitó, Barcelona, Spain) | Mediterranean |
| Thymus mastichina (L.) L. | Wild population. Villanueva de Gómez (20 August 2024) | Mediterranean |
| Thymus vulgaris L. | Commercial seeds (Eurogarden, Fitó, Barcelona, Spain) | Mediterranean |
| Thymus zygis L. | Commercial seeds (Eurogarden, Fitó, Barcelona, Spain) | Mediterranean |
| Ocimeae | ||
| Lavandula angustifolia subsp. angustifolia | Commercial seeds (Eurogarden, Fitó, Barcelona, Spain) | Mediterranean |
| Lavandula stoechas subsp. pedunculata (Mill.) Samp. Ex Rozeira | Wild population. Villanueva de Gómez (20 August 2024) | Mediterranean |
| Marsypianthes chamaedris (Vahl) Kuntze | Wild population, Puyo, Ecuador (October 2024) | Neotropical |
| Ocimum americanum L. | Cultivated plants, Puyo, Ecuador (October 2024) | Paleotropical |
| Ocimum basilicum L. | Comercial seeds (Eurogarden, Fitó, Barcelona, Spain) | Paleotropical/Australian |
| Ocimum campechianum Mill. | Wild population, Puyo, Ecuador (October 2024) | Neotropical |
| Ocimum gratissimum L. | Cultivated plants, Puyo, Ecuador (October 2024) | Paleotropical |
| Measurement | PC1 (Size) | PC2 (Roundness) | PC3 (Curvature Ratio) |
|---|---|---|---|
| Perimeter | 0.974 | ||
| Width | 0.972 | ||
| Area | 0.953 | ||
| Length | 0.939 | ||
| Mean curvature | −0.923 | ||
| Aspect ratio | −0.930 | ||
| Roundness | 0.918 | ||
| Circularity | 0.851 | ||
| Ratio Max to Mean curvature | −0.945 | ||
| Min. curvature | 0.885 | ||
| Max. curvature | −0.614 | −0.693 | |
| Percentage variation | 39.5 | 23.7 | 20.6 |
| Accumulated | 39.5 | 63.3 | 83.9 |
| Tribe | N | PC1 (Size) | PC2 (Roundness) | PC3 (Curvature Ratio) |
|---|---|---|---|---|
| Elsholtzieae (Perilla) | 6 | 0.96 (14.0) c | 1.24 (26.1) c | 0.37 (66.1) b |
| Mentheae (Clinopodium, Mentha, Origanum, Salvia, Thymus) | 74 | −0.20 (584.8) a | 0.10 (864.3) b | 0.41 (138.2) b |
| Ocimeae (Lavandula, Marsypianthes, Ocimum) | 42 | 0.21 (276.2) b | −0.36 (294.2) a | −0.77 (157.2) a |
| Genus | N | PC1 (Size) | PC2 (Roundness) | PC3 (Minimum Curvature) |
|---|---|---|---|---|
| Perilla (P. frutescens) | 6 | 0.96 (14.0) e | 1.24 (26.1) e | 0.37 (66.1) cd |
| Clinopodium (C. nepeta) | 6 | −0.54 (16.6) bc | 0.66 (49.6) cd | 0.13 (303.9) cd |
| Mentha (M. × piperita, M. pulegium, M. suaveolens) | 18 | −1.40 (16.7) a | −0.30 (155.7) b | 0.03 (3043.9) cd |
| Origanum (O. vulgare) | 5 | −0.90 (6.8) b | 0.04 (338.3) b | −0.15 (245.5) c |
| Salvia (S. hispanica, S. microphylla, S. officinalis, S. pratensis, S. rosmarinus) | 28 | 1.14 (47.4) e | −0.24 (452.4) b | 0.73 (23.2) e |
| Thymus (T. mastichina, T. vulgaris, T. zygis) | 17 | −0.79 (52.6) b | 0.93 (34.8) d | 0.53 (54.9) cd |
| Lavandula (L. angustifolia subsp. angustifolia, L. stoechas subsp. pedunculata) | 12 | −0.27 (310.6) bcd | −1.29 (79.8) a | 0.55 (66.6) de |
| Marsypianthes (M. chamaedris) | 6 | 0.31 (40.5) cd | 0.48 (57.5) bc | −1.99(19.8) a |
| Ocimum (O. americanum, O. basilicum, O. campechianum, O. gratissimum) | 24 | 0.43 (65.6) d | −0.10 (841.0) b | −1.12 (92.3) b |
| N | A | C | AR | S | Cmax | Cmin | Mean | Ratio | |
|---|---|---|---|---|---|---|---|---|---|
| M. × piperita | 6 | 0.23 a (7.9) | 0.84 b (1.7) | 1.38 ab (6.3) | 0.987 b (0.2) | 15.1 b (37.3) | 0.3 b (463) | 4.1 b (8.7) | 3.7 b (32.2) |
| M. pulegium | 6 | 0.30 c (9.3) | 0.84 b (2.4) | 1.35 a (7.7) | 0.991 c (0.1) | 9.6 a (11.1) | −0.5 ab (121) | 3.7 a (4.5) | 2.6 a (15.3) |
| M. suaveolens | 6 | 0.25 b (9.3) | 0.80 a (2.2) | 1.41 b (5.0) | 0.983 a (0.3) | 21.6 b (20.7) | −2.4 a (76) | 3.9 b (23.8) | 6.1 b (43) |
| Species | N | IJ MMpip | IJ MMpul | IJ MMsuav |
|---|---|---|---|---|
| M. × piperita | 20 | 92.3 b (1.6) | 93.0 b (1.5) | 91.6 ab (1.8) |
| M. pulegium | 20 | 91.8 ab (2.4) | 93.2 b (1.8) | 91.0 a (2.3) |
| M. suaveolens | 20 | 91.2 a (2.1) | 91.8 a (1.8) | 92.6 b (1.8) |
| N | A | C | AR | S | Cmax | Cmin | Mean | Ratio | |
|---|---|---|---|---|---|---|---|---|---|
| S. hispanica | 6 | 2.23 a (10.7) | 0.83 b (1.0) | 1.55 c (2.8) | 0.991 b (0.1) | 3.3 b (15.6) | 0.4 b (42.7) | 1.0 bc (8.9) | 3.3 ab (12.0) |
| S. microphylla | 6 | 3.50 c (7.1) | 0.83 b (1.3) | 1.62 d (3.5) e | 0.992 c (0.1) | 3.3 b (13.6) | 0.2 ab (29.4) | 0.9 b (11.9) | 3.8 ab (8.1) |
| S. officinalis | 6 | 5.11 d (12.3) | 0.89 d (0.9) | 1.16 a (5.1) | 0.991 c (0.1) | 1.8 a (12.2) | 0.3 ab (51.6) | 0.6 a (6.2) | 3.2 a (15.1) |
| S. pratensis | 6 | 2.80 b (11.3) | 0.84 c (1.4) | 1.41 b (3.5) | 0.988 a (0.2) | 3.9 b (16.6) | 0.3 ab (68.3) | 0.9 bc (6.0) | 4.3 b (18.0) |
| S. rosmarinus | 6 | 2.70 b (13.4) | 0.77 a (4.0) | 1.89 a (9.1) | 0.987 a (0.3) | 3.8 b (17.1) | 0.1 a (74.2) | 1.0 c (9.8) | 3.7 ab (18.2) |
| N | A | C | AR | S | Cmax | Cmin | Mean | Ratio | |
|---|---|---|---|---|---|---|---|---|---|
| T. mastichina | 6 | 0.65 b (13.1) | 0.88 b (0.8) | 1.09 a (3.7) | 0.988 a (0.2) | 7.5 a (17.7) | −0.8 a (129) | 2.4 a (6.4) | 3.2 b (17.1) |
| T. vulgaris | 6 | 0.62 b (15.4) | 0.88 b (0.7) | 1.12 a (3.8) | 0.992 a (0.1) | 6.1 a (16.6) | 0.4 b (178) | 2.5 a (11.3) | 2.4 a (19.6) |
| T. zygis | 6 | 0.21 a (12.5) | 0.86 a (1.5) | 1.23 b (7.8) | 0.988 b (0.2) | 12.4 b (7.1) | 0.3 ab (337) | 4.1 b (7.7) | 3.0 ab (9.2) |
| Species | N | IJ MTmast | IJ MTvulg | IJ MTzig |
|---|---|---|---|---|
| T. mastichina | 20 | 94.8 c (0.8) | 93.8 b (1.2) | 89.8 a (2.3) |
| T. vulgaris | 20 | 93.7 b (1.1) | 94.8 c (0.8) | 90.7 a (1.9) |
| T. zygis | 20 | 89.7 a (3.9) | 90.5 a (3.5) | 92.3 b (2.4) |
| N | A | C | AR | S | Cmax | Cmin | Mean | Ratio | |
|---|---|---|---|---|---|---|---|---|---|
| L. angustifolia | 6 | 2.36 b (7.7) | 0.73 a (3.1) | 2.07 b (5.1) | 0.986 a (0.1) | 5.0 a (24.6) | 0.2 b (14.8) | 1.7 a (6.2) | 3.0 a (23.1) |
| L. stoechas | 6 | 0.40 a (8.4) | 0.84 b (2.4) | 1.40 a (4.2) | 0.987 a (0.2) | 9.3 b (30.7) | −1.4 a (74) | 3.5 b (3.6) | 2.7 a (32.0) |
| N | A | C | AR | S | Cmax | Cmin | Mean | Ratio | |
|---|---|---|---|---|---|---|---|---|---|
| O. americanum | 6 | 2.57 d (5.0) | 0.74 a (4.3) | 1.68 c (5.9) | 0.985 b (0.2) | 13.4 b (25.7) | −9.2 a (27.1) | 1.0 a (11.7) | 14.2 b (34.0) |
| O. basilicum | 6 | 2.34 c (6.2) | 0.79 c (2.7) | 1.44 b (6.2) | 0.977 a (0.6) | 13.1 b (21.7) | −1.5 bc (66.9) | 1.4 c (5.4) | 9.5 b (22.4) |
| O. campechianum | 6 | 1.64 b (6.1) | 0.77 b (1.7) | 1.63 c (3.0) | 0.986 b (0.2) | 8.4 a (25.3) | −1.0 c (56.1) | 1.3 b (8.4) | 6.7 a (21.3) |
| O. gratissimum | 6 | 1.20 a (5.1) | 0.85 d (1.4) | 1.14 a (2.3) | 0.990 c (0.1) | 8.4 a (16.7) | −2.1 b (23.2) | 1.2 b (4.4) | 7.2 a (15.2) |
| N | MOam | MOba | MOca | MOgr | |
|---|---|---|---|---|---|
| O. americanum | 20 | 94.3 d (1.9) | 86.8 b (3.5) | 88.9 c (1.5) | 73.9 a (5.1) |
| O. basilicum | 20 | 88.1 b (3.2) | 93.3 c (1.3) | 87.8 b (2.3) | 84.9 c (3.5) |
| O. campechianum | 20 | 90.4 c (0.9) | 87.9 b (1.4) | 95.3 d (0.8) | 78.9 b (1.9) |
| O. gratisimum | 20 | 77.6 a (1.8) | 84.3 a (1.8) | 77.3 a (1.7) | 96.2 d (0.5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez del Pozo, D.; Martín-Gómez, J.J.; Reyes Tomala, N.I.; Tocino, Á.; Cervantes, E. Seed Geometry in Species of the Nepetoideae (Lamiaceae). Horticulturae 2025, 11, 315. https://doi.org/10.3390/horticulturae11030315
Gutiérrez del Pozo D, Martín-Gómez JJ, Reyes Tomala NI, Tocino Á, Cervantes E. Seed Geometry in Species of the Nepetoideae (Lamiaceae). Horticulturae. 2025; 11(3):315. https://doi.org/10.3390/horticulturae11030315
Chicago/Turabian StyleGutiérrez del Pozo, Diego, José Javier Martín-Gómez, Nick Israel Reyes Tomala, Ángel Tocino, and Emilio Cervantes. 2025. "Seed Geometry in Species of the Nepetoideae (Lamiaceae)" Horticulturae 11, no. 3: 315. https://doi.org/10.3390/horticulturae11030315
APA StyleGutiérrez del Pozo, D., Martín-Gómez, J. J., Reyes Tomala, N. I., Tocino, Á., & Cervantes, E. (2025). Seed Geometry in Species of the Nepetoideae (Lamiaceae). Horticulturae, 11(3), 315. https://doi.org/10.3390/horticulturae11030315







