Mass Modeling of Six Loquat (Eriobotrya japonica Lindl.) Varieties for Post-Harvest Grading Based on Physical Attributes

Abstract

Loquat fruit is valued for its pleasant taste and favorable ripening period. However, its delicate texture and high perishability make it highly vulnerable to damage during packaging, so the fruit is usually packed by hand. Developing a fruit-sizing machine could increase commercial market opportunities. Automated mass detection reduces manual sorting errors and labor requirements. Overall, it enhances grading accuracy, speed, and uniformity in loquat processing. It also helps distinguish between ripe, underripe, and overripe fruits through subtle mass differences. Mass modeling has proven to be an effective baseline approach for the development and optimization of grading machines, and its efficiency has been demonstrated across different fruit types. Here, we present a comparative analysis of various models for mass modeling of six international and Italian loquat varieties (“Algerie,” “Peluche,” “Golden Nugget,” “Virticchiara,” “Nespolone di Trabia,” and “Claudia”) cultivated in southern Italy. On fifty fruits per variety, singular mass and spatial diameters [longitudinal (DL), maximum transverse (DT1), and minimum transverse (DT2) were measured. Linear and non-linear regression analyses, including quadratic, polynomial, and cubic models, were applied to both the complete dataset and individual varieties. A set of predictors was used, including DL (length), DT1 (width), and DT2 (thickness), ellipsoid and oblate spheroid volume. Model performance was evaluated based on higher R² values, and lower RMSE and MBE values. The best general model was obtained using an ellipsoidal volume (R² = 0.97, RMSE = 2.76). Both linear and cubic models demonstrated high suitability across all varieties, with ellipsoidal volume emerging as the most effective predictor. Conversely, (DL) based models were the least suitable, yielding the lowest (R² = 0.41) values in “Virticchiara.” The developed general and specific-variety models and equations provide a solid foundation for establishing high-performance systems for mass and size estimation, which can be effectively integrated into a fruit sizer machine.

1. Introduction

Loquat (Eriobotrya japonica Lindl.) is an evergreen tree species belonging to the Rosaceae family, native to China, and the best adapted to subtropical and warm temperate climates [1]. Loquat is today mainly cultivated in China and Spain, followed by Turkey, Cyprus, Egypt, Greece, Pakistan, and Italy [2,3]. At the beginning of the last century, the loquat was introduced to Italy from Japan. According to the latest available data, loquat is cultivated mostly on the northern coast of Sicily, especially in Palermo Province, with about 400 hectares with an estimated production of approximately 4843 tons, representing 81.8% of the national production.

Loquat cultivation includes both international varieties like “Algerie,” “Magdal,” “Golden Nugget,” “Tanaka,” and “Peluche” [4], and local varieties such as “Virticchiara,” “Nespolone di Trabia,” and “Claudia” [5]. The fruit is a pome of different shapes (flat, round, oval, and elliptic) [6], with white, yellow, or orange flesh and a taste ranging from sweet to sub-acid or acid taste and varies depending on the variety [7]. Loquat fruits are particularly appreciated for their ripening period, occurring in spring in temperate climates, where few other fruits are available on the market. However, their limited storability, high perishability and short shelf life remain the greatest limitations for their commercialization [4,8]. In the local market, the fruit is generally marketed without a packaging process or by using a manual process. Growing competition in the food industry, coupled with new purchasing habits of consumers, has increased demand for higher fruit quality (uniformity of size and shape) [4,9,10]. To meet these requirements, automated grading machines have been increasingly adopted. Grading is often based on physical attributes such as size, shape, mass, or volume, which are critical for optimizing fruit quality and packaging [11,12]. Understanding the relationship between fruit physical attributes and mass could improve grading systems [13]. Since physical attributes are easily measured and detected, modelling them can support the design of accurate, fast, and low-cost postharvest machinery, handling, grading, and sorting equipment [14].

Among these approaches, mass modeling is considered the most reliable method for fruit grading based on robust regression equations. Mass modeling has been successfully applied to predict the mass of several fruits using regression models based on physical properties, such as diameter, length, width, and volume. Both single and multiple predictor models have been employed, including linear, quadratic, power, and polynomial regressions. Its application have been successfully reported for instance in prediction the mass of potato [15], guava [16], mandarin [17], strawberry [18], sweet cherry [19], chebula [20], black sapote [14], fig [21], pomegranate [22], banana [23], mango [24], and Spanish cherry [25].

As for loquat, to our knowledge, only a single study has been conducted on the loquat mass modeling of local Iranian varieties [26]. However, no studies have yet been conducted on Italian or international loquat varieties, and it is well known that different fruit shapes may require different sizing models. Even within the same species, mass modeling can vary from one variety to another.

This work aimed to determine the most suitable mass modeling equation for international and local varieties based on fruit physical attributes. A comparative analysis of three international (Algerie, Peluche, and Golden Nugget) and Italian (Virticchiara, Nespolone di Trabia, and Claudia) loquat varieties was conducted by using linear and non-linear regression analyses, including quadratic, polynomial, and cubic models. Obtained models can be integrated with machine vision techniques and serve effectively in the development of post-harvest machinery.

2. Materials and Methods

2.1. Sample Collection

Loquat fruits were collected at the commercial ripening degree using phenological development stages “BBCH” of the loquat plant (stage 807) [27], organically cultivated in an experimental orchard located in Palermo, Italy (38°07′77″ N, 13°37′27″ E). Fifty loquat fruits per variety were randomly collected, belonging to the international varieties “Algerie,” “Peluche,” and “Golden Nugget,” and to the local varieties “Virticchiara,” “Nespolone di Trabia,” and “Claudia” for a total of 300 fruits (Figure 1). The fruits were brought to the postharvest laboratory of the SAAF department of the University of Palermo, Italy where various physical attributes were measured.

The mass of each fruit was measured using a digital scale (Gibertini, Novate Milanese, Italy) with 0.01 g precision. Three spatial diameters of the loquat fruits, longitudinal diameter (DL), maximum transverse diameter (DT1), and minimum transverse diameter (DT2), were measured following the scheme in Figure 2, using a digital caliper precise to 0.01 mm (Turoni^@, Forlì, Italy). Geometric mean diameter (D_g) (1), aspect ratio (AR) (2), and sphericity (Ψ) (3) were also determined using the following equations.

D_g = (DL × DT1 × DT2)^1/3

(1)

AR = DL/DT1

(2)

Ψ = [(DL × DT1 × DT2)^1/3/DL]

(3)

Fruit volume was calculated following standard shapes. Depending on the variety, the fruits were classified as having either elliptical (ellip) shape or oblate spheroid (osp), and their volume was estimated using Equations (4) and (5), respectively. Then, the actual fruit volume of each fruit was determined using the water displacement method [28,29].

$${\mathrm{v}}_{\mathrm{e}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{p}}={\displaystyle \frac{4}{3}}·\mathrm{\pi }·\left({\displaystyle \frac{\mathrm{D}\mathrm{L}}{2}}\right)·\left({\displaystyle \frac{\mathrm{D}\mathrm{T}1}{2}}\right)·\left({\displaystyle \frac{\mathrm{D}\mathrm{T}2}{2}}\right)$$

(4)

$${\mathrm{v}}_{\mathrm{o}\mathrm{s}\mathrm{p}}={\displaystyle \frac{4}{3}}·\mathrm{\pi }·\left({\displaystyle \frac{\mathrm{D}\mathrm{L}}{2}}\right)·{\left({\displaystyle \frac{\mathrm{D}\mathrm{T}1}{2}}\right)}^2$$

(5)

2.2. Regression Analysis and Model Development

Measured physical attributes were then used for mass modeling prediction based on a single predictor regression model. For all six different varieties, Linear (6), Quadratic (7), Cubic (8), and Polynomial (first inverse (9), second inverse (10), and third inverse (11) order) univariate regression models were employed and tested using measured physical attributes.

$$\mathrm{M}=\mathrm{a}+\mathrm{b}\mathrm{x}$$

(6)

$$\mathrm{M}=\mathrm{a}+\mathrm{b}\mathrm{x}+\mathrm{c}{\mathrm{x}}^2$$

(7)

$$\mathrm{M}=\mathrm{a}+\mathrm{b}\mathrm{x}+\mathrm{c}{\mathrm{x}}^2+\mathrm{d}{\mathrm{x}}^3$$

(8)

$$\mathrm{M} ={\displaystyle \frac{\mathrm{a}}{\mathrm{x}}}+\mathrm{b}$$

(9)

$$\mathrm{M} ={\displaystyle \frac{\mathrm{a}}{{\mathrm{x}}^2}}+{\displaystyle \frac{\mathrm{b}}{\mathrm{x}}}+\mathrm{c}$$

(10)

$$\mathrm{M} ={\displaystyle \frac{\mathrm{a}}{{\mathrm{x}}^3}}+{\displaystyle \frac{\mathrm{b}}{{\mathrm{x}}^2}}+{\displaystyle \frac{\mathrm{c}}{\mathrm{x}}}+\mathrm{d}$$

(11)

where M indicates fruit mass (6)–(11); a, b, c, and d are the regression constants, and x is the tested physical attributes. A regression model was generated using DL, DT1, DT2, and volume V_osp and V_ellip. Although multiple regression was considered, only single-predictor models were developed. This approach was chosen to avoid redundancy among highly correlated predictors and to ensure models remain simple and applicable in post-harvest grading systems or for lab measurements.

Data was analyzed both pooled across varieties (general models) and by variety (variety-specific models). For each loquat variety, all possible models were evaluated, and the best-performing ones were retained and selected. Later, each predictor variable was tested for different types of regression to obtain the model that provided the best possible prediction. Within each regression type, the optimal equation was then identified using single predictor attributes. Goodness-of-fit and predictive accuracy were assessed using the coefficient of determination (R²), root mean square error (RMSE), and mean bias error (MBE), which was used to evaluate the bias of the model and its tendency to either underestimate or overestimate predicted values.

The best-fitting model was defined as the one with the highest R², the lowest RMSE, and the MBE closest to zero (in absolute value). Where applicable, a t-test on residual mean was used to assess whether bias differed from zero, yet none of the models showed significant bias, confirming that prediction errors were centered around zero). Anova was performed to compare physical attributes among the different varieties. All data analysis and models were performed on Rstudio (R 4.4.2) [30], using the “broom,” “tidyverse,” and “ggplot” packages.

3. Results

3.1. Physical Attributes

Fruit weight differed considerably among varieties, ranging from 33.36 ± 10.0 g in “Algerie” to 63.33 ± 20.88 g in “Peluche” (

Table 1. Descriptive physical attributes and characteristics of the six loquat varieties (three international and three local). Values presented here are mean ± SD. Dg (geometric mean diameter), AR (aspect ratio) and Ψ (sphericity), DL, DT1, and DT2 are in (mm), V, V_(osp), and V_(ellip) are in cm³ and fruit weight in (g). Statistical significance was indicated when applicable: p < 0.05 (*) and p < 0.01 (**), based on ANOVA.

Attributes	Algerie	Claudia	Golden Nugget	Nespolone di Trabia	Peluche	Virticchiara
Dg	38.35 ± 3.95	43.09 ± 3.96 *	41.53 ± 4.56	41.51 ± 4.45	48.56 ± 5.52 **	39.54 ± 3.77
Ψ	0.90 ± 0.05	0.86 ± 0.04	0.92 ± 0.06 *	0.92 ± 0.05 *	0.77 ± 0.06 **	0.89 ± 0.06
DL	42.66 ± 4.56	50.12 ± 5.06 *	45.05 ± 5.34	45.29 ± 5.99	63.31 ± 7.36 **	44.48 ± 4.88
DT1	37.50 ± 4.23	41.53 ± 4	41.23 ± 4.61	41.16 ±4.36	43.90 ± 5.94	38.81 ±3.94
DT2	35.34 ± 4.02	38.54 ± 4.05	38.70 ± 4.9	38.46 ± 3.88	41.42 ± 5.44 *	35.96 ± 4.05
V	32.13 ± 9.73	45.41 ± 11.83	39.91 ±12.57	41.60 ±12.53	63.44 ± 12 **	35.57 ±9.35
V(osp)	32.33 ± 9.72	46.24 ± 12.03	41.34 ± 12.94	41.53 ± 12.96	66.12 ± 22 **	35.82 ± 8.67
V(ellip)	30.45 ± 9.23	42.93 ± 11.46	38.84 ± 12.6	38.70 ±11.85	62.29 ± 21.6 **	33.19 ± 8.21
AR	1.14 ± 0.1	1.21 ± 0.1	1.10 ± 0.1	1.10 ± 0.08	1.46 ± 0.12 *	1.15 ± 0.17
Fruit weight	33.36 ± 10	46.56 ± 12.07 *	42.23 ± 13.2	42.80 ± 12.48	63.3 ± 20.88 **	37.45 ± 9.37

). Consistently, “Peluche” had significantly the longest DL dimensions (DL = 63.31 ± 7.36 mm; Dg = 48.56 ± 5.52 mm) and volume (V = 63.44 ± 12.0 cm³) (Anova; p < 0.01). By contrast, “Algerie” and “Virticchiara” had the smallest fruit, with average weights of 33.36 ± 10 and 33.19 ± 8.21 g, respectively. Geometric mean diameter (Dg) ranged between 38.35 ± 3.95 and 48.56 ± 5.52. Aspect ratio (AR) varied from 1.10 in “Golden Nugget” and “Nespolone di Trabia” to 1.46 in “Peluche,” indicating more elongated fruit in the latter. The sphericity (Ψ) value ranged between 0.77 for “Peluche” and 0.92 for “Golden Nugget”. Estimated ovoid and ellipsoid volumes followed trends like measured volume, confirming the reliability of the geometric approaches. Overall, international varieties “Claudia,” “Golden Nugget,” and “Algerie” displayed intermediate size and weight, whereas the local variety “Peluche” stood out for its markedly larger fruit. “Virticchiara” and “Algerie” had both small fruits. A summary of the physical attributes of the six studied loquat varieties is shown in Table 1.

3.2. Mass Modeling

Based on selected attributes (DL, DT1, DT2, V_(ellip), and V_(osp)), a general regression model and a variety-specific model were generated and selected. The top best-fitted models were selected based on statistical parameters (R², RMSE, and MBE). Models with higher R², lower RMSE and MBE near 0 were considered the best. Selected linear and non-linear model regression for mass modeling are shown in

Table 2. Best general model by attributes for the selected model of the pool of all loquat varieties. Mass model equations are presented with their coefficients, along with the coefficient of determination (R²), root mean square error (RMSE), and mean bias error (MBE).

		Statistical Parameters
Model (Attributes)	Model Equation	R2	RMSE	MBE
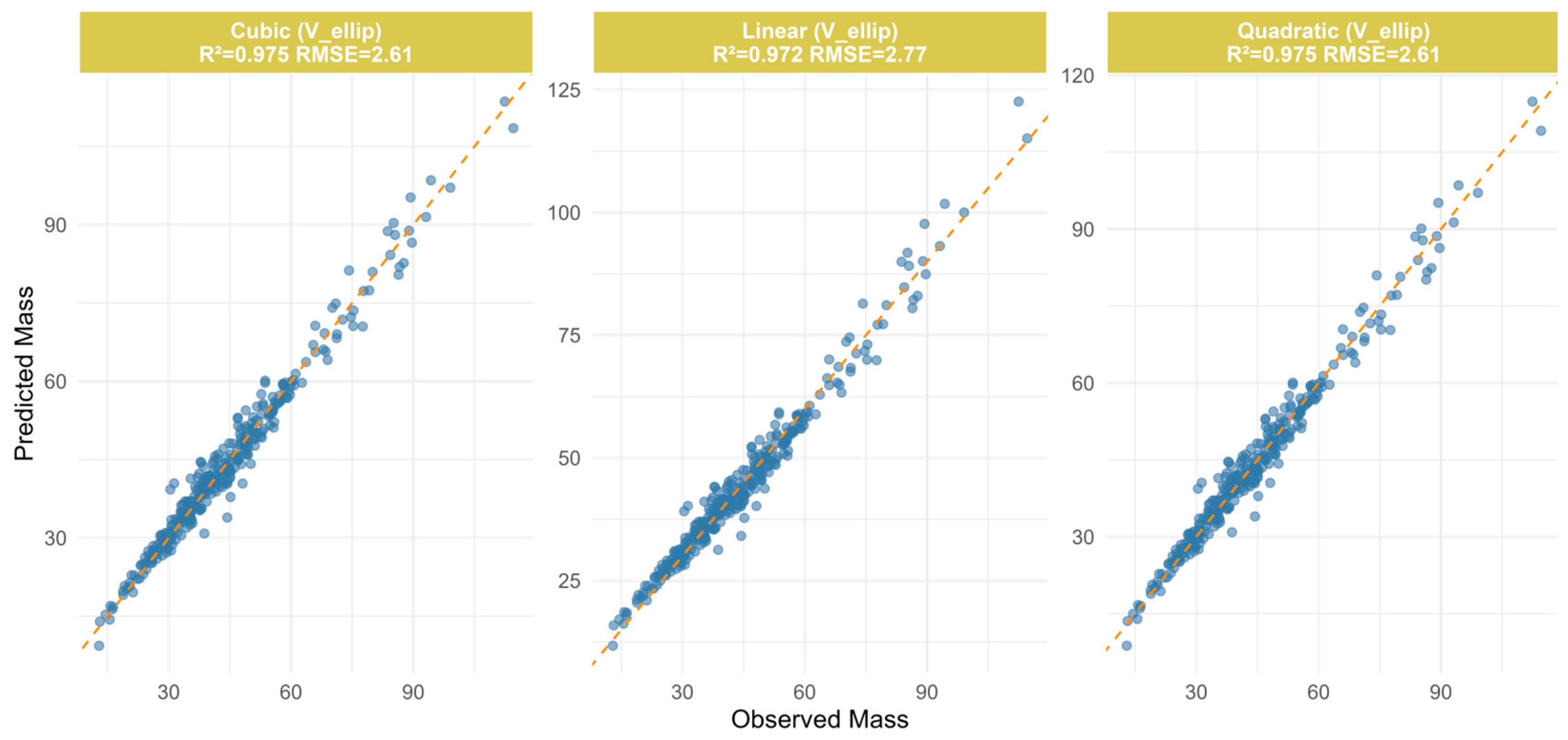
Cubic (DL)	−57.8142 + 3.3044 DL − 0.0368 DL2 + 0.0002 DL3	0.69	9.23	2.01 × 10−13
P. Inverse3 (DT1)	$765.8349-{\displaystyle \frac{66857.982}{\mathrm{D}\mathrm{T}1}}$$+{\displaystyle \frac{22047477.21}{{\mathrm{D}\mathrm{T}1}^2}}$$-{\displaystyle \frac{321394869}{{\mathrm{D}\mathrm{T}1}^3}}$	0.85	6.43	−2.27 × 10−12
Cubic (DT2)	−9.0169 + 1.2869 DT2 − 0.04 DT22 + 0.0011 DT23	0.88	5.86	1.23 × 10−13
Quadratic (V(ellip))	0.655 + 1.0863 V(ellip) − 0.0003 V(ellip)2	0.98	2.61	9.92 × 10−15
Cubic (V(osp))	2.7069 + 0.8904 V(osp) − 0.002 V(osp)2 + 0.011 V(osp)3	0.95	3.56	3.40 × 10−14

and

Table 3. Best regression model for mass prediction by variety. Mass model equations are presented with their regression coefficients (a–d) along with the coefficient of determination (R²), root mean square error (RMSE), and mean bias error (MBE).

		Regression Constants				Statistical Parameters
Variety	Model (Attributes)	a	b	c	d	R2	RMSE	MBE
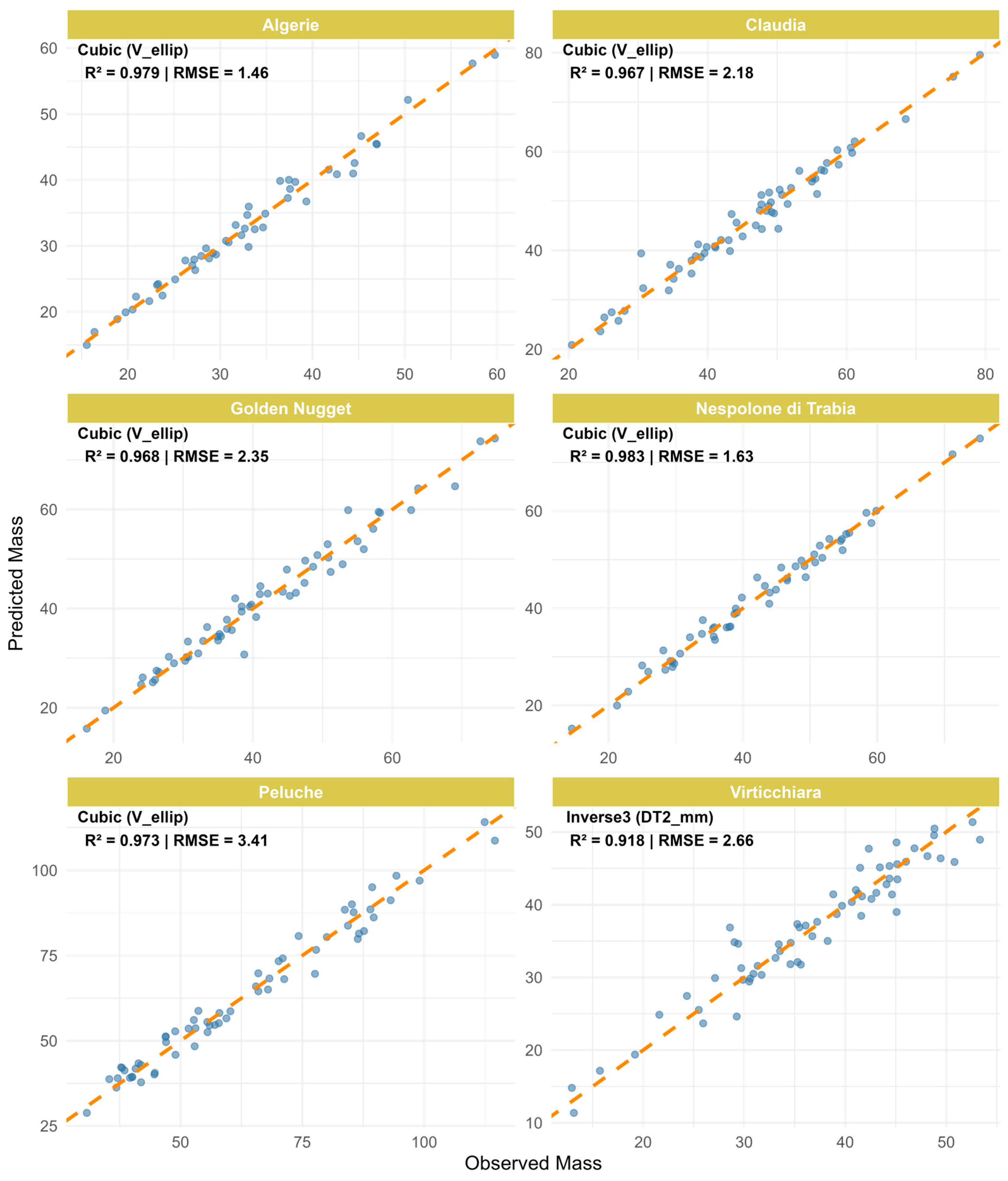
Algerie	Cubic (V(ellip))	6.584	0.463	0.017	−2 × 10−4	0.98	1.46	−3.70 × 10−15
	Quadratic (V(ellip))	1.8674	0.958	0.0019	-	0.98	1.48	5.63 × 10−15
	Linear (V(ellip))	0.0203	1.081	-	-	0.98	1.49	3.66 × 10−15
	Linear (V(osp))	0.1458	1.0144	-	-	0.96	2.12	−1.13 × 10−16
	P. Inverse3 (DT2)	297.67	−17,424.11	348,019	−2,244,065	0.94	2.51	7.94 × 10−14
	Linear (DT2)	−52.6804	2.422	-	-	0.93	2.62	−2.44 × 10−14
	Cubic (DT1)	53.3759	−3.8646	0.09	−3 × 10−4	0.92	2.76	−4.27 × 10−14
	P. Inverse2 (DT1)	269.24	−14,284.6	202,224	-	0.92	2.86	2.51 × 10−13
	Linear (DT1)	−51.95	2.2637	-	-	0.90	3.19	1.47 × 10−14
Claudia	Cubic (V(ellip))	−2.33	1.289	−0.0049	-	0.97	2.18	1.20 × 10−14
	Linear (V(ellip))	1.6795	1.034	-	-	0.97	2.19	7.34 × 10−15
	Cubic (V(osp))	−1.55	1.235	−0.0068	0.0004	0.91	3.54	3.92 × 10−14
	Linear (V(osp))	1.769	0.958	-	-	0.91	3.55	4.16 × 10−14
	P. Inverse3 (DT2)	332.15	−18,512.86	321,022.65	−1,276,363	0.90	3.75	6.44 × 10−14
	Linear (DT2)	−62.1645	2.7275	-	-	0.90	3.76	−5.60 × 10−14
	Cubic (DT1)	−153.464	11.3283	−0.3782	−0.003	0.90	3.84	7.46 × 10−15
	Linear (DT1)	−67.1645	2.7275	-	-	0.83	4.96	−5.50 × 10−14
	Cubic (DL)	303.6252	−20.2291	0.4578	−0.003	0.82	5.15	2.63 × 10−14
	Linear (DL)	−51.3776	1.9449	-	-	0.67	6.93	7.47 × 10−13
Golden nuggets	Cubic (V(ellip))	−2.1055	1.328	−0.074	0.001	0.97	2.35	2.23 × 10−14
	Linear (V(ellip))	1.4713	1.0332	-	-	0.97	2.35	1.70 × 10−14
	Cubic (V(osp))	−4.763	0.9384	−0.0112	0.004	0.95	2.97	1.80 × 10−15
	Quadratic (V(osp))	1.6004	0.9384	0.0006	-	0.95	2.99	3.73 × 10−15
	Linear (V(osp))	0.4539	0.9955	-	-	0.95	2.99	8.53 × 10−15
	P. Inverse3 (DT2)	893.7261	−78,032.20	2,355,205	−23,855,109	0.92	3.63	1.55 × 10−13
	P. Inverse3 (DT1)	665.8907	−57,834.986	1,772,408.4	−18,622,981	0.87	4.71	−7.18 × 10−14
	Linear (DT1)	−67.6165	2.6489	-	-	0.85	5.02	2.59 × 10−14
	Linear (DT2)	−54.3336	2.4792	-	-	0.84	5.21	−2.66 × 10−14
	Cubic (DL)	−193.0831	12.0711	−0.2326	0.00188	0.72	6.90	1.82 × 10−13
Nespolone di Trabia	Cubic (V(ellip))	−3.355	1.5413	−0.014	0.0001	0.98	1.63	4.69 × 10−15
	Linear (V(ellip))	1.8173	1.0433	-	-	0.98	1.68	5.83 × 10−15
	Cubic (V(osp))	−0.4581	1.2918	−0.0099	0.0001	0.95	2.64	1.67 × 10−16
	Cubic (DT1)	6.7845	−0.6501	0.0243	0.003	0.92	3.50	−4.290 × 10−15
	Quadratic (DT1)	24.0347	−1.9873	0.0584	-	0.92	3.50	5.429 × 10−15
	Linear (DT1)	−69.8441	2.722	-	-	0.90	3.83	−2.00 × 10−14
	Quadratic (DT2)	−52.9953	1.8906	0.015	-	0.90	3.87	1.97 × 10−14
	Linear (DT2)	−75.2735	3.0543	-	-	0.90	3.88	3.25 × 10−14
	Cubic (DL)	−169.2834	12.0549	−0.269	0.0022	0.80	5.52	−5.35 × 10−14
	Linear (DL)	−41.5972	1.8501	-	-	0.79	5.67	−3.01 × 10−15
Peluche	Quadratic (V(ellip))	−8.0154	1.3202	−0.0026	-	0.97	3.41	4.89 × 10−15
	Linear (V(ellip))	3.5717	0.9503	-	-	0.97	3.66	4.25 × 10−15
	Cubic (V(osp))	7.2528	0.6088	0.006	-	0.95	4.57	−2.69 × 10−14
	Linear (V(osp))	5.5	0.866	-	-	0.94	4.96	−1.10 × 10−15
	Cubic (DT2)	142.1188	−11.683	0.333	−0.002	0.91	6.29	9.72 × 10−14
	Quadratic (DT2)	−32.8939	0.9851	0.0314	-	0.91	6.31	−1.93 × 10−14
	Linear (DT2)	−88.4103	3.6498	-	-	0.90	6.39	−5.04 × 10−14
	Cubic (DT1)	362.901	−25.8721	0.6274	−0.0044	0.89	6.83	−6.09 × 10−13
	Linear (DT1)	−82.3454	3.3056	-	-	0.88	7.06	−9.26 × 10−15
	Cubic (DL)	1164.12	−54.6319	0.8588	−0.0043	0.55	13.82	−1.41 × 10−12
Virticchiara	P. Inverse3 (DT2)	564.38	−44,953.31	1,286,677	−12,709,763	0.92	2.66	−1.08 × 10−13
	Cubic (DT2)	−250.711	22.107	−0.6227	0.0064	0.92	2.68	−9.85 × 10−13
	Quadratic (V(ellip))	2.7468	0.9289	0.0027	-	0.92	2.71	1.40 × 10−15
	Linear (V(ellip))	0.5092	1.0919	-	-	0.91	2.72	4.73 × 10−15
	Linear (DT2)	−42.5747	2.2062	-	-	0.91	2.77	−3.75 × 10−14
	Cubic (DT1)	893.5024	−78.157	2.2504	−0.0207	0.87	3.41	1.45 × 10−12
	Cubic (V(osp))	19.6474	−1.5186	0.0956	−0.0207	0.84	3.71	−3.50 × 10−14
	Linear (V(osp))	1.8478	0.9744			0.81	4.02	−3.29 × 10−14
	Inverse3 (DL)	−40.0215	12,951.08	−583,873.36	7,171,246	0.41	7.11	2.19 × 10−13

.

3.3. General Regression Mass Model per Predictor

In the general mass modeling of loquat fruit, where variety was not considered as a factor, different model equations were obtained. Top models obtained were based on V_(ellip), either Cubic (M = 1.0863 V_(ellip) − 0.0003 V_(ellip)² + 0.011 V_(ellip)³ + 0.655), linear (M = 3.9519 + 0.9686 V_(ellip)), or Quadratic (M = 1.0863 V_(ellip) − 3 × 10⁻⁴ V_(ellip)² − 0.0018), with an R² of nearly 0.98 and RMSE < 2.8 (Figure 3). Regarding each predictor variable, the weakest model was a cubic regression using a univariate predictor (DL), which yielded the lowest R² (0.69) and the highest RMSE (9.23). The best-fitting model was the cubic regression based on V_(ellip), with an R² of 0.98 and a low RMSE (2.61). Two other cubic and quadratic regression models, based on DT2 and V_osp, also showed strong fits, with R² values of 0.88 and 0.95, respectively. For DT1, the best regression model was an inverse third-order polynomial, with an R² of 0.85 and an RMSE of 6.43. All models demonstrated very low MBE values, ranging from −2.27 × 10⁻¹² to 2.01 × 10⁻¹³ (Table 2).

3.4. Mass Modeling per Variety

All possible models were generated, and the top-performing models were selected. For all six varieties studied, a similar trend was observed. The model based on V_(ellip) as a predictor attribute showed the best fit model across all varieties except “Virticchiara.” All models based on V_(ellip) showed high R² values and low RMSE, ranging from 1.46 to 3.37. In contrast, models based on DL showed weaker performance and lower prediction accuracy. Across all varieties, mean bias error (MBE) values were negligible, indicating the absence of any systematic over- or underestimation bias (Table 3; Figure 4).

For “Algerie” loquat fruits, the cubic model based on V_(ellip) (R² = 0.9; RMSE = 1.46; MBE = −3.704 × 10⁻¹⁵) showed the best fit, followed by quadratic and linear models based on V_(ellip). Polynomial inverse third order and linear model based on DT2 presented a strong model with an R² of 0.92. DT1 also demonstrated good model fitting in the cubic, polynomial inverse second order, and linear regressions.

As to the “Claudia” variety, the cubic and linear models based on V_(ellip), V_(osp), and DT1 showed the best fit compared to other models, with R² values ranging between 0.83 for DT1 and 0.97 for V_(ellip) and RMSE varying between 2.18 and 4.96. The lowest R² value was obtained for the linear model based on DL, with an R² of 0.67 and the highest RMSE of 6.93.

For the “Golden nuggets” variety, also cubic and linear models based on V_(ellip) were the best-fitted models with an R² (0.97) and RMSE (2.35) values in both cases. V_(osp) was the second-best predictor-based model, with an R² value of 0.95 for cubic, quadratic, and linear models. By contrast, DL showed the weakest regression with an R² value of 0.72 and an RMSE of 6.19. Polynomial models performed better than linear models for both DT1 and DT2.

Regarding “Nespolone di Trabia” fruit, among all the models, the cubic and linear models based on V_(ellip) were the best fitted models, having the highest R² and RMSE. The cubic regression model based on V_(osp) also showed great model fitness, whereas the DT1 and DT2 models provided lower accuracy. DL-based models had the poorest performance for both linear and cubic regression models.

For “Peluche” fruit, among the ten selected models, the quadratic and linear models based on V_(ellip) were the best fitted, with the highest R² (0.97) and lowest RMSE (3.41). The least accurate model is the cubic model based on DL, with an R² (0.55) and an RMSE (13.82).

In “Virticchiara” fruit, the DT2 model-based, both polynomial inverse of third order and cubic regression yielded the best-fit model (R² = 0.92; RMSE = 2.67), whereas DL-based model showed poor fitness with an R² of 0.41 (Table 3; Figure 4).

4. Discussion

Physical characterization revealed distinct morphological differences among the studied varieties. Overall, “Algerie” and “Virticchiara” had the smallest fruits, whereas “Peluche” had the largest fruits. Such variation is often critical for the design and development of postharvest machinery, as machine dimensions and packaging systems are often calibrated based on fruit size [31]. Despite the differences among varieties, intra-varietal variation was relatively limited. Therefore, no grading within each variety was required, unlike other studies that reported considerable fruit-to-fruit variation within a single variety. Among the tested models, the cubic, linear, and quadratic models based on V_(ellip) showed the best general performance when all varieties were pooled together. Such an approach has also been tested in previous studies, and similar findings were obtained. For instance, when modeling ungraded strawberry, linear, and quadratic models showed the highest fitness (R² = 0.99, low RMSE). In guava, a quadratic model based on V_(ellip) was the most suitable (R² = 0.986, RMSE = 3.73) [16]. Similarly, a quadratic model, based on geometric mean diameter (Dg) of ungraded fruits (104.08 − 4.91 Dg + 0.09 Dg² with R² = 0.956), was recommended for kinnow mandarin fruit mass prediction [17]. At the variety-specific models’ level, the Cubic, Linear, and Quadratic models were the most suitable across all six loquat varieties. The obtained models were previously highlighted and described for their high and accurate performance in predicting fruit mass. Likewise, Shahbazi and Rahmati (2013a) reported that Linear and Quadratic models, based on ellipsoid volume and projected area, performed best in sweet cherry, while the same authors found Quadratic models suitable for figs [21]. Among graded strawberries, the most accurate model was Linear (M = −2.45 + 0.001 V, R² = 0.984). Quadratic and linear models also emerged as the most suitable models in mass modeling of Terminalia chebula fruit [20]. Although several viable models may be identified, selecting a single, robust model is essential. Although several viable models may be identified, selecting a single, robust model is essential. Linear and quadratic models are particularly advantageous because they are statistically reliable, computationally simple, cost-effective, and easily integrated into machine-learning frameworks and postharvest technologies.

Physical attributes, including volume, dimensional measurements, and other related traits, were considered for mass modeling. Our findings showed that volume-based models, particularly those derived from V_(ellip), were the most accurate predictors of loquat mass across all six studied varieties. These results align with previous studies, where volume has consistently emerged as the best predictor of fruit mass in numerous species, including Diospyros nigra [14] (R² = 0.8919) mandarin (R² = 0.955) [17], pomegranate (R² = 0.99) [22], and Thai apple ber [32] based on actual volume (R² = 0.973; RMSE = 1.184) and calculated volume (R² = 0.969; RMSE = 1.224). This accuracy is generally attributed to the strong correlation between fruit mass and volume, which is generally characterized by a linear relation. On the other hand, models based on diameters in particular length (DL) performed poorly, which is in line with [18], who reported the lowest R² (0.02) for length-based models of strawberry fruit, and [33], who also obtained low R² values (~0.15) using minor and major diameters of coconuts.

When comparing our results to the single other study on loquat mass modeling, conducted on three local Iranian varieties [26]. The results revealed that both mass and volume modeling were the best obtained based on intermediate diameter (M = 0.047 b² − 1.284 b + 12.076, R² = 0.94) and projected area M = 0.84 (PA2)1.45, R² = 0.96). By contrast, the most practical model for loquat was obtained as a linear model based on measured volume (R² = 0.99), M = 1.06 V_m −0.07 [26]. These results confirm the good performance of a linear model based on volume for loquat fruit in general. However, differences among varieties can influence the accuracy of the general models, thereby necessitating the development of variety-specific models.

5. Conclusions

This study demonstrated that loquat mass can be accurately predicted using simple geometric attributes, particularly based on fruit volume V_(ellip), providing the highest predictive performance across the six varieties. Linear, cubic, and quadratic models proved to be the most reliable both in general and in variety-specific models. In contrast, diameter-based predictors, especially DL, showed the lowest accuracy among the used predictors. The obtained models can be effectively integrated into machine-vision and deep-learning systems to enable automated grading of loquat fruits, reducing reliance on manual sorting and supporting more efficient, consistent, and cost-effective postharvest operations.