UAV Multispectral Data Combined with the PROSAIL Model Using the Adjusted Average Leaf Angle for the Prediction of Canopy Chlorophyll Content in Citrus Fruit Trees
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Field Test
2.2. UAV Multispectral Data Acquisition
2.3. Ground-Measured Data
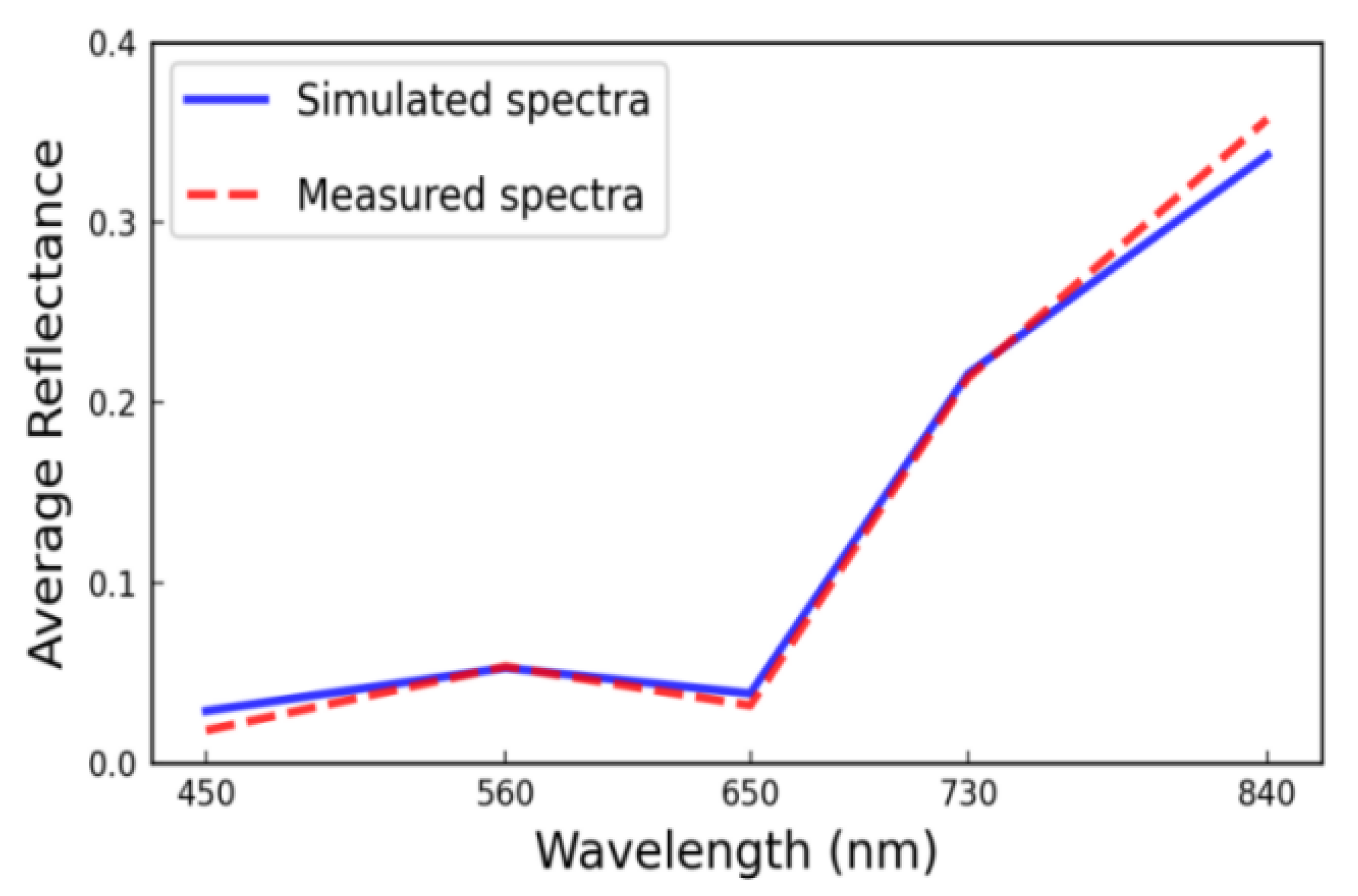
2.4. Simulated Spectrum
2.5. Research Methods
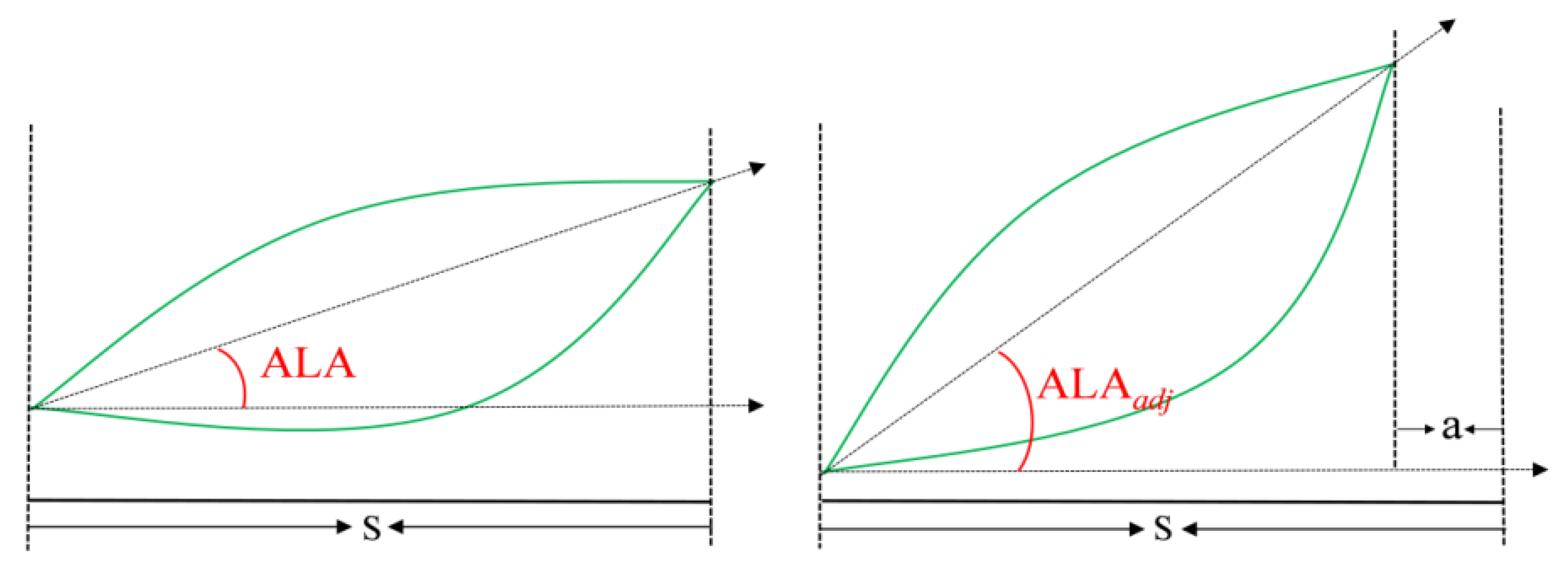
2.5.1. Optimization and Adjustment of ALAs
2.5.2. Hybrid Modeling and Precision Evaluation
3. Results and Analysis
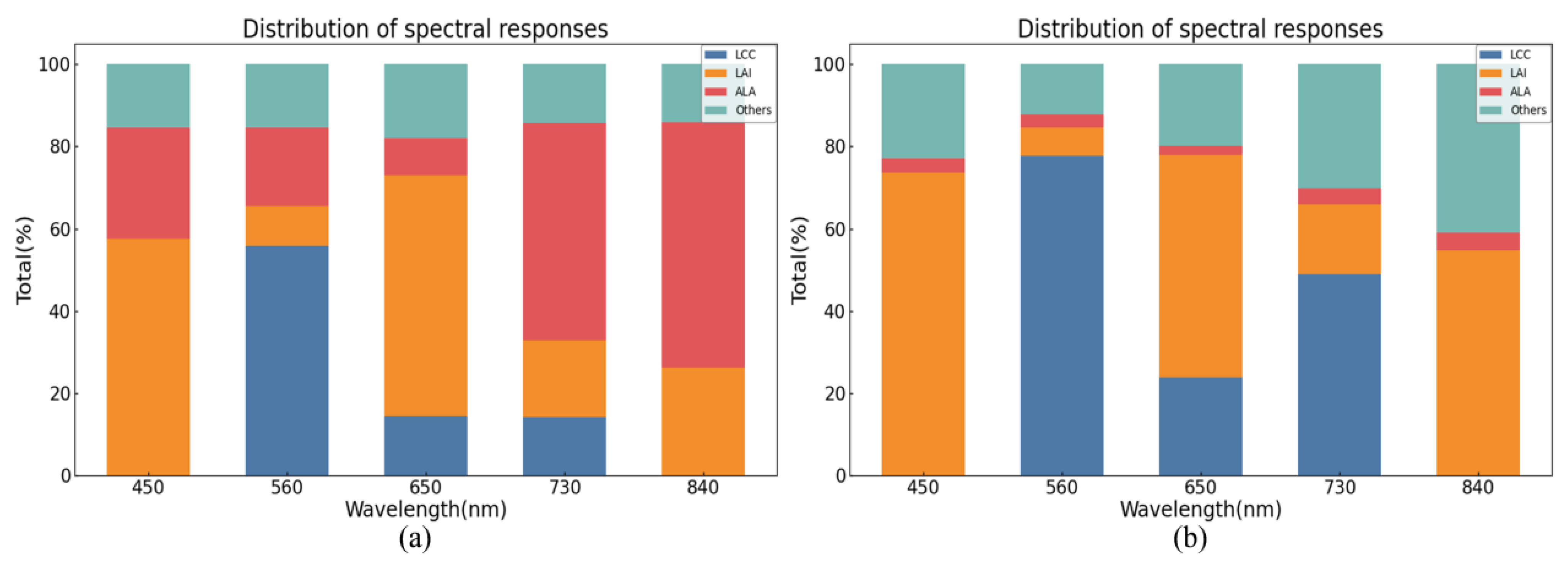
3.1. PROSAIL Parameter Sensitivity Analysis
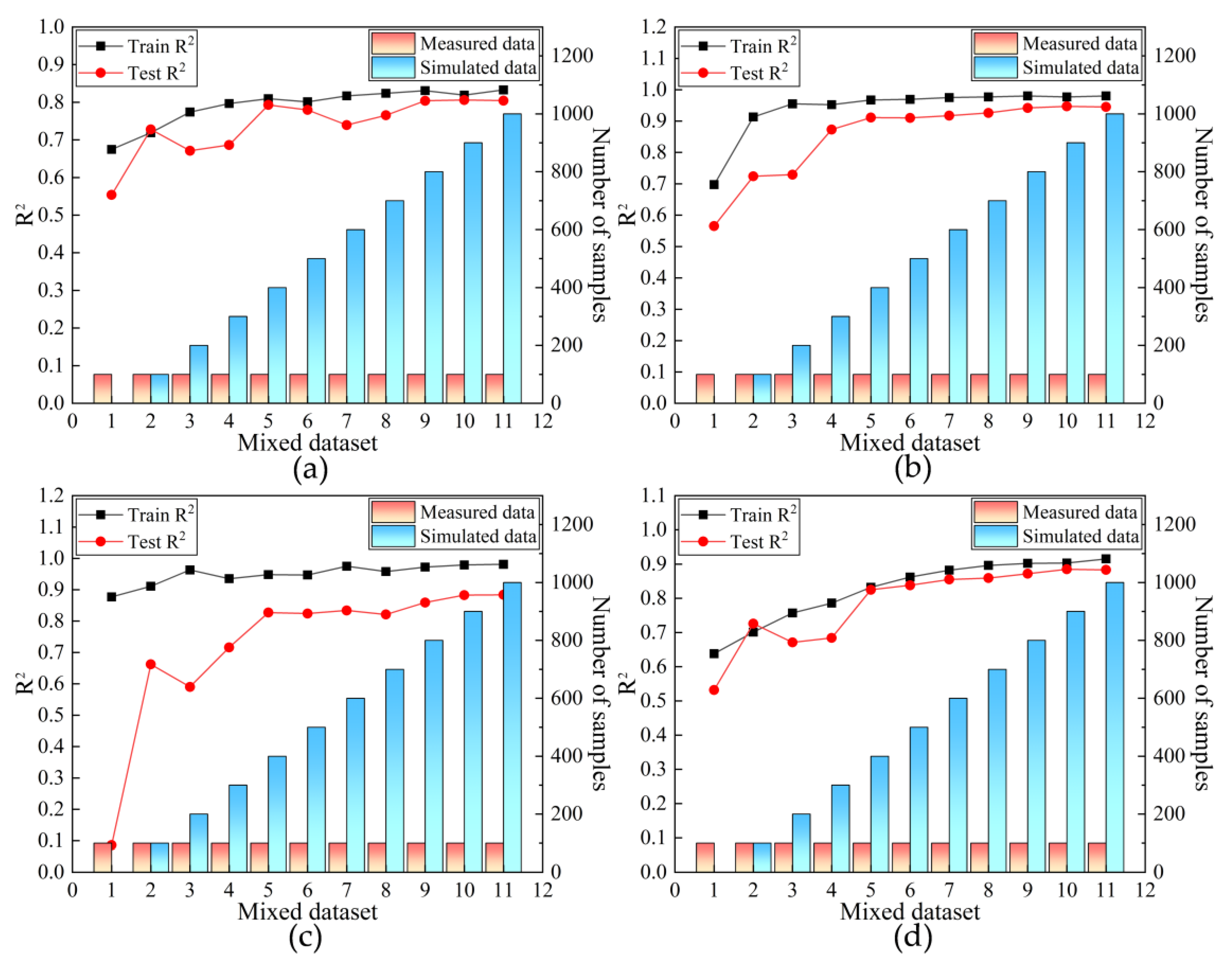
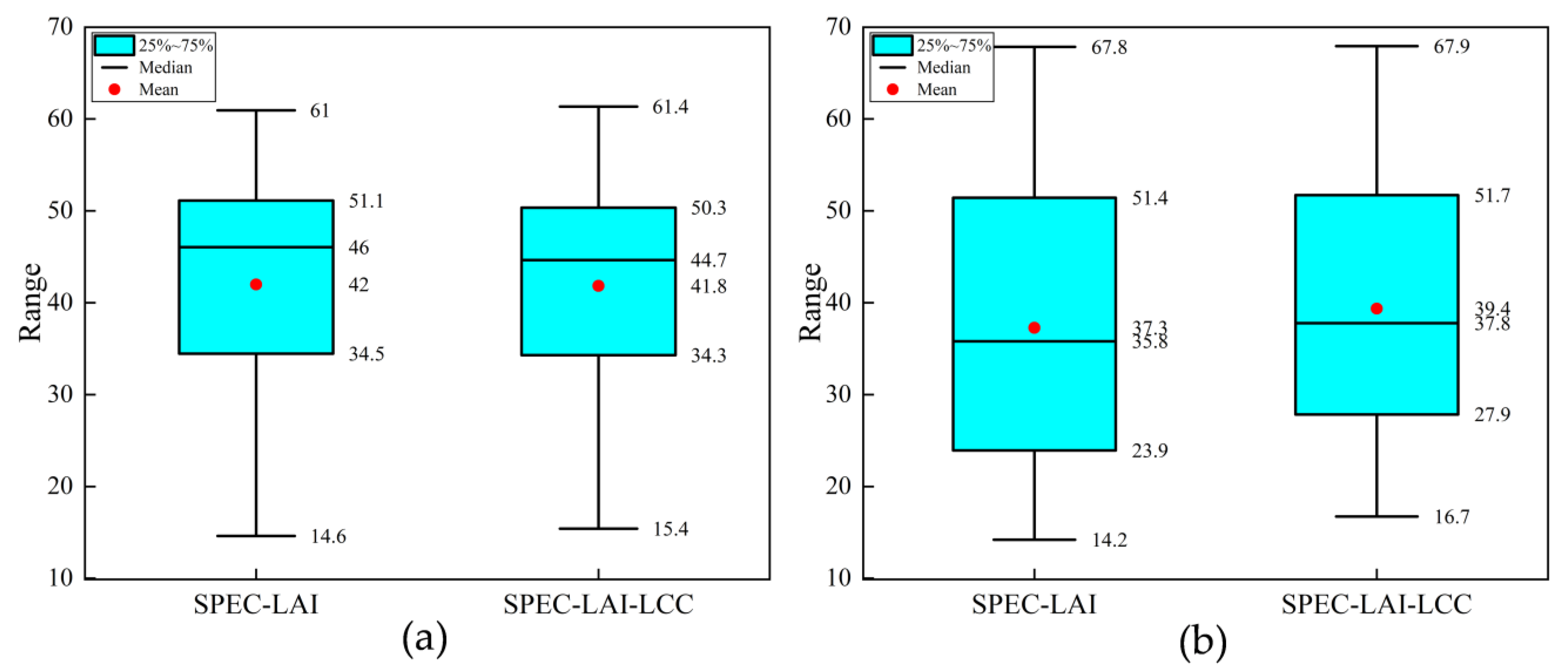
3.2. Experimental Analysis of the Mixing Ratio Between Measured and Simulated Data
3.3. Comparative Analysis of the ALA Optimization Results
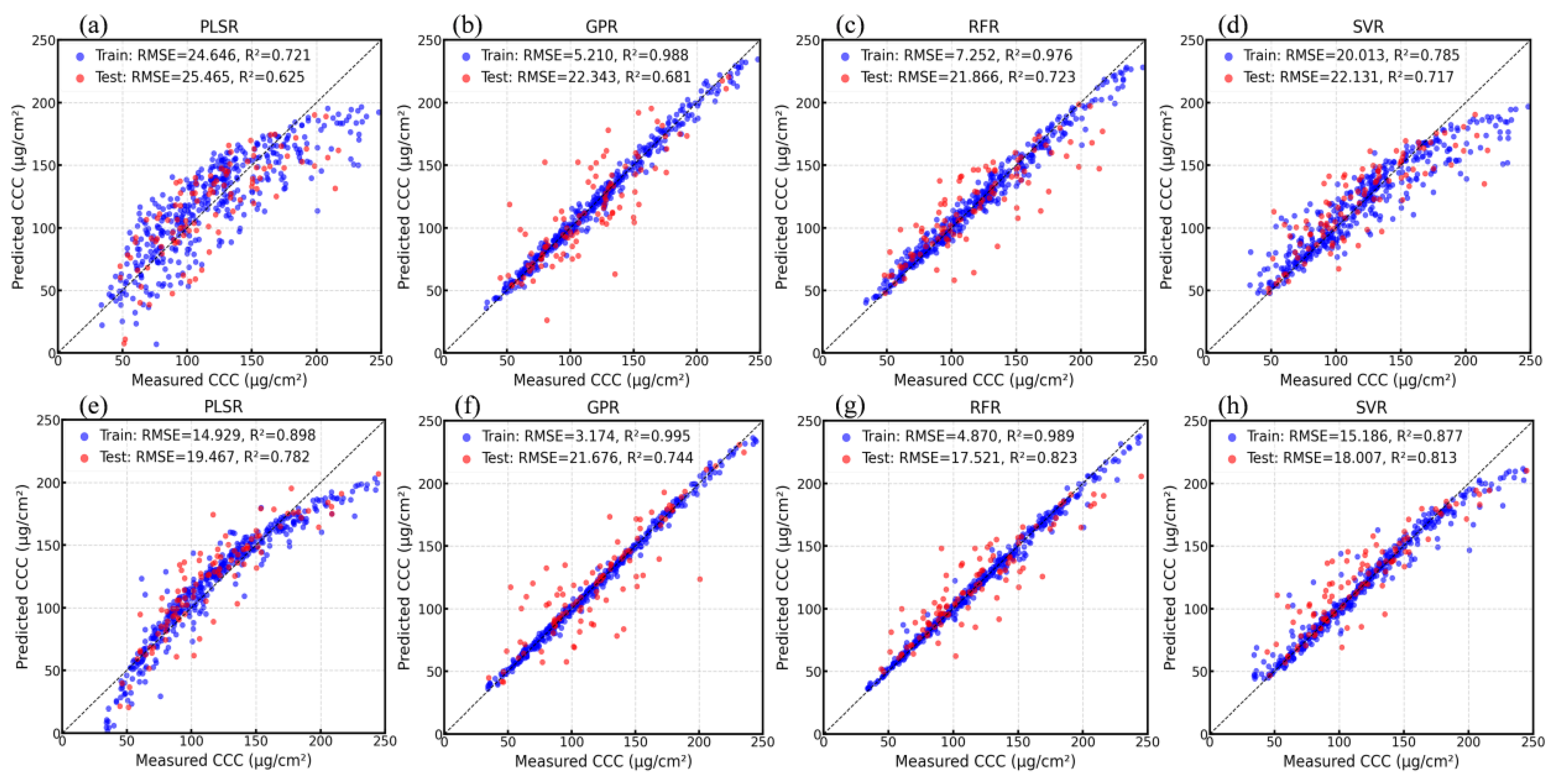
3.4. Performance Evaluation of the ALAadj Hybrid Inversion Model
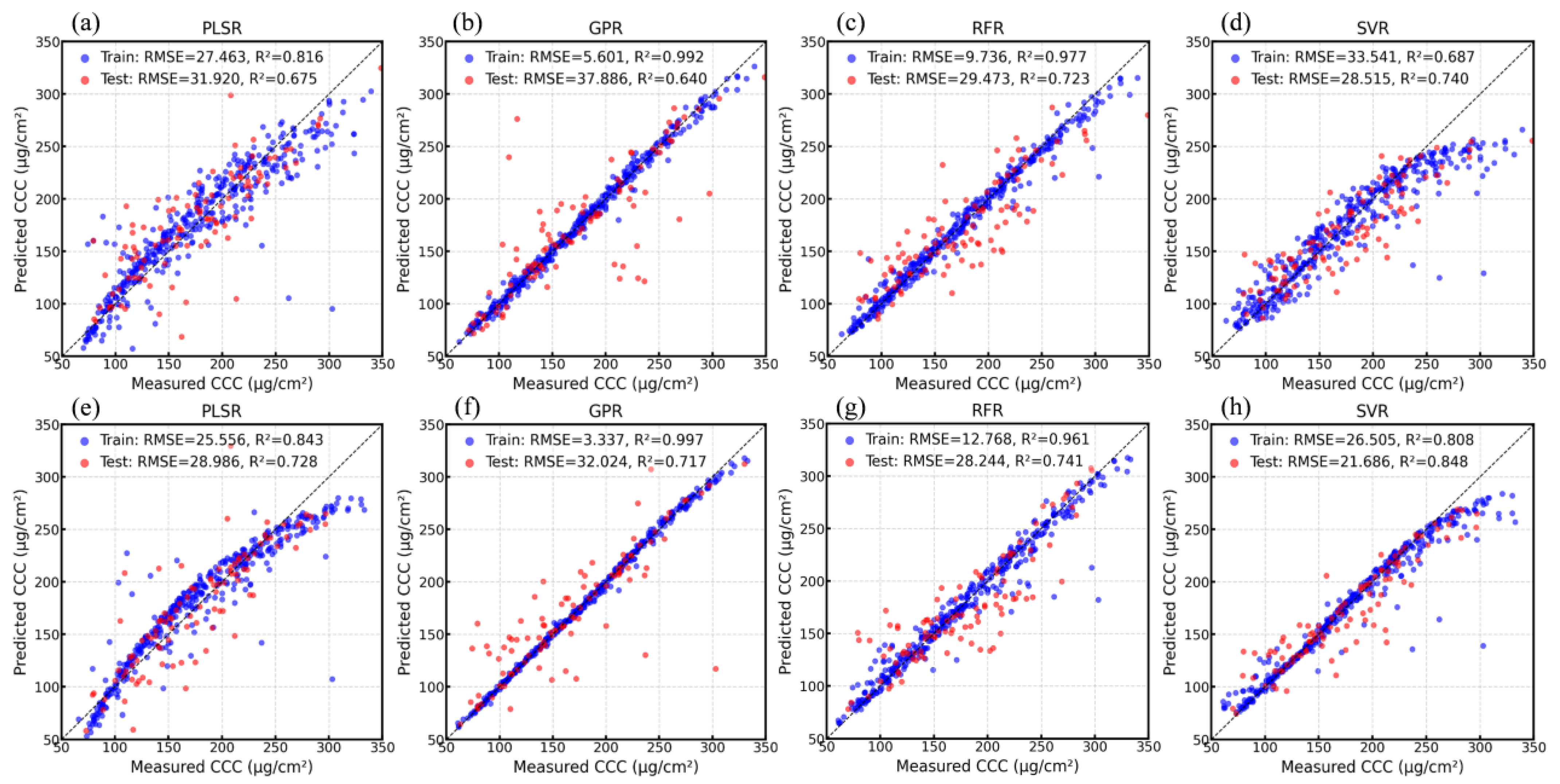
3.5. Performance Comparison Analysis of the ALAadj Hybrid Inversion Model in the Validation Area
4. Discussion
5. Conclusions
- (1)
- A 1:4 ratio of measured to simulated data was identified as the most pragmatic accommodation for the hybrid inversion model in this study;
- (2)
- The ALAadj value in the study area was 42°, with adjusted PROSAIL parameters showing enhanced spectral response regions favorable for LCC and LAI modeling in the CCC;
- (3)
- Compared with the unadjusted versions, the ALAadj hybrid inversion model demonstrated significant performance improvements across the four machine learning methods, with the peak R2 increasing by 13.8% from 0.723 to 0.823 and the RMSE decreasing by 19.9% from 21.866 μg/cm2 to 17.521 μg/cm2.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, M.W.; Fu, C.N.; Wang, C.C.; Xu, Y.J.; Jiang, M.L.; Xiao, Y.H.; Lu, F. Analysis of Countermeasures for the High-quality Development of Guilin’s Citrus Industry. South. Hortic. 2025, 36, 62–69. [Google Scholar]
- Wang, Y.N.; Sun, Y.; Chen, Y.N.; Wu, C.Y.; Huang, C.P.; Li, C.; Tang, X.G. Non-linear correlations exist between solar-induced chlorophyll fluorescence and canopy photosynthesis in a subtropical evergreen forest in Southwest China. Ecol. Indic. 2023, 157, 111311. [Google Scholar] [CrossRef]
- Lawson, T.; Chabrand, S.V. Imaging Spatial and Temporal Variation in Photosynthesis Using Chlorophyll Fluorescence. In Photosynthesis: Methods and Protocols; Methods in Molecular Biology; Springer: New York, NY, USA, 2024; Volume 2790, pp. 293–316. [Google Scholar] [CrossRef]
- Xu, Z.H.; He, A.Q.; Zhang, Y.W.; Hao, Z.B.; Li, Y.F.; Xiang, S.Y.; Li, B.; Chen, L.Y.; Yu, H.; Shen, W.L.; et al. Retrieving chlorophyll content and equivalent water thickness of Moso bamboo (Phyllostachys pubescens) forests under Pantana phyllostachysae Chao-induced stress from Sentinel-2A/B images in a multiple LUTs-based PROSAIL framework. For. Ecosyst. 2023, 10, 100108. [Google Scholar] [CrossRef]
- Cheng, J.P.; Yang, H.; Qi, J.B.; Sun, Z.D.; Han, S.Y.; Feng, H.K.; Jiang, J.Y.; Xu, W.M.; Li, Z.H.; Yang, G.J.; et al. Estimating canopy-scale chlorophyll content in apple orchards using a 3D radiative transfer model and UAV multispectral imagery. Comput. Electron. Agric. 2022, 202, 107401. [Google Scholar] [CrossRef]
- Cheng, Q.; Xu, H.; Fei, S.; Li, Z.; Chen, Z. Estimation of Maize LAI Using Ensemble Learning and UAV Multispectral Imagery under Different Water and Fertilizer Treatments. Agriculture 2022, 12, 1267. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Han, F.; Shi, Z.; Zhao, F.; Zhang, F.; Pan, W.; Zhang, Z.; Cui, Q. Estimation of Canopy Chlorophyll Content of Apple Trees Based on UAV Multispectral Remote Sensing Images. Agriculture 2025, 15, 1308. [Google Scholar] [CrossRef]
- Feng, H.; Fan, Y.; Yue, J.; Ma, Y.; Liu, Y.; Chen, R.; Fu, Y.; Jin, X.; Bian, M.; Fan, J.; et al. Enhancing potato leaf protein content, carbon-based constituents, and leaf area index monitoring using radiative transfer model and deep learning. Eur. J. Agron. 2025, 166, 127580. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Zhang, C.J.; Chen, Z.B.; Yang, G.J.; Xu, B.; Feng, H.K.; Chen, R.Q.; Qi, N.; Zhang, W.J.; Zhao, D.; Cheng, J.P.; et al. Removal of canopy shadows improved retrieval accuracy of individual apple tree crowns LAI and chlorophyll content using UAV multispectral imagery and PROSAIL model. Comput. Electron. Agric. 2024, 221, 108959. [Google Scholar] [CrossRef]
- Sun, B.; Wang, C.; Yang, C.; Xu, B.; Zhou, G.; Li, X.; Xie, J.; Xu, S.; Liu, B.; Xie, T.; et al. Retrieval of rapeseed leaf area index using the PROSAIL model with canopy coverage derived from UAV images as a correction parameter. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102373. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Yang, X.; Zhang, J.; Zhang, B.; Xie, P.; Wang, Y.; Chen, J.; Shi, L. UAV-based stomatal conductance estimation under water stress using the PROSAIL model coupled with meteorological factors. Int. J. Appl. Earth Obs. Geoinf. 2025, 137, 104425. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Z.; Bai, W.; Wang, E.; Wang, Q.; Zhang, D.; Zhang, Y.; Yang, N.; Liu, Y.; Nie, J.; et al. Canopy heterogeneity with border-row proportion affects light interception and use efficiency in maize/peanut strip intercropping. Field Crops Res. 2021, 271, 108239. [Google Scholar] [CrossRef]
- Li, K.; Jiang, C.; Guan, K.; Wu, G.; Ma, Z.; Li, Z. Evaluation of average leaf inclination angle quantified by indirect optical instruments in crop fields. Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104206. [Google Scholar] [CrossRef]
- Casa, R.; Baret, F.; Buis, S.; Lopez-Lozano, R.; Pascucci, S.; Palombo, A.; Jones, H.G. Estimation of maize canopy properties from remote sensing by inversion of 1-D and 4-D models. Precis. Agric. 2010, 11, 319–334. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; Francois, C.; Ustin, S.L. PROSPECT plus SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. Interdiscip. J. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Pan, Y.; Wu, W.; He, J.; Zhu, J.; Su, X.; Li, W.; Li, D.; Yao, X.; Cheng, T.; Zhu, Y.; et al. A novel approach for estimating fractional cover of crops by correcting angular effect using radiative transfer models and UAV multi-angular spectral data. Comput. Electron. Agric. 2024, 222, 109030. [Google Scholar] [CrossRef]
- Jiao, Q.; Sun, Q.; Zhang, B.; Huang, W.; Ye, H.; Zhang, Z.; Zhang, X.; Qian, B. A Random Forest Algorithm for Retrieving Canopy Chlorophyll Content of Wheat and Soybean Trained with PROSAIL Simulations Using Adjusted Average Leaf Angle. Remote Sens. 2021, 14, 98. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, M.; Hank, T. Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies. Remote Sens. 2019, 11, 1150. [Google Scholar] [CrossRef]
- Yang, G.; Qin, J.; Wang, L.; Fang, S.; Li, W.; Chen, Y.; Gong, Y.; Dian, Y.; Sun, C.; Wang, J.; et al. Accurate solution of the SAIL model by leaf inclination angle calculation based on laser point clouds. Geo-Spat. Inf. Sci. 2025, 28, 722–740. [Google Scholar] [CrossRef]
- Sun, Q.; Jiao, Q.; Chen, X.; Xing, H.; Huang, W.; Zhang, B. Machine Learning Algorithms for the Retrieval of Canopy Chlorophyll Content and Leaf Area Index of Crops Using the PROSAIL-D Model with the Adjusted Average Leaf Angle. Remote Sens. 2023, 15, 2264. [Google Scholar] [CrossRef]
- Mederer, D.; Feilhauer, H.; Cherif, E.; Berger, K.; Hank, T.B.; Kovach, K.R.; Dao, P.D.; Lu, B.; Townsend, P.A.; Kattenborn, T. Plant trait retrieval from hyperspectral data: Collective efforts in scientific data curation outperform simulated data derived from the PROSAIL model. ISPRS Open J. Photogramm. Remote Sens. 2025, 15, 100080. [Google Scholar] [CrossRef]
- Cao, L.; Chen, S.; Zhen, Z.; Li, Z.; Wang, K. Improved PROSAIL Inversion via Auto Differentiation for Estimating Leaf Area Index and Canopy Chlorophyll Content. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4411817. [Google Scholar] [CrossRef]
- de Sá, N.C.; Baratchi, M.; Hauser, L.T.; van Bodegom, P. Exploring the Impact of Noise on Hybrid Inversion of PROSAIL RTM on Sentinel-2 Data. Remote Sens. 2021, 13, 648. [Google Scholar] [CrossRef]
- Jin, Z.; Liu, H.; Cao, H.; Li, S.; Yu, F.; Xu, T. Hyperspectral Remote Sensing Estimation of Rice Canopy LAI and LCC by UAV Coupled RTM and Machine Learning. Agriculture 2025, 15, 11. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Y.P.; Chen, P.; Li, J.Y.; Liu, D.; Chu, X.L. Non-destructive spectroscopy assisted by machine learning for coal industrial analysis: Strategies, progress, and future prospects. Trends Anal. Chem. 2025, 192, 118322. [Google Scholar] [CrossRef]
- An, G.; Xing, M.; He, B.; Liao, C.; Huang, X.; Shang, J.; Kang, H. Using machine learning for estimating rice chlorophyll content from in situ hyperspectral data. Remote Sens. 2020, 12, 3104. [Google Scholar] [CrossRef]
- Li, S.; Lin, Y.; Zhu, P.; Jin, L.; Bian, C.; Liu, J. Combining UAV Multispectral Imaging and PROSAIL Model to Estimate LAI of Potato at Plot Scale. Agriculture 2024, 14, 2159. [Google Scholar] [CrossRef]
- Sibiya, B.S.; Odindi, J.; Mutanga, O.; Cho, M.A.; Masemola, C. The utility of radiative transfer models (RTM) on remotely sensed data in retrieving biophysical and biochemical properties of terrestrial biomes: A systematic review. Adv. Space Res. 2025, 75, 7424–7444. [Google Scholar] [CrossRef]
- Bullock, D.G.; Anderson, D.S. Evaluation of the Minolta SPAD-502 chlorophyll meter for nitrogen management in corn. J. Plant Nutr. 1998, 21, 741–755. [Google Scholar] [CrossRef]
- Cerovic, Z.G.; Masdoumier, G.; Ghozlen, N.B.; Latouche, G. A new optical leaf-clip meter for simultaneous non-destructive assessment of leaf chlorophyll and epidermal flavonoids. Physiol. Plant. 2012, 146, 251–260. [Google Scholar] [CrossRef]
- Xu, L.; Shi, S.; Gong, W.; Chen, B.; Sun, J.; Xu, Q.; Bi, S. Mapping 3D plant chlorophyll distribution from hyperspectral LiDAR by a leaf-canopyradiative transfer model. Int. J. Appl. Earth Obs. Geoinf. 2024, 127, 103649. [Google Scholar] [CrossRef]
- Verhoef, W. Theory of Radiative Transfer Models Applied in Optical Remote Sensing of Vegetation Canopies. Ph.D. Thesis, Wageningen Agricultural University, Wageningen, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Sha, X.; Ni, F.; Xie, P.; Shen, S.; Islam, A.R.M.T. Hyperspectral Characteristics and Scale Effects of Leaf and Canopy of Summer Maize under Continuous Water Stresses. Agriculture 2021, 11, 1180. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Vuolo, F.; Neugebauer, N.; Bolognesi, S.F.; Atzberger, C.; D’Urso, G. Estimation of Leaf Area Index Using DEIMOS-1 Data: Application and Transferability of a Semi-Empirical Relationship between two Agricultural Areas. Remote Sens. 2013, 5, 1274–1291. [Google Scholar] [CrossRef]
- Huttunen, J.; Kokkola, H.; Mielonen, T.; Mononen, M.E.J.; Lipponen, A.; Reunanen, J.; Lindfors, A.V.; Mikkonen, S.; Lehtinen, K.E.J.; Kouremeti, N.; et al. Retrieval of aerosol optical depth from surface solar radiation measurements using machine learning algorithms, non-linear regression and a radiative transfer-based look-up table. Atmos. Chem. Phys. 2016, 16, 8181–8191. [Google Scholar] [CrossRef]
- Yang, K.; Tang, B.-H.; Fu, W.; Zhou, W.; Fu, Z.; Fan, D. Estimation of Forest Canopy Fuel Moisture Content in Dali Prefecture by Combining Vegetation Indices and Canopy Radiative Transfer Models from MODIS Data. Forests 2024, 15, 614. [Google Scholar] [CrossRef]
- Thakur, B.; Danish, T.; Manashi, G. A Bibliometric Review of Machine Learning Applications in Soil Science Using Digital Spectroscopy (2008–2024). J. Exp. Agric. Int. 2025, 47, 536–549. [Google Scholar] [CrossRef]
- Li, X.; Yan, J.; Huang, C.; Ma, W.; Guo, Z.; Li, J.; Yao, X.; Da, Q.; Cheng, K.; Yang, H. Estimation of Silage Maize Plant Moisture Content Based on UAV Multispectral Data and Ensemble Learning Methods. Agriculture 2025, 15, 746. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Z.; Fan, X.; Hou, F. Synergistic Multi-Model Approach for GPR Data Interpretation: Forward Modeling and Robust Object Detection. Remote Sens. 2025, 17, 2521. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, H.; Liu, C.; Xie, Y.; Cao, Y.; Shi, Y. Self-adaptive data-driven evolutionary algorithm based on random forest feature selection and incremental Gaussian process regression on personalized antidepressant medication research. Appl. Intell. 2025, 55, 846. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. A hybrid training approach for leaf area index estimation via Cubist and random forests machine-learning. ISPRS J. Photogramm. Remote Sens. 2018, 135, 173–188. [Google Scholar] [CrossRef]
- Wei, Y.; Mo, X.; Yu, S.; Wu, S.; Chen, H.; Qin, Y.; Zeng, Z. An Optimized Multi-Stage Framework for Soil Organic Carbon Estimation in Citrus Orchards Based on FTIR Spectroscopy and Hybrid Machine Learning Integration. Agriculture 2025, 15, 1417. [Google Scholar] [CrossRef]
- Hasan, U.; Sawut, M.; Chen, S. Estimating the Leaf Area Index of Winter Wheat Based on Unmanned Aerial Vehicle RGB-Image Parameters. Sustainability 2019, 11, 6829. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, H.; Li, Q.; Fu, X.; Li, H. Estimating Canopy Chlorophyll Content of Potato Using Machine Learning and Remote Sensing. Agriculture 2025, 15, 375. [Google Scholar] [CrossRef]
- Yang, H.; Hu, Y.; Yin, H.; Jin, Q.; Li, F.; Yu, K. Improving potato leaf chlorophyll content prediction using a machine learning model with a hybrid dataset. Int. J. Remote Sens. 2025, 46, 3064–3088. [Google Scholar] [CrossRef]
- Duursma, R.A.; Falster, D.S.; Valladares, F.; Sterck, F.J.; Pearcy, R.W.; Lusk, C.H.; Sendall, K.M.; Nordenstahl, M.; Houter, N.C.; Atwell, B.J.; et al. Light interception efficiency explained by two simple variables: A test using a diversity of small- to medium-sized woody plants. New Phytol. 2012, 193, 397–408. [Google Scholar] [CrossRef]
- Sun, Q.; Jiao, Q.; Qian, X.; Liu, L.; Liu, X.; Dai, H. Improving the Retrieval of Crop Canopy Chlorophyll Content Using Vegetation Index Combinations. Remote Sens. 2021, 13, 470. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Foliage area and architecture of plant canopies from sunfleck size distributions. Agric. For. Meteorol. 1992, 60, 249–266. [Google Scholar] [CrossRef]
- Sun, J.; Wang, L.; Shi, S.; Li, Z.; Yang, J.; Gong, W.; Wang, S.; Tagesson, T. Leaf pigment retrieval using the PROSAIL model: Influence of uncertainty in prior canopy-structure information. Crop. J. 2022, 10, 1251–1263. [Google Scholar] [CrossRef]
- Injadat, M.; Moubayed, A.; Nassif, A.B.; Shami, A. Machine learning towards intelligent systems: Applications, challenges, and opportunities. Artif. Intell. Rev. 2021, 54, 3299–3348. [Google Scholar] [CrossRef]


| Multispectral Bands | Center Wavelength (Bandwidth)/nm | Radiation Correction Coefficient |
|---|---|---|
| Blue | 450 ± 16 | 0.537 |
| Green | 560 ± 16 | 0.538 |
| Red | 650 ± 16 | 0.537 |
| Red Edge | 730 ± 16 | 0.533 |
| NIR | 840 ± 26 | 0.536 |
| Parameter | Range | Mean Value | Unit |
|---|---|---|---|
| SPAD | [38.36, 73.86] | 58.89 | - |
| LCC | [32.63, 99.30] | 65.26 | μg/cm2 |
| LAI | [1.02, 2.46] | 1.81 | - |
| CCC | [51.23, 226.31] | 119.19 | μg/cm2 |
| Model | Parameter | Unit | Range | Step |
|---|---|---|---|---|
| PROSPECT 5- 4SAIL | Chlorophyll content (Cab) | μg/cm2 | 32–100 | 0.1 |
| Leaf structure index (N) | - | 1–2 | 0.1 | |
| Dry matter content (Cm) | g/cm2 | 0.016 | - | |
| Leaf water depth (Cw) | cm | 0.02 | - | |
| Carotenoid (Car) | μg/cm2 | 25%Cab | - | |
| Brown pigments (Cb) | - | 0 | - | |
| Leaf area index (LAI) | m2/m2 | 1–2.5 | 0.1 | |
| Soil coefficient (Psoil) | - | 0.1–0.4 | 0.1 | |
| Hot spot parameter (Hspot) | m/m | 0.1 | - | |
| Average leaf angle (ALA) | (°) | 10–80 | 5 | |
| Solar zenith angle (tts) | (°) | 30 | - | |
| Observe zenith angle (tto) | (°) | 0 | - | |
| Relative azimuth (psi) | (°) | 0 | - |
| Model | Hyperparameter Grids |
|---|---|
| PLSR | n_components: [5, 10, 15, 20] |
| GPR | kernel: [RBF, RBF + WhiteKernel] |
| alpha: [1 × 10−5, 1 × 10−3] | |
| n_restarts_optimizer: [3, 5] | |
| RFR | n_estimators: [100, 200] |
| max_depth: [10, 20, None] | |
| min_samples_split: [2, 5] | |
| min_samples_leaf: [1, 2] | |
| SVR | kernel: [‘rbf’, ‘linear’] |
| C: [0.1, 1, 10] | |
| epsilon: [0.1, 0.2] | |
| gamma: [‘scale’, 0.01, 0.1] |
| Data Source | Total Samples | Training | Testing | Training Proportion | Testing Proportion |
|---|---|---|---|---|---|
| Simulated Data | 400 | 350 | 50 | 87.5% | 12.5% |
| Measured Data | 100 | 50 | 50 | 50% | 50% |
| Total | 500 | 400 | 100 | 80% | 20% |
| Method | Hybrid Inversion Model | Experimental Area | Validation Area | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| PLSR | ALA-unadjusted | 0.625 | 25.465 | 0.675 | 31.920 |
| ALAadj | 0.782 | 19.467 | 0.728 | 28.986 | |
| GPR | ALA-unadjusted | 0.681 | 22.343 | 0.640 | 37.886 |
| ALAadj | 0.744 | 21.676 | 0.717 | 32.024 | |
| RFR | ALA-unadjusted | 0.723 | 21.866 | 0.723 | 29.473 |
| ALAadj | 0.823 | 17.521 | 0.741 | 28.244 | |
| SVR | ALA-unadjusted | 0.717 | 22.131 | 0.740 | 28.515 |
| ALAadj | 0.813 | 18.007 | 0.848 | 21.686 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, S.; Hou, Y.; Wang, R.; Li, M.; Yuan, S.; Mei, Z.; Song, Y.; Yan, J. UAV Multispectral Data Combined with the PROSAIL Model Using the Adjusted Average Leaf Angle for the Prediction of Canopy Chlorophyll Content in Citrus Fruit Trees. Horticulturae 2025, 11, 1223. https://doi.org/10.3390/horticulturae11101223
Dou S, Hou Y, Wang R, Li M, Yuan S, Mei Z, Song Y, Yan J. UAV Multispectral Data Combined with the PROSAIL Model Using the Adjusted Average Leaf Angle for the Prediction of Canopy Chlorophyll Content in Citrus Fruit Trees. Horticulturae. 2025; 11(10):1223. https://doi.org/10.3390/horticulturae11101223
Chicago/Turabian StyleDou, Shiqing, Yichang Hou, Rongbin Wang, Minglan Li, Shixin Yuan, Zhengmin Mei, Yaqin Song, and Jichi Yan. 2025. "UAV Multispectral Data Combined with the PROSAIL Model Using the Adjusted Average Leaf Angle for the Prediction of Canopy Chlorophyll Content in Citrus Fruit Trees" Horticulturae 11, no. 10: 1223. https://doi.org/10.3390/horticulturae11101223
APA StyleDou, S., Hou, Y., Wang, R., Li, M., Yuan, S., Mei, Z., Song, Y., & Yan, J. (2025). UAV Multispectral Data Combined with the PROSAIL Model Using the Adjusted Average Leaf Angle for the Prediction of Canopy Chlorophyll Content in Citrus Fruit Trees. Horticulturae, 11(10), 1223. https://doi.org/10.3390/horticulturae11101223





