Computing the Composition of Ethanol-Water Mixtures Based on Experimental Density and Temperature Measurements
Abstract
1. Introduction
2. Materials and Methods
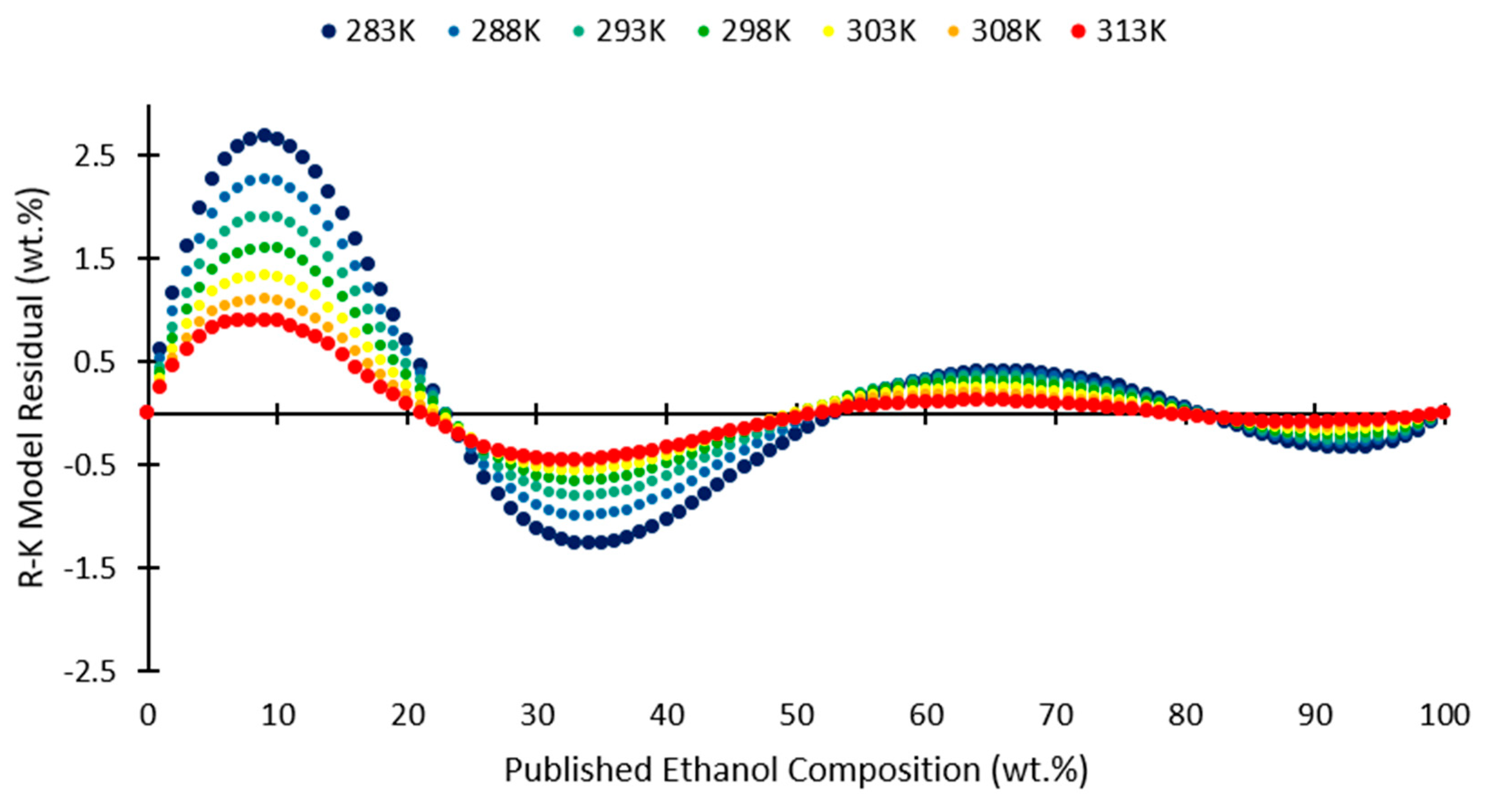
2.1. Redlich-Kister Model
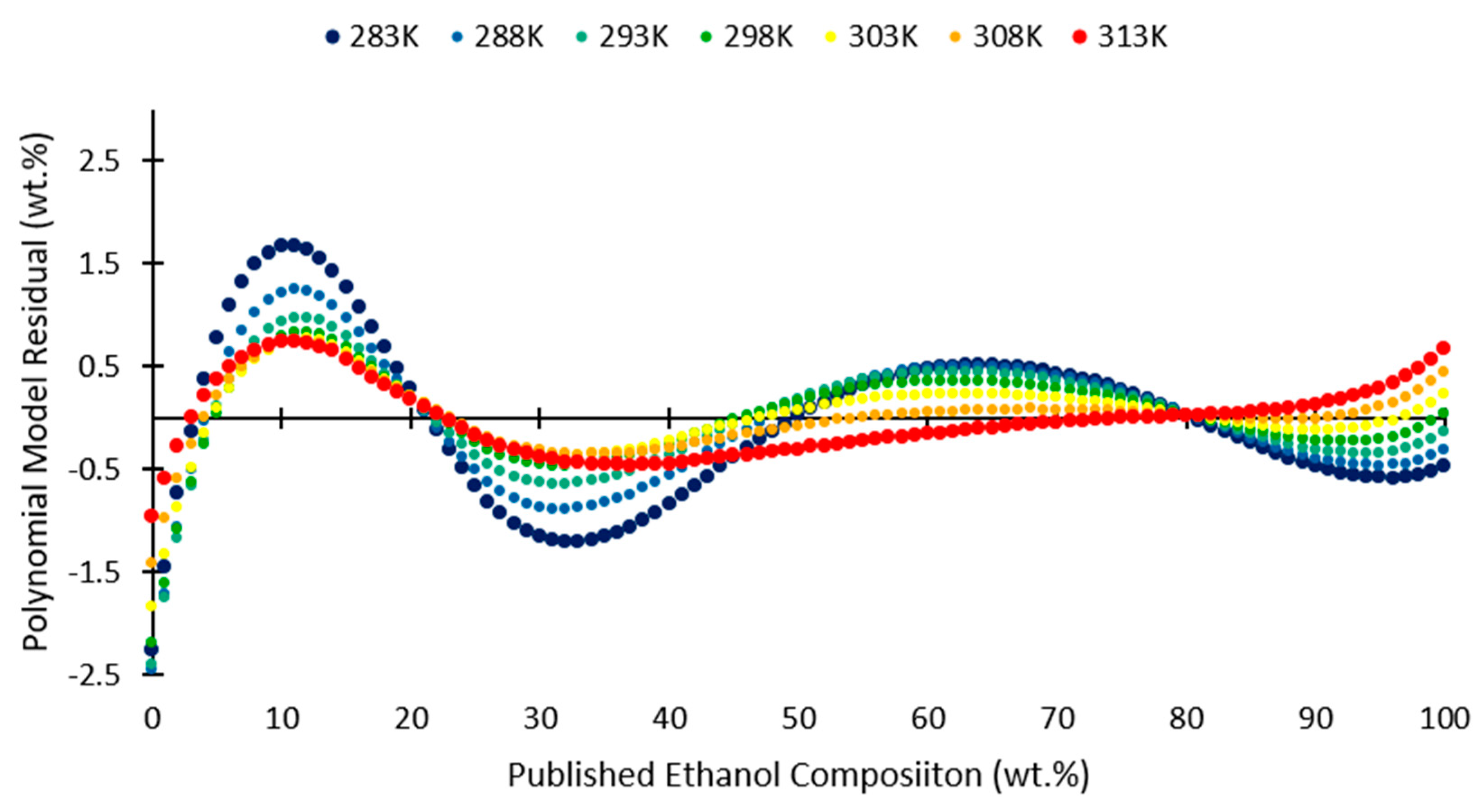
2.2. Polynomial Model
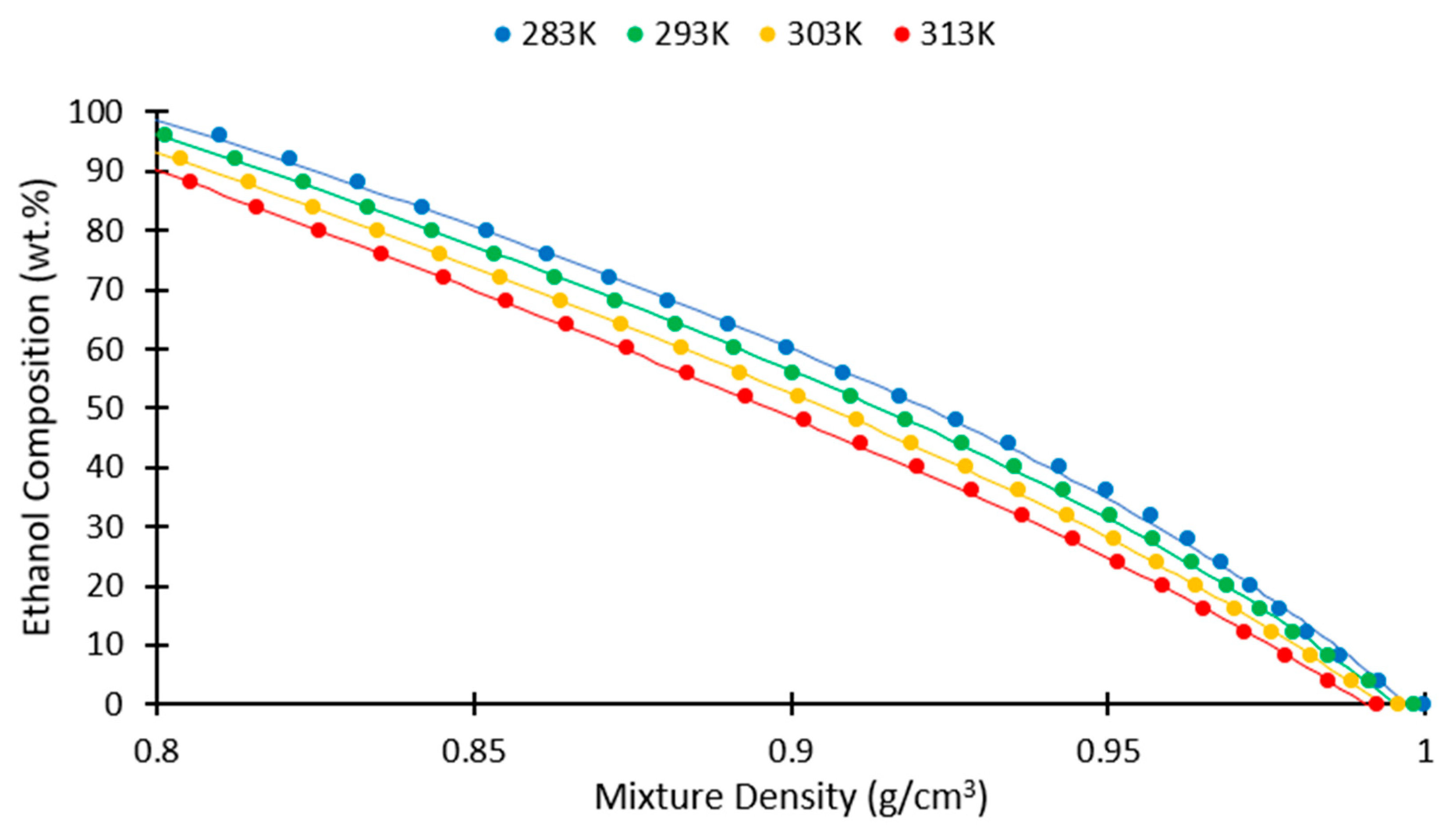
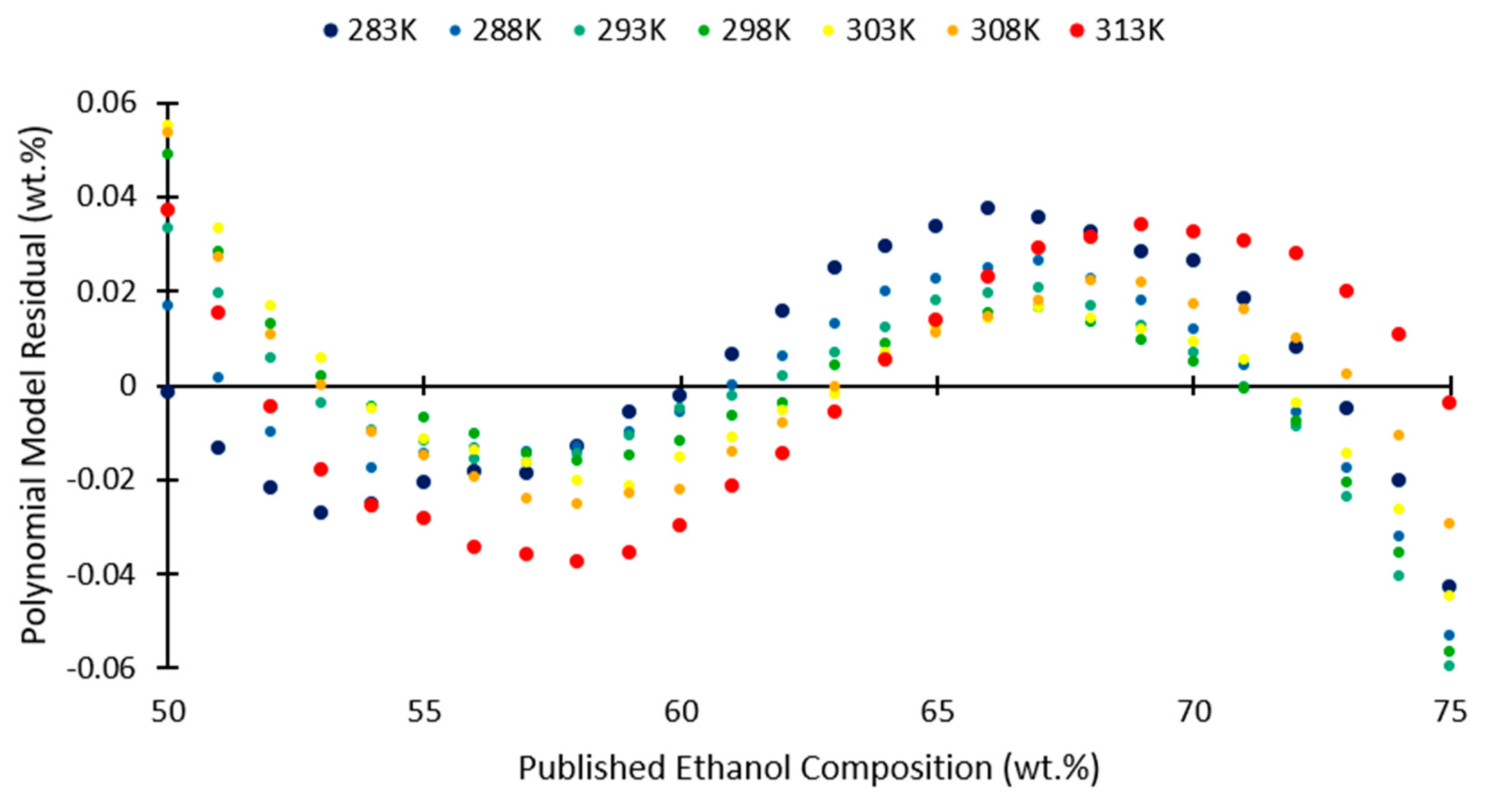
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zion Market Research. Available online: https://www.zionmarketresearch.com/news/fuel-ethanol-market (accessed on 10 March 2018).
- Lindsey, B.D.; Ayotte, J.D.; Jurgens, B.C.; Desimone, L.A. Using groundwater age distributions to understand changes in methyl tert-butyl ether (MtBE) concentrations in ambient groundwater, northeastern United States. Sci. Total Environ. 2017, 579, 579–587. [Google Scholar] [CrossRef] [PubMed]
- Condon, N.; Klemick, H.; Wolverton, A. Impacts of ethanol policy on corn prices: A review and meta-analysis of recent evidence. Food Policy 2015, 51, 63–73. [Google Scholar] [CrossRef]
- Li, H.; Chai, X.S.; Deng, Y.L.; Zhan, H.Y.; Fu, S.Y. Rapid determination of ethanol in fermentation liquor by full evaporation headspace gas chromatography. J. Chromatogr. A 2009, 1216, 169–172. [Google Scholar] [CrossRef] [PubMed]
- Weatherly, C.A.; Woods, R.M.; Armstrong, D.W. Rapid Analysis of Ethanol and Water in Commercial Products Using Ionic Liquid Capillary Gas Chromatography with Thermal Conductivity Detection and/or Barrier Discharge Ionization Detection. J. Agric. Food Chem. 2014, 62, 1832–1838. [Google Scholar] [CrossRef] [PubMed]
- Buttler, T.A.; Johansson, K.A.J.; Gorton, L.G.O.; Markovarga, G.A. Online Fermentation Process Monitoring of Carbohydrates and Ethanol Using Tangential Flow Filtration and Column Liquid-Chromatography. Anal. Chem. 1993, 65, 2628–2636. [Google Scholar] [CrossRef]
- Lidén, H.; Buttler, T.; Jeppsson, H.; Marko-Varga, G.; Volc, J.; Gorton, L. On-line monitoring of monosaccharides and ethanol during a fermentation by microdialysis sampling, liquid chromatography and two amperometric biosensors. Chromatographia 1998, 47, 501–508. [Google Scholar] [CrossRef]
- Terol, A.; Paredes, E.; Maestre, S.E.; Prats, S.; Todoli, J.L. Alcohol and metal determination in alcoholic beverages through high-temperature liquid-chromatography coupled to an inductively coupled plasma atomic emission spectrometer. J. Chromatogr. A 2011, 1218, 3439–3446. [Google Scholar] [CrossRef] [PubMed]
- Yarita, T.; Nakajima, R.; Otsuka, S.; Ihara, T.; Takatsu, A.; Shibukawa, M. Determination of ethanol in alcoholic beverages by high-performance liquid chromatography-flame ionization detection using pure water as mobile phase. J. Chromatogr. A 2002, 976, 387–391. [Google Scholar] [CrossRef]
- Buratti, S.; Ballabio, D.; Giovanelli, G.; Dominguez, C.M.Z.; Moles, A.; Benedetti, S.; Sinelli, N. Monitoring of alcoholic fermentation using near infrared and mid infrared spectroscopies combined with electronic nose and electronic tongue. Anal. Chim. Acta 2011, 697, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Mazarevica, G.; Diewok, J.; Baena, J.R.; Rosenberg, E.; Lendl, B. On-line fermentation monitoring by mid-infrared spectroscopy. Appl. Spectrosc. 2004, 58, 804–810. [Google Scholar] [CrossRef] [PubMed]
- Veale, E.L.; Irudayaraj, J.; Demirci, A. An on-line approach to monitor ethanol fermentation using FTIR spectroscopy. Biotechnol. Prog. 2007, 23, 494–500. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.Y.; Luo, F.; Xie, R.; Zhang, L.P.; Ju, X.J.; Wang, W.; Liu, Z.; Chu, L.Y. Online monitoring of ethanol concentration using a responsive microfluidic membrane device. Anal. Methods-UK 2016, 8, 4028–4036. [Google Scholar] [CrossRef]
- National Research Council (U.S.); Washburn, E.W.; West, C.J.; Hull, C. International Critical Tables of Numerical Data, Physics, Chemistry and Technology, 1st ed.; McGraw-Hill book company, Inc.: New York, NY, USA, 1926. [Google Scholar]
- Perry, R.H.; Green, D.W. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Micro Motion ELITE Peak Performance Coriolis Flow and Density Meter. Available online: https://www.emerson.com/en-us/catalog/micro-motion-elite-coriolis (accessed on 5 August 2018).
| Parameter | ai | bi | ci |
|---|---|---|---|
| i = 0 | −9.054199 | −4.930763 | 5.286817 |
| i = 1 | 0.01572057 | 0.01241796 | −0.01989784 |
| Ethanol Composition Range (wt.%) | θ1 | θ2 (K−1) | θ3 (cm3∙g−1) | θ4 (cm6∙g−2) | θ5 (g∙cm−3) | θ6 (cm3∙g−1∙K−1) | θ7 (K) |
|---|---|---|---|---|---|---|---|
| 0–100 | −96.32780 | −0.02856512 | 98.96611 | −37.81838 | 35.07342 | 0.02844898 | 36.74344 |
| 0–25 | 1722.515 | −0.04283923 | −1786.652 | 612.3505 | −548.0476 | 0.04246920 | −17.43558 |
| 25–50 | −357.4251 | −0.01758119 | 381.6007 | −138.9431 | 114.0415 | 0.01808855 | 155.2817 |
| 50–75 | −6.965499 | −0.02773449 | −5.967778 | 2.310737 | 8.993499 | 0.03055873 | 255.8742 |
| 75–100 | 16.57862 | −0.03431656 | −37.51686 | 15.19476 | 3.823482 | 0.03827332 | 272.0696 |
| Ethanol Composition Range (wt.%) | Average Absolute Residual (wt.% Ethanol) | Largest Residual (wt.% Ethanol) |
|---|---|---|
| 0–100 | 0.3739 | 2.447 |
| 0–25 | 0.1684 | 0.6908 |
| 25–50 | 0.0307 | 0.2435 |
| 50–75 | 0.01747 | 0.05981 |
| 75–100 | 0.01777 | 0.08352 |
| R-K 0–100 † | 0.4516 | 2.682 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danahy, B.B.; Minnick, D.L.; Shiflett, M.B. Computing the Composition of Ethanol-Water Mixtures Based on Experimental Density and Temperature Measurements. Fermentation 2018, 4, 72. https://doi.org/10.3390/fermentation4030072
Danahy BB, Minnick DL, Shiflett MB. Computing the Composition of Ethanol-Water Mixtures Based on Experimental Density and Temperature Measurements. Fermentation. 2018; 4(3):72. https://doi.org/10.3390/fermentation4030072
Chicago/Turabian StyleDanahy, Brooks B., David L. Minnick, and Mark B. Shiflett. 2018. "Computing the Composition of Ethanol-Water Mixtures Based on Experimental Density and Temperature Measurements" Fermentation 4, no. 3: 72. https://doi.org/10.3390/fermentation4030072
APA StyleDanahy, B. B., Minnick, D. L., & Shiflett, M. B. (2018). Computing the Composition of Ethanol-Water Mixtures Based on Experimental Density and Temperature Measurements. Fermentation, 4(3), 72. https://doi.org/10.3390/fermentation4030072