Dynamic Optimization of Xylitol Production Using Legendre-Based Control Parameterization

Abstract

This paper presents an improved methodology for optimizing the fed-batch fermentation process of xylitol production, aiming to maximize the final concentration in a bioreactor co-fed with xylose and glucose. Xylitol is a valuable sugar alcohol widely used in the food and pharmaceutical industries, and its microbial production requires precise control over substrate feeding strategies. The proposed technique employs Legendre polynomials to parameterize two control actions (the feeding rates of glucose and xylose), and it uses a hybrid optimization algorithm combining Monte Carlo sampling with genetic algorithms for coefficient selection. Unlike traditional optimization approaches based on piecewise parameterization, which produce discontinuous control profiles and require post-processing, this method generates smooth profiles directly applicable to real systems. Additionally, it significantly reduces mathematical complexity compared to strategies that combine Fourier series with orthonormal polynomials while maintaining similar optimization results. The methodology achieves good results in xylitol production using only eight parameters, compared to at least twenty in other approaches. This dimensionality reduction improves the robustness of the optimization by decreasing the likelihood of convergence to local optima while also reducing the computational cost and enhancing feasibility for implementation. The results highlight the potential of this strategy as a practical and efficient tool for optimizing nonlinear multivariable bioprocesses.

1. Introduction

Xylitol is a five-carbon sugar alcohol derived from xylose. Discovered in 1891, it has been widely used as a low-calorie sweetener due to its pleasant taste and beneficial properties. Since the 1960s, xylitol has been employed as a sweetening agent in various industries, including in food, pharmaceuticals, cosmetics, and oral hygiene products. Commercially, it is primarily obtained from plant sources, such as birch, other hardwood trees, and fibrous vegetation, through chemical processes that are both costly and environmentally demanding. Despite its natural occurrence in fruits and vegetables, large-scale production continues to rely on energy-intensive chemical methods that require high-pressure hydrogenation and expensive catalysts [1].

In response to these drawbacks, biotechnological production methods have gained significant attention due to their environmental sustainability and potential for cost reduction [2]. By harnessing microbial metabolism, xylitol can be obtained from renewable biomass through fermentation processes, avoiding harsh reaction conditions and reducing the dependency on fossil-derived chemicals. In particular, microbial fermentation using yeasts or bacteria allows for the selective conversion of xylose to xylitol under mild conditions, offering an attractive alternative to conventional synthesis. Additionally, these biological systems provide a framework for valorizing agro-industrial waste streams rich in hemicellulose, contributing to circular economy initiatives and the development of more sustainable value chains. Among the various fermentation strategies, fed-batch processes have proven especially effective for xylitol production [3]. In a fed-batch system, substrates are incrementally added to the bioreactor, enabling better control over nutrient availability, reducing inhibition effects, and maintaining favorable conditions for microbial activity. A common approach involves using glucose as the primary carbon source during the growth phase, followed by xylose feeding to enhance xylitol production. However, the design of optimal feeding profiles remains a complex task due to the nonlinear dynamics of microbial growth, substrate uptake, and product formation. Moreover, the metabolic behavior of microorganisms may vary significantly depending on factors such as oxygen availability, pH, temperature, or the presence of inhibitors, all of which add further layers of complexity to the optimization process.

Traditionally, the optimization of fed-batch fermentation relies on detailed first-principle models that describe biomass growth, substrate consumption, and product kinetics [4,5]. These models are essential for predicting system behavior and guiding process design. Nevertheless, their complexity often hinders their direct use in real-time control and optimization frameworks. Moreover, in practice, the accuracy of these models may be affected by parameter uncertainty, measurement noise, and biological variability, further complicating the implementation of optimal control strategies.

In industrial bioprocessing, mathematical optimization is a crucial tool to improve yield and efficiency [6]. A common technique involves parameterizing the control actions (typically the substrate feed rates) using piecewise constant or piecewise linear functions [7,8]. While conceptually simple, these strategies present several limitations. First, they require a large number of parameters to capture the desired feeding dynamics accurately, especially when finer time discretizations are used. Second, they often produce control profiles with discontinuities or abrupt changes between intervals. These non-smooth profiles can result in rapid variations in substrate concentration, leading to osmotic stress, metabolic imbalances, or even microbial inhibition.

Alternative approaches such as artificial neural networks [9], numerical search methods [10], and heuristic algorithms [11,12,13,14] have been proposed to address the challenges of dynamic optimization. These methods can be implemented either in offline or online frameworks, depending on the availability of real-time measurements and computational resources. While online strategies like Model Predictive Control continuously adjust control actions based on real-time process data [15], offline methods, such as the one employed in this study, compute optimal control trajectories in advance, without requiring real-time feedback. Furthermore, many existing approaches prioritize mathematical optimization without considering the physical or biological feasibility of the resulting control trajectories. In real systems, actuators such as pumps or valves cannot implement rapid setpoint changes, and microorganisms are sensitive to sudden environmental perturbations. Therefore, generating smooth feeding profiles is not only mathematically desirable but also essential for safe and effective bioprocess operation [16,17].

This work proposes an offline dynamic optimization methodology that uses process kinetics to pre-compute smooth feeding trajectories suitable for implementation in real systems. The focus is on offline optimization due to its lower computational burden and ease of implementation. The core of the methodology is a mathematical model that captures the key dynamics of biomass growth, substrate consumption, and xylitol production. Instead of discretizing the time domain into intervals with constant or linear values, the feeding rates are represented as continuous functions expanded in terms of orthogonal Legendre polynomials. Beyond bioprocesses, Legendre polynomials have been extensively applied in optimal control problems across various fields, including robotics, aerospace trajectory planning, and nonlinear dynamic systems, particularly through pseudospectral methods that exploit their orthogonality and numerical efficiency [18,19,20,21]. This orthonormal basis offers several advantages: it ensures smoothness and continuity, reduces the number of optimization parameters required, and allows for straightforward integration into gradient-free optimization frameworks, preventing abrupt variations that could lead to cell stress, inhibition, or even cell death [16].

As an enhancement over previous methods based on Fourier series and orthonormal polynomials [13,22,23,24], the use of Legendre polynomials reduces the mathematical complexity of the parameterization while preserving its flexibility. This leads to a more efficient formulation of the optimization problem, which can be solved with fewer degrees of freedom and improved numerical stability. In addition, a hybrid optimization algorithm is employed, combining the global exploration capabilities of Monte Carlo sampling with the convergence efficiency of genetic algorithms. This hybrid approach allows for a robust search of the optimal polynomial coefficients that define the feeding profiles.

The implementation of the proposed methodology is carried out in MATLAB^® and Simulink^®, and its effectiveness is demonstrated through numerical simulations of a fed-batch xylitol production process. The results are compared with a previously published optimal profile from [3], highlighting both the competitiveness of the xylitol yield and the simplicity of the resulting control trajectories. Importantly, the profiles obtained are immediately suitable for real application, as they require no post-processing or interpolation to ensure continuity.

In summary, this work presents a novel strategy for the optimization of substrate feeding in xylitol bioproduction processes. By integrating orthogonal polynomial parameterization with a hybrid optimization algorithm, the proposed approach addresses the key limitations of existing methods, offering an efficient, biologically consistent, and industrially viable solution. In addition, the reduction in the number of optimization parameters improves the robustness of the solution process by decreasing the likelihood of convergence to local optima, a frequent issue in high-dimensional heuristic optimization. Beyond its application to xylitol, the methodology is adaptable to a broad range of biotechnological systems where smooth control trajectories are required. The remainder of the manuscript is organized as follows: Section 2 presents the mathematical model of the xylitol production process. Section 3 introduces the proposed optimization strategy. Section 4 analyzes the simulation results. Finally, Section 5 summarizes the conclusions and outlines potential directions for future work.

2. Process of Mathematical Model

The mathematical model for xylitol production is formulated as a system of six differential equations. Originally proposed by Tochampa et al. [3], the model describes a bioreactor fed with two streams, namely, xylose and glucose, both at a concentration of 200 g/L. The state variables considered are the concentrations of biomass ($C_x$), xylose ($C_{xyl}$), glucose ($C_{glc}$), extracellular xylitol ($C_{xit}^{ex}$), and intracellular xylitol ($C_{xit}^{in}$), as well as the operating volume ($V_l$):

$${\displaystyle \frac{d{C}_x}{dt}}=-{\displaystyle \frac{F_{glc}+F_{xyl}}{V_l}}{C}_x+u{C}_x$$

(1)

$${\displaystyle \frac{d{C}_{xyl}}{dt}}=-{\displaystyle \frac{F_{xyl}}{V_l}}{C}_{xyl}^f-{\displaystyle \frac{F_{glc}+F_{xyl}}{V_l}}{C}_{xyl}-q_{xyl}{C}_x$$

(2)

$${\displaystyle \frac{d{C}_{glc}}{dt}}={\displaystyle \frac{F_{glc}}{V_l}}{C}_{glc}^f-{\displaystyle \frac{F_{glc}+F_{xyl}}{V_l}}{C}_{glc}-q_{glc}{C}_x$$

(3)

$${\displaystyle \frac{d{C}_{xit}^{ex}}{dt}}=-{\displaystyle \frac{F_{glc}+F_{xyl}}{V_l}}{C}_{xit}^{ex}-r_{t,xit}^{\prime }{C}_x$$

(4)

$${\displaystyle \frac{d{C}_{xit}^{in}}{dt}}=(r_{f,xit}-r_{u,xit}-r_{t,xit}^{\prime }){\rho }_x-u{C}_{xit}^{in}$$

(5)

$${\displaystyle \frac{d{V}_l}{dt}}=F_{glc}+F_{xyl}$$

(6)

where t denotes the time variable [h], defined over the fermentation horizon; $F_{glc}$ and $F_{xyl}$ are the volumetric flow rates of the glucose and xylose feed, respectively; u is the specific growth rate; $C_{glc}^f$ and $C_{xyl}^f$ are the concentrations of glucose and xylose in the feed; $q_{xyl}$ and $q_{glc}$ are the uptake rates of xylose and glucose; $r_{t,xit}^{\prime }$ is the mass flow rate of xylitol on a dry weight basis; $r_{f,xit}$ is the specific xylitol formation rate; $r_{u,xit}$ is the specific intracellular xylitol consumption rate; and ${\rho }_x$ is the cell density. Model parameters are listed in

Table 1. Description of model parameters.

Symbol	Description	Value	Unitis
$u_{xit}^{max}$	Max. specific growth rate with respect to xylitol.	$0.189$	h−1
$u_{glc}^{max}$	Max. specific growth rate with respect to glucose.	$0.662$	h−1
$K_{s,glc}$	Monod saturation constant for glucose.	$9.998$	${\mathrm{g}}_{\mathrm{gluc}}{\mathrm{L}}^{-1}$
$K_{s,xit}$	Monod saturation constant for xylitol.	$16.068$	${\mathrm{g}}_{\mathrm{xylitol}}{\mathrm{L}}^{-1}$
$K_{s,xyl}$	Monod saturation constant for xylose.	$11.761$	${\mathrm{g}}_{\mathrm{xyl}}{\mathrm{L}}^{-1}$
$K_r$	Repression constant for glucose.	$0.100$	${\mathrm{g}}_{\mathrm{gluc}}{\mathrm{L}}^{-1}$
$q_{glc}^{max}$	Max. specific uptake rate of glucose.	$0.342$	${{\mathrm{g}}_{\mathrm{gluc}}}^{-1}{\mathrm{h}}^{-1}$
$q_{xyl}^{max}$	Max. specific uptake rate of xylose.	$3.276$	${{\mathrm{g}}_{\mathrm{xyl}}}^{-1}{\mathrm{h}}^{-1}$
$K_{i,glc}$	Inhibition uptake constant of xylose by glucose.	$0.100$	${\mathrm{g}}_{\mathrm{gluc}}{\mathrm{L}}^{-1}$
$K_{i,xit}$	Inhibition uptake constant of glucose by xylose.	$14.780$	${\mathrm{g}}_{\mathrm{xyl}}{\mathrm{L}}^{-1}$
$P_{xit}$	Permeability coefficient of the cell membrane.	$7.591\times {10}^9$	ms−1
$a_{cell}$	Specific surface area of the cell.	$7.6$	${\mathrm{m}}^2{\mathrm{g}}^{-1}$
$M_{xit}$	Molar mass of xylitol.	152	gmol−1
$M_{xyl}$	Molar mass of xylose.	150	gmol−1
$Y_{x/xit}$	Biomass yield on xylitol.	$0.48$	${\mathrm{g}}_{\mathrm{cell}}{{\mathrm{g}}_{\mathrm{xylitol}}}^{-1}$

. The specific growth rate (u) depends on the glucose input and the xylitol produced, as shown in the following expression:

$$u=u_{glc}^{max}{\displaystyle \frac{C_{glc}}{K_{s,glc}+C_{glc}}}+u_{xit}^{max}{\displaystyle \frac{C_{xit}^{in}}{K_{s,xit}+C_{xit}^{in}}}{\displaystyle \frac{K_r}{K_r+C_{glc}}}$$

(7)

The specific uptake rates of xylose ($q_{xyl}$) and glucose ($q_{glc}$) are influenced by competitive inhibition between the substrates.

$$q_{glc}=q_{glc}^{max}{\displaystyle \frac{C_{glc}}{K_{s,glc}+C_{glc}(1+\frac{C_{xyl}}{K_{i,xyl}})}}$$

(8)

$$q_{xyl}=q_{xyl}^{max}{\displaystyle \frac{C_{xyl}}{K_{s,xyl}+C_{xyl}(1+\frac{C_{glc}}{K_{i,glc}})}}$$

(9)

The diffusive transport of xylitol from inside the cell to the outside ($r_{t,xit}^{\prime }$), the specific intracellular formation rate of xylitol ($r_{f,xit}$), and the specific intracellular consumption rate of xylitol ($r_{u,xit}$) are described by

$$r_{t,xit}^{\prime }=3.6\times {10}^6{P}_{xit}{a}_{cell}(C_{xit}^{in}-C_{xit}^{ex})$$

(10)

$$r_{f,xit}={\displaystyle \frac{M_{xit}}{M_{xyl}}}{q}_{xyl}$$

(11)

$$r_{u,xit}={\displaystyle \frac{u_{xit}}{Y_{x/xit}}}$$

(12)

To simplify the model, the equation assumes that xylitol is only consumed for cell growth, as its consumption for cell maintenance is insignificant. The state variables’ initial conditions for this process are as follows: $V_{l,0}$ = 2.5 L; $C_{x,0}$ = 6 g/L; $C_{gls,0}$ = 0 g/L; $C_{xyl,0}$ = 0 g/L; and $C_{xit,0}$ = 0 g/L. Additionally, the concentrations of glucose ($C_{glc}^f$) and xylose ($C_{xyl}^f$) in the feed are 200 g/L each.

3. Optimization Strategy

The optimization strategy consists of three stages. First, the optimization problem is formulated by defining the objective and system constraints. Then, the control actions are parameterized to ensure a suitable and continuous representation. Finally, the parameters involved in parameterization are optimized to achieve a solution that enhances process performance.

3.1. Optimal Control Problem Statement

The optimal control problem is formulated to determine two control action profiles, the glucose and xylose feeding rates, that maximize xylitol production over a 20 h time horizon ($t_f$ = 20 h). The objective function, constraints, and system dynamics are clearly defined to ensure feasibility and optimality. Specifically, the objective is to find the profiles of $F_{glc}\left(t\right)$ and $F_{xyl}\left(t\right)$ that maximize the concentration of xylitol at the final reaction time.

$$\underset{F_{glc}\left(t\right),F_{xyl}\left(t\right)}{max}J=\underset{F_{glc}\left(t\right),F_{xyl}\left(t\right)}{max}{C}_{xit}^{ex}\left(t_f\right)$$

(13)

This objective is subject to the equality constraints given by the mathematical model of the process (see Equations (1)–(6)), initial conditions (defined in [3]; see Equation (14)), and inequality constraints on the process variables (see Equation (15)).

$$[C_{x,0};C_{glc,0};C_{xyl,0};C_{xit,0}]=[6;0;0;0]\mathrm{g}/\mathrm{L}$$

(14)

$$\begin{array}{cc}\hfill V_{l,0}& =2.5\mathrm{L},\hfill \\ \hfill 2.5\mathrm{L}& \le V_l\left(t_f\right)\le 4\mathrm{L},\hfill \\ \hfill 0\mathrm{L}/\mathrm{h}& \le F_{\mathrm{glc}}\le 0.5\mathrm{L}/\mathrm{h},\hfill \\ \hfill 0\mathrm{L}/\mathrm{h}& \le F_{\mathrm{xyl}}\le 0.5\mathrm{L}/\mathrm{h}.\hfill \end{array}$$

(15)

3.2. Control Action Parameterization

The technique assumes the existence of an optimal control profile, represented as a function in the Hilbert space $L_2[0,t_f]$, where $t_f$ denotes the known final reaction time. This choice ensures that the control function remains square-integrable, a desirable property in many optimization frameworks [25]. Given that the optimal control profile $F^{*}\left(t\right)$ is assumed to be continuous, it can be approximated using a truncated expansion in a set of orthonormal polynomials adapted to the interval $[0,t_f]$. These polynomials are derived from the classical Legendre basis defined on $[-1,1]$, and they are mapped to the domain of interest through a change of variable detailed later (Equations (20)–(22)). The resulting approximate control profile is expressed as follows:

$$\tilde{F}\left(t\right)=a_0{P}_0+a_1{P}_1+a_2{P}_2+\dots +a_i{P}_i+\dots a_n{P}_n$$

(16)

Here, $\tilde{F}\left(t\right)$ is the approximated function, $a_i$ represents the polynomial coefficients, and $P_i\left(t\right)$ represents the orthonormal polynomials defined on $[0,t_f]$. Consequently, solving the optimization problem involves determining the coefficients that yield smooth feeding control actions. The control actions for xylitol production are represented by the feeding rates of glucose, ${\tilde{F}}_{glc}$, and xylose, ${\tilde{F}}_{xyl}$, which are modeled using a second-(Equation (17)) or third-degree (Equation (18)) polynomial:

$${\tilde{F}}_{glc}=c_0{P}_0+c_1{P}_1+c_2{P}_2;{\tilde{F}}_{xyl}=b_0{P}_0+b_1{P}_1+b_2{P}_2$$

(17)

$${\tilde{F}}_{glc}=c_0{P}_0+c_1{P}_1+c_2{P}_2+c_3{P}_3;{\tilde{F}}_{xyl}=b_0{P}_0+b_1{P}_1+b_2{P}_2+b_3{P}_3$$

(18)

By optimizing the coefficients $c_i$ and $b_i$ of the Legendre polynomials, the optimal control vectors ${\tilde{F}}_{glc}$ and ${\tilde{F}}_{xyl}$ are obtained, maximizing the objective function (Equation (13)). Consequently, the system achieves optimal control policies.

The control action parameterization strategy is based on Legendre polynomials, a family of orthogonal polynomials that are well behaved within the interval $[-1,1]$, facilitating the optimization process. These polynomials are redefined to fit the time interval $[0,t_f]$, ensuring their applicability to the problem’s temporal domain. One of their key properties is orthogonality [26], meaning that the inner product of two Legendre polynomials of different degrees n and m in $L_2$ over this interval is zero when $n\ne m$. Since Legendre polynomials form a complete and orthogonal set, any square-integrable function within the interval can be approximated as a weighted sum of these polynomials. This property ensures flexibility in representing control action profiles while maintaining mathematical tractability [27].

Another fundamental property that supports the parameterization of the control action is Rodrigues’ formula. This formula provides an explicit expression for generating Legendre polynomials of any degree, offering a systematic way to compute them efficiently [28].

$$Q_n\left(x\right)={\displaystyle \frac{1}{2^{n}n!}}{\displaystyle \frac{d^n}{d{x}^n}}{(x^2-1)}^n$$

(19)

where $Q_n$ are orthogonal polynomials in $L_2[-1,1]$, and n is their degree [27].

To find an orthogonal basis in $L_2[0,t_f]$, the following transformation is required [27]:

$$x=2{\displaystyle \frac{t}{t_f}}-1$$

(20)

Then,

$$Q_n\left(x\right)=Q_n\left(x\left(t\right)\right)=m_n\left(t\right)$$

(21)

where $m_n$ are the orthogonal polynomials. Thus, to obtain an orthonormal basis in $L_2[0,t_f]$, the following is defined:

$$P_n={\displaystyle \frac{m_n\left(t\right)}{\parallel m_n\left(t\right)\parallel }}$$

(22)

In this way, the orthonormal polynomials involved in Equations (17) and (18) are obtained. This transformation ensures that the polynomials remain well conditioned over the desired interval, enhancing numerical stability and computational efficiency.

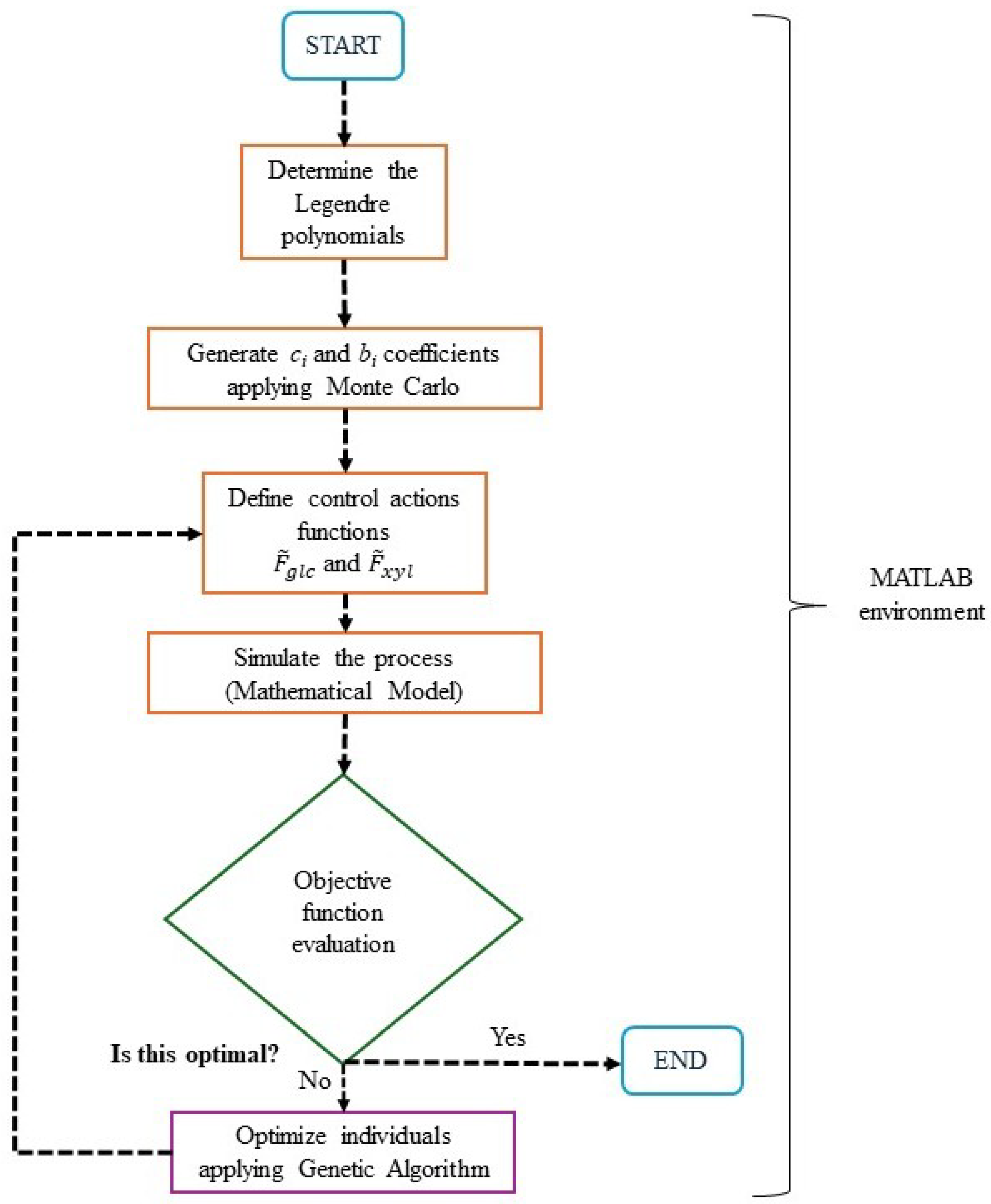
3.3. Control Action Optimization

This parameter optimization technique aims to maximize the xylitol concentration at the process endpoint by determining the optimal control actions within a dual-substrate feeding strategy. To achieve this, a hybrid approach combining Monte Carlo simulation and a genetic algorithm is implemented to efficiently explore the optimization space. Initially, the Monte Carlo method, a probabilistic technique that relies on extensive random sampling, is employed to generate a diverse population of candidate solutions. Each candidate consists of a specific set of coefficients associated with the Legendre polynomials, which define the smooth substrate feeding profiles over the fermentation period. These candidates, also referred to as individuals, are evaluated by simulating the bioprocess dynamics, and their performance is assessed based on the resulting xylitol concentration at the end of the batch. This initial sampling phase allows for a broad exploration of the solution space, reducing the risk of premature convergence to suboptimal regions. Following this, the genetic algorithm takes over to further refine the most promising individuals. This evolutionary optimization technique imitates natural selection through genetic operations such as selection, crossover, and mutation, enabling the progressive improvement of the feeding profiles over successive generations. The combination of both methods leverages the global search capabilities of Monte Carlo and the local refinement strength of genetic algorithms, yielding high-quality solutions with reduced computational costs and enhanced robustness against local minima. Using a population matrix derived from the Monte Carlo-generated individuals, the genetic algorithm iteratively optimizes the control actions. The hybrid algorithm follows a structured sequence to optimize the control actions ${\tilde{F}}_{glc}$ and ${\tilde{F}}_{xyl}$, ensuring smooth profiles suitable for direct application. The steps are as follows:

• Definition of the Individual and Parameter Scaling: Each individual represents a set of parameters to be optimized, defining the Legendre polynomial coefficients $c_i$ and $b_i$. These parameters allow for the construction of the control action profiles, which are used to simulate the process and evaluate the objective function J. Each parameter $a_i$ is determined using the following expression:

  $$a_i=a_{i,min}+{\delta }_i(a_{i,max}-a_{i,min})$$

  (23)

  where $\delta$ is a weighting coefficient varying between 0 and 1, and $a_{i,max}$ and $a_{i,min}$ represent the upper and lower bounds of the parameter’s variation range, respectively. A set of these coefficients uniquely defines each individual. The bounds for the optimization coefficients $a_i$ are not fixed in advance. Instead, they are initially based on the expected range of the control actions and then progressively refined during the exploratory phase of the simulations. As improved solutions tend to cluster within certain value ranges, the bounds are empirically narrowed to focus the search on the most promising regions of the parameter space. This strategy is commonly used in heuristic optimization to enhance convergence efficiency without compromising solution diversity [29].
• Initial Population Generation: A random initial population of $N=5000$ individuals is generated using the Monte Carlo method. The objective function of each individual is evaluated based on the process simulation results (Equation (13)).
• Selection: The best 20 individuals, based on their objective function value J, are selected using an elitist strategy.
• Crossover: A one-point crossover operator is applied to the selected individuals, combining parameter sets to explore the search space and generate 20 additional individuals.
• Mutation: By applying small perturbations to selected individuals, 40 new individuals are generated, where one randomly chosen parameter of each individual is modified within its variability range.
• Exploration Mechanism: To prevent convergence to local extrema, an additional set of 20 randomly generated individuals is introduced in each generation, adapting their distribution based on the algorithm’s evolution.

The process is repeated iteratively until convergence is reached or the predefined limit of $L=50$ generations is met. Convergence is determined when the variation in J becomes minimal, typically before reaching 50 generations. The selection of the hyperparameters N and L follows the methodological criteria established in a previous study [30], where the influence of population size and the number of generations on convergence and solution quality was systematically analyzed. While the specific values used here are adjusted to suit the current case study, the selection process is based on the same reasoning and is therefore not repeated in full. It should be noted that all process constraints defined in Equation (15), including those on feeding rates and final volume, are strictly enforced during the candidate generation stage. These constraints originate from the reference model [3] and are based on the physical limitations of the bioreactor setup and the feeding equipment. In the implementation, a while-loop structure is used to verify the feasibility of each proposed control profile. If any of the constraints are violated, the profile is discarded, and a new one is generated. This ensures that only feasible individuals are passed on to the simulation and evaluation stages and that the optimization process remains confined to the admissible region of the solution space. Figure 1 outlines the steps taken to optimize the process control actions.

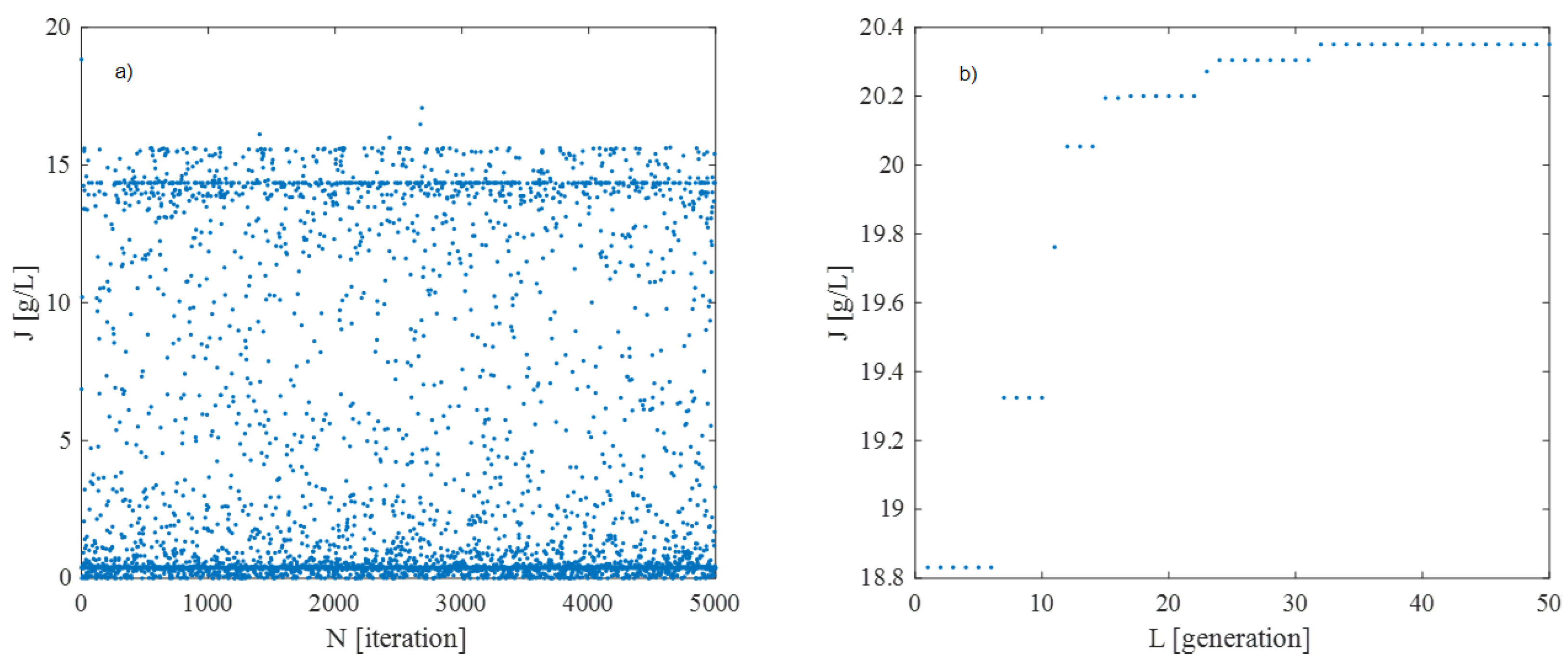
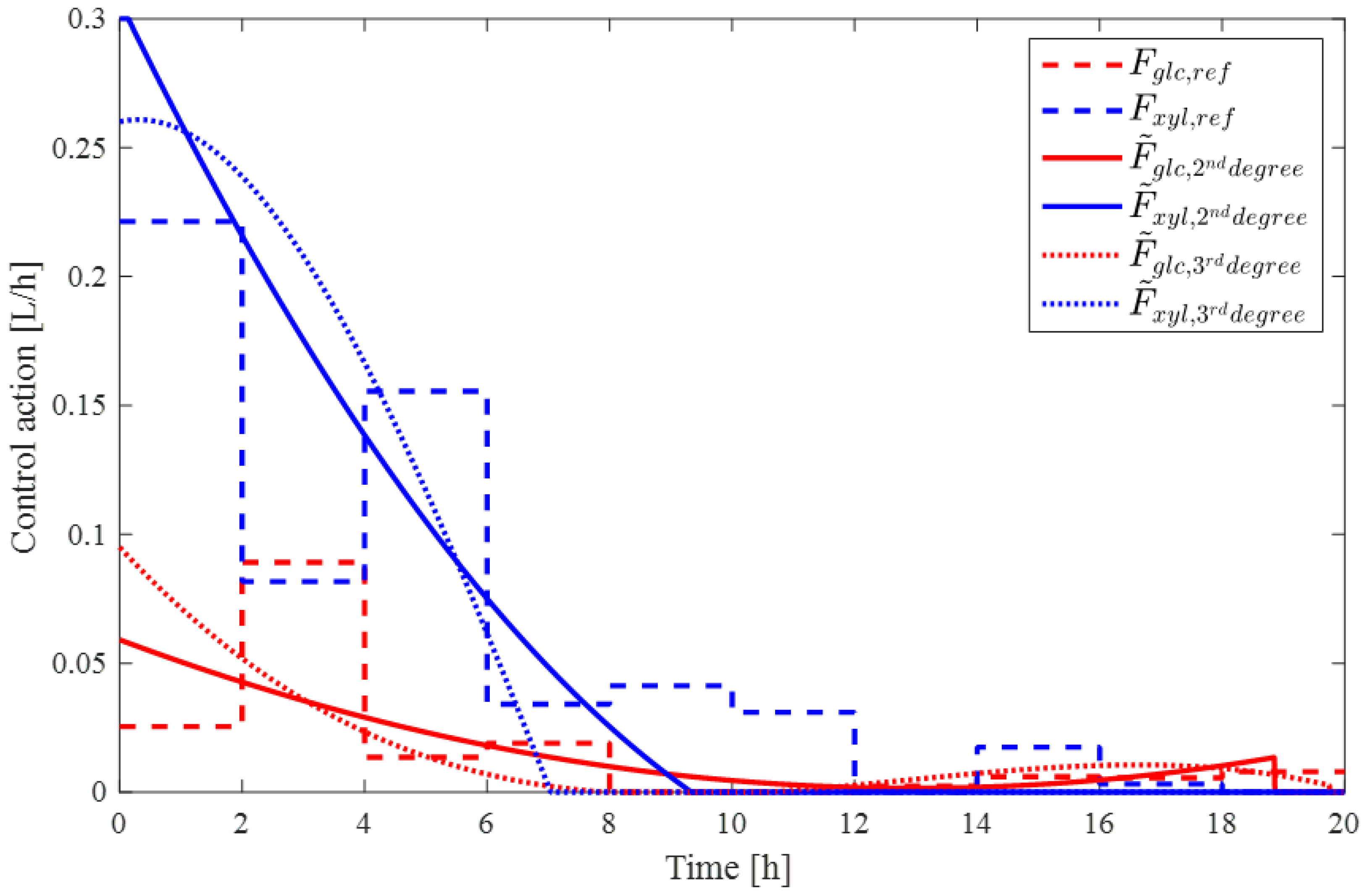
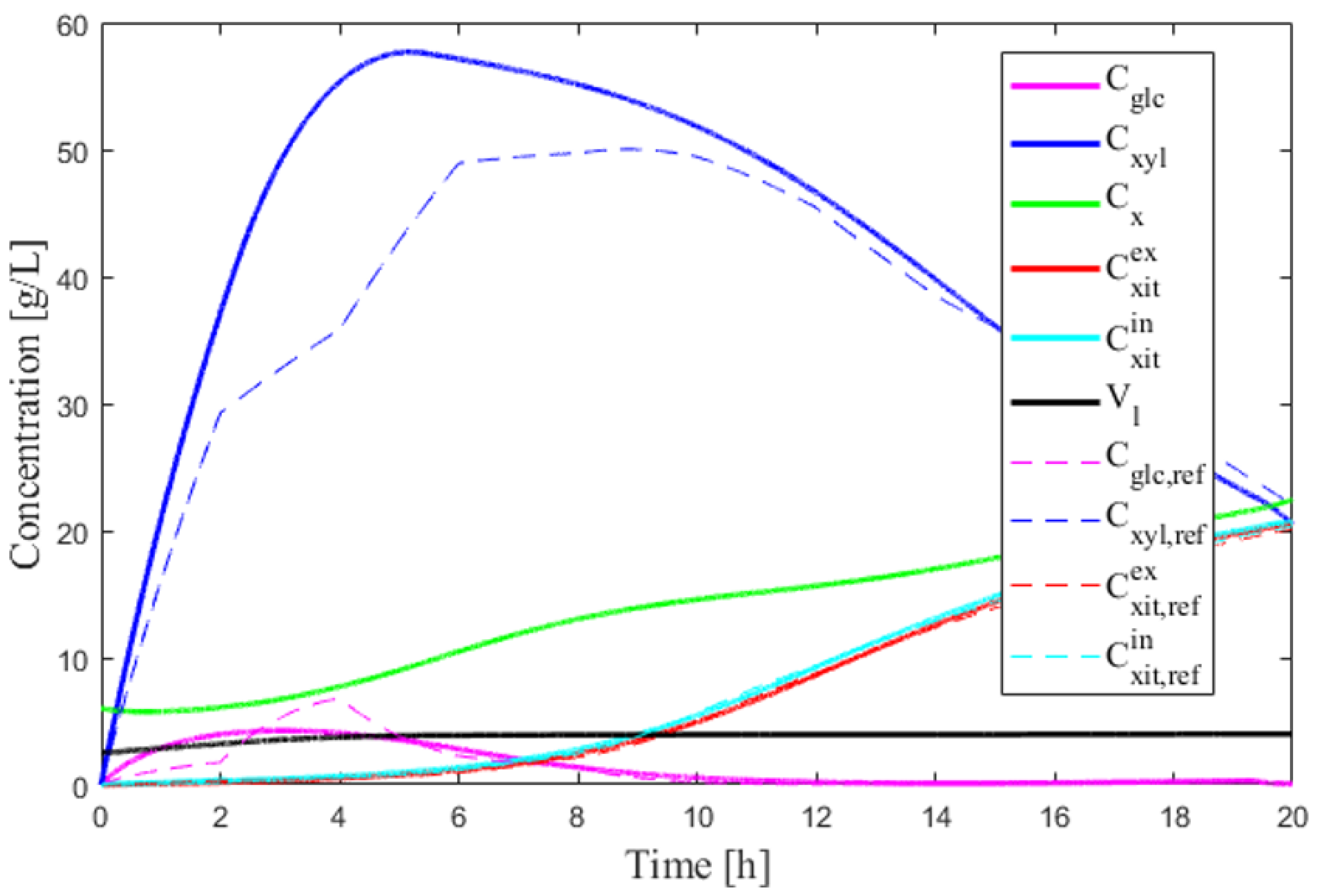
4. Results and Discussion

This section analyzes an alternative strategy for optimizing xylitol production through the parameterization of two control actions: the glucose and xylose feeding rates. The objective function is defined as the maximization of the xylitol concentration at the end of the process. To ensure a consistent and meaningful comparison, all simulations are carried out under the same operating conditions reported by Tochampa et al. [3]. While their method discretizes the time horizon into multiple intervals and optimizes each segment independently, the present approach employs continuous polynomial functions to represent the control profiles over the entire process duration. Specifically, second- and third-degree polynomials are considered to assess their ability to capture the system dynamics while maintaining a simple mathematical structure. Before introducing the results obtained with the proposed strategy, it is useful to examine in more detail the main limitations of the reference method.

In Tochampa’s method, the feeding profiles are obtained through a piecewise constant parameterization optimized using genetic algorithms. While this approach provides flexibility within each time interval, it results in discontinuous control signals with abrupt transitions. These discontinuities require additional signal filtering before implementation in real systems, which introduces distortions and deviations from the original optimized profiles. Consequently, the control actions applied in practice differ from those derived during the optimization stage, leading to suboptimal performance in real applications. Furthermore, this methodology demands the optimization of ten independent parameters per control action, significantly increasing the dimensionality of the search space, the computational cost, and the risk of convergence to local minima. Under these conditions, Tochampa et al. [3] reported a maximum xylitol concentration of $20.06$ g/L, which will serve as the benchmark for evaluating the effectiveness of the proposed continuous-parameter strategy.

As previously mentioned, this work explores the use of Legendre polynomials of the second and third degrees to parameterize the glucose and xylose feeding profiles in the xylitol production process. This strategy offers several advantages: it ensures smooth control actions, avoids the need for filtering before implementation in real systems, and reduces the mathematical complexity compared to other functional representations. Moreover, the use of orthogonal polynomials like Legendre allows for a compact and numerically stable formulation. To determine the optimal set of polynomial coefficients, a hybrid algorithm is employed. It combines the global search capabilities of Monte Carlo sampling with the local refinement offered by a genetic algorithm. This two-stage optimization effectively balances exploration and exploitation, increasing the likelihood of efficiently reaching near-optimal solutions. The evolution of the optimization process is illustrated in Figure 2. Figure 2a shows the distribution of solutions obtained during the Monte Carlo phase, characterized by a broad and random search. Figure 2b reveals how the genetic algorithm progressively improves the objective function, demonstrating its capacity to fine-tune the results. These visualizations highlight the stochastic nature of the initial phase and the convergence trend achieved during the refinement stage.

The resulting control profiles for each polynomial degree are represented in Equations (24) and (25), where the final form of the approximating polynomials is shown. The objective function values obtained in each case are $20.26$ g/L and $20.35$ g/L of xylitol, respectively. Although slight improvements are observed as the polynomial degree increases, the gains are not substantial enough to justify the added complexity and the increased number of parameters (considering the minimal improvement observed with the third-degree polynomials, higher-order expansions were not pursued to avoid overparameterization and to preserve the simplicity and implementability of the feeding profiles in real systems). The second-degree polynomial achieves a xylitol concentration comparable to that of the higher-degree cases and exceeds the $20.06$ g/L reported by Tochampa et al. [3]. This suggests that the second-degree approximation strikes an effective balance between simplicity and performance, requiring fewer parameters while preserving smoothness and feasibility for implementation.

$${\tilde{F}}_{glc}=0.059+0.009t+3.4\times {10}^{-4}{t}^2;{\tilde{F}}_{xyl}=0.307+0.049t+0.002t^2$$

(24)

$${\tilde{F}}_{glc}=0.095+0.026t+0.002t^2+5.6\times {10}^{-5}{t}^3;{\tilde{F}}_{xyl}=0.26+0.005t+0.009t^2+3.8\times {10}^{-4}{t}^3$$

(25)

These results are further illustrated in Figure 3, which includes the feeding profiles obtained using the proposed methodology, alongside those reported by Tochampa et al. [3] The figure highlights the smoother nature of the proposed profiles, which avoid the abrupt changes and post-optimization filtering required by the piecewise constant strategy. This improvement is reflected in the concentration values and the qualitative behavior of the control profiles. The presence of slope discontinuities in the optimal feeding profiles may appear counterintuitive given the smoothness of Legendre polynomial expansions. However, this behavior is consistent with strategies reported in the literature, where optimal feeding policies often include non-feeding phases to avoid substrate or product inhibition. Such profiles effectively switch between fed-batch and batch operation depending on the system dynamics and constraints [31]. Compared to previous methodologies that use Fourier series and orthonormal polynomials [13,22,23,24], this technique achieves equivalent optimization results with a considerably lower mathematical complexity. Figure 4 presents the evolution of the state variables during the process. Although the trajectories vary compared to the reference, the trend remains within the ranges reported in [3], with a smoother system evolution. This behavior is particularly beneficial for preventing microorganism stress, as abrupt changes in the feeding rate can negatively impact growth and metabolite production [16].

A key advantage of the proposed methodology is that the resulting feeding profiles can be directly applied in a real system without further modification. In contrast, the stepped profiles used by Tochampa et al. [3] are not physically realizable, since instantaneous changes in feeding rates are impractical due to actuator response limitations. The smoothness of the proposed profiles avoids this issue and makes implementation feasible using standard control hardware. Although the reported increase in the xylitol concentration is modest, such improvements can yield substantial benefits in industrial settings, where improved productivity reduces the consumption of raw materials per unit of product, optimizes reactor utilization, and contributes to the overall profitability of the process.

Furthermore, although a formal robustness analysis is beyond the scope of this work, preliminary simulations indicate that the system is not highly sensitive to small variations in the polynomial coefficients or to minor perturbations in initial conditions. This inherent stability suggests that the proposed approach may retain performance even under realistic process uncertainties, which is particularly relevant in biological systems where exact conditions are difficult to maintain. Together, these results support the use of low-degree Legendre polynomials as a simple and implementation-ready strategy for the open-loop optimization of biological production processes.

5. Conclusions

The proposed dynamic optimization strategy, based on low-degree Legendre polynomials, successfully parameterized the glucose and xylose feeding rates in a fed-batch xylitol production process. The resulting control profiles led to a $1.44\%$ increase in the final xylitol concentration, from $20.06$ g/L (reference) to $20.35$ g/L, using only four parameters per control action. This improvement, though moderate in absolute terms, was achieved with a significantly simplified mathematical structure, resulting in reduced computational costs and enhanced implementation feasibility.

Beyond performance enhancement, the method ensures smooth control actions, avoiding the abrupt variations associated with piecewise constant strategies. This feature is particularly relevant for practical applications, where real systems cannot accommodate discontinuous profiles due to actuator limitations and biological sensitivity. The results confirm that a second-degree polynomial representation offers an effective balance between simplicity and accuracy, fulfilling the initial objective of achieving implementable and efficient optimal control strategies.

Given its compact formulation and favorable numerical properties, the proposed methodology constitutes a promising alternative for the open-loop optimization of nonlinear multivariable bioprocesses. Future work will focus on extending this approach to closed-loop control schemes and evaluating its performance under process uncertainties and experimental conditions.