Dynamic Optimization of Xylitol Production Using Legendre-Based Control Parameterization
Abstract
1. Introduction
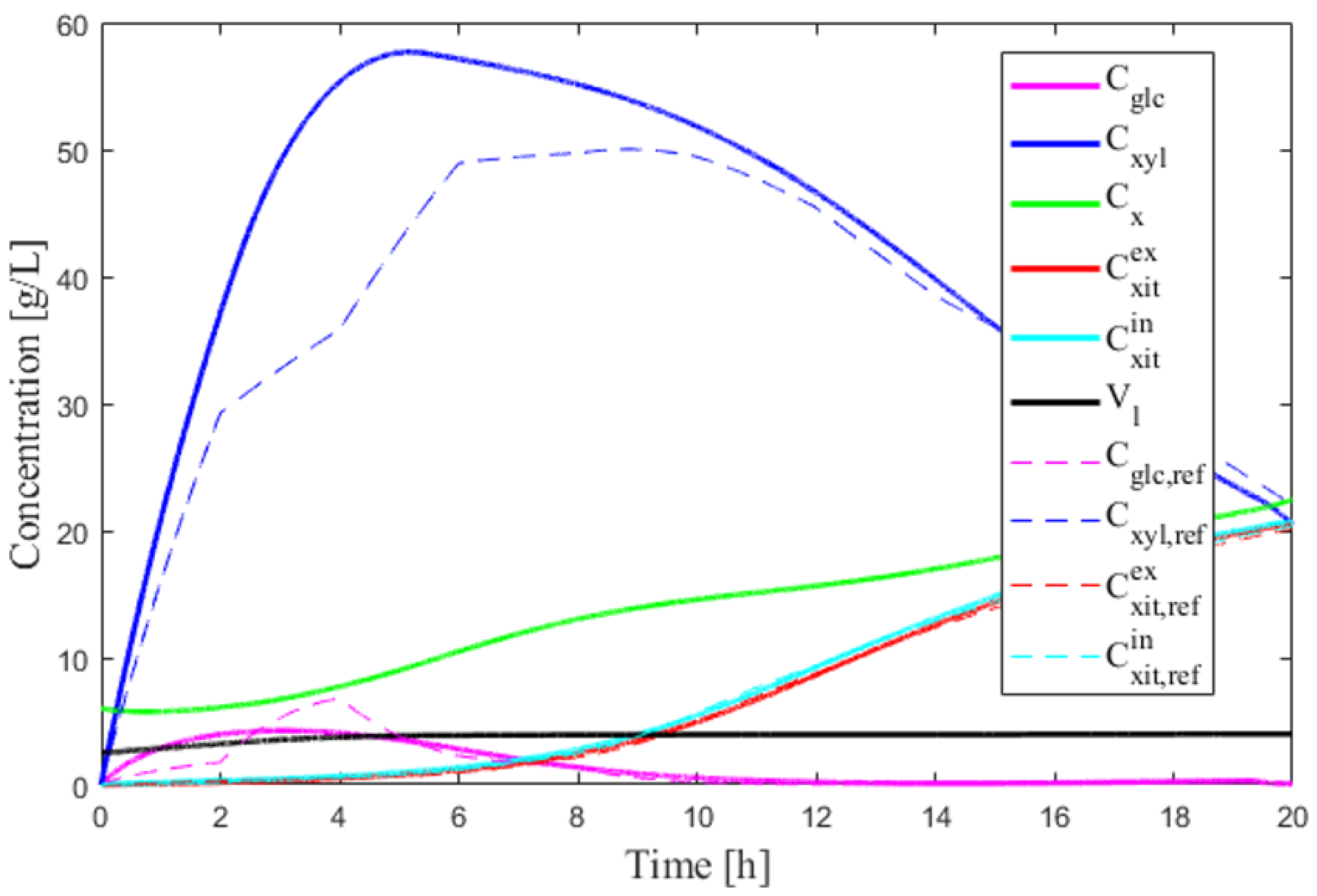
2. Process of Mathematical Model
3. Optimization Strategy
3.1. Optimal Control Problem Statement
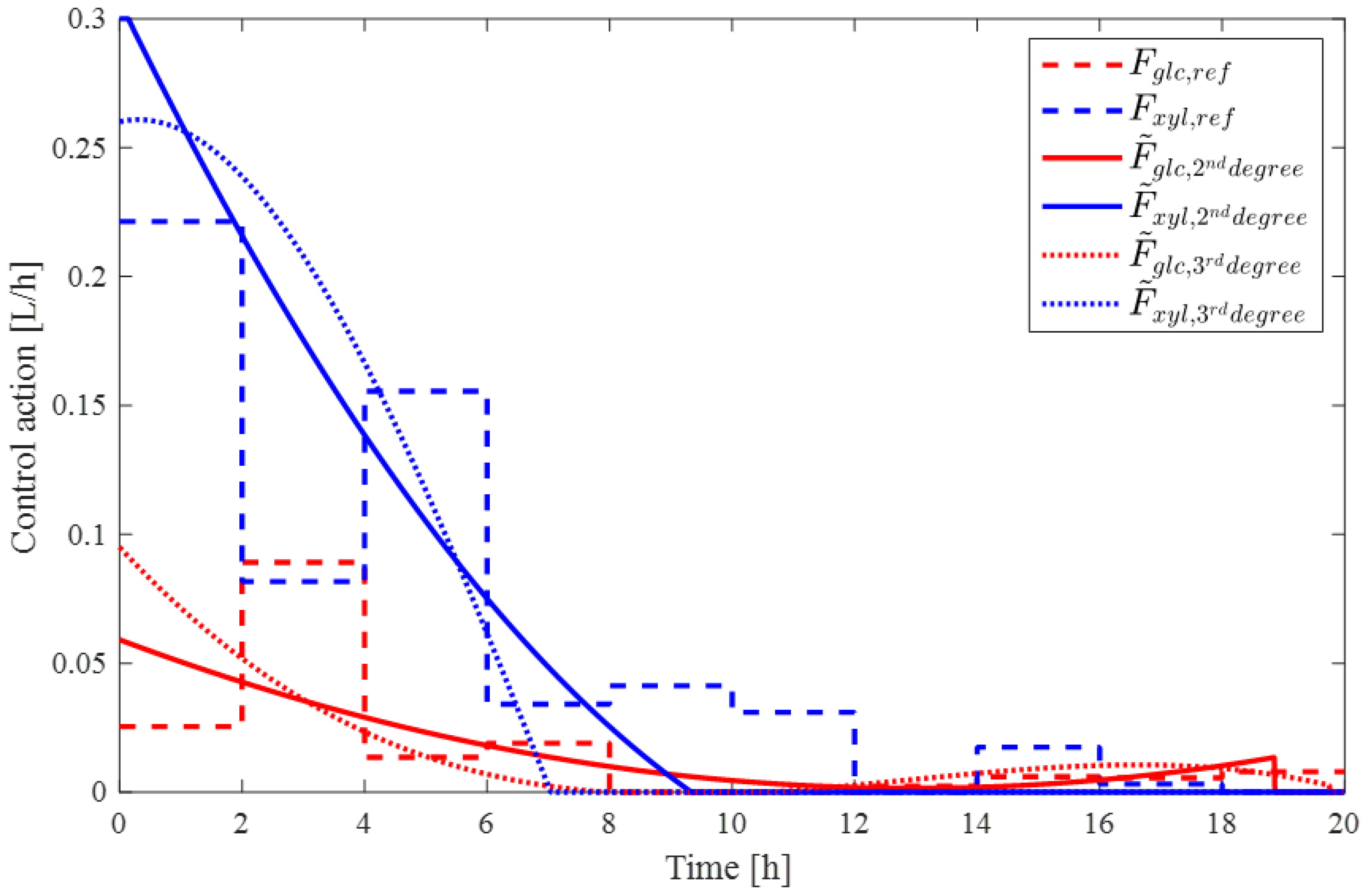
3.2. Control Action Parameterization
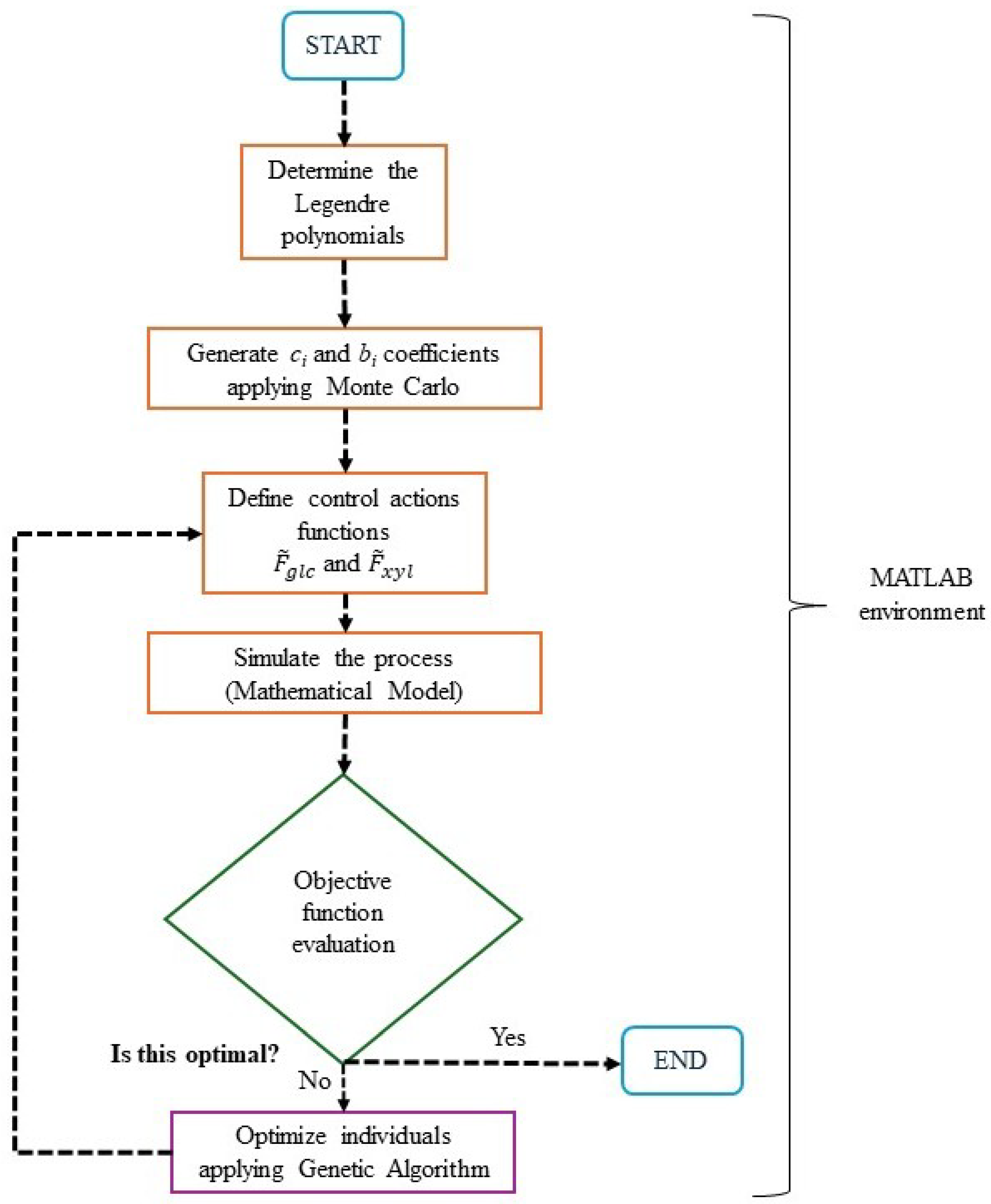
3.3. Control Action Optimization
- Definition of the Individual and Parameter Scaling: Each individual represents a set of parameters to be optimized, defining the Legendre polynomial coefficients and . These parameters allow for the construction of the control action profiles, which are used to simulate the process and evaluate the objective function J. Each parameter is determined using the following expression:where is a weighting coefficient varying between 0 and 1, and and represent the upper and lower bounds of the parameter’s variation range, respectively. A set of these coefficients uniquely defines each individual. The bounds for the optimization coefficients are not fixed in advance. Instead, they are initially based on the expected range of the control actions and then progressively refined during the exploratory phase of the simulations. As improved solutions tend to cluster within certain value ranges, the bounds are empirically narrowed to focus the search on the most promising regions of the parameter space. This strategy is commonly used in heuristic optimization to enhance convergence efficiency without compromising solution diversity [29].
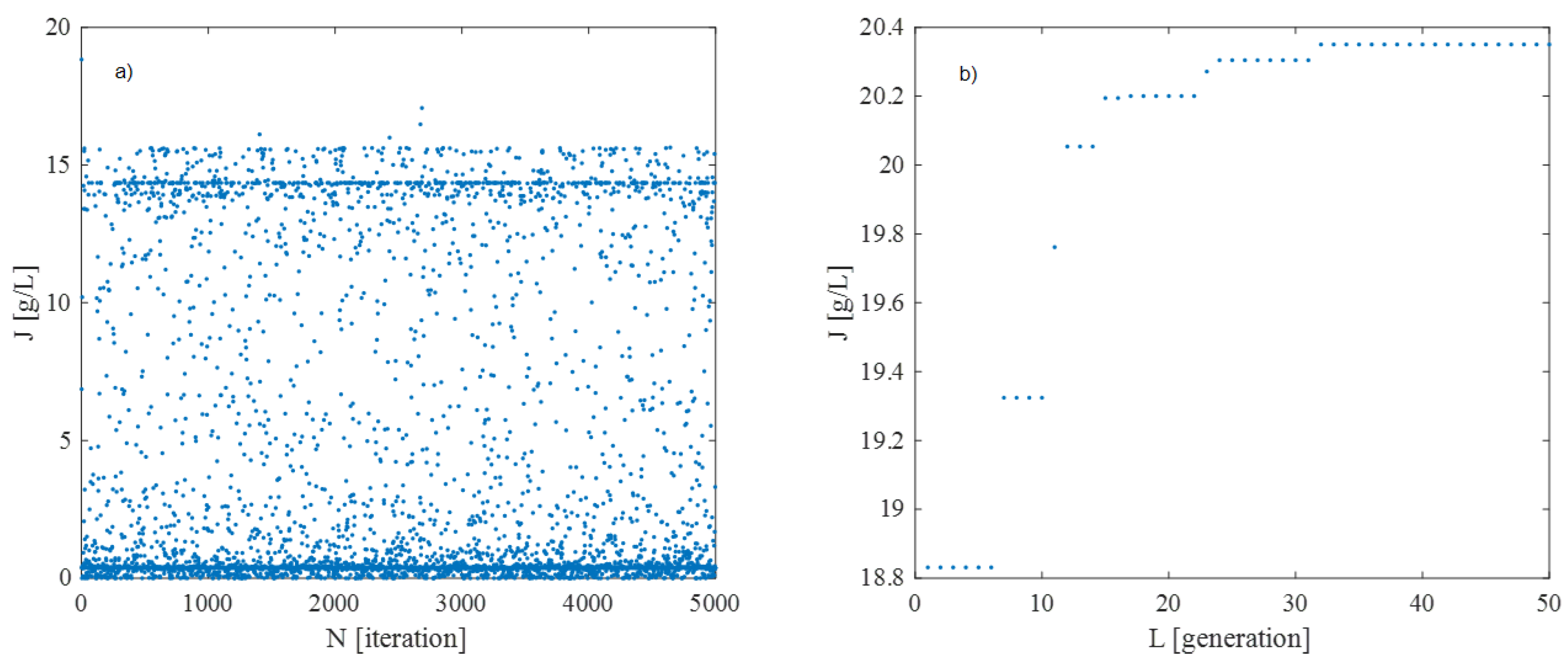
- Initial Population Generation: A random initial population of individuals is generated using the Monte Carlo method. The objective function of each individual is evaluated based on the process simulation results (Equation (13)).
- Selection: The best 20 individuals, based on their objective function value J, are selected using an elitist strategy.
- Crossover: A one-point crossover operator is applied to the selected individuals, combining parameter sets to explore the search space and generate 20 additional individuals.
- Mutation: By applying small perturbations to selected individuals, 40 new individuals are generated, where one randomly chosen parameter of each individual is modified within its variability range.
- Exploration Mechanism: To prevent convergence to local extrema, an additional set of 20 randomly generated individuals is introduced in each generation, adapting their distribution based on the algorithm’s evolution.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gasmi Benahmed, A.; Gasmi, A.; Arshad, M.; Shanaida, M.; Lysiuk, R.; Peana, M.; Pshyk-Titko, I.; Adamiv, S.; Shanaida, Y.; Bjørklund, G. Health benefits of xylitol. Appl. Microbiol. Biotechnol. 2020, 104, 7225–7237. [Google Scholar] [CrossRef] [PubMed]
- de Albuquerque, T.L.; da Silva, I.J., Jr.; de Macedo, G.R.; Rocha, M.V.P. Biotechnological production of xylitol from lignocellulosic wastes: A review. Process Biochem. 2014, 49, 1779–1789. [Google Scholar] [CrossRef]
- Tochampa, W.; Sirisansaneeyakul, S.; Vanichsriratana, W.; Srinophakun, P.; Bakker, H.H.; Wannawilai, S.; Chisti, Y. Optimal control of feeding in fed-batch production of xylitol. Ind. Eng. Chem. Res. 2015, 54, 1992–2000. [Google Scholar] [CrossRef]
- Luus, R. Optimization of fed-batch fermentors by iterative dynamic programming. Biotechnol. Bioeng. 1993, 41, 599–602. [Google Scholar] [CrossRef]
- Park, S.; Fred Ramirez, W. Optimal production of secreted protein in fed-batch reactors. AIChE J. 1988, 34, 1550–1558. [Google Scholar] [CrossRef]
- Setoodeh, P.; Jahanmiri, A.; Eslamloueyan, R. Hybrid neural modeling framework for simulation and optimization of diauxie-involved fed-batch fermentative succinate production. Chem. Eng. Sci. 2012, 81, 57–76. [Google Scholar] [CrossRef]
- Arpornwichanop, A.; Shomchoam, N. Studies on optimal control approach in a fed-batch fermentation. Korean J. Chem. Eng. 2007, 24, 11–15. [Google Scholar] [CrossRef]
- Srinivasan, B.; Palanki, S.; Bonvin, D. Dynamic optimization of batch processes: I. Characterization of the nominal solution. Comput. Chem. Eng. 2003, 27, 1–26. [Google Scholar] [CrossRef]
- Zhang, J. Developing robust neural network models by using both dynamic and static process operating data. Ind. Eng. Chem. Res. 2001, 40, 234–241. [Google Scholar] [CrossRef]
- Luus, R. Application of dynamic programming to differential-algebraic process systems. Comput. Chem. Eng. 1993, 17, 373–377. [Google Scholar] [CrossRef]
- Li, J.; Rhinehart, R.R. Heuristic random optimization. Comput. Chem. Eng. 1998, 22, 427–444. [Google Scholar] [CrossRef]
- Pantano, M.N.; Fernández, M.C.; Amicarelli, A.; Scaglia, G.J. Evolutionary algorithms and orthogonal basis for dynamic optimization in L2 space for batch biodiesel production. Chem. Eng. Res. Des. 2022, 177, 354–364. [Google Scholar] [CrossRef]
- Pantano, M.N.; Fernández, M.; Rodriguez, L.; Scaglia, G.J.E. Optimización Dinámica Basada en Fourier: Aplicación al Proceso de Producción de Biodiesel; Revista Iberoamericana de Automática e Informática Industrial: Valencia, Spain, 2020. [Google Scholar]
- Banga, J.R.; Balsa-Canto, E.; Moles, C.G.; Alonso, A.A. Dynamic optimization of bioprocesses: Efficient and robust numerical strategies. J. Biotechnol. 2005, 117, 407–419. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C.; Camacho, E.F.; Bordons, C. Constrained Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Weegman, B.P.; Essawy, A.; Nash, P.; Carlson, A.L.; Voltzke, K.J.; Geng, Z.; Jahani, M.; Becker, B.B.; Papas, K.K.; Firpo, M.T. Nutrient regulation by continuous feeding for large-scale expansion of mammalian cells in spheroids. J. Vis. Exp. JoVE 2016, 52224. [Google Scholar] [CrossRef]
- Lee, S.J.; Song, H.; Lee, S.Y. Genome-based metabolic engineering of Mannheimia succiniciproducens for succinic acid production. Appl. Environ. Microbiol. 2006, 72, 1939–1948. [Google Scholar] [CrossRef] [PubMed]
- Elnagar, G.N.; Kazemi, M.A.; Razzaghi, M. The pseudospectral Legendre method for discretizing optimal control problems. IEEE Trans. Autom. Control 1995, 40, 1793–1796. [Google Scholar] [CrossRef]
- Gong, Q.; Fahroo, F.; Ross, I.M. A pseudospectral method for the optimal control of constrained feedback linearizable systems. IEEE Trans. Autom. Control 2006, 51, 1115–1129. [Google Scholar] [CrossRef]
- Ross, I.M.; Fahroo, F. Pseudospectral methods for optimal motion planning of differentially flat systems. In Proceedings of the Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; pp. 1135–1140. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar] [CrossRef]
- Pantano, M.N.; Fernández, M.C.; Ortiz, O.A.; Scaglia, G.J.; Vega, J.R. A Fourier-based control vector parameterization for the optimization of nonlinear dynamic processes with a finite terminal time. Comput. Chem. Eng. 2020, 134, 106721. [Google Scholar] [CrossRef]
- Pantano, M.N.; Puchol, M.C.F.; Rossomando, F.G.; Scaglia, G.J. Open-Loop Dynamic Optimization for Nonlinear Multi-Input Systems. Application to Recombinant Protein Production. IEEE Lat. Am. Trans. 2021, 19, 1307–1314. [Google Scholar] [CrossRef]
- Fernández, C.; Pantano, N.; Groff, C.; Gil, R.; Scaglia, G. Bioethanol production optimization by direct numerical methods and evolutionary algorithms. IEEE Lat. Am. Trans. 2024, 22, 259–265. [Google Scholar] [CrossRef]
- Ito, K. Functional Analysis and Optimization. Lecture Monograph. 2016. Available online: https://kito.wordpress.ncsu.edu/files/2020/07/funa3-2.pdf (accessed on 30 March 2025).
- Ramírez Rincón, W.A. Elementos de Polinomio de Legendre. Bachelor’s Thesis, Universidad de Pamplona, Norte de Santander, Colombia, 2017. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley & Sons: Hoboken, NJ, USA, 1991; Volume 17. [Google Scholar]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 6th ed.; Arfken, G.B., Weber, H.J., Eds.; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA, 2005. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Fernández, C.; Pantano, N.; Godoy, S.; Serrano, E.; Scaglia, G. Optimización de parámetros utilizando los métodos de Monte Carlo y Algoritmos Evolutivos. Aplicación a un controlador de seguimiento de trayectoria en sistemas no lineales. Rev. Iberoam. Autom. Inform. Ind. 2019, 16, 89–99. [Google Scholar] [CrossRef]
- Hong, J. Optimal substrate feeding policy for a fed batch fermentation with substrate and product inhibition kinetics. Biotechnol. Bioeng. 1986, 28, 1421–1431. [Google Scholar] [CrossRef]
| Symbol | Description | Value | Unitis |
|---|---|---|---|
| Max. specific growth rate with respect to xylitol. | h−1 | ||
| Max. specific growth rate with respect to glucose. | h−1 | ||
| Monod saturation constant for glucose. | |||
| Monod saturation constant for xylitol. | |||
| Monod saturation constant for xylose. | |||
| Repression constant for glucose. | |||
| Max. specific uptake rate of glucose. | |||
| Max. specific uptake rate of xylose. | |||
| Inhibition uptake constant of xylose by glucose. | |||
| Inhibition uptake constant of glucose by xylose. | |||
| Permeability coefficient of the cell membrane. | ms−1 | ||
| Specific surface area of the cell. | |||
| Molar mass of xylitol. | 152 | gmol−1 | |
| Molar mass of xylose. | 150 | gmol−1 | |
| Biomass yield on xylitol. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez, E.; Noriega, M.; Fernández, C.; Pantano, N.; Rodriguez, L.; Scaglia, G. Dynamic Optimization of Xylitol Production Using Legendre-Based Control Parameterization. Fermentation 2025, 11, 308. https://doi.org/10.3390/fermentation11060308
Gutiérrez E, Noriega M, Fernández C, Pantano N, Rodriguez L, Scaglia G. Dynamic Optimization of Xylitol Production Using Legendre-Based Control Parameterization. Fermentation. 2025; 11(6):308. https://doi.org/10.3390/fermentation11060308
Chicago/Turabian StyleGutiérrez, Eugenia, Marianela Noriega, Cecilia Fernández, Nadia Pantano, Leandro Rodriguez, and Gustavo Scaglia. 2025. "Dynamic Optimization of Xylitol Production Using Legendre-Based Control Parameterization" Fermentation 11, no. 6: 308. https://doi.org/10.3390/fermentation11060308
APA StyleGutiérrez, E., Noriega, M., Fernández, C., Pantano, N., Rodriguez, L., & Scaglia, G. (2025). Dynamic Optimization of Xylitol Production Using Legendre-Based Control Parameterization. Fermentation, 11(6), 308. https://doi.org/10.3390/fermentation11060308






