ADM1-Based Modeling of Biohydrogen Production through Anaerobic Co-Digestion of Agro-Industrial Wastes in a Continuous-Flow Stirred-Tank Reactor System

Economou, Christina N.; Manthos, Georgios; Zagklis, Dimitris; Kornaros, Michael

doi:10.3390/fermentation10030138

Open AccessEditor’s ChoiceArticle

ADM1-Based Modeling of Biohydrogen Production through Anaerobic Co-Digestion of Agro-Industrial Wastes in a Continuous-Flow Stirred-Tank Reactor System

¹

Laboratory of Biochemical Engineering & Environmental Technology (LBEET), Department of Chemical Engineering, University of Patras, 26504 Patras, Greece

²

Institute of Circular Economy and Environment (ICEE), University of Patras’ Research and Development Center, 26504 Patras, Greece

^*

Author to whom correspondence should be addressed.

Fermentation 2024, 10(3), 138; https://doi.org/10.3390/fermentation10030138

Submission received: 8 February 2024 / Revised: 22 February 2024 / Accepted: 27 February 2024 / Published: 29 February 2024

(This article belongs to the Special Issue Biological Conversion of Biomass Residues and Waste Streams for the Sustainable Production of Biofuels and Bio-Based Products: 2nd Edition)

Download

Browse Figures

Versions Notes

Abstract

:

Biological treatment is a promising alternative for waste management considering the environmentally sustainable concept that the European Union demands. In this direction, anaerobic digestion comprises a viable waste treatment process, producing high energy-carrier gases such as biomethane and biohydrogen under certain operating conditions. The mathematical modeling of this bioprocess can be used as a valuable tool for process scale-up with cost-effective implications. The scope of this work was the evaluation of the well-established Anaerobic Digestion Model 1 (ADM1) for use in two-stage anaerobic digestion of agro-industrial waste. Certain equations for the description of the metabolic pathways for lactate and bioethanol accumulation were implemented in the existing mechanistic model in order to enhance the model’s accuracy. The model presents a high estimation ability regarding the final product (H₂ and biogas) reaching the same maximum value for the theoretical as the experimental data of these products (0.0012 and 0.0036 m³/d, respectively). The adapted ADM1 emerges as a useful instrument for designing anaerobic co-digestion processes with the goal of achieving high yields in fermentative hydrogen production, considering mixed biomass growth mechanisms.

Keywords:

modeling; hydrogen production; anaerobic co-digestion; olive mill wastewater; cheese whey; cow manure

1. Introduction

The disposal of agro-industrial wastes such as olive mill wastewater (OMW), cheese whey (CW) and cow manure (CM), which are characterized by a high organic content, present a serious environmental problem in the Mediterranean region [1]. These wastes, which are generated in millions of tonnes per year from processing industries, could serve as sustainable raw materials for the anaerobic digestion (AD) process, which is the most preferred technology for bio-energy production, reducing the organic content of wastewaters [2].

Hydrogen is a valuable gas generated from AD systems during the stage of acidogenesis [3,4]. Various studies have been conducted to study its production by dark fermentation using numerous wastes such as sweet sorghum extract, swine manure and food wastes as single substrates, while the hydrogen production rate depends on the initial feedstock composition and the operating conditions [5,6,7]. Anaerobic co-digestion (AcoD) (combining a mixture of different substrates) has been widely investigated in order to increase both the biogas and hydrogen production [2,8]. In addition, the hydrogen production from biological processes may contribute to the product’s environmental burden reduction compared to the most common hydrogen production processes such as steam reformation of methane and reforming oil/naphtha [9,10].

Mathematical models are a useful tool for the AcoD process optimization through kinetic parameters estimation and reactor design [8]. The Gompertz bacterial growth model has been applied to describe fermentative hydrogen or methane production, biomass synthesis and substrate degradation in batch operating mode under different pH values or mixing ratio of feedstocks [11,12,13]. The Anaerobic Digestion Model 1 (ADM1) is a structured model that integrates the five steps of disintegration, hydrolysis, acidogenesis, acetogenesis and methanogenesis [14]. Despite its high level of complexity, ADM1 has been successfully applied, sufficiently describing the biogas and methane production either in batch or continuous operating modes [15,16]. In addition, ADM1 modification by excluding methanogenic stage allows the prediction of biohydrogen production [17]. For example, Couto et al. [18] and Antonopoulou et al. [6] modified the ADM1 to describe the hydrogen production, including lactate and ethanol production processes, two metabolic products of acidogenesis that were not taken into account in the model due to negligible impact on methanogenic systems [18], while other researchers included the ethanol degradation process to acetic acid [19]. Montecchio et al. [20] used ADM1, including two processes for the uptake of lactose and lactose hydrolysis in order to simulate the continuous hydrogen production from anaerobic fermentation of cheese whey. Ntaikou et al. [21] applied a modified version of ADM1 in order to predict the hydrogen generation as well as the formation of ethanol and acetate from continuous and batch pure cultures of Ruminococcus albus using sweet sorghum extract as a sole substrate. Recently, Alexandropoulou et al. [4] used the modified ADM1 by Antonopoulou et al. [6], assuming different Monod-type kinetic rates of Volatile Fatty Acids (VFAs) in order to describe the experimental data derived from a continuously operated acidogenic reactor with suspended food wastes in deionized water as feed. Finally, in the work of de Araújo Cavalcante et al., the production of caproic acid from the ethanol and butyric acid accumulation via reverse β-oxidation reactions and chain elongation bacteria was modeled [22]. Based on the aforementioned studies, the mathematical simulation of fermentative hydrogen production using complex substrates, such as agro-industrial wastewaters, in a continuous-flow stirred-tank reactor (CSTR) is still limited.

The aim of the present study was to investigate the applicability of a modified ADM1 model to the continuous fermentative hydrogen production process using agro-industrial wastes as substrate under different Hydraulic Retention Times (HRTs). Long-term experimental data from a 1 L mesophilic continuous biohydrogen reactor were used in order to verify the modified ADM1 [23]. Although the dark fermentation’s mathematical modeling has been investigated by several authors, the application of ADM1 in continuous systems has been not performed in the existing literature. This work uses previously published data [23] for the estimation of the necessary parameters of the ADM1 model in order to satisfactorily describe these kinds of dark fermentation systems. The mathematical modeling of dark fermentation can be used as a valuable tool for process scale-up with cost-effective actions.

2. Materials and Methods

ADM1 Application for a Hydrogen Production Process

Detailed descriptions concerning the experimental set-up and CSTR operation are provided from [23]; however, a brief description for convenience will now follow. The ADM1 model was fitted to experimental data derived from a single-stage CSTR system using a mixture of OMW, CW and CM (in a ratio 55:40:5, v/v/v) as a substrate [23], which was operated at different HRTs (5, 3, 2, 1 and 0.75 d) aiming to evaluate hydrogen productivity and operational stability [23]. The scenarios with HRT values of 5, 3, 1 and 0.75 d were used for model calibration, while the scenario with an HRT value of 2 d was used for model validation. During the reactor operation, the pH value was 6, as in a previous work by Dareioti et al. [24] it was demonstrated that this was the optimal value for maximum hydrogen production using the aforementioned substrates, preventing, at the same time, methanogens from hydrogen consumption. The biogas produced was mainly composed of hydrogen and carbon dioxide [23]. The experimental data fitting was performed using the commercial numerical code Aquasim (Version 2.1d) [25] as a constant volume mixed reactor compartment connected by a diffusive link to a mixed biogas compartment [14]. The estimation of the parameters was carried out using the secant algorithm, which is well-suited for the minimization of the sum of squares between experimental data and model-predicted values [25].

Disintegration and hydrolysis are described in ADM1 using first order kinetics. The disintegration kinetic constant for composite degradation is described as k_dis (d⁻¹), and the hydrolysis constants for the carbohydrates, lipids and proteins are k_hyd,ch (d⁻¹), k_hyd,li (d⁻¹) and k_hyd,pr (d⁻¹), respectively [14]. Monod-type kinetics were used for substrates uptake (sugars, acetate, butyrate, propionate, amino acids, long chain fatty acids and hydrogen) (expressed in kg COD/m³), where k_m is the maximum specific uptake rate (kg COD/(kg COD·d)), k_s is the saturation constant (kg COD/m³) and X is the concentration of degrading microorganisms (kg COD/m³) [6]. The structure of the model was modified in order to make the model more reliable for describing the hydrogen production process from agro-industrial wastes. Thus, lactate uptake based on Monod kinetics (Equation (1)) and ethanol were included in the ADM1 model according to Antonopoulou et al. [6] and Mo et al. [26], since they were detected as by-products in significant amounts. Additionally, two acid-base equilibrium equations were added in the ADM1, due to lactate and ethanol contributions [6]. Furthermore, dynamic first-order rate equations for the decay of lactate (X_lac) degraders [6], as well as the decay of Lactobacillus (X_lac,su)-degrading microorganisms, were included. Also, Batstone et al. [14] proposed I_pH and I_IN,lim kinetics for pH inhibition and limitation of microbial growth due to the lack of inorganic nitrogen, respectively presented in Equations (1)–(3).

L a c t a t e u p t a k e r a t e : k_{m_l a c} \frac{S_{l a c}}{k_{s_l a c} + S_{l a c}} \cdot X_{l a c} \cdot I_{p H} \cdot I_{I N, l i m}

(1)

S u g a r s u p t a k e r a t e : k_{m_s u} \frac{S_{s u}}{k_{s_s u} + S_{s u}} \cdot X_{s u} \cdot I_{p H} \cdot I_{I N, l i m}

(2)

S u g a r s u p t a k e r a t e b y L a c t o b a c i l l o u s : k_{m_l a c_s u} \frac{S_{s u}}{k_{s_l a c_s u} + S_{s u}} \cdot X_{l a c, s u} \cdot I_{p H} \cdot I_{I N, l i m}

(3)

where k_{m_lac}, k_{m_su} and k_{m_lac_su} are the Monod maximum specific uptake rates (kg COD/(kg COD·d)), k_{s_lac}, k_{s_su} and k_{s_lac_su} are the half saturation constants (kg COD/m³), S_lac and S_su are the concentrations of lactate and sugars, respectively (kg COD/m³), and X_lac and X_lac,su are the concentrations of lactate and ethanol degrading microorganisms, respectively (kg COD/m³).

According to the experimental results described previously [23,24], products from the fermentation of sugars contained in mixtures of OMW, CW and CM included lactate, acetate and ethanol. The stoichiometric reactions for the production of lactate and ethanol are described by the homofermentative (Equation (4)), the heterofermentative (Equation (5)) and the bifidum pathway (Equation (6)) [24].

C₆H₁₂O₆ → 2CH₃CH(OH)COOH

(4)

C₆H₁₂O₆ → CH₃CH(OH)COOH + CH₃CH₂OH + CO₂

(5)

2C₆H₁₂O₆ → 3CH₃COOH + 2CH₃CH(OH)COOH

(6)

The fraction of monosaccharide, which is degraded via the first, second and third reaction of the above equations, can be expressed as n_1,su, n_2,su and n_3,su, respectively. Based on ADM1, the sum of aforementioned coefficients could be equal to one (Equation (7)). The stoichiometric coefficients of lactate, acetate and ethanol were calculated as a function of these fractions, and are presented in Table 1. Thus, the model was modified also in terms of sugar uptake based on new stoichiometric coefficients.

n_{1, s u} + n_{2, s u} + n_{3, s u} = 1

(7)

Lactate can be degraded mainly to butyrate, acetate, propionate and hydrogen according to the following reactions (Equations (8) and (9)):

3CH₃CH(OH)COOH → 2CH₃CH₂COOH + CH₃COOH + CO₂ + H₂O

(8)

2CH₃CH(OH)COOH → CH₃CH₂CH₂COOH + 2CO₂ + 2H₂

(9)

The fraction of lactate which is degraded via the first and second reaction of the above equations can be expressed as n_1,lac and n_2,lac, respectively, where the sum of these coefficients is also equal to one (Equation (10)). Table 2 presents the stoichiometric coefficient of each product of lactate degradation. It is noted that the stoichiometric coefficients of amino acids and composites degradation were used in the ADM1 as suggested by Batstone et al. [14].

In addition, a fraction of acetate could be transformed into butyrate according to the reaction presented in Equation (11) [24], and is expressed as n_1,bu,su,ac (Equation (12)). Equation (13) shows the stoichiometric coefficient of acetate degradation.

n_{1, l a c} + n_{2, l a c} = 1

(10)

2CH₃COOH + 2H₂ → CH₃CH₂CH₂COOH + 2H₂O

(11)

n_{1, b u, s u, a c} = 1

(12)

f_bu,su,ac = 1.25 n_{1_bu_su_ac}

(13)

The aforementioned metabolic transformation pathways, as well as the mass balances for hydrogen production, are described in detail by Dareioti et al. [24]. Also, an extra process (Reaction 14) was added in order to describe the consumption of hydrogen from homoacetogenic bacteria according to Antonopoulou et al. [6]. The fraction of hydrogen which is degraded into acetate is expressed as n_1,ac,h2 (Equation (15)). Equation (16) shows the stoichiometric coefficient of hydrogen degradation.

4H₂ + 2CO₂ → CH₃COOH + 2H₂O

(14)

n_{1, a c, h 2} = 1

(15)

f_ac,h2 = n_{1_ac_h2}

(16)

Furthermore, a dynamic first-order rate equation for the decay of hydrogen-degrading microorganisms (X_h2) and hydrogen uptake rate based on Monod kinetics (Equation (17)) were included in the ADM1 model according to Antonopoulou et al. [6].

H y d r o g e n u p t a k e r a t e : k_{m_a c_h 2} \frac{S_{h 2}}{k_{s_a c_h 2} + S_{h 2}} \cdot X_{h 2} \cdot I_{p H} \cdot I_{I N, l i m}

(17)

where k_{m_ac_h2} is the Monod maximum specific uptake rate (kg COD/(kg COD·d)), k_{s_ac_h2} is the half saturation constant (kg COD_S/m³), S_h2 is the concentration of hydrogen (kg COD/m³), X_h2 is the concentration of hydrogen-degrading microorganisms (kg COD/m³). A detailed presentation of the model is presented in Table A1 and Table A2 of the Appendix A Section.

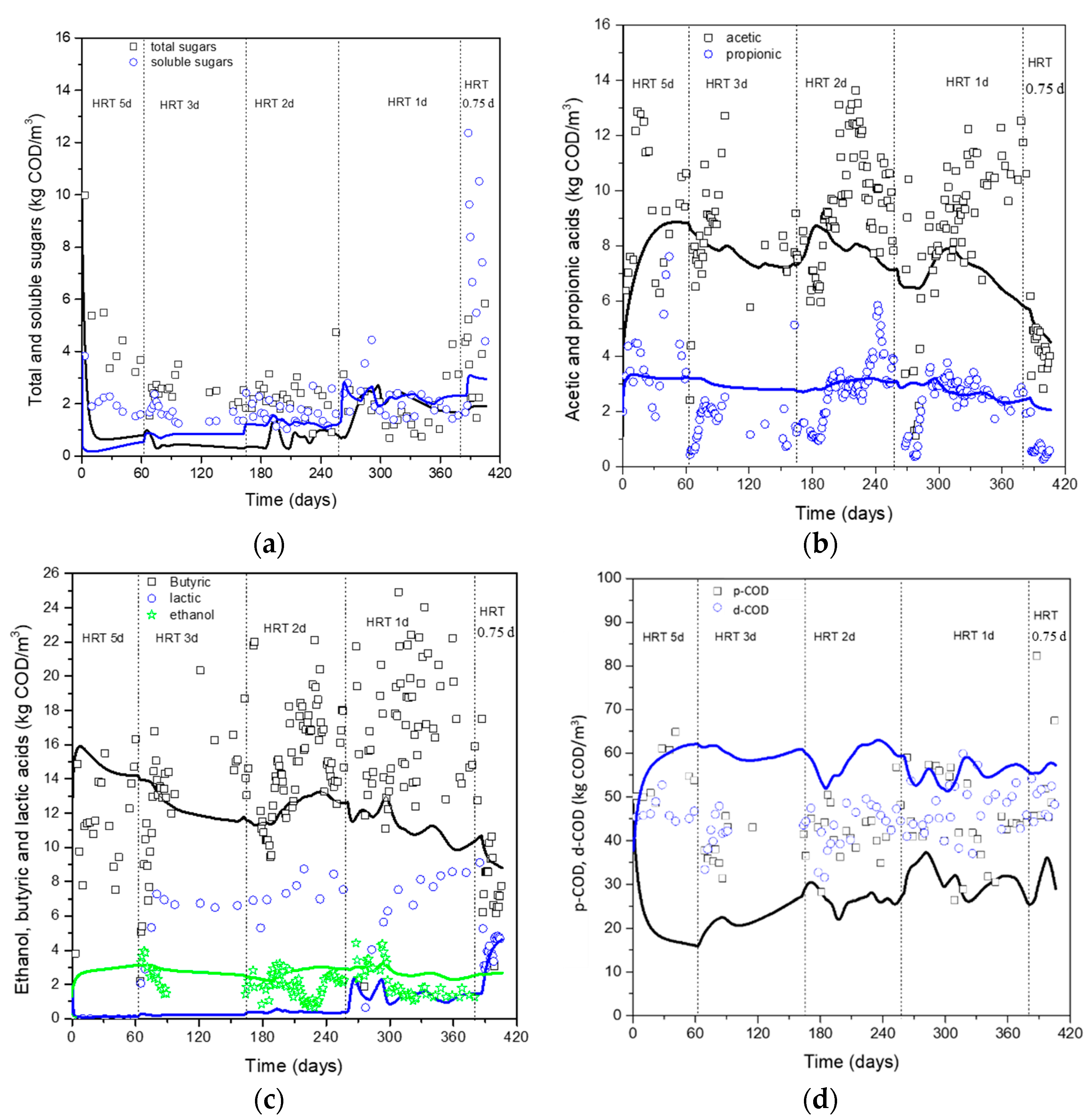
3. Results & Discussion

Estimation of Kinetic and Stoichiometric Parameters–Model Prediction

Figure 1 and Figure 2 depict the experimental data (scatter) from experiments with different HRTs together with the model fittings (solid lines) for biogas (hydrogen and carbon dioxide) and hydrogen production rates, carbohydrates consumption, particulate COD (p-COD), dissolved COD (d-COD), VFAs and ethanol concentrations.

It was observed that the hydrogen yield increased in lower HRTs [23,27]. It has also been demonstrated that short HRTs favor bacteria that produce biohydrogen [2]. On the other hand, the shortest HRT (0.75 d) negatively affected the total and soluble carbohydrates consumption (Figure 2), which were also converted to VFAs, lactic acid and ethanol [23,24]. The most abundant metabolic end-product was butyric acid (Figure 2c), which is only associated with hydrogen production [4]. Ethanol was also detected in lower concentrations in comparison with other constituent products (Figure 2c).

The values of the biochemical parameters, hydrolysis kinetic parameters for carbohydrates, lipids and proteins (k_{hydr_ch}, k_{hydr_li} and k_{hydr_pr,} respectively), the first order decay rate of biomass (k_{dec_all}) and the biomass yields were set as initial values, as suggested in the Scientific and Technical Report of ADM1 [14]. In addition, the yield of biomass on uptake of lactate (Y_lac) was set equal to the yield of biomass on sugars uptake (Y_su = 0.01 kg COD/kg COD) and the Monod maximum specific uptake rate for sugars consumption (k_{m_su}) was set equal to 20.4 kg COD/(kg COD·d) according to Antonopoulou et al. [6]. Nevertheless, some kinetic parameters had to be adjusted in order to achieve the best agreement between measured and simulated values. The kinetic parameters chosen to be adjusted were the maximum specific uptake rates of hydrogen degradation and acetate production (k_{m,ac_h2}), lactate (k_{m_lac}) and monosaccharides towards lactate production (k_{m_lac_su}), half saturation constants of hydrogen degradation towards acetate production (k_{s_ac_h2}) and monosaccharides degradation towards lactate production (k_{s_lac_su}). The stoichiometric coefficients of sugar, lactate, acetate and hydrogen degradation (n_1,su, n_2,su, n_3,su, n_1,lac, n_2,lac, n_1,bu,su,ac, n_1,ac,h2) as well as the yield of biomass on uptake of monosaccharides by Lactobacillus (Y_{lac_su}) were also estimated. The above parameters were estimated simultaneously by fitting the modified ADM1 model to all experimental data [28]. Table 3 and Table 4 present the new estimated stoichiometric coefficients and kinetic parameters, respectively obtained from the model fitting on experimental data.

Based on Table 4, the model-estimated value describing rate of hydrogen degradation was found to be k_{m,ac_h2} = 2.99 kg COD/(kg COD·d). A similar value (3.182 kg COD/(kg COD·d)) has been obtained by Antonopoulou et al. [6] using acidogenic batch experiments. The k_{s_ac_h2} was found equal to 2.28 × 10⁻⁴ kg COD/m³, and the respective proposed by Antonopoulou et al. [6] and Batstone et al. [14] were 0.7 × 10⁻⁶ and 2.5 × 10⁻⁵ kg COD/m³, respectively. The ADM1 simulation of the biogas and hydrogen production rates against the respective experimental data is shown in Figure 1. As can be seen in Figure 1 and Figure 2, the model was able to satisfactorily predict the experimental data obtained from different HRTs.

The kinetic parameter concerning lactate consumption (k_{m_lac}) was determined using the following standard parameter values reported by Antonopoulou et al. [6] and Batstone et al. [14] (Y_lac = 0.1 kg COD/kg COD, k_{s_lac} = 0.5 kg COD/m³ and the first order decay rate for the lactate degrading microorganisms, k_dec,all = 0.02 d⁻¹). The model parameter estimation led to a k_{m_lac} = 2.281 kg COD/(kg COD·d), whereas the respective proposed by Antonopoulou et al. [6] and Alexandropoulou et al. [4] were 10.883 and 0.760 kg COD/(kg COD·d), respectively. These differences of estimated values may be due to the different feedstocks and operational systems [4]. The estimated kinetic parameters concerning sugar uptake towards lactate production by Lactobacillus, k_{m_lac_su}, k_{s_lac_su} and Y_{lac_su}, were 37.820 kg COD/(kg COD·d), 13.182 kg COD/m³ and 0.03 kg COD/kg COD, respectively. The obtained kinetic parameters indicate that Lactobacillus have a significant impact on sugar consumption. However, the biomass yield on the uptake of sugars by Lactobacillus is the lowest in comparison with the other yields proposed by Antonopoulou et al. [6] and Batstone et al. [14]. In addition, the estimated stoichiometric coefficients of sugar, lactate, acetate and hydrogen degradation (Table 3) were different in comparison with previous studies, maybe due to the presence of different microbial populations in the system [4,6].

Simulated curves and experimental data for p-COD and d-COD variations are presented in Figure 2. It can be seen that the p-COD concentration is underestimated by the model, while the concentration of d-COD is overestimated. However, a satisfying prediction of modified ADM1 model was obtained between p-COD and d-COD concentrations and fitting curve, especially after the 200 h of bioreactor operation at lower HRTs. The experimental data and simulation results of VFAs (acetic, propionic, butyric and lactic) and ethanol concentrations are presented in Figure 2b,c. The modified ADM1 was able to adequately simulate the concentrations of acetate, propionate, butyrate and ethanol over the course of experiments at different HRTs. However, the modified ADM1 predictions on the lactate experimental data (Figure 2c) were not very successful, maybe due to some types of inhibitors (e.g., phenolic compounds derived from OMW) that were contained into the tested substrate [23] and are not included in the proposed ADM1 model. Similar ADM1 model failures have been also observed in the literature [8,29]. As an example, the proposed modified ADM1 model by Alexandropoulou et al. [4] was not able to predict lactate concentration at high HRTs, while the lactate simulation was more accurate at the lower HRTs. Therefore, it is difficult to simulate and verify the high number of different processes, variables, stoichiometric coefficients and kinetic parameters in a long-term operation [30,31].

4. Conclusions

The aim of this study was to simulate the AcoD process of agro-industrial residues in a CSTR acidogenic reactor under different HRTs, using a modified version of ADM1. The lactate and ethanol metabolites were included into the model structure, while some stoichiometric and kinetic parameters were estimated using experimental data from a previous study. The obtained results indicate that the ADM1 is capable of satisfactorily simulating biohydrogen and biogas production, as well as the acetate, propionate, and butyrate concentrations. However, the ADM1 predictions on the lactate experimental values were not very successful, maybe due to some types of inhibitors that were present in the substrate according to the previous study. Nevertheless, the modified ADM1 could be a valuable tool for AcoD process design aiming fermentative hydrogen production, whereas further modifications are required to improve the predictions for lactate concentrations.

Author Contributions

Conceptualization, C.N.E. and M.K.; methodology, C.N.E.; software, C.N.E.; validation, C.N.E. and G.M.; formal analysis, C.N.E., G.M. and D.Z.; investigation, C.N.E.; resources, M.K.; data curation, G.M. and D.Z.; writing—original draft preparation, C.N.E.; writing—review and editing, G.M., D.Z. and M.K.; visualization, C.N.E. and G.M.; supervision, M.K.; project administration, M.K.; funding acquisition, M.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by H.F.R.I. under the call “National Recovery and Resilience Plan (Greece 2.0), Action: Basic Research Financing (Horizontal support of all Sciences)” (project I.D.: 014943 entitled “Fate and impact of bioplastics in the bioprocesses of anaerobic digestion and composting in the context of sustainable waste management, VALOPLAST”).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available on request.

Acknowledgments

The authors gratefully acknowledge Katerina Stamatelatou for providing Aquasim platform with the ADM1 model equations.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

AcoD	Anaerobic Co-Digestion
AD	Anaerobic Digestion
ADM1	Anaerobic Digestion Model 1
CM	Cow Manure
COD	Chemical Oxygen Demand
CSTR	Continuous Stirred Tank Reactor
CW	Cheese Whey
d-COD	Dissolved Chemical Oxygen Demand
HRT	Hydraulic Retention Time
OMW	Olive Mill Wastewater
p-COD	Particulate Chemical Oxygen Demand
TSS	Total Suspended Solids
VSS	Volatile Suspended Solids

Appendix A

Table A1. Biochemical rate coefficients (v_i,j) and kinetic rate equations (ρ_j) for soluble components (i = 1–14; j = 1–23). Bold letters indicate additional processes or components added to the ADM1 model in this work, beyond what was in initially included in [14].

	Component → i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	Rate (ρ_j, kg COD/(m³·d))
j	Process ↓	S_su	S_aa	S_fa	S_va	S_bu	S_pro	S_ac	S_h2	S_ch4	S_IC	S_IN	S_I	S_eth	S_lac
1	Disintegration												f_SI,XC			$k_{d i s} X_{C} I_{p H}$
2	Hydrolysis of Carbohydrates	1														$k_{h y d, c h} X_{c h}$
3	Hydrolysis of Proteins		1													$k_{h y d, p r} X_{p r}$
4	Hydrolysis of Lipids	1 − f_fa,li		f_fa,li												$k_{h y d, l i} X_{l i}$
5	Uptake of Sugars	−1				(1 − Y_su)·f_bu,su	(1 − Y_su)·f_pro,su	(1 − Y_su)·f_ac,su	(1 − Y_su)·f_h2,su		$- \sum_{i = 1 - 9, 11 - 28} C_{i} v_{i, 5}$	$-$ (Y_su)·N_bac		(1 − Y_su)·f_eth,su		$k_{m, s u} \frac{S_{s u}}{k_{s} + S_{s u}} X_{s u} I_{1}$
6	Uptake of Amino Acids		−1		(1 − Y_aa)·f_va,aa	(1 − Y_aa)·f_bu,aa	(1 − Y_aa)·f_pro,aa	(1 − Y_aa)·f_ac,aa	(1 − Y_aa)·f_h2,aa		$- \sum_{i = 1 - 9, 11 - 28} C_{i} v_{i, 6}$	N_aa − (Y_aa)·N_bac				$k_{m, a a} \frac{S_{a a}}{k_{s} + S_{a a}} X_{a a} I_{1}$
7	Uptake of LCFA			−1				(1 − Y_fa)·0.7	(1 − Y_fa)·0.3			$-$ (Y_fa)·N_bac				$k_{m, f a} \frac{S_{f a}}{k_{s} + S_{f a}} X_{f a} I_{2}$
8	Uptake of Valerate				−1		(1 − Y_c4)·0.54	(1 − Y_c4)·0.31	(1 − Y_c4)·0.15			$-$ (Y_c4)·N_bac				$k_{m, c 4} \frac{S_{v a}}{k_{s} + S_{v a}} X_{c 4} \frac{1}{1 + (S_{b u} + S_{c a p}) / S_{v a}} I_{2}$
9	Uptake of Butyrate					−1		(1 − Y_c4)·0.8	(1 − Y_c4)·0.2			$-$ (Y_c4)·N_bac				$k_{m, c 4} \frac{S_{b u}}{k_{s} + S_{b u}} X_{c 4} \frac{1}{1 + (S_{v a} + S_{c a p}) / S_{b u}} I_{2}$
10	Uptake of Propionate						−1	(1 − Y_pro)·0.57	(1 − Y_pro)·0.43		$- \sum_{i = 1 - 9, 11 - 28} C_{i} v_{i, 10}$	$-$ (Y_pro)·N_bac				$k_{m, p r o} \frac{S_{p r o}}{k_{s} + S_{p r o}} X_{p r o} I_{2}$
11	Uptake of Acetate							−1		(1 − Y_ac)	$- \sum_{i = 1 - 9, 11 - 28} C_{i} v_{i, 11}$	$-$ (Y_ac)·N_bac				$k_{m, a c} \frac{S_{a c}}{k_{s} + S_{a c}} X_{a c} I_{3}$
12	Uptake of Hydrogen								−1	(1 − Y_h2)	$- \sum_{i = 1 - 9, 11 - 28} C_{i} v_{i, 12}$	$-$ (Y_h2)·N_bac				$k_{m, h 2} \frac{S_{h 2}}{k_{s} + S_{h 2}} X_{h 2} I_{1}$
13	Decay of X_su															$k_{d e c, X s u} X_{s u}$
14	Decay of X_aa															$k_{d e c, X a a} X_{a a}$
15	Decay of X_fa															$k_{d e c, X f a} X_{f a}$
16	Decay of X_c4															$k_{d e c, X c 4} X_{c 4}$
17	Decay of X_pro															$k_{d e c, X p r o} X_{p r o}$
18	Decay of X_ac															$k_{d e c, X a c} X_{a c}$
19	Decay of X_h2															$k_{d e c, X h 2} X_{h 2}$
20	Decay of X_lac															$k_{d e c, X l a c} X_{l a c}$
21	Uptake of Lactate					(1 − Y_lac)·f_bu,lac	(1 − Y_lac)·f_pro,lac	(1 − Y_lac)·f_ac,lac	(1 − Y_lac)·f_h2,lac						−1	$k_{m_l a c} \frac{S_{l a c}}{k_{s_l a c} + S_{l a c}} \cdot X_{l a c} \cdot I_{1}$
22	Sugars uptake rate by Lactobacillus														(1 − Y_su)·f_lac,su	$k_{m_l a c_s u} \frac{S_{s u}}{k_{s_l a c_s u} + S_{s u}} \cdot X_{l a c, s u} \cdot I_{1}$
23	Decay of Lactobacillus															$k_{d e c, X l a c, s u} X_{l a c, s u}$
		Monosaccharides (kg COD m⁻³)	Amino Acids (kg COD m⁻³)	Long chain fatty acids (kg COD m⁻³)	Total valerate (kg COD m⁻³)	Total butyrate (kg COD m⁻³)	Total propionate (kg COD m⁻³)	Total acetate (kg COD m⁻³)	Hydrogen gas (kg COD m⁻³)	Methane gas (kg COD m⁻³)	Inorganic Carbon (kg mole C m⁻³)	Inorganic Nitrogen (kg mole N m⁻³)	Soluble Inerts (kg COD m⁻³)	Total Ethanol (kg COD m⁻³)	Total Lactate (kg COD m⁻³)	Inhibition factors $I_{1} = I_{p H_{i}} I_{I N, l i m}$ $I_{2} = I_{p H_{i}} I_{h 2} I_{I N, l i m}$ $I_{3} = I_{p H_{i}} I_{N H 3} I_{I N, l i m}$

Table A2. Biochemical rate coefficients (v_i,j) and kinetic rate equations (ρ_j) for particulate components (i = 15–28; j = 1–23). Bold letters indicate additional processes or components added to the ADM1 model in this work, beyond what was in initially included in [14].

	Component → i	15	16	17	18	19	20	21	22	23	24	25	26	27	28	Rate (ρ_j, kg COD/(m³·d))
J	Process ↓	X_c	X_ch	X_pr	X_li	X_su	X_aa	X_fa	X_c4	X_pro	X_ac	X_h2	X_I	X_lac	X_lac,su	Rate (ρ_j, kg COD/(m³·d))
1	Disintegration	−1	f_ch,XC	f_pr,XC	f_li,XC								f_SI,XC			$k_{d i s} X_{C}$
2	Hydrolysis of Carbohydrates		−1													$k_{h y d, c h} X_{c h}$
3	Hydrolysis of Proteins			−1												$k_{h y d, p r} X_{p r}$
4	Hydrolysis of Lipids				−1											$k_{h y d, l i} X_{l i}$
5	Uptake of Sugars					Y_su										$k_{m, s u} \frac{S_{s u}}{k_{s} + S_{s u}} X_{s u} I_{1}$
6	Uptake of Amino Acids						Y_aa									$k_{m, a a} \frac{S_{a a}}{k_{s} + S_{a a}} X_{a a} I_{1}$
7	Uptake of LCFA							Y_fa								$k_{m, f a} \frac{S_{f a}}{k_{s} + S_{f a}} X_{f a} I_{2}$
8	Uptake of Valerate								Y_c4							$k_{m, c 4} \frac{S_{v a}}{k_{s} + S_{v a}} X_{c 4} \frac{1}{1 + (S_{b u} + S_{c a p}) / S_{v a}} I_{2}$
9	Uptake of Butyrate								Y_c4							$k_{m, c 4} \frac{S_{b u}}{k_{s} + S_{b u}} X_{c 4} \frac{1}{1 + (S_{v a} + S_{c a p}) / S_{b u}} I_{2}$
10	Uptake of Propionate									Y_pro						$k_{m, p r o} \frac{S_{p r o}}{k_{s} + S_{p r o}} X_{p r o} I_{2}$
11	Uptake of Acetate										Y_ac					$k_{m, a c} \frac{S_{a c}}{k_{s} + S_{a c}} X_{a c} I_{3}$
12	Uptake of Hydrogen											Y_h2				$k_{m, h 2} \frac{S_{h 2}}{k_{s} + S_{h 2}} X_{h 2} I_{1}$
13	Decay of X_su	1				−1										$k_{d e c, X s u} X_{s u}$
14	Decay of X_aa	1					−1									$k_{d e c, X a a} X_{a a}$
15	Decay of X_fa	1						−1								$k_{d e c, X f a} X_{f a}$
16	Decay of X_c4	1							−1							$k_{d e c, X c 4} X_{c 4}$
17	Decay of X_pro	1								−1						$k_{d e c, X p r o} X_{p r o}$
18	Decay of X_ac	1									−1					$k_{d e c, X a c} X_{a c}$
19	Decay of X_h2	1										−1				$k_{d e c, X h 2} X_{h 2}$
20	Decay of X_lac	1												−1		$k_{d e c, X l a c} X_{l a c}$
21	Uptake of Lactate													Y_lac		$k_{m_l a c} \frac{S_{l a c}}{k_{s_l a c} + S_{l a c}} \cdot X_{l a c} \cdot I_{1}$
22	Sugars uptake rate by Lactobacillus														Y_lac,su	$k_{m_l a c_s u} \frac{S_{s u}}{k_{s_l a c_s u} + S_{s u}} \cdot X_{l a c, s u} \cdot I_{1}$
23	Decay of Lactobacillus	1													−1	$k_{d e c, X l a c, s u} X_{l a c, s u}$
		Composites (kg COD m⁻³)	Carbohydrates (kg COD m⁻³)	Proteins (kg COD m⁻³)	Lipids (kg COD m⁻³)	Sugar degraders (kg COD m⁻³)	Amino acid degraders (kg COD m⁻³)	LCFA degraders (kg COD m⁻³)	Caproate, valerate and butyrate degraders (kg COD m⁻³)	Propionate degraders (kg COD m⁻³)	Acetate degraders (kg COD m⁻³)	Hydrogen degraders (kg COD m⁻³)	Particulate inerts (kg mole C m⁻³)	Lactate Degraders (kg COD m⁻³)	Lactobacillus (kg COD m⁻³)	Inhibition factors $I_{1} = I_{p H_{i}} I_{I N, l i m}$ $I_{2} = I_{p H_{i}} I_{h 2} I_{I N, l i m}$ $I_{3} = I_{p H_{i}} I_{N H 3} I_{I N, l i m}$

References

Manthos, G.; Dareioti, M.; Zagklis, D.; Kornaros, M. Using Biochemical Methane Potential Results for the Economic Optimization of Continuous Anaerobic Digestion Systems: The Effect of Substrates’ Synergy. Renew. Energy 2023, 211, 296–306. [Google Scholar] [CrossRef]
Gomez-Romero, J.; Gonzalez-Garcia, R.A.; Chairez, I.; Torres, L.; García-Peña, E.I. Continuous Two-staged Co-digestion Process for Biohydrogen Production from Agro-industrial Wastes. Int. J. Energy Res. 2016, 40, 257–272. [Google Scholar] [CrossRef]
Alexandropoulou, M.; Antonopoulou, G.; Trably, E.; Carrere, H.; Lyberatos, G. Continuous Biohydrogen Production from a Food Industry Waste: Influence of Operational Parameters and Microbial Community Analysis. J. Clean. Prod. 2018, 174, 1054–1063. [Google Scholar] [CrossRef]
Alexandropoulou, M.; Antonopoulou, G.; Lyberatos, G. A Novel Approach of Modeling Continuous Dark Hydrogen Fermentation. Bioresour. Technol. 2018, 250, 784–792. [Google Scholar] [CrossRef]
Zappi, A.; Hernandez, R.; Holmes, W.E. A Review of Hydrogen Production from Anaerobic Digestion. Int. J. Environ. Sci. Technol. 2021, 18, 4075–4090. [Google Scholar] [CrossRef]
Antonopoulou, G.; Gavala, H.N.; Skiadas, I.V.; Lyberatos, G. Modeling of Fermentative Hydrogen Production from Sweet Sorghum Extract Based on Modified ADM1. Int. J. Hydrogen Energy 2012, 37, 191–208. [Google Scholar] [CrossRef]
Jurado, E.; Antonopoulou, G.; Lyberatos, G.; Gavala, H.N.; Skiadas, I.V. Continuous Anaerobic Digestion of Swine Manure: ADM1-Based Modelling and Effect of Addition of Swine Manure Fibers Pretreated with Aqueous Ammonia Soaking. Appl. Energy 2016, 172, 190–198. [Google Scholar] [CrossRef]
Hagos, K.; Zong, J.; Li, D.; Liu, C.; Lu, X. Anaerobic Co-Digestion Process for Biogas Production: Progress, Challenges and Perspectives. Renew. Sustain. Energy Rev. 2017, 76, 1485–1496. [Google Scholar] [CrossRef]
Balaji, R.K.; Rajan, K.P.; Ragula, U.B.R. Modeling & Optimization of Renewable Hydrogen Production from Biomass via Anaerobic Digestion & Dry Reformation. Int. J. Hydrogen Energy 2020, 45, 18226–18240. [Google Scholar]
Smit, R.; Whitehead, J.; Washington, S. Where Are We Heading with Electric Vehicles? Air Qual. Clim. Chang. 2018, 52, 18–27. [Google Scholar]
Khadka, A.; Parajuli, A.; Dangol, S.; Thapa, B.; Sapkota, L.; Carmona-Martínez, A.A.; Ghimire, A. Effect of the Substrate to Inoculum Ratios on the Kinetics of Biogas Production during the Mesophilic Anaerobic Digestion of Food Waste. Energies 2022, 15, 834. [Google Scholar] [CrossRef]
Abudi, Z.N.; Hu, Z.; Sun, N.; Xiao, B.; Rajaa, N.; Liu, C.; Guo, D. Batch Anaerobic Co-Digestion of OFMSW (Organic Fraction of Municipal Solid Waste), TWAS (Thickened Waste Activated Sludge) and RS (Rice Straw): Influence of TWAS and RS Pretreatment and Mixing Ratio. Energy 2016, 107, 131–140. [Google Scholar] [CrossRef]
Kafle, G.K.; Kim, S.H.; Sung, K.I. Ensiling of Fish Industry Waste for Biogas Production: A Lab Scale Evaluation of Biochemical Methane Potential (BMP) and Kinetics. Bioresour. Technol. 2013, 127, 326–336. [Google Scholar] [CrossRef] [PubMed]
Batstone, D.J.; Keller, J.; Angelidaki, I.; Kalyuzhnyi, S.V.; Pavlostathis, S.G.; Rozzi, A.; Sanders, W.T.M.; Siegrist, H.A.; Vavilin, V.A. The IWA Anaerobic Digestion Model No 1 (ADM1). Water Sci. Technol. 2002, 45, 65–73. [Google Scholar] [CrossRef] [PubMed]
Satpathy, P.; Biernacki, P.; Uhlenhut, F.; Cypionka, H.; Steinigeweg, S. Modelling Anaerobic Digestion in a Biogas Reactor: ADM1 Model Development with Lactate as an Intermediate (Part I). J. Environ. Sci. Health Part A 2016, 51, 1216–1225. [Google Scholar] [CrossRef] [PubMed]
Satpathy, P.; Biernacki, P.; Cypionka, H.; Steinigeweg, S. Modelling Anaerobic Digestion in an Industrial Biogas Digester: Application of Lactate-Including ADM1 Model (Part II). J. Environ. Sci. Health Part A 2016, 51, 1226–1232. [Google Scholar] [CrossRef] [PubMed]
Guellout, Z.; Clion, V.; Benguerba, Y.; Dumas, C.; Ernst, B. Study of the Dark Fermentative Hydrogen Production Using Modified ADM1 Models. Biochem. Eng. J. 2018, 132, 9–19. [Google Scholar] [CrossRef]
Couto, P.T.; Eng, F.; Naessens, W.; Nopens, I.; Zaiat, M.; Ribeiro, R. Modelling Sugarcane Vinasse Processing in an Acidogenic Reactor to Produce Hydrogen with an ADM1-Based Model. Int. J. Hydrogen Energy 2020, 45, 6217–6230. [Google Scholar] [CrossRef]
Shi, E.; Li, J.; Zhang, M. Application of IWA Anaerobic Digestion Model No. 1 to Simulate Butyric Acid, Propionic Acid, Mixed Acid, and Ethanol Type Fermentative Systems Using a Variable Acidogenic Stoichiometric Approach. Water Res. 2019, 161, 242–250. [Google Scholar] [CrossRef]
Montecchio, D.; Yuan, Y.; Malpei, F. Hydrogen Production Dynamic during Cheese Whey Dark Fermentation: New Insights from Modelization. Int. J. Hydrogen Energy 2018, 43, 17588–17601. [Google Scholar] [CrossRef]
Ntaikou, I.; Gavala, H.N.; Lyberatos, G. Application of a Modified Anaerobic Digestion Model 1 Version for Fermentative Hydrogen Production from Sweet Sorghum Extract by Ruminococcus Albus. Int. J. Hydrogen Energy 2010, 35, 3423–3432. [Google Scholar] [CrossRef]
de Araújo Cavalcante, W.; Leitão, R.C.; Gehring, T.A.; Angenent, L.T.; Santaella, S.T. Anaerobic Fermentation for N-Caproic Acid Production: A Review. Process Biochem. 2017, 54, 106–119. [Google Scholar] [CrossRef]
Dareioti, M.A.; Kornaros, M. Effect of Hydraulic Retention Time (HRT) on the Anaerobic Co-Digestion of Agro-Industrial Wastes in a Two-Stage CSTR System. Bioresour. Technol. 2014, 167, 407–415. [Google Scholar] [CrossRef]
Dareioti, M.A.; Vavouraki, A.I.; Kornaros, M. Effect of PH on the Anaerobic Acidogenesis of Agroindustrial Wastewaters for Maximization of Bio-Hydrogen Production: A Lab-Scale Evaluation Using Batch Tests. Bioresour. Technol. 2014, 162, 218–227. [Google Scholar] [CrossRef] [PubMed]
Reichert, P. User Manual of AQUASIM 2.0 for the Identification and Simulation of Aquatic Systems; Swiss Federal Institute for Environmental Science and Technology (EAWAG): Dubendorf, Switzerland, 1998. [Google Scholar]
Mo, R.; Guo, W.; Batstone, D.; Makinia, J.; Li, Y. Modifications to the Anaerobic Digestion Model No. 1 (ADM1) for Enhanced Understanding and Application of the Anaerobic Treatment Processes—A Comprehensive Review. Water Res. 2023, 244, 120504. [Google Scholar] [CrossRef]
Scoma, A.; Bertin, L.; Fava, F. Effect of Hydraulic Retention Time on Biohydrogen and Volatile Fatty Acids Production during Acidogenic Digestion of Dephenolized Olive Mill Wastewaters. Biomass Bioenergy 2013, 48, 51–58. [Google Scholar] [CrossRef]
Bułkowska, K.; Białobrzewski, I.; Klimiuk, E.; Pokoj, T. Kinetic Parameters of Volatile Fatty Acids Uptake in the ADM1 as Key Factors for Modeling Co-Digestion of Silages with Pig Manure, Thin Stillage and Glycerine Phase. Renew. Energy 2018, 126, 163–176. [Google Scholar] [CrossRef]
Kunatsa, T.; Xia, X. A Review on Anaerobic Digestion with Focus on the Role of Biomass Co-Digestion, Modelling and Optimisation on Biogas Production and Enhancement. Bioresour. Technol. 2022, 344, 126311. [Google Scholar] [CrossRef]
Soda, S.; Wada, K.; Okuda, M.; Ike, M. Application of Modified ADM1 to Long-Term Experiments for Methane/Hydrogen Production from Model Organic Waste. Water Pract. Technol. 2011, 6, wpt2011009. [Google Scholar] [CrossRef]
Feldman, H.; Flores-Alsina, X.; Kjellberg, K.; Jeppsson, U.; Batstone, D.J.; Gernaey, K.V. Model-based Analysis and Optimization of a Full-scale Industrial High-rate Anaerobic Bioreactor. Biotechnol. Bioeng. 2018, 115, 2726–2739. [Google Scholar] [CrossRef]

Figure 1. Experimental values (points) and model predictions (lines) for biogas and hydrogen production during acidogenesis of OMW/CM/LCM mixture (55/40/5, v/v/v) for each HRT tested.

Figure 2. Experimental values (points) and model predictions (lines) for total and soluble carbohydrates consumption (a), acetic and propionic acid accumulation (b), ethanol and lactic acid accumulation (c), and p-COD and d-COD (d) during acidogenesis of OMW/CM/LCM mixture (55/40/5, v/v/v) for each HRT tested.

Table 1. Stoichiometric coefficients from sugars uptake.

Products of Sugars Degradation	Stoichiometric Coefficients, kg COD/kg COD
Lactate	f_lac,su = 0.5 (1 + n_1,su)
Acetate	f_ac,su = 0.5 (n_3,su)
Ethanol	f_eth,su = 0.5 n_2,su

Table 2. Stoichiometric coefficients from lactate uptake.

Products of Lactate Degradation	Stoichiometric Coefficients, kg COD/kg COD
Butyrate	f_bu,lac = 0.83 (1 − n_1,lac)
Acetate	f_ac,lac = 0.22 n_1,lac
Propionate	f_pro,lac = 0.78 n_1,lac
Hydrogen	f_h2,lac = 0.17 (1 − n_1,lac)

Table 3. Estimated coefficients for sugars and lactate degradation obtained from the ADM1 simulation on experimental results.

Coefficient	Estimated Value
n_1,su	0.605
n_2,su	0.150
n_3,su	0.245
n_1,lac	0.200
n_2,lac	0.800

Table 4. Estimated kinetic parameters obtained from the ADM1 simulation on experimental results.

Kinetic Parameter	Units	Estimated Value
k_{m,ac_h2}	kg COD/(kg COD·d)	2.99
k_{m_lac}	kg COD/(kg COD·d)	2.281
k_{m_lac_su}	kg COD/(kg COD·d)	37.820
k_{s_ac_h2}	kg COD/m³	2.28 × 10⁻⁴
k_{s_lac_su}	kg COD/m³	13.182
Y_{lac_su}	kg COD/kg COD	0.03

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Economou, C.N.; Manthos, G.; Zagklis, D.; Kornaros, M. ADM1-Based Modeling of Biohydrogen Production through Anaerobic Co-Digestion of Agro-Industrial Wastes in a Continuous-Flow Stirred-Tank Reactor System. Fermentation 2024, 10, 138. https://doi.org/10.3390/fermentation10030138

AMA Style

Economou CN, Manthos G, Zagklis D, Kornaros M. ADM1-Based Modeling of Biohydrogen Production through Anaerobic Co-Digestion of Agro-Industrial Wastes in a Continuous-Flow Stirred-Tank Reactor System. Fermentation. 2024; 10(3):138. https://doi.org/10.3390/fermentation10030138

Chicago/Turabian Style

Economou, Christina N., Georgios Manthos, Dimitris Zagklis, and Michael Kornaros. 2024. "ADM1-Based Modeling of Biohydrogen Production through Anaerobic Co-Digestion of Agro-Industrial Wastes in a Continuous-Flow Stirred-Tank Reactor System" Fermentation 10, no. 3: 138. https://doi.org/10.3390/fermentation10030138

APA Style

Economou, C. N., Manthos, G., Zagklis, D., & Kornaros, M. (2024). ADM1-Based Modeling of Biohydrogen Production through Anaerobic Co-Digestion of Agro-Industrial Wastes in a Continuous-Flow Stirred-Tank Reactor System. Fermentation, 10(3), 138. https://doi.org/10.3390/fermentation10030138

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

ADM1-Based Modeling of Biohydrogen Production through Anaerobic Co-Digestion of Agro-Industrial Wastes in a Continuous-Flow Stirred-Tank Reactor System

Abstract

1. Introduction

2. Materials and Methods

ADM1 Application for a Hydrogen Production Process

3. Results & Discussion

Estimation of Kinetic and Stoichiometric Parameters–Model Prediction

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

Appendix A

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI