Bioprocess Intensification of a Continuous-Flow Enzymatic Bioreactor via Productivity Dynamic Optimization under Modeling Uncertainty

Abstract

In this contribution, a class of observer-based optimal feedback control is designed. The proposed feedback control is based on the Euler–Lagrange theoretical framework, and it is motivated by the productivity intensification from the chemical reactors, which is optimally increased. A Lagrangian is computed by employing the corresponding mass balance equation of a specifically selected biochemical compound. The resulting optimal controller is coupled with a novel uncertainty estimator with bounded feedback to derive an accurate estimation of the unknown terms and functions, mostly related to the reaction rate. Via Lyapunov analysis, it was shown that the proposed observer is asymptotically stable. The estimation of the unknown terms and functions is used by the proposed controller. The proposed methodology is applied to a generic model of an enzymatic biochemical continuous reactor with complex oscillatory dynamic behavior described by mass balance equations, so, in general, the proposed controller may be applied to any continuous stirred tank bioreactor; that is, the controller is independent of the specific kinetic functions. Numerical simulations show a satisfactory performance of the proposed control strategy.

1. Introduction

The continuous stirred tank bioreactor (CSTB) is a classical benchmark because it is one of the most popular types of equipment employed in the chemical and biochemical industries. This type of operation is flexible for production and ensures a suitable mixing operation in which the concentrations of chemical products and reactive products are adequately uniform throughout the bioreaction volume and within the outlet product stream. Despite such advantages, under an actual operation at an industrial-scale bioreactor, the operation is often far from idealized lab-scale bioreaction design because the influence of non-ideal flow, mass, and heat transport phenomena must be compensated for or attenuated toward the bioprocess intensification. The term ‘process intensification’ was introduced in the early 2000s. In the first years, the intensification concept was related to the optimal dimension design of the process equipment under predetermined operating conditions; however, industrial plants were required to provide a flexible and wide operational policy to respond to the high and changing demand of the market and the strict environmental legislation, along with process sustainability related to safe operation, high-quality products, energy saving, etc. Here, a new multidisciplinary conceptualization of industrial plants in design and operation is needed, so high predictive process modeling, multi-objective optimization, on-line monitoring, and control processes under the above-mentioned restrictions must be performed simultaneously.

Moreover, the bioprocess intensification via feedback is relevant because of the unpredictability caused by the strong influence of the highly nonlinear behavior on the chemical kinetics, which can induce dynamic complexity such as steady-state multiplicity, operational instability, or even more, oscillatory dynamic behavior [1,2].

Bioprocess intensification is a relatively recent concept that consists of searching for increased efficiency. Intensification combines optimization of capital, energy, environmental, and safety benefits with a radical reduction in a plant-scale fashion. Although the process intensification can be addressed via the reactor configuration strategies (see, for instance, ref. [3] for the photocatalytic case), a suitable alternative for the bioprocess intensification is to exploit the feedback control approaches to promote efficiency at the bioreaction yield, which allows users to overcome stable operation. In this sense, distinct problems can be formulated from the perspective of feedback control, such as, for example, the stabilization of the chemostat under maximum production concerns [4] or extremum seeking via robust sliding-mode control [5], which introduces an extremum-seeking control scheme using sliding mode techniques to guarantee the dynamic optimization of methane outflow rate in anaerobic digestion processes. The proposed control method includes an observer-based uncertain estimator that computes the unknown terms related to the growth kinetics and the inlet composition. Moreover, self-optimizing control of dynamical processes and extremum-seeking control are two techniques to handle these kinds of dynamic optimization problems [6,7,8]. The main goal of extremum-seeking methods is to determine the operating set-points, such that a performance function reaches its extremum values. That is, a feedback control step is a valuable tool to achieve secure and intensified operation while maintaining adequate bioreactor conditions and enhancing the system dynamics at previously selected set-points via a closed-loop operation under regulatory tasks. In this sense, an appropriate problem formulation and its solution can derive from intensification politics. Such an operational policy can be reached via lineal proportional–integral–derivative (PID), adaptive, predictive, and linearizing, among several other controllers [9,10,11,12,13,14,15,16,17,18], with certain success. Nevertheless, a different approach lies in the framework of optimal control, where the control engineers have tuned controller parameters through cost function optimization. There are several error cost functions, like integrated time-weighted absolute error (ITAE), integrated squared error (ISE), integrated exponential time squared error (IETSE), integrated squared time cubed error (ISTCE), and integrated time exponential time squared error (ITETSE), that are employed for obtaining optimal controller parameters [19,20]. Also, iterative methods such as numerical optimization, fminsearch subroutine, and soft computing-based optimization methods, which include artificial bee colony (ABC) optimization, particle swarm optimization (PSO), genetic algorithm, cuckoo optimization, and quasi-opposition-based equilibrium optimizer, are used to minimize the cost functions [21,22,23,24,25].

As mentioned above, the intensification of the practical operation of continuous bioreactors remains an important challenge for process engineers in the design, analysis, optimization, and control stages. This contribution addresses bioprocess intensification from the perspective of optimal feedback control. The underlying idea is to tackle the necessity of increasing the quality of the reactor operation under an optimal operational policy that includes optimal cost and maximum productivity. The underlying idea is to solve the tracking trajectory problem. The proposed intensification scheme is such that it accounts for the structured uncertainties and output-bounded disturbances, including uncertain initial and ambient conditions, variations in feed quality, and uncertainty in the process description [26]. This makes sense because the optimal design may lead to deviation from the optimal and potentially high-risk solution if the uncertainties are not considered. Therefore, the need to incorporate methodologies for uncertainty compensation in chemical processes is essential to achieving a robust process operation.

This manuscript is organized as follows. Section 2 describes the mathematical model of the CSTB. The proposed optimal control and the uncertainty observers are given in Section 3, together with their main technical characteristics. Section 4 contains a description of the main results obtained, and, finally, the concluding remarks of this work are provided in Section 5.

2. Bioreactor Modeling

In traditional model-based optimization techniques, the accuracy of the mathematical models of the processes is especially important. Particularly, the kinetic modeling in chemical reactors contains a wide set of model parameters that are subject to uncertainty in their thermodynamic and/or kinetic parameters, determined from experiments [27]. Besides the uncertainty and fluctuations present in the process, operations affect the reliability of model-based optimization, among others pressure, feed composition, or temperature. Such sensitivity might cause a violation of safety constraints and, hence, result in an infeasible process design. In general, system optimization under uncertainty is an important and active research issue. Diverse approaches that consider uncertainties have been reported for the optimization of chemical processes [28,29,30,31].

Let us consider a class of continuous-flow bioreactors where enzymatic reactions take place. As is well known, enzymatic reactions can present complex dynamic behaviors, such as sustained oscillations or, even more, chaotic behavior. This work has taken an enzymatic kinetics model under continuous operation, which can even exhibit chaotic oscillations [32]. The considered mathematical model is based on the classical mass conservation principle by considering a four-state variable dynamical system. For the considered bioreactor model, some assumptions are established: (a) the chemical reactions are performed in perfect homogeneous conditions in a well-stirred tank reactor under isothermal operation; (b) first-order kinetics are supposed for the reactions from $C_4$ to $C_1$ and $C_2$ and $C_1$ to $C_2$; (c) the reactive $C_1$ catalyzes the production of the compound $C_3$; both reactions from $C_1$ are catalyzed by $C_2$ and $C_3$, and the reaction from $C_4$ is also catalyzed by $C_3$; and (d) all the chemical species are involved in autocatalytic reactions and their kinetics are governed by the Michaelis–Menten structures.

The general chemical kinetic pathway is as follows [32]:

$$C_1\to C_1^{*}\to C_2+C_3$$

$$C_1\leftrightarrow C_4\to C_2$$

$$C_2\to 2C_2^{*}\to Product$$

$$C_3\to 2C_3^{*}\to Product$$

$$C_4\to 2C_4^{*}\to C_3+Product$$

where $C_i^{*}$ for i = 1, 2, 3, 4 are the corresponding activate chemical complexes, which are considered, as usual, in a pseudo-steady state.

The above kinetic model is extended to continuous reactor operation, showing complex oscillations. The mathematical model is defined by a set of four nonlinear ordinary differential equations, and it represents the mass balances for each one of the chemical compounds at the corresponding mass concentrations.

Mass balancing:

$${\dot{c}}_1=d_0+k_8{c}_4-k_1\frac{c_1{c}_2}{c_1+K}-k_2\frac{c_1{c}_3}{c_1+K}+\left(c_{1,in}-c_1\right)u$$

(1)

$${\dot{c}}_2=k_3{c}_1+k_4{c}_2+k_9{c}_4-k_5\frac{c_2}{c_2+K}+\left(c_{2,in}-c_2\right)u$$

(2)

$${\dot{c}}_3=d_1+k_6{c}_1{c}_3-k_7{c}_3+\left(c_{3,in}-c_3\right)u$$

(3)

$${\dot{c}}_4=\left(k_{10}-k_8-k_9\right)c_4-k_{11}\frac{c_3{c}_4}{c_4+K}+\left(c_{4,in}-c_4\right)u$$

(4)

Here, C = [c₁ c₂ c₃ c₄]^T is the vector of mass concentrations. The inlet concentrations to the reactor have the following nominal values: $c_{1,in}=150$ and $c_{2,in}=c_{3,in}=c_{4,in}=0$, whereas the nominal value of the control input is given by u = 0.015. As usual, for these processes, let us consider that the control input is defined as u = Q/V, where Q is the volumetric inlet flow and V is the volume of the reactor, which is assumed as constant, as usual for these systems. As reported in [32], the set of kinetic parameters is given as follows: k₁ = 1.0, k₂ = 1.0, k₃ = 1.0, k₄ = 0.25, k₅ = 152.5, k₆ = 1.0, k₇ = 130, k₈ = 0.001, k₉ = 1.0, k₁₀ = 1.051, k₁₁ = 0.5, and K = 0.001. The corresponding initial conditions are arbitrarily assumed to be $c_{10}=$129.1, $c_{20}=$ 76.06, $c_{30}=$0.5895, and $c_{40}=$ 21.38. Here, d₀ =90 and d₁ = 2.2 are constant load disturbances, which are included to simulate realistic process operation.

Killory’s model [32] is selected for its capacity to generate complex oscillatory dynamic behavior; this is an important drawback for the operation of (bio)chemical reactors.

3. Controller Design

Generally, the theoretical framework of the optimal control is related to the calculus of variations, which concerns trajectory optimization tasks, where a functional $\mathfrak{I}\left(\mathcal{L}\left(·\right)\right)≔{\mathbb{R}}^q\to \mathbb{R}$ is a scalar called performance index, cost function, or cost index, which is for maximizing or minimizing, accordingly with the corresponding objectives to be reached by solving the Euler–Lagrange equation [33]. That is,

$$\frac{\partial \mathcal{L}}{\partial x_1}-\frac{d}{d{x}_2}\left(\frac{\partial \mathcal{L}}{\partial {\dot{x}}_1}\right)=0$$

(5)

The term $\mathcal{L}$ is named as the Lagrangian of the system under study.

In the most common case, the performance index $\mathfrak{I}$ can be represented by the following integral functional form as:

$$\mathfrak{I}={\int }_{t_0}^{t_f}\mathcal{L}\left(t,x,u\right)dt+\mathcal{H}\left(x_f,t_f\right)$$

(6)

where $\mathcal{H}\left(x_f,t_f\right)$ is an algebraic term to be minimized (or maximized) at final conditions, subject to the following terminal constraints:

$$\mathcal{H}\left(x_f,t_f\right)=0$$

(7)

As the state equation, a class of nonlinear systems is considered as follows:

$$\dot{x}=f\left(x\right)+g\left(x\right)u$$

(8)

Its initial conditions are as follows:

$$x\left(t_0\right)=x_0$$

(9)

As usual, f(x) = [f₁(x) f₂(x) f₃(x) … f_n(x)]^T; then, $f\left(x\right): {\mathbb{R}}^{\mathrm{n}}\to {\mathbb{R}}^{\mathrm{n}}$ is a nonlinear and bounded smooth vector field, and $g^{-1}\left(x\right)$ exists as the inverse of $g\left(x\right)$. Also, x = [x_1, x₂, x₃, … x_n]^T; here, $\mathrm{x}\text{∈}{\mathbb{R}}^{\mathrm{n}}$ is the vector of state variables, such that $x\subset \mathcal{W};\mathcal{W}=\left\{x_i, i=\mathrm{1,2},\dots ,n∕x_i\in \left[0 x_{i,max}\right]\right\}$, where $\mathcal{W}$ is a compact set, i.e., $\mathcal{W}$ is bounded and closed under the vector field operations.

Now, the following functional form [31] is considered:

$$\mathcal{P}\left(x,\dot{x},u\right)={\int }_0^T\mathcal{L}\left(x,\dot{x},u\right)dt$$

(10)

Minimizing the functional (10) is required; therefore,

$$\delta \mathcal{P}\left(x,\dot{x},u\right)={\int }_0^T\delta \mathcal{L}\left(x,\dot{x},u\right)dt$$

(11)

Here, the differential form of the Lagrangian $\mathcal{L}$ is given as

$$\delta \mathcal{L}\left(x,\dot{x},u\right)=\frac{\partial \mathcal{L}}{\partial x}\delta x+\frac{\partial \mathcal{L}}{\partial \dot{x}}\delta \dot{x}+\frac{\partial \mathcal{L}}{\partial u}\delta u=0$$

(12)

Now, to construct the corresponding Lagrangian for our purposes, let us consider the following alternative system representation based on Equation (8):

$$\dot{x}=f\left(x\right)+\alpha u+p\left(x,u\right)$$

(13)

From Equation (13):

$$p\left(\dot{x},x,u\right)=\dot{x}-f\left(x\right)-\alpha u$$

(14)

Therefore, from Equation (14), the corresponding Lagrangian for the performance index is proposed as

$$\mathcal{L}\left(x,\dot{x},u\right)\equiv \dot{x}-f\left(x\right)-\alpha u$$

(15)

From Equations (10) and (15), the functional that represents the performance index is

$$\mathcal{P}\left(x,\dot{x},u\right)={\int }_0^T(\dot{x}-f\left(x\right)-\alpha u) dt$$

(16)

Here, the differential form of Equation (16) is

$$\delta \mathcal{P}\left(x,\dot{x},u\right)={\int }_0^T\delta (\dot{x}-f\left(x\right)-\alpha u)dt$$

(17)

Applying Equation (12), the following differential equation for the control input u is performed:

$$\alpha u^{\prime }+f^{\prime }=0$$

(18)

By solving Equation (18), with $f\left(x_0\right)=0$, we have that

$$u=-{\alpha }^{-1}{\int }_{x_0}^x{f}^{\prime }\left(z\right)dz+u_0$$

(19)

or

$$u=-{\alpha }^{-1}f\left(x\right)-u_0$$

(20)

As can be observed, the control law (20) is realizable as feedback control only if the nonlinear term f(x) is available. However, as is well known, the nonlinear terms are hard to model accurately, being an important source of parametric and/or structured uncertainties.

From the above, an alternative form of the controller (20) must be considered to avoid the above-mentioned drawbacks. Indeed, as non-ideal conditions and uncertain terms are present, the control approach given by Equation (20) is not realizable. So, a strategy must be proposed to compensate for the uncertain terms and reach a realizable control design. For this purpose, an uncertainty observer-based controller must be considered.

Uncertainty Observer-Based Estimator Design

Let us consider system (13), where the nonlinear term f(x) is unknown, which is now considered a new unknown state variable, and the term h(x) is the uncertain nonlinear dynamic behavior of f(x), constituting an extended dynamical system as

$$\dot{x}=f\left(x\right)+a_{1}u+p\left(x,u\right)$$

(21)

$$\dot{f}=h\left(x\right)$$

(22)

Coupled with a linearly measured output, y = Cx.

To analyze the convergence of the proposed observer, the following assumptions are introduced.

Assumption 1. h(x) is a bounded unknown nonlinear vector field, i.e.,

$$‖h\left(x\right)‖\le \mathrm{M}<\infty$$

Assumption 2. $‖f\left(x\right)-\widehat{f}\left(\widehat{x}\right)‖\le \mathsf{{\rm K}}<\infty$. Here, f(x) is a nonlinear and unknown term of system (21) with uncertain dynamic h(x) and $\widehat{f}\left(\widehat{x}\right)$ is the corresponding estimation of f(x).

Now, the design of the uncertainty observer is established.

Proposition 1.

The following nonlinear system (23)–(24) is an asymptotic observer of the system (21)–(22):

$$\dot{\widehat{x}}=\widehat{f}\left(x,u\right)+\alpha u+p\left(x,u\right)+g_{1}sin\left(e_1\right)$$

(23)

$$\dot{\widehat{f}}=g_{2}sin\left(e_1\right)$$

(24)

where g₁ and g₂ are the observer gains and $e_1=y-\widehat{y}=Cx-C\widehat{x}$, with C = [1 0] and $e_2=f-\widehat{f}$ being the observation errors.

Proof of Proposition 1. 

Let us define the observation error vector as:

$$\epsilon ={\left[e_1 e_2\right]}^T$$

Let us consider the observation error dynamic from Equations (21)–(22) and (23)–(24):

$$\frac{d\epsilon }{dt}\equiv \dot{\epsilon }=\left[\begin{array}{c}{\dot{e}}_1\\ {\dot{e}}_2\end{array}\right]=\left[\begin{array}{c}f\left(x\right)-\widehat{f}\left(\widehat{x}\right)-g_{1}sin\left(e_1\right)\\ h\left(x\right)-g_{2}sin\left(e_1\right)\end{array}\right]$$

(25)

Now, Assumptions 1 and 2 and the Cauchy–Schwartz inequality are applied to Equation (25):

$$‖\dot{\epsilon }‖\le \left[\begin{array}{c}K\\ M\end{array}\right]-\left[\begin{array}{c}\left|g_1\right|\\ \left|g_2\right|\end{array}\right] sin\left(e_1\right)$$

(26)

Note that

$$‖sin\left(e_1\right)‖\le 1$$

(27)

Then,

$$‖\dot{\epsilon }‖\le \wp -G$$

(28)

$$\mathrm{Here}\text{:} \mathrm{\wp }=\left[\begin{array}{c}K\\ M\end{array}\right] \mathrm{and} G=\left[\begin{array}{c}\left|g_1\right|\\ \left|g_2\right|\end{array}\right]$$

(29)

Let us propose the following quadratic form of a Lyapunov function:

$$V={\epsilon }^T\epsilon$$

(30)

Note that this scalar function is a positive definite function.

The time derivative of the scalar function V is defined as

$$\dot{V}={\dot{\epsilon }}^T\epsilon +{\epsilon }^T\dot{\epsilon }$$

(31)

Now, considering Equations (26)–(27):

$$\dot{V}\le {\left(\wp -G\right)}^T‖\epsilon ‖+{‖\epsilon ‖}^T\left(\wp -G\right)$$

(32)

By adequately selecting the observer gains of the vector G:

$$\mathrm{\wp }-G=-Q$$

(33)

Finally:

$$\dot{V}\le -Q^T‖\epsilon ‖-{‖\epsilon ‖}^{T}Q\le 0$$

(34)

As can be observed, Equation (34) satisfies the stability condition of the Lyapunov criteria; therefore, it can be concluded that the proposed observer is asymptotically stable.

Note that an asymptotic observer, by definition, can lead the named estimation or observation error to zero at a large enough time, i.e., $\underset{t\to \infty }{\lim }e=0$. The conclusion of this point is that the estimated terms converge to the real ones. □

Finally, under the proposal of the above uncertainty observer design, the realizable controller can be defined as

$$u=-{\alpha }^{-1}\widehat{f}-u_0$$

(35)

4. Results and Discussion

Numerical experiments were conducted to explore the reliability and performance of the proposed methodology. The experiments were performed on a PC with an Intel^® Core™ i7 processor, employing MATLAB (v. 2022a) and the 23s library to solve ordinary differential equations under the initial conditions previously mentioned in Section 2.

From the bioreactor model, the selected productivity of the chemical compound corresponds to C₁, where ${f\left(x\right)=d}_0+k_8{c}_4-k_1\frac{c_1{c}_2}{c_1+K}-k_2\frac{c_1{c}_3}{c_1+K}$ is the reaction rate term, which, as usual, is the most difficult term to be known, so it is considered the uncertain term, which is a realistic assumption. The considered control input corresponds to the input flow u. Considering that the application example shows complex and nonlinear oscillatory dynamic behavior, there are generally no rules for the tuning of the control’s parameters. Therefore, via numerical simulations (not shown), we realize some experiments to calculate, via trial and error, the best selection of the corresponding parameters. As usual, in the control process for nonlinear systems, the parameters of the proposed optimal control are assumed to be α = 1 and u₀ = 0.015, yielding the following control structure: u = 1×f − 0.015.

The uncertainty observer (23)–(24), coupled with the proposed controller (35), considers that C₁ is available as measured system output and as parameters g₁ = 10 and g₂ = 100, under the following initial conditions: $C_{10}=1$ and ${\widehat{f}}_0=1$. The proposed control strategy is turned on at t = 50 time units.

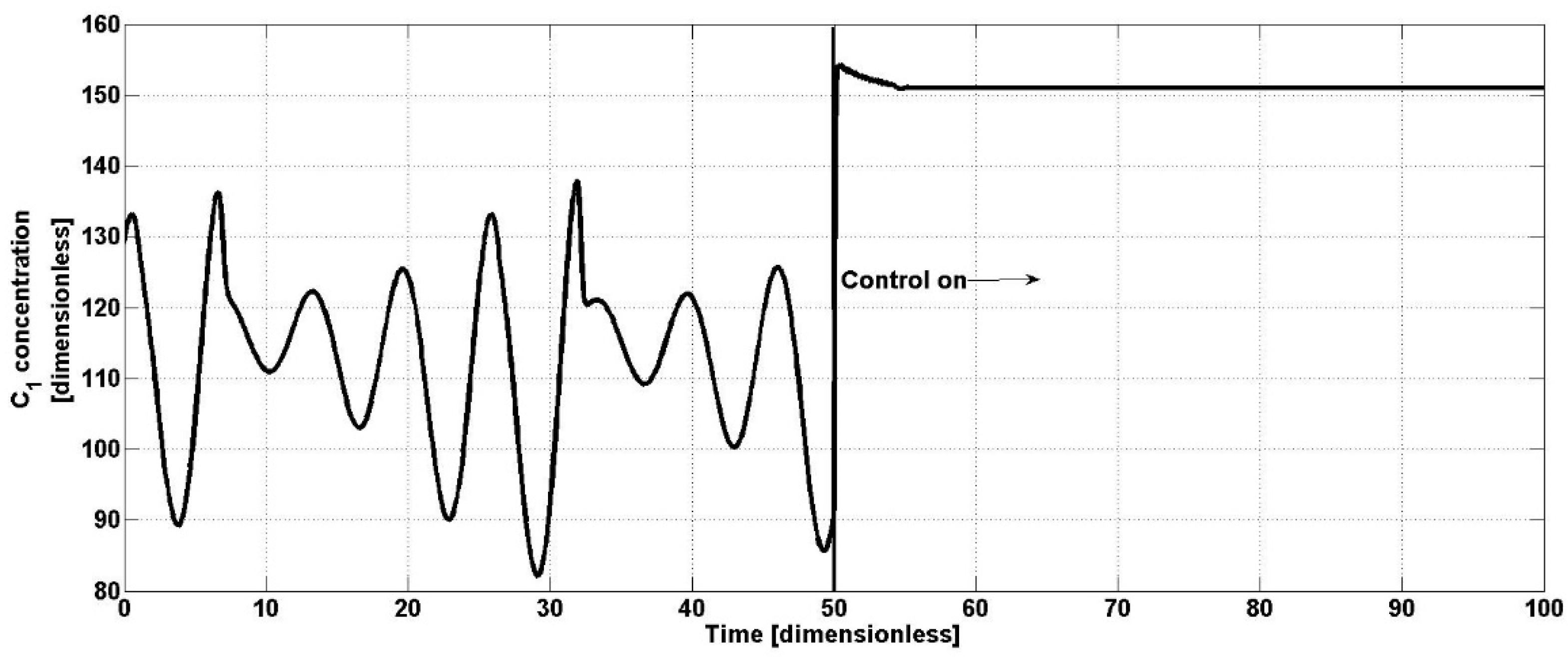
Now, Figure 1 shows the open-loop performance of C₁ concentration and the oscillatory dynamics of the bioreactor from the operation start-up until the controller start-up. When the proposed controller acts, the C₁ concentration responds immediately, eliminating the oscillatory behavior and increasing the C₁ concentration to a constant value of C₁ = 150, which is the first satisfactory response of the bioreactor.

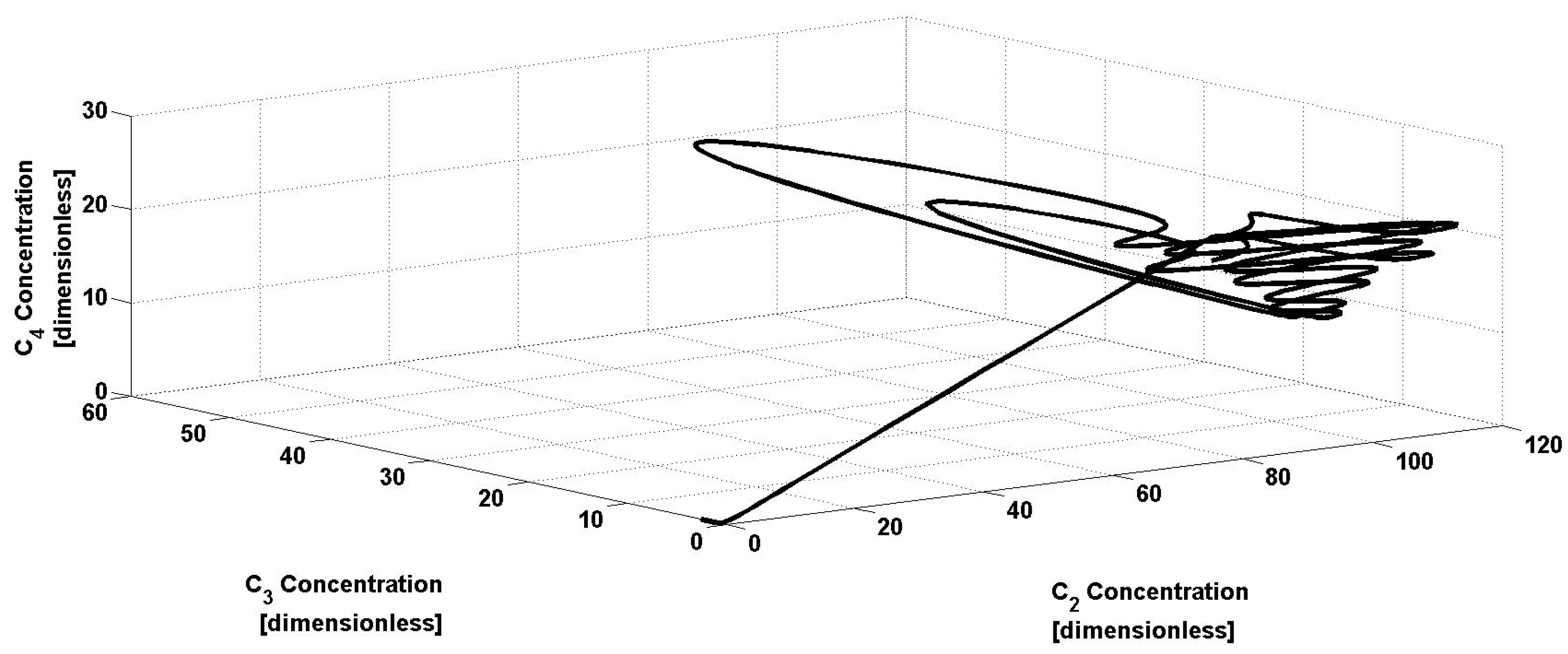
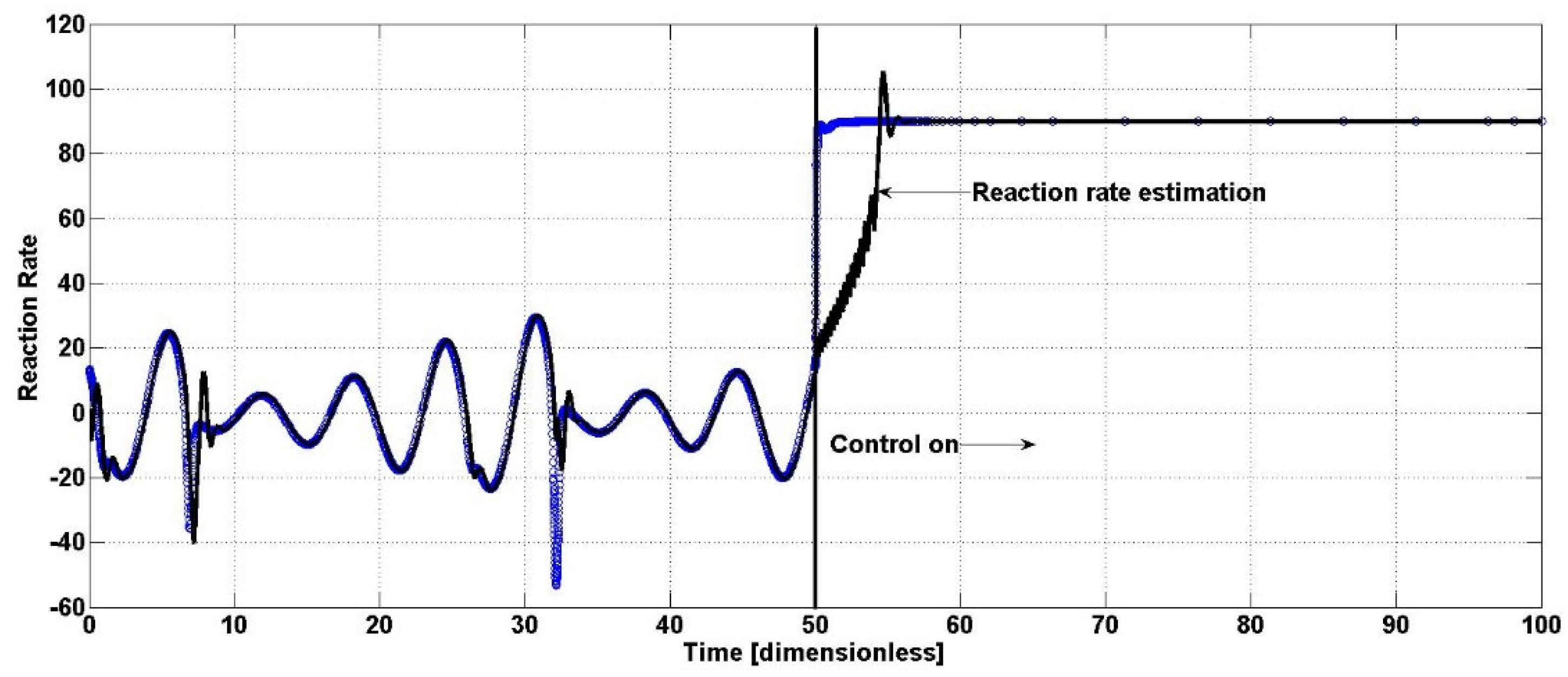
Figure 2 is related to a phase portrait, where the uncontrolled concentrations, C₂, C₃, and C_4, are presented. Note that the oscillatory behavior is also eliminated, leading the bioreactor to a fixed closed-loop steady state. Now, it can be observed in Figure 3 that the performance of the uncertainty observer varies from the oscillatory open-loop operation to the closed-loop operation. The estimation methodology has satisfactory performance, as when the controller is active, the estimator again reaches the real reaction rate f without a large setting time (only 5 time units) and without large overshoots.

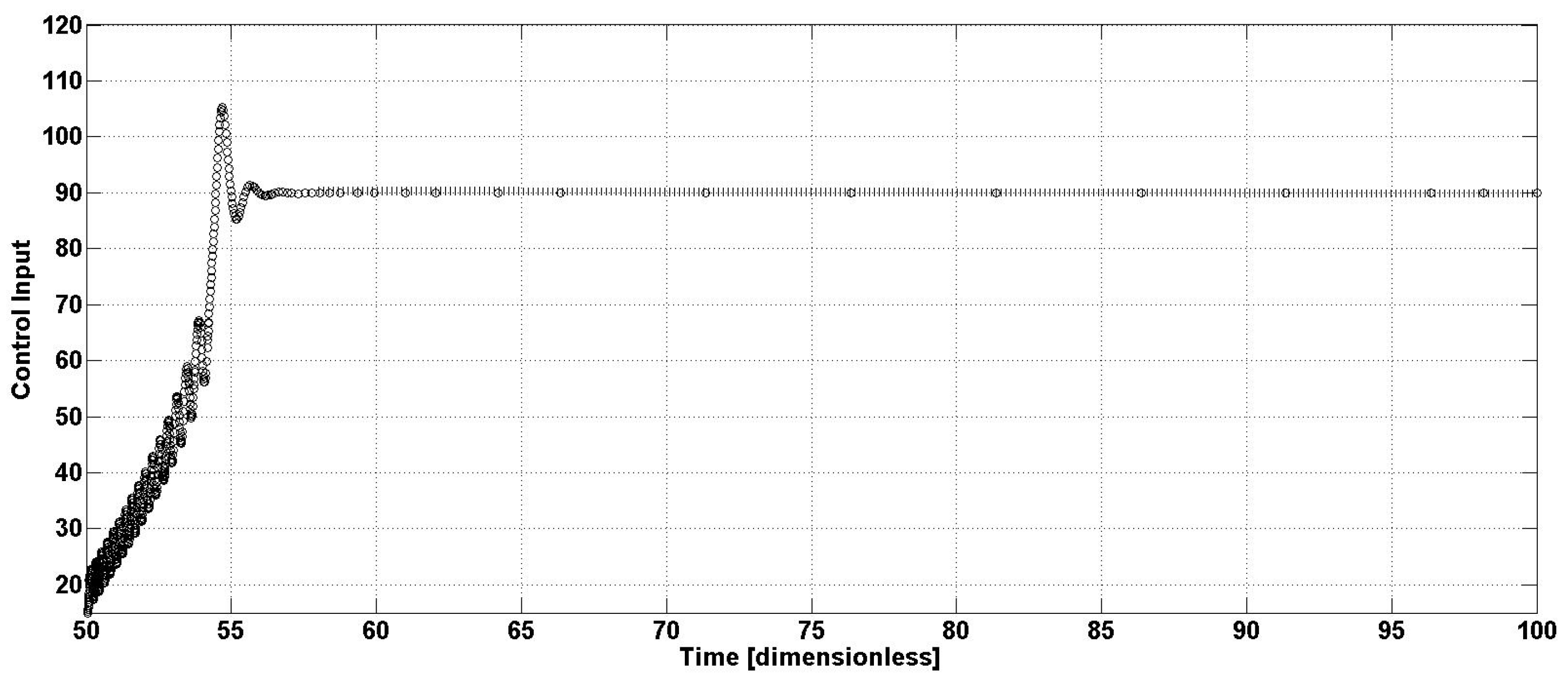
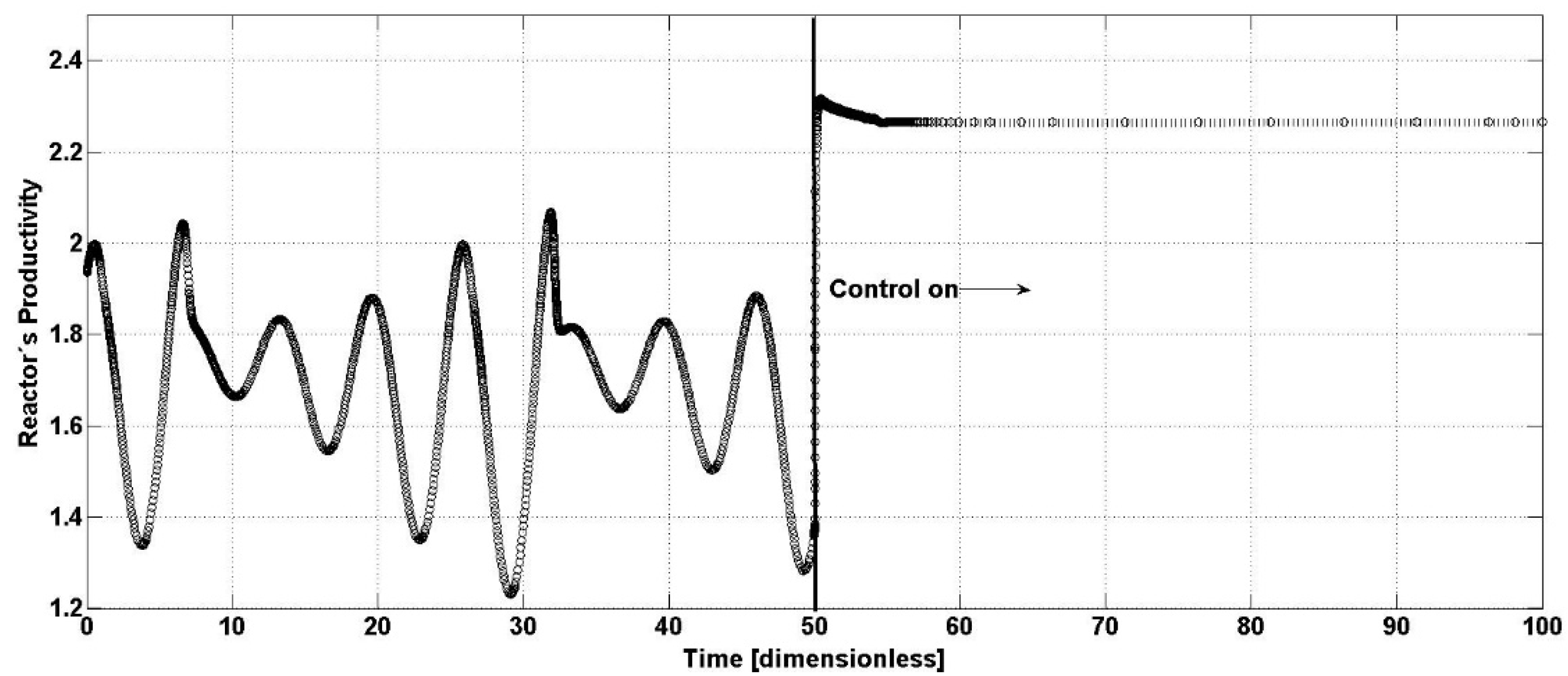
Figure 4 is related to the corresponding control effort; as can be seen, an important increase in the input flow is caused by the control law (35). This is a second important characteristic of the proposed methodology, considering that the bioreactor productivity p, in a continuous operation, is directly proportional to the output concentration and the corresponding flow. From the above and because of the previous results, the open-loop and closed-loop bioreactor productivity is presented in Figure 5. The closed-loop productivity is stable and has increased by around 12.5%.

The intensification of biochemical processes is still an open and challenging problem. This is mainly because distinct approaches can be addressed towards biochemical process intensification. Among others, high productivity with a lower possible process scale, economical or yielding costs, or an increment in bioprocess efficiency aim for intensification. Meanwhile, feedback control strategies accompany most of the intensification goals. Robust and optimization properties of the feedback control are open problems whose solutions support biochemical process intensification.

5. Conclusions

This work presents a class of observer-based optimal controllers whose task is to maximize productivity in a continuous stirred tank bioreactor under the framework of Euler–Lagrange theory and the intensification concept. The proposed controller requires online information on the reaction rate for the selected chemical compound, so a novel uncertainty observer is presented with success to develop the proposed optimal control strategy. The observer has asymptotic convergence under the Lyapunov theoretical framework. The proposed controller is applied to a highly nonlinear bioreactor model, where the maximum bioreactor productivity is reached in a stable closed-loop steady-state operation by suppressing the open-loop oscillations of the mass concentrations in the bioreactor. The closed-loop productivity is also stable and is increased by around 12.5% in comparison with the highest open-loop productivity reached.