Next Article in Journal
Chemical Activation of Apricot Pit-Derived Carbon Sorbents for the Effective Removal of Dyes in Environmental Remediation
Next Article in Special Issue
Highly Effective Electrochemical Water Splitting with Enhanced Electron Transfer between Ni2Co Layered Double Hydroxide Nanosheets Dispersed on Carbon Substrate
Previous Article in Journal
Recent Advances in Graphene-Based Mesoporous Nanosheets for Supercapacitors
Previous Article in Special Issue
Sustainable Supercapacitors Based on Polypyrrole-Doped Activated Biochar from Wood Waste Electrodes
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
C
Volume 9
Issue 4
10.3390/c9040092
carbon-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

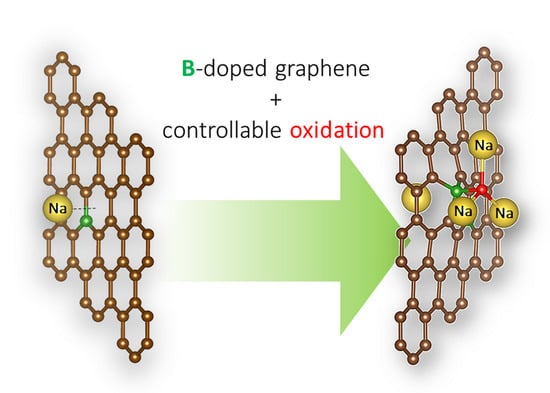
Density Functional Theory Analysis of the Impact of Boron Concentration and Surface Oxidation in Boron-Doped Graphene for Sodium and Aluminum Storage

by
Milica S. Ritopečki
1,
Natalia V. Skorodumova
2,3,
Ana S. Dobrota
1,* and
Igor A. Pašti
1,*
1
Faculty of Physical Chemistry, University of Belgrade, Studentski Trg 12-16, 11158 Belgrade, Serbia
2
Department of Materials Science and Engineering, School of Industrial Engineering and Management, KTH—Royal Institute of Technology, Brinellvägen 23, 10044 Stockholm, Sweden
3
Applied Physics, Division of Materials Science, Department of Engineering Sciences and Mathematics, Luleå University of Technology, 97187 Luleå, Sweden
*
Authors to whom correspondence should be addressed.
C 2023, 9(4), 92; https://doi.org/10.3390/c9040092
Submission received: 5 September 2023 / Revised: 21 September 2023 / Accepted: 26 September 2023 / Published: 28 September 2023
(This article belongs to the Special Issue Nanoporous Carbons for Hydrogen Sorption and Electrochemical Energy Storage)
Browse Figures
Versions Notes

Abstract

:
Graphene is thought to be a promising material for many applications. However, pristine graphene is not suitable for most electrochemical devices, where defect engineering is crucial for its performance. We demonstrate how the boron doping of graphene can alter its reactivity, electrical conductivity and potential application for sodium and aluminum storage, with an emphasis on novel metal-ion batteries. Using Density Functional Theory calculations, we investigate both the influence of boron concentration and the oxidation of the material on the mentioned properties. It is demonstrated that the presence of boron in graphene increases its reactivity towards atomic hydrogen and oxygen-containing species; in other words, it makes B-doped graphene more prone to oxidation. Additionally, the presence of these surface functional groups significantly alters the type and strength of the interaction of Na and Al with the given materials. Boron-doping and the oxidation of graphene is found to increase the Na storage capacity of graphene by a factor of up to four, and the calculated sodiation potentials indicate the possibility of using these materials as electrode materials in high-voltage Na-ion batteries.

Graphical Abstract

1. Introduction

Graphene is a two-dimensional material with a graphite monolayer structure and sp2-hybridized carbon (C) atoms arranged in a honeycomb lattice [1,2]. Due to its rare properties, such as good electric conductivity and a large surface area, graphene has attracted interest as a potential anode material. However, the fact that it is a zero-bandgap semiconductor, along with its chemical inertness, limits its application possibilities [3,4,5,6,7]. Therefore, the graphene lattice is usually changed by chemical doping or by introducing covalent bonds with certain chemical groups or even molecules [8,9]. It should, however, be noted that the defects in graphene can also occur spontaneously during synthesis, and they can be sometimes difficult to predict and control [10]. The simplest modification method of pristine is chemical doping by heteroatoms, which improves the properties of pristine graphene by improving the metal–surface interaction, adsorption and charge transfer abilities [2,4,11,12]. Heteroatoms such as boron (B), nitrogen (N), sulfur (S), fluorine (F), and phosphorus (P) are frequently chosen for this purpose since they change the bandgap and the position of the Fermi level, which depends on their concentration [4,13].
Carbon-based materials, including graphene, are widely investigated as candidates for electrode materials in metal-ion batteries (MIBs). For MIBs, the strength and the nature of the interactions of the metal (and/or metal-based ions) with electrode materials are essential. Novel types of MIBs focus on metals other than Li as the electroactive species due to the problems associated with Li-ion batteries [14] and Li abundance in general. These other metals include Na and Al, as they have small a mass and radius and a high abundance in Earth’s crust [15]. Additionally, further advantages of Al are its three-electron redox property and low flammability. However, both Na and Al interact with pristine graphene relatively weakly [16], resulting in low voltages in hypothetical novel MIBs with graphene as the electrode material. Thus, chemical functionalization is needed to boost graphene’s Na and Al storage capacity. Some reports of Al- and Na-ion batteries, which use carbon-based electrodes, can already be found in the literature [17,18,19,20].
Boron-doped graphene is an especially good candidate for the doping of graphene since B- and C-atoms have similar radii, making a C-B bond in a monolayer only ~0.5% longer than the C-C one. Because of this, doping does not affect the planarity of the graphene sheet or the sp2 hybridization of the carbon atoms within [11,21]. Boron is less electronegative than carbon, which causes a difference in electron density between boron and carbon atoms, leaving the boron site with an electron deficit [22]. In addition, since boron has one electron less, B-graphene acts as a p-type semiconductor [23]. B-graphene also has, similarly to pristine graphene, a very low or nondetectable total magnetization [12,23]. For now, B-graphene has primarily found its place in energy-related applications, such as batteries and supercapacitors [24,25], but there are also studies where it is used as a gas and optical sensor material [26,27] and in the biomedical field of study [28]. For example, Ling and Mizuno used first-principle calculations to demonstrate that the sodiation of boron-doped graphene preserves its structural integrity, avoids the formation of dendrites and allows for approx. 2 times the capacity of the graphite anode in Li-IB and approx. 2.5 times higher than hard carbon in Na-IB [29]. Zhang et al. presented the facile synthesis of boron-doped reduced graphene oxide, which can be used as a sodium-ion battery anode [30]. Recently, Yiqun et al. demonstrated that the cathode based on boron-doped reduced graphene oxide displays a high Al-storage capacity and outstanding long-term stability [31].
In this study, we continue our previous work [32,33], where it was shown that the introduction of dopants (B, N, P or S) into oxidized graphene or the controlled oxidation of doped graphene can enhance the Na storage capabilities of the material, with boron found to be a very suitable dopant for this purpose. Thus, we investigate the effects of different concentrations of boron as a dopant in graphene on its properties, which are not addressed in detail in the literature but are of high importance for the electrochemical applications of B-doped graphene. First, we focus on the reactivity of the material towards H, O and OH, and next, we investigate the adsorption of Na and Al onto bare and oxidized boron-doped graphene to explore the possibility of using such modified graphene surfaces in novel energy storage devices.

2. Methods

In order to carry out Density Functional Theory (DFT) calculations, the open-source program packet Quantum ESSPRESO [34,35] was used. GGA and PBE functionals were used as part of this package. Since the adsorption of sodium and aluminum on graphene-based materials was investigated, dispersion interactions need to be included by utilizing the DFT-D2 correction [36]. The kinetic energy cut-off of plane waves was set at 36 Ry, and the density cut-off was set at 576 Ry. Spin polarization was included in all the conducted calculations. The first irreducible Brillouin zone was obtained using a Γ -centered 4 × 4 × 1 grid utilizing the general Monkhorst–Pack scheme [37]. Löwdin charges were used for discussing charge transfer. To investigate electronic structure, a denser centered 20 × 20 × 1 grid was used.
Pristine graphene was modelled as a (3 3  × 3 3 )R30° structure containing 54 carbon atoms, C54. Boron-doped graphene was constructed by replacing one, two or three carbon atoms with boron, obtaining graphene with 1.85, 3.70 or 5.56 at.% of B, respectively. To evaluate the stability of boron-doped graphene, the binding energy (Eb) of boron at the vacancy sites was used. The binding energy of the nth (n   ∈   {1, 2, 3}) substitutionally introduced boron atom is calculated as
Eb(nth B) = E(C54−nBn) − E(C54−nBn−1) − E(B)
where E(C54−nBn) stands for the total energy of graphene doped with n atoms of B, E(C54−nBn−1) is the total energy of graphene doped with n − 1 atoms of B and a vacancy at the site where the nth B will be introduced and E(B) the total energy of an isolated boron atom. Since the adsorption of atomic hydrogen, atomic oxygen and hydroxyl groups on C54−nBn was also investigated, their corresponding adsorption energies (Eads) were calculated using the following formula:
Eads(A) = Esubs+A − Esubs − EA
where Esubs+A, Esubs and EA stand for the total energies of the optimized adsorbate–substrate system, bare substrate (C54−nBn), and isolated adsorbate atom/group (A = H, O, or OH), respectively. The most stable O@C54−nBn and OH@C54−nBn structures were further used as models of oxidized C54−nBn.
Finally, the adsorption of Na and Al on bare C54−nBn and its oxidized forms (O@C54−nBn and OH@C54−nBn) was investigated, while the strength of their interaction with the substrate was estimated in terms of differential and integral adsorption energies. The differential adsorption energy (Eads,diff) was calculated as
Eads,diff (M) = Esubs+mM − Esubs+(m−1)M − EM
where “subs” can be C54−nBn, O@C54−nBn or OH@C54−nBn, while Esubs+mM stands for the total energy of the chosen substrate with m atoms of metal M adsorbed (i.e., m is the number of atoms M, M = Na or Al). Similarly, Esubs+(m−1)M stands for the total energy of the chosen substrate with m − 1 atoms of metal M adsorbed. The integral adsorption energy (Eads,int) was calculated as
Eads,int (M) = (Esubs+mM − Esubs − m∙EM)/m
where Esubs stands for the total energy of the optimized substrate without any M adsorbed. Charge redistribution caused by metal interaction with the chosen model systems was investigated through a 3D plot of charge difference (Δρ), defined as:
Δρ = ρsubs+M − ρsubs,frozen − ρM
where ρsubs+M, ρsubs,frozen and ρM stand for the ground state charge densities of the substrate interacting with M, the ground state charge densities of the substrate when M is removed (with frozen geometry) and that of the isolated M atom, respectively.
Graphical representations of all the graphene structures in this paper were made using VESTA [38].

3. Results

3.1. Graphene Doping by Boron

Pristine graphene, C54, was used as a starting model. Its optimization resulted in a C-C bond length of 1.43 Å, which is in agreement with previous studies [12,39,40]. B-doped graphene was modelled by replacing n carbon atoms by boron, as described in the Computational Details section. While the position of the first boron atom can be chosen arbitrarily, it is necessary to perform additional calculations to find the optimal positions of the second and the third boron atom relative to the first one, or the first and second one, respectively. In the case of C52B2 systems, we find that the energetically least stable configuration is the one where the two B atoms are next to each other (Figure 1). The systems become more stable as the two B atoms separate, and the optimal structure corresponds to the state where they are one across from the other, on opposite sides of the same C4B2 hexagon (Figure 1). We note that substitutional B atom clustering was recently observed for B-doped graphene single layers on the Ir(111) surface [41]. Boron atoms did not prefer direct bonding, that is, the configuration in which they are adjacent to each other in a C4H2 ring. The situation we find is not identical to that described in ref. [41], which also included the geometric deformation of the B-doped graphene sheet caused by its bending towards the Ir(111) surface.
A similar pattern was found upon the introduction of the third boron atom—the dopant atoms are one across from the other on opposite sides of one hexagon, while it is optimal to have two boron atoms inside one hexagon. The first boron atom (the case of C53B) is found to be incorporated into the graphene lattice with a binding energy of −12.90 eV and a C-B bond length of 1.49 Å, which is in agreement with our previous studies [12,42]. When more B atoms are introduced, the binding energies follow the following trend: Eb(1st B) < Eb(2nd B) < Eb(3rd B), i.e., the first B is bound the strongest. The differences in their Eb are up to 6.2%. The results are summarized in Table 1. The results presented here suggest that boron atoms at higher doping levels could form a 2D array even in a self-standing B-doped graphene sheet, similarly to B-doped graphene on Ir(111) [41]. All the investigated C54−nBn systems were found to be nonmagnetic. We observed that there was no disruption to the planarity, even with the addition of three B atoms, which is a consequence of the similar atomic radii of B and C. Upon the introduction of boron, the Bader charge of its first neighbouring carbon atoms increased by 0.1 e. On the other hand, the charge of boron atoms decreased by 0.1–0.2 e, which is expected since boron is less electronegative than carbon.
Upon boron insertion into a graphene lattice, the Fermi energy is shifted towards higher energies. In Figure S3, the electronic structures of pristine graphene and doped species were also compared. The energy range in this figure is chosen so that the p states of boron atoms can be clearly seen. For the full range DOS plots please see Figure S3, right. It is well known that pristine graphene is a semimetal with a zero-band gap [23]. This was also observed here, and it is also shown that doped models behave as conductors. This is very important for the materials’ potential electrochemical purposes.
After setting the models of boron-doped graphene with various concentrations of B, we move on to exploring their reactivity towards species of interest.

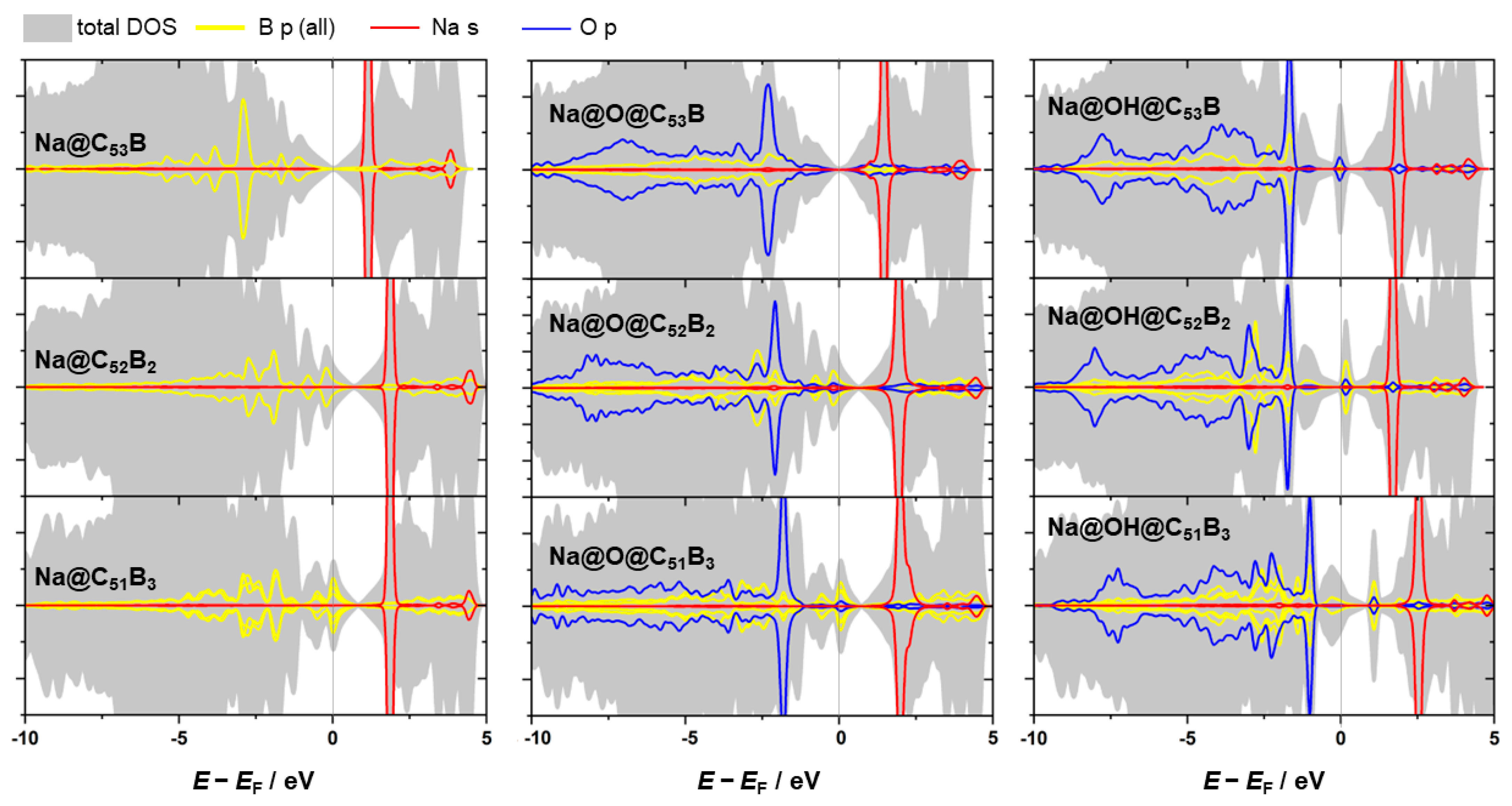
3.2. Reactivity and Oxidation

The H, O and OH adsorption trends of C54−nBn are summarized in Figure 2. When investigating H adsorption (Figure 2, top), the C-top sites were found to be the most favourable ones. For the B-doped surfaces, the carbon atom that is the closest to a boron atom is the one where H prefers to adsorb. This is in agreement with some previous research [12,43]. We find that with the increment of boron percentage in the system, the H adsorption energy decreases, i.e., H is bound more strongly. For pristine graphene, the energy of H adsorption is −0.79 eV, while for C51B3, it is −2.06 eV. The C-H bond length does not change significantly upon B introduction (1.13–1.15 Å).
The situation is somewhat different when looking at the adsorption of O (Figure 2, middle). The preferred site is the bridge site, which in the case of pristine graphene implies the site between two carbon atoms. In the investigated cases of B-doped graphene, the preferred bridge site is the C-B bridge. The energy of adsorption behaves in the same way as for the H adoption—the boron percentage and adsorption energies of O are negatively correlated, the lowest energy being −4.30 eV for O@C51B3.
The adsorption of OH (Figure 2, bottom) gave similar results as in previously conducted research [12]—OH binds via creating a C-O bond in the case of pristine graphene and a B-O bond in the case of C54−nBn. When there are two boron atoms in the model, the adsorption to each one of them gives similar results, with the more stable one having a binding energy of −2.21 eV and B-O and O-H bond lengths of 1.52 Å and 0.98 Å, respectively. However, for the C51B3 structure, it is most favourable for the OH group to adsorb on top of the boron atom that is in the middle, obtaining a binding energy of −2.21 eV and the same bond lengths as in C52B2. It is also interesting to note that, unlike the cases where the adsorption of H and O was investigated, the most stable model with adsorbed OH is not the C51B3 structure but C52B2. The bond lengths do not vary much when increasing the number of boron atoms. It is also noted that the re-hybridization from sp2 to sp3 occurs in all the cases upon H, O or OH adsorption, meaning that the models lose their initial planarity.
Obviously, all the investigated adsorbates bind more strongly to B-doped graphene than to pristine graphene, with the strength of the interaction rising with B percentage. This means that the introduction of B into the graphene lattice results in an enhanced reactivity of the material towards H, O and OH. The increased reactivity towards H is of significance for the possible applications of such materials for hydrogen production and storage. The adsorption energy of atomic hydrogen is used as one of the basic descriptors for the hydrogen evolution reaction (HER) activity of the material. In fact, metal-free substitutionally B-doped graphene (1.85 at.% of B) was previously demonstrated to have significantly higher HER activity compared to defective graphene and glassy carbon, with a HER onset potential of around −0.3 V vs. RHE (Reversible Hydrogen Electrode) [44]. This value agrees well with the calculated hydrogen binding energy on B-doped graphene (~−2.1 eV, Figure 2). Moreover, from the results presented here, it is clear that the HER active sites are not the B site but the carbon atoms adjacent to the dopant sites, whose activity is rendered by B incorporation into the graphene lattice.
On the other hand, the enhanced reactivity of C54−nBn towards O-containing groups signals that boron doping makes graphene more prone to oxidation, i.e., that O-groups will be more stable on the surface containing B than the pristine one. This is very important from the aspect of metal interaction with such surfaces, which is crucial for applications of materials in metal-ion batteries. It is known that the oxygen-containing groups on graphene can play a very important role in this case, allowing for a stronger interaction of the chosen metal with the surface [38,40]. However, there is a risk of the O-group interacting “too strongly” with the metal and detaching from the surface irreversibly. Therefore, the stabilization of O-groups on graphene by its doping with B could be a good strategy for the better performance of graphene-based materials in metal-ion batteries. Another important question, when it comes to electrochemical applications, is the electrical conductivity of the material. The electronic structures of C54−nBn upon the adsorption of H, O and OH are given in Figure 3. It can be seen that the oxidized forms of C54−nBn (i.e., C54−nBn with O and OH adsorbed) act as conductors, making them good candidates for further research. However, we note that there is a DOS change around the Fermi level upon oxidation, which indicates that even though there is no band gap opening, the conductivity of the material is altered by the presence of oxygen-containing groups. The adsorption of the two metals of interest, Na and Al, onto bare and oxidized C54−nBn surfaces will be investigated in the next sections.

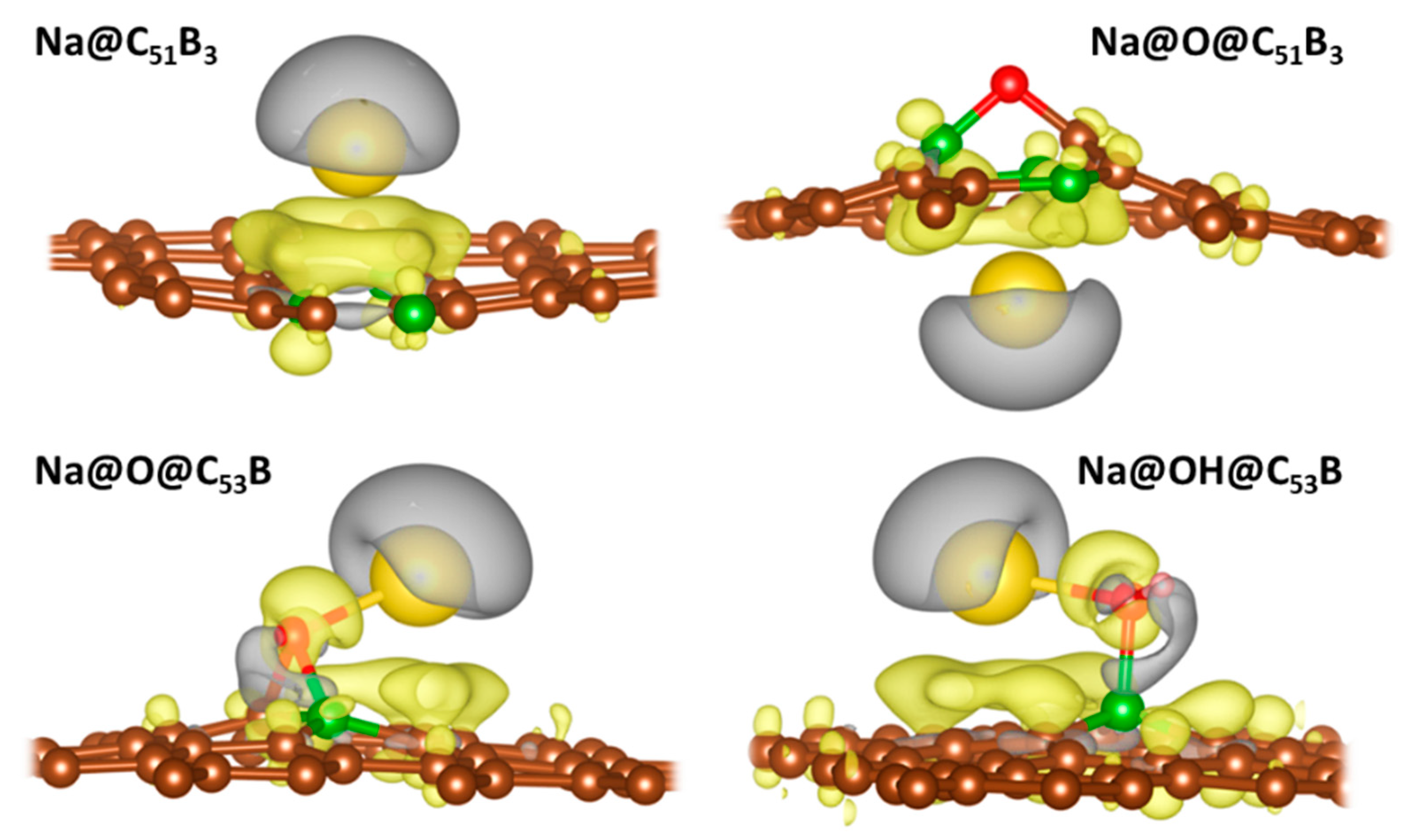
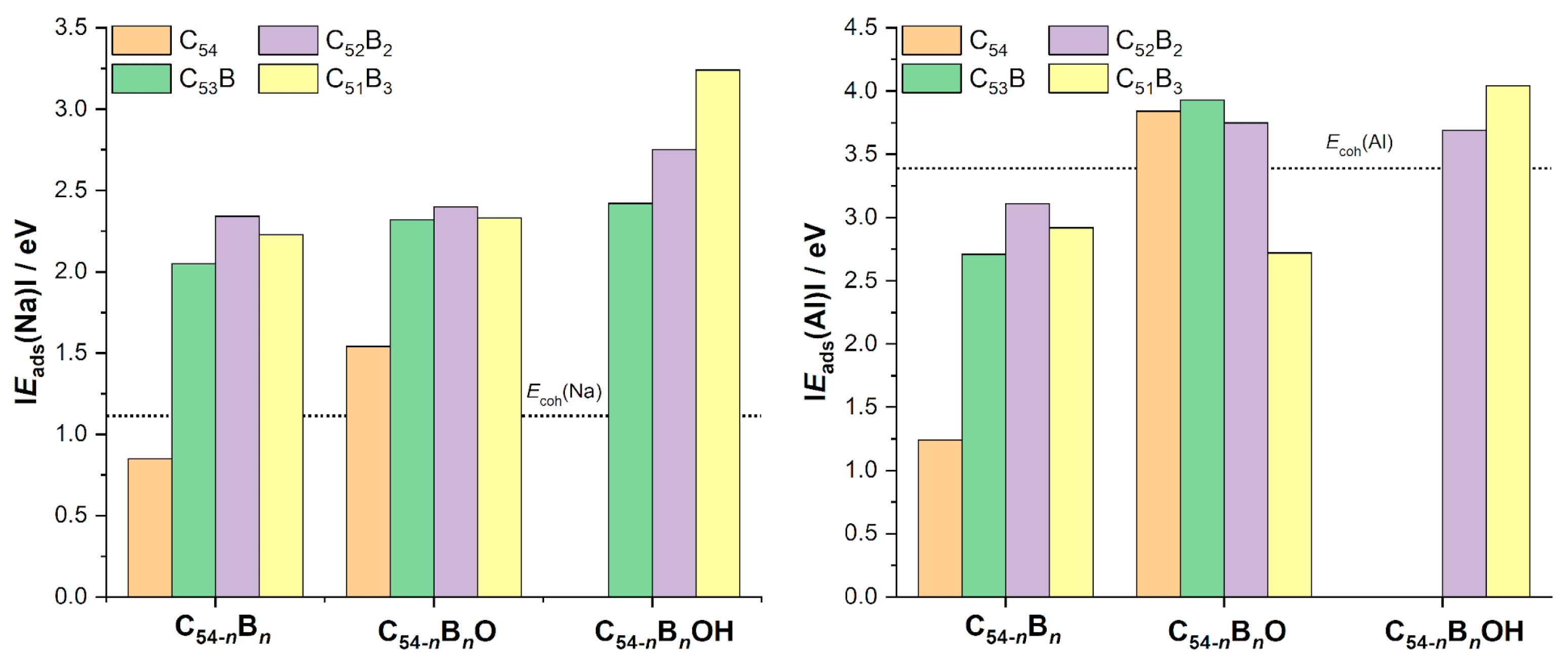
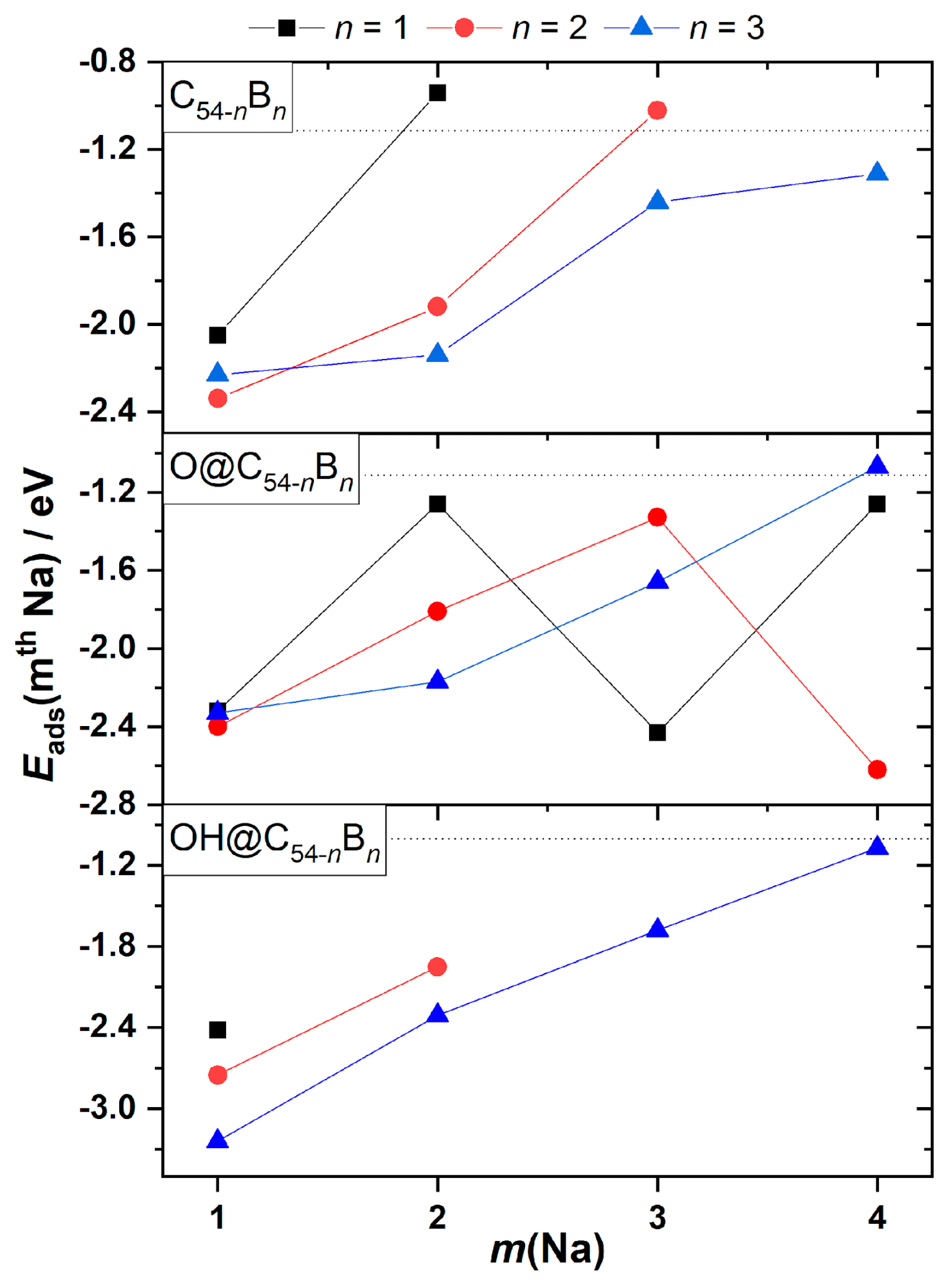
3.3. Metal Adsorption

Sodium is known to adsorb on pristine graphene at the C6-hollow site with an adsorption energy of −0.93 eV [16]. Aluminum also adsorbs to a hollow site on pristine graphene, with an adsorption energy amounting to −1.09 eV [16]. The reported energies vary depending on the computational approach (especially the chosen dispersion correction) and the size of the supercell. Regarding the adsorption of Na onto oxidized (nondoped) graphene, it is known that Na can directly interact with OH group, resulting in its detachment from the basal plane and NaOH phase separation [33]. We confirm all the mentioned facts regarding pristine graphene here and, additionally, investigate the adsorption of sodium and aluminum onto C54−nBn, O@C54−nBn and OH@C54−nBn. The calculated metal adsorption energies on pristine graphene are found to be −0.85 eV and −1.26 eV for Na and Al, respectively. When it comes to OH@C54, we find that both Na and Al adsorption result in metal hydroxyde phase separation. On the other hand, for O@C54, there is no detachment of the O-group, and we find that the adsorption energy of Na is −1.54 eV and that of Al is −3.84 eV. In the case of C54−nBn, the metal can occupy various top, bridge, or hollow adsorption sites. For the oxidized surfaces, the metal generally interacts directly with the oxygen-containing group. Three different outcomes can be identified, and they are represented in Figure 4. Here we have shown only the representatives of the three main groups of adsorption geometries. All optimized structures of Na and Al adsorption on the investigated (oxidized) B-doped graphene can be found in SI, Figures S2 and S3.
The first outcome is for the cases where the metal atom is adsorbed on the same side of the basal plane as O or OH. In these cases, the metal atom interacts directly with the oxygen-containing group. Most of the investigated systems behave like this. In the second outcome, the adsorbed Al or Na is on the opposite side of the basal plane from oxygen. This was only found for C51B3 models with an adsorbed oxygen atom. This can be explained by the combination of a high dopant concentration and the presence of the O-group, which significantly alter the planarity and charge of the surface. Because of this, it is easier for the metal atom to approach the other side of the plane. In both cases, the adsorbed metal occupies a hollow site on the opposite side from Oads. This is similar to the case of Na adsorption on corrugated doped graphene [45]. The third outcome represent the cases where the new phase emerges upon the adsorption of the metal. This happens in three cases: Na@OH@pristine graphene, Al@OH@pristine graphene and when OH is bounded on top of the C53B after the adsorption of Al. Therefore, these new phases represent the formation of metal hydroxyde. These models were not considered further since the formation of a new phase is not favourable for electrochemical purposes. Additionally, the charge redistribution is considered through charge difference plots. Again, for brevity, the mentioned plots are given in Figure 5 only for the chosen systems, which are representatives of the different types of interaction of the metals with the surfaces.
It can be clearly seen that in all the cases, the metal atoms are the ones that lose their charge and transfer it either completely to the graphene basal plane (in the cases of nonoxidized surfaces) or partially to oxygen and partially to the basal plane (in the cases of oxidized surfaces). The only exception when it comes to the oxidized surfaces is the already mentioned M@O@C51B3 (Figure 5, top right), where M adsorbs on the opposite side of the basal plane from O, so that no charge transfer from M to O is found. According to Löwdin charges, Na transfers 0.65–0.75 e to the substrate in all the cases, while Al transfers 0.46–0.52 e to the substrate.
In order to avoid forming a metal precipitate, the interaction energy between the metal and the substrate needs to be higher than the cohesive energies of the metals [46]. Thus, one of the main points of interest was comparing the absolute value of the calculated adsorption energies with the cohesive energies of Na 1.113 eV atom–1, and Al 3.39 eV atom–1 [47,48], as shown in Figure 6. It can be seen that in the case of sodium, only one system has an energy lower than the cohesive energy, and that is O@C54. On the other hand, for aluminum, half of the systems, not counting the ones where a new phase emerges, do not fulfil this condition. This is intuitive since Al has higher cohesive energy compared to Na. The systems where the precipitation of Al does not occur are O@C54, O@C53B, O@C52B2, OH@C52B2 and OH@C51B3.
For electrochemistry purposes “the intermediate” adsorption energy is the one that is preferable, meaning that it is high enough for metals not to precipitate but the adsorption is not so strong that it becomes irreversible.
For substrates without pre-adsorbed O or OH, the absolute value of the adsorption energies of sodium and aluminum increases with the increment of boron atoms in the structure up to a point where there are two boron atoms, and then it decreases again, making the C52B2 model the one with the most exothermic adsorption energy for both metals. The same trend is observed for Na when O is pre-adsorbed on the surface. However, this is not the case for Al, for which the highest absolute value of the adsorption energy is for the O@C52B2 structure. When OH is bonded to the surface, for both metals, the absolute value of the adsorption energy increases with the percentage of boron.
Another important point is determining whether the systems are conducting. They need to be conducting to be used as electrode materials. This is why the analysis of the electronic structure, in particular, the density of states (DOS), was carried out for all the investigated systems. Figure 7 shows them for the case of sodium (for brevity).
Out of the considered models that fulfil the previous conditions, almost all behave as conductors, except Na@C53B and Na@O@C53B, which, upon adsorbing sodium, have a very low DOS around the Fermi energy (Figure 7).
Next, we investigated how the presence of boron dopant atoms in different concentrations, as well as the presence of O/OH groups on the surface, affect the adsorption capacity for Na and Al (Figure 8). We compare the calculated differential adsorption energies of each added Na atom to its cohesive energy and find that up to four Na atoms can be adsorbed onto C51B3, O@C53B and O@C52B2. For the oxidized forms of C51B3, the absolute value of Eads,diff of the fourth Na atom is lower than Na’s cohesive energy, which indicates that metal phase precipitation would occur. On the other hand, for OH@C53B, the Na-O phase separation occurs upon the addition of the second Na atom, while for C53B and OH@C52B2, it happens upon adding the third Na atom, and for C52B2, after the addition of the fourth Na atom. The optimized structures of two, three and four Na atom adsorption onto the models for which no phase separation occurs and the adsorption energies overcome the cohesive energy of Na are shown in Figure 9. From this figure, it is obvious that, in the case of nonoxidized boron-doped graphene, Na prefers adsorbing on B-containing hollow sites. On the other hand, in the case of the oxidized surfaces, it mostly interacts with the O-group, which can bind up to three Na atoms.
When it comes to Al adsorption (Table 2), upon the addition of the second Al atom, most cases result in adsorption energies lower than the Al cohesive energy (comparing absolute values), while for others, Al-O phase separation occurs. The only case with a stable adsorption of 2Al is 2Al@O@C52B2, which also results in Al-O phase separation upon the addition of the third Al atom.
Finally, as we see clear improvement in the materials’ capacity for Na induced by B-doping, we calculate the sodiation potentials of the studied materials as electrode materials in a galvanic cell. For this consideration, a proper reference point needs to be taken, since potential cannot be directly compared to the adsorption energies of an isolated Na atom. Therefore, we use the approach explained in detail in ref. [33] and consider a galvanic cell (potential secondary sodium-ion battery) with solid Na as the anode and the investigated boron-doped graphene surfaces as the cathodes. The half reactions in this cell (equivalent to battery discharging) would be, at the anode:
Na (s) → Na+ + e−
and at the cathode:
Na+ + e− + *(O/OH)C54−nBn → Na@(O/OH)C54−nBn,
where *(O/OH)C54−nBn stands for the adsorption site on the investigated surface, i.e., C54−nBn, O@C54−nBn or OH@C54−nBn. We note that this consideration assumes that the activity of Na+ in the electrolyte is 1, that the changes in volume and entropy due to adsorption are negligible [49], and that the Na+ ions interact with B-graphene free of their solvation spheres. This way, the change in the Gibbs free energy of the adsorption, ΔG, can be estimated as the energy change in the Na transfer from the metallic Na anode to the B-graphene cathode. As explained in ref. [33], under the mentioned assumptions, the electrode potential at which the sodiation of graphene-based material takes place, E0 (Na+/Na@(O/OH)C54−nBn), referred to as the Standard Hydrogen Electrode, SHE, is
E0(Na+/Na@(O/OH)C54−nBn) ≈ E0(Na+/Na) − ΔE/F
where E0(Na+/Na) is the standard electrode potential of the Na+/Na electrode (−2.71 V vs. SHE, from tables of standard electrode potentials), ΔE is the energy change upon Na adsorption and F is the Faraday constant. When we look at the average adsorption of 1Na (1e− in the reaction), ΔE reduces to Eads,int(Na) + Ecoh(Na), and we get
E0(Na+/Na@(O/OH)C54−nBn) ≈ E0(Na+/Na) – [Eads(Na) + Ecoh(Na)]/e
where Ecoh(Na) is the already mentioned cohesive energy of Na, and Eads,int(Na) is the integral (average) Na adsorption energy (both Ecoh and Eads,int are given in eVs, per one Na atom, and therefore divided only by e in Equation (9), where Ecoh(Na) = 1.113 eV atom–1 [47,48]). From Equation (9), it can be seen that E0(Na+/Na@(O/OH)C54−nBn) is a linear function of Eads(Na). Given that Eads(Na) is negative, the stronger the Na binding is to the surface, the more positive E0(Na+/Na@(O/OH)C54−nBn) will be. The calculated sodiation potentials are shown in Table 3.
It is obvious from Table 3 that the calculated sodiation potentials for all the investigated (oxidized) B-doped graphene surfaces are negative, with −2.34 V vs. SHE for Na+/Na@C53B for m = 2 as the lowest (most negative). However, none of them are more negative than the standard electrode potential of the Na+/Na electrode (−2.71 V vs. SHE), which indicates that in the considered galvanic cell, solid Na would indeed dissolve to release Na+ ions, which would then adsorb at the B-doped surfaces of graphene. The material with the most positive sodiation potential (the case of Na+/Na@OH@C51B3 for m = 2) combined with an Na+/Na electrode would yield the most positive standard electromotive force (ε0) of the cell, ε0 = −1.07 V − (−2.71 V) = 1.64 V, resulting in a high-voltage sodium-ion battery. The possibility of obtaining high-voltage sodium-ion batteries is in line with our previous findings on (oxidized) doped graphene, ref. [33]. However, in the mentioned study, the dopant concentration was not investigated as a variable. Here, we can clearly see (Table 3) that for the case of 2Na adsorption, an increase in B concentration makes the sodiation potential more positive. However, this is not the case when we consider three and four Na atom adsorption, where C52B2 is found to be optimal.
It is interesting to compare pristine graphene and its oxidized forms with the boron-doped analogues studied here. If we were to calculate the sodiation potential for pristine, nonoxidized graphene, based only on 1Na adsorption, it renders a very negative E0(Na+/Na@C54), amounting to −2.99 V. Obviously, this case surpasses (is more negative than) the standard electrode potential for pure Na+/Na, indicating that in such a galvanic cell, Na+/Na would actually act as the cathode, where Na+ would reduce, while Na+/Na@C54 would act as the anode, i.e., the half reactions (R1) and (R2) would go in opposite directions than previously stated. The resulting ε0 would be 0.28 V. This means that the pristine graphene material would have to be filled with Naads before the start of the battery operation to provide Na, which would oxidate during the battery discharge. Additionally, next to low battery voltage, we add the fact that pristine graphene shows a rather poor Na capacity, with already the second Na not being able to surpass Ecoh(Na), making room for Na–metal phase separation and deteriorating the possibility of preparing the Na-filled graphene electrode material. When it comes to the oxidized forms of nondoped graphene, in O-functionalized graphene, one epoxy group is found to be able to bind up to three Na atoms, while the presence of OH allows for its interaction with just one Na. The B-doping of the material is found to improve this situation—the sodiation potentials are more positive than Na+/Na, the cohesive energy problem is surpassed and the Na+ (battery) capacity is improved up to four times.

4. Conclusions

DFT calculations were utilized to investigate the influence of boron dopant concentration and surface oxidation on the potential for Na and Al storage in graphene. The obtained results demonstrated that the introduction of boron into graphene has a significant effect on its reactivity towards oxygen-containing species, rendering the material more susceptible to oxidation. Consequently, when modeling such materials, it is crucial to consider the oxidation of the B centers. In terms of electrochemical applications, the oxidation of B-doped graphene modifies its electronic structure but does not induce a bandgap. As a result, the controllable doping of graphene with boron, followed by oxidation, appears to be a promising approach for enhancing its electrochemical performance with respect to Na and Al storage. Specifically, this strategy optimizes the strength of the interaction between Na and Al and the graphene surface and its storage capacity, thereby opening up possibilities for its applications in metal-ion batteries and energy storage in general. In both cases, the adsorbate atoms tend to bind to or near B atoms, which are additionally functionalized by surface groups such as O or OH. Depending on the B-dopant concentration and the oxidation of the surface, such functionalized materials can store up to four Na atoms per dopant atom and are possible candidates for high-voltage (up to approx. 1.6 V) and high-capacity Na-ion batteries.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/c9040092/s1: Figure S1. Investigated configurations of C52B2. Figure S2. Investigated configurations of C51B3. Figure S3. Electronic structures (total DOS) of pristine graphene (C54, first row) and investigated boron-doped graphene C54−nBn (bottom three rows), zoomed in to the range of −5 to +5 eV (left) and in full energy range (right). The p states of boron dopant atoms are shown separately (in the case of C52B2, the p states of two B atoms overlap). For clarity, all total DOS plots are divided by 5. The Fermi level (dashed, black line) is set to 0. Figure S4. Optimized structures of Na adsorption onto (oxidized) C54−nBn systems (first row: bare C54−nBn, middle row: C54−nBn oxidized by Oads, bottom row: C54−nBn oxidized by OHads). Graphical representations were made using VESTA. Figure S5. Optimized structures of Al adsorption onto (oxidized) C54−nBn systems (first row: bare C54−nBn, middle row: C54−nBn oxidized by Oads, bottom row: C54−nBn oxidized by OHads). Graphical representations were made using VESTA.

Author Contributions

Conceptualization, A.S.D. and I.A.P.; data curation, N.V.S. and I.A.P.; formal analysis, M.S.R. and A.S.D.; funding acquisition, N.V.S. and I.A.P.; investigation, M.S.R. and A.S.D.; methodology, M.S.R., N.V.S., A.S.D. and I.A.P.; resources, N.V.S. and I.A.P.; supervision, N.V.S. and A.S.D.; validation, N.V.S. and I.A.P.; writing—original draft, M.S.R. and A.S.D.; writing—review and editing, N.V.S. and I.A.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Serbian Ministry of Science, Technological Development, and Innovations (contract number: 451-03-47/2023-01/200146). I.A.P. is also indebted to the Research Fund of the Serbian Academy of Sciences and Arts, project F-190, for supporting this study. The computations and data handling were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC) at Linköping University, partially funded by the Swedish Research Council through grant agreement No. 2018-05973.

Data Availability Statement

The raw/processed data required to reproduce these findings cannot be shared at this time as the data also form part of an ongoing study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
  2. Liu, J.; Liang, T.; Tu, R.; Lai, W.; Liu, Y. Redistribution of π and σ Electrons in Boron-Doped Graphene from DFT Investigation. Appl. Surf. Sci. 2019, 481, 344–352. [Google Scholar] [CrossRef]
  3. Brownson, D.A.C.; Kampouris, D.K.; Banks, C.E. An Overview of Graphene in Energy Production and Storage Applications. J. Power Sources 2011, 196, 4873–4885. [Google Scholar] [CrossRef]
  4. Shanmugam, S.; Nachimuthu, S.; Subramaniam, V. DFT Study of Adsorption of Ions on Doped and Defective Graphene. Mater. Today Commun. 2020, 22, 100714. [Google Scholar] [CrossRef]
  5. Ali, S.; Lone, B. Adsorption of Cytosine on Si and Ge Doped Graphene: A DFT Study. Mater. Today Proc. 2023, 80, 774–781. [Google Scholar] [CrossRef]
  6. Tiwari, S.K.; Sahoo, S.; Wang, N.; Huczko, A. Graphene Research and Their Outputs: Status and Prospect. J. Sci. Adv. Mater. Devices 2020, 5, 10–29. [Google Scholar] [CrossRef]
  7. Soldano, C.; Mahmood, A.; Dujardin, E. Production, Properties and Potential of Graphene. Carbon 2010, 48, 2127–2150. [Google Scholar] [CrossRef]
  8. Agnoli, S.; Favaro, M. Doping Graphene with Boron: A Review of Synthesis Methods, Physicochemical Characterization, and Emerging Applications. J. Mater. Chem. A 2016, 4, 5002–5025. [Google Scholar] [CrossRef]
  9. Liu, L.; Qing, M.; Wang, Y.; Chen, S. Defects in Graphene: Generation, Healing, and Their Effects on the Properties of Graphene: A Review. J. Mater. Sci. Technol. 2015, 31, 599–606. [Google Scholar] [CrossRef]
  10. Yang, G.; Li, L.; Lee, W.B.; Ng, M.C. Structure of Graphene and Its Disorders: A Review. Sci. Technol. Adv. Mater. 2018, 19, 613–648. [Google Scholar] [CrossRef]
  11. Riyaz, M.; Garg, S.; Kaur, N.; Goel, N. Boron Doped Graphene as Anode Material for Mg Ion Battery: A DFT Study. Comput. Theor. Chem. 2022, 1214, 113757. [Google Scholar] [CrossRef]
  12. Dobrota, A.S.; Pašti, I.A.; Mentus, S.V.; Skorodumova, N.V. A DFT Study of the Interplay between Dopants and Oxygen Functional Groups over the Graphene Basal Plane-Implications in Energy-Related Applications. Phys. Chem. Chem. Phys. 2017, 19, 8530–8540. [Google Scholar] [CrossRef] [PubMed]
  13. Zhang, Q.; Zhou, Y.; Yu, Y.; Chen, B.-Y.; Hong, J. Exploring Catalytic Performance of Boron-Doped Graphene Electrode for Electrochemical Degradation of Acetaminophen. Appl. Surf. Sci. 2020, 508, 145111. [Google Scholar] [CrossRef]
  14. Etacheri, V.; Marom, R.; Elazari, R.; Salitra, G.; Aurbach, D. Challenges in the Development of Advanced Li-Ion Batteries: A Review. Energy Environ. Sci. 2011, 4, 3243–3262. [Google Scholar] [CrossRef]
  15. Liang, Y.; Dong, H.; Aurbach, D.; Yao, Y. Current Status and Future Directions of Multivalent Metal-Ion Batteries. Nat. Energy 2020, 5, 646–656. [Google Scholar] [CrossRef]
  16. Pašti, I.A.; Jovanović, A.; Dobrota, A.S.; Mentus, S.V.; Johansson, B.; Skorodumova, N.V. Atomic Adsorption on Pristine Graphene along the Periodic Table of Elements—From PBE to Non-Local Functionals. Appl. Surf. Sci. 2018, 436, 433–440. [Google Scholar] [CrossRef]
  17. Lin, M.C.; Gong, M.; Lu, B.; Wu, Y.; Wang, D.Y.; Guan, M.; Angell, M.; Chen, C.; Yang, J.; Hwang, B.J.; et al. An Ultrafast Rechargeable Aluminium-Ion Battery. Nature 2015, 520, 324–328. [Google Scholar] [CrossRef]
  18. Zhou, W.; Jia, J.; Lu, J.; Yang, L.; Hou, D.; Li, G.; Chen, S. Recent Developments of Carbon-Based Electrocatalysts for Hydrogen Evolution Reaction. Nano Energy 2016, 28, 29–43. [Google Scholar] [CrossRef]
  19. Zhang, T.; Li, C.; Wang, F.; Noori, A.; Mousavi, M.F.; Xia, X.; Zhang, Y. Recent Advances in Carbon Anodes for Sodium-Ion Batteries. Chem. Rec. 2022, 22, e202200083. [Google Scholar] [CrossRef]
  20. Benti, N.E.; Tiruye, G.A.; Mekonnen, Y.S. Boron and Pyridinic Nitrogen-Doped Graphene as Potential Catalysts for Rechargeable Non-Aqueous Sodium–Air Batteries. RSC Adv. 2020, 10, 21387–21398. [Google Scholar] [CrossRef]
  21. Panchakarla, L.S.; Subrahmanyam, K.S.; Saha, S.K.; Govindaraj, A.; Krishnamurthy, H.R.; Waghmare, U.V.; Rao, C.N.R. Synthesis, Structure, and Properties of Boron- and Nitrogen-Doped Graphene. Adv. Mater. 2009, 21, 4726–4730. [Google Scholar] [CrossRef]
  22. Yu, X.; Han, P.; Wei, Z.; Huang, L.; Gu, Z.; Peng, S.; Ma, J.; Zheng, G. Boron-Doped Graphene for Electrocatalytic N2 Reduction. Joule 2018, 2, 1610–1622. [Google Scholar] [CrossRef]
  23. Rao, C.N.R.; Gopalakrishnan, K.; Govindaraj, A. Synthesis, Properties and Applications of Graphene Doped with Boron, Nitrogen and Other Elements. Nano Today 2014, 9, 324–343. [Google Scholar] [CrossRef]
  24. Liu, Y.; Artyukhov, V.I.; Liu, M.; Harutyunyan, A.R.; Yakobson, B.I. Feasibility of Lithium Storage on Graphene and Its Derivatives. J. Phys. Chem. Lett. 2013, 4, 1737–1742. [Google Scholar] [CrossRef]
  25. Hao, Q.; Xia, X.; Lei, W.; Wang, W.; Qiu, J. Facile Synthesis of Sandwich-like Polyaniline/Boron-Doped Graphene Nano Hybrid for Supercapacitors. Carbon 2015, 81, 552–563. [Google Scholar] [CrossRef]
  26. Zhang, L.; Zhang, Z.Y.; Liang, R.P.; Li, Y.H.; Qiu, J.D. Boron-Doped Graphene Quantum Dots for Selective Glucose Sensing Based on the “Abnormal” Aggregation-Induced Photoluminescence Enhancement. Anal. Chem. 2014, 86, 4423–4430. [Google Scholar] [CrossRef]
  27. Choudhuri, I.; Patra, N.; Mahata, A.; Ahuja, R.; Pathak, B. B-N@Graphene: Highly Sensitive and Selective Gas Sensor. J. Phys. Chem. C 2015, 119, 24827–24836. [Google Scholar] [CrossRef]
  28. Fan, Z.; Li, Y.; Li, X.; Fan, L.; Zhou, S.; Fang, D.; Yang, S. Surrounding Media Sensitive Photoluminescence of Boron-Doped Graphene Quantum Dots for Highly Fluorescent Dyed Crystals, Chemical Sensing and Bioimaging. Carbon 2014, 70, 149–156. [Google Scholar] [CrossRef]
  29. Ling, C.; Mizuno, F. Boron-Doped Graphene as a Promising Anode for Na-Ion Batteries. Phys. Chem. Chem. Phys. 2014, 16, 10419–10424. [Google Scholar] [CrossRef]
  30. Zhang, Y.; Qin, J.; Batmunkh, M.; Zhong, Y.L. Facile Synthesis of Boron-Doped Reduced Electrochemical Graphene Oxide for Sodium Ion Battery Anode. JOM 2021, 73, 2531–2539. [Google Scholar] [CrossRef]
  31. Du, Y.; Zhang, B.; Kang, R.; Zhou, W.; Zhang, W.; Jin, H.; Wan, J.; Zhang, J.; Chen, G. Boron-Doping-Induced Defect Engineering Enables High Performance of a Graphene Cathode for Aluminum Batteries. Inorg. Chem. Front. 2022, 9, 925–934. [Google Scholar] [CrossRef]
  32. Diklić, N.P.; Dobrota, A.S.; Pašti, I.A.; Mentus, S.V.; Johansson, B.; Skorodumova, N.V. Sodium Storage via Single Epoxy Group on Graphene—The Role of Surface Doping. Electrochim. Acta 2019, 297, 523–528. [Google Scholar] [CrossRef]
  33. Dobrota, A.S.; Pašti, I.A.; Mentus, S.V.; Johansson, B.; Skorodumova, N.V. Functionalized Graphene for Sodium Battery Applications: The DFT Insights. Electrochim. Acta 2017, 250, 185–195. [Google Scholar] [CrossRef]
  34. Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
  35. Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
  36. Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
  37. Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  38. Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  39. Dobrota, A.S.; Pašti, I.A.; Skorodumova, N.V. Oxidized Graphene as an Electrode Material for Rechargeable Metal-Ion Batteries—A DFT Point of View. Electrochim. Acta 2015, 176, 1092–1099. [Google Scholar] [CrossRef]
  40. Dobrota, A.S.; Gutić, S.; Kalijadis, A.; Baljozović, M.; Mentus, S.V.; Skorodumova, N.V.; Pašti, I.A. Stabilization of Alkali Metal Ions Interaction with OH-Functionalized Graphene: Via Clustering of OH Groups-Implications in Charge Storage Applications. RSC Adv. 2016, 6, 57910–57919. [Google Scholar] [CrossRef]
  41. Cuxart, M.G.; Perilli, D.; Tömekce, S.; Deyerling, J.; Haag, F.; Muntwiler, M.; Allegretti, F.; Di Valentin, C.; Auwärter, W. Spatial Segregation of Substitutional B Atoms in Graphene Patterned by the Moiré Superlattice on Ir(111). Carbon 2023, 201, 881–890. [Google Scholar] [CrossRef]
  42. Pašti, I.A.; Jovanović, A.; Dobrota, A.S.; Mentus, S.V.; Johansson, B.; Skorodumova, N.V. Atomic Adsorption on Graphene with a Single Vacancy: Systematic DFT Study through the Periodic Table of Elements. Phys. Chem. Chem. Phys. 2018, 20, 858–865. [Google Scholar] [CrossRef] [PubMed]
  43. Miwa, R.H.; Martins, T.B.; Fazzio, A. Hydrogen Adsorption on Boron Doped Graphene: An Ab Initio Study. Nanotechnology 2008, 19, 155708. [Google Scholar] [CrossRef] [PubMed]
  44. Sathe, B.R.; Zou, X.; Asefa, T. Metal-Free B-Doped Graphene with Efficient Electrocatalytic Activity for Hydrogen Evolution Reaction. Catal. Sci. Technol. 2014, 4, 2023–2030. [Google Scholar] [CrossRef]
  45. Dobrota, A.S.; Pašti, I.A.; Mentus, S.V.; Johansson, B.; Skorodumova, N.V. Altering the Reactivity of Pristine, N- and P-Doped Graphene by Strain Engineering: A DFT View on Energy Related Aspects. Appl. Surf. Sci. 2020, 514, 145937. [Google Scholar] [CrossRef]
  46. Oh, J.S.; Kim, K.N.; Yeom, G.Y. Graphene Doping Methods and Device Applications. J. Nanosci. Nanotechnol. 2014, 14, 1120–1133. [Google Scholar] [CrossRef]
  47. Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
  48. Kaxiras, E. Atomic and Electronic Structure of Solids; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
  49. Yao, L.H.; Cao, M.S.; Yang, H.J.; Liu, X.J.; Fang, X.Y.; Yuan, J. Adsorption of Na on Intrinsic, B-Doped, N-Doped and Vacancy Graphenes: A First-Principles Study. Comput. Mater. Sci. 2014, 85, 179–185. [Google Scholar] [CrossRef]
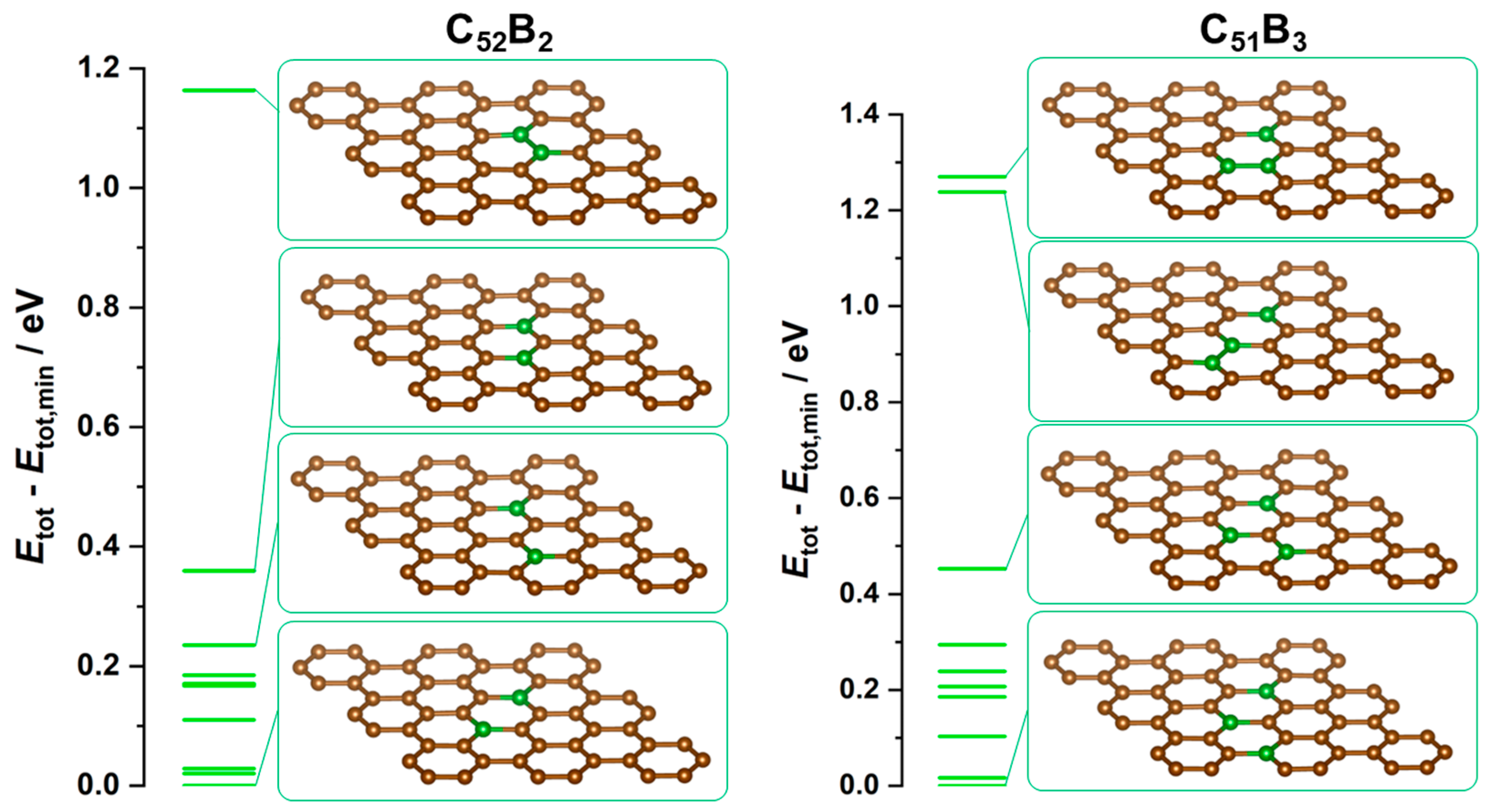
Carbon 09 00092 g001
Figure 1. Relative stabilities (in terms of total energies, Etot) of the investigated C52B2 (left) and C51B3 (right) structures compared to the most stable one with Etot,min, which corresponds to Etot − Etot,min = 0.
Figure 1. Relative stabilities (in terms of total energies, Etot) of the investigated C52B2 (left) and C51B3 (right) structures compared to the most stable one with Etot,min, which corresponds to Etot − Etot,min = 0.
Carbon 09 00092 g001
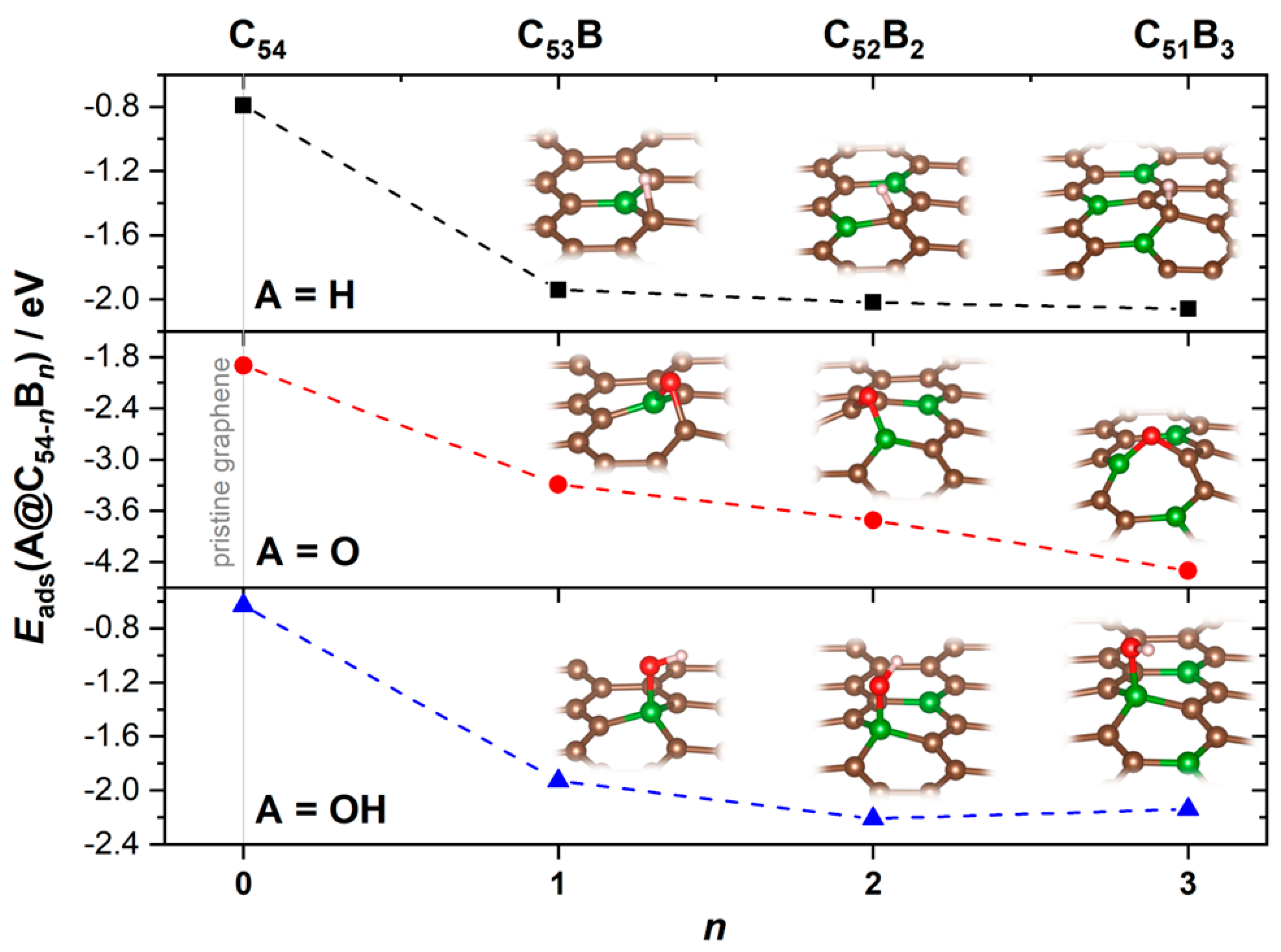
Carbon 09 00092 g002
Figure 2. The adsorption trends of H, O and OH on C54−nBn models: the relationship between the adsorption energies and the number of boron atoms, n, in the system. For boron-containing models, optimized adsorption structures are given for each system.
Figure 2. The adsorption trends of H, O and OH on C54−nBn models: the relationship between the adsorption energies and the number of boron atoms, n, in the system. For boron-containing models, optimized adsorption structures are given for each system.
Carbon 09 00092 g002
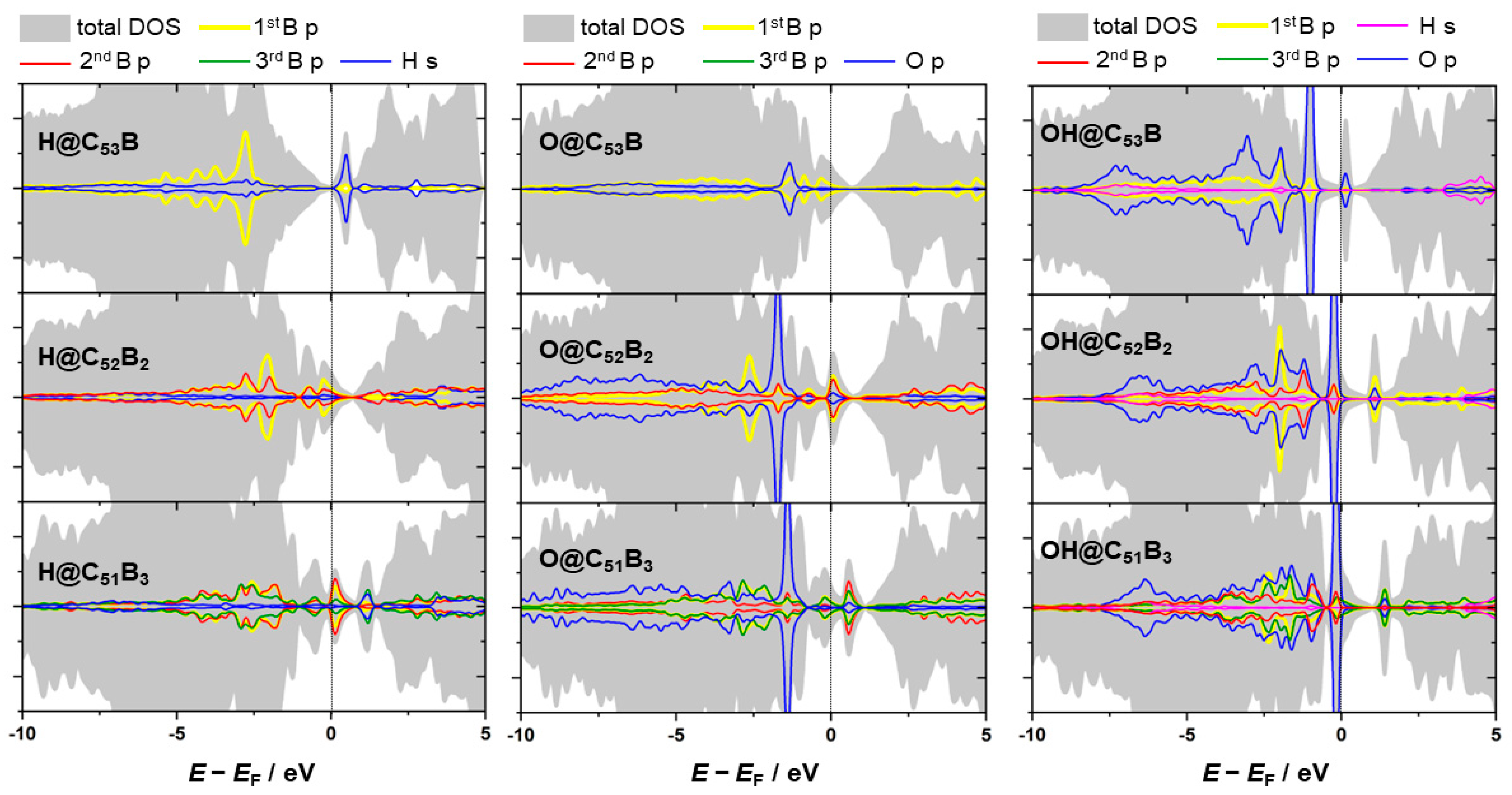
Carbon 09 00092 g003
Figure 3. Electronic structures of the optimized H@ C54−nBn (left), O@C54−nBn (middle) and OH@C54−nBn systems (right). Except for the total DOSs and p states of dopant atoms, the states of the adsorbate are also given as follows: p states of O (cases of Oads and OHads) and s states of H (cases of Hads and OHads).
Figure 3. Electronic structures of the optimized H@ C54−nBn (left), O@C54−nBn (middle) and OH@C54−nBn systems (right). Except for the total DOSs and p states of dopant atoms, the states of the adsorbate are also given as follows: p states of O (cases of Oads and OHads) and s states of H (cases of Hads and OHads).
Carbon 09 00092 g003
Carbon 09 00092 g004
Figure 4. Examples of different outcomes of the metal adsorption on top of the obtained models for the case of Al: Al adsorbed at O@C53B (left), Al at O@C51B3 (middle) and Al at nonoxidized C53B (right).
Figure 4. Examples of different outcomes of the metal adsorption on top of the obtained models for the case of Al: Al adsorbed at O@C53B (left), Al at O@C51B3 (middle) and Al at nonoxidized C53B (right).
Carbon 09 00092 g004
Carbon 09 00092 g005
Figure 5. Charge difference plots for the indicated chosen systems of Na adsorption. Grey isosurfaces indicate charge loss, while the yellow ones indicate charge gain. The isosurface values are ±0.002 eV/Å.
Figure 5. Charge difference plots for the indicated chosen systems of Na adsorption. Grey isosurfaces indicate charge loss, while the yellow ones indicate charge gain. The isosurface values are ±0.002 eV/Å.
Carbon 09 00092 g005
Carbon 09 00092 g006
Figure 6. Adsorption energies of Na (left) and Al (right) in C54−nBn models compared to their cohesive energies (Ecoh), given by dotted lines. The missing columns (Na@C54OH, Al@C54OH and Al@C53BOH) indicate metal–hydroxyde phase separation.
Figure 6. Adsorption energies of Na (left) and Al (right) in C54−nBn models compared to their cohesive energies (Ecoh), given by dotted lines. The missing columns (Na@C54OH, Al@C54OH and Al@C53BOH) indicate metal–hydroxyde phase separation.
Carbon 09 00092 g006
Carbon 09 00092 g007
Figure 7. Electronic structures of sodium adsorption onto nonoxidized and oxidized C54−nBn models. Except for total DOS, the s states of sodium are given, as well as the p states of boron dopant atoms and p states of O (when present, as in the cases of O@ C54−nBn and OH@C54−nBn).
Figure 7. Electronic structures of sodium adsorption onto nonoxidized and oxidized C54−nBn models. Except for total DOS, the s states of sodium are given, as well as the p states of boron dopant atoms and p states of O (when present, as in the cases of O@ C54−nBn and OH@C54−nBn).
Carbon 09 00092 g007
Carbon 09 00092 g008
Figure 8. Differential adsorption energies of m Na atoms (m goes from 1 to 4) onto the investigated substrates. Lacking data points indicate M-O phase separation (e.g., in the case of 2Na@OH@C53B). For comparison, the cohesive energy of Na is given as dotted, grey horizontal lines.
Figure 8. Differential adsorption energies of m Na atoms (m goes from 1 to 4) onto the investigated substrates. Lacking data points indicate M-O phase separation (e.g., in the case of 2Na@OH@C53B). For comparison, the cohesive energy of Na is given as dotted, grey horizontal lines.
Carbon 09 00092 g008
Carbon 09 00092 g009
Figure 9. Optimized structures of 2–4 Na adsorption onto C51B3 (top row), O@C53B (middle row), and O@C52B2 (bottom row).
Figure 9. Optimized structures of 2–4 Na adsorption onto C51B3 (top row), O@C53B (middle row), and O@C52B2 (bottom row).
Carbon 09 00092 g009
Table 1. Binding energies of boron atom (Eb(B)), C-B bond lengths (d(C-B)) and partial Löwdin charges of B (∆q(B)) for the studied C54−nBn models.
Table 1. Binding energies of boron atom (Eb(B)), C-B bond lengths (d(C-B)) and partial Löwdin charges of B (∆q(B)) for the studied C54−nBn models.
ModelEb(B)/eVd(C-B)/Å∆q(B)/e
C53B–12.901.49−0.1
C52B2–12.461.51−0.2
C51B3–12.151.51−0.2
Table 2. Differential adsorption energies of 1-2 Al atoms onto the investigated substrates. Lacking values indicate M-O phase separation. Bolded values indicate that the adsorption energy overcomes Al’s cohesive energy.
Table 2. Differential adsorption energies of 1-2 Al atoms onto the investigated substrates. Lacking values indicate M-O phase separation. Bolded values indicate that the adsorption energy overcomes Al’s cohesive energy.
m(Al)Eads(mth Al@subs)/eV
C53BC52B2C51B3O@
C53B		O@
C52B2		O@
C51B3		OH@
C53B		OH@
C52B2		OH@
C51B3
1−2.71−3.11−2.92−3.93−3.75−2.72−3.80−3.69−4.05
2----−3.70---−2.81
Table 3. Integral adsorption energies (Eads,int) of 2–4 Na atoms on (O/OH)C54−nBn surfaces and corresponding sodiation potentials (E(Na+/Na@subs, bold values), where subs = (O/OH)C54−nBn). “*” indicates that phase separation has occurred, and such systems were not taken into further account.
Table 3. Integral adsorption energies (Eads,int) of 2–4 Na atoms on (O/OH)C54−nBn surfaces and corresponding sodiation potentials (E(Na+/Na@subs, bold values), where subs = (O/OH)C54−nBn). “*” indicates that phase separation has occurred, and such systems were not taken into further account.
Subs2Na3Na4Na
Eads,int
/eV		E0(Na+/Na@subs)
/V		Eads,int
/eV		E0(Na+/Na@subs)
/V		Eads,int
/eV		E0(Na+/Na@subs)
/V
C53B–1.50–2.34****
C52B2–2.13–1.71****
C51B3–2.19–1.65–1.94–1.90–1.78–2.06
O@C53B–1.79–2.05–2.00–1.84–1.82–2.02
O@C52B2–2.10–1.74–1.84–2.00–2.04–1.80
O@C51B3–2.25–1.59–2.05–1.79**
OH@C52B2–2.35–1.49****
OH@C51B3–2.77–1.07–2.41–1.43**
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ritopečki, M.S.; Skorodumova, N.V.; Dobrota, A.S.; Pašti, I.A. Density Functional Theory Analysis of the Impact of Boron Concentration and Surface Oxidation in Boron-Doped Graphene for Sodium and Aluminum Storage. C 2023, 9, 92. https://doi.org/10.3390/c9040092

AMA Style

Ritopečki MS, Skorodumova NV, Dobrota AS, Pašti IA. Density Functional Theory Analysis of the Impact of Boron Concentration and Surface Oxidation in Boron-Doped Graphene for Sodium and Aluminum Storage. C. 2023; 9(4):92. https://doi.org/10.3390/c9040092

Chicago/Turabian Style

Ritopečki, Milica S., Natalia V. Skorodumova, Ana S. Dobrota, and Igor A. Pašti. 2023. "Density Functional Theory Analysis of the Impact of Boron Concentration and Surface Oxidation in Boron-Doped Graphene for Sodium and Aluminum Storage" C 9, no. 4: 92. https://doi.org/10.3390/c9040092

APA Style

Ritopečki, M. S., Skorodumova, N. V., Dobrota, A. S., & Pašti, I. A. (2023). Density Functional Theory Analysis of the Impact of Boron Concentration and Surface Oxidation in Boron-Doped Graphene for Sodium and Aluminum Storage. C, 9(4), 92. https://doi.org/10.3390/c9040092

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop