Abstract
The low selectivity of materials to gases of a similar nature may limit their use as sensors. Knowledge of the adsorption kinetic characteristics of each gas on the surface of the material may enable the ability to identify them. In this work, copper-containing silicon–carbon films were formed using electrochemical deposition on the Al2O3 substrate with interdigitated Cr/Cu/Cr electrodes. These films showed good adsorption characteristics with several different gases. The adsorption kinetics of nitrogen dioxide, sulfur dioxide, and carbon monoxide on the film surface were investigated by the change in the resistivity of the material. Pseudo-first-order and pseudo-second-order kinetics, Elovich, Ritchie, and Webber intraparticle diffusion models were applied. It was found that the largest approximation factor and the lowest Root-Mean-Square Error and Mean Bias Error for all three gases were for the Elovich model. The advantages of silicon–carbon copper-containing films for gas sensor applications were shown. An algorithm for gas recognition was proposed based on the dependence of the change in the resistivity of the material under stepwise gas exposure. It was found that parameters such as the values of the extrema of the first and second derivatives of the R vs. t dependence during adsorption and the slope of R vs. t dependence in the Elovich coordinates are responsible for gas identification among several one-nature gases.
1. Introduction
Silicon–carbon films and their composites with enhanced sorption, adhesion, and mechanical properties are promising materials for gas sensor applications [1,2,3,4,5,6,7,8]. Silicon carbide gas sensors can detect a range of gases—NO, O2, CH4, NH3, H2S, CO, and SO2—by varying the composition of the composite gas-sensing layer, operating temperature, and design.
Due to cross-sensitivity, the selectivity problem is worthy of serious research for the wider use of such materials. There are a few approaches to solving this problem, such as the use of temperature modulation [9,10,11,12,13], surface decoration [14], the doping of materials [15,16,17,18,19], the use of sensor arrays (e-nose) [20], machine-learning methods [21,22,23,24], and various software solutions for signal processing [25,26,27].
The use of several characteristics of the response-curve transition part of the stepwise supply of the gas mixture to the sensor can be a promising approach to ensure selectivity since this part of the response reflects the mechanism and kinetics of adsorption. The adsorption mechanism and kinetics of different gases on the same surface may be different. One of the first attempts to use transition parameters was made by Müller and Lange, who showed that the identification of individual gases is possible if more than one parameter from the response curve is used [28].
In other studies, responses at different periods [29,30], combinations of responses, integrals, derived responses [31,32], and response-curve modeling using curve-fitting algorithms [33] were used to predict or identify gas mixture or odor content.
The studies showed that there is a relationship between derivative extrema and gas concentration; the time-derived signal is stable for short exposure times [34,35] and has a stable baseline [36,37] even in the presence of signal drift. Therefore, to apply this approach, a sharp stepwise effect of gas is necessary [38,39,40]. The response dynamics section is usually not used for processing during desorption [41].
To describe the kinetics of gas adsorption, researchers use various models, including pseudo-first-order and pseudo-second-order models, as well as Langmuir, intraparticle diffusion of Weber, Elovich, and Ritchie models [42,43,44,45,46]. An optimally selected model can be an identifier for an adsorbate–adsorbent pair for a particular material. This material can be used to estimate the concentration of several gases.
Thus, this work aimed to study the adsorption kinetics of NO2, CO, and SO2 gases on the surface of silicon–carbon copper-containing films and to identify the characteristics of the transition part of the response during a stepped gas supply. A change in the resistance of the material was used as the response. It was also necessary to determine the most optimal model from the following list: pseudo-first-order and pseudo-second-order kinetics models and the Elovich, Ritchie, and Weber models of intraparticle diffusion to develop a method for gas identification from a known list of one-type gases and to estimate the concentration of each gas.
This paper shows that it is possible to identify similar gases with silicon–carbon–copper sensors by processing the response based on a fitted adsorption kinetics model. Previously, the kinetics of NO2, CO, and SO2 adsorption in the same concentration range on the materials being studied and the adsorption mechanisms have not been investigated.
2. Materials and Methods
A gas-sensitive layer was formed on interdigitated electrodes using the electrochemical deposition technique [47,48,49]. In the first stage, the deposition of the pure silicon–carbon film from methanol and hexamethyldisilazane (HMDSN) (ratio 9:1) solution was carried out for 40 min at 150 V. In the second stage, copper acetate (0.14 wt.%) was added to the electrolyte, and the film deposition continued for 5 min at 50 V. Finally, a methanol/HMDSN (ratio 9:1) solution was deposited onto the silicon–carbon film layer for 40 min at 150 V. Then, the films were annealed at 200 °C for 2 h.
Interdigitated electrodes were formed via the vacuum vapor deposition of Cr/Cu/Cr (hCr = 15 nm, hCu = 2 μm) layers on the Al2O3 substrate with the following laser demetallization (MicroSET-M Granite RA, Russia): step between electrodes—50 μm; electrode width—50 μm. The laser method of topology formation was used to reduce the cost of the sensor manufacturing (modern laser equipment allows the formation of a conductor–gap topology of up to 6–20 μm without using the liquid methods of classical photolithography).
The adsorption experiments were carried out in a test chamber equipped with a heating element, as shown in Figure 1. The gas sensor was heated by a DC power source for the purpose of maintaining the required temperature of 100 ± 1 °C. Measurements were made by injecting a mixture of air with different gas concentrations (the test gas met the requirements of ISO 6142-1: 2015) into the chamber. The gas mixture was generated by mixing test gases (NO2, CO, and SO2) with the synthetic air (Microgaz-FM02 installation (Russia)) to obtain different concentrations in the range of 10–50 ppm. A Keithley 2450 Source Meter connected to a computer was used as a signal receiver. The gas mixture was supplied forcibly, while the sensor resistance reached 10% of the initial value.
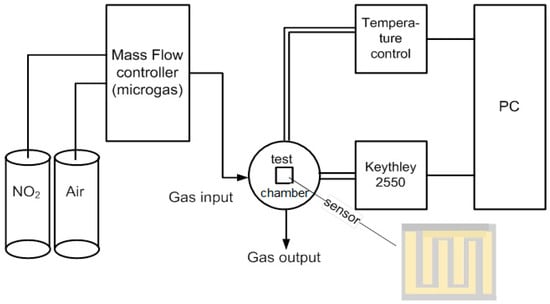
Figure 1.
Schematic diagram of the experimental setup [32].
The gas exposure reversibly changed the film resistance. After purging the test chamber with the synthetic air, the film resistance returned to the initial value. The initial processing of resistance data was carried out as reported in [32]. Gas mixtures were injected cyclically. The cycle included the sequential supply of a gas mixture and purging with synthetic air for each type of gas from higher to lower concentrations. Three or more cycles were done for each gas type. There were no breaks between cycles. After the end of the cycle with a concentration of 10 ppm, the next cycle immediately began with a concentration of 50 ppm. Averaging was performed for each kinetic parameter.
The sensor response was normalized according to Equation (1):
where R0 is the film resistance before the gas exposure and R(t) is the film resistance under the gas exposure at time.
Next, graphs of the first derivative S′(t) and the second derivative S″(t) of the response were plotted, and the minimums and maximums were determined, respectively. The values of the extrema were used as parameters characterizing the “rate” and “rate of change” of the adsorption process. The preferential adsorption mechanism was determined by comparison with known kinetic models.
Kinetic equations of pseudo-first and pseudo-second order, Elovich, Ritchie models, and intraparticle Webber diffusion models were used to simulate the dynamics of the gas sensor response during adsorption [42].
Pseudo-first order kinetic Equation (2):
where K1 is a pseudo-first-order adsorption rate constant; qe is the equilibrium amount of adsorbate; and qt is the amount of adsorbate at time t. K1 is found to be the slope of the straight line from the graph of ln(qe − qt) vs. t.
ln(qe − qt) = ln qe − K1 × t,
Pseudo-second-order kinetic Equation (3):
where K2—pseudo-second-order adsorption rate constant. The K2 value is calculated from the slope of the linear curve of the t/qt vs. t.
t/qt = 1/(K2 × qe2) + t/qe,
Equation (4) of adsorption kinetics using the Weber model is
where Kdif is the constant diffusion rate inside the particles, and the C values provide information about the thickness of the boundary layer. The parameters Kdif and C are calculated using the linear graph of qt vs. t1/2. The presence of several linear regions in the plots indicates that adsorption is affected not only by intraparticle diffusion.
qt = Kdif × t1⁄2 + C,
The kinetic Equation (5), according to the Elovich model, describes adsorption on a heterogeneous surface with exponential growth of the adsorption sites.
where α is the initial adsorption rate constant, and β is a constant associated with the measure of the potential barrier for sequential adsorption. The constants of the equation are calculated from the slope and intersection of the qt vs. lnt linear plot, respectively.
qt = 1/β × ln(αβ) + 1/β × lnt,
The Ritchie model assumes that the adsorption rate depends on unoccupied adsorption sites and that the adsorption process is a second-order reaction [43]. It is considered to be an alternative to the Elovich model. The integral form of the kinetics Equation (6) is
where α is the adsorption rate constant; graph (1/qt) vs. (1/t) must be a straight line.
1/qt = 1/(α × qe t) + 1/qe,
In our case, the value of qt is proportional to the value of S, ΔS = 1 − S(t).
To implement the gas-identification algorithm, the MATLAB R2023a software complex was applied. Three parameter values called “informative features” were estimated for each gas and all gas concentrations: (1) extreme of the first derivative; (2) extreme of the second derivative; (3) the slope coefficient of the approximating direct response in the coordinates of the Elovich equation. These parameters characterized the response dynamics of the sensor based on a copper-containing silicon–carbon film to the stepped effect of gas: The coordinates of the three points were determined in the space of informative features. The least-squares method was used to build lines through the found points in space.
The lines are represented by the following Equation (7):
where p1, p2, and p3 are the coordinates of the guide vector not equal to zero. A unique straight line in the operating concentration range was plotted for each gas.
Identification was supposed to be carried out by the minimum distance from the measurement point of an unknown gas in three-dimensional space to a straight line characterizing one of the gases NO2, CO, and SO2.
Let M1 (x1, y1, z1) be a point lying on a line, then the distance from the point M0 (x0, y0, z0) to the line is found by Formula (8):
3. Results and Discussion
A series of experiments showed a stable response of sensors based on a copper-containing silicon–carbon film. Typical dependencies of resistance change on time under gas mixture step exposure are shown in Figure 2 (Real response—Figure 2a–c; reduced response—Figure 2d–f.
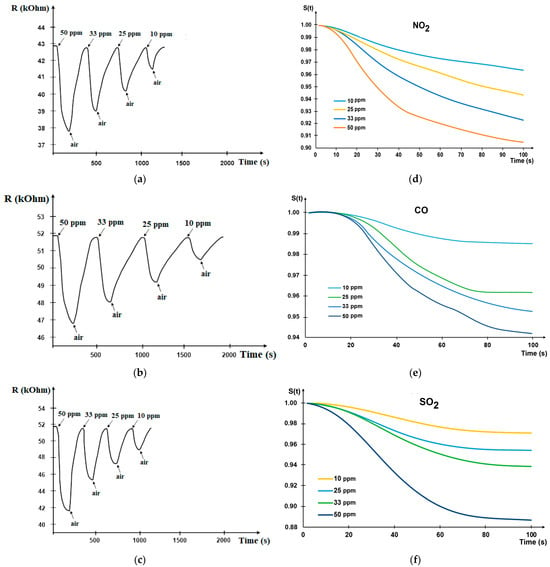
Figure 2.
The real-time sensor response to various concentrations: (a) NO2; (b) CO; (c) SO2. Reduced response of gas sensor under gas exposure: (d) NO2; (e) CO; (f) SO2.
The sensor response to NO2 gas is higher due to the electronic structure: the number of electrons taking part in the adsorption interactions is higher.
The kinetics of the first S′(t) and the second derivative S″(t) of the gas sensor response are presented in Figure 3. It can be noted that the minimum and maximum points differ depending on the concentration of each gas.
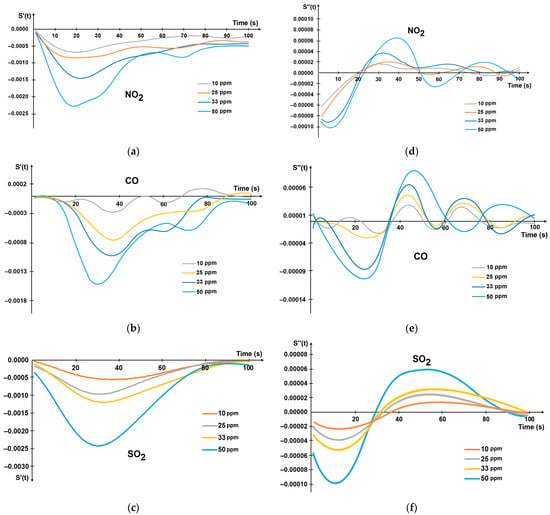
Figure 3.
The kinetics of the first derivative of gas sensor response S(t) at different concentrations: (a) NO2; (b) CO; (c) SO2. The kinetics of the second derivative S(t) at different concentrations: (d) NO2; (e) CO; (f) SO2.
The adsorption equilibrium time occurred at 100 ± 10 s for all three gases.
The time to reach the extremes of the first and second derivative of the response varies depending on the gas, but in all cases, it does not exceed 40 s and 60 s for the minimum of the first derivative and the maximum of the second derivative, respectively. The important fact is that the extremes of sensor response derivatives do not depend on the possible resistance drift of the sensor material caused by its aging or external effects. Since there are significant differences between the values of the extrema for each gas and the patterns when the concentration changes, it is advisable to use these parameters as informative features characterizing the gas.
In the next step, experimentally obtained graphs of the sensor response to the gas exposure were checked for compliance with known models.
Figure 4 shows plots based on the experimental data obtained during the exposure of three gases (33 ppm) in coordinates corresponding to kinetic models: pseudo-first order (Figure 4a), pseudo-second order (Figure 4b), intraparticle diffusion model (Figure 4c), Elovich model (Figure 4d) and Ritchie model (Figure 4e). Linear sections are observed in all the plots.
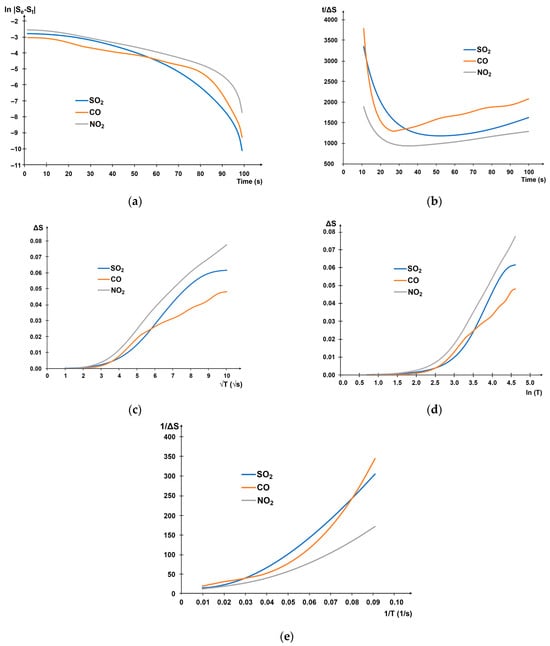
Figure 4.
Kinetic adsorption in coordinates corresponding to kinetic models: (a) pseudo-first order, (b) pseudo-second order, (c) intraparticle diffusion model, (d) Elovich model, and (e) Ritchie model.
Table 1 shows the equations of approximating curves and the determinative coefficients (R2), Root-Mean-Square Error (RMSE), and Mean Bias Error (MBE) for kinetics response experiments under study.

Table 1.
Parameters of kinetic models.
The same calculations were also done for 10, 25, and 50 ppm gas concentrations. As a result, it was shown that the intraparticle diffusion and Elovich models are most suitable for describing the experimental data: determination coefficients R2 are higher than 0.9, and an MBE and RMSE are minimum. However, unlike the intraparticle diffusion model, the time interval between the minimum of the first derivative (S′) and the maximum of the second derivative (S″), in which the linearization is maximal, was determined for the Elovich model. Table 1 shows the example for 33 ppm gas concentration. The surface of the adsorbing material is porous, so a high degree of linearity for the Weber model is evident, but the time intervals with the highest degree of linearity were found to be different for the three types of gases. The pseudo-second-order model showed the lowest coefficient of determination, indicating the only physical adsorption process without chemical interaction [50].
In general, since no model has a graph of all-linear kinetics over the entire range, it can be noted that several factors influence the adsorption process. The linearity of the plots in the coordinates of the models at a particular time interval shows that it is a moment when the adsorption mechanism for this model prevails, and the factor that controls the kinetic process can be assumed. The Elovich model assumes multilayer adsorption on energetically heterogeneous active sites.
The heterogeneity of the active sites leads to different activation energies of chemisorption, which may be due to the combined composition of the sensitive layer: the presence of carbide, carbon, and copper-containing phases. As the gas concentration increases, the slope of the approximating straight line in Elovich coordinates increases, which is proportional to the increase in the value of the β and indicates an increase in the occupancy of the surface.
A change in the predominant adsorption mechanism for the test materials may be due to a change in adsorption rates. Therefore, a high degree of linearity in the time interval between the extremes of the response derivatives is observed.
The detected features, characterizing the adsorption of different gases on the same surface, were used to identify gases by one sensor. In this study, gas sensors based on silicon–carbon materials doped with copper and showed response to the one-nature gases CO, SO2, and NO2 were investigated.
The following algorithm was developed for gas identification:
- (1)
- preliminary processing of data coming from the sensor, including signal filtering; normalization of resistance values; construction of auxiliary graphs of the normalized signal, the first derivative, and the second derivative in the coordinates of the Elovich equation;
- (2)
- finding informative features: the values of the extrema of the first and second derivatives of the normalized response, the slope of the approximating line in the coordinates of the Elovich equation in the time interval between the extrema of the first and second derivatives (in order to determine the response section that will be used to construct the equation in the coordinates Elovich; determination the time at which the extrema of the first and second derivatives of the response are observed);
- (3)
- compiling an array of data on the values of three informative features for each reference concentration in the operating range of the sensor for each gas;
- (4)
- normalization of the values of the informative features by the maximum value and construction of straight lines characterizing gas in the space of informative features, using the method of least squares in space;
- (5)
- for identification of an unknown gas, data from the sensor is processed according to paragraphs 1 and 2 and are normalized by the same coefficients as when constructing the straight lines characterizing gas in the space of informative features;
- (6)
- determination of a point in a multidimensional space corresponding to a dimension;
- (7)
- calculation and comparison of the minimum distances to all straight lines characterizing gas in space of informative features;
- (8)
- determination of the gas type by the minimum distance to the straight lines characterizing gas in space of informative features;
- (9)
- determination of gas concentration based on the calibration dependence of the sensor for the recognized gas;
- (10)
- output of results.
Based on experimental data of five reference concentrations in the range from 10 to 50 ppm, points were built in the multidimensional space of parameters that had been found by the sensor response to gases: the minimum of the first derivative, the maximum of the second derivative, and the slope of the approximating line in the Elovich equation coordinates. To avoid an error in estimating the distance between points in space, the parameters were normalized by the maximum value (Equation (9)):
Xj = Xi/Xmax; Yj = Yi/Ymax; Zj = Zi/Zmax
Applying the least-squares method to a set of five points of the corresponding measurement, we obtain canonical equations for straight lines, characterizing gases.
SO2:
(X − 0.1630)/0.3139 = (Y − 0.1678)/0.3121 = (Z − 0.2088)/0.2069.
NO2:
(X − 0.2236)/0.1322 = (Y − 0.2685)/0.2685 = (Z − 0.2008)/0.2997.
CO:
(X − 0.0903)/0.1487 = (Y − 0.1834)/0.2148 = (Z − 0.3803)/0.1837.
At the same time, partial determination coefficients are calculated:
- -
- for SO2 R21 = 0.9999; R22 = 0.9433;
- -
- for NO2 R21 = 0.9516; R22 = 0.9043;
- -
- for CO R21 = 0.9867; R22 = 0.9563.
A high degree of linearity of approximating curves is observed. Figure 5 shows the obtained straight lines in the space of the response dynamics parameters. Such a curve is unique for each gas. The straight lines do not cross each other in the concentration range under study. The gas-identification algorithm is also shown in Figure 5. The M0 point is based on the sensor response parameters to the unknown gas. The distances d1, d2, and d3 are calculated from point M0 to the lines characterizing the gases CO, SO2, and NO2. Gas is identified by the shortest distance. After the gas becomes known, its concentration can be found using calibration curves pre-constructed for each gas by reference concentrations. In this study, we use calibration curves based on the extremes of the first and second derivatives, as shown in [32].
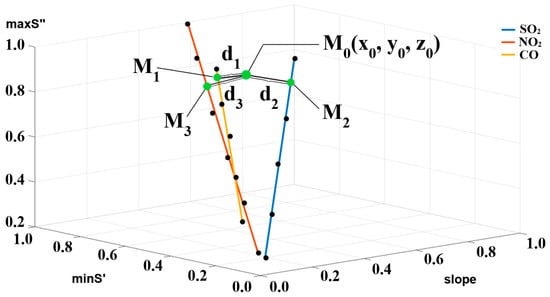
Figure 5.
Straight lines characterizing gas in the space of response dynamics parameters. Green points—projection of the point M0 onto characteristic lines; black points—experimental points.
A series of experiments with gas concentrations different from the reference one used in the plotting of the straight lines showed 100% gas identification. Further quantification of the gas concentration by the sensors being studied was carried out with a relative error of not more than 5%. Results are presented in Table 2.

Table 2.
The quantitative determination of gas concentration.
4. Conclusions
A kinetic study has shown that the adsorption of nitrogen dioxide, sulfur dioxide, and carbon monoxide on the surface of copper-containing silicon–carbon films is best described by the Webber intraparticle diffusion and the Elovich models. It was found that in the time interval between the minimum of the first derivative and the maximum of the second derivative for sensor response kinetics, the R2 of the approximating curve in the Elovich equation coordinates is close to 1, which shows the predominance of the multilayer adsorption mechanism on energetically heterogeneous centers. An algorithm for gas recognition was proposed based on the dependence of the change in the resistivity of the material under stepwise gas exposure. It was found that gas identification is possible using the extreme values of the first and second derivatives of the R vs. t dependence during gas adsorption, as well as the slope of this dependence in Elovich coordinates in the working concentrations range. If we take these parameters and build a dependence in the parametric space of these characteristics at points corresponding to different concentrations, then it will be a straight and characteristic line of each gas. Straight lines for different gases will not intersect, and the gas can be identified by the shortest distance from the corresponding point to the line.
Author Contributions
Conceptualization, N.K.P.; methodology, N.K.P. and S.P.N.; software, N.K.P.; validation, N.K.P., S.P.N. and T.N.M.; formal analysis, N.K.P. and S.P.N.; investigation, S.P.N. and T.S.M.; resources, N.K.P., S.P.N. and T.N.M.; data curation, S.P.N.; writing—original draft preparation, N.K.P. and S.P.N.; writing—review and editing, T.N.M., T.S.M. and S.P.N.; visualization, S.P.N. and T.S.M.; supervision, N.K.P.; project administration, N.K.P.; funding acquisition, N.K.P. and T.N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was supported by the Ministry of Science and Higher Education of the Russian Federation in the framework of the state task in the field of scientific activity, grant number FENW-2022-0001.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, X.; Xun, Q.; Li, Z.; Du, S. Silicon carbide converters and MEMS devices for high-temperature power electronics: A critical review. Micromachines 2019, 10, 406. [Google Scholar] [CrossRef]
- Platonov, V.B.; Rumyantseva, M.N.; Frolov, A.S.; Yapryntsev, A.D.; Gaskov, A.M. High-temperature resistive gas sensors based on ZnO/SiC nanocomposites. Beilstein J. Nanotechnol. 2019, 10, 1537–1547. [Google Scholar] [CrossRef]
- Sasago, Y.; Nakamura, H.; Odaka, T.; Isobe, A.; Komatsu, S.; Nakamura, Y.; Yamawaki, T.; Yorita, C.; Ushifusa, N.; Yoshikawa, Y.; et al. SiC-FET gas sensor for detecting sub-ppm gas concentrations. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 151–158. [Google Scholar] [CrossRef]
- Andersson, M.; Bastuck, M.; Huotari, J.; Spetz, A.L.; Lappalainen, J.; Schütze, A.; Puglisi, D. SiC-FET sensors for selective and quantitative detection of VOCs down to ppb level. Procedia Eng. 2016, 168, 216–220. [Google Scholar] [CrossRef]
- Gaiardo, A.; Bellutti, P.; Fabbri, B.; Gherardi, S.; Giberti, A.; Guidi, V.; Landini, N.; Malagù, C.; Pepponi, N.; Valt, M.; et al. Chemoresistive gas sensor based on SiC thick film: Possible distinctive sensing properties between H2S and SO2. Procedia Eng. 2016, 168, 276–279. [Google Scholar] [CrossRef]
- Semenov, A.V.; Lubov, D.V.; Kozlovskyi, A.A. The chemresistive properties of SiC nanocrystalline films with different conductivity type. J. Sens. 2020, 2020, 7587314. [Google Scholar] [CrossRef]
- Sun, L.; Han, C.; Wu, N.; Wang, B.; Wang, Y. High temperature gas sensing performances of silicon carbide nanosheets with an n–p conductivity transition. RSC Adv. 2018, 8, 13697–13707. [Google Scholar] [CrossRef]
- Kim, S.; Choi, J.; Jung, M. Silicon carbide-based hydrogen gas sensors for high-temperature applications. Sensors 2013, 13, 13575–13583. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, Y.; Meng, X.; Zhang, Z.; Cao, J. A gas sensor based on Ag-modified ZnO flower-like microspheres: Temperature-modulated dual selectivity to CO and CH4. Surf. Interfaces 2021, 24, 101110. [Google Scholar] [CrossRef]
- Ding, H.; Ge, H.F.; Liu, J.H. High performance of gas identification by wavelet transform-based fast feature extraction from temperature modulated semiconductor gas sensors. Sens. Actuators B Chem. 2005, 107, 749–755. [Google Scholar] [CrossRef]
- Roth, M.; Hartinger, R.; Faul, R.; Endres, H.-E. Drift reduction of organic coated gas-sensors by temperature modulation. Sens. Actuators B Chem. 1996, 36, 358–362. [Google Scholar] [CrossRef]
- Martinelli, E.; Polese, D.; Catini, A.; D’Amico, A.; Di Natale, C. Self-adapted temperature modulation in metal-oxide semiconductor gas sensors. Sens. Actuators B Chem. 2012, 161, 534–541. [Google Scholar] [CrossRef]
- Lee, A.P.; Reedy, B.J. Temperature modulation in semiconductor gas sensing. Sens. Actuators B Chem. 1999, 60, 35–42. [Google Scholar] [CrossRef]
- Sun, K.; Zhan, G.; Zhang, L.; Wang, Z.; Lin, S. Highly sensitive NO2 gas sensor based on ZnO nanoarray modulated by oxygen vacancy with Ce doping. Sens. Actuators B Chem. 2023, 379, 133294. [Google Scholar] [CrossRef]
- Ghosh, R.; Santra, S.; Ray, S.K.; Guha, P.K. Pt-functionalized reduced graphene oxide for excellent hydrogen sensing at room temperature. Appl. Phys. Lett. 2015, 107, 153102. [Google Scholar] [CrossRef]
- Manna, B.; Chakrabarti, I.; Guha, P.K. Platinum nanoparticles decorated graphene oxide based resistive device for enhanced formaldehyde sensing: First-principle study and its experimental correlation. IEEE Trans. Electron. Dev. 2019, 66, 1942–1949. [Google Scholar] [CrossRef]
- Kim, T.-H.; Jeong, S.-Y.; Moon, Y.K.; Lee, J.-H. Dual-mode gas sensor for ultrasensitive and highly selective detection of xylene and toluene using Nb-doped NiO hollow spheres. Sens. Actuators B Chem. 2019, 301, 127140. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, C.; De, Q.; Gu, F.; Han, D. One-step synthesis of Co-doped In2O3 nanorods for high response of formaldehyde sensor at low temperature. ACS Sens. 2018, 3, 468–475. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Neri, G. Nanostructured materials for room-temperature gas sensors. Adv. Mater. 2016, 28, 795–831. [Google Scholar] [CrossRef]
- Anisimov, D.S.; Chekusova, V.P.; Trul, A.A.; Abramov, A.A.; Borshchev, O.V.; Agina, E.V.; Ponomarenko, S.A. Fully integrated ultra-sensitive electronic nose based on organic field-effect transistors. Sci. Rep. 2021, 11, 10683. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, J.; Du, T.; Zhu, Z.; Zhang, J.; Liu, Q. A gas sensor array for the simultaneous detection of multiple VOCs. Sci. Rep. 2017, 7, 1960. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.; Li, W.; Yang, X.; Wu, Y.; Wang, D.; Yang, A.; Yuan, H.; Wang, X.; Li, Y.; Rong, M. Identification of gas mixtures via sensor array combining with neural networks. Sens. Actuators B Chem. 2021, 39, 129090. [Google Scholar] [CrossRef]
- Yaqoob, U.; Younis, M.I. Chemical Gas Sensors: Recent Developments, Challenges, and the Potential of Machine Learning—A Review. Sensors 2021, 21, 2877. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-S.; Li, H.-Y.; Kim, B.-Y.; Jo, Y.-M.; Byun, H.-G.; Hwang, I.-S.; Abdel-Hady, F.; Wazzan, A.A.; Lee, J.H. Discriminative detection of indoor volatile organic compounds using a sensor array based on pure and Fe-doped In2O3 nanofibers. Sens. Actuators B. Chem. 2019, 285, 193–200. [Google Scholar] [CrossRef]
- Acharyya, S.; Nag, S.; Guha, P.K. Selective detection of VOCs with WO3 nanoplates based single chemiresistive sensor device using machine learning algorithms. IEEE Sens. J. 2021, 21, 5771–5778. [Google Scholar] [CrossRef]
- Vergara, A.; Llobet, E.; Martinelli, E.; Di Natale, C.; D’Amico, A.; Correig, X. Feature extraction of metal oxide gas sensors using dynamic moments. Sens. Actuators B Chem. 2007, 122, 219–226. [Google Scholar] [CrossRef]
- Rodner, M.; Bahonjic, J.; Mathisen, M.; Gunnarsson, R.; Ekeroth, S.; Helmersson, U.; Ivanov, I.G.; Yakimova, R.; Eriksson, J. Performance tuning of gas sensors based on epitaxial graphene on silicon carbide. Mater. Design. 2018, 153, 153–158. [Google Scholar] [CrossRef]
- Nanto, H.; Tsubakino, S.; Ikeda, M.; Endo, F. Identification of aromas from wine using quartz-resonator gas sensors in conjunction with neural-network analysis. Sens. Actuators B Chem. 1995, 25, 794–796. [Google Scholar] [CrossRef]
- Endres, H.E.; Go, W.; Jander, H.D.; Drost, S.; Sberveglieri, G.; Faglia, G.; Perego, C. A systematic investigation on the use of time-dependent sensor signals in signal-processing techniques. Sens. Actuators B Chem. 1995, 25, 785–789. [Google Scholar] [CrossRef]
- Hongmei, W.; Lishi, W.; Wanli, X.; Baogni, Z.; Chengjun, L.; Jianxing, F. An application of artificical neural networks. Simultaneous determination of the concentration of sulfur dioxide and relative humidity with a single coated piezoelectric crystal. Anal. Chem. 1997, 69, 699–702. [Google Scholar] [CrossRef]
- Du, H.; Xie, G.; Su, Y.; Tai, H.; Du, X.; Yu, H.; Zhang, Q. A new model and its application for the dynamic response of RGO resistive gas sensor. Sensors 2019, 19, 889. [Google Scholar] [CrossRef] [PubMed]
- Plugotarenko, N.K.; Novikov, S.P.; Myasoedova, T.N.; Mikhailova, T.S. Comparative Analysis of Derivative Parameters of Chemoresistive Sensor Signals for Gas Concentration Estimation. Chemosensors 2022, 10, 126. [Google Scholar] [CrossRef]
- Somboon, P.; Wyszynski, B.; Nakamoto, T. Realization of recording a wide range of odor by utilizing both of transient and steady-state sensor responses in recording process. Sens. Actuators B Chem. 2007, 124, 557–563. [Google Scholar] [CrossRef]
- Newton, M.I.; Starke, T.K.H.; Willis, M.R.; McHale, G. NO2 detection at room temperature with copper phthalocyanine thin film devices. Sens. Actuators B Chem. 2000, 67, 307–311. [Google Scholar] [CrossRef]
- Mazein, P.; Zimmermann, C.; Rebière, D.; Déjous, C.; Pistré, J.; Planade, R. Dynamic analysis of Love waves sensors responses: Application to organophosphorus compounds in dry and wet air. Sens. Actuators B Chem. 2003, 95, 51–57. [Google Scholar] [CrossRef]
- Rodner, M.; Eriksson, J. First-order time-derivative readout of epitaxial graphene-based gas sensors for fast analyte determination. Sens. Actuators Rep. 2020, 2, 100012. [Google Scholar] [CrossRef]
- Marco, S.; Gutierrez-Galvez, A. Signal and data processing for machine olfaction and chemical sensing: A review. IEEE Sens. J. 2012, 12, 3189–3214. [Google Scholar] [CrossRef]
- Rakow, N.A.; Suslick, K.S. A colorimetric sensor array for odour visualization. Nature 2000, 406, 710–713. [Google Scholar] [CrossRef]
- Arbayani Zaidan, M.; Hossein Motlagh, N.; Fung, P.L.; Khalaf, A.S.; Matsumi, Y.; Ding, A.; Tarkoma, S.; Petäjä, T.; Kulmala, M.; Hussein, T. Intelligent air pollution sensors calibration for extreme events and drifts monitoring. IEEE Trans. Ind. Inform. 2023, 19, 1366–1379. [Google Scholar] [CrossRef]
- Yang, L.; Ji, H.; Meng, C.; Li, Y.; Zheng, G.; Chen, X.; Niu, G.; Yan, J.; Xue, Y.; Guo, S.; et al. Intrinsically breathable and flexible NO2 gas sensors produced by laser direct writing of self-assembled block copolymers. Am. Chem. Soc. 2022, 14–15, 17818–17825. [Google Scholar] [CrossRef]
- Acharyya, S.; Nag, S.; Guha, P.K. Ultra-selective tin oxide-based chemiresistive gas sensor employing signal transform and machine learning techniques. Anal. Chim. Acta 2022, 1217, 339996. [Google Scholar] [CrossRef] [PubMed]
- El-Desouky, M.G.; El-Bindary, A.A.; El-Bindary, M.A. Low-Temperature Adsorption Study of Carbon Dioxide on Porous Magnetite Nanospheres Iron Oxide. Biointerface Res. Appl. Chem. 2021, 12, 6252–6268. [Google Scholar]
- Urfa, Y.; Çorumlu, V.; Altındal, A. Gamma ray irradiation dose dependent methanol sensing with ZnO nanoparticles. Mater. Chem. Phys. 2021, 264, 124473. [Google Scholar] [CrossRef]
- Xie, T.; Xie, G.; Du, H.; Su, Y.; Ye, Z.; Chen, Y.; Jiang, Y. Two novel methods for evaluating the performance of OTFT gas sensors. Sens. Actuators B Chem. 2016, 230, 176–183. [Google Scholar] [CrossRef]
- Myasoedova, T.N.; Plugotarenko, N.K.; Moiseeva, T.A. Copper-containing films obtained by the simple citrate sol–gel route for NO2 detection: Adsorption and kinetic study. Chemosensors 2020, 8, 79. [Google Scholar] [CrossRef]
- Saleh, T.A. Chapter 2—Adsorption technology and surface science. Interface Sci. Technol. 2022, 34, 39–64. [Google Scholar]
- Mikhailova, T.S.; Grigoryev, M.N.; Myasoedova, T.N. The two-stage electrochemical deposition of a manganese-doped silicon-carbon film onto the silicon (100) substrate. J. Phys. Conf. Ser. 2019, 1410, 012027. [Google Scholar] [CrossRef]
- Plugotarenko, N.K.; Myasoedova, T.N.; Grigoryev, M.N.; Mikhailova, T.S. Electrochemical deposition of silicon-carbon films: A study on the nucleation and growth mechanism. Nanomaterials 2019, 9, 1754. [Google Scholar] [CrossRef]
- Myasoedova, T.N.; Grigoryev, M.N.; Plugotarenko, N.K.; Mikhailova, T.S. Fabrication of gas-sensor chips based on silicon-carbon films obtained by electrochemical deposition. Chemosensors 2019, 7, 52. [Google Scholar] [CrossRef]
- Hassan, N.; Shahat, A.; El-Didamony, A.; El-Desouky, M.; El-Bindary, A. Equilibrium, kinetic and thermodynamic studies of adsorption of cationic dyes from aqueous solution using ZIF-8. Moroc. J. Chem. 2020, 8, 627–637. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).