Novel Ultrahard Extended Hexagonal C10, C14 and C18 Allotropes with Mixed sp2/sp3 Hybridizations: Crystal Chemistry and Ab Initio Investigations

Matar, Samir F.; Eyert, Volker; Solozhenko, Vladimir L.

doi:10.3390/c9010011

Open AccessArticle

Novel Ultrahard Extended Hexagonal C₁₀, C₁₄ and C₁₈ Allotropes with Mixed sp²/sp³ Hybridizations: Crystal Chemistry and Ab Initio Investigations

by

Samir F. Matar

¹

,

Volker Eyert

²

and

Vladimir L. Solozhenko

^3,*

¹

CMMS, Lebanese German University (LGU), Jounieh P.O. Box 206, Lebanon

²

Materials Design SARL, 92120 Montrouge, France

³

LSPM–CNRS, Université Sorbonne Paris Nord, 93430 Villetaneuse, France

^*

Author to whom correspondence should be addressed.

C 2023, 9(1), 11; https://doi.org/10.3390/c9010011

Submission received: 30 December 2022 / Revised: 11 January 2023 / Accepted: 16 January 2023 / Published: 18 January 2023

(This article belongs to the Section Carbon Materials and Carbon Allotropes)

Download

Browse Figures

Versions Notes

Abstract

:

Based on 4H, 6H and 8H diamond polytypes, novel extended lattice allotropes C₁₀, C₁₄ and C₁₈ characterized by mixed sp³/sp² carbon hybridizations were devised based on crystal chemistry rationale and first-principles calculations of the ground state structures and energy derived properties: mechanical, dynamic (phonons), and electronic band structure. The novel allotropes were found increasingly cohesive along the series, with cohesive energy values approaching those of diamond polytypes. Regarding mechanical properties, C₁₀, C₁₄, and C₁₈ were found ultrahard with Vickers hardness slightly below that of diamond. All of them are dynamically stable, with positive phonon frequencies reaching maxima higher than in diamond due to the stretching modes of C=C=C linear units. The electronic band structures expectedly reveal the insulating character of all three diamond polytypes and the conductive character of the hybrid allotropes. From the analysis of the bands crossing the Fermi level, a nesting Fermi surface was identified, allowing us to predict potential superconductive properties.

Keywords:

diamond; polytypes; hardness; phonons; electron structure; hybridization; DFT

1. Introduction

Diamond is mainly known in the cubic form (space group Fd-3m); a less common form is hexagonal one (space group P6₃/mmc) called lonsdaleite. Such structures are also adopted by silicon carbide SiC known to crystallize in different structures called polytypes. This appellation pertains to the stacking of layers generically named A/B/C: AB in 2H (2 layers; hexagonal system), ABC in 3C (3 layers; cubic system), ABCB in 4H (4 layers; hexagonal system), ABCACB 6H (6 layers; hexagonal system) [1]. Si and C are isoelectronic regarding the external valence shell, and diamond possesses similar polytypes such as best known 3C and 2H. The closeness of electronic structures, and despite the larger size of Si compared to C, nanostructured diamond polytypes were epitaxially grown on silicon [2]. Other diamond polytypes (8H and 9R; R for rhombohedral) were identified with calculated X-ray diffraction data published by Ownby et al. [3]. Later, first-principles studies of diamond polytypes were performed by Wen et al. [4], indicating the absence of phase transitions between them.

In 3C and 2H diamond polytypes, the carbon hybridization is purely tetrahedral sp³, characterizing ultrahard large band gap insulating electronic systems. The electronic structure properties can be modified by introducing trigonal C(sp²). Indeed, recent works showed that nanodiamonds with sp²/sp³ mixed carbon hybridization play an important role in the design of advanced electronic materials [5]. Zhai et al. showed progress in the electrochemistry of hybrid diamond/sp²-C nanostructures [6]. As for other carbon hybridizations, mixed sp³-sp¹ were recently identified in superhard “yne-diamond” categorized as semi-metallic [7].

In this context, a model sp³/sp² C₅ was proposed as the simplest hybrid form with 3 C(sp³) and 2 C(sp²) atoms per unit cell characterized by ultrahardness close to that of diamond and semi-metallic electronic structure due to the presence of C(sp²) [8]. The purpose of the present work was to show the effects of introducing small amounts of sp² carbon into 4H, 6H and 8H diamond polytypes leading to increasingly extended C(sp³)/C(sp²) networks exhibiting smaller amounts of trigonal carbon. The investigations were based on crystal chemistry and first-principles calculations within the well-established quantum mechanics framework of the density functional theory DFT [9,10].

2. Brief Presentation of the Computational Framework

The methodology was developed in the former works (cf. [8] and therein cited papers). Summarizing the essentials, the search for the ground state structures with minimal energies was carried out with unconstrained geometry optimizations using a DFT-based plane-wave Vienna Ab initio Simulation Package (VASP) [11] with an energy cutoff of 500 eV. The program uses the projector augmented wave (PAW) method for atomic potentials [12]. Within DFT, the effects of exchange and correlation were treated using a generalized gradient approximation (GGA) scheme [13].

The relaxation of the atoms onto ground state geometry was done by applying a conjugate-gradient algorithm [14]. Blöchl tetrahedron method [15] with corrections according to the Methfessel–Paxton scheme [16] were applied for geometry optimization and energy calculations, respectively. A special k-point sampling [17] was used to calculate the Brillouin-zone (BZ) integrals. For better reliability, the optimization of the structural parameters was carried out along with successive self-consistent cycles with increasing Brillouin zone mesh up to k_x = 22, k_y = 22, k_z = 4 until the forces on atoms were less than 0.02 eV/Å and the stress components below 0.003 eV/Å³.

Investigation of the mechanical properties was based on the calculations of the elastic properties determined by performing finite distortions of the lattice and deriving the elastic constants from the strain–stress relationship. The calculated elastic constants C_ij were then used to obtain the bulk (B) and the shear (G) moduli via Voigt’s [18] averaging method based on a uniform strain. Besides the mechanical properties, the dynamic stability was determined from the calculated phonon spectra. They are illustrated with phonon band structures obtained using the “Phonopy” code [19]. The structure representations were obtained by the VESTA visualization software [20]. For assessing the electronic properties, the band structures were obtained by the all-electron augmented spherical wave method (ASW) [21] using the GGA functional [13] and similar Brillouin zone meshes for VASP calculations.

3. Crystal Chemistry Results

The three diamond polytypes 4H (C₈), 6H (C₁₂) and 8H (C₁₆), where H stands for hexagonal (space group P6₃/mmc, No. 194), are shown in Figure 1 in two representations: ball-and-stick (left) and tetrahedral stacking (right). C₈, C₁₂ and C₁₆ are, respectively, characterized by four layers (ABAA’), six layers (ABCC’B’A’), and eight layers (ABCBACC’A’) of C4 tetrahedra. Such tetrahedral representations allow a better illustration of the layers in primed letters A’ and C’, designating upside-down tetrahedra of the A and C regular layers.

Introducing trigonal sp² carbon was done through the occupation of 2a Wyckoff position with two carbon atoms at 0,0,0 and 0,0,½ in 4H and 8H polymorphs, and 2b Wyckoff position with two carbon atoms at 0,0, ¼ and 0,0, -¼ in 6H polytype. Since these carbon atoms bring C(sp²) into the crystal structure, they are labeled ‘trig’ (trigonal), and C₁₀, C₁₄, and C₁₈ structures are labeled ‘hybrid’ (Table 1). The resulting structural templates, as well as the pristine polytypes, were submitted to full geometry relaxation leading to energy ground state structures. Fully relaxed C₁₀, C₁₄ and C₁₈ structures are shown in Fig. 2. In the tetrahedral representations, they are characterized by four layers ABAB for hybrid C₁₀, seven layers ABB’CBB’A’ for hybrid C₁₄, and eight layers ABB’CC’DD’A’ for hybrid C₁₈, respectively. However, the observed less compact stacking from the spacing of the tetrahedral layers compared to pristine structures allows one to expect different physical properties such as larger compressibility as shown in the next sections, on the one hand, and different crystal fingerprint versus SiC (or ZnS) polytypes, on the other hand.

In Table 1a, giving the resulting structural properties, the calculated values for pristine 4H and 8H polytypes (in parentheses) show good agreement with the literature, thus providing reliability to the calculational framework (plane waves) and the GGA. In all polytypes, there is a unique interatomic distance of ~1.54 Å, characteristic for diamond. From the total energy, the atom averaged cohesive energy values are obtained by subtracting the atomic energy of single isolated carbon (−6.6 eV in the present work), and all polytypes possess the same magnitude of E_coh/atom = −2.49 eV, also characterizing diamond.

Turning to hybrid C₁₀, C₁₄ and C₁₈, there is a significant change in the lattice parameters and atomic positions. The resulting large increase of the unit cell volumes is consistent with less compact crystal structures (Figure 2). Besides interatomic C(sp³) characterizing the pristine polytypes, there is now a shorter bond d{C(tet)-C(trig)} = 1.46 Å due to the presence of C(sp²). The atom-averaged cohesive energy of hybrid allotropes is lower, but interestingly, there is an increase in E_coh/atom values along the series with a closer value of hybrid C₁₈ to polytype 8H, illustrating the effect of a smaller sp²/sp³ ratio. Consequently, it can be assumed that C(sp³) networks with a small amount of C(sp²) in extended hybrid allotropes C₁₀, C₁₄ and C₁₈ are models capable of approaching diamond nanostructures, with better results with the latter. All three allotropes’ structures were deposited on CCDC (Cambridge Crystallographic Data Center) database.

4. Charge Density

Further qualitative illustration of the different types of carbon hybridization (sp³ and sp²) is obtained from the charge density projections shown by yellow volumes in Figure 3. In C₈, C₁₂ and C₁₆ diamond polytypes (Figure 3a,c,e, respectively), the sp³ hybridization is clearly observed as expected from the only presence of C(tet), with the yellow volumes taking the shape of a tetrahedron; and like diamond all three polytypes are perfectly covalent.

Large changes are observed in hybrid C₁₀, C₁₄ and C₁₈ (Figure 3b,d,f). Besides the C(tet) tetrahedral charge density, there appears to be continuous charge density along vertically arranged C=C=C fragments due to the inserted C(trig). In all three subfigures, the charge density is no more localized as in covalent polytypes but rather continuously distributed. Thus, we are dealing with a decrease in covalence from diamond polytypes to hybrid C₁₀, C₁₄ and C₁₈. Such observation will be further illustrated with the electronic band structures.

5. Mechanical Properties from Elastic Constants

For assessing the mechanical characteristics, calculations of elastic properties were carried out by performing finite distortions of the lattice. The elastic constants C_ij were derived from the strain–stress relationship in the large-scale statistically isotropic material approximation. Subsequently, C_ij were used to calculate the bulk (B) and shear (G) moduli by averaging using Voigt’s method [18]. The calculated sets of elastic constants are given in Table 2.

All C_ij values are positive, and their combinations obey rules pertaining to the mechanical stability of the chemical system: C₁₁ > C₁₂, C₁₁C₃₃ > C₁₃² and (C₁₁+C₁₂) C₃₃ > 2C₁₃². The equations providing bulk B_V and shear G_V moduli are as follows for the hexagonal system:

B_V = 1/9 {2(C₁₁ + C₁₂) + 4C₁₃ + C₃₃}

G_V = 1/30 {C₁₁ + C₁₂ + 2C₃₃ − 4C₁₃ + 12C₄₄ + 6(C₁₁ − C₁₂)}

Diamond polytypes C₈, C₁₂ and C₁₆ have the largest B_V and G_V, close to the accepted values for diamonds (B_V = 445 GPa and G_V = 550 GPa [22]). Regarding hybrid C₁₀, C₁₄ and C₁₈, large B_V and G_V are obtained, but they are smaller than those of pristine diamond polytypes. The larger moduli observed for C₁₈ versus C₁₀ can be attributed to the lower C(trig)/C(tet), which leads to a mechanical behavior close to that of a diamond.

Vickers hardness (H_V) of carbon allotropes was predicted using four modern theoretical models [23,24,25,26]. The thermodynamic model [23] is based on thermodynamic properties and crystal structure, empirical Mazhnik–Oganov [24] and Chen–Niu [25] models use the elastic properties, and the Lyakhov–Oganov approach [26] considers the topology of the crystal structure, strength of covalent bonding, degree of ionicity and directionality. The fracture toughness (K_Ic) was evaluated using Mazhnik–Oganov model [24]. Table 3 and Table 4 present the hardness values calculated using all four models, as well as other mechanical properties such as bulk (B), shear (G) and Young’s (E) moduli, the Poisson’s ratio (ν) and fracture toughness (K_Ic).

Table 3 shows that X-ray density ρ systematically decreases in the C₁₈–C₁₄–C₁₀ row of hybrid allotropes, while pristine 4H, 6H and 8H polytypes have expected diamond density. Obviously, the introduction of additional trigonal carbon atoms leads to the formation of less dense phases. A similar trend is observed for bulk moduli of hybrid allotropes calculated in the framework of the thermodynamic model (see Table 3).

As shown earlier [27], in the particular case of ultrahard compounds of light elements, the thermodynamic model shows surprising agreement with available experimental data. Moreover, its use is preferable in the case of dense hybrid carbon allotropes, for which the Lyakhov–Oganov model usually gives underestimated hardness values, whereas the empirical models are not reliable. As it follows from Table 3, Vickers hardness of all three polytypes (H_V = 97 GPa) is close to that of diamond, while the hardness of hybrids is expectedly lower (94 GPa for C₁₈ and C₁₄, and 92 GPa for C₁₀). Other used models of hardness show similar trends between diamond polytypes and hybrids with respect to hardness, Young’s modulus, Poisson’s ratio and fracture toughness. Concomitantly, E, ν and K_Ic of all hybrids were found to be smaller than calculated for diamond polytypes. Thus, all phases under study have exceptional mechanical properties and can be considered prospective ultrahard phases [28].

Table 3. Vickers hardness (H_V) and bulk moduli (B₀) of carbon allotropes calculated in the framework of the thermodynamic model of hardness [23].

	Space Group	a=b (Å)	c (Å)	ρ (g/cm³)	H_V (GPa)	B₀ (GPa)
Polytype 4H: C₈	P6₃/mmc	2.5221	8.2371	3.5164	97	443
Hybrid C₁₀	P6₃/mmc	2.4960	11.1775	3.3073	92	417
Polytype 6H: C₁₂	P6₃/mmc	2.5221	12.3557	3.5164	97	443
Hybrid C₁₄	P6₃/mmc	2.5000	15.2330	3.3867	94	427
Polytype 8H: C₁₆	P6₃/mmc	2.5221	16.47429	3.5164	97	443
Hybrid C₁₈	P6₃/mmc	2.5019	19.3964	3.4146	94	430
Lonsdaleite	P6₃/mmc	2.5221 ^†	4.1186 ^†	3.5164	97	443
Diamond	Fd-3m	3.56661 ^‡		3.5169	98	445 ^§

^† Ref. [3]; ^‡ Ref. [29]; ^§ Ref. [22].

Table 4. Mechanical properties of carbon allotropes: Vickers hardness (H_V), bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν) and fracture toughness (K_Ic).

	H_V				B		G_V	E **	ν **	K_Ic^‡
	T *	LO ^†	MO ^‡	CN ^§	B₀ *	B_V	G_V	E **	ν **	K_Ic^‡
	GPa									MPa·m^½
Polytype 4H: C₈	97	90	106	102	443	445	557	1179	0.058	6.5
Hybrid C₁₀	92	79	82	74	417	408	440	971	0.103	5.4
Polytype 6H: C₁₂	97	90	94	85	443	445	502	1094	0.090	6.2
Hybrid C₁₄	94	72	88	80	427	417	467	1020	0.092	5.7
Polytype 8H: C₁₆	97	90	103	100	443	432	539	1142	0.059	6.3
Hybrid C₁₈	94	66	92	88	430	412	488	1050	0.075	5.7
Lonsdaleite	97	90	99	94	443	432	521	1115	0.070	6.2
Diamond	98	90	100	93	445 ^††		530 ^††	1138	0.074	6.4

* Thermodynamic model [23]; ^† Lyakhov–Oganov model [26]; ^‡ Mazhnik–Oganov model [24]; ^§ Chen–Niu model [25]; ** E and ν values calculated using isotropic approximation; ^†† Ref. [22].

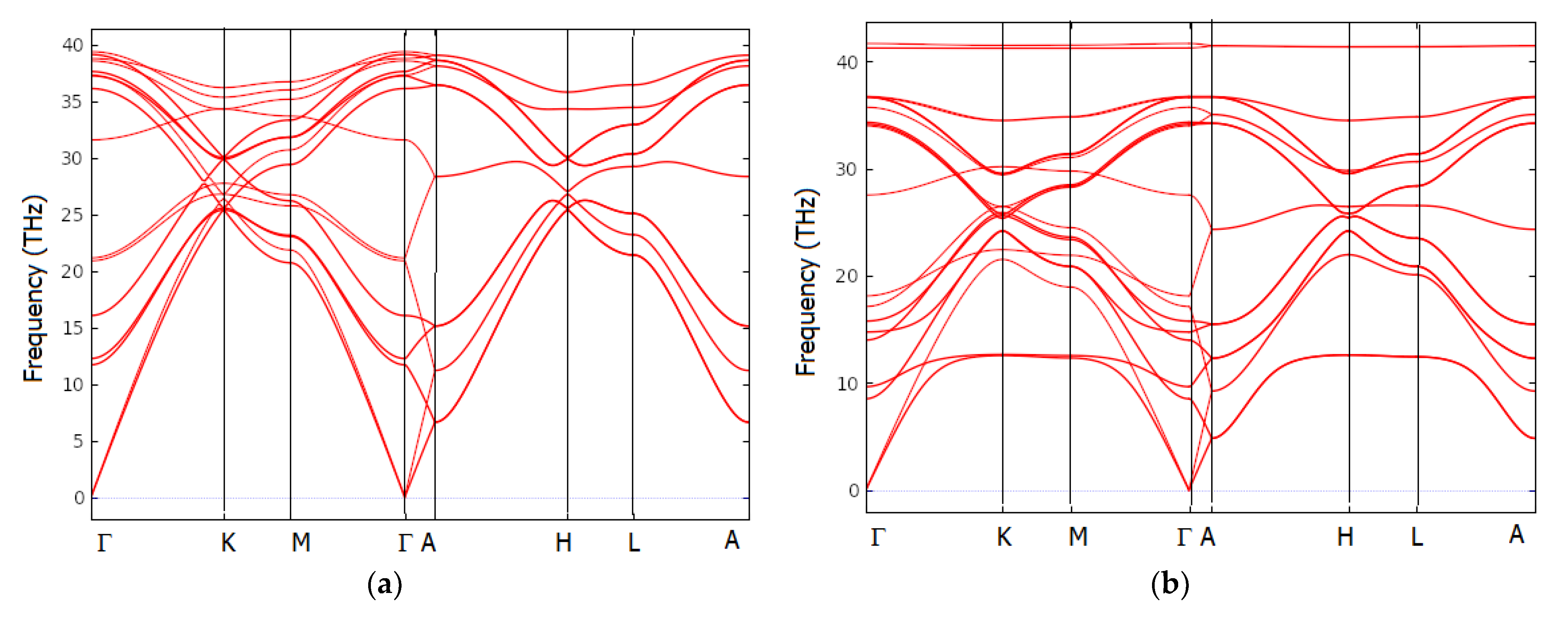
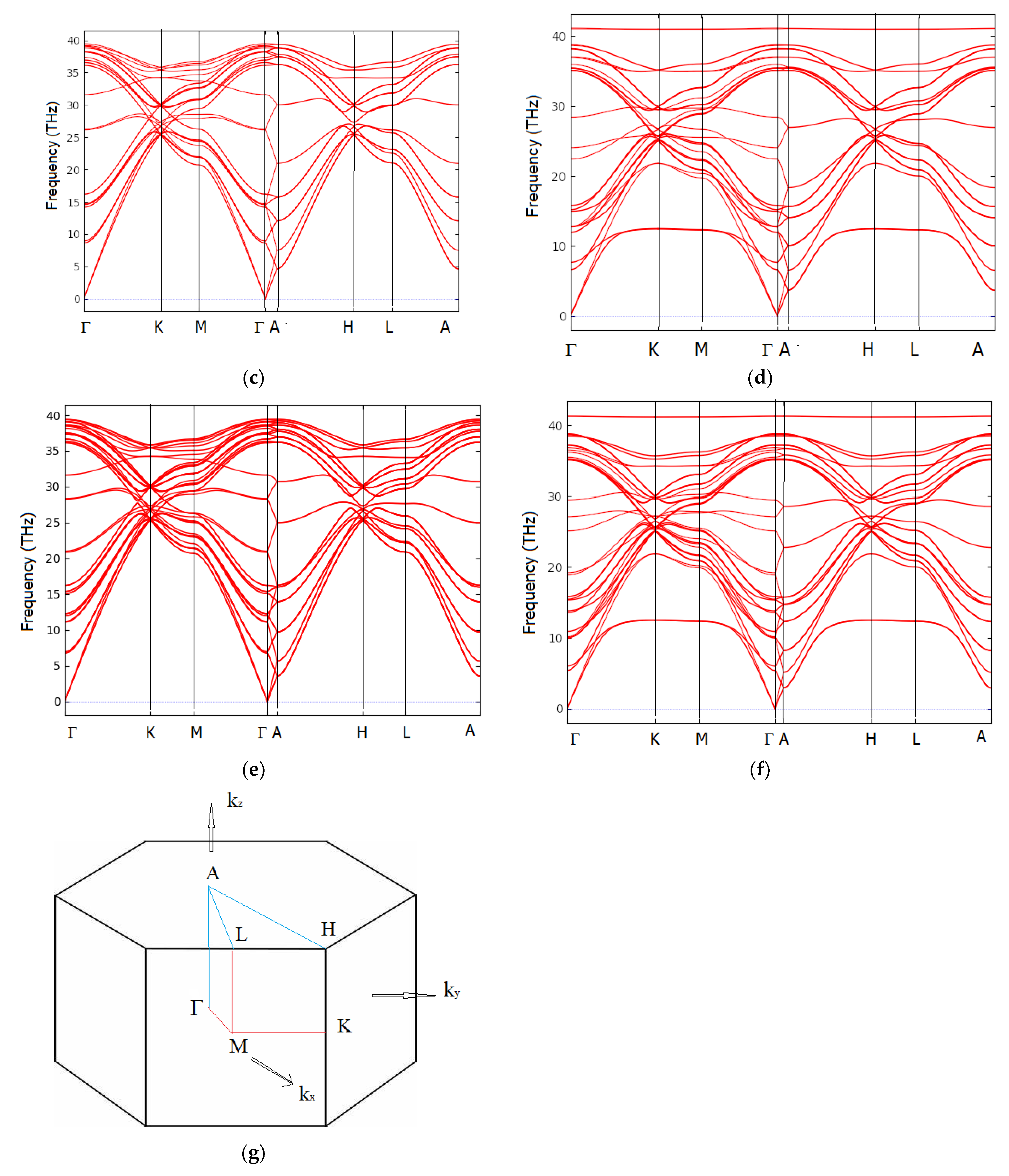
6. Dynamic Properties from the Phonons

Further confirmation of phase stability can be obtained from the phonon band structures, which are shown in Figure 4 for 4H, 6H and 8H diamond polytypes and the novel C₁₀, C₁₄ and C₁₈ allotropes along the high-symmetry lines of the hexagonal Brillouin zone provided in Figure 4g as a guide for the eye. The vertical axis shows the frequencies given in units of terahertz (THz). Since no negative frequency magnitudes are observed, expectedly for diamond polytypes, as well as for hybrid carbon allotropes, all structures should be considered dynamically stable. There are 3N-3 optical modes found at higher energy than three acoustic modes that start from zero energy (ω = 0) at the Γ-point, the center of the Brillouin Zone, up to a few Terahertz. They correspond to the lattice rigid translation modes of the crystal (two transverse and one longitudinal). Flat bands (no band dispersion) that can be observed in hybrid carbon allotropes correspond to the aligned C-C-C fragments. The remaining bands correspond to the optical modes. They culminate at ω ~ 40 THz in C₈, C₁₂ and C₁₆, the magnitude observed for diamond by Raman spectroscopy [30], and ω ~ 42 THz in C₁₀, C₁₄ and C₁₈ with flat bands corresponding to antisymmetric C-C-C stretching as recently observed in allene (propadiene) molecule and tetragonal C₆ [31].

7. Electronic Band Structures and Density of States

The electronic band structures shown in Figure 5 along the high-symmetry lines of the hexagonal Brillouin zone were obtained using the ASW method [21] and calculated crystal parameters (Table 1a,b). For diamond-like insulating C₈, C₁₂ and C₁₆, the energy levels are referred to the top of the valence band (VB), E_V. As a specific character of diamond, the band gap is indirect along k_z between Γ_VB and Z_CB with a magnitude close to 5 eV.

Oppositely, hybrid C₁₀, C₁₄ and C₁₈ behave as metals with the energy zero at the Fermi level E_F. E_F is crossed with dispersed four bands due to the 2p electrons of the trigonally coordinated carbon atoms. This feature was subsequently analyzed by calculating the four corresponding Fermi surfaces (FS) of the C₁₈ hybrid allotrope shown in Figure 6a. While confirming the almost perfect two-dimensional nature of this allotrope, the Fermi surface (especially the hexagonal ring in the center of the displayed FS) reveals a strong tendency towards nesting, which is also obvious from the metallic bands in the band structure that cross the Fermi energy almost halfway between the Γ-point and the M-point. Hypothesizing that doubling of the in-plane cell vectors would bring the Fermi surface close to the boundaries of the hexagonal Brillouin zone and may induce a charge density wave and a concomitant lattice instability or pave the wave to a superconducting phase [32,33], further calculations were done with 2 × 2 × 1 cell of C₁₄ allotrope presenting fewer atoms than C₁₈. The corresponding FS presented in Figure 6b shows similar features of nesting as in Figure 6a, but FS is closer to the BZ borders due to the supercell construction. The observed results further stress the hypothesis of potential superconducting behavior with 2D character generalized to all three hybrid allotropes.

8. Conclusions

The purpose of this work was to propose model carbon allotropes based on 4H, 6H and 8H diamond polytypes, modified through crystal chemistry rationale by the introduction of trigonal (sp²) carbon, thus creating mixed C(sp³)/C(sp²) hybridizations in C₁₀, C₁₄ and C₁₈ hybrid allotropes. DFT calculations allowed us to identify the hybrid forms as cohesive and stable both mechanically and dynamically, with very high hardness approaching that of diamonds. The electronic band structures revealed metallic-like behavior due to the trigonal carbons with nested Fermi surfaces indicative of potential superconductivity.

Author Contributions

S.F.M.: Conceptualization, crystal chemistry, calculations. V.E.: ASW method, Fermi surface, calculations. V.L.S.: Hardness models, mechanical properties, calculations. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Bhattacharya, P.; Fornari, R.; Kamimura, H. (Eds.) Comprehensive Semiconductor Science and Technology; Reference work; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
Ownby, P.D.; Yang, X.; Liu, J. Calculated X-ray diffraction data for diamond polytypes. J. Am. Ceram. Soc. 1992, 75, 1876–1883. [Google Scholar] [CrossRef]
Lifshitz, Y.; Duan, X.F.; Shang, N.G.; Li, Q.; Wan, L.; Bello, I.; Lee, S.T. Epitaxial diamond polytypes on silicon. Nature 2001, 412, 404. [Google Scholar] [CrossRef]
Wen, B.; Zhao, J.; Bucknum, M.J.; Yao, P.; Li, T. First-principles studies of diamond polytypes. Diam. Relat. Mater. 2008, 17, 356–364. [Google Scholar] [CrossRef]
Lin, Y.; Sun, X.; Su, D.S.; Centi, G.; Perathoner, S. Catalysis by hybrid sp²/sp³ nanodiamonds and their role in the design of advanced nanocarbon materials. Chem. Soc. Rev. 2018, 47, 8438–8473. [Google Scholar] [CrossRef] [Green Version]
Zhai, Z.; Huang, N.; Jiang, X. Progress in electrochemistry of hybrid diamond/sp²-C nanostructures. Curr. Opin. Electrochem. 2022, 32, 100884. [Google Scholar] [CrossRef]
Hu, M.; Huang, Q.; Zhao, Z.; Xu, B.; Yu, D.; He, J. Superhard and high-strength yne-diamond semimetals. Diam. Relat. Mater. 2014, 46, 15–20. [Google Scholar] [CrossRef]
Matar, S.F. C₅ as simplest ultrahard allotrope with mixed sp²/sp³ carbon hybridizations from first principles. arXiv 2022, arXiv:2210.04210. [Google Scholar]
Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef] [Green Version]
Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef] [Green Version]
Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
Blöchl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar]
Perdew, J.; Burke, K.; Ernzerhof, M. The Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, 2nd ed.; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
Blöchl, P.E.; Jepsen, O.; Anderson, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [Green Version]
Monkhorst, H.J.; Pack, J.D. Special k-points for Brillouin zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
Voigt, W. Über die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annal. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef] [Green Version]
Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
Eyert, V. The Augmented Spherical Wave Method, Lect. Notes Phys. 849; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
Brazhkin, V.V.; Solozhenko, V.L. Myths about new ultrahard phases: Why materials that are significantly superior to diamond in elastic moduli and hardness are impossible. J. Appl. Phys. 2019, 125, 130901. [Google Scholar] [CrossRef]
Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. The interrelation between hardness and compressibility of substances and their structure and thermodynamic properties. J. Superhard Mater. 2008, 30, 368–378. [Google Scholar] [CrossRef]
Mazhnik, E.; Oganov, A.R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. [Google Scholar] [CrossRef]
Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
Lyakhov, A.O.; Oganov, A.R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO₂. Phys. Rev. B 2011, 84, 092103. [Google Scholar] [CrossRef] [Green Version]
Matar, S.F.; Solozhenko, V.L. Crystal chemistry and ab initio prediction of ultrahard rhombohedral B₂N₂ and BC₂N. Solid State Sci. 2021, 118, 106667. [Google Scholar] [CrossRef]
Solozhenko, V.L.; Le Godec, Y. A hunt for ultrahard materials. J. Appl. Phys. 2019, 126, 230401. [Google Scholar] [CrossRef] [Green Version]
Bindzus, N.; Straasø, T.; Wahlberg, N.; Becker, J.; Bjerg, L.; Lock, N.; Dippel, A.-C.; Iversen, B.B. Experimental determination of core electron deformation in diamond. Acta Cryst. A 2014, 70, 39–48. [Google Scholar] [CrossRef] [Green Version]
Krishnan, R.S. Raman spectrum of diamond. Nature 1945, 155, 171. [Google Scholar] [CrossRef]
Matar, S.F. Crystal chemistry rationale and DFT investigations of novel hard tetragonal C₆ built from tetrahedral C(sp³) lattice embedding allene-like sp² linear tricarbon. ChemArxiv 2022. [Google Scholar] [CrossRef]
Arita, R.; Ikeda, H. Is Fermi-surface nesting the origin of superconductivity in iron pnictides?: A fluctuation–exchange-approximation study. J. Phys. Soc. Japan 2009, 78, 113707. [Google Scholar] [CrossRef] [Green Version]
Dugdale, S.B. Life on the edge: A beginner’s guide to the Fermi surface. Phys. Scr. 2016, 91, 053009. [Google Scholar] [CrossRef]

Figure 1. Sketches of hexagonal diamond polytypes (left) and their polyhedral representation (right): (a) 4H (C₈), (b) 6H (C₁₂) and (c) 8H (C₁₆).

Figure 2. Sketches of hybrid carbon allotropes (left) and their polyhedral representation (right): (a) C₁₀, (b) C₁₄ and (c) C₁₈.

Figure 3. Charge density projections (yellow volumes) of diamond polytypes 4H (C₈), 6H (C₁₂) and 8H (C₁₆), and novel hybrid carbon allotropes: (a) 4H, (b) C₁₀, (c) 6H, (d) C₁₄, (e) 8H, and (f) C₁₈.

Figure 4. Phonons band structures along major directions of the hexagonal Brillouin zone shown in the last panel: (a) 4H polytype, (b) hybrid C₁₀, (c) 6H polytype, (d) hybrid C₁₄, (e) 8H polytype, (f) hybrid C₁₈, (g) hexagonal Brillouin zone.

Figure 5. Electronic band structures along major directions of the hexagonal Brillouin zone. (a) 4H polytype, (b) Hybrid C₁₀, (c) 6H polytype, (d) Hybrid C₁₄, (e) 8H polytype, (f) Hybrid C₁₈.

Figure 6. Fermi surface corresponds to the bands crossing E_F of hybrid C₁₈ allotrope (a) and Fermi surface for 2 × 2 × 1 supercell of hybrid C₁₄ allotrope (b).

Table 1. Crystal structure parameters of hexagonal carbon polytypes and derived hybrid allotropes.

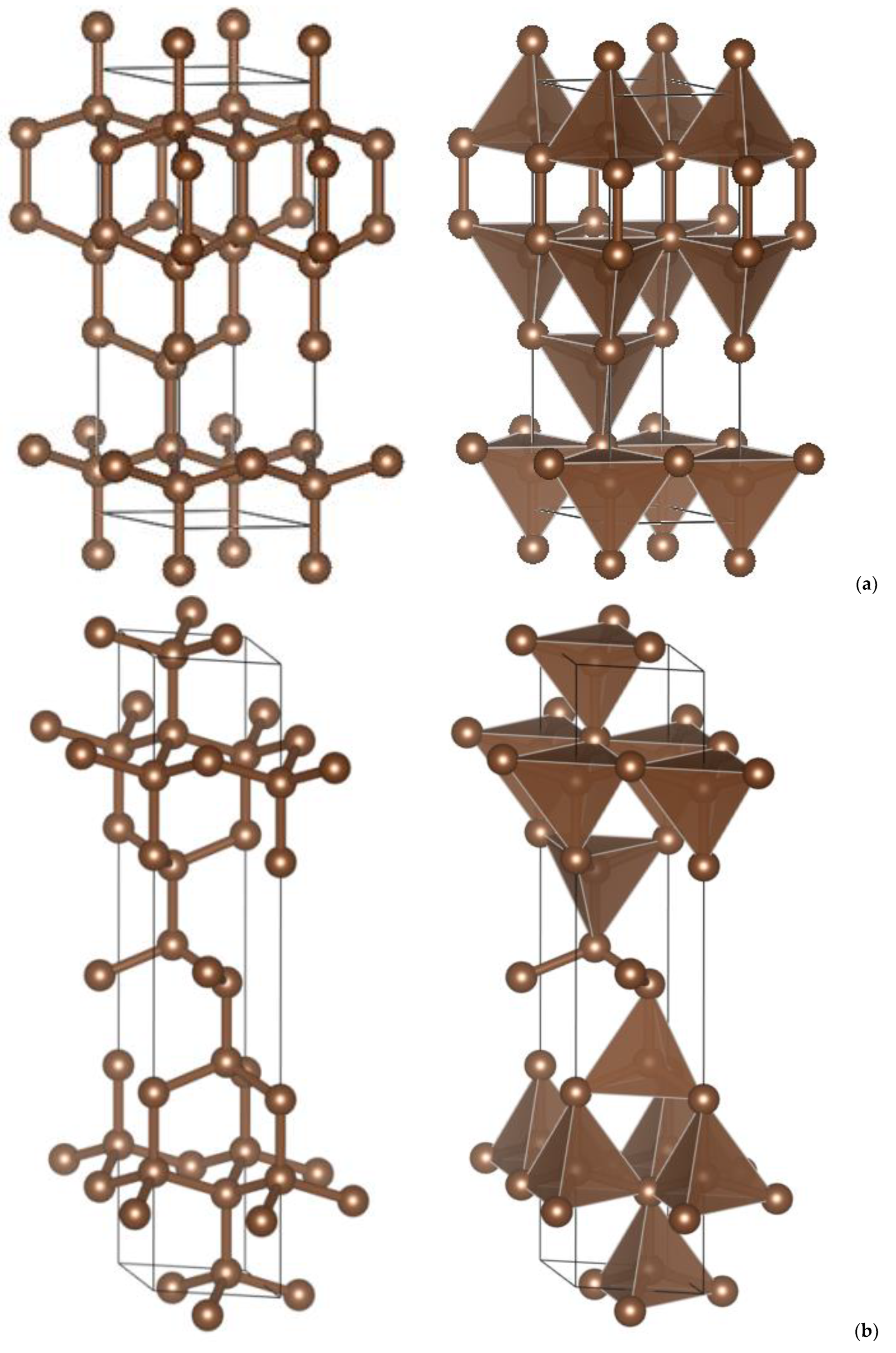
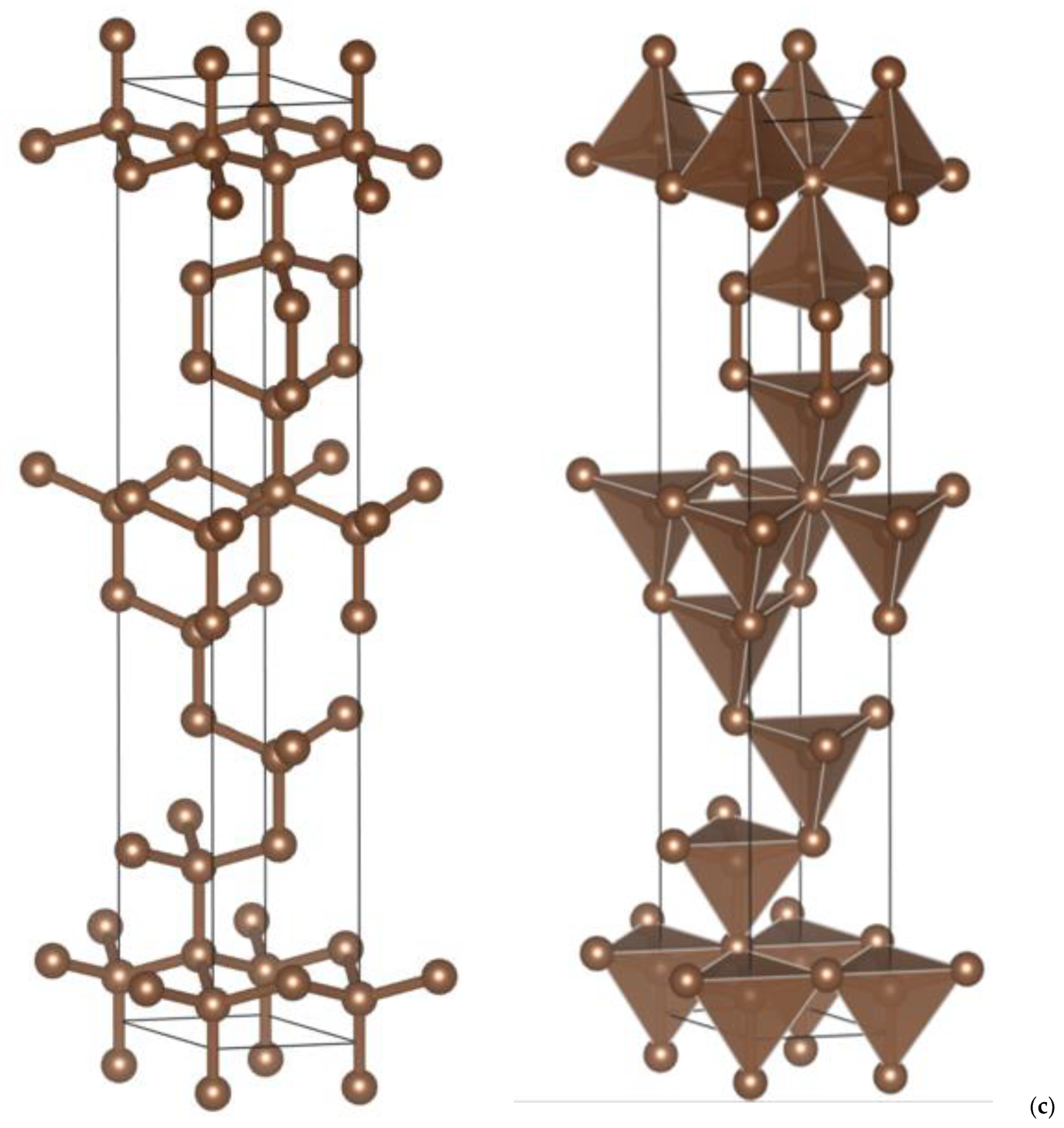
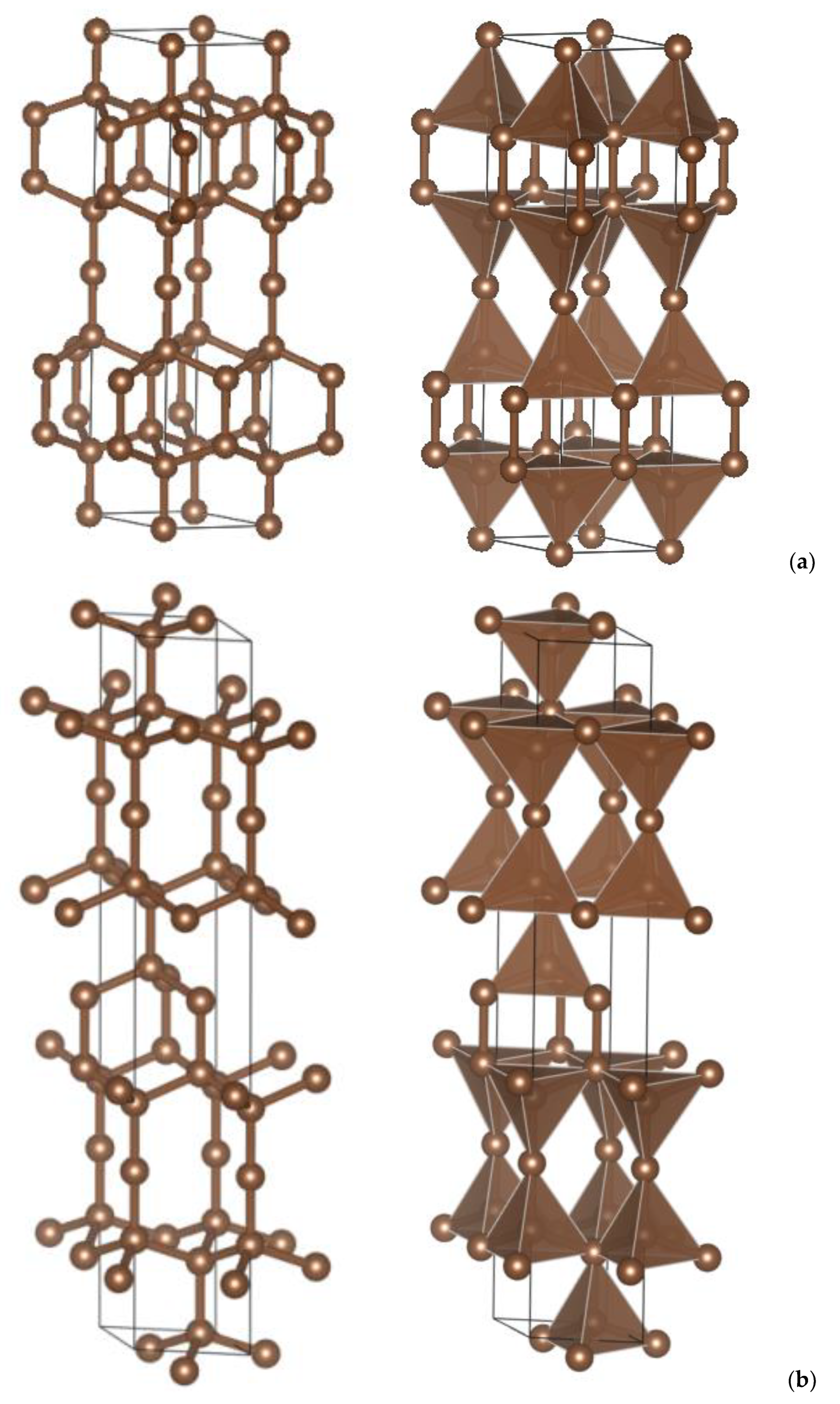
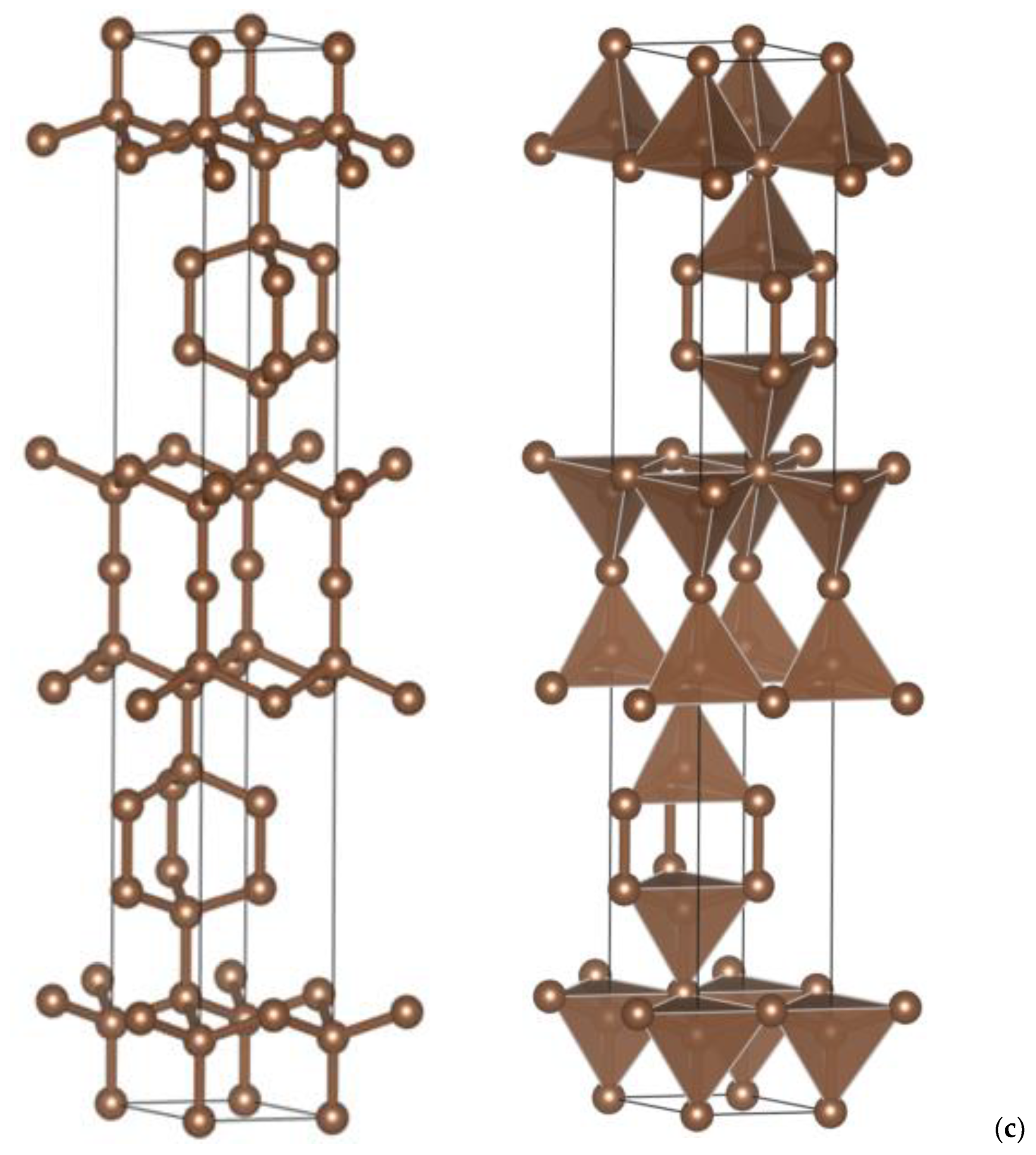
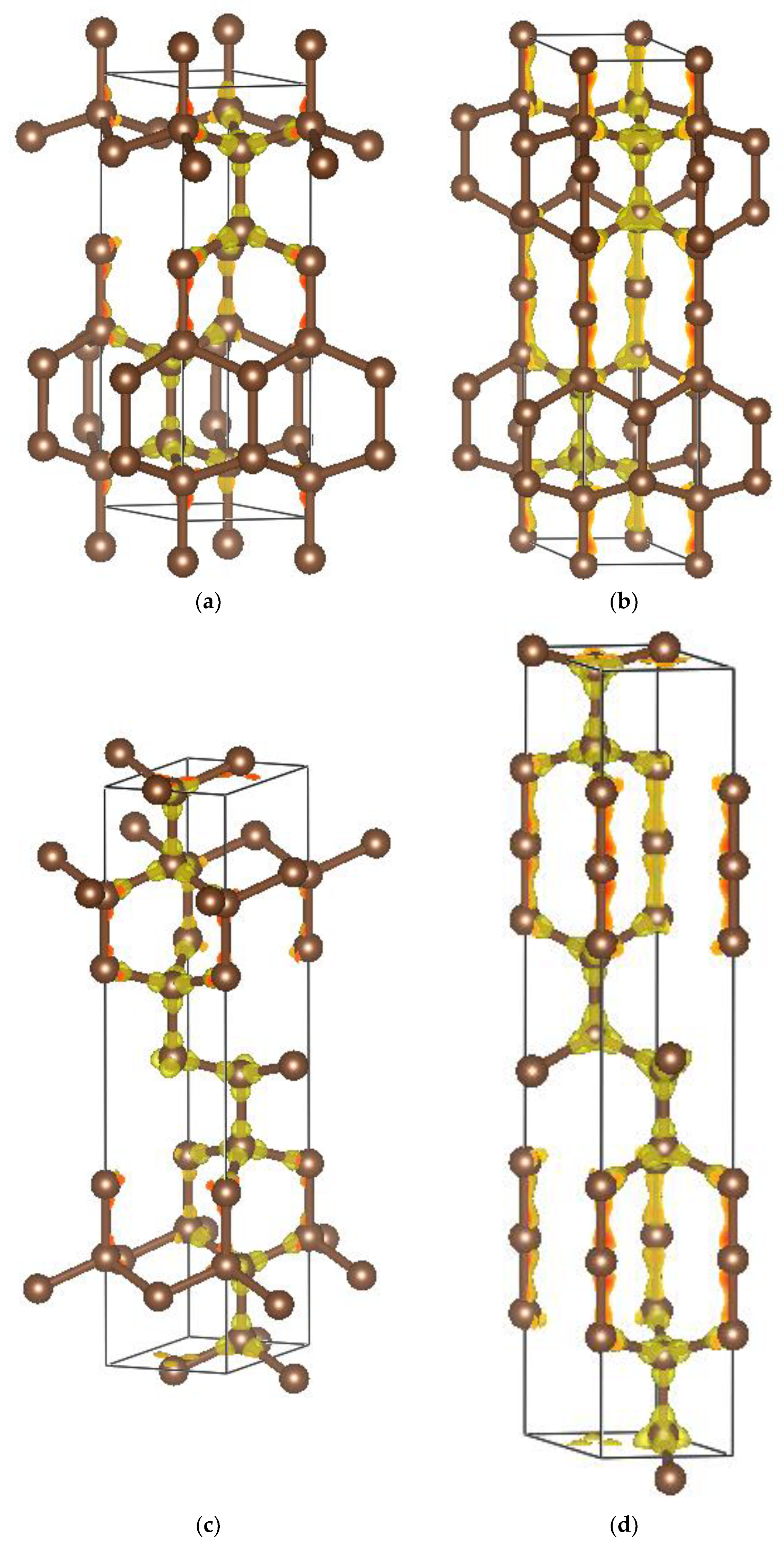
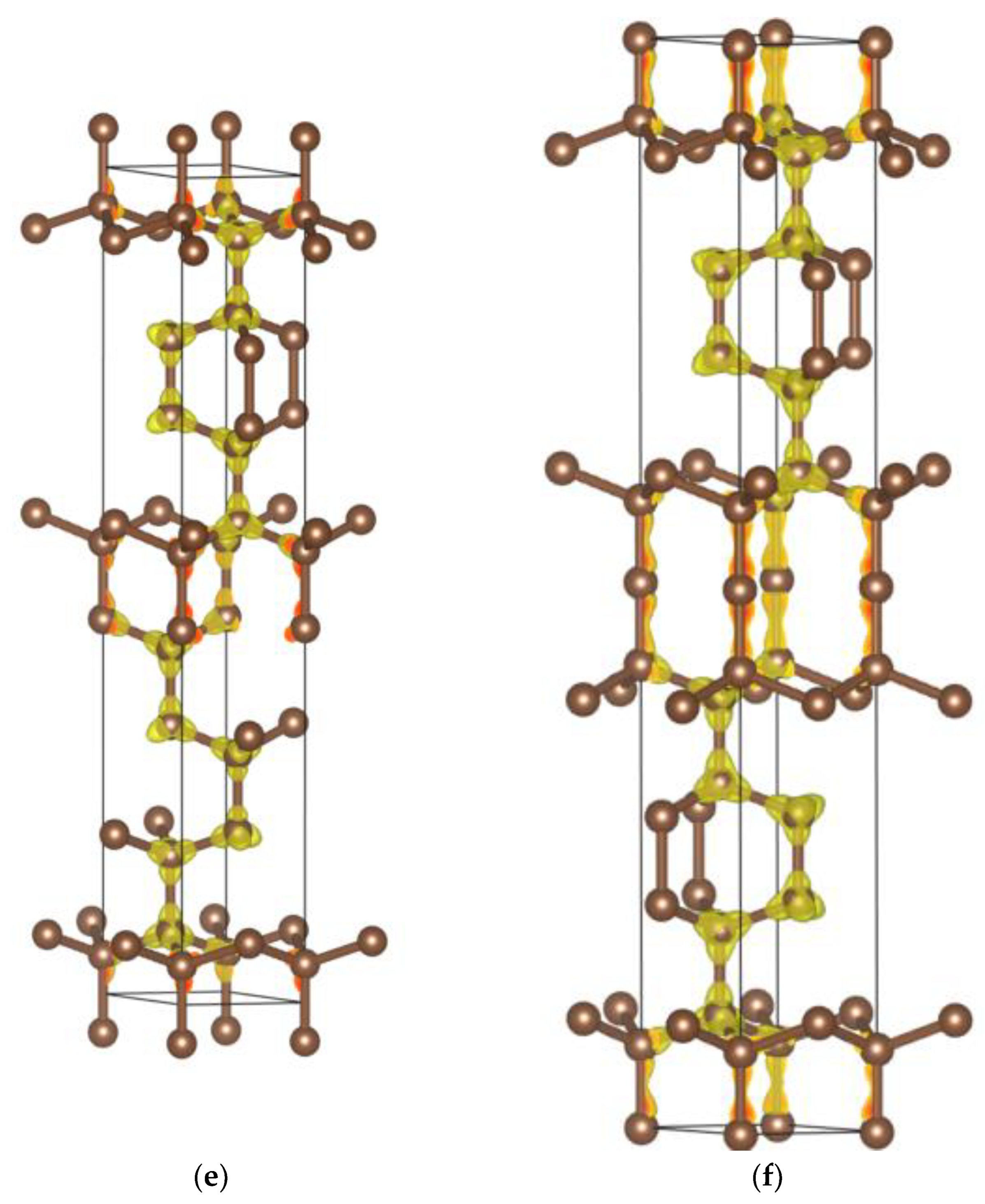
(a) 4H, 6H and 8H Polytypes [2] (Presently Calculated Values Are in Parentheses)
P6₃/mmc N°194	Polytype 4H: C₈	Polytype 6H: C₁₂	Polytype 8H: C₁₆
a, Å	2.522 (2.511)	2.522 (2.514)	2.522 (2.516)
c, Å	8.237 (8.279)	12.356 (12.394)	16.474 (16.505)
C1(4e) 0 0 z	0.0938 (0.093)	0.1875 (0.187)	0.0469 (0.047)
C2(4f) 1/3 2/3 z	0.1563 (0.156)	0.5208 (0.521)	0.0781 (0.0780)
C3(4f) 1/3 2/3 z	–	0.6458 (0.645)	0.1719 (0.1710)
C4(4f) 1/3 2/3 z	–	–	0.797 (0.797)
Volume, Å³	45.376 (45.25)	68.064 (67.87)	90.75 (90.45)
d_{C1(tet)-C2(tet)}, Å	1.544	1.544	1.544
E_total, eV	−72.68	−109.06	−145.43
E_coh/atom, eV	−2.49	−2.49	−2.49
(b) Hybrid C8, C14 and C16
P6₃/mmc No. 194	C₁₀	C₁₄	C₁₈
a, Å	2.496	2.500	2.502
c, Å	11.178	15.233	19.396
C(2a) (trig)	0 0 0	–	0 0 0
C(2b) (trig)	–	0 0 ¼	–
C1(4e) 0 0 z	0.3692	0.1541	0.0753
C2(4f) 1/3 2/3 z	0.1807	0.5171	0.1035
C3(4f) 1/3 2/3 z	–	0.6180	0.1828
C4(4f) 1/3 2/3 z	–	–	0.7903
Volume, Å³	60.307	82.451	105.14
d_{C1(tet)-C2(tet)}, Å	1.545	1.544	1.536
d_{C(tet)-C(trig)}, Å	1.462	1.462	1.461
E_total, eV	−84.94	−121.45	−157.73
E_coh/atom, eV	−1.89	−2.08	−2.16

Table 2. Elastic constants C_ij and Voigt values of bulk (B_V) and shear (G_V) moduli of diamond polytypes and novel hybrid carbon allotropes (all values are in GPa).

	C₁₁	C₁₂	C₁₃	C₃₃	C₄₄	B_V	G_V
Polytype 4H: C₈	1190	105	37	1271	542	445	557
Hybrid C₁₀	922	101	39	1469	410	408	440
Polytype 6H: C₁₂	1129	160	43	1256	485	445	502
Hybrid C₁₄	972	93	69	1343	439	417	467
Polytype 8H: C₁₆	1152	99	48	1211	526	432	539
Hybrid C₁₈	1012	90	45	1325	461	412	488

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Matar, S.F.; Eyert, V.; Solozhenko, V.L. Novel Ultrahard Extended Hexagonal C₁₀, C₁₄ and C₁₈ Allotropes with Mixed sp²/sp³ Hybridizations: Crystal Chemistry and Ab Initio Investigations. C 2023, 9, 11. https://doi.org/10.3390/c9010011

AMA Style

Matar SF, Eyert V, Solozhenko VL. Novel Ultrahard Extended Hexagonal C₁₀, C₁₄ and C₁₈ Allotropes with Mixed sp²/sp³ Hybridizations: Crystal Chemistry and Ab Initio Investigations. C. 2023; 9(1):11. https://doi.org/10.3390/c9010011

Chicago/Turabian Style

Matar, Samir F., Volker Eyert, and Vladimir L. Solozhenko. 2023. "Novel Ultrahard Extended Hexagonal C₁₀, C₁₄ and C₁₈ Allotropes with Mixed sp²/sp³ Hybridizations: Crystal Chemistry and Ab Initio Investigations" C 9, no. 1: 11. https://doi.org/10.3390/c9010011

APA Style

Matar, S. F., Eyert, V., & Solozhenko, V. L. (2023). Novel Ultrahard Extended Hexagonal C₁₀, C₁₄ and C₁₈ Allotropes with Mixed sp²/sp³ Hybridizations: Crystal Chemistry and Ab Initio Investigations. C, 9(1), 11. https://doi.org/10.3390/c9010011

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu