1. Introduction
In addition to a hair sensor’s flow sensitivity and response range, the frequency or range of frequencies for which the sensor is useful is of high importance. Sensitivity has been previously discussed and includes both the ability to measure a small amplitude of air perturbation and the magnitude of response per change in air velocity past this threshold [
1,
2,
3,
4]. The frequency bandwidth of useful operation has been discussed to a smaller extent. It typically includes the in-phase response recorded from quasi-static deflection (DC) to the first natural resonance of the system. For auditory or sonar applications of hair sensors and more exotic frequency-tuned air flow response schemes, the change in air flow at a specific frequency can be isolated by operating an individual hair sensor at its resonance frequency or with a collection of resonance-tailored sensors effectively serving as a bandpass detector [
5,
6,
7]. In this case, a strong resonant response would be desired at the frequency of interest. Artificial hair sensors which have a strong and frequency-tunable resonance response as well as high sensitivity before the first resonance could function both as a proportional flow sensor below resonance and as a bandpass detector at the selected resonance frequencies.
A number of artificial hair sensor schemes have been previously developed with different hair dimensions, transduction element types, and performance metrics, with the resonance properties only reported for a few. Krijnen et al. suggested the product of the threshold and frequency response bandwidth as a figure of merit for hair sensors [
3]. Their 1-mm-long SU8 polymer hairs were mounted on a suspended capacitive membrane which rotated at the base under air flow to give a resonance frequency of 500 Hz. The devices were fabricated using microelectromechanical systems (MEMS) processes, and they have been measured in an air flow tube [
8]. Chen et al. also use MEMS processes to fabricate a silicon cantilever arm for 600-μm-long SU8 hairs that resonate at 3.1 kHz [
9]. Tamaddoni et al. demonstrated cantilever bending and a 293 Hz primary resonance in a sensor with a hydrogel-supported lipid bilayer transducer and a 12-mm-long glass fiber [
10], and Sarlo et al. recently investigated arrays of similar sensors and the mapping of velocity [
11]. Yilmazoglu et al. recently used arrays of carbon nanotubes (CNTs) as both the piezoresistive transduction element and the hair pillars and reported that the sensors maintained functionality even after deflection at 2 kHz [
12].
Here we discuss the frequency response of non-MEMS hair flow sensors consisting of a piezoresistive, radial array of CNTs grown on a glass microfiber hair partially within an electroded glass capillary. The length of the glass fiber hair is adjustable in height to a predictable and tunable first resonance frequency as well as a sensitive response before first resonance. Due to the strong resonance, higher-order resonant modes are accessible at even higher frequencies. The fabrication, sensitivity to steady aerodynamics, internal mechanics, and integration of arrays into aerodynamic structures of these CNT-based sensors have been previously discussed [
1,
4,
13]. Essentially, the external aerodynamic loading induces a moment inside the capillary which compresses the radially grown CNT array, providing a sigmoidal resistance change (decrease) as a function of flow velocity or deflection.
In now considering the response as a function of dynamic flow (e.g., frequency of deflection), the natural frequencies of a vibrating Euler-Bernoulli beam are known to be
where
I,
E,
ρ,
A, and
LE are the moment of inertia, Young’s modulus, density, cross-sectional area, and length of the beam, respectively. This assumes the bending stiffness (
EI) and mass per length (
ρA) do not greatly vary along the length of the beam. The
αn values are determined from the boundary conditions of the beam. Assuming a beam that is free at one end (moment, shear = 0) and fixed at the other (slope = 0), the first four
αn values are 1.875, 4.694, 7.854, and 10.996 [
14]. While the total length of the hair (
LT) includes the portion of fiber enclosed by the capillary, this model most closely matches these devices if the beam is considered only as the length of the fiber external to the capillary (
LE) and the hair is assumed to be fixed at the opening of the capillary.
Going further, it has been previously shown that these sensors can be more accurately modeled as beams supported by an elastic foundation [
4,
15,
16]. In the case of the dynamic response of the sensor, a stiffness constant k appears in the time-varying Euler beam equation:
where
k is zero outside the capillary (
x ≥ 0). This “partial elastic base” condition can be solved by treating the two sections of the beam independently and matching the solutions at the opening of the capillary. The resonance frequencies are found from the relationship
where the
βn values are determined from the boundary conditions [
15,
17]. In this case, for these devices, the hair is modeled as having a free end outside of the capillary (
x =
LE) and a fixed end at the bottom of the capillary (
x =
LE −
LT). In the absence of an elastic base (
k = 0), the
βn values are identical to the
αn values in Equation (1) and the natural frequencies are the same as those found from the fixed base model but with
LE replaced by
LT. Further, for an infinite value of k in the elastic base model, the two models predict the same resonance frequencies. Using this approach, the frequency response of the experiment response of the fabricated hair sensors can be compared with their predicted responses.
The nanotubes surrounding the glass fiber inside the capillary act as the elastic base, supporting the fiber along the length of hair internal to the capillary. The value of the stiffness constant can be determined by characterizing the bending and deflection of the hair under mechanical loading or by measuring the electrical response under various loading conditions, noting that the electrical response is uniquely a function of the bending moment on the hair [
4]. It has been shown that the relationship between the elastic base stiffness and the compressive modulus of the CNTs (
κ) can be approximated as
where
r is in the radius of the glass fiber and
R is the inner radius of the capillary.
2. Results
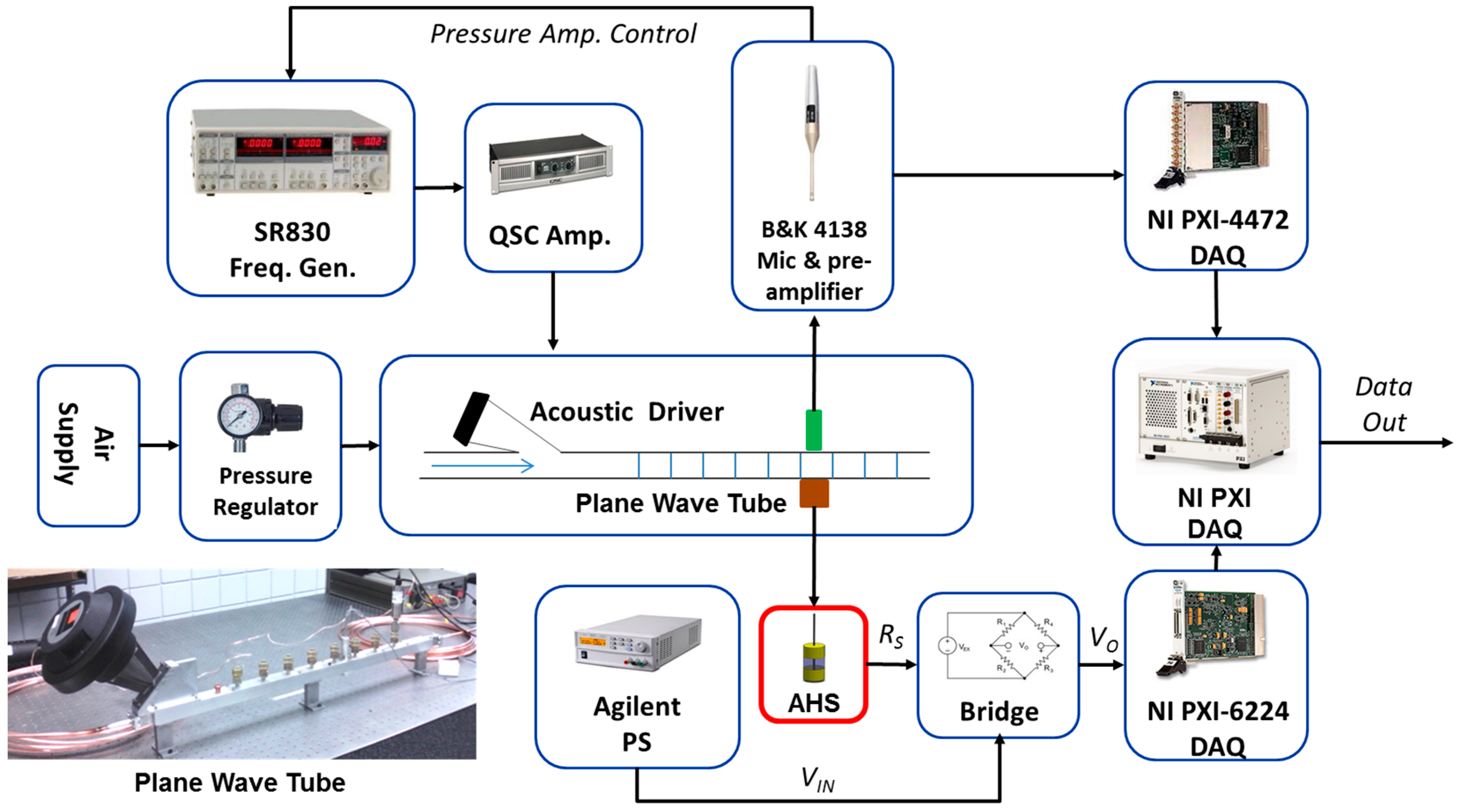
Three sensors were investigated in terms of their frequency response using a plane-wave tube. The air flow was dynamically modulated by an audio speaker connected to a 1-m-long, 5-mm-square inner diameter aluminum alloy tube. The speaker was coupled into to the tube at an angle and driven by a power amplifier receiving a sinusoidal input signal from a lock-in amplifier to expose the hairs to air flows at acoustic frequencies. The sound pressure near the sensor was measured with a microphone mounted at the top of the tube at its lengthwise and widthwise center. A proportional–integral–derivative (PID) controller was used to adjust the output of the speaker to maintain a constant signal on the microphone at each frequency. The sensors were mounted at the bottom of the tube directly below the microphone. Propagating plane waves were expected up to a cutoff frequency of about 34 kHz for this tube [
18]. The setup is more completely described in the Materials and Methods Section.
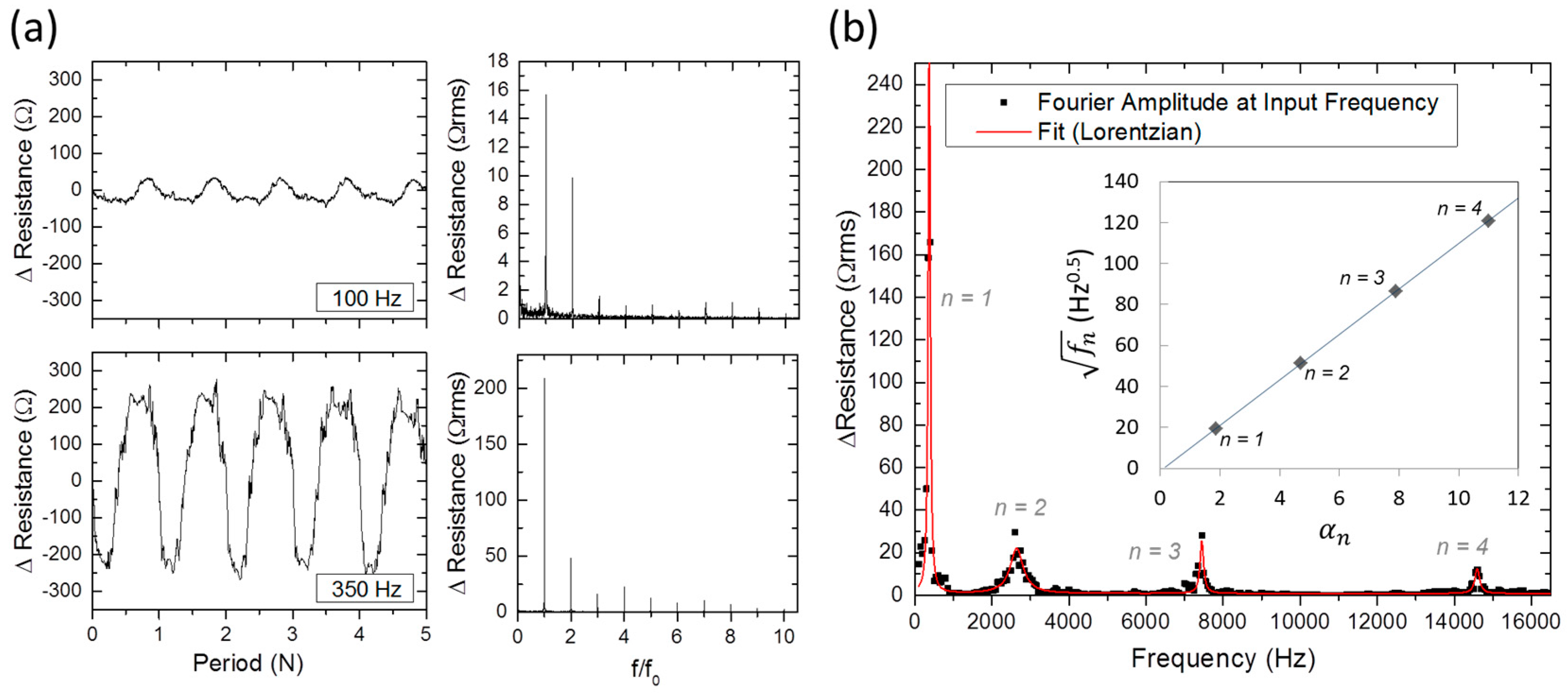
The response of Sensor 1 (
LE = 4.00 mm) to dynamically modulated air flow is shown in
Figure 1a over five periods at two drive frequencies (100 Hz and 350 Hz), along with the corresponding Fourier transformed frequency response. In both cases, the root mean square (RMS) amplitude of the supplied modulation was 300 Pa RMS as measured by the microphone. At 350 Hz, the hair was in resonance with the air flow, as suggested by the large increase in the magnitude of the resistance change and the sinusoidal response to the sinusoidal input. The magnitude of the Fourier transformed response at the driving frequency is plotted in
Figure 1b versus the driving frequency. The square root of the resonance frequencies can be seen to vary linearly with the fixed-base
αn of Equation (1) (inset of
Figure 1b), indicating a well-behaved elastic response.
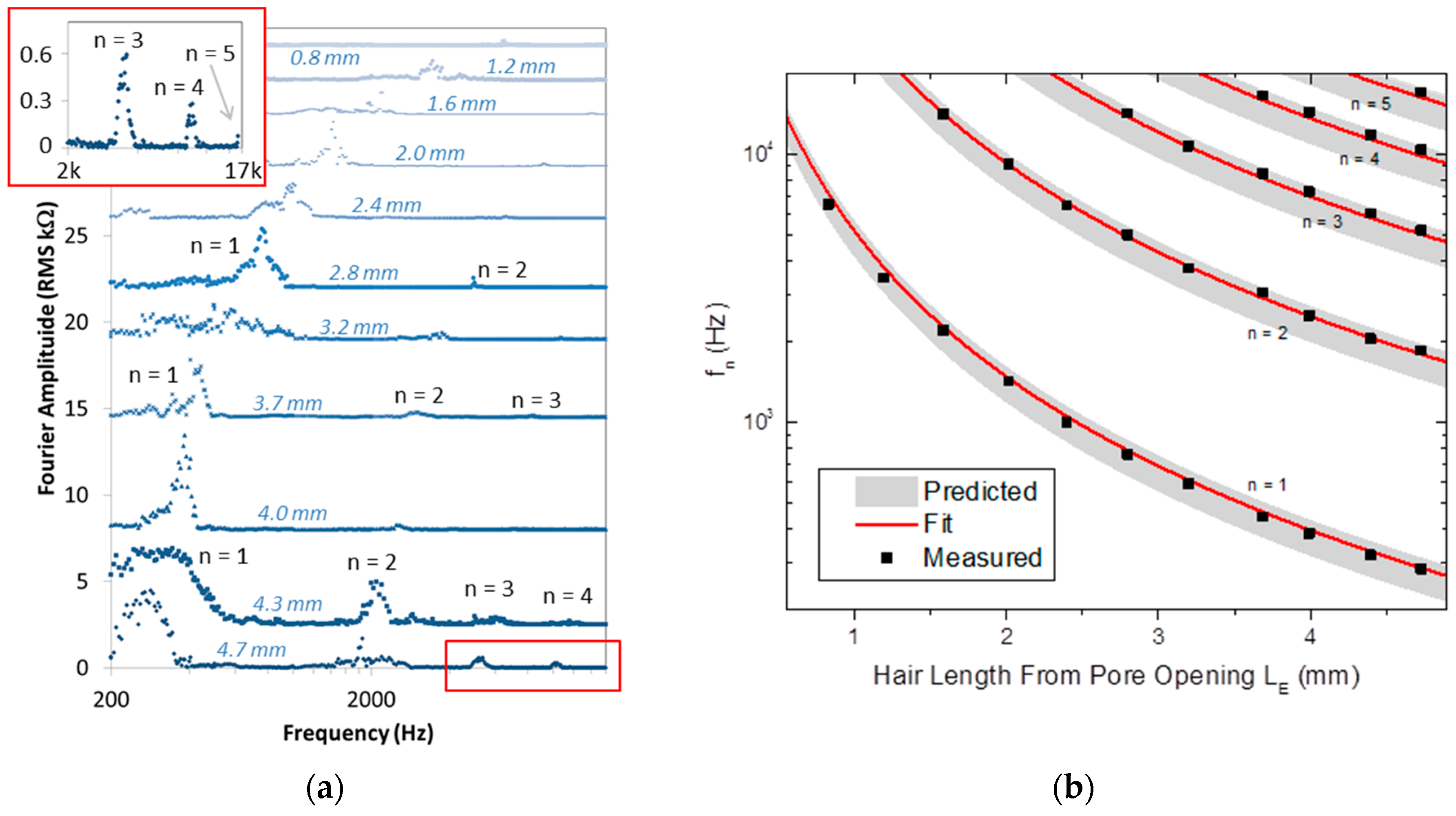
To investigate the relationship between the vibrational response of the sensors and their exposed hair length, a second sensor (Sensor 2) was incrementally reduced from an initial
LE of 4.73 mm to a final
LE of 0.83 mm. This sensor was one of 25 sensors previously examined in steady flow conditions [
4]. The magnitude of the Fourier transformed response is plotted versus the frequency in
Figure 2a for each length. Up to five resonance peaks are visible at the initial hair length and progressively shift to higher frequencies as
LE is reduced as expected. The peaks corresponding to the primary mode can be fit to the expression for a damped oscillator with a small damping coefficient (e.g., 0.008 for
LE of 2.78 mm). The resonance frequencies were extracted and are plotted versus the exposed length in
Figure 2b.
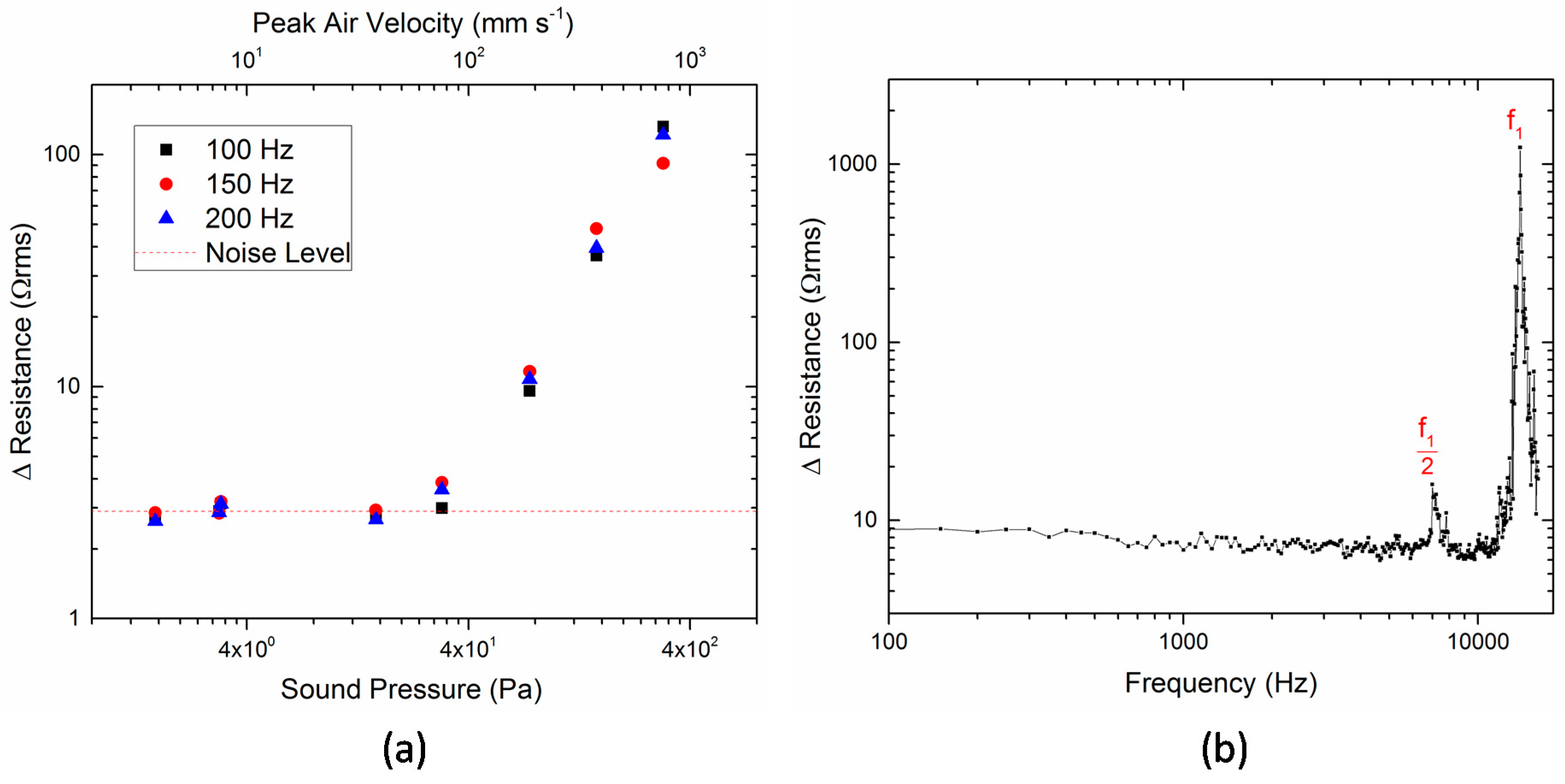
To assess the minimum detectable threshold of sensors such as these, the amplitude of the response is shown in
Figure 3a for Sensor 3 (
LE = 4.37 mm) versus the measured sound pressure amplitudes (
p0). The peak air velocity (
upeak) calculated from the sound pressure
is also indicated, where p is the pressure amplitude,
us is the speed of sound, and
ρair is density of air [
18]. The three frequencies shown below are the first resonance frequency. The RMS noise level of the setup was seen to be about 2.9 Ω·rms with no detectable change in resistance above this value for low air velocities. The resistance change increased linearly above a threshold of 70 mm·s
−1 air velocity, which is considered the dynamic detectable threshold for this sensor and measurement setup.
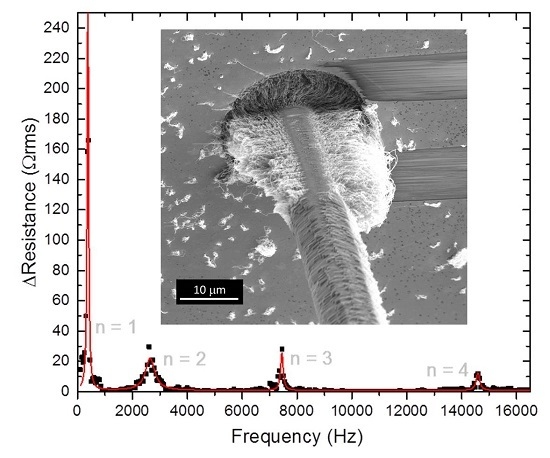
At a much shorter external length (0.62 mm), the sensitivity was decreased but the first resonance bandwidth was greatly increased. The frequency of the sinusoidal plane wave was swept from 100 Hz to 16 kHz at constant sound pressure amplitude of 300 Pa. The RMS change in the resistance of the sensor was seen to be approximately constant with the increasing frequency until the frequency approached the first resonance of the sensor at 13.9 kHz and the response of the sensor reached a peak (
Figure 3b). A small peak was also seen around half this frequency due to the increased contribution of the higher modes of the input in the plane wave tube at integer multiples of the applied frequency. The response of 6 to 9 Ω·rms below resonance is above the noise limit, making this a viable sensor for ultra-large-bandwidth applications even though the cross-section is greatly reduced.
3. Discussion
It can be seen from Equation (1) or Equation (3) that the resonance frequency will vary inversely with the square root of the mass per length of the beam (
ρA). For the S2 glass microfiber used in these experiments,
ρA is 1.6 × 10
−7 kg/m as calculated from the reported density. It is expected to be increased by the additional mass of the nanotubes. To determine the upper bound on ρA, the typical density of the CNT array (
ρCNT = 0.5 g·cm
−3) was estimated from mass and volume change measurements of CNT growth by the same method on large planar substrates. This density is somewhat larger than many reported values for CNT arrays since iron is continually fed to the system during synthesis, resulting in nanoparticles of iron within the volume of the CNT array [
19]. The areal density is assumed to be preserved for the glass fiber such that the additional mass per length on a cylindrical fiber is given by 2π·r
fiber·L
CNT·
ρCNT. The average length of the CNTs (L
CNT) was measured to be 12 μm, so the predicted maximum
ρA is 2.7 × 10
−7 kg/m.
The resonance frequencies predicted by the partial elastic base model in Equation (3) are compared to the measured resonance frequencies in
Figure 2b. The predicted resonance frequencies are within the bounded range of CNT densities expected, from negligible compared to the density of the glass fiber up to the maximum value estimated above. The measured resonance frequencies are found to fall within this band. The solid red line represents the best fit of the elastic base model to the measured resonance frequencies across all the modes and hair lengths. The mass per length is the only fit parameter and the best fit corresponds to a value of 1.9 × 10
−7 kg/m.
The first resonance bandwidth at any given length, e.g., 5.2 kHz at
LE = 1 mm, is large compared to other hair sensors. This is most obviously due to the large bending stiffness of the hair coupled with the low mass per density (e.g., the ratio of EI to
ρA). Similarly, for hair sensors that rotate at the base, the resonance frequency is proportional to the square root of the ratio of the torsional stiffness of the hinge at the base of the hair to the mass per length of the hair [
3,
20]. The hair will move in rotation rather than bending as long as this torsional stiffness is small relative to the bending stiffness of the hair. In both the torsional and bending cases, the bandwidth can be increased by choosing hair materials with large specific stiffness.
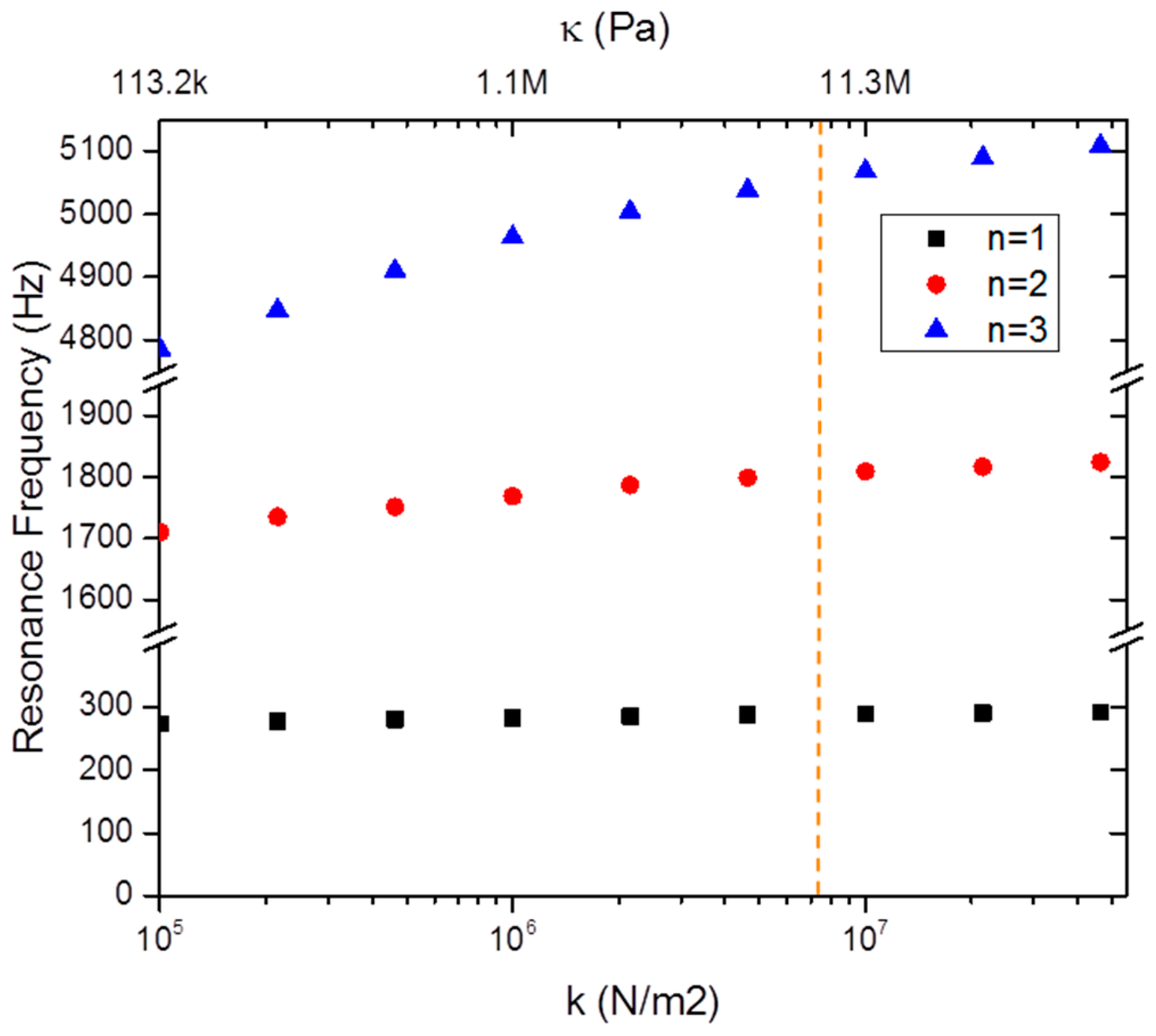
Using the elastic base model, the predicted role of the nanotube stiffness in the resonance frequencies of the sensors is shown in
Figure 4 assuming the other properties of the sensor are identical to Sensor 3 and with
LE = 4.37 mm. Reported values for the measured stiffness of nanotube arrays vary by as much as three orders of magnitude, most likely due to differences in synthesis conditions and substrate characteristics [
21,
22,
23]. As the stiffness is changed in this system, there is little predicted change to the useful frequency bandwidth before first resonance even though the higher-order modes show an obvious decrease in frequency with decreasing nanotube stiffness.
Whereas the bandwidth shows little dependence on k, the sensitivity and possibly the detectable threshold should be enhanced by decreasing the nanotube array stiffness. Indeed, a quasi-static analysis by Slinker et al. indicates the sensitivity decreases as
k1/2 [
4]. Conversely, the quasi-static deflection range over which a change in resistance is significant (i.e., span of the middle section of the sigmoidal response) and the percent resistance change per deflection (the slope of the middle of the sigmoidal response) have opposite dependence on the length and fiber bending stiffness, with the former going as
L−2 and (
EI)
1/2, while the latter goes as
L and (
EI)
−1/2. Control of the stiffness of the support material and alternative means for signal generation (piezoelectric, etc.) may provide opportunities in the future to optimize the sensitivity of these devices without impacting the observed large bandwidth.