Next Article in Journal
Pulsed Laser Annealing of Deposited Amorphous Carbon Films
Previous Article in Journal
Carbon Dot Nanozymes in Orthopedic Disease Treatment: Comprehensive Overview, Perspectives and Challenges
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
C
Volume 11
Issue 3
10.3390/c11030059
carbon-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

In Silico Exfoliation of ReaxFF Graphite—Temperature, Speed, Angle Dependence, and the Effect of Gold Overlayer

by
Teruki Ando
1,
Seiya Yokokura
1,
Hiroki Waizumi
1,
Hironori Suzuki
2,
Kenji Kawashima
2 and
Toshihiro Shimada
1,*
1
Division of Applied Chemistry, Faculty of Engineering, Graduate School of Chemical Science and Engineering, Hokkaido University, Kita 13-Nishi 8, Kita-ku, Sapporo 060-8628, Japan
2
IMRA Japan, 2-36 Hachiken-Cho, Kariya 448-8650, Japan
*
Author to whom correspondence should be addressed.
C 2025, 11(3), 59; https://doi.org/10.3390/c11030059
Submission received: 31 May 2025 / Revised: 31 July 2025 / Accepted: 31 July 2025 / Published: 7 August 2025
(This article belongs to the Section Carbon Materials and Carbon Allotropes)
Browse Figures
Versions Notes

Abstract

Exfoliation of layered materials is an important technique for preparing atomic-layer materials. To provide fundamental mechanistic insights for optimizing this process, we investigated the exfoliation process of nano graphite using molecular dynamics simulations with the ReaxFF force field. The impact of temperature, speed, and angle of removing the top layer has been examined to gain insight into obtaining thin, uniform layers. The bending rigidity of the ReaxFF graphite is temperature-dependent and affects the cleavage behavior. The impact of the Au overlayer, which has recently been utilized to obtain a large area, was also studied, and it was confirmed to be effective in improving repeatability.

Graphical Abstract

1. Introduction

Graphene and other atomic layer materials are expected to find applications in a wide variety of fields, including next-generation electronics, energy storage, and composite materials, due to their unique electronic, mechanical, and thermal properties [1,2]. One of the primary methods for fabricating these materials is exfoliation from bulk layered materials. The mechanical exfoliation of graphene from graphite has been widely studied as a fundamental approach to obtain high-quality mono- and few-layer graphene [3,4]. However, it remains challenging to control the single-layer thickness of layered materials during mechanical exfoliation over a wide area, which often exceeds several hundred micrometers. Despite its widespread use, the mechanism of mechanical exfoliation remains incompletely understood in many aspects. Experimental studies include nanoscale exfoliation experiments using atomic force microscopy (AFM) [5] and exfoliation energy measurements [6]. These studies have demonstrated that the exfoliation force and energy are dependent on the number of layers and environmental conditions. In addition, various peeling techniques, such as ultrasonic-assisted liquid-phase peeling [7], shear force-based peeling [8], and electrochemical methods [9] have been developed to improve their efficiency. Many theoretical and computational studies have been reported to support the exfoliation experiments; however, they are primarily focused on the liquid phase [10,11,12,13,14,15,16], powder exfoliation [17,18], or the fundamental development of the methodology, including the creation of novel force fields [19]. The knowledge about the effects of temperature [20], peeling speed, and lift angles on exfoliation is very limited, based on both simulations and experiments.
Recently, exfoliation techniques using metal deposition layers have garnered significant attention as a transfer method for large-area graphene. For example, it has been demonstrated that thin metal films, such as Au, can be deposited on graphite and layered materials. Then, the atomic layers can be exfoliated along with the metal film [21,22,23]. The advantage of this technique is that it can efficiently exfoliate single or a few layers of graphene due to the moderate interaction between the metal and graphene, compared to the organic adhesives used in scotch tapes.
The primary objective of this study is to elucidate the underlying mechanisms by which exfoliation parameters determine the outcome of delamination at the atomic scale, and to provide physical insight into the dynamic process. Additionally, the second objective is to establish guiding principles for optimizing scalable production technologies based on knowledge of these mechanisms. Therefore, we here report the MD simulation of graphene exfoliation using the Reactive force field (ReaxFF) [24,25], which is particularly useful for analyzing complex systems involving the formation and breaking of atomic bonds, and the effect of metallic species. A wide variety of studies on carbon materials using ReaxFF have been reported, including the fracture of carbon materials [26], the formation mechanism of graphene oxide, pyrolysis of hydrocarbons, and the frictional properties of diamond-like carbon [27]. We also examined the bending behavior of ReaxFF graphite to assess the limitations of using this force field for simulating the mechanical properties of graphite involved in exfoliation. In the following, we refer to the simulated material as “ReaxFF graphite (or graphene)” to avoid confusion with the real graphite.
The exfoliation of layered materials can be considered as a model case of mechanical fracture of strongly anisotropic materials. During the analysis of the kinetic aspects of the exfoliation process, we found that layer bouncing, likely related to thermal rippling, plays a crucial role in determining the exfoliation thickness, providing new insights into atomic-scale fracture processes [28].

2. Materials and Methods

We have employed LAMMPS with ReaxFF [29,30]. The structure we have calculated consists of 7 layers of supercoronene (C733H69), i.e., hydrogen-terminated circular graphene stacked in the same manner as 2H-graphite (Figure 1). The initial bond distances were taken from bulk graphite and aromatic hydrocarbons. The top and bottom layers were thermally frozen, and the top layer was moved with various speeds and motions. The temperature was set to a specific value using the NVT scheme with a Nosé–Hoover thermostat [31,32]. Timestep was 0.1 fs. A periodic boundary cell of 10 nm × 10 nm × 10 nm was employed. Before the mechanical motion was initiated for exfoliation, the system was thermally stabilized at designated temperatures for 1 to 10 ps. Thermal equilibrium was confirmed by monitoring the temperature. The top and bottom layers were frozen, and their atomic positions were controlled as a function of time.
We examined the various speeds of lifting and oblique lifting of the top layer and conducted five simulations under the same conditions with different random seeds. We used the OVITO program package (version 3.12.4) [33] for visualization. To explore the effects of the Au overlayer, three atomic layers of fcc-structured Au with the bulk lattice constant were put on the supercoronene. The atomic distance between Au and the top-layer carbon was determined by energy minimization of the ReaxFF simulation. Au atoms were frozen. The ReaxFF potentials for C, H, and Au were obtained from the literature [34,35,36]. For the estimation of bending rigidity, we applied constant forces to the edges and centerline of a nearly square (50 Å × 50 Å) single graphene sheet (C960). We measured the curvature after stabilization at various temperatures.

3. Results

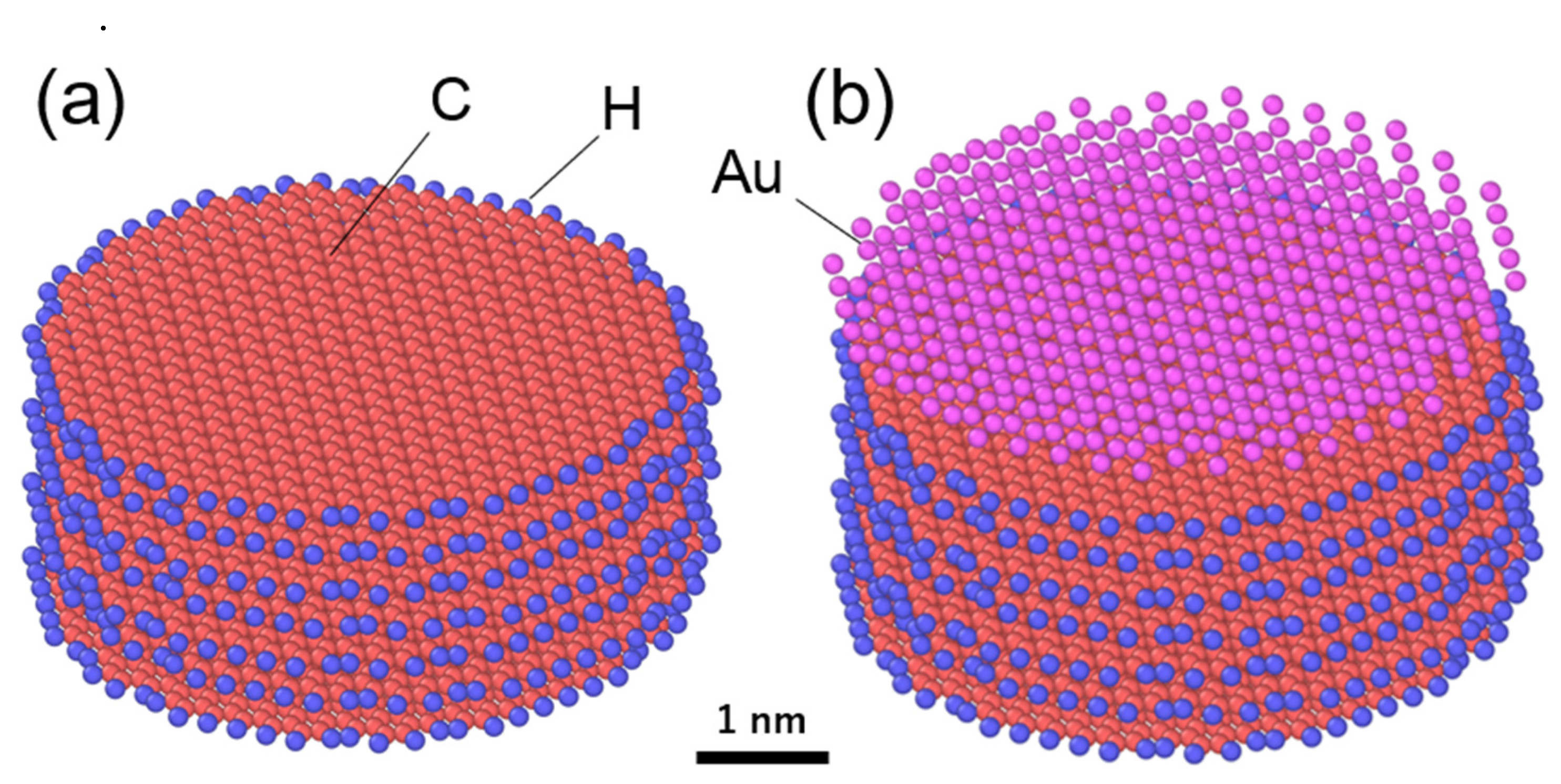
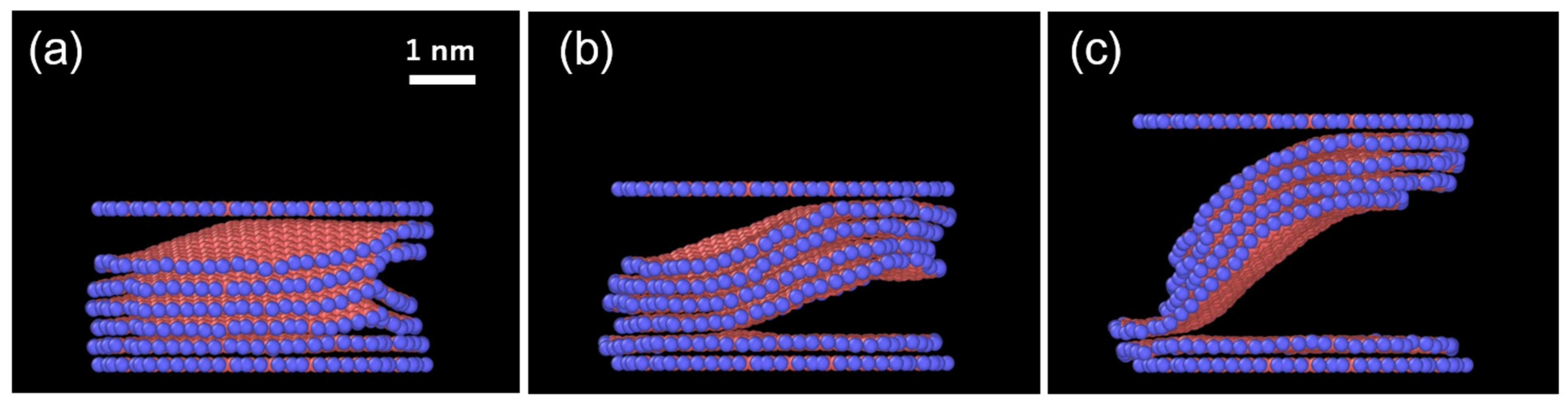
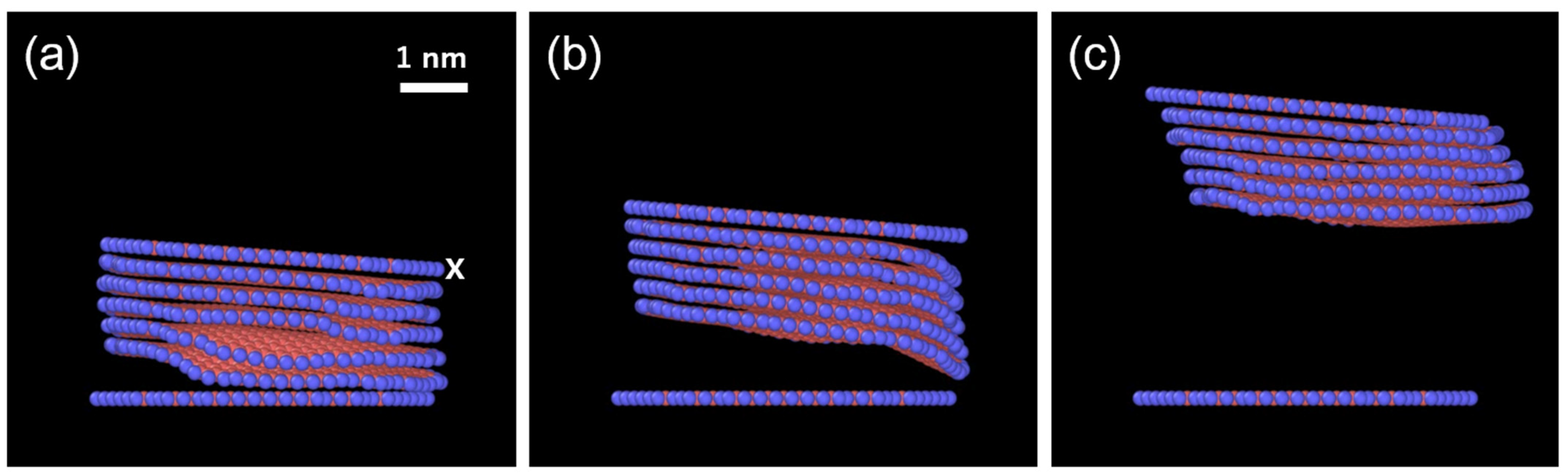
3.1. Exfoliation Behavior of ReaxFF Nanographite (Supercoronene)

First, we examined continuous speed vertical lifting of the top layer at various temperatures. The result is summarized in Table 1, which shows the average and standard deviations (indicated after ‘±’) from five replica simulations with different random seeds. We notice the following:
(1)
The speed of lifting intensely affects the number of layers, and there is a certain threshold. Multiple layers are lifted with the top layers when the speed is 0.5~1 Å/ps (50~100 m/s), but the top layer is removed alone at the speed of 5 Å/ps (500 m/s). These values of lifting speed are higher than those in the real experiments, but the result can be scaled using the calculated bending rigidity of ReaxFF graphene, as explained later.
(2)
The effect of temperature is not straightforward. Pristine graphene exhibits a reduced number of exfoliated layers at a rate of 1 Å/ps as the temperature increases, whereas the number of exfoliated layers increases at a rate of 2 Å/ps.
(3)
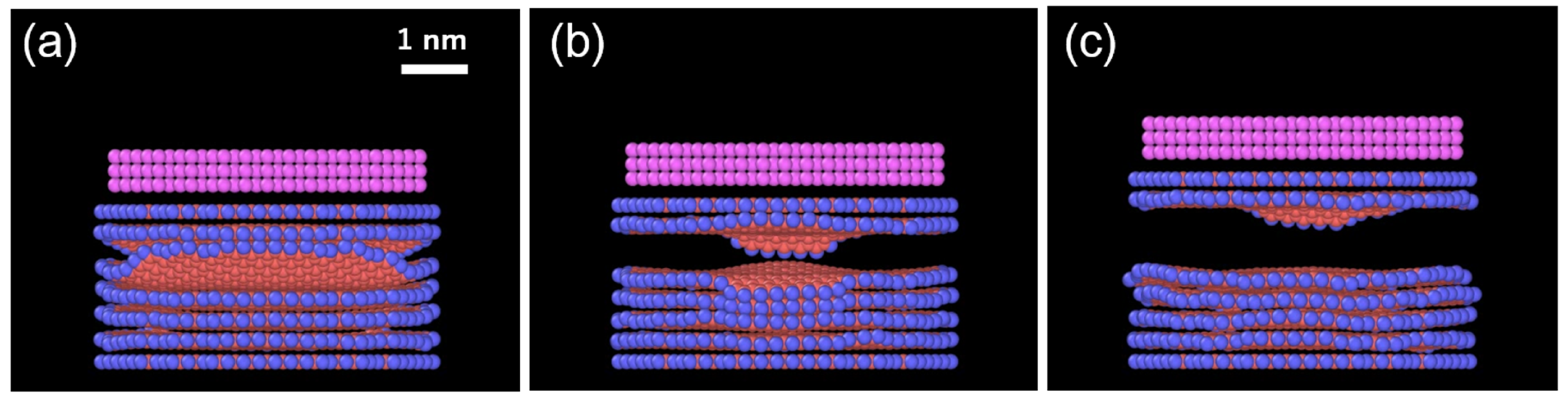
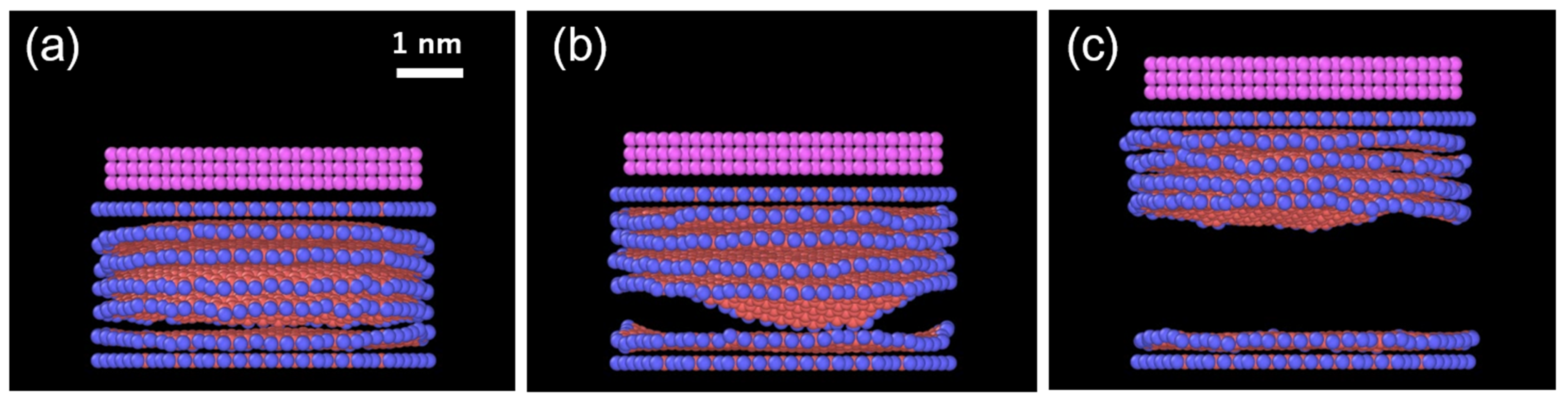
The Au overlayer affects the result (Table 2). The deviation of the results is significantly reduced, especially in the case of 1 Å/ps, as all the replicas show identical numbers of exfoliated layers. Since the top graphene layer is lifted with the Au layers, the Au only modifies the interaction between the top layer and the second layer of the graphene sheets. It is noted that this minor sublayer modification is enough to control the results. By analyzing the total energy before and after exfoliation at 10 K, the interaction energy between the layers of ReaxFF graphene without an Au overlayer was found to be 39.8 meV/atom. This falls within the range in the literature: 30–52 meV/atom [37,38,39] from theory, and approximately 50 meV/atom from experiments using carbon nanotubes and aromatic molecules [40,41]. With an Au overlayer, our simulations yield 79.8 and 48.6 meV/atom for the first–second layers (zero-layer exfoliation) and second–third layers (one-layer exfoliation), respectively. They are substantially greater than that without an Au overlayer and steeply decrease as the layer number increases, which accounts for the present result. The critical implication of this result is that there is an appropriate speed range for the exfoliation, depending on the strength of interlayer interactions.
The feature (1) can be explained easily by the fact that the acceleration (a) of the second layer (next to the top layer) by the attraction via van der Waals force (F) derived from Newton’s law (F = ma, where m is the mass involved) is not enough to follow the motion of the top layer. However, features (2) and (3) are complicated, and their behavior seems exemplary in fracture processes. We need to examine the mechanism in detail from the snapshots of the exfoliation. First, we examine the feature (2), which is typically observed at the speed of 2 Å/ps. Figure 2 shows the snapshots taken at the critical scene of the cleavage. In Figure 2a, the second layer (next to the top) is half cleaved from the top layer, and the third layer is almost parallel to the second layer, while the fourth, fifth, and sixth layers are sticking to the bottom layer. Then a wavy motion occurs in the fourth and fifth layer at the right-hand side of the image. This wavy motion seems to be induced by thermal rippling of the graphene sheet. In Figure 2b, the right-hand side of the fourth and fifth layer is attached to the third layer. Then, in Figure 2c, a “tag of war” happens between the first–second and the fifth–sixth layer. The result appears stochastic, as both zero-layer and four-layer cleavage occur. In different runs with varying random seeds, different behaviors are observed, resulting in varying numbers of exfoliated layers at this threshold temperature and speed. This does not happen at lower temperatures, but occurs at temperatures higher than 400 K. For example, Figure 3 shows snapshots at 200 K with the top layer lifted at a speed of 2 Å/ps. The distinct difference is that the “wavelength” of the wavy motion is longer than that at 400 K or higher, making the inertia larger and the amplitude smaller. Mechanical properties exemplified by “bending rigidity” should be examined as a function of temperature. Before doing so, we will see the impact of the pre-tilting. Figure 4 and Figure 5 show the typical snapshots with an Au overlayer, which show excellent reproducibility, although the thermal rippling also exists.

3.2. Impact of Pre-Tilting of the Top Layer Before Lifting

Exfoliation of layered materials can be achieved in various ways, including the use of classical scotch tapes [3], robot-operated lens-like rubber with an adhesive structure [4], and ultrasonic cavitation in liquids, among others. All are involved in the force applied in the tilted directions, not only vertical lifting. We examined the effect of pre-tilting the top layer before lifting it. The top layer was rotated around an axis 1 Å from the edge, and the height of the top layer in equilibrium (indicated by a white “x” mark in Figure 6a) was adjusted so as not to apply a compressive force. After rotating by a certain angle (1°, 2°, 5°), it was lifted at a speed of 2 Å/ps, which appears to be a threshold value for the number of exfoliated layers. The results are tabulated in Table 3, which shows a distinct difference from the normal lifting. From the snapshot shown in Figure 6b, the asymmetric adhesion between layers induced by the tilted top layer plays an important role. This pre-tilting mimics the real exfoliation process by using a scotch-tape or lens-shaped rubber structure. The present result strongly suggests that careful real-time control of the pre-tilting can be a strategy of mechanical exfoliation to obtain uniform atomic layers with a large area.

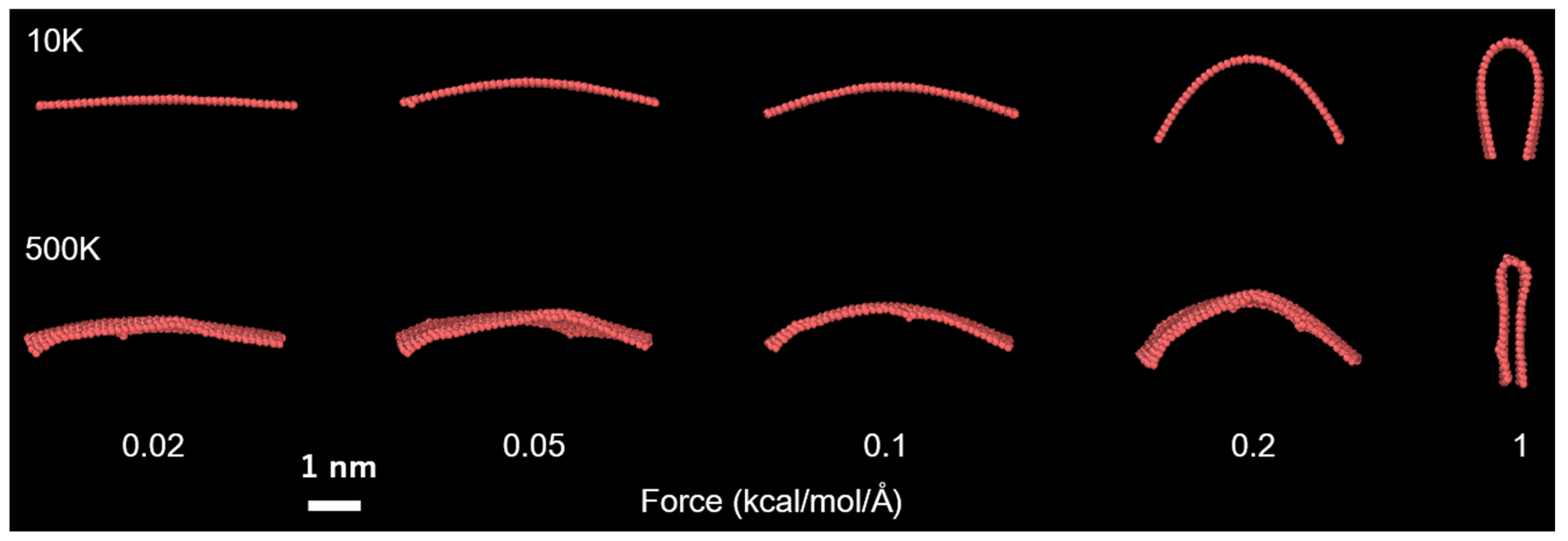
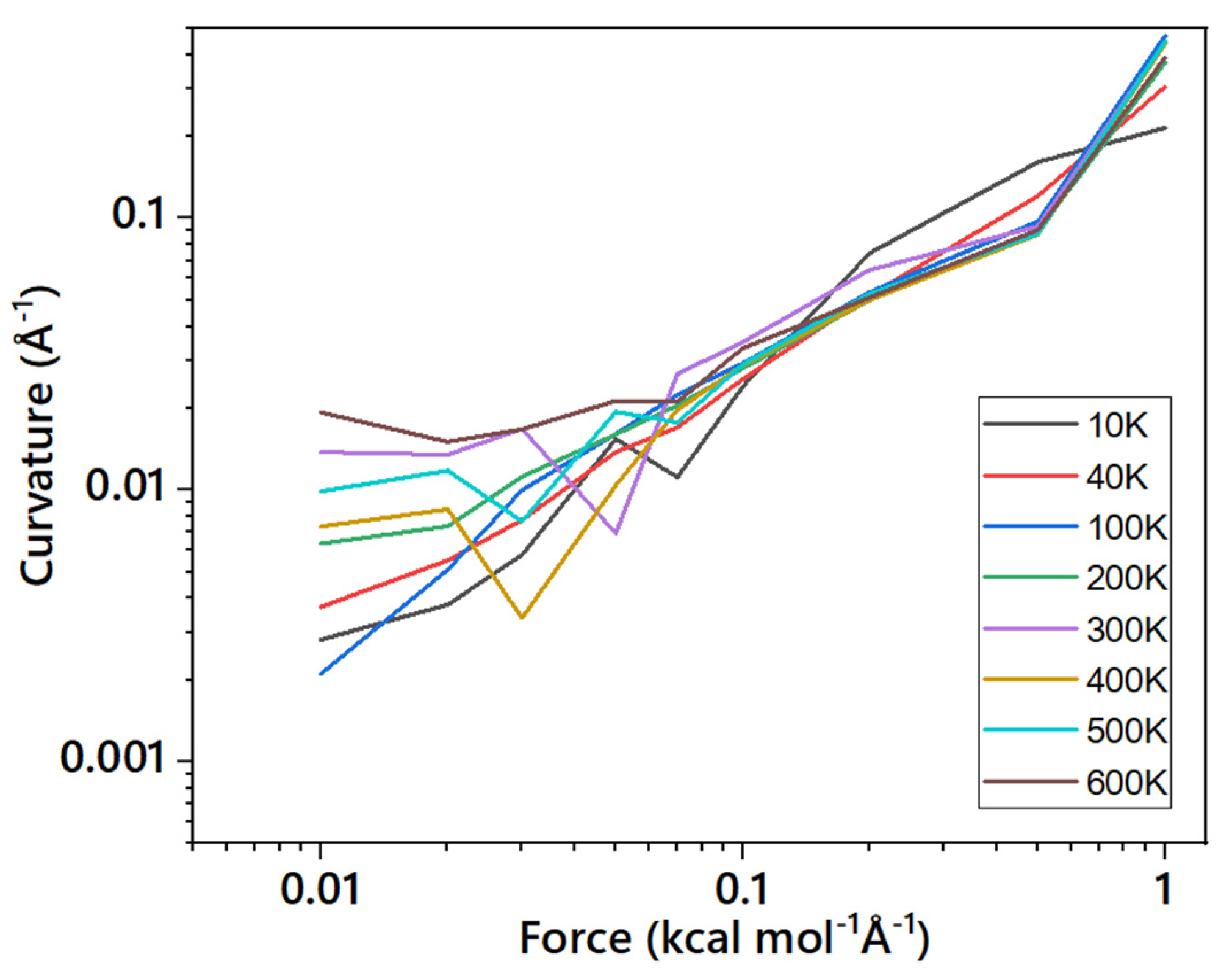
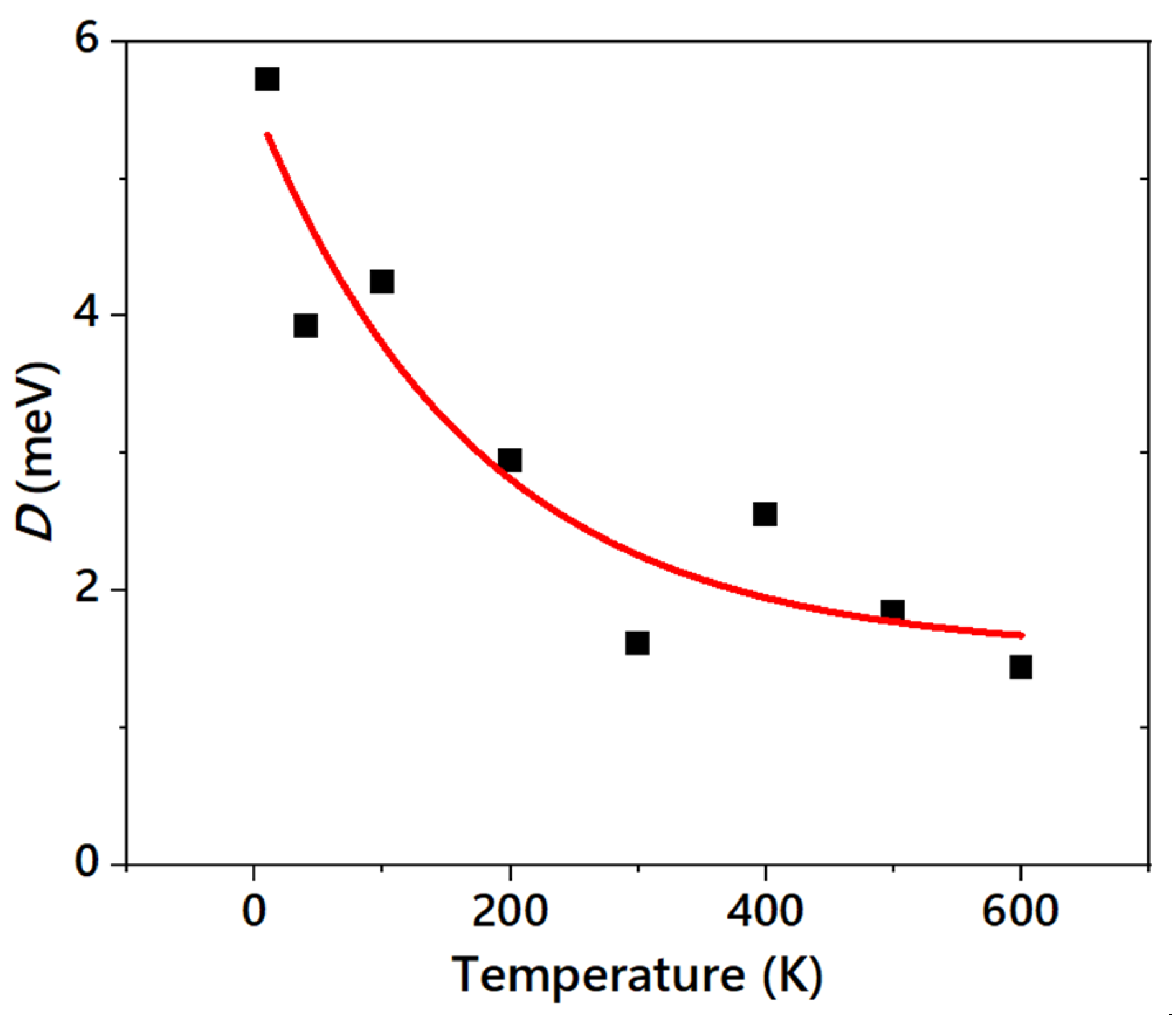
3.3. Estimation of the Bending Rigidity of ReaxFF Graphene

Bending rigidity is considered a crucial parameter for discussing the mechanical properties of graphene [42,43,44,45,46,47,48,49,50,51,52]. Many theoretical and experimental results have been published, and researchers are still actively concerned about the atomic nature of two-dimensional flexibility. The value of the bending rigidity has converged to ~1.1 eV, but the temperature dependence is still under active discussion [52]. Since the bending of graphene layers plays a crucial role in the exfoliation process, as stated above, we estimated the temperature and force dependence of the bending rigidity of ReaxFF graphene.
We prepared a nearly square sheet of graphene (50 Å × 50 Å) and used a three-point bending scheme. A certain force (F) was applied to lift the center row atoms in the graphene sheet, and opposite forces (−F/2) were applied at the edges to keep the center of mass. The forces were applied along the direction of the zigzag edge. After the NVT simulation has run for a sufficient time to equilibrate the system, the curvature of the centered 4 to 10 rows is measured by a least-squares fit to a portion of a circle. Figure 7 illustrates some of the results of the curvature measurement.
The resulting curvatures as a function of temperature and applied forces are shown in Figure 8. We observe that the curvature is strongly dependent on temperature when the force is small, but converges at large forces. Additionally, we notice dips in the curve. We consider this to be related to thermal ripples in graphene, which are also observed in other calculations. From the curvature and forces, the bending rigidity can be estimated. Since the values are dependent on the forces (curvatures), we have taken F = 0.02 kcal/mol/Å, which shows strong temperature dependence. The curvature of ~0.01 Å−1 corresponds to the bending radius of 100 Å, which is typically observed in this simulation of the exfoliation.
The bending rigidity, D, was calculated using the following formula.
D = F L 4 W κ
where L and W are the length and width of the sheet, κ is the curvature. The result is shown in Figure 9, which demonstrates the “softening” of the ReaxFF graphene at higher temperatures. However, this “softening” with increasing temperature contradicts recent experimental evidence [52], which reports a “hardening” of real graphene. This fundamental discrepancy highlights a limitation of the ReaxFF potential in accurately capturing the subtle entropic effects that govern the temperature-dependent mechanics of real graphene. It should also be noted that the D values for ReaxFF graphene (1.6~6 meV) differ significantly from the reported actual graphene values (~1.1 eV) [42,43,44,45,46,47,48,49,50,51,52]. This significant discrepancy is primarily attributed to the fundamental parameterization of the ReaxFF force field. The parameters used [34,35,36] are taken from drastically different molecular systems with respect to graphene; they were optimized for simulating covalent bonding in Au-S-C-H systems, not specifically for reproducing the high bending stiffness of graphene, which arises from its unique, planarπ-conjugated system with non-covalent interlayer interaction.

3.4. Implications on the Real Graphene and Other Layered Materials

Since the bending rigidity (D) values differ from those of real graphene, it is inappropriate to compare the present results with the real graphite exfoliation directly. Instead, since ReaxFF graphene is much softer against bending, this simulation can be compared with the softer 2D polymers, such as covalent organic frameworks [53,54,55,56]. The study also provides several guiding principles for experiments. The critical speed of ~1 Å/ps (100 m/s) found in our simulation, when scaled by the two- to three-orders-of-magnitude difference in bending rigidity, suggests a realistic critical speed of approximately 1 m/s for mechanical exfoliation of real graphite. This provides a quantitative target for experimental setups, such as AFM-based exfoliation or roll-to-roll processes. Furthermore, our results, which show a dramatic change in outcome with a slight pre-tilt angle (Table 3), highlight that precise, dynamic control of the peeling angle is a critical parameter for achieving uniform, large-area exfoliation, rather than seeking a single optimal angle. It is essential to acknowledge the discrepancies between this idealized simulation and experimental reality. Our model uses a defect-free and size-limited nanographene, whereas real graphite contains grain boundaries, point defects, and surface adsorbates. These imperfections can act as stress concentration points, likely promoting exfoliation at lower forces and speeds, and contributing to the stochastic nature often seen in experiments. Therefore, our findings should be considered a baseline for an ideal system. Regarding the transferability of these conclusions, the qualitative behaviors—such as the existence of a critical speed and the importance of temperature and tilt angle—are likely universal for other 2D materials like MoS2 or h-BN, as they stem from the fundamental competition between interlayer adhesion and bending stiffness. However, the quantitative parameters (e.g., the exact critical speed) will require recalibration for each material, as they depend heavily on material-specific parameters. Finally, while the Au overlayer was used as a model to modify interlayer interactions, its practical use involves challenges such as cost, potential contamination, and complex post-processing removal steps. Future work could explore alternatives, such as charge-transfer polymers or other metals, which might offer similar benefits without such drawbacks.
Finally, we comment on the effects of the finite size and the edges in this simulation. There are various ways to increase the scale of the simulation, such as using a larger supercell or applying periodic boundary conditions [20]. Upon initial evaluation of those directions, we found that many additional factors became involved, including the increased contribution of curvature and enhanced thermal rippling. Bond breaking and formation, as well as atmospheric pressure, may be involved on a realistic scale, as observed in the experiments. Considering this, we limit this study to a size-limited but well-defined system, which is primarily governed by van der Waals interactions in chemically saturated materials.

4. Conclusions

We investigated the exfoliation process of graphite using molecular dynamics simulations with the ReaxFF force field, aiming to uncover fundamental mechanisms to guide the development of large-area exfoliation techniques. Although the bending rigidity of ReaxFF graphene differs from reported values of real graphene, essential features of the exfoliation have been derived, which can be generalized to the exfoliation of layered materials. There is a critical speed of lifting that determines the number of exfoliated layers. Temperature dependence exists. Pre-tilting the top layer, which is realistic by applying peeling forces using Scotch Tape, significantly affects the number of layers. Modification of the first–second layer interaction by the Au overlayer alters the critical speed and temperature behavior, thereby enhancing reproducibility. These uplifting results suggest that precise real-time control of speed and tilt angle will enable the exfoliation of atomic layers with a large area, as designed. We hope the significant technical barriers, including the need for extreme precision in mechanical control over large areas, the challenge of substrate non-uniformity (such as defects and grain boundaries), and the complexity of integrating real-time feedback systems for process control, will someday be overcome.

Author Contributions

Conceptualization, H.S., K.K. and T.S.; methodology, T.A.; software, T.A. and T.S.; validation, S.Y. and H.W.; writing, T.A. and T.S.; writing—review and editing, S.Y. and H.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data for this research are available from the corresponding author upon reasonable request.

Acknowledgments

The authors are grateful to the Supercomputer time from the Institute of Solid State Physics, The University of Tokyo (2024-Ba-0054) and the Research Center for Computational Science, Okazaki, Japan (Projects: 25-IMS-C358 and 24-IMS-C072), which were partly used for the present research.

Conflicts of Interest

The authors declare no conflicts of interest. This significant discrepancy is primarily attributed to the fundamental parameterization of the ReaxFF force field.

References

  1. Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
  2. Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F.; et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef] [PubMed]
  3. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
  4. Kinoshita, K.; Moriya, R.; Onodera, M.; Wakafuji, Y.; Masubuchi, S.; Watanabe, K.; Taniguchi, T.; Machida, T. Dry release transfer of graphene and few-layer h-BN by utilizing thermoplasticity of polypropylene carbonate. npj 2D Mater. Appl. 2019, 3, 22. [Google Scholar] [CrossRef]
  5. Li, X.; Cai, W.; An, J.; Kim, S.; Nah, J.; Yang, D.; Piner, R.; Velamakanni, A.; Jung, I.; Tutuc, E.; et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef]
  6. Koenig, S.P.; Boddeti, N.G.; Dunn, M.L.; Bunch, J.S. Ultrastrong adhesion of graphene membranes. Nat. Nanotechnol. 2011, 6, 543–546. [Google Scholar] [CrossRef]
  7. Hernandez, Y.; Nicolosi, V.; Lotya, M.; Blighe, F.M.; Sun, Z.; De, S.; McGovern, I.T.; Holland, B.; Byrne, M.; Gun’ko, Y.K.; et al. High-yield production of graphene by liquid-phase exfoliation of graphite. Nat. Nanotechnol. 2008, 3, 563–568. [Google Scholar] [CrossRef]
  8. Paton, K.R.; Varrla, E.; Backes, C.; Smith, R.J.; Khan, U.; O’Neill, A.; Boland, C.; Lotya, M.; Istrate, O.M.; King, P.; et al. Scalable production of large quantities of defect-free few-layer graphene by shear exfoliation in liquids. Nat. Mater. 2014, 13, 624–630. [Google Scholar] [CrossRef]
  9. Munuera, J.M.; Paredes, J.I.; Enterría, M.; Pagán, A.; Villar-Rodil, S.; Pereira, M.F.R.; Martins, J.I.; Figueiredo, J.L.; Cenis, J.L.; Martínez-Alonso, A.; et al. Electrochemical Exfoliation of Graphite in Aqueous Sodium Halide Electrolytes toward Low Oxygen Content Graphene for Energy and Environmental Applications. ACS Appl. Mater. Interfaces 2017, 9, 24085–24099. [Google Scholar] [CrossRef]
  10. Gotzias, A.; Lazarou, Y.G. Graphene Exfoliation in Binary NMP/Water Mixtures by Molecular Dynamics Simulations. ChemPlusChem 2023, 88, e202300758. [Google Scholar] [CrossRef]
  11. Gotzias, A.; Tocci, E.; Sapalidis, A. Solvent-Assisted Graphene Exfoliation from Graphite Using Umbrella Sampling Simulations. Langmuir 2023, 39, 18437–18446. [Google Scholar] [CrossRef]
  12. Cai, L.; Hou, S.; Wei, X.; Tan, G.; Peng, Z.; Yan, Y.; Wang, L.; Lei, D.; Wu, Y.; Liu, Z. Exfoliation and stabilization mechanism of graphene in carbon dioxide expanded organic solvents: Molecular dynamics simulations. Phys. Chem. Chem. Phys. 2020, 22, 2061–2070. [Google Scholar] [CrossRef] [PubMed]
  13. Biswas, R. Molecular dynamics studies on the exfoliation of graphene in room temperature ionic liquids. J. Mol. Liq. 2021, 337, 116592. [Google Scholar] [CrossRef]
  14. Cai, L.; Tan, G.; Jing, X.; Wu, Y.; Liu, Z. How to obtain high monolayer content in liquid phase exfoliation of graphene: A molecular dynamic simulation. J. Mol. Liq. 2023, 382, 121873. [Google Scholar] [CrossRef]
  15. He, Y.; Qian, X.; Queiroz da Silva, G.C.; Gabellini, C.; Lucherelli, M.A.; Biagiotti, G.; Richichi, B.; Ménard-Moyon, C.; Gao, H.; Posocco, P.; et al. Unveiling Liquid-Phase Exfoliation of Graphite and Boron Nitride Using Fluorescent Dyes Through Combined Experiments and Simulations. Small 2024, 20, 2307817. [Google Scholar] [CrossRef]
  16. Chen, S.; Li, Q.; He, D.; Liu, Y.; Wang, L.; Wang, M. Dynamic exfoliation of graphene in various solvents: All-atom molecular simulations. Chem. Phys. Lett. 2022, 804, 139900. [Google Scholar] [CrossRef]
  17. Wu, P.; Wei, T.; Wei, J.; Zhou, Q.; Zhang, W.; Liu, M. Simulation on fabricating graphene-coated nickel powders through micromechanical exfoliation. Mater. Today Commun. 2024, 38, 109853. [Google Scholar] [CrossRef]
  18. Nishad, W.; Subbiah, S.; Swaminathan, N. A qualitative understanding of high intensity mechanical shearing and exfoliation of graphite nanoplatelets in a three-body contact using molecular dynamic simulations. J. Manuf. Process. 2021, 71, 645–652. [Google Scholar] [CrossRef]
  19. Sinclair, R.C.; Suter, J.L.; Coveney, P.V. Graphene–Graphene Interactions: Friction, Superlubricity, and Exfoliation. Adv. Mater. 2017, 29, 1705791. [Google Scholar] [CrossRef]
  20. Prodanov, N.V.; Khomenko, A.V. Computational investigation of the temperature influence on the cleavage of a graphite surface. Surf. Sci. 2010, 604, 730–740. [Google Scholar] [CrossRef]
  21. Velický, M.; Donnelly, G.E.; Hendren, W.R.; McFarland, S.; Scullion, D.; DeBenedetti, W.J.I.; Calinao Correa, G.; Han, Y.; Wain, A.J.; Hines, M.A.; et al. Mechanism of Gold-Assisted Exfoliation of Centimeter-Sized Transition-Metal Dichalcogenide Monolayers. ACS Nano 2018, 12, 10463–10472. [Google Scholar] [CrossRef]
  22. Chen, S.; Li, B.; Dai, C.; Zhu, L.; Shen, Y.; Liu, F.; Deng, S.; Ming, F. Controlling Gold-Assisted Exfoliation of Large-Area MoS2 Monolayers with External Pressure. Nanomaterials 2024, 14, 1418. [Google Scholar] [CrossRef]
  23. Ziewer, J.; Ghosh, A.; Hanušova, M.; Pirker, L.; Frank, O.; Velicky, M.; Gruning, M.; Huang, F. Strain-Induced Decoupling Drives Gold-Assisted Exfoliation of Large-Area Monolayer 2D Crystals. Adv. Mater. 2025, 37, 2419184. [Google Scholar] [CrossRef]
  24. van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
  25. Chenoweth, K.; van Duin, A.C.T.; Goddard, W.A. ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef]
  26. Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF Potential for Carbon Condensed Phases and Its Application to the Thermal Fragmentation of a Large Fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef]
  27. de Tomas, C.; Suarez-Martinez, I.; Marks, N.A. Graphitization of amorphous carbons: A comparative study of reactive force fields. Carbon 2016, 109, 681–693. [Google Scholar] [CrossRef]
  28. Bitzek, E.; Kermode, J.R.; Gumbsch, P. Atomistic aspects of fracture. Int. J. Fract. 2015, 191, 13–30. [Google Scholar] [CrossRef]
  29. Aktulga, H.M.; Fogarty, J.C.; Pandit, S.A.; Grama, A.Y. Parallel Reactive Molecular Dynamics: Numerical Methods and Algorithmic Techniques. Parallel Comput. 2012, 38, 245–259. [Google Scholar] [CrossRef]
  30. Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
  31. Nosé; S A unified formulation of the constant temperature molecular-dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [CrossRef]
  32. Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A. 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
  33. Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
  34. Järvi, T.T.; van Duin, A.C.; Nordlund, K.; Goddard, W.A. III. Development of interatomic reaxff potentials for Au−S−C−H systems. J. Phys. Chem. A 2011, 115, 10315–10322. [Google Scholar] [CrossRef]
  35. Bae, G.-T.; Aikens, C.M. Improved ReaxFF force field parameters for Au–S–C–H systems. J. Phys. Chem. A 2013, 117, 10438–10446. [Google Scholar] [CrossRef] [PubMed]
  36. Monti, S.; Carravetta, V.; Ågren, H. Simulation of gold functionalization with cysteine by reactive molecular dynamics. J. Phys. Chem. Lett. 2016, 7, 272–276. [Google Scholar] [CrossRef] [PubMed]
  37. Girifalco, L.A.; Lad, R.A. Energy of cohesion, compressibility, and the potential energy functions of the graphite system. J. Chem. Phys. 1956, 25, 693–697. [Google Scholar] [CrossRef]
  38. Chakarova-Käck, S.D.; Schröder, E.; Lundqvist, B.I.; Langreth, D.C. Application of van der Waals density functional to an extended system: Adsorption of benzene and naphthalene on graphite. Phys. Rev. Lett. 2006, 96, 146107. [Google Scholar] [CrossRef]
  39. Dappe, Y.J.; Basanta, M.A.; Flores, F.; Ortega, J. Weak chemical interaction and van der Waals forces between graphene layers: A combined density functional and intermolecular perturbation theory approach. Phys. Rev. B 2006, 74, 205434. [Google Scholar] [CrossRef]
  40. Zacharia, R.; Ulbricht, H.; Hertel, T. Interlayer cohesive energy of graphite from thermal desorption of polyaromatic hydrocarbons. Phys. Rev. B 2004, 69, 155406. [Google Scholar] [CrossRef]
  41. Benedict, L.X.; Chopra, N.G.; Cohen, M.L.; Zettl, A.; Louie, S.G.; Crespi, V.H. Microscopic determination of the interlayer binding energy in graphite. Chem. Phys. Lett. 1998, 286, 490–496. [Google Scholar] [CrossRef]
  42. Zakharchenko, K.V.; Los, J.H.; Katsnelson, M.I.; Fasolino, A. Atomistic simulations of structural and thermodynamic properties of bilayer graphene. Phys. Rev. B 2010, 81, 235439. [Google Scholar] [CrossRef]
  43. Shen, Y.K.; Wu, H.A. Interlayer shear effect on multilayer graphene subjected to bending. Appl. Phys. Lett. 2012, 100, 101909. [Google Scholar] [CrossRef]
  44. Costamagna, S.; Neek-Amal, M.; Los, J.H.; Peeters, F.M. Thermal rippling behavior of graphane. Phys. Rev. B 2012, 86, 041408. [Google Scholar] [CrossRef]
  45. Ramírez, R.; Chacón, E.; Herrero, C.P. Anharmonic effects in the optical and acoustic bending modes of graphene. Phys. Rev. B 2016, 93, 235419. [Google Scholar] [CrossRef]
  46. Yi, L. Temperature dependence bending rigidity of 2D membranes: Graphene as an example. AIP Adv. 2018, 8, 075104. [Google Scholar] [CrossRef]
  47. Liu, P.; Zhang, Y.W. Temperature-dependent bending rigidity of graphene. Appl. Phys. Lett. 2009, 94, 231912. [Google Scholar] [CrossRef]
  48. Han, E.; Jaehyung, Y.; Annevelink, E.; Son, J.; Kang, D.A.; Watanabe, K.; Taniguchi, T.; Ertekin, E.; Huang, P.U.; van der Zande, A.M. Ultrasoft slip-mediated bending in few-layer graphene. Nat. Mater. 2020, 19, 305–309. [Google Scholar] [CrossRef]
  49. Nicklow, R.; Wakabayashi, N.; Smith, H.G. Lattice dynamics of pyrolytic graphite. Phys. Rev. B 1972, 5, 4951. [Google Scholar] [CrossRef]
  50. Chen, X.; Yi, C.; Ke, C. Bending stiffness and interlayer shear modulus of few-layer graphene. Appl. Phys. Lett. 2015, 106, 101907. [Google Scholar] [CrossRef]
  51. Taleb, A.A.; Yu, H.K.; Anemone, G.; Farias, D.; Wodtke, A.M. Helium diffraction and acoustic phonons of graphene grown on copper foil. Carbon 2015, 95, 731–737. [Google Scholar] [CrossRef]
  52. Tømterud, M.; Hellner, S.K.; Eder, S.D.; Forti, S.; Convertino, D.; Manson, J.R.; Coletti, C.; Frederiksen, T.; Holst, B. Observation of increasing bending rigidity of graphene with temperature. Carbon 2025, 238, 120150. [Google Scholar] [CrossRef]
  53. Côté, A.P.; Benin, A.I.; Ockwig, N.W.; O’Keeffe, M.; Matzger, A.J.; Yaghi, O.M. Porous, Crystalline, Covalent Organic Frameworks. Science 2005, 310, 1166. [Google Scholar] [CrossRef]
  54. Geng, K.; He, T.; Liu, R.; Dalapati, S.; Tan, K.T.; Li, Z.; Tao, S.; Gong, Y.; Jiang, Q.; Jiang, D. Covalent Organic Frameworks: Design, Synthesis, and Functions. Chem. Rev. 2020, 120, 8814. [Google Scholar] [CrossRef]
  55. Kato, M.; Ota, R.; Endo, T.; Yanase, T.; Nagahama, T.; Shimada, T. Free-Standing Nanometer-Thick Covalent Organic Framework Films for Separating CO2 and N2. ACS Appl. Nano Mater. 2022, 5, 2367. [Google Scholar] [CrossRef]
  56. Kato, M.; Yanase, T.; Waizumi, H.; Yokokura, S.; Shimada, T. Solvent-vapor-assisted crystallization of covalent organic framework films for CO2/CH4 separation. Chem. Lett. 2024, 53, upae191. [Google Scholar] [CrossRef]
Carbon 11 00059 g001
Figure 1. Seven layers of hydrogen-terminated circular graphene or supercoronene (C733H69). (a) Pristine graphene (b) with three Au overlayers in fcc structure.
Figure 1. Seven layers of hydrogen-terminated circular graphene or supercoronene (C733H69). (a) Pristine graphene (b) with three Au overlayers in fcc structure.
Carbon 11 00059 g001
Carbon 11 00059 g002
Figure 2. Snapshots of the exfoliation process at 400 K. The top layer is lifted upward at a speed of 2 Å/ps (Red:C, Blue:H). (a) 2.65 ps (b) 4.50 ps (c) 9.50 ps.
Figure 2. Snapshots of the exfoliation process at 400 K. The top layer is lifted upward at a speed of 2 Å/ps (Red:C, Blue:H). (a) 2.65 ps (b) 4.50 ps (c) 9.50 ps.
Carbon 11 00059 g002
Carbon 11 00059 g003
Figure 3. Snapshots of the exfoliation process at 200 K. The top layer is lifted upward at a speed of 2 Å/ps (Red:C, Blue:H). (a) 3.00 ps (b) 4.33 ps (c) 8.50 ps.
Figure 3. Snapshots of the exfoliation process at 200 K. The top layer is lifted upward at a speed of 2 Å/ps (Red:C, Blue:H). (a) 3.00 ps (b) 4.33 ps (c) 8.50 ps.
Carbon 11 00059 g003
Carbon 11 00059 g004
Figure 4. Snapshots of the exfoliation process at 300 K with a 3-atomic overlayer of Au. The top layer is lifted upward at a speed of 1 Å/ps (Red:C, Blue:H, Pink:Au). (a) 6.55 ps (b) 8.83 ps (c) 11.72 ps.
Figure 4. Snapshots of the exfoliation process at 300 K with a 3-atomic overlayer of Au. The top layer is lifted upward at a speed of 1 Å/ps (Red:C, Blue:H, Pink:Au). (a) 6.55 ps (b) 8.83 ps (c) 11.72 ps.
Carbon 11 00059 g004
Carbon 11 00059 g005
Figure 5. Snapshots of the exfoliation process at 600 K with a 3-atomic overlayer of Au. The top layer is lifted upward at a speed of 2 Å/ps (Red:C, Blue:H, Pink:Au). (a) 4.14 ps (b) 6.90 ps (c) 20.00 ps.
Figure 5. Snapshots of the exfoliation process at 600 K with a 3-atomic overlayer of Au. The top layer is lifted upward at a speed of 2 Å/ps (Red:C, Blue:H, Pink:Au). (a) 4.14 ps (b) 6.90 ps (c) 20.00 ps.
Carbon 11 00059 g005
Carbon 11 00059 g006
Figure 6. Snapshots of pre-tilt (5 °) followed by lifting (2 Å/ps) at 100 K. White “x” in (a) indicates the axis of rotation for pre-tilting (Red:C, Blue:H). (a) 2.57 ps (b) 6.00 ps (c) 14.00 ps.
Figure 6. Snapshots of pre-tilt (5 °) followed by lifting (2 Å/ps) at 100 K. White “x” in (a) indicates the axis of rotation for pre-tilting (Red:C, Blue:H). (a) 2.57 ps (b) 6.00 ps (c) 14.00 ps.
Carbon 11 00059 g006
Carbon 11 00059 g007
Figure 7. Equilibrized structure at 10 K and 500 K applying opposite forces indicated in the figure at the center and a 50 Å × 50 Å square graphene sheet.
Figure 7. Equilibrized structure at 10 K and 500 K applying opposite forces indicated in the figure at the center and a 50 Å × 50 Å square graphene sheet.
Carbon 11 00059 g007
Carbon 11 00059 g008
Figure 8. Curvature vs. bending force at various temperatures.
Figure 8. Curvature vs. bending force at various temperatures.
Carbon 11 00059 g008
Carbon 11 00059 g009
Figure 9. Bending rigidity D at 0.02 kcal/mol/Å. The curve is guide to eyes.
Figure 9. Bending rigidity D at 0.02 kcal/mol/Å. The curve is guide to eyes.
Carbon 11 00059 g009
Table 1. Number of exfoliated layers from the pristine seven layers of ReaxFF graphene.
Table 1. Number of exfoliated layers from the pristine seven layers of ReaxFF graphene.
Lifting Speed
(Å/ps)		Temperature (K)
10100200300400500600
0.52.6 ± 0.53.8 ± 1.64.8 ± 0.43.8 ± 1.12.4 ± 0.93.8 ± 0.43.2 ± 0.8
14.0 ± 0.04.0 ± 0.04.0 ± 0.02.4 ± 1.54.0 ± 0.01.6 ± 0.51.4 ± 0.5
20.0 ± 0.00.0 ± 0.01.6 ± 2.22.6 ± 1.72.6 ± 1.72.6 ± 1.73.4 ± 0.5
50.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.0
Table 2. Number of exfoliated layers with a 3-atomic Au overlayer.
Table 2. Number of exfoliated layers with a 3-atomic Au overlayer.
Lifting Speed
(Å/ps)		Temperature (K)
10100200300400500600
0.51.2 ± 0.41.0 ± 0.72.4 ± 2.21.6 ± 2.22.4 ± 1.51.6 ± 1.12.0 ± 1.2
14.0 ± 0.01.0 ± 0.01.0 ± 0.01.0 ± 0.01.0 ± 0.01.0 ± 0.01.0 ± 0.0
20.2 ± 0.44.0 ± 0.04.0 ± 0.04.0 ± 0.04.0 ± 0.04.0 ± 0.04.0 ± 0.0
50.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.0
Table 3. Number of exfoliated layers with pre-tilting before the lifting. The lifting speed is 2 Å/ps.
Table 3. Number of exfoliated layers with pre-tilting before the lifting. The lifting speed is 2 Å/ps.
Angle of Pre-Tilting (o)Temperature (K)
10100200300400500600
10.0 ± 0.00.0 ± 0.00.0 ± 0.02.2 ± 2.02.6 ± 1.72.6 ± 1.72.4 ± 1.1
20.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.00.0 ± 0.02.6 ± 1.72.2 ± 1.5
50.0 ± 0.01.0 ± 2.21.0 ± 2.21.0 ± 2.20.0 ± 0.00.0 ± 0.00.0 ± 0.0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ando, T.; Yokokura, S.; Waizumi, H.; Suzuki, H.; Kawashima, K.; Shimada, T. In Silico Exfoliation of ReaxFF Graphite—Temperature, Speed, Angle Dependence, and the Effect of Gold Overlayer. C 2025, 11, 59. https://doi.org/10.3390/c11030059

AMA Style

Ando T, Yokokura S, Waizumi H, Suzuki H, Kawashima K, Shimada T. In Silico Exfoliation of ReaxFF Graphite—Temperature, Speed, Angle Dependence, and the Effect of Gold Overlayer. C. 2025; 11(3):59. https://doi.org/10.3390/c11030059

Chicago/Turabian Style

Ando, Teruki, Seiya Yokokura, Hiroki Waizumi, Hironori Suzuki, Kenji Kawashima, and Toshihiro Shimada. 2025. "In Silico Exfoliation of ReaxFF Graphite—Temperature, Speed, Angle Dependence, and the Effect of Gold Overlayer" C 11, no. 3: 59. https://doi.org/10.3390/c11030059

APA Style

Ando, T., Yokokura, S., Waizumi, H., Suzuki, H., Kawashima, K., & Shimada, T. (2025). In Silico Exfoliation of ReaxFF Graphite—Temperature, Speed, Angle Dependence, and the Effect of Gold Overlayer. C, 11(3), 59. https://doi.org/10.3390/c11030059

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop