Diffusion of C-O-H Fluids in a Sub-Nanometer Pore Network: Role of Pore Surface Area and Its Ratio with Pore Volume

Abstract

Porous materials are characterized by the pore surface area (S) and volume (V) accessible to a confined fluid. For mesoporous materials NMR measurements of diffusion are used to assess the S/V ratio, because at short times, only the diffusivity of molecules in the adsorbed layer is affected by confinement and the fractional population of these molecules is proportional to the S/V ratio. For materials with sub-nanometer pores, this might not be true, as the adsorbed layer can encompass the entire pore volume. Here, using molecular simulations, we explore the role played by S and S/V in determining the dynamical behavior of two carbon-bearing fluids—CO₂ and ethane—confined in sub-nanometer pores of silica. S and V in a silicalite model representing a sub-nanometer porous material are varied by selectively blocking a part of the pore network by immobile methane molecules. Three classes of adsorbents were thus obtained with either all of the straight (labeled ‘S-major’) or zigzag channels (‘Z-major’) remaining open or a mix of a fraction of both types of channel blocked, resulting in half of the total pore volume being blocked (‘Half’). While the adsorption layers from opposite surfaces overlap, encompassing the entire pore volume for all pores except the intersections, the diffusion coefficient is still found to be reduced at high S/V, especially for CO₂, albeit not so strongly as would be expected in the case of wider pores. This is because of the presence of channel intersections that provide a wider pore space with non-overlapping adsorption layers.

1. Introduction

The behavior of fluids confined in nanoporous media is interesting from both a fundamental as well as application point of view [1,2]. When the pore size is smaller than a nanometer, the resulting strict confinement gives rise to the exhibition of a peculiar behavior by the confined fluids [3,4]. Carbon-bearing fluids are particularly interesting, as understanding their behavior under confinement is important in several industrial applications, including subsurface gas recovery and catalysis [5]. Further, the contrasting behavior exhibited by CO₂ and non-wetting fluids like alkanes, due to the difference in their interaction with the confining medium, can be useful in determining pore tortuosity—an important parameter characterizing the pore shapes in porous rock samples [6,7]. Several studies have reported the behavior of ethane and CO₂ confined in nanoporous silica [8,9].

While the interaction of the confined fluids with the porous medium determines their behavior, geometrical characteristics of the pore network also play an important role [10]. Two important characteristics that define a pore network are the accessible surface area (S) and volume (V) of the pores [11]. A good adsorbent is expected to have a high surface area, and values of S typically range from a few hundred to even thousands of m²/g [12]. Whilea high pore volume is favorable for confining fluids by making more pore space available; if the pores are too wide, an increase in the pore volume may no longer be favorable to efficient adsorption [13]. As the properties of the confined fluids are strongly determined by the interaction of the fluid with the porous medium, which in turn is strongly dependent on the surface area, the ratio S/V is an important factor that can influence fluid behavior. Indeed, NMR measurement of the diffusion of fluids confined in nanoporous media is useful in determining the S/V ratio of the confining media [14,15,16]. In a porous medium, only molecules adsorbed on the surface within a layer of a thickness proportional to the square root of the bulk diffusion coefficient (D₀) and diffusion time (t) feel the effect of geometric hindrance by the pore wall, whereas others in the pore center are free and exhibit bulk-like behavior (see Figure 1). The fraction of molecules in this adsorption layer is Sl_a/V, where l_a (=$\sqrt{D_{0}t})$ is the thickness of the layer. The diffusion coefficient in confinement (D) is thus reduced by a term proportional to S/V (with proportionality constant a = 4/(3d√π) and d being the spatial dimension), and a first approximation can be written as [14,15,16]

$$D=D_0(1-a(S/V\left)\sqrt{D_{0}t}\right)$$

(1)

In a microporous material (right panel, Figure 1) with a pore size comparable to the size of the adsorbed molecule, this layer covers the entire pore volume, and thus all molecules feel the geometrical restriction imposed by the pore walls; therefore relation 1 might not be valid and diffusivity might not even vary with S/V. It is thus important to investigate the relation between diffusion coefficient and S/V in such porous materials. In an experiment using powdered samples, it is difficult to distinguish between the signals coming from fluids confined in micropores and those in the relatively larger inter-crystalline pores that might exist between particles. Indeed, while several studies have reported fluid diffusivity in microporous materials like silicalite using NMR, the dependence of diffusivity on S/V is not addressed [17,18,19].

In an experiment on confined fluids, the sample material is often limited to a few specimens, and so the range of S and S/V investigated in an experiment is quite limited. In this regard, computer simulations can be useful by providing a wider range of these characteristics by artificially manipulating the confining medium to provide a richer diversity of pore shapes and topologies [20], thereby making a systematic study of the effects of characteristics like S and S/V feasible. In previous works we explored the roles of pore connectivity and tortuosity in determining the behavior of ethane and CO₂ confined in silicalite [21,22,23]. A variety of pore connectivities and tortuosities were achieved by selectively blocking a few pores with immobile methane molecules representing organic matter in nanopores. Here we explore the diffusion of ethane and CO₂ in these media in terms of variation in S and S/V. In particular, we investigate whether diffusion in sub-nanometer pores can have S/V dependence, as expected for wider pores and described by Equation (1).

2. Materials and Methods

Detailed information on the models of the confining media and computer simulations used can be found in previous publications [21,22,23]. Here, we provide a brief description for ready reference.

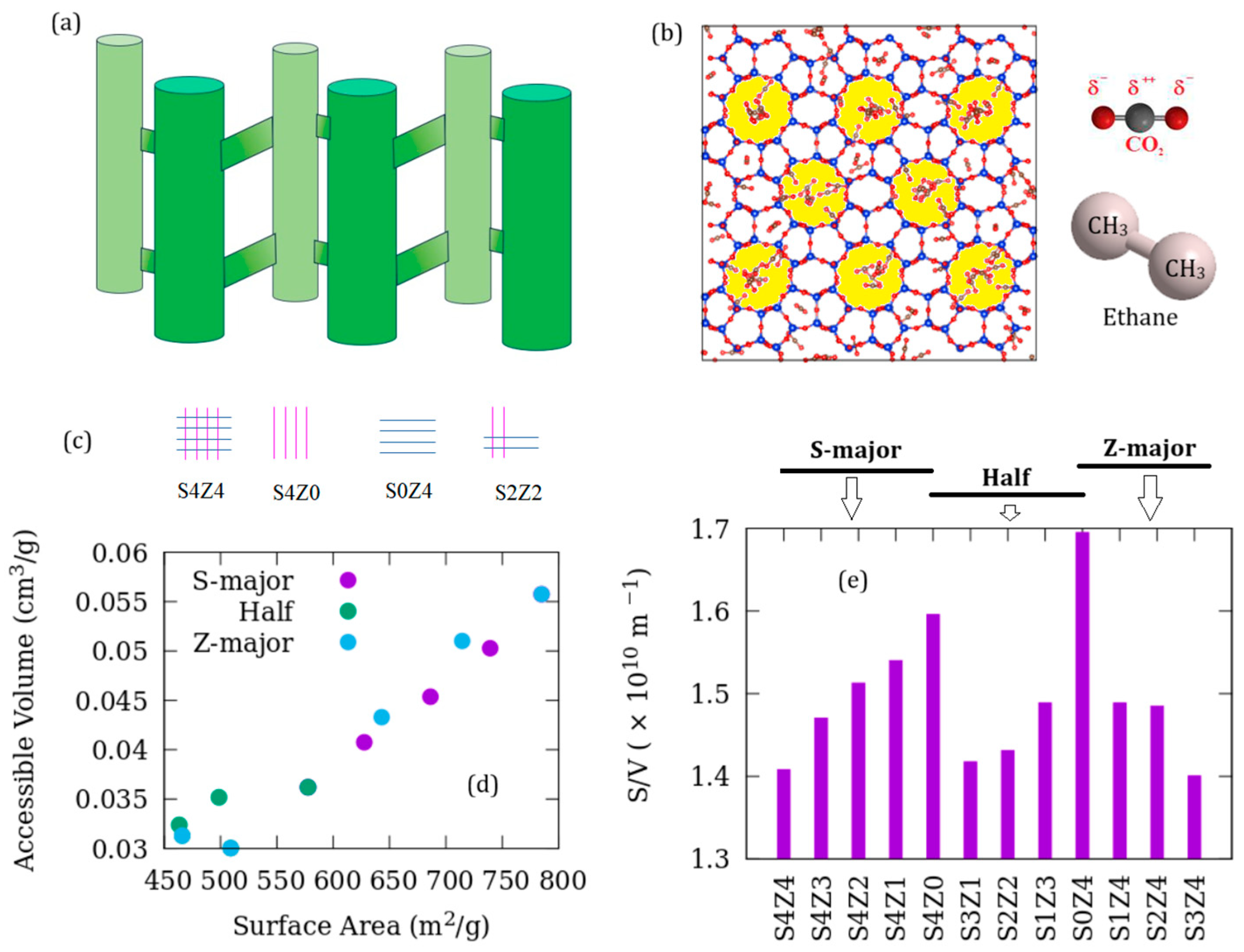
2.1. Adsorbent Models

A simulation cell made up of 2 × 2 × 3 unit cells of silicalite (40.044 × 39.798 × 40.149 ų) was prepared with the visualization software VESTA version 3.5.7 [24] using the atomic coordinates provided by Koningsveld et al. [25]. This simulation cell without any modification is an ideal silicalite crystal and has a total of 12 straight channel-like pores of width ~0.55 nm running along the Cartesian Y-direction, intersecting at 48 ellipsoidal intersections with 12 tortuous channels with similar dimensions exhibiting a zigzag configuration in the X-Z plane (see Figure 2a). Pore characteristics were systematically varied by selectively blocking different combinations of straight and/or zigzag channels. For this, methane was initially adsorbed at 200 K and 200 atm pressure using GCMC simulations, filling the entire pore space available to saturation. Subsequently, methane molecules were removed from some channels selectively to make them open and available for adsorbing other fluids. This resulted in a total of 12 model adsorbents with different values of S and S/V. These adsorbents were named SnZm (n, m = 0, 1, 2, 3 or 4), with n and m denoting, respectively, the fraction (out of 4) of straight and zigzag channels of silicalite that were available for adsorption. For example, S4Z4 is the unmodified silicalite with all channels open, S4Z0 has all straight channels open and all zigzag channels blocked, S0Z4 has all straight channels blocked and all zigzag channels open, and S2Z2 has half of each of the straight and zigzag channels open while the other half are blocked (see Figure 2c).

2.2. Force-Fields

We used a combination of TraPPE [26,27] and ClayFF [28] force-fields to represent the adsorbate and the adsorbent, respectively. The pore-blocking methane and the adsorbate ethane were represented in the united atom formalism TraPPE-UA [26], while the CO₂ molecules were represented by a rigid three-point potential TraPPE [27]. The interactions between the blocker methane and the adsorbates, as well as those between the silicalite framework and the adsorbates, were obtained by using the Lorentz–Berthelot mixing rules [29]. As shown earlier, this combination of the force-field provided good agreement between the simulated and experimental adsorption isotherms of ethane and CO₂ in silicalite [30,31].

2.3. Simulations

Fluids were adsorbed in the adsorbent models with GCMC simulations carried out using DL_Monte version 2.0.3 [32], while dynamical behavior was probed with molecular dynamics simulations carried out using DL_Poly version 4.10 [33]. All simulations were carried out at 308 K. Both ethane and CO₂ become supercritical at this temperature for pressures lower than 100 atm [34]. MD simulations were carried out on the equilibrated configurations obtained from the GCMC simulations that corresponded to a partial pressure of the adsorbed fluid of 1 atm. This corresponded to 128 molecules of either fluid adsorbed in the cell. A time step of 1 fs was used, and long-range interactions were cut-off at 14 Å. Further details about these simulations can be found in [21,22,23].

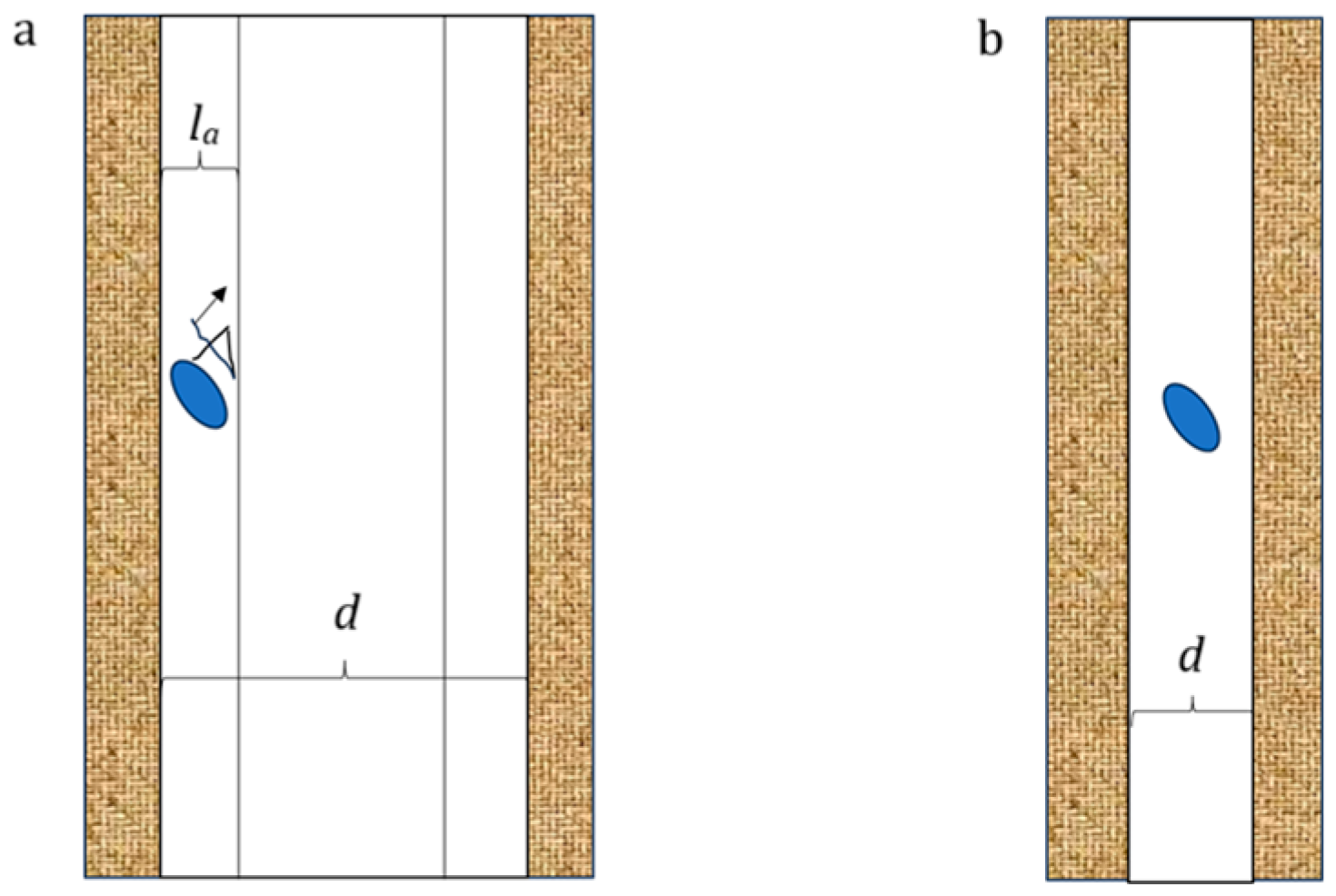
2.4. Pore Characterization

Pore characteristics, including the surface area and volume of the pores accessible to a spherical test particle of radius 1.2 Å, for all the 12 adsorbent models were determined using the pore characterization package Zeo++0.3 [35]. A small spherical test particle was used to efficiently probe the surface area and pore volume available with reasonable resolution. With a spherical probe of radius 1.2 Å, we made sure that the calculation provided better resolution than the use of either fluid molecules, which have kinetic radii larger than this, and also that two probes could fit into the pores with a diameter of 5.5 Å. In what follows, adsorbents in which all straight channels are free while some or all zigzag channels are blocked for sorption are labeled as ‘S-major’. Similarly, adsorbents with all zigzag channels open are labeled ‘Z-major’, whereas adsorbents where half or all channels (straight or zigzag) are free are labeled ‘Half’. Schematics illustrating some representative adsorbents are shown in Figure 2c, where each open straight (or zigzag) channel is represented by a vertical (or horizontal) line colored magenta (or blue). Figure 2d shows the pore characteristics of all 12 adsorbents. In general, surface area and accessible pore volume seem to be correlated such that an increase in the accessible pore volume results in an increase in the surface area. Nevertheless, this correlation is not ideal, and deviations result in a variation in S/V, as shown in Figure 2c, for all adsorbents. It is noteworthy that the surface area mentioned here is exclusively the surface area provided by the pore structure. In a real sample, an experimental determination of the surface area might also include the area of the nonporous external surface of the particles of the sample [36]. Subtracting the S and V of S4Z0 and/or S0Z4 from those for S4Z4, an estimate for the S/V ratio for the straight and zigzag channels and their intersections in S4Z4 can be obtained. We estimate the S/V ratio of intersections in S4Z4 to be 2.88 × 10¹⁰ m⁻¹, while that for the straight and zigzag channels are, respectively, 1.07 × 10¹⁰ m⁻¹ and 1.06 × 10¹⁰ m⁻¹. The void space in the intersections is wider than the diameter of the straight or zigzag channels. Further, while the straight and zigzag channels are cylindrical, the intersections are more sphere-like. Note that while the S/V for a cylindrical geometry with radius r is proportional to 2/r, that for a spherical geometry is 3/r. This makes the S/V ratio of the intersections significantly larger.

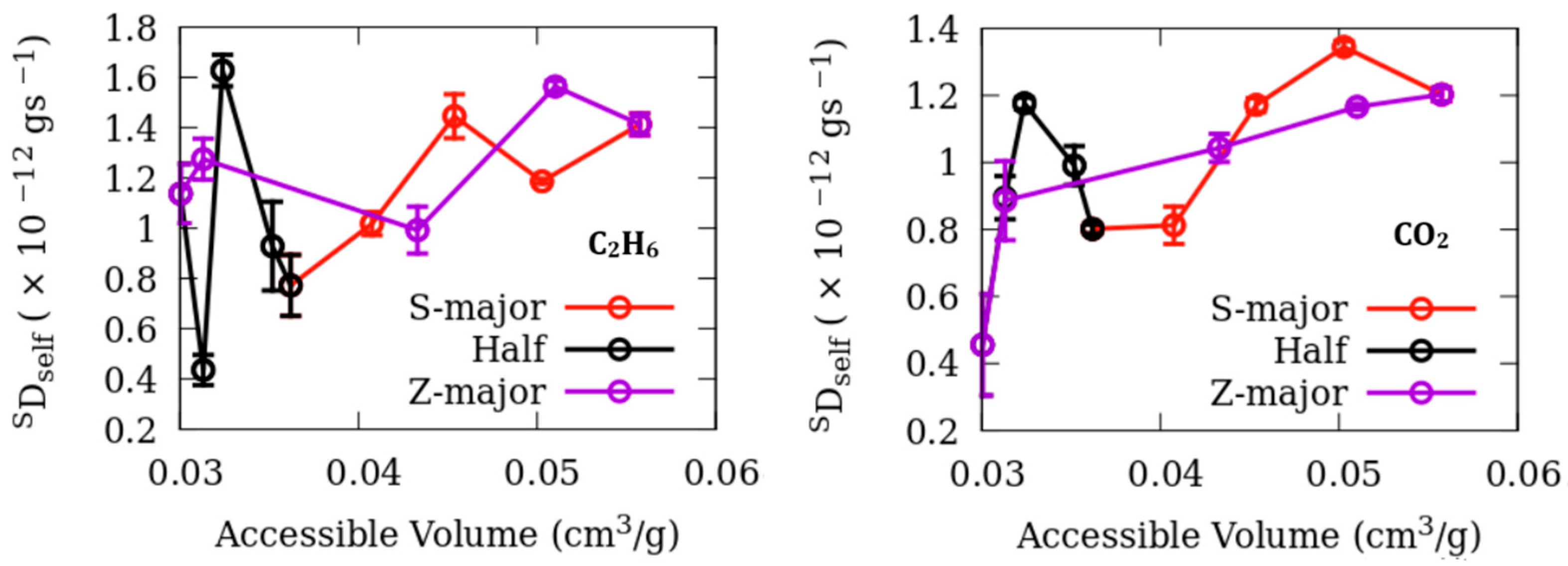
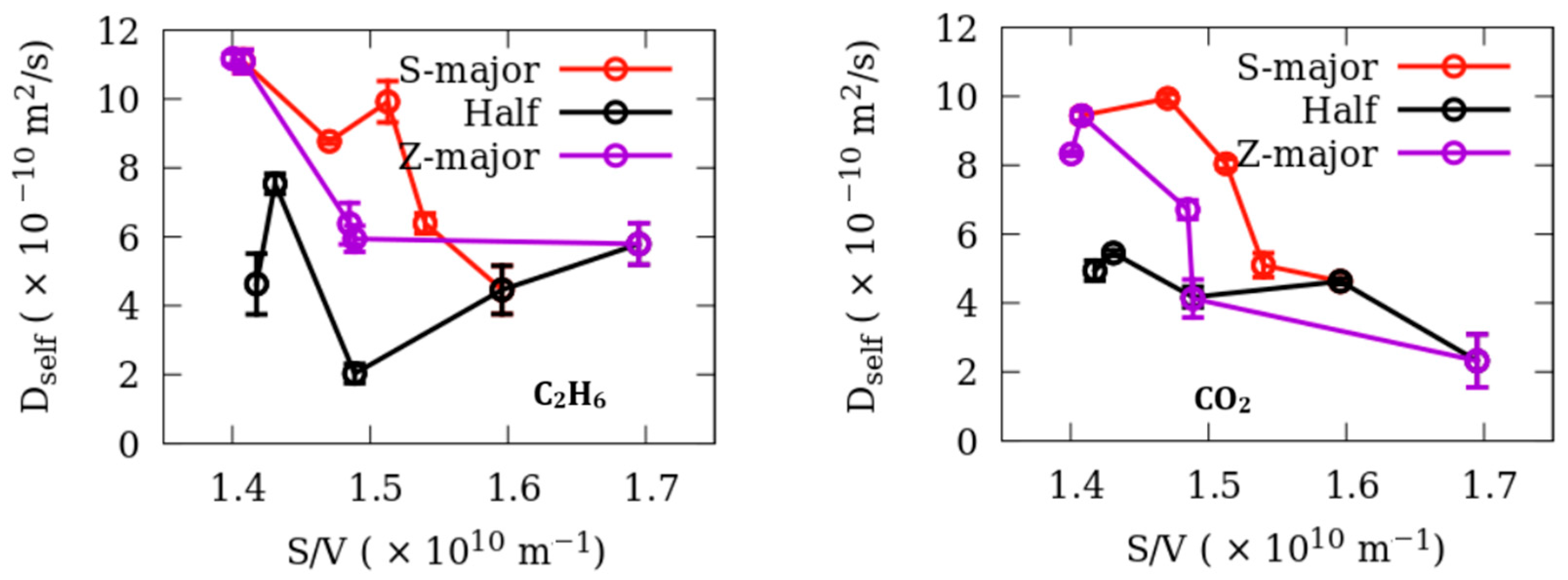
3. Results

Figure 3 displays the probability distribution of the location of the center of mass of an adsorbed molecule in a straight or zigzag channel obtained from the MD simulation trajectories consisting of 75,000 frames. Notably, for both fluids, multiple high-intensity points can be seen only at the intersections (highlighted with circles), while the regions away from the intersections in both the straight as well as the zigzag channels exhibit only single regions of high intensity. This is because the adsorption layers on the opposite pore surfaces overlap into a single layer with no bulk-like regions. In the intersections of straight and zigzag channels, however, the void volume is large enough to accommodate non-overlapping adsorption layers at the opposite surfaces, with a bulk-like region at the center. This small bulk-like region at the center of the intersections is especially visible for CO₂ in Figure 3 as a very small low-intensity region in the circled part. While CO₂ tends to cover a larger volume of the channel-like pores (wider regions of non-zero probability), ethane prefers to occupy a smaller region away from the pore walls. Further, while CO₂ exhibits several discontinuous regions of high probability (yellow), ethane exhibits a relatively homogenous distribution, with smaller number of high-intensity regions with smoother transitions between them.

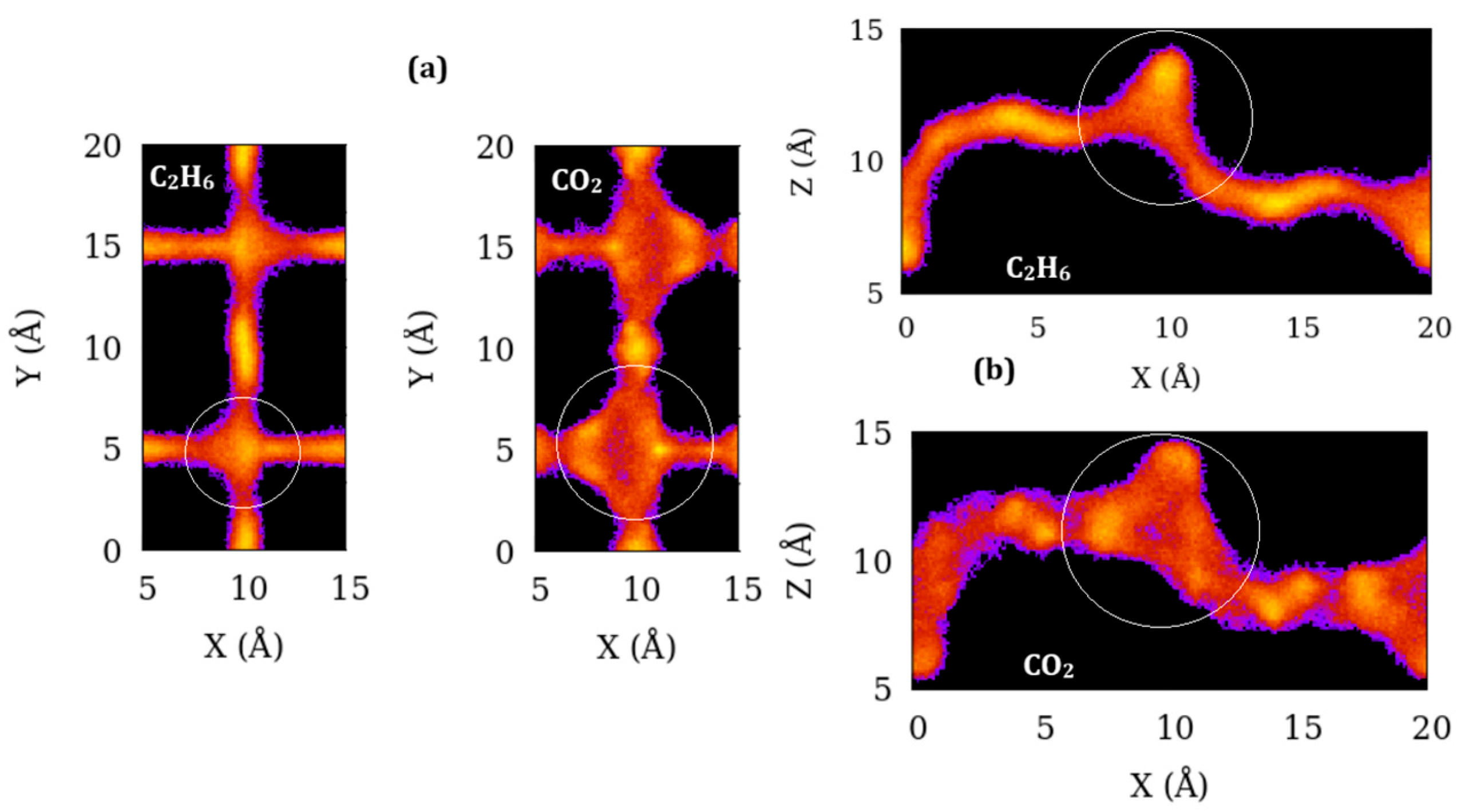
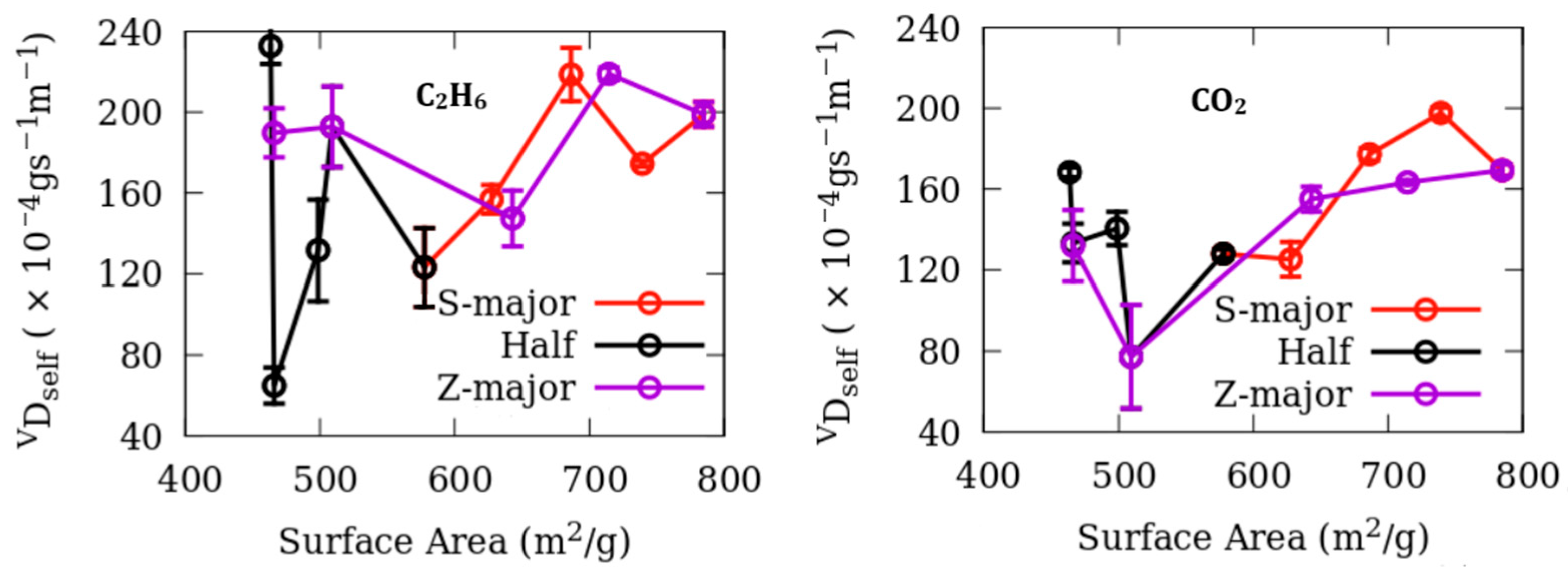
Dynamics

The dynamic behavior of a molecule is altered with a suppression of mobility when it is confined in a porous medium. In general, a larger volume available to the molecule can be expected to facilitate its mobility. For a fair assessment of the variation in mobility with surface area, we normalize the self-diffusion coefficient with the pore accessible volume. This volume-normalized self-diffusion coefficient (^VD_self = D_self/V) calculated from MD simulation trajectories is shown in Figure 4 as a function of the pore surface area. Overall, the diffusion coefficient does not seem to exhibit a systematic variation, except for in the S-major adsorbents, which seem to show slightly higher mobility with a higher surface area, although the variation is non-monotonic.

The effect of accessible volume on diffusivity is relatively clearer for CO₂, as shown in Figure 5 with the self-diffusion coefficient normalized to the available surface area (^SD_self = D_self/S). For ethane, the trend is relatively less prominent, although higher pore volume adsorbents, in general, do exhibit higher diffusivities. The difference in the prominence of the effects of pore volume on the mobility of CO₂ vs. ethane is a consequence of the interplay of the kinetic diameter and the fluid–adsorbent interactions. As seen in Figure 3, and reported in previous studies [22,23], while ethane prefers to occupy the pore centers, CO₂ molecules are distributed close to the pore surfaces. This means that the effective pore volume available for CO₂ in silicalite channels is larger compared to that for ethane, as the former can be adsorbed much closer to the pore surface. This difference is further enhanced as CO₂, with a smaller kinetic diameter of 0.38 nm [37] (compared to 0.44 nm for ethane [38]), requires a relatively smaller volume for free motion.

Figure 6 shows the combined effects of the pore accessible surface area and volume on the self-diffusion coefficients of ethane and CO₂ in silicalite. Here the effects of S/V are clearly visible for CO₂, for which a higher S/V seems to suppress diffusivity. The effect of S/V on the diffusion of ethane, however, is relatively weak.

4. Discussion and Conclusions

While the diffusion coefficients of fluids confined in porous media are related to the S/V ratio, as in Equation (1), for pore sizes comparable to the molecular size of the fluid, this is no longer valid because of an absence of a bulk-like region away from the pore surface. For such porous media, the reduction in the diffusion coefficient of the confined fluid compared to the bulk state is expected to be stronger than that suggested by Equation (1) and independent of S/V. For silicalite, with a pore size of ~0.55 nm, comparable to the kinetic diameters of ethane and CO₂, as we have seen, there is no bulk-like region in its straight or zigzag channel-like pores (see Figure 3). However, at the intersections of the straight and zigzag channels, the geometrical restriction is somewhat relaxed. This is especially true for CO₂, which fills the pores more effectively due to (i) a smaller kinetic diameter and (ii) stronger interaction with the silicalite atoms. This difference between the two fluids is reflected in the weaker dependenceof D_self for ethane on S/V as compared to that of CO₂. Despite a stricter restriction imposed by the channels of silicalite, there is nevertheless a significant decrease in D_self at a higher S/V. This is because of the presence of intersections that provide a fraction of pore space wide enough to accommodate non-overlapping adsorption layers and a very small bulk-like region. The presence of this small bulk-like region in a small fraction of the pore space gives rise to the S/V dependence of the diffusion coefficient seen in Figure 6. While blocking the channels with immobile methane molecules, the original shape of the intersections can be distorted depending upon whether the methane molecules are present on the straight or the zigzag side of the intersection. Thus, while the intersections contribute to the second term on the right side of Equation (1), this contribution is not uniform. This non-uniformity results in the scattering of the data in Figure 6. Nevertheless, in the case of CO₂ the trend is clear.

A linear fit to the data in Figure 6 was used to estimate the bulk diffusion coefficient (see Figure 7). The values obtained for CO₂ range between 53.23 × 10⁻¹⁰ m²/s and 17.62 × 10⁻¹⁰ m²/s (

Table 1. Fit parameters D₀ and a obtained from fits in Figure 7.

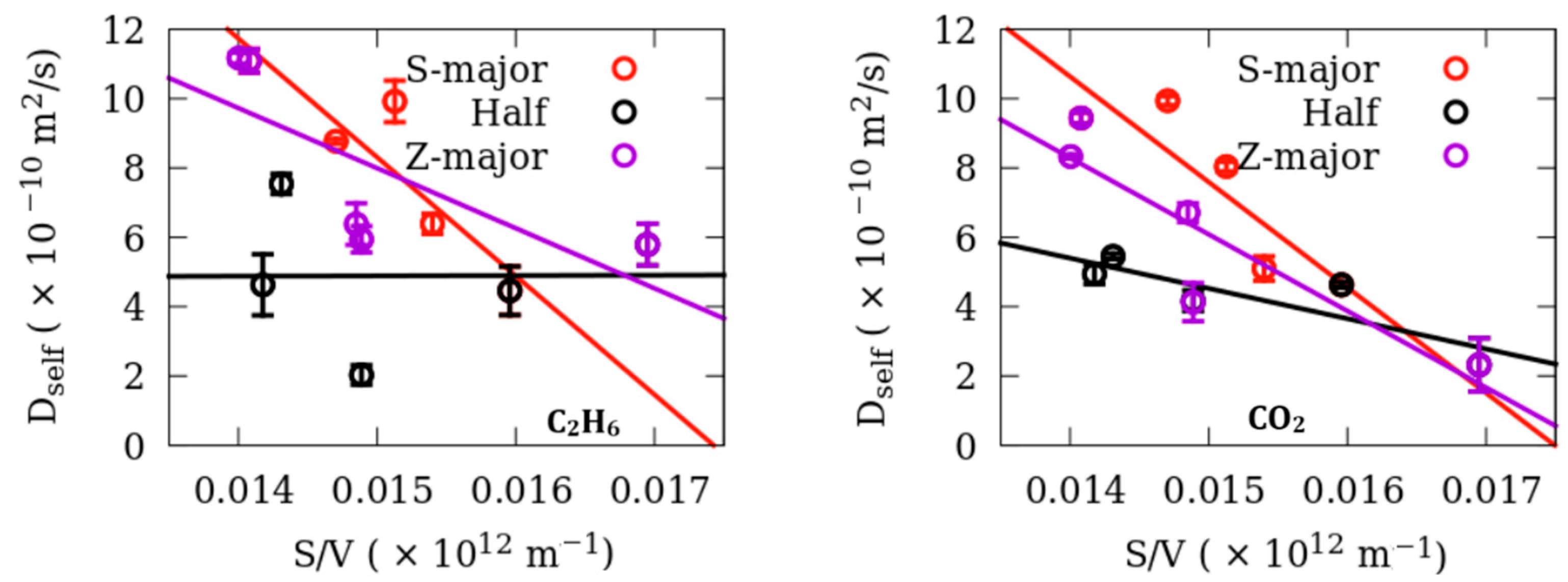
Fluid	Adsorbent	D0 (×10−10 m2/s)	a (×10−12 m)	RMS Residuals
Ethane	S-major	59.66 ± 14.07	57.38 ± 2.2	1.33
	Half	4.75 ± 15.1	−1.91 ± 213	2.33
	Z-major	33.99 ± 13.75	50.99 ± 6.57	2.18
CO2	S-major	53.23 ± 14.16	57.16 ± 2.55	1.33
	Half	17.62 ± 4.65	49.55 ± 4.31	0.71
	Z-major	39.22 ± 9.61	56.32 ± 2.76	1.52

). These are orders of magnitude smaller than the experimental value of 9510 × 10⁻¹⁰ m²/s at a slightly lower temperature of 298 K and an elevated pressure of 10.34 bar [39]. Similar values are obtained for ethane (Table 1) that are almost an order of magnitude smaller than the bulk value at 294 K and an elevated pressure of 250 bar of 187 × 10⁻¹⁰ m²/s [40], confirming that the reduction in the diffusion coefficient in silicalite is stronger than that expected by the S/V scaling of porous materials using Equation (1). Further, the linear fits for CO₂ in all adsorbents are significantly better than those for ethane (rightmost column, Table 1), suggesting a more systematic S/V dependence of diffusivity for CO₂ compared to that for ethane.

Among the three types of adsorbents, the adsorbent type with only half of the volume available for adsorption exhibits the weakest dependence. For ethane, this dependence is too weak and is overshadowed by the scatter in the data. The combined effect of a weak dependence and large scatter results in a small value of ‘a’ (Table 1) with a large error margin for ethane in ‘Half’ adsorbents. It is noteworthy that the ‘Half’ adsorbents have the smallest number of open pore connections (0–12, compared to 48 for S4Z4 and >12 for S-major and Z-major), i.e., intersections which have open access to molecules from all sides [22]. The contribution of intersections to the diffusivity of adsorbed molecules is therefore suppressed even further in these adsorbents because of their partial inaccessibility from either straight or zigzag channels.

As noted earlier, the S/V values reported in this work pertain exclusively to the pore surface area and volumes. While in simulations, this is easy to control, in an experiment with a powdered sample, excluding the contributions of fluid adsorbed in the inter-particle voids to S/V can be extremely challenging. This means that for microporous samples with extremely narrow pores, the diffusion coefficient can be expected to vary with S/V, due to the contribution from the inter-particle voids and particle surfaces. However, for highly mobile fluids, if the confinement is strong enough, the time scales involved in the motion of the fluid molecules in the pores and the inter-particle voids and surfaces can differ significantly. This can provide a means of excluding the contribution of the inter-particle and particle-surface-adsorbed fluid in a study of the S/V dependence of the diffusion coefficient of the confined fluid. To summarize, for porous media with very narrow pores comparable to the size of the confined molecule (this would translate to very high S/V ratios), the reduction in diffusion coefficient is stronger than the linear dependence in Equation (1) suggests.