Influence of a Background Shear Flow on Cyclone–Anticyclone Asymmetry in Ageostrophic Balanced Flows

Abstract

In this paper, we study how cyclonic and anticyclonic vortices adapt their shape and orientation to a background shear flow in an effort to understand geophysical vortices. Here we use a balanced model that incorporates the effects of rotation and density stratification to model the case of an isolated vortex of uniform potential vorticity subjected to a background shear flow that mimics the effect of surrounding vortices. We find equilibrium states and analyze their linear stability to determine the vortex characteristics at the margin of stability. Differences are found between the cyclonic and anticyclonic equilibria depending on the background flow parameters. When there is only horizontal strain, the vertical aspect ratio of the vortex does not change, whereas increasing the imposed background strain rate causes a change in the horizontal cross section, with cyclones being more deformed than anticyclones for a given value of strain. Vertical shear not only causes changes in the vertical axis but also causes the vortex to tilt away from it upright position. Overall, anticyclonic equilibria tend to have a more circular horizontal cross section, a longer vertical axis, and a larger tilt angle with respect to cyclonic equilibria. The strongest asymmetry between the horizontal cross section of cyclonic and anticyclonic vortices occurs for low values of vertical shear, while the strongest asymmetry in the vertical axes and tilt angle occurs for large vertical shear. Finally, by expanding the vortex shape and orientation in terms of the strain rate, we derive simple formulas that provide insights into how the vortex equilibria depend on the background flow.

1. Introduction

Large-scale flows in the ocean and atmosphere contain vortices. These vortices can evolve over long periods of time [1], having the potential to transport many physical properties, such as temperature and salinity, as well as biological properties over long distances [2,3]. These vortices are strongly influenced by the Earth’s rotation, referred to as the Coriolis effect, as well as the effects of density stratification [4]. As the sense of the Earth’s rotation is always the same (counterclockwise in the Northern Hemisphere, clockwise in the Southern Hemisphere), it affects cyclonic (anticlockwise) and anticyclonic (clockwise) vortices differently, leading to an asymmetry in their dynamical behavior. This asymmetry has been observed in large-scale observations [5,6] as well as in numerical simulations [7,8,9,10,11,12,13]. Despite these many studies, there is still much that is not understood about the factors that influence this asymmetry. In fact, a recent study [14] shows that there is a bias in the altimetry satellite measurements of large-scale eddies, with cyclonic eddies being under-detected; thus, there is still an important role for theoretical approaches in developing our understanding of cyclone–anticyclone asymmetry.

Here we consider an idealized model of a single vortex in the presence of a background shear flow in order to characterize the cyclonic–anticyclonic asymmetry induced by background shear flow. The model we consider is the nonlinear quasi-geostrophic model [15], a balanced model, i.e., one where all the dynamics are controlled by the evolution of the potential vorticity (PV) field, $\varpi$, a materially conserved scalar field. The model assumes an f-plane with a fixed value for the planetary rotation rate, i.e., the Coriolis frequency, f, and the model is derived from an expansion of the full equations in the Rossby number up to the second order, where the Rossby number is defined as $Ro\equiv {\left|\varpi \right|}_{max}/f$. For the first order in the Rossby number, we obtain the quasi-geostrophic (QG) equations, whereas at the second order, we obtain the so-called QG + 1 equations. We use this model and study analytical solutions previously derived for an ellipsoidal vortex in the presence of a background shear flow [16,17]. We find equilibria and analyze their linear stability to determine the vortex characteristics at the margin of stability for a given background flow. As the QG solutions depend linearly on the PV, there is no dynamical difference in the behavior of cyclonic and anticyclonic vortices at this order, only the sign changes. However, the solutions up to the second order contain a linear and a quadratic term in the PV which, when combined, cause an asymmetry in dynamical behavior. Here we examine how this asymmetry changes as the background flow is changed in order to understand the impact of both horizontal strain and vertical shear.

In Section 2, we review the model of the ellipsoidal vortex and the method for obtaining equilibria and computing their linear stability. In Section 3, we present the results, showing how the vortex shape and orientation depend on the background flow and deriving an approximate model of the vortex shape characteristics that apply when the background flow is weak, in order to quantify the asymmetry between cyclonic and anticyclonic vortices. In Section 4, we discuss these results and draw our conclusions.

2. Problem Formulation

2.1. Balanced Ellipsoidal Vortex Model

We consider the nonlinear quasi-geostrophic model [15], which is a balanced model derived from the full non-hydrostatic Oderdeck–Boussinesq equations [18]. The equations are expanded in terms of the PV-based Rossby number, $ϵ\equiv {\left|\varpi \right|}_{max}$, where $\varpi$ is the PV anomaly given by:

$$\varpi ={\displaystyle \frac{\zeta }{f}}+{\displaystyle \frac{1}{N^2}}{\displaystyle \frac{\partial b}{\partial z}}+{\displaystyle \frac{\mathit{\omega }·\mathbf{\nabla }b}{f{N}^2}},$$

(1)

where $\mathit{\omega }$ is the relative vorticity with $\zeta$ being its vertical component, $b$ is the buoyancy anomaly, and $N$ and $f$ are the buoyancy and Coriolis frequencies, respectively. The other variables in the system are determined by the PV anomaly, which is materially conserved, i.e.,:

$${\displaystyle \frac{\partial \varpi }{\partial t}}+\mathbf{u}·\mathbf{\nabla }\varpi =0.$$

(2)

The velocity field can be expressed in terms of a vector potential, $\mathit{\phi }\equiv (\phi ,\psi ,\varphi )$:

$$\mathbf{u}=-f\mathbf{\nabla }\times \mathit{\phi },$$

(3)

where the vector potential can be solved through an inversion problem at different orders in the Rossby number [15]. At the first order, we have the QG equations:

$${\mathbf{\nabla }}^2{\varphi }^{\left(1\right)}=\varpi ,$$

(4)

where bracketed superscripts on field variables denote order in Rossby number (note ${\phi }^{\left(1\right)}={\psi }^{\left(1\right)}=0$). Note here that the vertical coordinate z is stretched by $\chi =N/f$, whereas the buoyancy and Coriolis frequencies are considered constant here. At the next order $\mathcal{O}\left({ϵ}^2\right)$, we have the QG + 1 equations:

$$\begin{array}{ccc}\hfill {\nabla }^2{\phi }^{\left(2\right)}& =& (2/\chi )\left({\varphi }_{yy}^{\left(1\right)}{\varphi }_{zx}^{\left(1\right)}-{\varphi }_{yz}^{\left(1\right)}{\varphi }_{xy}^{\left(1\right)}\right),\hfill \end{array}$$

(5a)

$$\begin{array}{ccc}\hfill {\nabla }^2{\psi }^{\left(2\right)}& =& (2/\chi )\left({\varphi }_{xx}^{\left(1\right)}{\varphi }_{yz}^{\left(1\right)}-{\varphi }_{zx}^{\left(1\right)}{\varphi }_{xy}^{\left(1\right)}\right),\hfill \end{array}$$

(5b)

$$\begin{array}{ccc}\hfill {\nabla }^2{\varphi }^{\left(2\right)}& =& {\left|\mathbf{\nabla }{\varphi }_z^{\left(1\right)}\right|}^2-\left({\mathbf{\nabla }}^2{\varphi }^{\left(1\right)}\right){\varphi }_{zz}^{\left(1\right)},\hfill \end{array}$$

(5c)

where subscripts x, y, and z on the fields denote partial differentiation.

These equations have been solved for the case of an isolated uniform ellipsoid of PV [16,19] and for the case where the vortex is embedded in a linear background shear flow [17]. We wish to revisit the latter solutions. The shape of the ellipsoid is specified by its axis half lengths a, b, and c, and by the unit vectors $\widehat{\mathbf{a}}=({\widehat{a}}_1,{\widehat{a}}_2,{\widehat{a}}_3)$, $\widehat{\mathbf{b}}=({\widehat{b}}_1,{\widehat{b}}_2,{\widehat{b}}_3)$, and $\widehat{\mathbf{c}}=({\widehat{c}}_1,{\widehat{c}}_2,{\widehat{c}}_3)$ directed along these axes. When the flow field depends linearly on spatial coordinates, i.e., $\mathbf{u}=\mathbf{S}\mathbf{x}$, then the equation of motion for the ellipsoid can be written as [20]:

$${\displaystyle \frac{d\mathbf{B}}{dt}}=\mathbf{S}\mathbf{B}+\mathbf{B}{\mathbf{S}}^T,$$

(6)

where $\mathbf{B}$ and $\mathbf{S}$ are $3\times 3$ matrices. The matrix $\mathbf{B}$ defines the shape and orientation of the vortex (the “shape” matrix) and is given by:

$$\mathbf{B}=\mathbf{M}\mathbf{E}{\mathbf{M}}^T,$$

(7)

where $\mathbf{M}$ is a rotation matrix defined by:

$$\mathbf{M}=\left(\begin{array}{ccc}\widehat{\mathbf{a}}& \widehat{\mathbf{b}}& \widehat{\mathbf{c}}\end{array}\right),$$

(8)

where the superscript T denotes transpose, and where matrix $\mathbf{E}$ is a diagonal matrix:

$$\mathbf{E}=\left(\begin{array}{ccc}{a}^2& 0& 0\\ 0& b^2& 0\\ 0& 0& c^2\end{array}\right).$$

(9)

We refer to $\mathbf{S}$ as the “flow” matrix, and it is composed of two parts when $\mathbf{S}={\mathbf{S}}_v+{\mathbf{S}}_b$: the self-induced motion, ${\mathbf{S}}_v$, and the motion induced by the external background shear flow, ${\mathbf{S}}_b$.

The self-induced motion of the vortex is obtained through the solutions to the equations above, where the QG $\mathcal{O}\left(ϵ\right)$ solution is obtained by inverting Equation (4), giving [21]:

$${\varphi }_v^{\left(1\right)}={\displaystyle \frac{1}{2}}{\mathbf{x}}^T{\mathbf{\Phi }}_v^{\left(1\right)}\mathbf{x},$$

(10)

where ${\mathbf{\Phi }}_v^{\left(1\right)}$ is a $3\times 3$ symmetric matrix:

$${\mathbf{\Phi }}_v^{\left(1\right)}=\mathbf{M}\mathbf{D}{\mathbf{M}}^T,$$

(11)

where the matrix $\mathbf{D}$ is a diagonal matrix with:

$$\begin{array}{ccc}\hfill D_{11}={\xi }_a& =& {\kappa }_v{R}_D(b^2,c^2,a^2),\hfill \end{array}$$

(12a)

$$\begin{array}{ccc}\hfill D_{22}={\xi }_b& =& {\kappa }_v{R}_D(c^2,a^2,b^2),\hfill \end{array}$$

(12b)

$$\begin{array}{ccc}\hfill D_{33}={\xi }_c& =& {\kappa }_v{R}_D(a^2,b^2,c^2),\hfill \end{array}$$

(12c)

where ${\kappa }_v=\varpi abc/3$ is the vortex strength, and where $R_D$ is the symmetric elliptic integral of the second kind [22] given by:

$$R_D(f,g,h)\equiv {\displaystyle \frac{3}{2}}{\int }_0^{\infty }{\displaystyle \frac{dt}{\sqrt{(t+f)(t+g){(t+h)}^3}}}.$$

(13)

The solution at the next order, $\mathcal{O}\left({ϵ}^2\right)$, is obtained by solving the QG + 1 Equation (5), whose solutions are [16]:

$$\begin{array}{ccc}\hfill {\phi }_v^{\left(2\right)}& =& {\displaystyle \frac{1}{2}}{\mathbf{x}}^T{\mathbf{\Gamma }}_v^{\left(2\right)}\mathbf{x},{\mathbf{\Gamma }}_v^{\left(2\right)}\equiv {\displaystyle \frac{1}{\chi }}\mathbf{M}{\mathbf{H}}^1{\mathbf{M}}^T,\hfill \end{array}$$

(14a)

$$\begin{array}{ccc}\hfill {\psi }_v^{\left(2\right)}& =& {\displaystyle \frac{1}{2}}{\mathbf{x}}^T{\mathbf{\Psi }}_v^{\left(2\right)}\mathbf{x},{\mathbf{\Psi }}_v^{\left(2\right)}\equiv {\displaystyle \frac{1}{\chi }}\mathbf{M}{\mathbf{H}}^2{\mathbf{M}}^T,\hfill \end{array}$$

(14b)

$$\begin{array}{ccc}\hfill {\varphi }_v^{\left(2\right)}& =& {\displaystyle \frac{1}{2}}{\mathbf{x}}^T{\mathbf{\Phi }}_v^{\left(2\right)}\mathbf{x},{\mathbf{\Phi }}_v^{\left(2\right)}\equiv -\mathbf{M}{\mathbf{H}}^3{\mathbf{M}}^T,\hfill \end{array}$$

(14c)

where ${\mathbf{H}}^k$ are $3\times 3$ symmetric matrices whose elements are given by:

$$\begin{array}{ccc}\hfill H_{11}^k& =& \left({\Omega }_{ab}+{\Omega }_{ca}\right){\xi }_a{\widehat{\mathbf{a}}}^T{\mathbf{J}}^k\widehat{\mathbf{a}}+\left({\xi }_a-{\Omega }_{ab}\right){\xi }_b{\widehat{\mathbf{b}}}^T{\mathbf{J}}^k\widehat{\mathbf{b}}+\left({\xi }_a-{\Omega }_{ca}\right){\xi }_c{\widehat{\mathbf{c}}}^T{\mathbf{J}}^k\widehat{\mathbf{c}},\hfill \end{array}$$

(15a)

$$\begin{array}{ccc}\hfill H_{22}^k& =& \left({\Omega }_{bc}+{\Omega }_{ab}\right){\xi }_b{\widehat{\mathbf{b}}}^T{\mathbf{J}}^k\widehat{\mathbf{b}}+\left({\xi }_b-{\Omega }_{bc}\right){\xi }_c{\widehat{\mathbf{c}}}^T{\mathbf{J}}^k\widehat{\mathbf{c}}+\left({\xi }_b-{\Omega }_{ab}\right){\xi }_a{\widehat{\mathbf{a}}}^T{\mathbf{J}}^k\widehat{\mathbf{a}},\hfill \end{array}$$

(15b)

$$\begin{array}{ccc}\hfill H_{33}^k& =& \left({\Omega }_{ca}+{\Omega }_{bc}\right){\xi }_c{\widehat{\mathbf{c}}}^T{\mathbf{J}}^k\widehat{\mathbf{c}}+\left({\xi }_c-{\Omega }_{ca}\right){\xi }_a{\widehat{\mathbf{a}}}^T{\mathbf{J}}^k\widehat{\mathbf{a}}+\left({\xi }_c-{\Omega }_{bc}\right){\xi }_b{\widehat{\mathbf{b}}}^T{\mathbf{J}}^k\widehat{\mathbf{b}},\hfill \end{array}$$

(15c)

$$\begin{array}{ccc}\hfill H_{12}^k& =& \left[{\xi }_a{\xi }_b-{\Omega }_{ab}\left({\xi }_a+{\xi }_b\right)\right]{\widehat{\mathbf{a}}}^T{\mathbf{J}}^k\widehat{\mathbf{b}},\hfill \end{array}$$

(15d)

$$\begin{array}{ccc}\hfill H_{31}^k& =& \left[{\xi }_c{\xi }_a-{\Omega }_{ca}\left({\xi }_c+{\xi }_a\right)\right]{\widehat{\mathbf{c}}}^T{\mathbf{J}}^k\widehat{\mathbf{a}},\hfill \end{array}$$

(15e)

$$\begin{array}{ccc}\hfill H_{23}^k& =& \left[{\xi }_b{\xi }_c-{\Omega }_{bc}\left({\xi }_b+{\xi }_c\right)\right]{\widehat{\mathbf{b}}}^T{\mathbf{J}}^k\widehat{\mathbf{c}},\hfill \end{array}$$

(15f)

where

$${\Omega }_{ab}\equiv {\displaystyle \frac{a^2{\xi }_a-b^2{\xi }_b}{a^2-b^2}};{\Omega }_{ca}\equiv {\displaystyle \frac{c^2{\xi }_c-a^2{\xi }_a}{c^2-a^2}};{\Omega }_{bc}\equiv {\displaystyle \frac{b^2{\xi }_b-c^2{\xi }_c}{b^2-c^2}};$$

(16)

and where the matrices ${\mathbf{J}}^k$ are:

$${\mathbf{J}}^1=\left(\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ 1& 0& 0\end{array}\right),{\mathbf{J}}^2=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),{\mathbf{J}}^3=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right).$$

(17)

As the interior potentials at the first and second order have a quadratic dependence on spatial coordinates, the self-induced velocity field is linear and preserves the ellipsoidal form. Thus, the self-induced velocity field has the form ${\mathbf{u}}_v={\mathbf{S}}_v\mathbf{x}$, where the self-induced flow matrix ${\mathbf{S}}_v$ is given by:

$${\mathbf{S}}_v={\mathbf{L}}_{\phi }{\mathbf{\Gamma }}_v^{\left(2\right)}+{\mathbf{L}}_{\psi }{\mathbf{\Psi }}_v^{\left(2\right)}+{\mathbf{L}}_{\varphi }\left({\mathbf{\Phi }}_v^{\left(1\right)}+{\mathbf{\Phi }}_v^{\left(2\right)}\right),$$

(18)

where the skew matrices are defined as:

$${\mathbf{L}}_{\phi }=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -\chi \\ 0& 1& 0\end{array}\right),{\mathbf{L}}_{\psi }=\left(\begin{array}{ccc}0& 0& \chi \\ 0& 0& 0\\ -1& 0& 0\end{array}\right),{\mathbf{L}}_{\varphi }=\left(\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right),$$

(19)

and where the scaling factor $\chi =N/f$ arises where the velocity field depends on z derivatives of the vector potential components.

For the background shear flow field, we use the form derived by [20] for the QG case. They considered the effect of a single distant vortex of strength ${\kappa }_b$, located at $\mathbf{x}={\mathbf{X}}_b$, at a distance R from the ellipsoidal vortex of strength ${\kappa }_v$ located at the origin (see Figure 1); then, the background flow matrix can be written as:

$${\mathbf{S}}_b^{\left(1\right)}=\gamma \left(\begin{array}{ccc}0& {\displaystyle \frac{1}{2}}\left(1+3cos2\theta \right)+\beta & {\displaystyle \frac{3}{2}}sin2\theta \\ 1-\beta & 0& 0\\ 0& 0& 0\end{array}\right),$$

(20)

where $\gamma$ is the “strain rate”, defined as:

$$\gamma \equiv {\kappa }_b/R^3,$$

(21)

where

$$\beta \equiv ({\kappa }_b+{\kappa }_v)/{\kappa }_b=1+{\kappa }_v/{\kappa }_b$$

(22)

is a parameter depending only the ratio of the vortex strengths, and where $\theta$ is the angle of the vortices in the $y-z$ plane. For the case of a cyclonic (anticyclonic) vortex where $\varpi >0$ ($\varpi <0$), this implies that ${\kappa }_v>0$ (${\kappa }_v<0$) and $\gamma >0$ ($\gamma <0$). Thus, as was noted in [23], for both the cyclonic and anticyclonic vortices when $\beta <1$ we have opposite-signed interactions, while for $\beta >1$, we have like-signed interactions. The case where $\beta =1$ implies $|{\kappa }_b/{\kappa }_v|\to \infty$, corresponding to the special cases of adverse shear for $\gamma >0$ and cooperative shear for $\gamma <0$. In what follows, we only consider the case of adverse shear when $\beta =1$. The second-order corrections were considered in [17], although they found that they had negligible impact on the equilibria found; therefore, we neglect them here.

Thus, given the background flow parameters and an initial vortex strength, shape, and orientation, the vortex evolves according to Equation (6), with the self-induced flow matrix ${\mathbf{S}}_v$ given by Equation (18) and with the background flow matrix ${\mathbf{S}}_b$ given by Equation (20). For the background flow, we consider here that the matrix component $B_{33}$ is constant. This arises because the time dependence of the $B_{33}$ component in Equation (6) is equal to $2\left(S_{31}{B}_{31}+S_{32}{B}_{23}+S_{33}{B}_{33}\right)$ and, for the background flow considered here, $B_{31}=S_{32}=S_{33}=0$. While this is always the case in QG, this is only true for certain configurations of the background flow matrix ${\mathbf{S}}_b$ in the QG + 1 system. As noted in [23], this implies that the height-to-width aspect ratio, given by $h/r=\sqrt{4\pi /3V}{\mathbf{B}}_{33}^{3/4}$, is constant. Thus, the vortex system can be specified by the parameter values $(\varpi ,f/N,h/r,\gamma ,\beta ,\theta )$. In what follows, we consider $f/N=0.1$, typical in large-scale flows, and we fix the magnitude of the PV anomaly, $\left|\varpi \right|=0.5$. While we fix the magnitude of the PV anomaly, we explore the cyclonic–anticyclonic asymmetries considering $\varpi =\pm 0.5$.

2.2. Vortex Equilibria and Linear Stability

From the equation governing the evolution of the vortex, Equation (6), we can determine steady states that satisfy the following:

$$\mathbf{S}\mathbf{B}+\mathbf{B}{\mathbf{S}}^T=0.$$

(23)

This equation can be solved numerically using an iterative linear method introduced by [23]. An initial guess for the matrix $\mathbf{B}$ is used, and then the linearized form of Equation (23) is used to obtain the next iteration. Equation (23) cannot be inverted directly, but instead one equation must be removed and conservation of volume enforced to close the equations. For the lowest strain value, the initial guess is a vortex having a circular cross section aligned with the coordinate axes, while for the initial guess, for each further increment of the strain value, we use the equilibrium obtained for the previous strain values. We apply the iterative process until the root mean square difference between the elements of the matrix $\mathbf{B}$ at successive iterations is less than ${10}^{-10}$. If the difference between iterations is greater than 1 or if the number of iterations exceeds 10,000, then the procedure is stopped, and we assume there is no steady state for the particular parameters considered. This procedure is applied for each set of specified parameter values $(h/r,\beta ,\theta )$ and for the QG, QG + 1 cyclonic, and QG + 1 anticyclonic cases. The procedure is first applied to the smallest value of the strain rate, $\left|\gamma \right|={10}^{-5}$ and, once the equilibrium is found, the strain rate is incremented by $d\gamma ={10}^{-5}$. The procedure is repeated until we reach a critical turning point strain, ${\gamma }_c$, i.e., the strain value beyond which there are no more steady states. In general, the critical strain is different for the QG, QG + 1 cyclonic, and QG + 1 anticyclonic equilibria.

As well as determining the equilibria, we wish to analyze their linear stability to ellipsoidal modes, i.e., the $m=2$ mode that corresponds to changes in the vortex shape that preserve its ellipsoidal form. This mode has been shown to be the marginal mode of instability for QG ellipsoids [24]. We compute the linear stability following the method of [24], where the shape matrix is decomposed into:

$$\mathbf{B}\left(t\right)={\mathbf{B}}_e+\widehat{\mathbf{B}}{e}^{\sigma t},$$

(24)

where ${\mathbf{B}}_e$ is the equilibrium part, and the second term is an infinitesimal perturbation. By Taylor expansion of the flow matrix $\mathbf{S}$ and by substituting Equation (24) into Equation (6), one can obtain an eigenvalue problem where $\sigma$ and $\widehat{\mathbf{B}}$ are the eigenvalue and eigenvector, respectively, and where $\sigma ={\sigma }_r+i{\sigma }_i$, where the real and imaginary parts are the growth rate and frequency of the mode, respectively (see [24] for details).

3. Results

Here we compute the equilibria for a range of values of the background flow parameters $\beta$ and $\theta$ and for a number of values of the height-to-width aspect ratio $h/r$. For each height-to-width aspect ratio considered, we examine both like-signed interactions with $1\le \beta \le 6$ and opposite-signed interactions with $-4\le \beta <1$, while we consider values of the angle of incidence $0^{\circ }\le \theta <{90}^{\circ }$. For every case, we will compute the QG, QG + 1 cyclonic, and QG + 1 anticyclonic equilibria up to the margin of stability, and we define the magnitude of the marginal strain rate for QG, QG + 1 cyclonic, and QG + 1 anticyclonic equilibria as ${\gamma }_m^{qg}$, ${\gamma }_m^{cy}$, and ${\gamma }_m^{ac}$, respectively.

The steady states of this system have recently been solved in [17], although the focus there was on the magnitude of the marginal and critical turning point strain and how they change with the background flow parameters. Here we wish to revisit this, although we focus on how the vortex shape and orientation change with the background flow and quantify the asymmetry between the cyclonic and the anticyclonic equilibria. We characterize the shape of the vortex by defining the horizontal aspect ratio as $\delta \equiv a/b$ and the vertical aspect as $\tau \equiv c/\sqrt{ab}$, while the orientation is specified by the tilt angle $\eta$ (Figure 1). Using these aspect ratios, the ellipsoid semi-axis lengths are given by $a={\delta }^{1/2}/{\tau }^{1/3}$, $b=1/\left({\delta }^{1/2}{\tau }^{1/3}\right)$, and $c={\tau }^{2/3}$, where $abc=1$, thus fixing the volume of the ellipsoid without loss of generality. Note that the vertical aspect ratio is different than the height-to-width aspect ratio $h/r$ and that it can vary with different strain values.

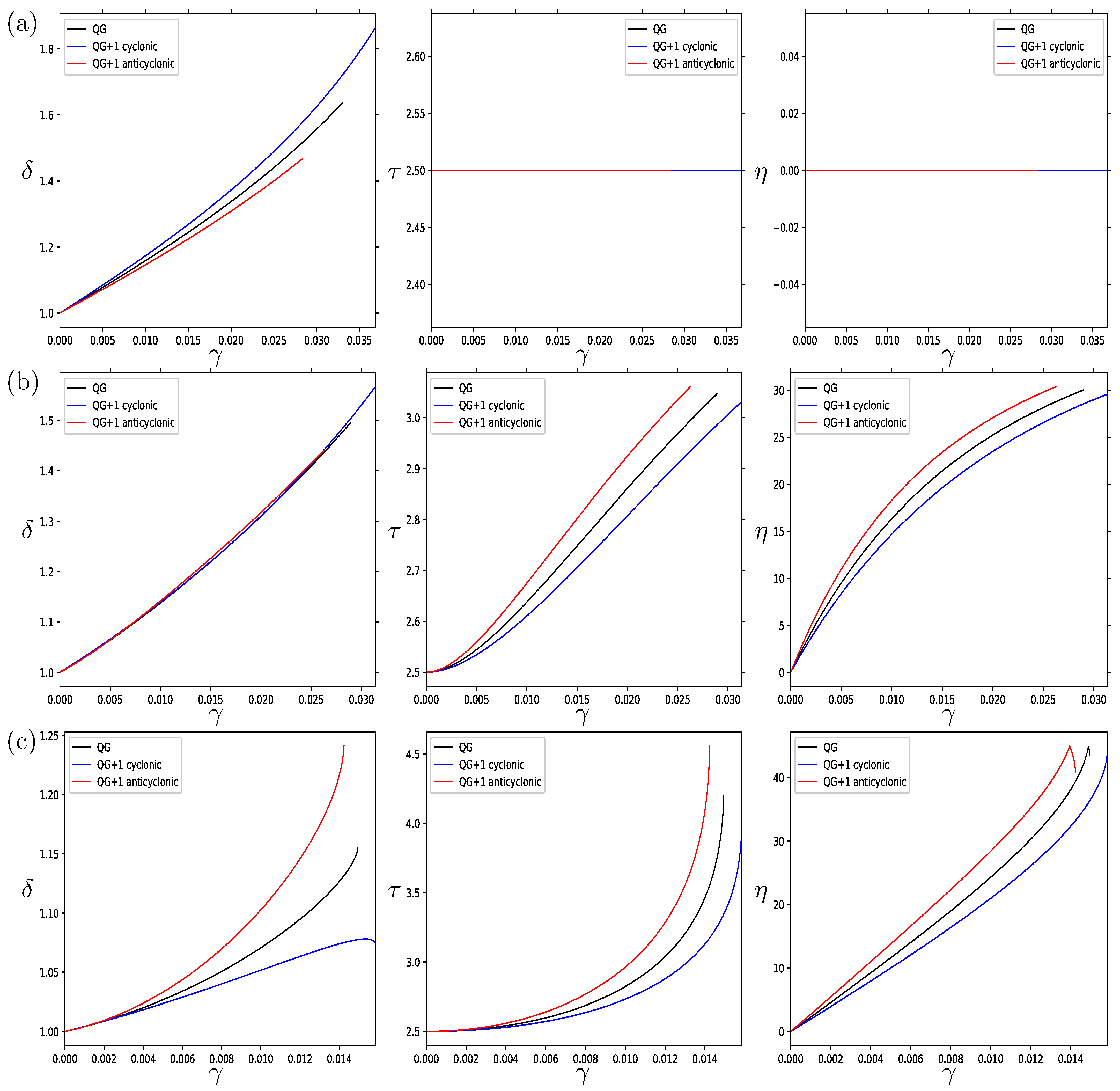
3.1. Vortex Characteristics as a Function of Strain

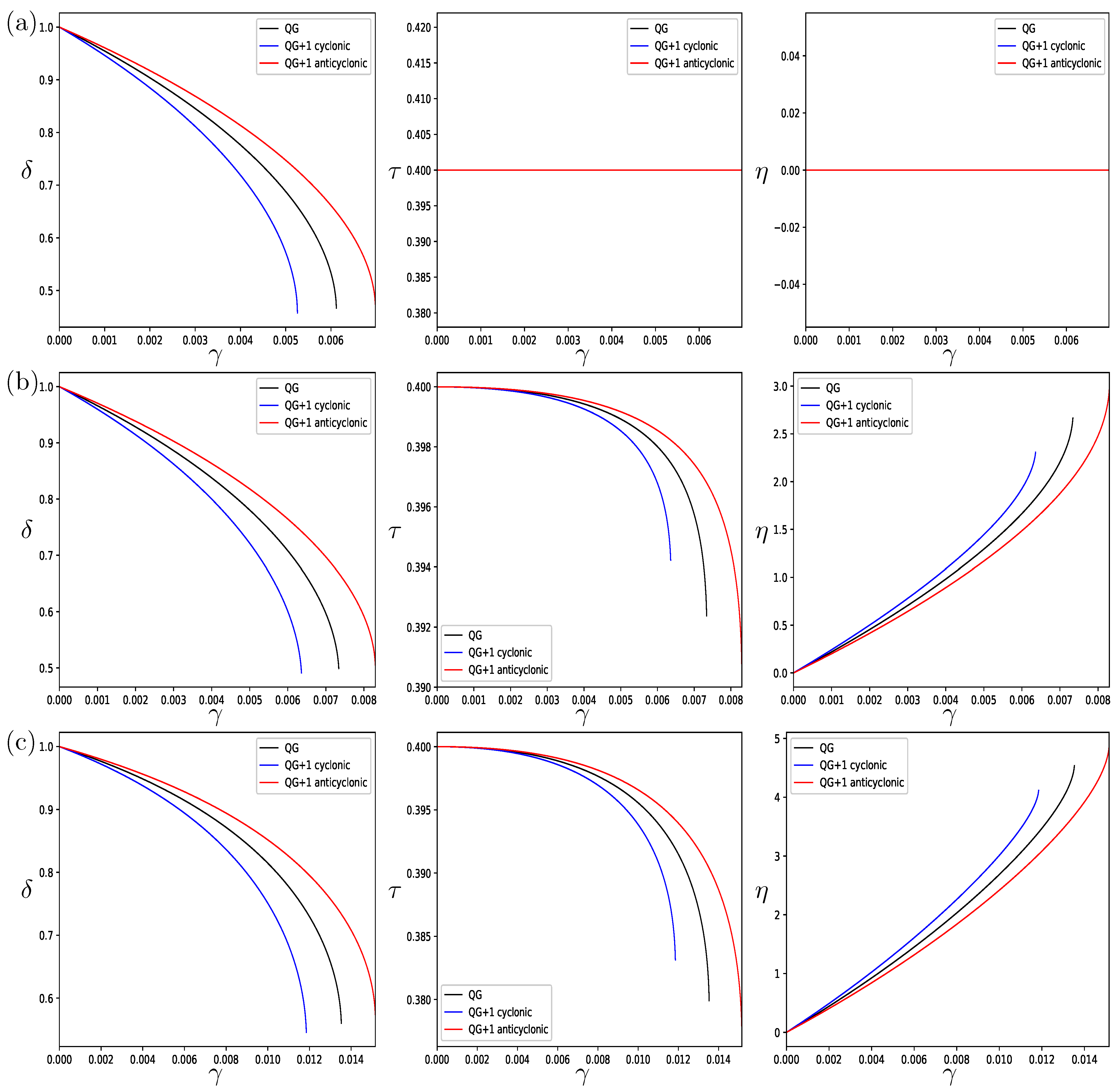
In Figure 2, we plot the horizontal and vertical aspect ratios and the tilt angle as a function of strain for QG (black), QG + 1 cyclonic (blue), and QG + 1 anticyclonic (red) equilibria for three different values of $\theta$ in the case of an oblate vortex with $h/r=0.4$ and considering the case of like-signed interactions with $\beta =2$.

For the case when $\theta =0$, Figure 2a, only the horizontal aspect ratio varies with the strain. That is, when there is no vertical shear, there is no tilting of the vortex, and the vertical aspect ratio is equal to the height-to-width aspect ratio. On the other hand, the horizontal aspect ratio decreases with increasing strain, with the cyclonic values being less than the anticyclonic values for a given strain value. However, as the marginal strain rate of the anticyclonic equilibria are higher than those of the cyclones, the marginal horizontal aspect ratio ends up being the same for anticyclones and cyclones. For the cases $\theta ={30}^{\circ }$ and $\theta ={60}^{\circ }$ in Figure 2b and Figure 2c, respectively, the equilibria tilt angle increases as the strain increases. As the equilibria increasingly tilt with the strain, the vertical aspect ratio $\tau$ decreases. For a given strain rate, the deformation of the cyclonic vortex is greater than the anticyclonic case. However, the marginal strain is greater for the anticyclonic vortex, and so at the marginal strain, the anticyclone is more tilted and has a smaller vertical aspect ratio than the cyclone.

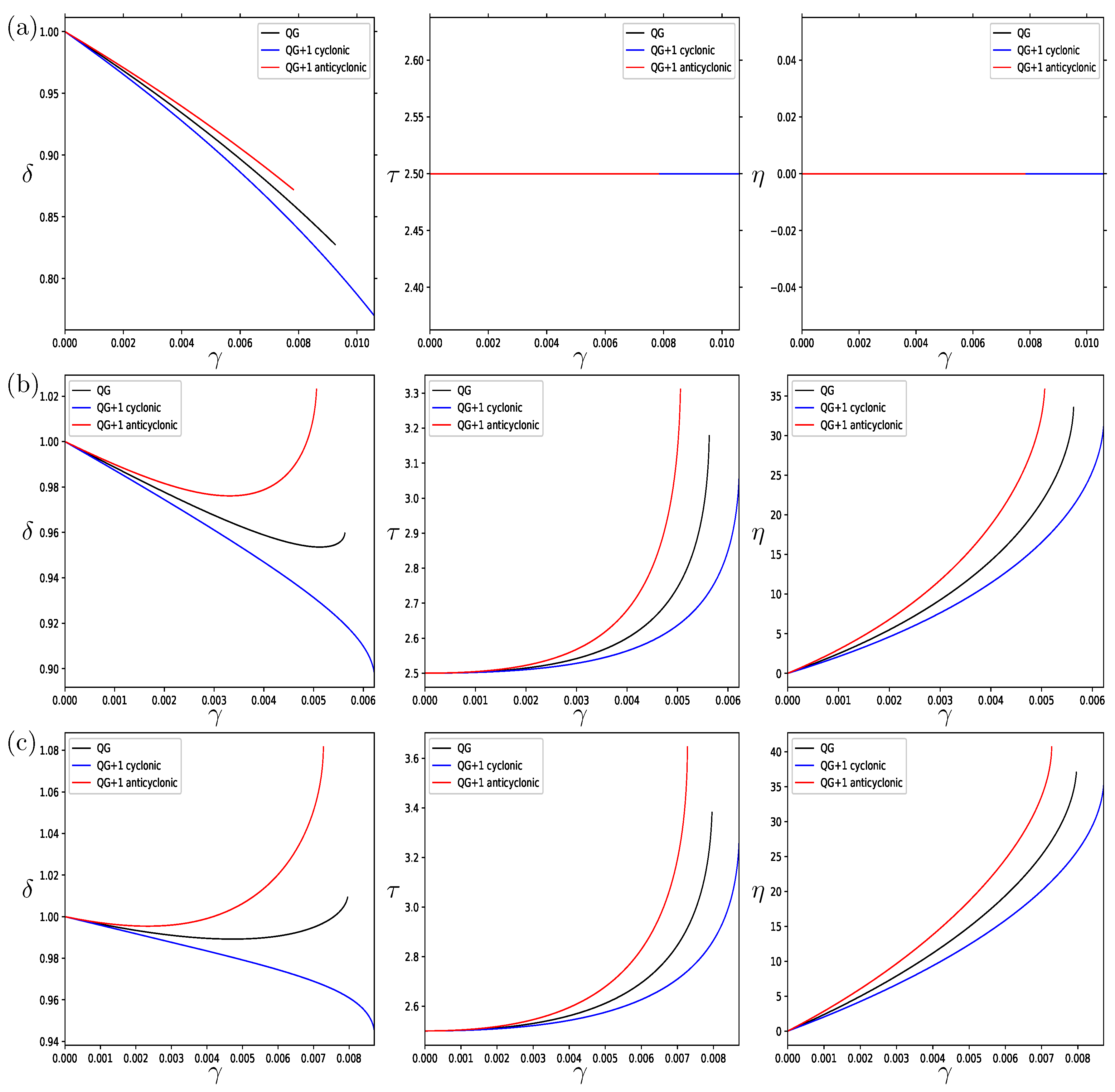
In Figure 3, we plot the parameters for the case of a prolate vortex with $h/r=2.5$. When there is no vertical shear, $\theta =0$ (Figure 3a), the behavior is similar to that which was seen for the oblate case, although in this case, at the marginal strain, there is stronger asymmetry of the horizontal aspect ratio, with the horizontal aspect ratio of the cyclonic equilibrium being much less than the anticyclonic equilibrium.

When there is vertical shear, Figure 3b,c, there is even stronger asymmetry in the horizontal aspect ratio, with the cyclonic case decreasing with strain, while the anticyclonic case initially decreases but eventually increases and becomes larger than its initial value. Unlike the oblate case, the vertical aspect ratio increases with the strain rate, while the vortex has a much larger degree of tilting. Additionally, conversely to the oblate case, for a given value of the strain rate, the anticyclonic vortex is more deformed and has a greater tilt angle than the cyclonic case.

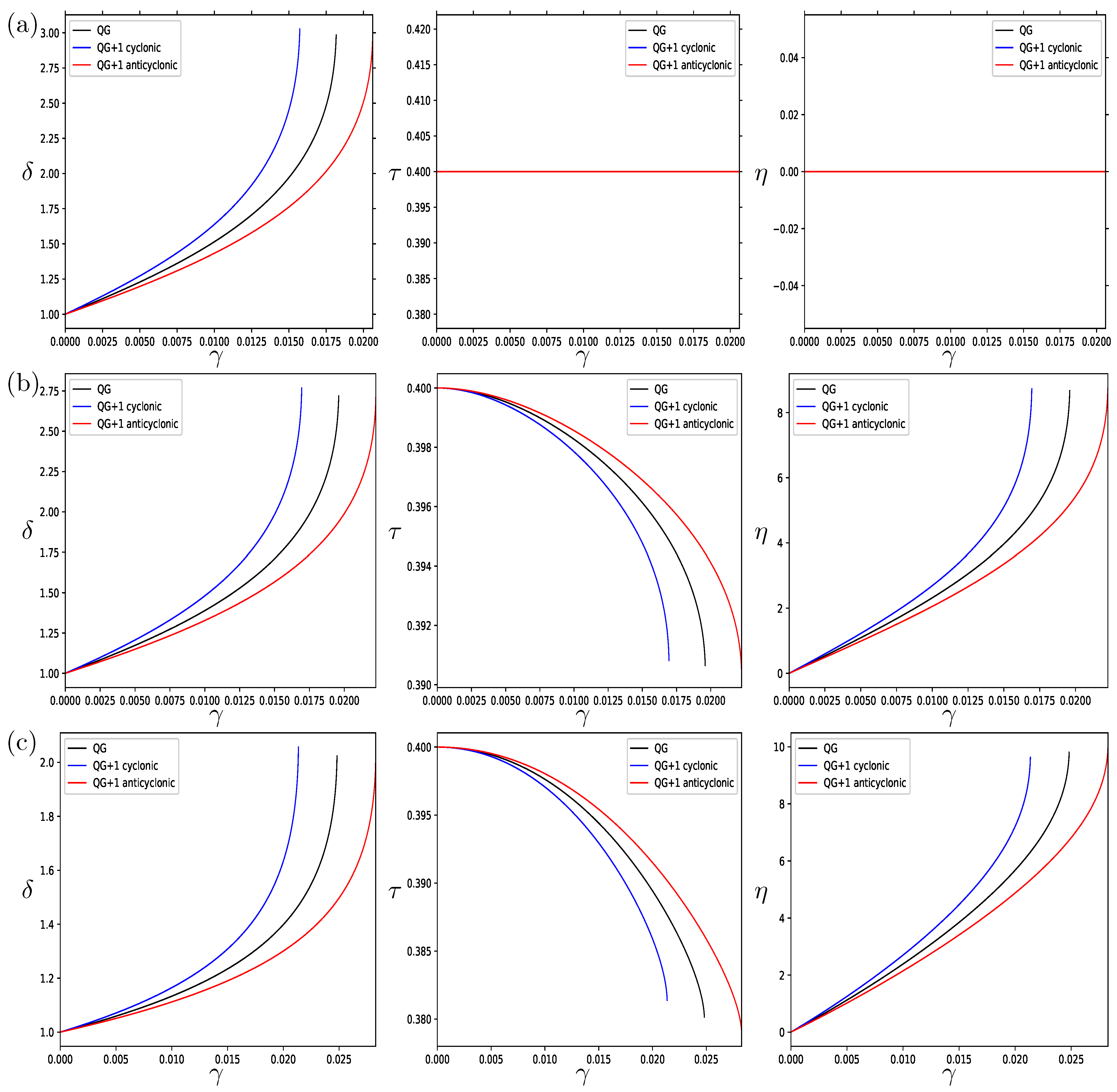
Next, we consider the case of opposite-signed interactions with $\beta =0$ and show the cases $h/r=0.4$ and $h/r=2.5$ in Figure 4 and Figure 5, respectively.

One significant difference between the opposite and like-signed cases is that the opposite-signed horizontal aspect ratio increases with the strain rate for both oblate and prolate cases, whereas this only occurs for anticyclonic prolate equilibria when there is vertical shear. Overall, the opposite-signed equilibria are more deformed than the like-signed equivalent cases, probably linked to the fact that the marginal strain values for opposite-signed interactions are much larger those for like-signed interactions. However, the overall asymmetry between the cyclonic and anticyclonic equilibria for the opposite-signed interactions is reduced in nearly all cases, except for the prolate case with $\theta ={60}^{\circ }$ (Figure 5c).

3.2. Asymmetry at the Marginal Strain

Now we examine how the shape characteristics of the cyclonic and anticyclonic equilibria at the marginal strain rate change with the background flow parameters. Similar to how we refer to the marginal strain rates for QG, QG + 1 cyclonic, and QG + 1 anticyclonic equilibria, we define the marginal shape characteristics for the QG, QG + 1 cyclonic, and QG + 1 anticyclonic respectively as: ${\delta }_m^{qg}$, ${\delta }_m^{cy}$, and ${\delta }_m^{ac}$ for the marginal horizontal aspect ratio; ${\tau }_m^{qg}$, ${\tau }_m^{cy}$, and ${\tau }_m^{ac}$ for the marginal vertical aspect ratio; and ${\eta }_m^{qg}$, ${\eta }_m^{cy}$, and ${\eta }_m^{ac}$ for the marginal tilt angle. First, we will consider the dependence on the vertical offset $\theta$, beginning with the case of like-signed interactions in Figure 6.

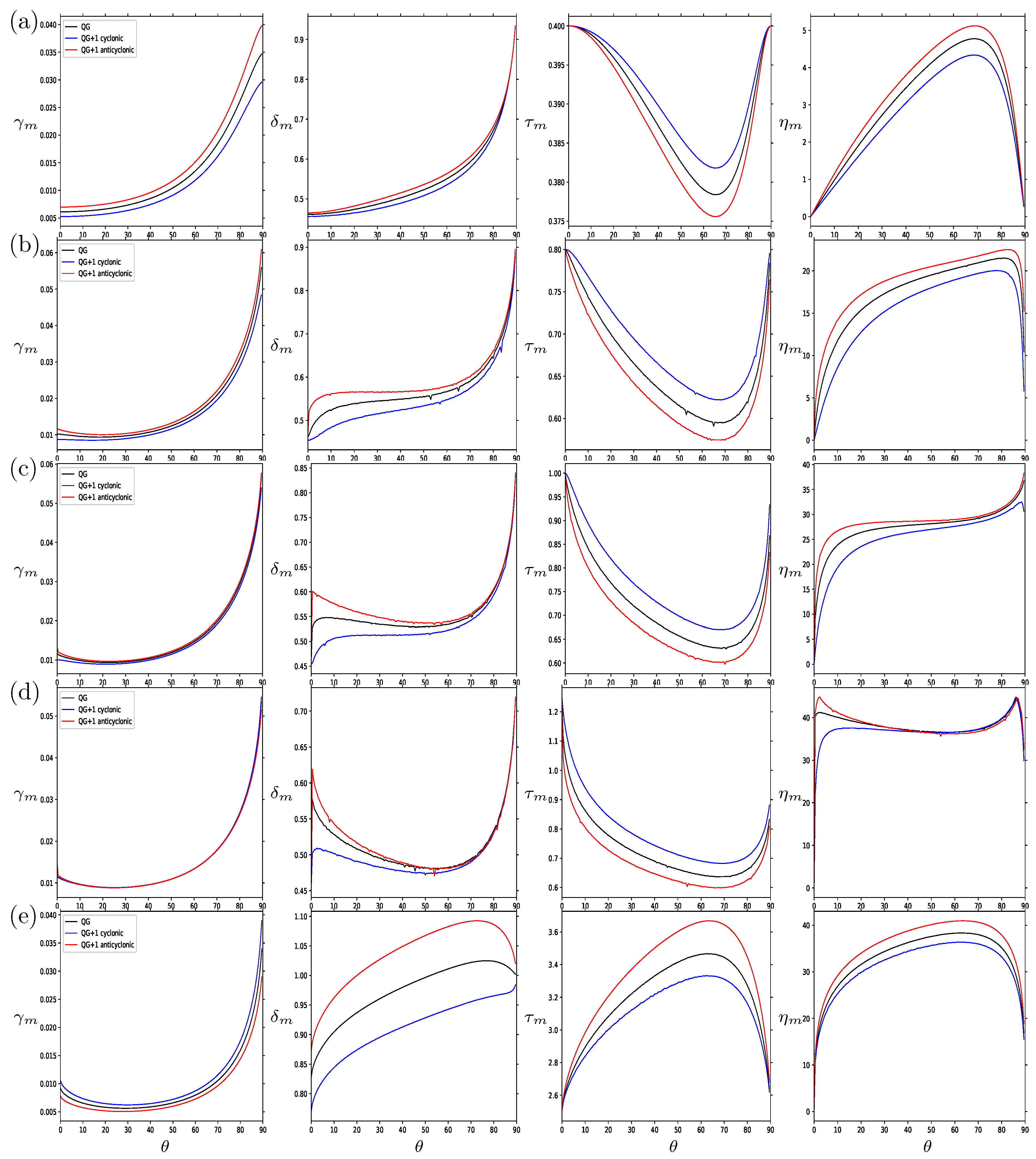
We plot the marginal strain rate ${\gamma }_m$ and the shape and orientation variables at the marginal strain rate as a function of $\theta$ for the cases when $\beta =2$ and for (a) $h/r=0.4$, (b) $h/r=0.8$, (c) $h/r=1$, (d) $h/r=1.25$, and (e) $h/r=2.5$. The marginal strain rate shows similar dependence on $\theta$, with the the largest values occurring at $\theta ={90}^{\circ }$. However, for the oblate cases ($h/r\le 1$), ${\gamma }_m^{ac}>{\gamma }_m^{cy}$, meaning that the anticyclonic oblate vortices are more stable, while the reverse is the case for the prolate cases ($h/r>1$). The horizontal aspect ratio ${\delta }_m$ also tends towards larger values for large $\theta$, although the dependence on $\theta$ changes with $h/r$. In particular, the most prolate case $h/r=2.5$ differs from the other cases, as it has the strongest cyclone–anticyclone asymmetry at large $\theta$, whereas for the other values of $h/r$, the asymmetry is strongest for low $\theta$. For all aspect ratios, ${\delta }_m^{ac}>{\delta }_m^{cy}$, and the value of $\delta$ is closest to unity for $\theta ={90}^{\circ }$, i.e., for the largest value of vertical shear, the equilibrium horizontal cross section becomes more circular. For the vertical aspect ratio, there is similar behavior for the cases where $h/r<2.5$, with ${\tau }_m$ decreasing with $\theta$ until it reaches $\theta \approx {70}^{\circ }$, at which point it increases again, returning to near the initial value, with ${\tau }_m^{ac}<{\tau }_m^{cy}$. However, for $h/r=2.5$ (Figure 6e), ${\tau }_m$ increases with $\theta$, reaching a maximum at about $\theta \approx {70}^{\circ }$, before returning to the initial value. In this case, ${\tau }_m^{ac}>{\tau }_m^{cy}$. The marginal tilting angle ${\eta }_m$ for all $h/r$ initially increases with $\theta$, although this increase is more abrupt for $h/r$ close to unity. For most values of $h/r$, the tilting angle decreases at large $\theta$, except for the case $h/r=1$, where the value remains high for the largest $\theta$. Overall, looking at the asymmetry in the shape and orientation, it is clear that the anticyclonic equilibria undergo greater deformation than the cyclonic ones. The greatest difference between the anticyclonic and cyclonic marginal shape most often occurs at $\theta \approx {70}^{\circ }$, with the exception of when $h/r$ is close to unity (Figure 6b,c,e), with ${\delta }_m$ and ${\eta }_m$ having the largest asymmetry when $\theta =0^{\circ }$.

In Figure 7, we consider the dependence on $\theta$ for the opposite-signed case with $\beta =0$. Here, there is very different behavior for the most oblate case, $h/r=0.4$, and for the other cases. For the strongly oblate case in Figure 7a, we see that ${\gamma }_c^{ac}>{\gamma }_c^{cy}$, although there are very few differences between the shape and orientation of the cyclonic and anticyclonic equilibria. The horizontal aspect ratio decreases with $\theta$, while the vertical aspect ratio initially decreases to a minimum at $\theta \approx {60}^{\circ }$ before increasing back to its original value. Conversely, the tilt angle increases to a maximum of ${10}^{\circ }$ before returning to zero. For $h/r>0.4$, the behavior of all the variables looks dramatically different from the most oblate case, with a kink appearing in the dependence at $\theta \approx {60}^{\circ }$. This kink has been seen before in [17,24] and is associated with a swap in the horizontal axes a and b of the equilibria when the shape matrix component $B_{11}=B_{22}$. It marks a transition in the behavior of the variables, with the vertical aspect ratio and the tilt angle reaching a maximum at this point before decreasing, while for the horizontal aspect ratio, it is close to the point where we go from ${\delta }_m^{ac}<{\delta }_m^{cy}$ to ${\delta }_m^{ac}>{\delta }_m^{cy}$. For ${\delta }_m$, interestingly, when there is no vertical shear, $\theta =0^{\circ }$, and the horizontal cross section is more deformed, with ${\delta }_m$ much larger than 1; however, as the vertical shear increases, the horizontal cross section becomes more circular. In the case of the vertical aspect ratio and the tilt angle, the greatest asymmetry between the cyclonic and anticyclonic equilibria occurs where the kink occurs, whereas for the horizontal aspect ratio, the strongest asymmetry occurs for $\theta =0^{\circ }$. Overall, the asymmetry is largest for the prolate cases ($h/r>1$).

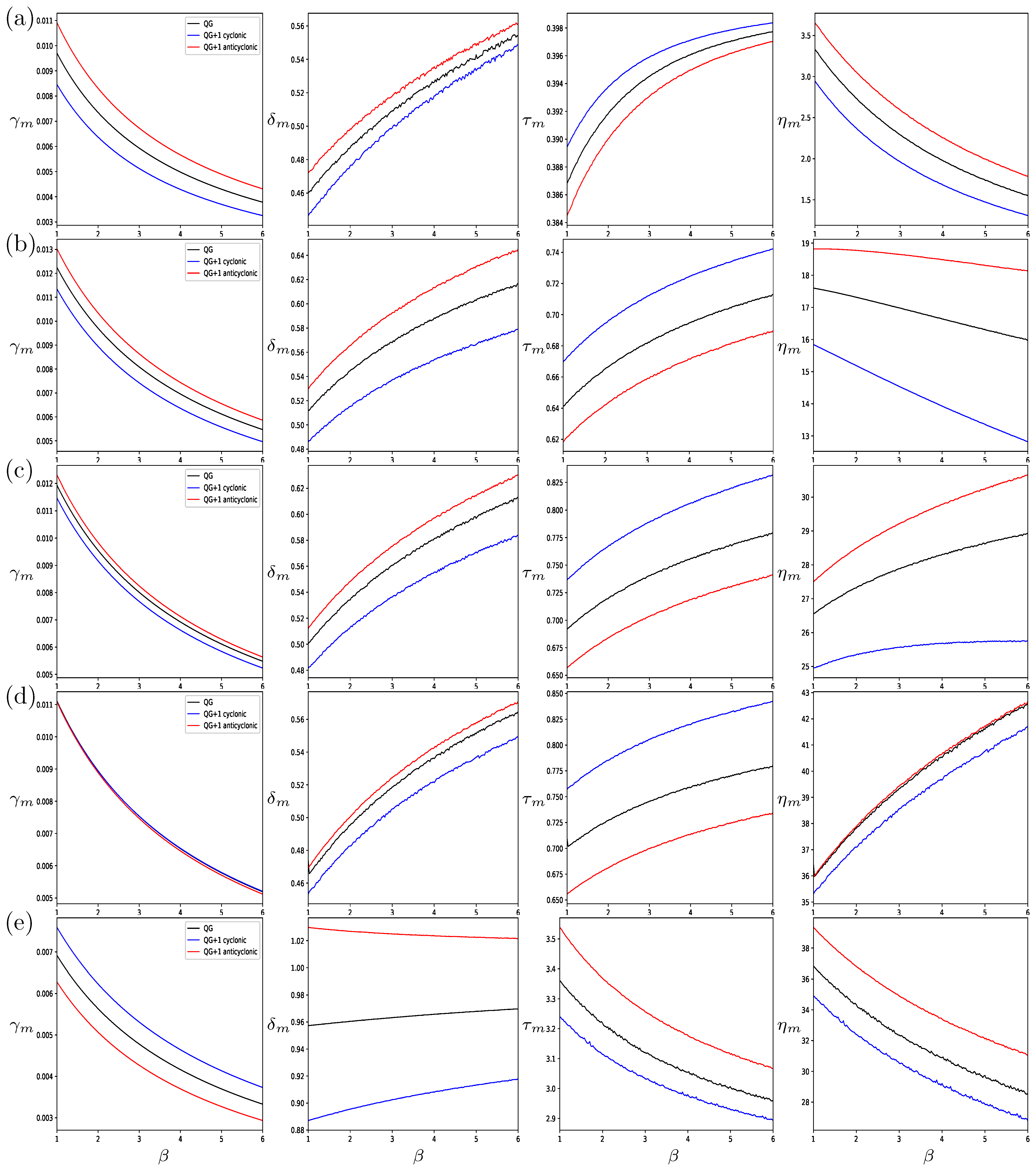
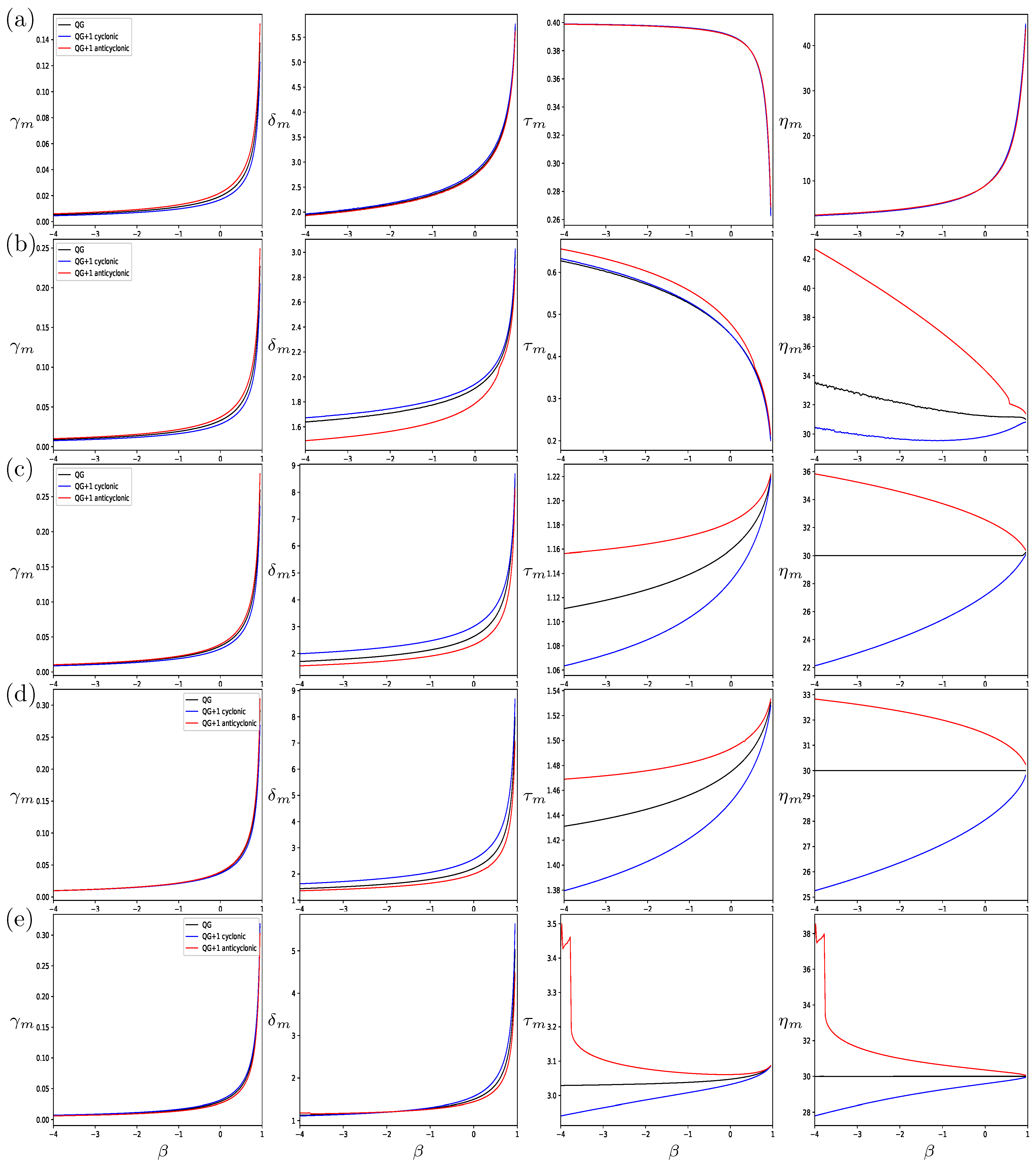
Next, we look at how the shape characteristics of the equilibria at the marginal strain rate change with the parameter $\beta$. In Figure 8, we plot the equilibria conditions at the marginal strain as a function of $\beta$ for the case of like-signed interactions.

For all values of $h/r$, the marginal strain ${\gamma }_m$ decreases with increasing $\beta$, although there is a difference between the oblate and prolate cases, with the oblate anticyclonic equilibria being more stable than the cyclonic equilibria, ${\gamma }_m^{ac}>{\gamma }_m^{cy}$, while the reverse is true for the prolate cases. The marginal horizontal aspect ratios have similar dependence on $\beta$ for all values of $h/r$, with ${\delta }_m$ increasing with $\beta$, moving towards unity; the only exception is ${\delta }_m^{ac}$ for the most prolate case, where the value decreases as $\beta$ increases. In all cases, ${\delta }_m^{ac}>{\delta }_m^{cy}$, with the strongest asymmetry occurring for $h/r=2.5$. Similarly, for the vertical aspect ratio, we see different behavior for the most prolate case, with ${\tau }_m$ decreasing with $\beta$, while for all the other values of $h/r$, ${\tau }_m$ increases with $\beta$. In all cases, ${\tau }_m$ approaches $h/r$ as $\beta$ increases. For the tilting angle ${\eta }_m$, there seems to be a separation between the cases with $h/r$ close to unity and the extremely oblate and prolate cases, with the most oblate and prolate values decreasing with $\beta$, while the other cases increase with $\beta$. Overall, the asymmetry tends to increase with $\beta$, with only the most oblate and prolate cases defying this trend for ${\delta }_m$.

In Figure 9, we look at the dependence on $\beta$ for opposite-signed interactions.

Here, the marginal strain behaves the same for all values of $h/r$, with ${\gamma }_m$ increasing rapidly as $\beta$ goes to 1. These larger marginal strain values on the approach to $\beta =1$ mark extreme deformation of the horizontal cross section of the equilibria, with ${\delta }_m$ increasing dramatically for all values of $h/r$. Instead, the behavior of the marginal vertical aspect ratio ${\tau }_m$ changes with $h/r$, with the most oblate cases (Figure 9a,b) decreasing with $\beta$, whereas for the other values of $h/r$, it increases with $\beta$, except for ${\tau }_m^{ac}$ for $h/r=2.5$ (Figure 9e). Apart from the most oblate case $h/r=0.4$, both the vertical aspect ratio ${\tau }_m$ and the tilt angle ${\eta }_m$ show increasing asymmetry as $\beta$ decreases, with the anticyclonic values tending to increase while the cyclonic values decrease. Generally, it appears that, as we move away from $\beta =1$ for both like-signed and opposite-signed interactions, the asymmetry increases.

3.3. Approximate Equilibrium Solutions

In order to clarify how the vortex characteristics depend on the background flow, it is worth trying to find approximate solutions for the equilibria. Given the form of the background flow, we have found that the equilibria are always tilted about the x-axis, implying that the axis vectors are:

$$\widehat{\mathbf{a}}=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),\widehat{\mathbf{b}}=\left(\begin{array}{c}0\\ cos\eta \\ -sin\eta \end{array}\right),\widehat{\mathbf{c}}=\left(\begin{array}{c}0\\ sin\eta \\ cos\eta \end{array}\right).$$

(25)

This means that the shape matrix always has a particular form, with $B_{12}=B_{31}=0$, and so the other components can be written in terms of the parameters $\delta$, $\tau$, and $\eta$:

$$\begin{array}{ccc}\hfill B_{11}& =& {\displaystyle \frac{\delta }{{\tau }^{2/3}}},\hfill \end{array}$$

(26a)

$$\begin{array}{ccc}\hfill B_{22}& =& {\displaystyle \frac{\delta }{{\tau }^{2/3}}}\left[1-(1-\delta {\tau }^2){sin}^2\eta \right],\hfill \end{array}$$

(26b)

$$\begin{array}{ccc}\hfill B_{33}& =& {\displaystyle \frac{\delta }{{\tau }^{2/3}}}\left[\delta {\tau }^2+(1-\delta {\tau }^2){sin}^2\eta \right],\hfill \end{array}$$

(26c)

$$\begin{array}{ccc}\hfill B_{23}& =& {\displaystyle \frac{\delta }{{\tau }^{2/3}}}\left(\delta {\tau }^2-1\right)sin\eta cos\eta .\hfill \end{array}$$

(26d)

Similarly the self-induced flow matrix has only certain non-zero components, which can be written as:

$$\begin{array}{ccc}\hfill S_{v12}& =& q_0+q_1{sin}^2\eta +q_2{sin}^4\eta ,\hfill \end{array}$$

(27a)

$$\begin{array}{ccc}\hfill S_{v13}& =& \left[r_0+r_1{sin}^2\eta \right]sin\eta cos\eta ,\hfill \end{array}$$

(27b)

$$\begin{array}{ccc}\hfill S_{v21}& =& s_0+s_1{sin}^2\eta ,\hfill \end{array}$$

(27c)

$$\begin{array}{ccc}\hfill S_{v31}& =& t_{0}sin\eta cos\eta ,\hfill \end{array}$$

(27d)

where the coefficients are:

$$\begin{array}{ccc}\hfill q_0& =& {\xi }_b(-1+2{\xi }_c)-{\Omega }_{bc}({\xi }_b+2{\xi }_c),\hfill \end{array}$$

(28a)

$$\begin{array}{ccc}\hfill q_1& =& {\xi }_b-{\xi }_c-6{\xi }_b{\xi }_c+3({\xi }_b{\Omega }_{ab}+{\xi }_c{\Omega }_{ca})+{\Omega }_{bc}(7{\xi }_b+9{\xi }_c),\hfill \end{array}$$

(28b)

$$\begin{array}{ccc}\hfill q_2& =& 8\left[{\xi }_b{\xi }_c-{\Omega }_{bc}({\xi }_b+{\xi }_c)\right]-3({\xi }_b{\Omega }_{ab}+{\xi }_c{\Omega }_{ca}),\hfill \end{array}$$

(28c)

$$\begin{array}{ccc}\hfill r_0& =& {\xi }_b-{\xi }_c-6{\xi }_b{\xi }_c+3{\xi }_c{\Omega }_{ca}+{\Omega }_{bc}(5{\xi }_b+7{\xi }_c),\hfill \end{array}$$

(28d)

$$\begin{array}{ccc}\hfill r_1& =& 12\left[{\xi }_b{\xi }_c-{\Omega }_{bc}({\xi }_b+{\xi }_c)\right]-3({\xi }_b{\Omega }_{ab}+{\xi }_c{\Omega }_{ca}),\hfill \end{array}$$

(28e)

$$\begin{array}{ccc}\hfill s_0& =& {\xi }_a(1-2{\xi }_c)+{\Omega }_{ca}(2{\xi }_c+{\xi }_a),\hfill \end{array}$$

(28f)

$$\begin{array}{ccc}\hfill s_1& =& 2{\xi }_a({\xi }_c-{\xi }_b)+{\Omega }_{ab}({\xi }_a+2{\xi }_b)-{\Omega }_{ca}(2{\xi }_c+{\xi }_a),\hfill \end{array}$$

(28g)

$$\begin{array}{ccc}\hfill t_0& =& {\displaystyle \frac{f}{N}}\left[{\Omega }_{ca}({\xi }_c-{\xi }_a)+{\Omega }_{ab}({\xi }_a-{\xi }_b)+{\xi }_a({\xi }_b-{\xi }_c)\right].\hfill \end{array}$$

(28h)

As a result of the form of the shape and flow matrices, equilibrium Equation (23) reduces significantly to just two equations:

$$\begin{array}{ccc}\hfill S_{31}{B}_{11}+S_{13}{B}_{33}+S_{12}{B}_{23}& =& 0,\hfill \end{array}$$

(29a)

$$\begin{array}{ccc}\hfill S_{21}{B}_{11}+S_{12}{B}_{22}+S_{13}{B}_{23}& =& 0.\hfill \end{array}$$

(29b)

Given these two equations, as well as the fact that the $B_{33}$ component is constant, we have three equations in the three unknown variables $\delta$, $\tau$, and $\eta$. However, since the self-induced flow matrix ${\mathbf{S}}_v$ depends on these variables through the elliptical integrals, these equations cannot be directly solved. However, we can obtain approximate solutions by expanding these variables in the strain rate, i.e.,:

$$\begin{array}{ccc}\hfill \delta & =& {\delta }_0+\gamma {\delta }_1+{\gamma }^2{\delta }_2+\mathcal{O}\left({\gamma }^3\right),\hfill \end{array}$$

(30a)

$$\begin{array}{ccc}\hfill \tau & =& {\tau }_0+\gamma {\tau }_1+{\gamma }^2{\tau }_2+\mathcal{O}\left({\gamma }^3\right),\hfill \end{array}$$

(30b)

$$\begin{array}{ccc}\hfill \eta & =& {\eta }_0+\gamma {\eta }_1+{\gamma }^2{\eta }_2+\mathcal{O}\left({\gamma }^3\right).\hfill \end{array}$$

(30c)

We assume that the unperturbed solution when no strain is applied has a circular cross section, ${\delta }_0=1$, is upright, ${\eta }_0=0$, and that the initial vertical aspect ratio is equal to the height-to-width aspect ratio, i.e., ${\tau }_0=h/r$. We can Taylor expand the self-induced flow matrix components about this unperturbed configuration as follows:

$${\mathbf{S}}_v(\delta ,\tau ,\eta )={\mathbf{S}}_v({\delta }_0,{\tau }_0,{\eta }_0)+{\left.{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial \delta }}\right|}_{{\delta }_0}(\delta -{\delta }_0)+{\left.{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial \tau }}\right|}_{{\tau }_0}(\tau -{\tau }_0)+{\left.{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial \eta }}\right|}_{{\eta }_0}(\eta -{\eta }_0)+\dots ,$$

(31)

where derivatives with respect to the aspect ratios can be related to derivatives with respect to the axis lengths by:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial \delta }}& =& {\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial a^2}}{\displaystyle \frac{\partial a^2}{\partial \delta }}+{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial b^2}}{\displaystyle \frac{\partial b^2}{\partial \delta }}+{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial c^2}}{\displaystyle \frac{\partial c^2}{\partial \delta }}={\displaystyle \frac{1}{{\delta }^2{\tau }^{2/3}}}\left({\delta }^2{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial a^2}}-{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial b^2}}\right),\hfill \end{array}$$

(32a)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial \tau }}& =& {\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial a^2}}{\displaystyle \frac{\partial a^2}{\partial \tau }}+{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial b^2}}{\displaystyle \frac{\partial b^2}{\partial \tau }}+{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial c^2}}{\displaystyle \frac{\partial c^2}{\partial \tau }}=-{\displaystyle \frac{2}{3\delta {\tau }^{5/3}}}\left({\delta }^2{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial a^2}}+{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial b^2}}-2\delta {\tau }^2{\displaystyle \frac{\partial {\mathbf{S}}_v}{\partial c^2}}\right),\hfill \end{array}$$

(32b)

and where we use formulas for the derivatives of the elliptical integrals that have been derived in previous works [17,24]. By applying these formulas in the equilibrium relations in Equation (29) and matching the coefficients at different orders, we get, at the first order:

$${\delta }_1=-{\displaystyle \frac{3\left(1+cos2\theta \right)}{A_1}};{\tau }_1=0;{\eta }_1=-{\displaystyle \frac{3{\tau }_0^{2}sin2\theta }{A_2}},$$

(33)

and at the second order, we find:

$$\begin{array}{ccc}\hfill {\delta }_2& =& {\displaystyle \frac{A_3{\eta }_1^2+{\tau }_0^2\left[8(\beta -1)-A_1{\delta }_1\right]{\delta }_1}{2{\tau }_0^2{A}_1}},\hfill \end{array}$$

(34a)

$$\begin{array}{ccc}\hfill {\tau }_2& =& {\displaystyle \frac{3({\tau }_0^2-1){\eta }_1^2}{4{\tau }_0}},\hfill \end{array}$$

(34b)

$$\begin{array}{ccc}\hfill {\eta }_2& =& {\displaystyle \frac{\left[A_4{\delta }_1+2({\tau }_0^2-1)(1-\beta )\right]{\eta }_1}{A_2}},\hfill \end{array}$$

(34c)

where

$$\begin{array}{ccc}\hfill A_1& =& 4\left(s_0+{\displaystyle \frac{\partial s_0}{\partial \delta }}\right),\hfill \end{array}$$

(35a)

$$\begin{array}{ccc}\hfill A_2& =& 2[s_0+t_0+{\tau }_0^2(r_0-s_0)],\hfill \end{array}$$

(35b)

$$\begin{array}{ccc}\hfill A_3& =& 4[({\tau }_0^2-1)(s_0+t_0)-{\tau }_0^2(q_1+s_1)],\hfill \end{array}$$

(35c)

$$\begin{array}{ccc}\hfill A_4& =& 2\left[{\tau }_0^2\left(2s_0-{\displaystyle \frac{\partial r_0}{\partial \delta }}\right)-t_0-{\displaystyle \frac{\partial t_0}{\partial \delta }}\right]+{\displaystyle \frac{({\tau }_0^2-1)A_1}{2}},\hfill \end{array}$$

(35d)

where all of these coefficients are evaluated at the unperturbed state with $\delta ={\delta }_0$, $\tau ={\tau }_0$, and $\eta ={\eta }_0$. From these equations, we see that, when there is no vertical shear ($\theta =0$), the $\tau$ and $\eta$ disturbance terms vanish, with only the horizontal aspect ratio $\delta$ varying. In fact, the vertical aspect ratio has no linear dependence on the strain-rate, i.e., ${\tau }_1=0$. Additionally, there is no dependence on $\beta$ at the first order. The dependence of ${\delta }_1$ on $cos2\theta$ implies that the values with the largest magnitude will tend to occur for $\theta =0^{\circ }$; therefore, as the cyclonic and anticyclonic strain rates are differently signed, we would expect the strongest asymmetry to occur at this value, i.e., when there is no vertical shear. This is overall what we have seen when examining the dependence on $\theta$ in Figure 6 and Figure 7 for like-signed and opposite-signed interactions, respectively. On the other hand, the dependence of ${\tau }_2$ on $sin\theta$ means that the largest magnitudes occur for $\theta ={45}^{\circ }$. This explains to some extent why the strongest asymmetries in $\tau$ seen in Figure 6 and Figure 7 occur for larger values of $\theta$, although it tends to occur at even higher values, $\theta \approx {60}^{\circ }$, implying that higher-order terms play a role.

The dependence on $\beta$ first appears at the second order for $\delta$ and $\eta$, but not for ${\tau }_2$. The appearance of $\beta -1$ in ${\delta }_2$ and ${\eta }_2$ means there will be a change in sign for these terms passing from the like-signed ($\beta \ge 1$) and opposite-signed cases ($\beta <1$). In order to see the dependence of $\tau$ on $\beta$, we have to go to the next order, which can be easily done using the condition of constant $B_{33}$ and gives:

$${\tau }_3={\displaystyle \frac{3\left[{\delta }_1{\eta }_1+2({\tau }_0^2-1){\eta }_2\right]{\eta }_1}{4{\tau }_0}}.$$

(36)

while ${\tau }_3$ has a relatively simple form, the third order of $\delta$ and $\eta$ is significantly more complicated depending on second- and third-order derivatives of the elliptical integrals, and so we do not compute them here. However, the third-order coefficient for $\tau$ reveals the dependence on $\beta$ through the appearance of ${\eta }_2$ in Equation (36). For ${\eta }_2$, the $\beta -1$ term is multiplied by ${\tau }_0^2-1$, meaning that the sign of this term also depends on whether the vortex is oblate or prolate, and so both $\eta$ and $\tau$ will have a strong dependence on $h/r$, as we have seen in Figure 8 and Figure 9.

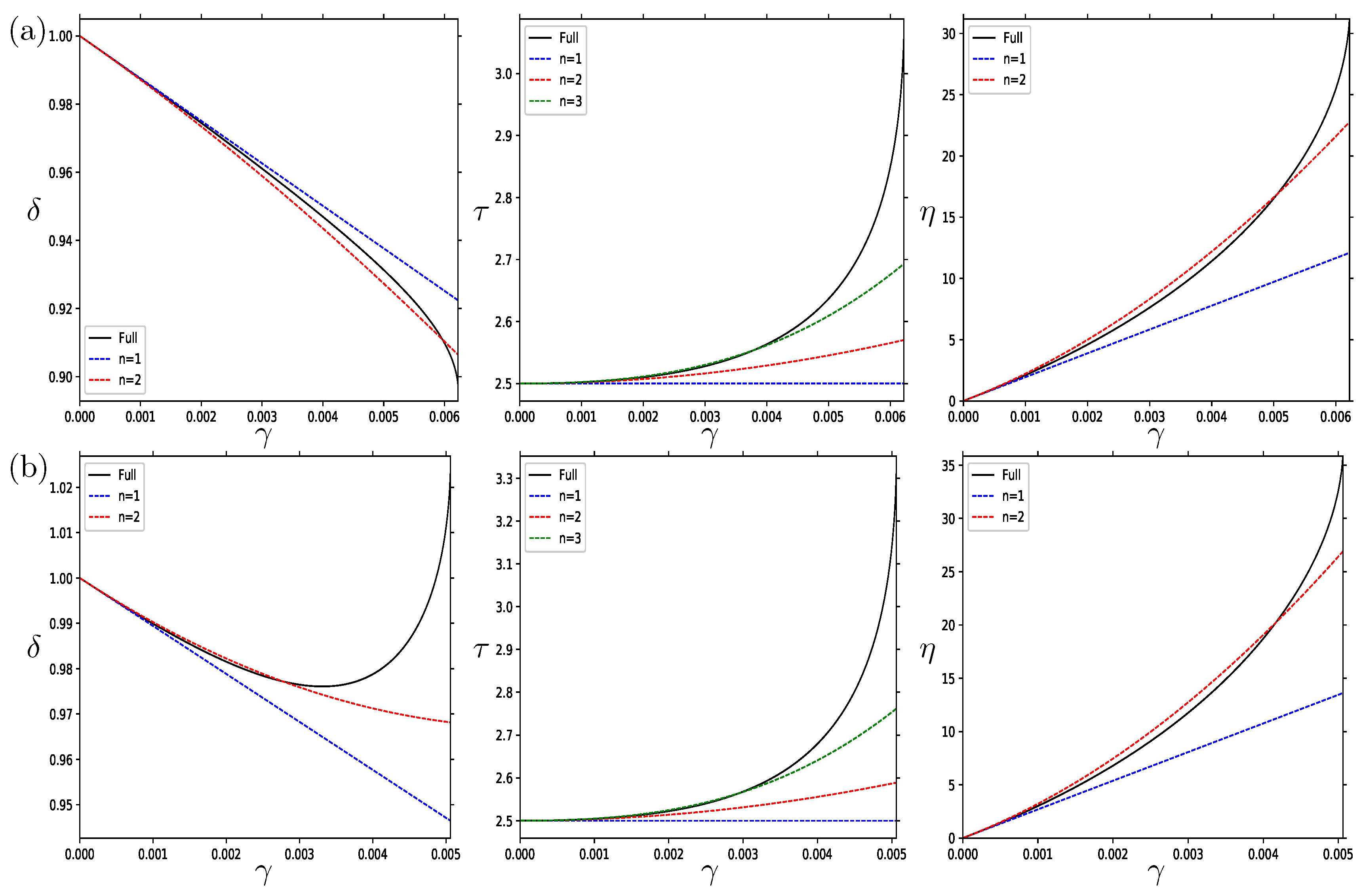
In Figure 10a,b we plot $\delta$, $\tau$, and $\eta$ as a function of $\gamma$ for the cyclonic and anticyclonic cases, respectively, where $h/r=2.5$, $\beta =2$, and $\theta ={30}^{\circ }$.

We plot the perturbation solutions at the first order (dashed blue curve) and the second order (dashed red curve), as well as the full solution (solid black curve). For the vertical aspect ratio, we also plot the third-order solution (green curve). For low values of the strain, both the first- and second-order perturbation solutions remain close to the full solution. At larger strain rates, the variables depart from the linear solution, with the direction of this deformation being captured by the higher-order perturbation solutions. In particular, the large asymmetry in $\delta$, with the cyclonic value decreasing as the anticyclonic value increases, is initially captured by the second-order perturbation. The change in the anticyclonic trend is due to the fact that, for like-signed interactions, the anticyclonic strain is negative, and so there is a sign change between the first- and second-order terms, i.e., ${\delta }^{ac}\approx {\delta }_0-\gamma {\delta }_1+{\gamma }^2{\delta }_2$. However, as the strain-rate approaches the marginal value, even the second-order and third-order corrections cannot capture the change in the shape and orientation, implying that even higher-order terms are needed to fully capture the deformation.

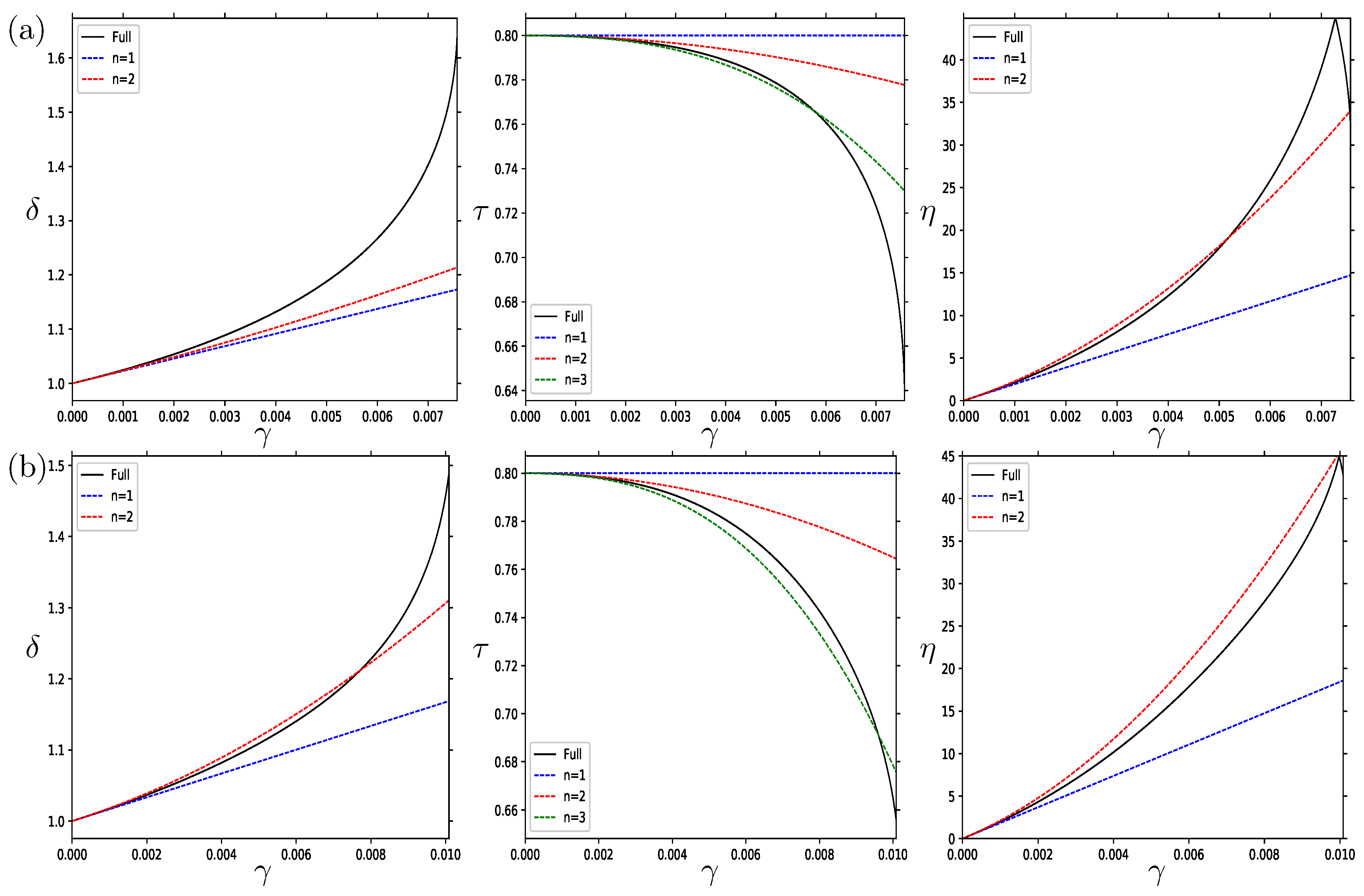
In Figure 11, we plot the perturbation values for the opposite-signed case of an oblate vortex, with $h/r=0.8$, $\beta =-4$, and $\theta ={30}^{\circ }$.

This case is one in which we have previously seen (Figure 9b) that there is strong asymmetry in the tilt angle. This asymmetry in $\eta$ is fairly well captured up to high strain values. For $\delta$ and $\tau$, the perturbation approximation captures the equilibria for low strain rates. However, as was seen for the like-signed case, as we approach the marginal strain rate, the error grows, particularly for ${\delta }^{cy}$, implying the need for higher-order corrections.

4. Discussion and Conclusions

In this work, we have examined how the shape and orientation of a vortex subjected to a background shear flow change as the background flow parameters are changed. In particular, we looked at how differences between cyclonic and anticyclonic equilibria can be induced by changing the level of strain and shear. It was shown that, in the absence of vertical shear, horizontal strain had the greatest impact on the horizontal cross section of the ellipsoidal vortices. Horizontal strain produced the strongest asymmetry in the horizontal aspect ratio of cyclonic and anticyclonic vortices, with cyclonic vortices becoming more deformed. This has been seen in shallow water turbulence, where anticyclones tend to be more axisymmetric than cyclones [7,11,25]. Instead, vertical shear tends to tilt the vortex from an upright position and changes the vertical aspect ratio. Vertical shear affects anticyclonic vortices more strongly than cyclonic vortices, with the strongest asymmetry occurring for large values of vertical shear. A mechanism that can damp the tilt angle produced by vertical shear has been seen in QG columnar vortices [26,27], although it is not known if this produces cyclonic–anticyclonic asymmetry in such vortices at the next order to QG. However, more recently, a study of a vortex merger at the finite Rossby number [28] showed that anticyclonic vortices are more susceptible to vertical shear, with vertically offset anticyclones merging from further apart than the equivalent cyclonic cases.

We also found that the shape and orientation of the equilibria also depend on the parameter $\beta \equiv 1+{\kappa }_v/{\kappa }_b$, i.e., the ratio of the target and background vortex strengths, with the vortex shape being most deformed as $\beta \to 1$. However, the asymmetry between the cyclonic and anticyclonic equilibria increases as $\beta$ moves away from $\beta =1$ for both like-signed ($\beta \ge 1$) and opposite-signed interactions ($\beta <1$). The importance of both the PV ratio and the vortex volume have recently been investigated in the case of counter-rotating vortex pairs at the finite Rossby number [29] and for vertically aligned hetons [30]. Both these studies point out that, as a result of stronger motions induced by the anticyclonic vortex relative to the cyclone, this leads to the anticyclone dominating the evolution of the two vortices. Here we have seen that, over the range of values of the parameter $\beta$, the horizontal aspect ratio of the cyclonic vortex is more deformed than the anticyclone, while the vertical aspect ratio of the anticyclone is generally more deformed. This deformation of the vertical aspect ratio when there is vertical shear is compensated by the increased tilting of the anticyclone with respect to the cyclone, an effect that is seen in the two vortex merger experiments of [28,29] for co-rotating and counter rotating vortices, respectively.

In order to understand the dependence of the equilibria on the background flow parameters, we derived an approximate model based on an expansion in the strain rate $\gamma$. While the formulas derived capture the equilibria shape and orientation up to intermediate values of the strain rate, they cannot fully capture the dependence at high strain values up to the marginal strain, where strong interactions like mergers between vortices would be expected to take place. However, the higher-order terms do provide some insights into how the asymmetry between cyclonic and anticyclonic cases arises and its dependence on the background flow parameters. Future work extending the QG + 1 ellipsoidal model to the multi-vortex case would help provide better insights into this asymmetry by first providing a better understanding of ageostrophic corrections in two vortex interactions.

Here we have considered an idealized case of an isolated vortex in the presence of a background shear flow. This case can provide insights into cyclone–anticyclone asymmetry when there is no forcing, such as subsurface eddies in the deep ocean. However, in the upper ocean boundary, forcing and Ekman effects can also drive cyclone–anticyclone asymmetry [9,31,32,33]. Further work is needed to understand how the approach considered here can be applied to the case where there is such forcing.