A Numerical Approach to Analyzing Shallow Flows over Rough Surfaces

Abstract

The hydraulic characteristics (such as velocity profiles, near-bed velocity profile, bed shear stress, and resistance coefficients) of shallow flows over rough surfaces were investigated using numerical simulations. A novel method is presented to simulate shallow flows over rough surfaces in a two-dimensional (2D) numerical domain, where the physical numerical domain represents bed topography. Results reveal that the model can accurately predict spatially averaged velocity profiles, turbulence characteristics, shear stresses, and uniform flow depths. The analysis identified two distinct flow regions based on mean and turbulent flow profiles. Results show that the turbulent shear stress profiles provide a more accurate estimation of the bed shear stresses. Resistance coefficients (friction factor or Manning’s roughness coefficient) vary with Froude number and submergence ratio (depth divided by roughness height).

1. Introduction

Shallow water flow represents one of the most common flows in the real world (e.g., sheet flows, overland flows, and gravel-bed river flows). Sheet flows are an integral component of the hydrologic cycle and are considered to have a depth of less than 0.03 m [1]. Shallow flows over gravel surfaces are generally considered to have depths in the range of 0.04 m to 0.1 m [2].

The major difference between a shallow and deep flow is the low submergence ratio (water depth to roughness height ratio). The presence of water surface and channel bed at such proximity uniquely shapes shallow flow characteristics. The surface roughness height becomes comparable to the flow depth, which changes the behavior of the resistance characteristics (friction factor or Manning’s roughness coefficient). The submergence ratio can be less than 5 under normal flow conditions, whereas it can vary from 10 to 20 under flood conditions [2] in shallow flows. The cases of shallow flows considered in this work represent the flows under normal and flood conditions.

The prediction of roughness characteristics in shallow flows is important for understanding flow behavior and sediment transport processes. In general, bed roughness and viscous forces exert resistance to the flow. The average velocity $\left(V\right)$ of free-surface flows is related to hydraulic radius $\left(R\right)$ and energy gradient $\left(S_f\right)$ through Chezy’s coefficient $\left(C\right)$, friction factor $\left(f\right)$, or Manning’s roughness coefficient $\left(n\right)$ as shown in Equation (1), respectively [3], where $g$ is the gravitational acceleration. The bed shear stress $\left({\tau }_o\right)$ and shear velocity $\left(u_{\ast }\right)$ are defined by Equation (2). For uniform flows in a wide channel, energy slope and hydraulic radius are replaced by bed slope $\left(S_o\right)$ and uniform flow depth $\left(h\right)$, respectively.

$$V=C\sqrt{R{S}_f}=\sqrt{{\displaystyle \frac{8g}{f}}}\sqrt{R{S}_f}={\displaystyle \frac{R^{1/6}}{n}}\sqrt{R{S}_f}$$

(1)

$$u_{\ast }=\sqrt{{\displaystyle \frac{{\tau }_o}{\rho }}}=\sqrt{gR{S}_f}$$

(2)

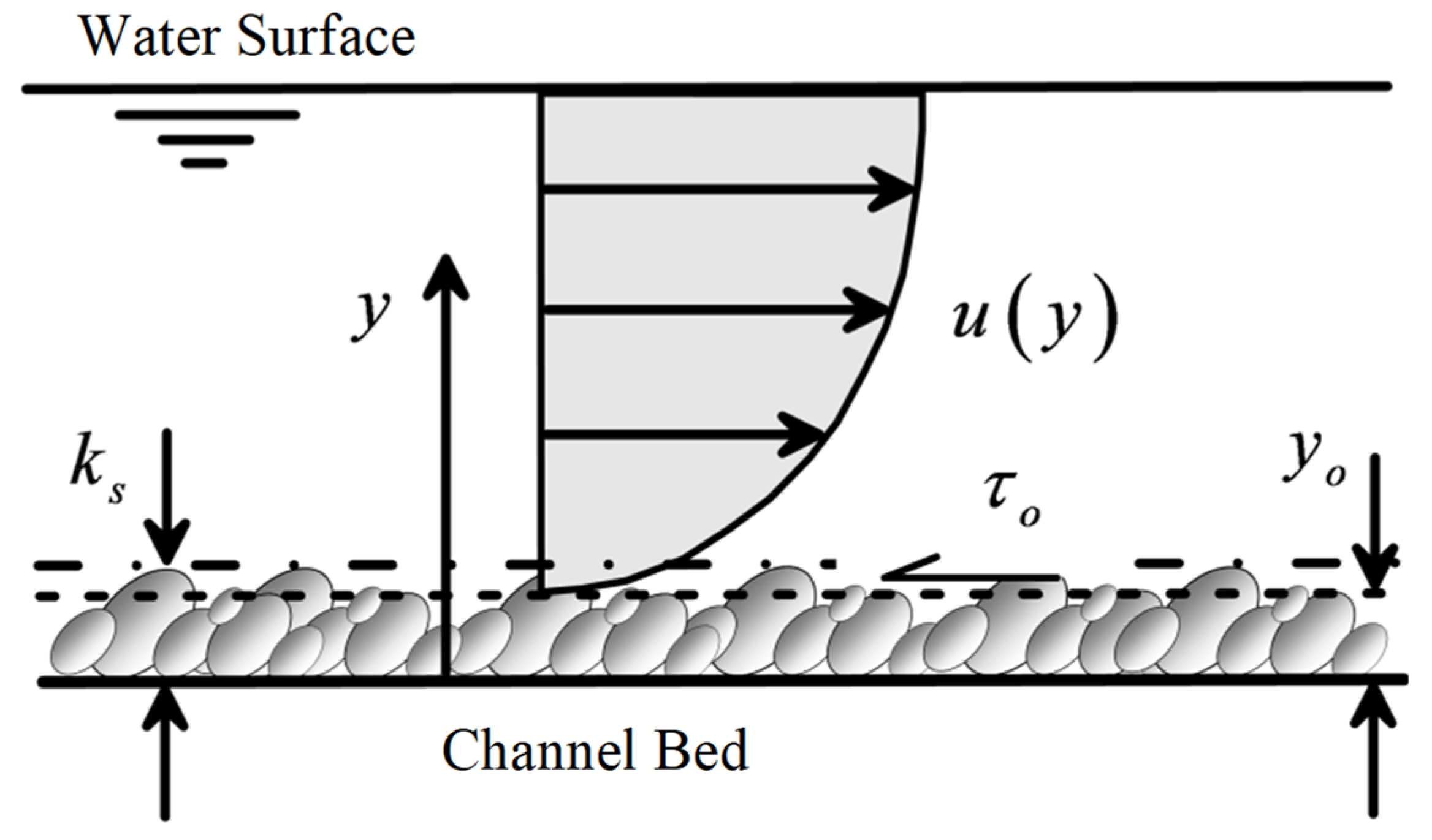
The turbulent boundary layer theory can approximate the velocity profile in shallow flows [4]. The schematic of the velocity distribution of flow over a rough bed is shown in Figure 1 and can be approximated by Equation (3), where $\kappa$ (=0.4) is the von Kármán constant, $U^{+}=u/u_{*}$, $Y^{+}=y{u}_{*}/\nu$, $B$ is an intercept, $u$ is the velocity at a distance $y$ from the bed, and $\nu$ is the kinematic viscosity [5,6]. The roughness function $\Delta U^{+}$ is a correction needed for rough beds and depends on the shear velocity and the roughness height [5], suggesting that the $k_s$ (equivalent surface roughness) may change with depth for shallow flows. Equation (4) provides an alternate form of the velocity profile where $y_o=0.033k_s$ is the location of $u=0$ [6].

$$U^{+}={\displaystyle \frac{1}{\kappa }}\ln \left(Y^{+}\right)+B-\Delta U^{+}$$

(3)

$$U^{+}={\displaystyle \frac{1}{\kappa }}\ln \left({\displaystyle \frac{y}{y_o}}\right)$$

(4)

Ferguson [2] reviewed various theoretical velocity profile models for shallow water flows with and without wake functions. The logarithmic velocity profile was found to work as well as the other alternatives. However, the assumption of the logarithmic profile for the velocity near the bed may not be accurate for rough-bed flows [7] as shown in Figure 1. Nikora et al. [7] showed that the velocity profile in the interfacial layer (a zone near the bed roughness) might be constant, exponential, or linear depending upon the flow conditions (such as flow depth, Reynolds number, and Froude number).

Ferro and Baiamonte [8] presented an experimental study using gravel beds in a rectangular flume. Velocities were measured by a current meter. The study used four different grain shapes and various flow depths to find an accurate representation of the velocity profile. The analysis showed that the velocity profile could mostly be described using a logarithmic function. However, for certain cases (based on the depth to grain size ratio and bed type), the velocity profile was found to be S-shaped. In a similar study, Ferro [9] measured velocity profiles over a gravel bed for five different gravel mixes and various flow depths in a horizontal rectangular flume. An ADV system was used to measure the velocities across the depth. The results obtained were similar to those of Ferro and Baiamonte [8].

Nichols [10] investigated shallow turbulent flows using a Particle Image Velocimetry (PIV) system. The primary objective of the study was to investigate the correlation between the free surface and the turbulent structure in the flow. The study also measured mean velocities across the flow depth for several cases of flow rates, bed slopes, and surface roughness (river gravels with $d_{50}=4.4$ mm and uniform size polymer spheres of 25 mm diameter). The free surface pattern was compared to the hydraulic properties of shallow flows. The submergence ratio had a profound impact on free surface and flow characteristics.

Lawrence [11] analyzed the hydraulics of overland flow/sheet flows using the submergence ratio as the governing parameter, instead of the Reynolds number. The study defined the submergence ratio $\left(h/d_g\right)$ using the flow depth $\left(h\right)$ and the grain height $\left(d_g\right)$. Three regimes were identified based on the submergence ratio: partially, marginally, and well-inundated regimes. The study concluded that the Reynolds number is significant in well-inundated regimes, whereas the relative surface coverage, surface slope, and the submergence ratio are the potential influencing factors for partially and marginally inundated regimes. However, Reynolds number, Froude number, and discharge should also be considered to characterize the flow resistance adequately [12,13].

Shallow free surface flows have been studied widely; however, there is still uncertainty involved in fully understanding the hydraulic behavior of such flows. The primary reason is that measuring flow depths and mean velocities accurately is complicated in such shallow flows [14]. Furthermore, the precision and applicability of Acoustic Doppler Velocimeters (ADV) and electromagnetic current meters are questionable in shallow flows [15]. Numerical simulations may be an effective way to investigate and understand the behavior of shallow flows.

Nicholas [16] numerically investigated shallow open channel flows over gravel beds considering the water surface as a fixed lid. The non-uniform gravel size was represented by a random elevation model based on Gaussian distribution, and surface roughness was added to the bed topography. The study discussed the advantages and disadvantages of the above approach with the flatbed simulations (where surface roughness, $k_s$, was used to represent the gravel on the bed) in modeling the turbulent characteristics of the flow. However, the performance of these two approaches in estimating the bed shear stresses and the near-bed velocity profiles was not explored. Singh et al. [17] simulated flow over gravel bed using Direct Numerical Simulation (DNS) and found good correlation between the simulated and the experimental velocity profiles. Bomminayuni and Stoesser [18] used Large Eddy Simulation (LES) for flow over closely packed hemisphere to analyze turbulence characteristics and coherent structures of shallow flow at Reynolds number of 13680 and Froude number of 0.17. The study found reasonable agreement with some of the experimental results. However, the bed shear stress was not analyzed. Furthermore, the model considered water surface as a rigid lid with zero shear stress. Kazemi et al. [19] simulated shallow water flow with regular spheres using the smooth particle hydrodynamics method. The study conducted 12 sets of experiments of various flow depths and bed slopes on a rough bed ($d_g=24$ mm) to investigate the effect of bed roughness under different flow conditions. The study found reasonable correlation between the experimental and numerical results.

Although there are various models available to describe shallow flows, there is no unanimous model (theoretical and numerical) available that can generate behavior of shallow flows accurately for different submergence ratios. In addition, there is a lack of a general method to estimate resistance coefficients (friction factor and Manning’s roughness) in shallow flows as most sheet flows are modeled using shallow water flow equations that require the knowledge of Manning’s roughness coefficient a priori.

The primary objective of this research is to use a 2D (vertical plane) numerical model to predict spatially averaged flow characteristics of shallow flows. A new approach where the channel bed is represented as uniformly distributed, closely packed semicircles (resembling the bed topography) is proposed. The hypothesis of the study is that the channel bed must be represented physically as part of the domain of a numerical model in order to predict velocity profiles and bed shear stress accurately in shallow flows. The predicted bed shear stresses and velocity profiles are investigated and compared with the available experimental data. The results will also allow the accurate prediction of Manning’s roughness coefficient or friction factor in shallow flows that can be used in 1D and 2D depth-averaged models. This will allow these models to simulate accurately the depth-discharge relationship and bed shear stress needed for flow and sediment transport modelling.

2. Numerical Simulations Setup

Steady-state simulations were performed using ANSYS Fluent software version 15.0 for two-dimensional (2D) shallow flows in a vertical plane. The Reynolds-Averaged Navier-Stokes (RANS) equation along with a standard $k-\epsilon$ turbulent closure scheme was solved in a vertical plane. This is the most widely used model to simulate turbulent flows and can simulate flows accurately where pressure gradients and mean streamline curvature are relatively small. As the extent of rotation, streamline curvature, and pressure gradient is limited for the flow cases simulated in this study, the RANS model with a standard $k-\epsilon$ turbulent closure scheme may be sufficient to predict the flow behavior [20]. The pressure–velocity field was solved using the SIMPLE scheme, and the spatial derivatives were solved using second-order upwinding schemes. The simulation convergence was verified using the velocity profiles as well as the residuals of mass balance, turbulent kinetic energy, and dissipation rate where the difference tolerance was set at ${10}^{-6}$.

The free surface was simulated using a two-phase model (air and water) using the Volume of Fluid (VOF) method. This approach does not require the knowledge of the uniform flow depth a priori. Thus, only discharge with an arbitrary initial flow depth as a boundary condition is sufficient at the inlet. The flow is allowed to develop, and water depths are therefore a result of the balance between the gravity and friction forces. Uniform flow depths were verified using the velocity profiles at different sections along the length of the domain. The domain length was selected as 25 m to ensure that uniform flow conditions are achieved and there is no effect from the downstream boundary into the domain. The channel bed was modelled as a non-slip wall with standard wall function. The downstream boundary was modelled as a pressure boundary. The longitudinal slope of the channel was incorporated by resolving the gravitational acceleration along the x and y direction in the computational model.

The mesh validation process is the first step for any computational model. In the present study, the meshes near the bed were selected such that they can capture the profile of the bed topography. As this study involves various types of bed topography (grain sizes), it required different sizes of cells in the near-bed region. At least 5 cells were provided along the curved surface of an individual grain to capture the topographical geometry of the bed. A typical configuration of the mesh near the bed and across an individual grain is shown in Figure 2.

The results presented here are mesh independent. Velocity profiles across the flow depth in the middle third of the domain (at ten different locations) were compared for different mesh sizes. Figure 3 shows a typical comparison of velocity profiles for the coarse and fine meshes for a 25 mm grain size case. The total number of cells was changed by 300% from coarse to fine mesh. Analysis showed that the maximum differences in the relative velocities of the course and fine meshes were within 3%. The same mesh independent criterion has been followed for all the cases in this study.

The initial values of $k$ and $\epsilon$ throughout the domain were exactly the same as the boundary condition defined at the inlet. The inlet boundary conditions for $k$ and $\epsilon$ were based on turbulent intensity (5% of the mean flow velocity) and hydraulic diameter. To ensure that boundary conditions did not influence the solutions obtained, the results in the middle portion of the channel, away from the boundaries, were used for analysis.

In the case of open channel flow simulations with comparatively larger depths or submergence ratios, simple flat-bed domain and surface roughness $\left(k_s\right)$ defined at the bed are capable of predicting the flow characteristics accurately. However, the mesh size adjacent to the bed must be selected appropriately. As per Fluent Inc. [21], the centroid of the cell adjacent to the bed must be higher than the roughness height. Nicholas [16] found that in cases where the above condition was violated, the near-bed simulated velocities were over-predicted. Generally, the mesh near the bed should be fine enough to capture the large velocity gradient and to model the near-bed velocity accurately. However, larger roughness heights (i.e., gravel bed flow) with low submergence will necessitate relatively larger mesh size near the bed that may result in poor predictions of velocity profiles throughout the depth. This study found that using a flat-bed model with low submergence leads to inaccurate prediction of the velocity profiles over the whole depth and is shown in the model validation section. Another criterion is to accurately model shear stress at the bed, as it is essential for accurate simulation of velocity profile. Since wall function is used, it was made sure that the centroid of the first cell was between 30 and 40, i.e., within the log-law region [21], thus satisfying both conditions for mesh size near the wall.

One of the main purposes of this study is to investigate whether representing the bed as uniformly distributed, closely packed semicircles (resembling the bed topography) would predict the flow behavior accurately. As such, the grain size is defined as a part of the bed topography (as shown in Figure 2) and is represented as closely packed semicircles of diameter $d_g$. The diameter $d_g$ is equal to $d_{90}$ for non-uniform grain sizes. The surface roughness of individual grains is represented as $k_{su}$ in the standard wall function. The hypothesis is that the semicircles at the bottom will represent the large-scale roughness of length $d_g$, whereas the surface roughness of the semicircles will represent the small-scale roughness of length $k_{su}$. A typical near-bed mesh setup is shown in Figure 2. The surface roughness of single grains $\left(k_{su}\right)$ is an essential factor for simulating shallow flows. In the case of large grain sizes, the surface area of single grains is significant and consequently has a profound impact on the flow characteristics. For small grain sizes, the surface area of single grains is not large enough to contribute significantly to the flow and can be ignored $\left(k_{su}=0\right)$.

In gravel beds, bed-topography variation occurs both along and across the flow direction. As such, the velocity profiles at different points on the bed may vary, and a 3D simulation is needed to capture these profile variations. However, all the reported experimental as well as 3D numerical simulations analyze and compare spatially averaged velocity profiles. Therefore, a 2D numerical model in a vertical plane with appropriate grain size and surface roughness representation may be sufficient to predict spatially averaged flow characteristics.

3. Model Validation

In this section, the mean velocity profiles resulting from the simulations are compared with the experimental results of Ferro and Baiamonte [8], Ferro [9], and Nichols [10]. Mass flow rate, channel slope, and roughness height corresponding to each condition were calculated from the experimental data summarized in

Table 1. Various cases and corresponding conditions applied for numerical simulations.

Case	Roughness Height	Submergence Ratio, $\mathit{h}/{\mathit{d}}_{\mathit{g}}$	Bed Slope, ${\mathit{S}}_{\mathit{o}}$	Experimental Study
1	$d_{90}=$ 6	7.5	0.004	Nichols [10]
2	$d_{90}=$ 6	10.8	0.004	Nichols [10]
3	$d_{90}=$ 6	14.3	0.004	Nichols [10]
4	$d_{90}=$ 6	17.7	0.004	Nichols [10]
5	$d=$ 25	2.0	0.004	Nichols [10]
6	$d=$ 25	2.7	0.004	Nichols [10]
7	$d=$ 25	3.5	0.004	Nichols [10]
8	$d=$ 25	4.3	0.004	Nichols [10]
9	$d_{90}=$ 29	6.3	0	Ferro [9]
10	$d_{90}=$ 44	4.9	0.0025	Ferro and Baiamonte [8]

(Case 1–10). The velocity profiles were averaged over different points along three grain lengths for numerical simulations. There were no noticeable differences among the velocity profiles taken at different points along the grains. The experimental velocity profiles were taken and averaged at different points along a cross section. As the cases presented in this study represent uniform flows, there was no significant variation of the flow profile along the channel.

The diameter of the semicircle $\left(d_g\right)$ was selected based on $d_{90}$ for distributed grain size cases and $d$ for the uniform grain size cases. For model validation, four sizes of grains (6 mm, 25 mm, 29 mm, and 44 mm) from studies mentioned above are used. The surface roughness $\left(k_{su}\right)$ of the bed was determined to achieve the best fit between simulated and measured velocity profiles for all grains. The variation of surface roughness $\left(k_{su}\right)$ will be discussed in detail later.

Velocity profiles are compared with the experimental results in Figure 4. The experimental and numerical velocity profiles were compared using the same datum in the vertical direction. This same comparison is represented as log-linear scale in Figure 5. The non-dimensional form of the velocity profiles is shown in the later part of the manuscript. The results clearly show that a 2D model in the vertical plane can be efficiently used to simulate the spatially averaged flow characteristics by choosing appropriate representation of bed topography and surface roughness of individual grains.

The traditional flat-bed model over-predicts the velocities in the near-bed region and consequently under-predicts flow depths, as shown in Figure 6 for selected cases. The reason for such behavior has been discussed in the preceding section. Therefore, flatbed model results are unreliable and are not discussed further.

4. Results and Discussion

4.1. Analysis of the Turbulence Profiles

Non-dimensional turbulent shear stress profiles are shown in Figure 7. In general, open channel flows, the turbulent shear stress is maximum just above the bed and varies linearly to zero at the water surface [22]. However, for shallow flows, the linear variation of the turbulent shear stress is limited to a certain depth below the water surface (as shown by Franca [23] as well), and this limit depends on the submergence ratio (0.25 h above the bed for the shallowest case). This may be due to the bed topography causing an increase in turbulent shear stress. Bed shear stresses calculated from the linear part of the turbulent shear stress profiles (from 0.25 h above the bed to h) are found to be the most accurate approach and are discussed later.

A region near the bed (called near-bed region) can be identified based on the turbulence shear stress profiles where the flow behavior is significantly different from the flow behavior above the zone. This zone is dominated by surface roughness height and topography of the channel bed. The extent of this region relative to the depth of water depends on the submergence ratio and decreases with it as shown in Figure 8. In comparison, the extent of the near-bed region relative to the depth is comparatively higher for lower submergence ratio cases. The result clearly shows that the influence of the channel bed is more pronounced in shallow flows.

4.2. Analysis of Velocity Profiles

In open channel flows, the velocity profile in the bottom 20% of the depth can be modeled with logarithmic profile [22]. Charbeneau et al. [4] suggested that the logarithmic region could be extended to the surface for shallow flows. This would imply that the wake component [24] of the velocity profile might be neglected. For shallow flows, Nikora et al. [7] found experimentally that the velocity profile in the near-bed region might be exponential, linear, or constant depending upon the flow condition. The velocity profiles for the simulated cases are presented as non-dimensional form on a log-linear scale in Figure 9. As shown in the figure, velocity profiles have two distinct regions; the near-bed region is affected by the bed topography and deviates from log-law, while the upper region still follows the log-law. In the near-bed regions, the velocity profile is linear for low submergence and logarithmic for higher submergence. This finding is in agreement with Nikora et al. [7]. This behavior of shallow flows would make bed shear stress prediction based on the velocity profiles difficult, which are generally based on the log-law profile fitted to the bottom 20% of the flow depth. As discussed in the preceding section, beyond the near-bed zone, the flow behavior is similar to that of an open channel flow and hence it follows log-law profile.

Figure 10 shows all the velocity profiles in a Clauser type plot. The bed shear stress and the $k_s$ value are obtained by plotting u versus y and fitting log-law above the near-bed region. The profiles consistently exhibit similar behavior near the bed and follow logarithmic velocity profile above the near-bed region. Typically, for a smooth bed, the log-law region exists between $Y^{+}=30–1000$ [5]. The results from the simulated cases show that the log-law region can exist between $Y^{+}=30–15000$. The extent of the near-bed zone or the lower limit of the logarithmic region in the shallow flows increases with roughness and the shear velocity. For cases 1 through 4, the extent of near-bed zone varies from $Y^{+}$ of 150 to 500, respectively, whereas for cases 5 through 10, this extent varies from 700 to 1200.

Table 2. Summary of velocity profile analysis.

Case	$\mathbf{Combined} \mathbf{Roughness} \mathbf{Length}, {\mathit{k}}_{\mathit{s}}$	Non-Dimensional $\mathbf{Combined} \mathbf{Roughness} \mathbf{Length}, {\mathit{k}}_{\mathit{s}}^{+}$	Roughness $\mathbf{Function}, \Delta {\mathit{U}}^{+}$
1	$1.4 d_g$	341.5	10.9
2	$2.0 d_g$	594.5	12.2
3	$2.3 d_g$	874.6	13.4
4	$2.8 d_g$	958.6	13.9
5	$0.2 d_g$	240.8	10.4
6	$0.4 d_g$	525.4	10.7
7	$0.5 d_g$	734.4	12.2
8	$0.7 d_g$	1203.9	13.6
9	$1.7 d_g$	1899.6	14.8
10	$0.9 d_g$	3113.8	15.3

summarizes the analysis of velocity profile based on the logarithmic region. The roughness function $\left(\Delta U^{+}\right)$ increases with the roughness height and the shear velocity. Average surface roughness, $k_s$ (derived from Equation (4)) is approximately $2.1d_g$ for relatively higher submergence ratios (cases 1 to 4), whereas the average surface roughness is $0.7d_g$ for relatively lower submergence ratios (cases 5 to 10). All the presented cases represent fully rough, turbulent flow cases (${k_s}^{+}>>70$, [25]). One important point to note is that even for the same grain size (Cases 1 and 4), the $k_s$ values vary significantly with submergence ratio. Similar behavior will be expected in the Manning’s roughness coefficient and friction factor.

4.3. Comparison of Bed Shear Stress

Bed shear stress in an open channel flow can be estimated by either velocity profile, turbulent shear stress profile, or channel bed slope using uniform flow condition [22]. Bed shear stress estimation based on the turbulent shear stress profiles was calculated by a fitting straight line above the near-bed region and extrapolating it to the bed. Log-law was fitted to the velocity profiles (u versus y) in the zone above the near-bed region. The slope and the intercept were used to calculate the bed shear stress and $k_s$. Bed shear stress was also calculated using the channel slope and the uniform flow depth obtained from the simulations. The three bed shear stress estimations are shown in

Table 3. Comparison of bed shear stress.

Case	Simulated Bed Shear Stress (N/m2)			Experimental Bed Shear Stress (N/m2)
	From Turbulent Shear Stress	From Velocity Profile	$\mathbf{From} \mathbf{Bed} \mathbf{Slope}, {\mathit{\tau }}_{\mathit{o}}=\mathit{\gamma }\mathit{R}{\mathit{S}}_{\mathit{o}}$
1	1.70	1.58	1.77	1.77
2	2.40	2.27	2.55	2.55
3	3.20	3.28	3.38	3.34
4	4.09	4.03	4.16	3.92
5	1.85	1.12	1.96	1.88
6	2.50	1.58	2.68	2.55
7	3.30	2.57	3.45	3.34
8	4.24	3.65	4.24	4.16
9	1.45	1.45	-	-
10	5.78	4.23	5.40	5.47

along with experimental bed shear stress determined from the bed slope and the flow depth provided in the experimental studies.

Bed shear stresses obtained from the turbulent shear stress profiles are within 5% of the experimental bed shear stress values (see Table 3). The uniform flow depths obtained through simulations match closely to those of the experimental set, and hence the bed shear stress estimated using the uniform flow depth is predicted accurately. However, the bed shear stress calculated using velocity profile yields inaccurate results for lower submergence ratio cases (5–10). This suggests that turbulent shear stress profiles should be used when calculating bed shear stress in shallow flows. The different zones of the velocity and shear stress variations play an important role in simulating shallow rough flows. As such, using the $k_s$ estimate (provided in Table 2) with flatbed topography is not capable of capturing the shallow rough flows accurately. The current method of representing grains with semicircles with the surface roughness of the individual grains as $k_{su}$ is a viable method for simulating shallow rough flows.

5. Estimating Resistance Coefficients

The resistance coefficients, friction factor ($f$) and Manning’s roughness ($n$), vary with the flow conditions. In general, the friction factor depends on Reynolds number (Re) of the flow and relative roughness ($k_s/h$). However, the submergence ratio ($h/d_g$) is more likely to be dominant [11] for shallow flows over a coarse grain bed. In addition to the submergence ratio, the friction factor is found to vary with Froude number [12,13]. 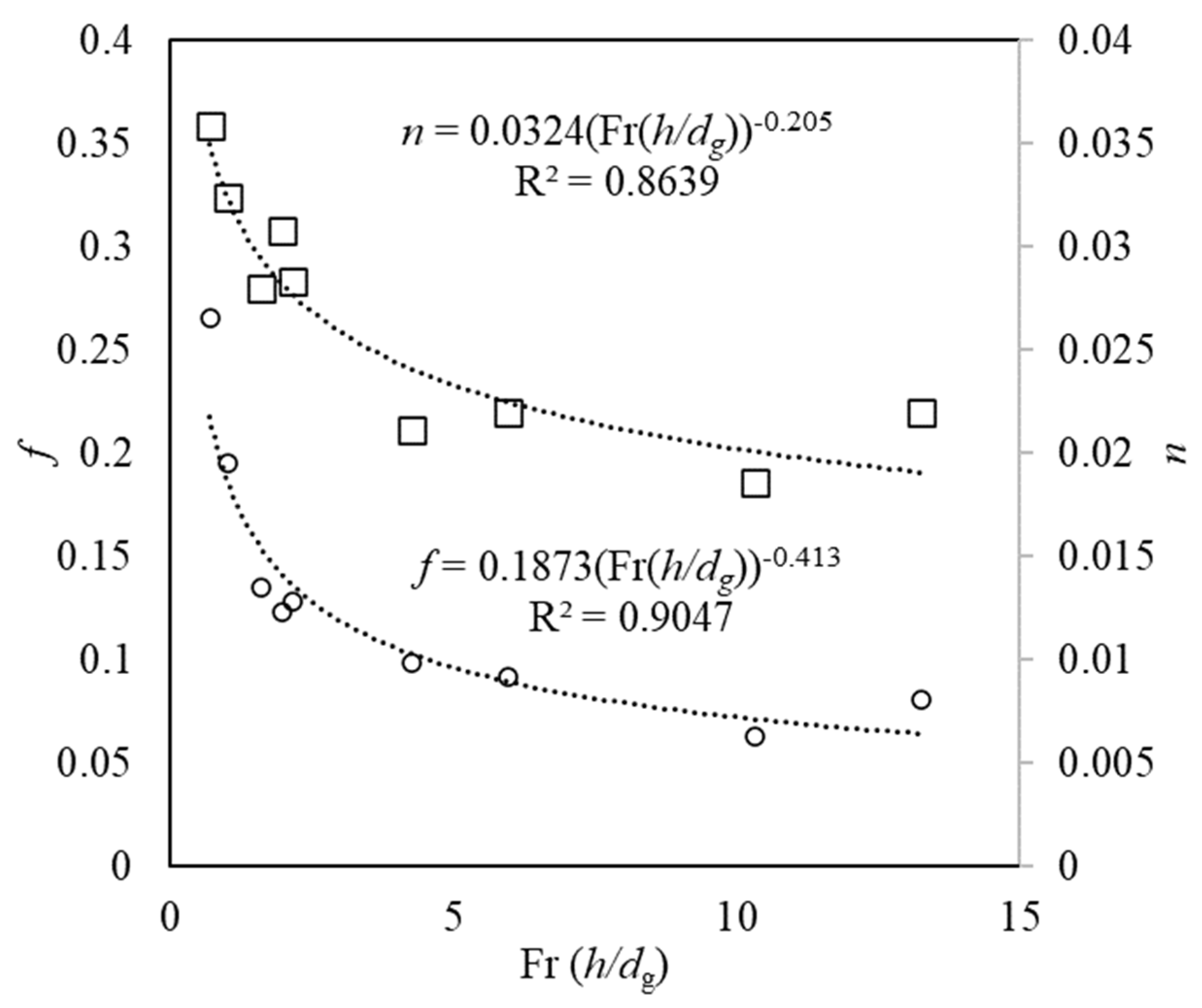All the cases considered in this study are in the rough, turbulent flow regime and friction factor and Manning’s roughness coefficient are found to be independent of Reynolds number; however, f and n are found to vary with the submergence ratio and Froude number for the test cases considered in this study. Froude number and submergence ratio are combined to express the variation of friction factor and Manning’s roughness coefficient, as shown in Figure 11. This is consistent with the findings of Wang et al. [25], where the general expression for friction factor is given by $f={10}^a{\left(h/d_g\right)}^{b}F{r}^c$. For the present study, the values of coefficients a, b, and c are found to be −0.727, −0.413 and −0.413, respectively, using least square regression method. For gravel bed cases, Manning’s roughness, n approaches $0.038 d_{90}^{1/6}$ [26] as submergence ratio increases.

6. Surface Roughness of Individual Grain

Analysis reveals that representing the bed topography in the domain is not adequate to simulate the flow behavior accurately for larger roughness elements or lower submergence ratios (cases 5–10). The surface roughness of the individual grain $\left(k_{su}\right)$ is a crucial component to accurately simulate velocity profiles for rough shallow flows for such cases. The most probable reason is that the flow length along the surface of each grain becomes comparable to the flow depth. As such, roughness from the surface of each grain becomes a significant factor that influences the flow behavior in shallow flows. The $k_{su}$ was determined using the best fit between the simulated and experimental velocity profiles for uniform flow depths ranging from 40 mm to 200 mm and grain sizes from 25 to 44.1 mm. The surface roughness, $k_{su}$, is zero for cases corresponding to 6 mm or less. Figure 12 shows the variation of $k_{su}/d_g$ with submergence ratio $\left(h/d_g\right)$. The surface roughness of the individual grain of the bed topography varies from $0.1d_g-0.3d_g$ and increases with the submergence ratio. Clifford et al. [27], through theoretical analysis, suggested that the surface roughness of the grains can be estimated as $0.4d_{50}$ for flows over gravel bed (which is equivalent to $k_{su}$). The surface roughness of the bed topography in this study varied from $0.17d_{50}-0.5d_{50}$ (for shallow to deep flows, respectively), thereby showing that $k_{su}$ is a function of both grain size and flow depth. Please note that the $k_{su}$ values reported in this manuscript are applicable for submergence ratios of (2–8) for various sizes of grain sizes. As shallow flows generally have submergence ratios less than 10, the range of $k_{su}$ values can be used to simulate shallow flow over rough surfaces.

7. Summary and Conclusions

The hydraulic characteristics of shallow turbulent flows were investigated using numerical simulations. Characteristics such as velocity profile, bed shear stress, and resistance coefficients were analyzed. A new approach is proposed where the bed topography is represented physically on the domain geometry. Numerical results were validated with the experimental data for various flow depths (40 mm–200 mm) and grain sizes (6 mm–44 mm). The results show that representation of the grain size as bed topography is essential for simulating shallow flows accurately (such as velocity profile, bed shear stress, and turbulence characteristics) using a 2D RANS model with a standard $k-\epsilon$ turbulent closure scheme. The velocity profile in the near-bed region is linear or logarithmic, but it follows log-law above it.

Two distinct flow regimes (near-bed region and upper region) are identified based on the velocity and the turbulent shear stress profiles. The extent of the near-bed region was found to be as high as 0.25 h for the shallowest flow, and it decreases as the submergence ratio increases. Turbulent shear stress profiles and velocity profiles can be used to estimate the bed shear stresses with the current methodology. Friction factor and Manning’s roughness can be estimated for shallow flows based on the submergence ratio and Froude number. Analysis shows that the surface roughness of the bed topography depends on the grain size and the relative submergence. The Manning’s roughness coefficient estimate for the shallow rough flows may be used in depth-averaged models for accurately predicting flow depth and bed stress in shallow flows.