POD Analysis of the Wake of Two Tandem Square Cylinders
Abstract
:1. Introduction
2. Experimental Details & POD Method
2.1. Experimental Setup
2.2. Hotwire Measurements
2.3. PIV Measurements
2.4. POD Analysis of PIV Data
2.5. POD Analysis of Hotwire Data
- The rms values of the K columns in U are nearly equal.
- N is significantly larger than K (N >> K).
- Each column statistically contains the same information across all turbulent scales, meaning the velocity spectra of all columns collapse.
- The velocity correlation matrix is given by Equation (10).
3. Results and Discussions
3.1. POD Modes and Energy Distribution
3.2. Wake Characteristics
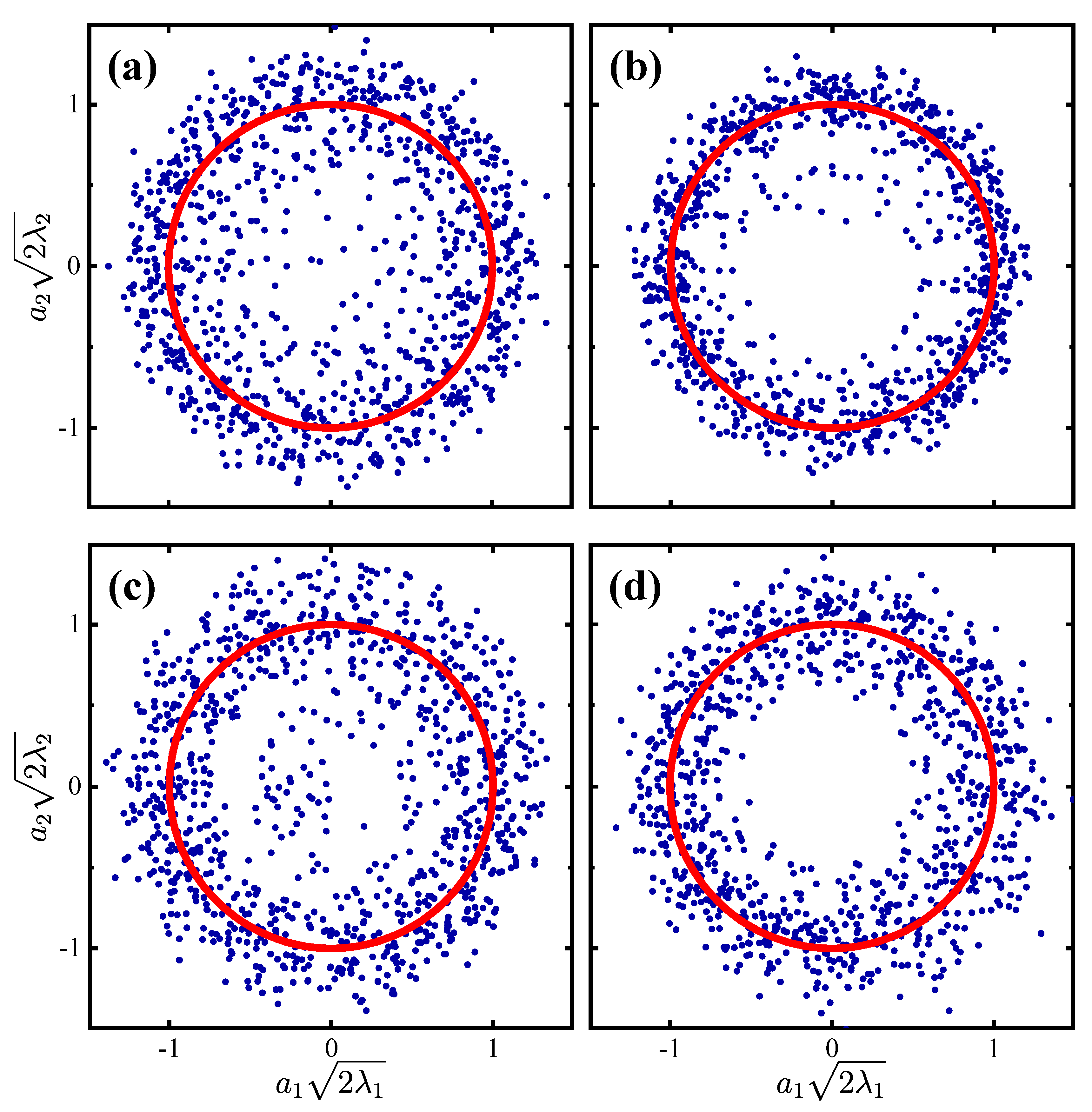
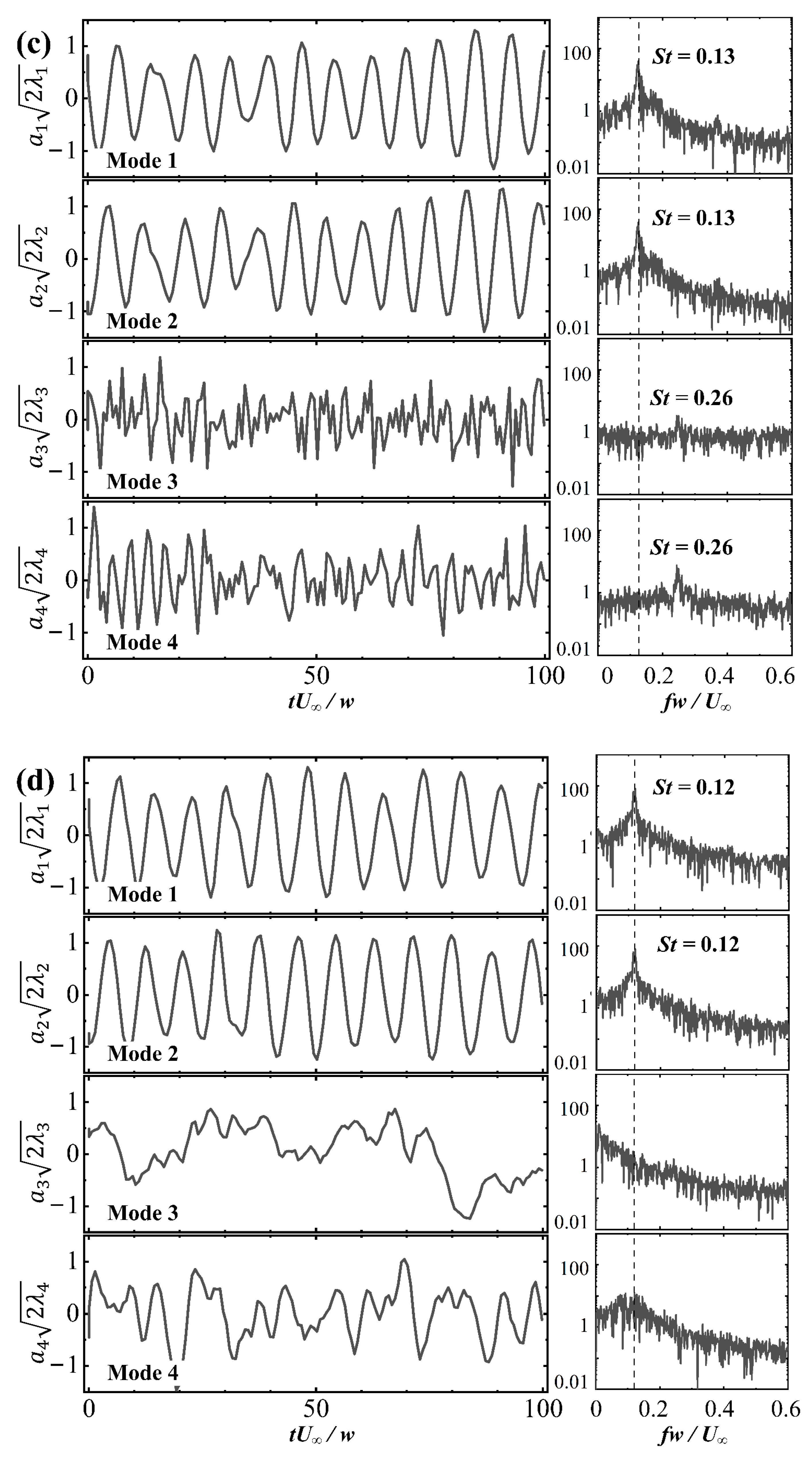
3.3. Identification of Flow Configurations Using PODPIV Coefficients
3.4. Further Analysis of Transition Flow
4. Conclusions
- A POD technique PODHW has been developed for the analysis of single-point hotwire data. The traditional POD method is usually performed on data obtained either from PIV measurements or hotwire array or direct numerical simulations data where the two-point space-correlation tensor should include information at two different space points at least. However, PODHW may be applied for the analysis of single-point hotwire measurements, which are characterized by high-frequency response and fine spatial resolution. More importantly, this method can be used for all other data from a single point such as the single-point 3-D vorticity data, obtained from an 8-wire vorticity probe [60,61], where it would be highly challenging to simultaneously measure vorticity at two points.
- It has been found from the data analysis using PODHW that the transition flow regime (L/w = 2.8) is characterized by two distinct states, i.e., reattachment and co-shedding, characterized by St = 0.13 and 0.10, respectively, thus confirming convincingly for the first time the proposition by Zhou et al. (2024) [1]. On the other hand, PODPIV fails to capture this flow feature. As shown from the hotwire signal, the switch from reattachment to co-shedding or vice versa in the transition regime is intermittent, the interval being in the order of 10 or dozens of seconds. As such, this physical phenomenon can be captured by the hotwire data with a duration of 10 min but missed by the high-speed PIV data (about 1000 images) in the duration of a couple of seconds, which explains the different results between PODHW and PODPIV analyses.
- The contribution from the predominant coherent structures to the total fluctuating velocity energy is documented for different regimes. The first two PODPIV modes contribute 58.0%, 54.5%, and 42.5% to the total fluctuating energy in the extended-body, reattachment, and co-shedding regimes, respectively. The two modes are highly correlated, exhibiting alternating vortex-shedding patterns, irrespective of L/w, apparently representing the Karman vortex streets, while the higher-order modes (3 and beyond) exhibited more random and chaotic behaviour. Since the PODPIV fails to capture both co-shedding and reattachment states, we have to rely on PODHW to determine the contribution from the predominant coherent structures to the total fluctuating velocity energy. The transition regime behaves differently from the other three regimes. The first, second and third PODHW modes make significant contributions to the total fluctuating velocity energy, accounting for 16.2%, 15.6%, and 13.2%, respectively (with the contribution of 4.7% from the fourth mode), due to the presence of both co-shedding and reattachment states. The Karman vortex strength in the transition regime (L/w = 2.8) is weakest of all, as indicated by the least pronounced peak at St in the power spectra of the first two PODPIV modes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| normalized POD coefficients | |
| a1&a2 | modal coefficients corresponding to the first and second modes |
| Ai | eigenvector associated with the matrix C |
| an | POD coefficients |
| C | covariance or correlation matrix |
| f | Vortex shedding frequency |
| L | Distance between the cylinder centres |
| L/w | Centre-to-centre spacing ratio |
| r2i | reconstruction error or the residual energy of the ith snapshot using the first two POD modes |
| Re | Reynolds number based on the square cylinder width (=U∞w/υ) |
| St | Strouhal number (=fw/U∞) |
| t | evolution time, s |
| Tu | freestream turbulence intensity |
| u | streamwise fluctuating velocities in the wake of the downstream cylinder, m/s |
| U | matrix of data or set of vectors |
| U∞ | freestream velocity, m/s |
| uLOM | reconstructed instantaneous velocity field |
| un | nth snapshot of the system |
| UT | transposition of the matrix U |
| v | lateral fluctuating velocities in the wake of the downstream cylinder |
| w | width of the square cylinder |
| x′-O′-y′ | Cartesian coordinates with origin at the centre of the downstream cylinder |
| x-O-y | Cartesian coordinates with origin at the centre of the upstream cylinder |
| η | measure of the magnitude or energy of the vector |
| λ1&λ2 | eigenvalues associated with the first and second modes |
| λi | eigenvalue corresponding to the eigenvector Ai |
| υ | kinematic viscosity of freestream |
| ϕ | angle or phase variable |
| φ | vortex-shedding phase angle |
| normalized POD modes |
References
- Zhou, Y.; Hao, J.; Alam, M.M. Wake of Two Tandem Square Cylinders. J. Fluid Mech. 2024, 983, A3. [Google Scholar] [CrossRef]
- Heidari, M. Wake Characteristics of Single and Tandem Emergent Cylinders in Shallow Open Channel Flow. Doctoral Dissertation, University of Windsor, Windsor, ON, Canada, 2016. [Google Scholar]
- Marble, E.; Morton, C.; Yarusevych, S. Pod Analysis of the Wake Development of a Pivoted Circular Cylinder Undergoing Vortex Induced Vibrations. Presented at the Fluids Engineering Division Summer Meeting 2017, Waikoloa, HI, USA, 30 July–3 August 2017. [Google Scholar]
- Alam, M.M.; Zhou, Y.; Wang, X. The Wake of Two Side-by-Side Square Cylinders. J. Fluid Mech. 2011, 669, 432–471. [Google Scholar] [CrossRef]
- Higham, J.; Brevis, W. Modification of the Modal Characteristics of a Square Cylinder Wake Obstructed by a Multi-Scale Array of Obstacles. Exp. Therm. Fluid Sci. 2018, 90, 212–219. [Google Scholar] [CrossRef]
- Chang, X.; Chen, W.-L.; Huang, Y.; Gao, D. Dynamics of the Forced Wake of a Square Cylinder with Embedded Flapping Jets. Appl. Ocean Res. 2022, 120, 103078. [Google Scholar] [CrossRef]
- Yoon, D.-H.; Yang, K.-S.; Choi, C.-B. Flow Past a Square Cylinder with an Angle of Incidence. Phys. Fluids 2010, 22, 043603. [Google Scholar] [CrossRef]
- Huang, R.; Hsu, C.; Chiu, P. Flow Behavior around a Square Cylinder Subject to Modulation of a Planar Jet Issued from Upstream Surface. J. Fluids Struct. 2014, 51, 362–383. [Google Scholar] [CrossRef]
- Sohankar, A.; Mohagheghian, S.; Dehghan, A.A.; Dehghan Manshadi, M. A Smoke Visualization Study of the Flow over a Square Cylinder at Incidence and Tandem Square Cylinders. J. Vis. 2015, 18, 687–703. [Google Scholar] [CrossRef]
- Hsu, C.M.; Huang, R.F.; Chung, H.C. Flow Characteristics and Drag Force of a Square Cylinder in Crossflow Modulated by a Slot Jet Injected from Upstream Surface. Exp. Therm. Fluid Sci. 2016, 75, 235–248. [Google Scholar] [CrossRef]
- Bai, H.; Alam, M.M. Dependence of Square Cylinder Wake on Reynolds Number. Phys. Fluids 2018, 30, 015102. [Google Scholar] [CrossRef]
- Yang, H.; Yang, W.; Yang, T.; Li, Q. Experimental Investigation of Flow around a Square Cylinder with Very Small Aspect Ratios. Ocean Eng. 2020, 214, 107732. [Google Scholar] [CrossRef]
- Martinuzzi, R.J.; Havel, B. Turbulent Flow around Two Interfering Surface-Mounted Cubic Obstacles in Tandem Arrangement. J. Fluids Eng. 2000, 122, 24–31. [Google Scholar] [CrossRef]
- Bhatt, R.; Alam, M.M. Vibrations of a Square Cylinder Submerged in a Wake. J. Fluid Mech. 2018, 853, 301–332. [Google Scholar] [CrossRef]
- Sakamoto, H.; Haniu, H. Effect of Free-Stream Turbulence on Characteristics of Fluctuating Forces Acting on Two Square Prisms in Tandem Arrangement. J. Fluids Eng. 1988, 110, 140–146. [Google Scholar] [CrossRef]
- Rastan, M.; Alam, M.M. Transition of Wake Flows Past Two Circular or Square Cylinders in Tandem. Phys. Fluids 2021, 33, 081705. [Google Scholar] [CrossRef]
- Sakamoto, H.; Hainu, H.; Obata, Y. Fluctuating Forces Acting on Two Square Prisms in a Tandem Arrangement. J. Wind Eng. Ind. Aerodyn. 1987, 26, 85–103. [Google Scholar] [CrossRef]
- Shui, Q.; Duan, C.; Wang, D.; Gu, Z. New Insights into Numerical Simulations of Flow around Two Tandem Square Cylinders. AIP Adv. 2021, 11, 045315. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chen, J.M. Observations of Hysteresis in Flow around Two Square Cylinders in a Tandem Arrangement. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1019–1050. [Google Scholar] [CrossRef]
- Hasebe, H.; Watanabe, K.; Watanabe, Y.; Nomura, T. Experimental Study on the Flow Field between Two Square Cylinders in Tandem Arrangement. In Proceedings of the Seventh Asia-Pacific Conference on Wind Engineering 2009, Taipei, Taiwan, 8–12 November 2009. [Google Scholar]
- Kim, D.-K.; Lee, J.-M.; Seong, S.-H.; Yoon, S.-H. A Study on Characteristics of the Flow around Two Square Cylinders in a Tandem Arrangement Using Particle Image Velocimetry. Trans. Korean Soc. Mech. Eng. B 2005, 29, 1199–1208. [Google Scholar] [CrossRef]
- Yen, S.-C.; San, K.; Chuang, T. Interactions of Tandem Square Cylinders at Low Reynolds Numbers. Exp. Therm. Fluid Sci. 2008, 32, 927–938. [Google Scholar] [CrossRef]
- Lankadasu, A.; Vengadesan, S. Interference Effect of Two Equal-Sized Square Cylinders in Tandem Arrangement: With Planar Shear Flow. Int. J. Numer. Methods Fluids 2008, 57, 1005–1021. [Google Scholar] [CrossRef]
- Yetik, Ö.; Mahir, N. Flow Structure around Two Tandem Square Cylinders Close to a Free Surface. Ocean Eng. 2020, 214, 107740. [Google Scholar] [CrossRef]
- Rajpoot, R.S.; Anirudh, K.; Dhinakaran, S. Numerical Investigation of Unsteady Flow across Tandem Square Cylinders near a Moving Wall at Re = 100. Case Stud. Therm. Eng. 2021, 26, 101042. [Google Scholar] [CrossRef]
- Zhao, M.; Mamoon, A.-A.; Wu, H. Numerical Study of the Flow Past Two Wall-Mounted Finite-Length Square Cylinders in Tandem Arrangement. Phys. Fluids 2021, 33, 093603. [Google Scholar] [CrossRef]
- Zhou, C.Y. The Wake and Force Statistics of Flow Past Tandem Rectangles. Ocean Eng. 2021, 236, 109476. [Google Scholar]
- Zhang, J.; Jing, H.; Han, M.; Yu, C.; Liu, Q. Effects of Taper Ratio on the Aerodynamic Forces and Flow Field of Two Tandem Square Cylinders. Phys. Fluids 2023, 35, 105152. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the Dynamics of Coherent Structures. I. Coherent Structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Oudheusden, B.v.; Scarano, F.; Hinsberg, N.v.; Watt, D. Phase-Resolved Characterization of Vortex Shedding in the near Wake of a Square-Section Cylinder at Incidence. Exp. Fluids 2005, 39, 86–98. [Google Scholar] [CrossRef]
- Kostas, J.; Soria, J.; Chong, M.S. A Comparison between Snapshot Pod Analysis of Piv Velocity and Vorticity Data. Exp. Fluids 2005, 38, 146–160. [Google Scholar] [CrossRef]
- Paul, S.; Agelinchaab, M.; Tachie, M. Flow around Finite Circular and Square Cylinders in an Open Channel. In Proceedings of the Fluids Engineering Division Summer Meeting 2009, Vail, CO, USA,, 2–6 August 2009. [Google Scholar]
- Lumley, J.L. The Structure of Inhomogeneous Turbulent Flows. Atmos. Turbul. Radio Wave Propag. 1967, 166–178. [Google Scholar]
- Kosambi, D. Statistics in Function Space. In DD Kosambi: Selected Works in Mathematics and Statistics; Springer: New Delhi, India, 1943; pp. 115–123. [Google Scholar]
- Loève, M. Functions Aleatoire De Second Ordre. Comptes Rendus l’Académie Sci. 1945, 220. [Google Scholar]
- Karhunen, K. Zur Spektraltheorie Stochastischer Prozesse. Ann. Acad. Sci. Fenn. AI 1946, 34. [Google Scholar]
- Pougachev, V.S. The general theory of correlation of random functions. Izvestiya Akademii Nauk SSSR Seriya Mat. Bull. l’Académie Sci. l’URSS 1953, 17, 401–420. [Google Scholar]
- Obukhov, A. Statistical Description of Continuous Fields. Trans. Geophys. Int. Acad. Nauk. USSR 1954, 24, 3–42. [Google Scholar]
- Wang, F.; Lam, K.M.; Zu, G.; Cheng, L. Coherent Structures and Wind Force Generation of Square-Section Building Model. J. Wind Eng. Ind. Aerodyn. 2019, 188, 175–193. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Shi, L.L.; Zhang, Q.S. Proper Orthogonal Decomposition of Wall-Pressure Fluctuations under the Constrained Wake of a Square Cylinder. Exp. Therm. Fluid Sci. 2011, 35, 1325–1333. [Google Scholar] [CrossRef]
- West, G.; Apelt, C. The Effects of Tunnel Blockage and Aspect Ratio on the Mean Flow Past a Circular Cylinder with Reynolds Numbers between 104 and 105. J. Fluid Mech. 1982, 114, 361–377. [Google Scholar] [CrossRef]
- Flagan, R.C.; Seinfeld, J.H. Fundamentals of Air Pollution Engineering; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Ramalingam, S.; Huang, R.F.; Hsu, C.M. Effect of Crossflow Oscillation Strouhal Number on Circular Cylinder Wake. Phys. Fluids 2023, 35, 095118. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, Y. Axisymmetric Jet Manipulated Using Two Unsteady Minijets. J. Fluid Mech. 2016, 808, 362–396. [Google Scholar] [CrossRef]
- Melling, A. Tracer Particles and Seeding for Particle Image Velocimetry. Meas. Sci. Technol. 1997, 8, 1406–1416. [Google Scholar] [CrossRef]
- Graftieaux, L.; Michard, M.; Grosjean, N. Combining Piv, Pod and Vortex Identification Algorithms for the Study of Unsteady Turbulent Swirling Flows. Meas. Sci. Technol. 2001, 12, 1422. [Google Scholar] [CrossRef]
- Meyer, K.E.; Pedersen, J.M.; Özcan, O. A Turbulent Jet in Crossflow Analysed with Proper Orthogonal Decomposition. J. Fluid Mech. 2007, 583, 199–227. [Google Scholar] [CrossRef]
- Wang, H. Pod Analysis of the Finite-Length Square Cylinder Wake. In Proceedings of the Seventh International Colloquium on Bluff Body Aerodynamics and Applications 2012, Shanghai, China, 2–6 September 2012. [Google Scholar]
- Kikitsu, H.; Okuda, Y.; Ohashi, M.; Kanda, J. Pod Analysis of Wind Velocity Field in the Wake Region Behind Vibrating Three-Dimensional Square Prism. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2093–2103. [Google Scholar] [CrossRef]
- Kawai, H.; Okuda, Y.; Ohashi, M. Near Wake Structure Behind a 3d Square Prism with the Aspect Ratio of 2.7 in a Shallow Boundary Layer Flow. J. Wind Eng. Ind. Aerodyn. 2012, 104, 196–202. [Google Scholar] [CrossRef]
- Broomhead, D.S.; King, G.P. Extracting Qualitative Dynamics from Experimental Data. Phys. D 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Zhou, T.; Zhou, Y.; Yiu, M.; Chua, L. Three-Dimensional Vorticity in a Turbulent Cylinder Wake. Exp. Fluids 2003, 35, 459–471. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Y.; Zhou, T.; Antonia, R. Three-Dimensional Vorticity, Momentum and Heat Transport in a Turbulent Cylinder Wake. J. Fluid Mech. 2016, 809, 135–167. [Google Scholar] [CrossRef]
- Wang, H.; Cao, H.; Zhou, Y. Pod Analysis of a Finite-Length Cylinder near Wake. Exp. Fluids 2014, 55, 1790. [Google Scholar] [CrossRef]
- Durao, D.; Heitor, M.; Pereira, J. Measurements of Turbulent and Periodic Flows around a Square Cross-Section Cylinder. Exp. Fluids 1988, 6, 298–304. [Google Scholar] [CrossRef]
- Zafar, F.; Alam, M.M. A Low Reynolds Number Flow and Heat Transfer Topology of a Cylinder in a Wake. Phys. Fluids 2018, 30, 083603. [Google Scholar] [CrossRef]
- Zheng, Q.; Alam, M.M. Evolution of the Wake of Three Inline Square Prisms. Phys. Rev. Fluids 2019, 4, 104701. [Google Scholar] [CrossRef]
- Zhou, Y.; Du, C.; Mi, J.; Wang, X. Turbulent Round Jet Control Using Two Steady Minijets. AIAA J. 2012, 50, 736–740. [Google Scholar] [CrossRef]
- Djenidi, L.; Elavarasan, R.; Antonia, R. The Turbulent Boundary Layer over Transverse Square Cavities. J. Fluid Mech. 1999, 395, 271–294. [Google Scholar] [CrossRef]
- Antonia, R.; Zhou, T.; Romano, G.P. Small-Scale Turbulence Characteristics of Two-Dimensional Bluff Body Wakes. J. Fluid Mech. 2002, 459, 67–92. [Google Scholar] [CrossRef]


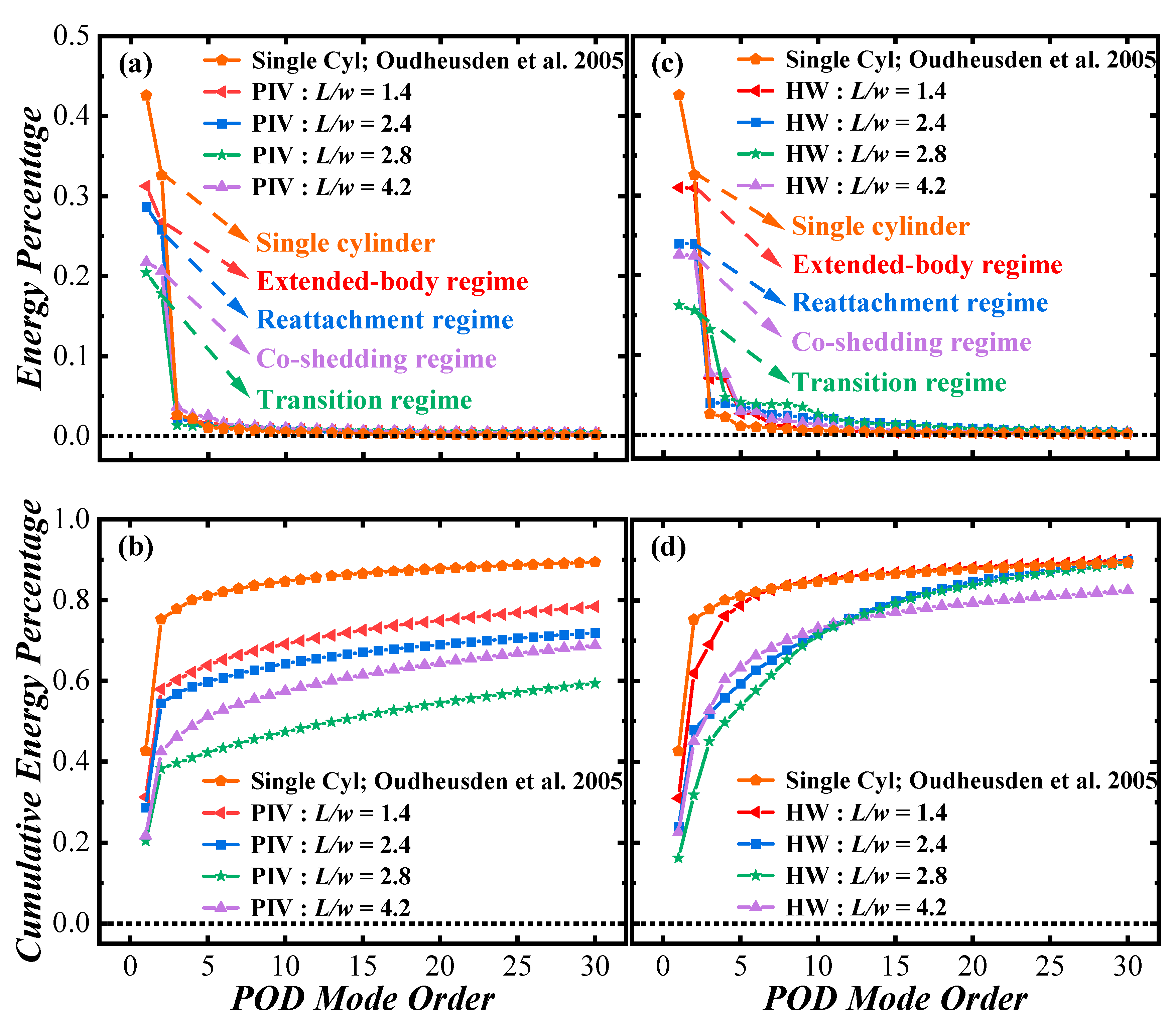







| L/w = 1.4 | L/w = 2.4 | L/w = 2.8 | L/w = 4.2 | Single Cylinder | |
|---|---|---|---|---|---|
| Mode 1 | 31.25% | 28.66% | 20.4% | 21.8% | 42.6% |
| Mode 2 | 26.7% | 25.83% | 17.8% | 20.7% | 32.6% |
| Mode 3 | 2.25% | 2.30% | 1.4% | 3.68% | 2.6% |
| Mode 4 | 1.97% | 1.76% | 1.3% | 2.60% | 2.2% |
| Mode 5 | 1.63% | 1.19% | 1.2% | 2.55% | 1.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, J.; Ramalingam, S.; Alam, M.M.; Tang, S.; Zhou, Y. POD Analysis of the Wake of Two Tandem Square Cylinders. Fluids 2024, 9, 196. https://doi.org/10.3390/fluids9090196
Hao J, Ramalingam S, Alam MM, Tang S, Zhou Y. POD Analysis of the Wake of Two Tandem Square Cylinders. Fluids. 2024; 9(9):196. https://doi.org/10.3390/fluids9090196
Chicago/Turabian StyleHao, Jingcheng, Siva Ramalingam, Md. Mahbub Alam, Shunlin Tang, and Yu Zhou. 2024. "POD Analysis of the Wake of Two Tandem Square Cylinders" Fluids 9, no. 9: 196. https://doi.org/10.3390/fluids9090196
APA StyleHao, J., Ramalingam, S., Alam, M. M., Tang, S., & Zhou, Y. (2024). POD Analysis of the Wake of Two Tandem Square Cylinders. Fluids, 9(9), 196. https://doi.org/10.3390/fluids9090196






