Abstract
Experimental and numerical investigations are conducted on a rotating disk from the perspective of convective heat transfer to understand the effect of heating on the stability of flow. A non-invasive approach with a thermal camera is employed to determine local Nusselt numbers for different rotational rates and perturbation parameters, i.e., the strength of the heat transfer. A novel transient temperature data extraction over the disk radius and an evaluation method are developed and applied for the first time for the air on a rotating disk. The evaluation method utilizes the lumped capacitance approach with a constant heat flux input. Nusselt number distributions from this experimental study show that there is a good agreement with the previous experimental correlations and linear stability analysis on the subject. A significant result of this approach is that by using the experimental setup and developed approach, it is possible to qualitatively show that instability in the flow starts earlier, i.e., an earlier departure from laminar behavior is observed at lower rotational Reynolds numbers with an increasing perturbation parameter, which is due to the strength of heating. Two experimental setups are modeled and simulated using a validated in-house Python code, featuring a three-dimensional thermal model of the disk. The thermal code was developed for the rotating disks and brake disks with a simplified geometry. Experimentally evaluated heat transfer coefficients are implemented and used as convective boundary conditions in the thermal code. Radial temperature distributions are compared with the experimental data, and there is good agreement between the experiment and the model. The model was used to evaluate the effect of radial conduction, which is neglected when using the lumped capacitance approach to determine heat transfer coefficients. It was observed that the radial conduction has a slight effect. The methodology and approach used in this experimental study, combined with the numerical model, can be used for further investigations on the subject.
1. Introduction
Convective flow over a rotating disk has been the subject of a wide range of research studies [1,2,3,4,5]. The subject has also been an active R&D area in turbomachinery, brake disks and other related areas. Convective heat transfer on a rotating disk has been investigated by several authors for a long time with different crossflow combinations, such as axial flow and parallel flow on a rotating disk. Convective heat transfer studies were mainly aimed at the determination of local or average Nusselt number dependence on rotational Reynolds and Prandtl numbers for different fluids [6,7,8]. It is important to emphasize that De Vere’s doctoral dissertation [9] contains comprehensive and relevant work on free rotating disk and parallel flow configurations. His research yielded accurate determination of heat transfer coefficients/Nusselt numbers for various flow configurations and rotating speeds. Even though the experimental equipment was not very sophisticated in his time, long ago, he managed to have accurate and precise results that were in relatively good agreement, both with theoretical studies (before him) and experimental studies (after him).
The transition of the boundary layer on a rotating disk in a still fluid has also attracted considerable attention [10,11] since some practical systems can be idealized using the physical interaction over the rotating disk, and the transitional flow is one of the typical phenomena in a three-dimensional boundary layer accompanied by a secondary flow, which is complex in principle [12]. In those studies, one of the objectives was the determination of the critical Reynolds number , the point at which a given infinitesimal perturbation is amplified and, thus, the laminar flow becomes destabilized.
Heat transfer was reported to have a significant influence in stability investigations as early as 1960, as found by Schlichting [13]. Temperature-dependent properties of a fluid pose a challenge for a precise stability analysis. Therefore, a physical concept named perturbation parameter is invented for this kind of analysis.
The perturbation parameter given in Equation (1) with the Kelvin unit is an essential and carefully reasoned concept in the early investigations [14,15] on the convective flat plate flow. It defines the strength of heat transfer. The critical Reynolds number dependence on the perturbation parameter is given in [16] for a flat plate flow as
This general expression is valid for every Newtonian fluid and with a small perturbation parameter. The thermophysical coefficients in Equation (2)
And the coefficients and depend on both the Prandtl number and mean flow. Equation (2) represents the change of the critical Reynolds number for sufficiently normalized wall temperature differences in both two-dimensional and three-dimensional boundary layers [17]. It is also important to mention that the air shows a destabilized convective behavior with the temperature increase, which also means a higher perturbation parameter . On the other hand, the water exhibits a stabilized behavior with a higher perturbation parameter.
Although it has long been known that heating can considerably influence the stability of laminar boundary layer flows [13,18], only a few recent studies have focused on this issue for the rotating disk case. A linear stability analysis of the flow over a rotating disk is conducted while considering the temperature-dependent thermophysical properties of fluids in a study [19]. Recent experimental studies [8,17] on the subject have focused on the Prandtl number effect combined with different wall temperatures on water over a rotating disk. However, air as a fluid in these experimental studies has not been investigated since an experimental study with such a fluid raises some challenges due to its rather low rate of change of thermophysical parameters with respect to temperature compared to liquids like water.
Another issue regarding the experiments with air is the effect of vibrations from the rotating equipment, as air is very sensitive to these vibrations, and in some cases, vibrations dominate the behavior of the boundary layer. The problem was reported in several instability studies on rotating disk flow in still air [10,11]. It has been stated in a previous study [11] that the data from the Hot-Wire Anemometry (HWA) device have an artificial noise arising from the vibration of the experimental setup, and in turn, these considerably affect the investigation, particularly the onset of instability. This issue was also observed in the initial phase of the current study. Measurements with HWA that are less than 1 mm close to the rotating disk surface had highly noisy data, especially around the frequencies under investigation.
Experimental convective heat transfer research with air has also been conducted with infrared thermal cameras in several studies [6,20,21,22]. As known to the authors, the first study with an IR camera on rotating disks was undertaken by Cardone et al. [20], and they conducted experiments on a heated disk with (only one wall temperature) a constant wall heat flux. It has been demonstrated that using an IR camera for such a study is advantageous, as their Nusselt number correlations agreed well with previous theoretical studies. Later, the same authors investigated the existence of spiral vortices with an IR camera [23], and they visualized the spiral vortices in a transitional regime on a heated rotating disk. With their approach, they were able to explain the effect of heating on a rotating disk in a qualitative and indirect way. This is because only one wall temperature is considered, and their statement was “the stability characteristics may, therefore, change significantly” with the heating.
In other related studies [21,22], the main objective was the heat transfer in a rotor (rotating disk)–stator system with an air gap in between. However, in those experiments, they also measured the case of rotating free disks in still air and applied a novel method for the determination of Nusselt numbers. In this novel method, they first calculated the local heat flux heat transfer from the known transient temperature obtained by the IR camera and interface temperatures measured by thermocouples. After calculating the local heat flux, they obtained the local heat transfer coefficients and, hence, Nusselt numbers.
Another study with an IR camera on a rotating disk in still air has been conducted for only laminar flow with low rotational speed [6]. Their experimental correlation was in good agreement with previously developed laminar correlations.
The aim of this paper is to investigate and demonstrate the applicability of a newly developed experimental evaluation method on a heated rotating disk for various rotational speeds, where the novelty of the work lies. The investigations include the effect of the perturbation parameter on the onset of instability of the flow over a rotating disk. To have a non-invasive measurement system, the experimental setup does not include a thermocouple and HWA. Two experimental setups are modeled and simulated with a three-dimensional thermal model, which is a validated in-house Python (Version 3.10.9) code [24]. Transient temperature data, with the help of another Python code provided by thermal camera setup are processed to reconstruct the precise transient temperature distributions over the radius of the disk. The directly measured transient temperature distributions are used to calculate Nusselt number distributions for a range of rotational speed and perturbation parameters. Then, they are compared with the previous data in the literature.
The results are presented in such a way that the effect of the strength of heat transfer on the onset of instability on the rotating disk for several rotational speeds is tractable. Furthermore, a thermal numerical model of the heated rotating disk is used to support the investigation. In the numerical model, an experimental case in this study is simulated using an in-house Python code. Three-dimensional transient heat conduction of rotating disk problem with heat flux and convective boundary conditions is solved. The most important outcome of this experimental study is the determination of Nusselt number distribution and how they change with the strength of heat transfer. The numerical thermal model supports the developed experimental evaluation method by quantitively showing the effect of radial conduction.
2. Convection over a Rotating Disk: The Theoretical Background
The first essential understanding and similarity solutions of the flow over a rotating disk in still air have been realized by von Karman [25]. Flow over a rotating disk has a unique behavior, as the rotating wall creates a radial pump effect through the no-slip condition and centrifugal force. Due to the continuity (mass conversation), new fluid molecules are axially driven toward the disk plane. This flow structure continuously repeats itself as the disk rotates.
Regarding the flow behavior, there exists three-dimensional flow with radial, tangential and axial velocity components (, and ). These components form three boundary layers, and a temperature boundary layer also occurs when the disk wall has a different temperature level than the ambient air (see Figure 1).
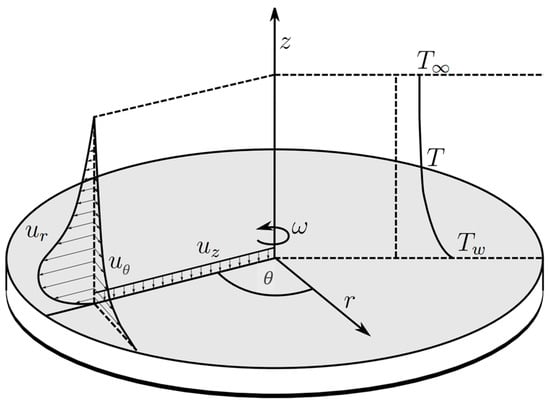
Figure 1.
Hydrodynamic and thermal boundary layer over a heated rotating disk in still air [26].
A key parameter in this study is the Nusselt number over a rotating disk. The experimental local Nusselt number correlation for convective flow over a free-rotating disk is defined in the literature as follows [27]:
The coefficient K is governed by the flow behavior (laminar, transition, or turbulent), the Prandtl number of the air and the temperature distribution at the disk surface [28]. The coefficient K for laminar flow is found within the range of 0.32–0.4, but a relatively recent study in this area has yielded K = 0.36, while for laminar flow is 0.5 [7]. For a turbulent flow over a rotating disk, Dorfman [27] has derived a relation for the Nusselt number using an integral method:
where is 0.6 for the constant heat flux boundary condition, and is 0.8 in Equation (4). This correlation will be compared with current experimental results.
Experimental studies on the determination of critical Reynolds number (at the onset of instability) yielded several values over the smooth rotating disk in still air. Experiments with HWA [11,12,29,30,31] showed consistently that the range of was between . It is clear that a unique number does not exist since it depends on the experimental conditions. However, a sudden change of a flow or thermal parameter such as skin friction and Nusselt number with respect to the rotational Reynolds number is a strong indication of the onset of instability, i.e., laminar behavior is no longer present. After a certain rotational Reynolds number, the flow enters the transition regime, and when the rotational Reynolds number is high enough, it becomes turbulent. In this study, the Nusselt number distributions are analyzed closely to track the onset of instability.
Other measurement techniques, such as acoustic measurements, visualization with kaolin, naphthalene and mass transfer coefficient (electrochemistry), have reported values that differ somewhat from the range provided by HWA measurements given above [32]. Apart from the measurement technique, different levels of roughness, vibrations, and other factors that could have occurred during experimental investigations could have contributed to the discrepancies between various sets of data. Therefore, the reference range for will be taken from the experiments with HWA [11,12,29,30,31] to compare with the experimental data in this study.
3. Experimental Methods and Test Rig
3.1. Test Rig
A test rig of heated rotating disk combined with a suitable IR camera can provide specific data from which a remarkable insight can be obtained on convective heat transfer. Particularly, local Nusselt number and its dependence on local rotational Reynolds number can be determined through the transient thermal behavior of the disk. Therefore, a specially designed test rig is employed in this investigation. The test rig in this study has already been used in several studies [26,28,33,34] on convective heat transfer subjected to forced flow. Readers should refer to the article [33], in particular, for a detailed explanation of the test rig. However, in those studies, the test rig was used to determine and analyze mean Nusselt numbers under different flow configurations. In the current study, IR camera is utilized to evaluate the transient temperature distribution of the disk surface, which is heated through constant heat flux, achieving a sufficiently uniform temperature distribution before rotation starts. Thus, the test rig is appropriate for determining local Nusselt numbers using the lumped capacitance approach, and the suitability of the approach will be explained in the next section.
Schematic and actual views of the test rig are shown in Figure 2 and Figure 3, respectively. It consists of an electrically heated composite disk with a radius of R = 200 mm and total thickness of 55 mm, with details of components mounted to the disk, as shown in Figure 4. The shaft is driven by a speed-controlled electric motor. The IR thermal camera and the blackboard are located as shown in Figure 2. The composite disk comprises multiple layers joined to a 2 mm thick heating pad. The main function of setup is to create rotational motion of the disk with a predefined rotational speed, heating the disk with an adjusted heat flux before and during the rotation, and acquire transient disk surface temperature data. The heat flux values are adjusted to ensure that the disk has a uniform temperature distribution at the desired temperature before the rotation starts.
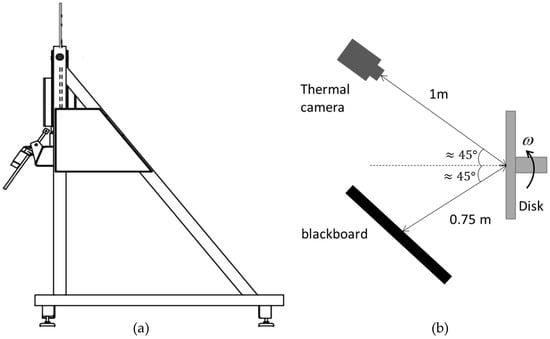
Figure 2.
(a) Construction of the measurement system; (b) thermal camera and blackboard position with geometrical details.

Figure 3.
Heated rotating disk system with the thermal camera on the left.
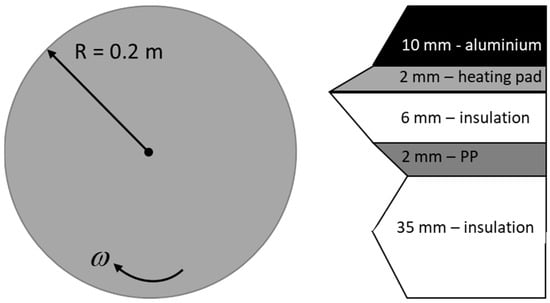
Figure 4.
Construction of the heated disk.
A disk with black surface for minimizing errors in related studies is a common way to minimize errors regarding higher emissivity of black surface. However, the surface of the aluminum disk is not painted in this study. The engineering applications targeted by this study, such as gas turbine rotor disks and brake disks, have low roughness levels. Considering this fact and to have as few excitation mechanisms as possible for the investigation of convective flow stability, the surface roughness has been kept low. There were other shiny metallic components in the room. Regarding these facts, the IR camera with a blackboard is used in dark rooms to reduce reflection effects and to have temperature data with minimum noise. Measured temperatures (just before and at the end of experiments) from IR camera and portable thermocouples have been compared and calibrated to have accurate temperature data. The effect of camera angle that is not perpendicular to the surface of rotating disk has been overcome by data processing algorithm code in Python that was provided by the manufacturer. Therefore, temperature data of rotating radial line have been accordingly stored during data processing. Adjustment of the IR camera angle, location of the IR camera and using blackboard have significantly helped with having accurate temperature results
FLIR IR camera is used with the ResearchIR software (Version 4.40.12.38), which is designed for thermographic data acquisition and analysis in R&D investigations. The software supports FLIR R&D cameras and provides an environment for factory and user calibrations [35]. Properties of the thermal camera, FLIR E60, used in this study are given in Table 1.

Table 1.
Properties of the thermal camera FLIR E60.
The experiments were conducted with different duration times. This has been undertaken to check the dependence of the test setup and the evaluation method on the test duration. After several test evaluations, it was found that the method is applicable in the range of 60–180 s, which provides a good compromise between accuracy and measurement time.
Sample raw thermal images taken in ResearchIR software from an experiment are given in Appendix A section. Figure A1 shows the raw image of the heated disk just before the start of motor. The disk in this image has a uniform temperature distribution around 40.3 °C. Figure A2 shows the raw image after the motor stopped.
3.2. Calculation of the Heat Transfer Coefficient
Heat transfer coefficients of each pixel—over which thermal camera records—are calculated by lumped capacitance method, including the mixed boundary condition (heat flux and convection) with a new data extraction method. The method uses transient temperature data of a rotating radial line over the course of rotation. For that reason, a Python code was developed to extract accurate temperature values of the radial line T(r, t) in time and space while it is rotating. One novelty of this study lies in combination of lumped capacitance method with the developed data extraction method applied for the first time in convective heat transfer experiment of rotating disk in still air. This approach enables us to have a precise and densely populated data set due to the high number of pixels across the radius of the disk. In a sense, there is quite finely distributed array of temperature sensors across a radial line, but in a non-invasive way (see Figure 5).
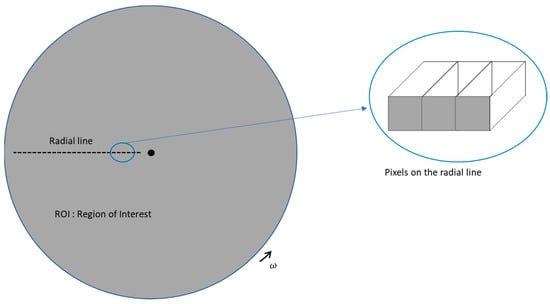
Figure 5.
Schematic presentation of the radial line created for each experiment with pixels having prismatic extension in axial direction.
To use the lumped capacitance approach, the condition Bi < 0.1 must be satisfied. The significance of the Biot number for the application of the lumped capacitance approach lies in its physical definition Bi = h/(k/L), which is the ratio of convection to the specific conductance of the solid. Therefore, the constraint on the Biot number imposes a condition on the solid that it should have a sufficiently uniform temperature distribution [36]. Calculations with the lumped capacitance approach are executed for each pixel of interest that the IR camera monitors in this study. A pixel with a backward axial extension forms a rectangular prism with a square section. Initially, the disk has a uniform temperature distribution just before the rotation starts, and the constant heat flux to the disk from the back side provides a sufficiently uniform temperature distribution all over the disk and, by definition, also in the rectangular prisms (pixels) that constitute a radial line as defined earlier. Once the rotation has started, forced convection causes the surface of the disk to cool and, thus, the pixels. The distribution of heat transfer coefficients over the radius is determined by the physics of the flow over a rotating disk. The Biot number for the highest rotational speed is between 0.0008 and 0.0037, where the range of the heat transfer coefficient from previous theoretical/experimental correlations is lying between 20 and 90 for the given range of Reynolds number in this study. Therefore, it is considered that the Biot number for the lumped capacitance approach is satisfied.
Another important point is that only axial heat transfer is considered for heat transfer coefficient calculations in our approach. The rear side of the disk well is insulated, and heating pad is deployed to achieve well-uniformly heated disk. Additionally, enough time is given to have uniform temperature distribution all over the disk before each experiment. Lastly, the thickness to diameter is quite small. These facts support the assumption that the conduction heat transfer within the disk is dominated by axial direction. Therefore, radial heat transfer is considered negligible, and this assumption will be further supported by the analysis of a 3D thermal model of the experimental setups.
ResearchIR software from the FLIR company allows the user to create ROIs (Regions of Interest) on the measured object. An ROI provides the temperature distribution of a chosen section to be saved in a datasheet for only one time instance. A radial line is created in ResearchIR to determine the dependency of local Nusselt number on the local rotational Reynolds number. The radial line is drawn slightly away from the geometric center of the disk’s surface toward the end edge of the disk. Thermo-optical interaction of the IR Camera with the shiny surface of the disk creates a bit unrealistically higher temperature just at the center of the disk despite a particular effort to avoid the reflection effects in measurement room. Therefore, the starting point of the radial line (radius start in Table 5) is placed slightly away from the center of the disk. In addition, circumferential surface convection effects are avoided by placing the endpoint of the radial line (radius end in Table 5) 9 mm away, on average, from the disk edge. The radial line consists of several pixels, from each of which transient temperature data are obtained by saving the measurement data to the PC in the online mode.
Thermal image is constructed through square-shaped pixels. A pixel has an extension in the axial direction that has the thickness of disk. It can be sad that any radial line is composed of adjacent rectangular prisms in principle. Accordingly, geometries of rectangular prisms that constitute a radial line will be used in the lumped capacitance approach [36] as shown in Figure 6.
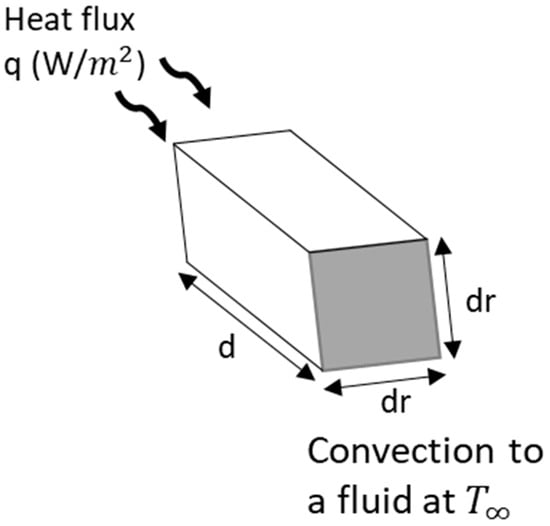
Figure 6.
Schematic view of the lumped analysis with heat flux for transient heat transfer adopted for a prism.
The equation that gives the transient thermal behavior of a rectangular prism (pixel) is given as follows [36]:
with the initial condition of . A variable Θ is defined for convenience in the solution of the ordinary differential equation such that Using Θ and the initial condition, Equation (6) becomes
Variables in Equation (7) are
The solution of the ordinary differential equation results in
Equation (9) gives the temperature value of a pixel after the thermophysical geometrical parameters, along with the time instance, are substituted into it. The equation is manipulated such that the local heat transfer coefficient becomes the only unknown parameter.
where
The determination of heat transfer coefficient of each pixel is reduced to the problem of finding the real root of Equation (10). After local heat transfer coefficients are determined, the local Nusselt number for each pixel is calculated by substituting the local radius of each pixel in Equation (12).
3.3. Uncertainty Analysis
Heat losses are calculated using the analogy of the electrical resistance. Thermal conductivity data from manufacturers are used for calculations together with the geometry of each component (see Figure 4). Heat losses (to the back side) are found to be less than 1% thanks to reliable insulation materials. A calculation according to the law of error propagation is carried out for Reynolds and Nusselt numbers. Here, a range is given for Nusselt numbers for all realized experiments since there is a temperature range that affects the calculation of uncertainty of the Nusselt number. Relative errors for properties used in this study are given in Table 2. Thermophysical parameters are the thermal conductivity and kinematic viscosity of air and the thermal conductivity of the disk. For the Prandtl number, the relative error is assumed to be 0.25%, as given in the study of [8].

Table 2.
Relative errors for measured and calculated properties.
The film temperature and Property Ratio Method.
The temperature-dependent thermophysical properties of the fluids should be taken into consideration very carefully [8]. There are two methods mainly used for this kind of analysis, namely, the arithmetic mean temperature of thermal boundary layer (film temperature) and property ratio method. The film temperature method is calculated as
However, this method may lead to unfavorable results when there are high temperature differences between wall and fluid temperature. To account for this problem, the property ratio method is developed for the evaluation of skin friction coefficient and Nusselt number for the case of external flow over surfaces [15]. In the method, heat and momentum transfer are obtained through fluid properties depending on the ambient temperature and pressure of the undisturbed free stream multiplied by a correction factor. The formulation for the evaluation of Nusselt number for air with Pr = 0.71 is [15]
Although it is stated that for air, the use of film temperature method is sufficient, both methods are used for a comparison of them in the context of the current study.
Furthermore, there are several temperature ranges in the experimental configuration. Therefore, Sutherland’s law [37] is used for the calculation of kinematic viscosity and the thermal conductivity of air for any given ambient temperature.
3.4. Determination of Critical Reynolds Number with the Landau Model
The study of stability using mathematical methods can be quite complex, but valuable insights can often be gained through a simple model suggested by Landau [38]. This model suggests that below a critical value of a control variable ( − )/, all perturbation modes of a specific order parameter O become negligible. When instability begins, at least one mode starts to grow. This leads to a straightforward relation like a Hopf bifurcation, with an empirical constant denoted as KL, as explained in detail in [38].
By linking the order parameter O and assuming a laminar heat transfer mechanism (i.e., ΔNu ∝ O1/2), the resulting heat transfer correlation is as follows:
This equation enables us to identify the stability threshold Reynolds number Recr for each perturbation parameter using a data fitting approach and Landau model. In other words, if − > 0, then it means that there is a greater deviation ΔNu = Nuexp − Nucorr from the laminar heat transfer mechanism. Reference critical Reynolds numbers are chosen as Recr,ref = . It is expected that for the air, the experimental Recr will be lower with increased perturbation parameter, and in this study, it is the function of wall temperature difference.
4. Thermal Modeling and Simulation of the Rotating Disk
The model of a three-dimensional brake disk for transient temperature and thermal stress distributions was built using the Python programming language in a study [24]. The three-dimensional transient energy equation with corresponding boundary conditions for the rotating disk in polar coordinates is as follows:
The boundary conditions are as follows:
Uniform heat flux is defined on the right surface of the disk (see Figure 7). The convective boundary condition is applied to the left and circumferential surface of the disk.
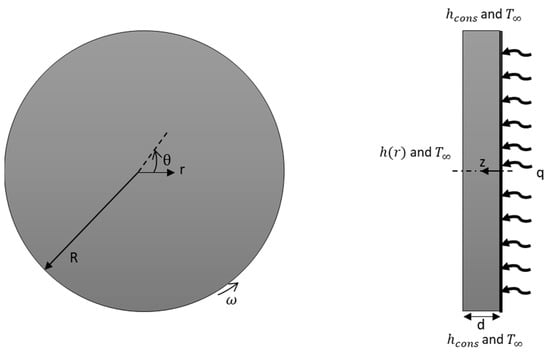
Figure 7.
Schematic presentation of thermal disk model of the rotating disk with boundary conditions.
On the side, the fitting function of heat transfer coefficients is implemented using the experimental data.
The governing Equation (19) is discretized with the implicit finite difference scheme, which is unconditionally stable with respect to time-step size.
The simulated experimental cases are 157.07 rad/s with (Table 5, no. 2) and 138.22 rad/s with (Table 5, no. 4). The disk is made of aluminum, and the fluid is air. The thermophysical and geometrical properties of the disk are given in Table 3, while the thermophysical properties of air are given in Table 4.

Table 3.
Thermophysical and geometrical properties of the disk.

Table 4.
Thermophysical properties of the air.
5. Results
Details of the parameters for each experiment are given in Table 5. A range of different rotational speed and perturbation parameters is considered to study the effects of heating on the stability of the flow over a rotating disk. Emissivity is set up at 0.04 in all experiments. The emissivity value for all experiments is set as 0.07 during the calibration of the thermal camera for the particular configuration in this study. Also, this value falls in the range for typical polished aluminum surfaces. Although perturbation parameters are quantitively smaller, they actually reflect the wide temperature range in experiments. The aim of the first experiment is to analyze the laminar flow over the disk. The Reynolds number is chosen such that there is only a laminar boundary layer existing over the whole radius of the disk. Other experiments are performed at higher Reynolds numbers, resulting in laminar, transitional and turbulent regimes coexisting over the radius of the disk. Radius start and end parameters are explained in the experimental method and test rig section.

Table 5.
Experimental parameters.
5.1. Results of Experiments
The outcomes of the experiment are compared with those obtained from an early investigation by de Vere [9] and a somewhat recent investigation by Pelle and Harmand [22]. In the following, the local Nusselt correlation for the laminar part of the flow (low Reynolds number) is given in Equation (4), with laminar flow coefficients shown in the graphical presentation of the results. These laminar curves are presented with local Reynolds numbers that are calculated by the radial distance of each pixel in the radial line.
The result of the experiment at a rotational speed of 34.55 rad/s, with the laminar boundary layer covering the whole of the disk radius, is shown in Figure 8. The local Nusselt number dependence on local Reynolds agrees well with the theoretical/experimental correlation. The coefficient of Equation (4) here is taken as K = 0.36. This value was also found to be more suitable in a relatively late study in this research area, as mentioned in the second section.
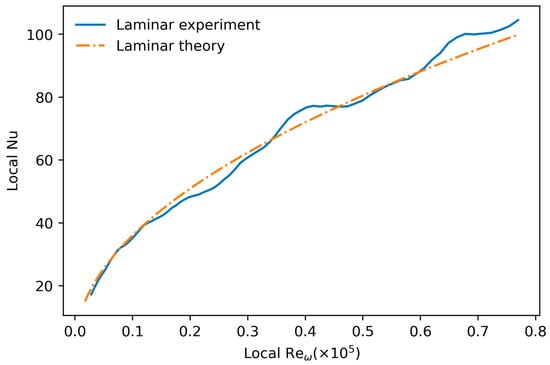
Figure 8.
Local Nu distribution with respect to local —laminar experiment and theoretical laminar correlation.
Figure 9 shows three plots with three different rotational speeds; each plot has two experimental graphs with different perturbation parameters and results of two previous studies with corresponding theoretical laminar Nusselt number distribution. The experiments with the highest rotational speed of 157.07 rad/s are shown in Figure 9a. Both experimental curves show a similar trend to the local Nusselt number dependence at other velocities. They also correlate well with the corresponding theoretical laminar curve.
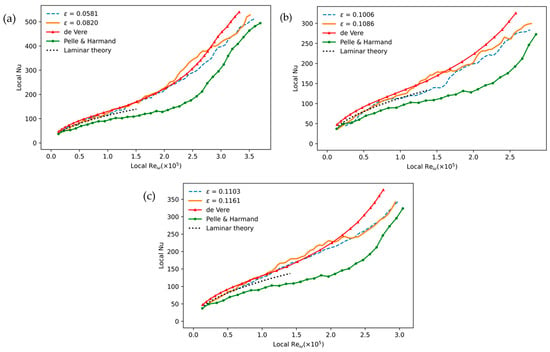
Figure 9.
Local Nusselt distribution with respect to local —(a) 157.07 rad/s; (b) 125.66 rad/s; (c) 138.22 rad/s.
Graphs for the rotational speed of 125.66 rad/s are shown in Figure 9b, and the results of both experiments fall within the range reported by de Vere [9] and Pelle and Harmand [22]. In this figure, it is clearly seen that the experimental curves fall within the range of both previous studies. However, for both up to about = the experiments correlate better with the theoretical laminar curve than the de Vere and Pelle and Harmand. It is stated in de Vere’s paper that the laminar part of the rotational flow field correlates well with the study [5] that concluded that the K value in Equation (4) is 0.38. Based on this, the laminar part of de Vere’s curve tends to be somewhat higher.
Figure 9c shows the experimental results having a 138.22 rad/s rotational speed. In this figure, it can also be said that the experimental curves are in good agreement with de Vere and again fall within the range of both previous studies. There is also a quite earlier deviation from laminar behavior, which can be attributed to the fact that it has the highest perturbation parameter among the others.
An important observation about the experimental curves at a given rotational speed is that those with greater perturbation parameters result in slightly higher local Nusselt numbers. This is particularly visible after = for rotational speeds of 125.66 rad/s and 138.22 rad/s. For the rotational speed of 157.07 rad/s, the higher tendency of the local Nusselt number (with ) starts after about = . And in general, all experiments follow a pattern that is closer to de Vere.
The fifth-degree polynomial functions from the local Nusselt distributions are generated in Python by utilizing a polyfit function that employs the least square method to fit the measured values. The local Nusselt distribution and the local Reynolds number of each experiment are used as input parameters to the Python function.
Fitted local Nusselt distribution results are compared to each other together with the corresponding laminar flow, as shown in Figure 10a–c. It can again be observed that the increase in the perturbation parameter results in an early instability. All three rotational speeds show the same pattern when looking at Figure 10, and an increase in the perturbation parameter results in an early departure from the laminar behavior at a given rotational speed. Another observation is that although the difference in the perturbation parameter is higher between and for the case of 157.07 rad/s than in the others, there is no stronger, earlier deviation from laminar behavior as expected. This may indicate that the early departure from stability at a given speed is not proportionally affected by variations in the perturbation parameters. An alternative explanation could be that the effect of the perturbation parameter may only be pronounced after certain higher levels of the perturbation parameter.
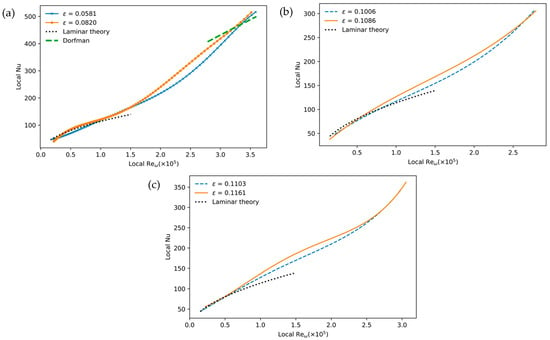
Figure 10.
Fitted local Nusselt distribution with respect to local —(a) 157.07 rad/s; (b) 125.66 rad/s; (c) 138.22 rad/s.
Research has mainly focused not on the turbulent part of the flow but rather on the laminar part and the onset of instability. Nevertheless, for the case of 157.07 rad/s, it was realized that after about = the tendency of the local Nusselt number follows the correlation given by Dorfman [27] for the turbulent regime of convective flow over a rotating disk (see Figure 10a). Other rotational speeds are also compared, but they do not follow the Dorfman relation, as in the case of 157.07 rad/s, and they are somewhat below that curve. This is not surprising as the turbulence starts after at least at = and on average, = according to a quite detailed review of for the end of transition, as given in Shevchuk’s book [32].
The final remark on the experimental results is that the evaluation of the local Nusselt number using the property ratio method makes almost no difference compared to the film temperature method, as expected for the fluid air. Therefore, the results evaluated by the property ratio method have not been presented.
5.2. Results of the Thermal Model
In the last stage, experiments and the thermal model are compared. The comparisons are based on thermal characteristics, such as the temperature evolutions of radial points and distributions along the radial line from both cases. Results are taken from experiment numbers 4 and 7 (see Table 5), and the boundary conditions of the numerical model are based on those experiments.
The created fitted heat transfer coefficients distribution using the experimental heat transfer coefficients are shown in Figure 11.
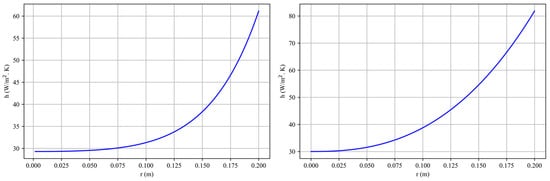
Figure 11.
The distribution of heat transfer coefficient over the radius of rotating disk (left: experiment number 4; right: experiment number 7).
5.3. Comparison of Results of Experiments and the Thermal Model
Temperature distributions for several time instants over a radial line obtained from experiment number 4 and simulation are shown in Figure 12. All time instants of simulation in the figure match the experimental results well.
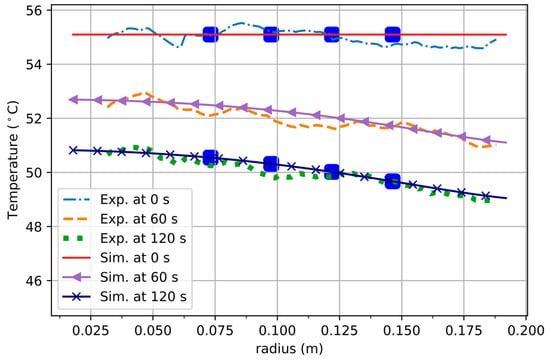
Figure 12.
Comparison of temperature distributions over the radius at several time instants (experiment number 4).
There are also four points with blue squares in the figure; these are the location of nodes (pixels) at radial points r = 0.073, 0.097, 0.121 and 0.146 m. The time evolution of those points is shown in Figure 13. The cooling curves are also in good agreement with each other, although there is some high scatter in the experimental values.
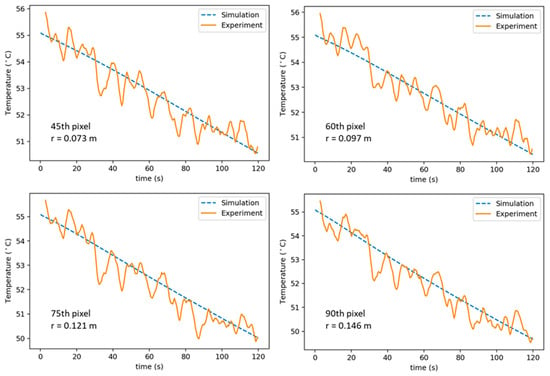
Figure 13.
Comparison of temperature evolutions for several pixels or radial points (experiment number 4).
The same thermal behavior was observed in experiment 7 as in experiment 4 (see Figure 14). It is clear from the comparison of temperatures that the cooling behavior of the uniformly heated disk with constant heat flux is well captured through the numerical model of the rotating disk.
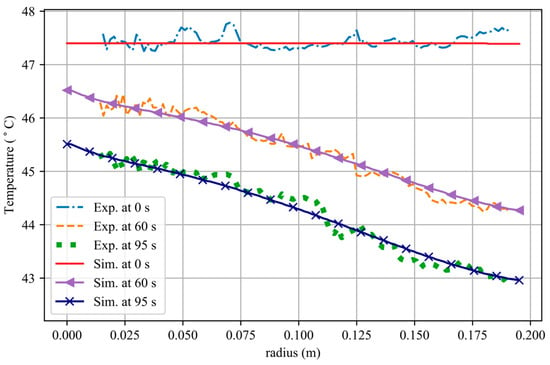
Figure 14.
Comparison of temperature distributions over the radius at several time instants (experiment number 7).
The effect of radial heat conduction is analyzed through the results of the 3D thermal model. Equation (9) is used to calculate the temperature values with a lumped capacitance approach. Inputs are initial temperature values Θ0(r), heat flux q, determined heat transfer coefficient distribution h(r) and parameter. The calculation is carried out for each pixel, and its results are denoted as .
Also, radial heat flux going in and out to each node (pixel) is calculated using the results of the thermal model for the end time.
where (i) denotes the index of nodes (pixels) in the radial direction. This equation gives the radial heat flux distribution over a radial line. Differences in incoming and outgoing fluxes are obtained using Equation (21) for each node of the thermal model (or pixel in experiments), giving a distribution over a radial line, as shown in Figure 15.
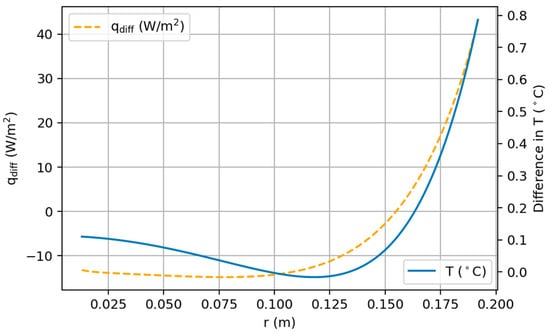
Figure 15.
Difference between temperatures calculated by lumped approach and thermal model together with over a radial line (experiment number 4).
The temperature differences between the thermal model and for the last time point are also plotted to show the effect of neglecting the radial conduction in the determination of heat transfer coefficients (see Figure 15). The differences are quite low, up to about r = 0.160 m, and then there is a sharp increase after that point, which can be explained by the increased convection effect at the circumferential section of the disk. The maximum difference is less than 0.8 °C. Also, there is a rather good correlation between the distributions of and differences in temperature.
Using the thermal model results, a final check was made for the uniformity of the axial temperature distributions of the nodes (corresponding to pixels). The calculation was based on the axial maximum and minimum temperatures of a node, and the percentage difference was found to be in the range of 0.09%, which is quite low and acceptable for the application of the lumped capacitance approach.
5.4. Dependence of Critical Reynolds Number on the Heating
To quantify the deviation of each experimental data point from the laminar correlation, the range of is considered, as shown in Figure 16. This range was chosen to have the same frame for all six datasets due to their slight differences in starting radius value and, hence, the Reynolds number. Furthermore, all the data within the selected range follows laminar correlation up to a point, followed by deviation, which means the onset of instability. Since there is uncertainty in experimental Nusselt numbers, it is necessary to use a suitable data evaluation model, such as the Landau model, to extract a meaningful dependence of critical Reynolds number on the perturbation parameter.
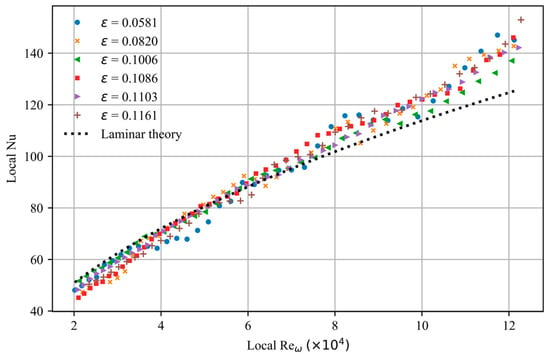
Figure 16.
Local Nusselt distribution in the range .
After proving that the lumped capacitance approach is reliable for the given experimental conditions, such as the effect of radial heat conduction, uniform temperature distribution and Biot number for each pixel, it is safe to apply Equation (18), which is derived from the Landau model for the current study.
Therefore, using the Nusselt numbers for the selected range, the term is calculated with the corresponding laminar correlation equation (). This calculation is performed for each pixel for a given experimental data, and then their mean value is calculated. The obtained variable is used to predict the variation of the critical Reynolds number with the varying perturbation parameters, as shown in Figure 17. The figure shows the perturbation parameter of each experiment together with the exponential fit function in the form , where a, b and c are, respectively, , 14.01 and . The tendency of predicted critical Reynolds number seems quasi-exponential as the variation in perturbation parameter is not strong. The predicted data tend to vary slightly with respect to the Landau parameter KL; that is, changing it results in small variations of Recr. However, this curve still provides valuable insights into the cases in this study, as it correlates the deviation from laminar behavior with an increasing perturbation parameter and a progressively decreasing critical Reynolds number.
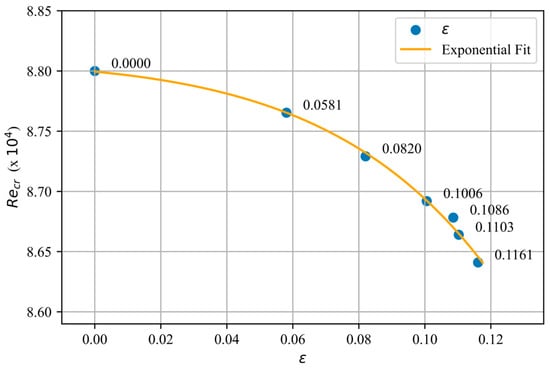
Figure 17.
Dependence of critical Reynolds number with the perturbation parameter.
6. Conclusions and Recommendations
In this study, the results of an experimental study employing an electrically heated rotating disk in still air together with its 3D thermal modeling were reported. Local surface temperatures of the disk were measured employing an IR camera and specialized software. Then, using the Python code with a novel evaluation approach, the heat transfer coefficients were determined over the disk radius. A lumped capacitance approach equation with axial heat flux term neglecting the radial flux is used in the novel approach. The results from all experiments in this study support this assumption. The effect of the heating strength (by varying the perturbation parameter) on the stability of the rotational flow field over the disk was investigated systematically under different rotational speeds. Furthermore, results are compared in terms of thermophysical values calculated by the property ratio method and the film temperature method. Apart from the experimental studies, two experimental setups are modeled using an in-house Python code. The main features of the model are that it is transient and three-dimensional, and it was validated for complex rotating disk scenarios in a previous study.
Experimental Nusselt numbers are compared with valuable studies in the field, and the outcomes are in good agreement with those studies. The approach used to set up the experiment, together with the developed evaluation method, seems promising. The neglection of the radial heat flux component in the new calculation method is analyzed and justified by the thermal modeling using the experimental data.
As it was already estimated, using the complicated property ratio method has not yielded noticeable differences due to the thermal character of the air, together with relatively low temperature differences between the disk surface and the ambient air. Fitting functions are created from the experimental results except for the laminar one (Table 5, no. 1). Then, comparisons are made between the theoretical laminar curve and fitting experimental curves for each rotational speed having two different perturbation parameters. This helped to analyze and compare the deviation from laminar flow from the point of view of heat transfer. Comparisons show that there is a similar behavior in early deviation with the increasing perturbation parameter for each given rotational speed. It is qualitatively observed that differences in perturbation parameters affect the onset of instability and that the departure from the laminar behavior occurs earlier for increased perturbation parameters. This is a remarkable finding because air as a fluid has not been previously investigated for this type of experimental stability analysis. Having a non-invasive experimental setup with a suitable evaluation method has been decisive for having such a result for the air as a fluid. Furthermore, the Landau model with data fitting procedure is applied to the experimental data to have a quantitative variation of critical Reynolds number with perturbation parameters. The analysis showed a reasonable dependence of the critical Reynolds number on perturbation parameters.
The thermal model of the rotating disk is compared firstly with transient temperature values. These parameters are in quite good agreement with the experimental data. Overall, the methodology in this study provides a non-invasive method with good accuracy for convective heat transfer analyses on a rotating disk. It can be recommended that an experimental setup with a fixed and high Reynolds number and perturbation parameters at higher levels than in this study (wall temperature difference) can greatly improve the knowledge of convective heat transfer. Also, different crossflow configurations, such as parallel flow or axial flow with this methodology, can provide meaningful and more precise data, as it is a non-invasive method.
Author Contributions
Conceptualization, S.a.d.W.; Methodology, Y.C.; Writing—original draft, Y.C.; Writing—review & editing, S.a.d.W. and M.D.; Visualization, Y.C.; Supervision, S.a.d.W. and M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was conducted during the first author’s research stay at Münster University of Applied Sciences. The research stay has been funded by the German Academic Exchange Service (DAAD) with the reference number 91807703.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We gratefully recognize the valuable contributions made by students and employees Fabio Fadda, Leon Chakiev, Stephan Sundermeier, and Leander Hake at the Muenster University of Applied Sciences. The first author thanks his company, TCDD (Turkish State Railways), for granting him the sabbatical leave that made the research stay possible.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| c | specific heat, J/(kg K) |
| d | thickness, mm |
| f | frequency, Hz |
| h | heat transfer coefficient, |
| k | thermal conductivity, |
| q | heat flux, W/m2 |
| r | radial coordinate, m |
| t | time, s |
| z | axial coordinate, m |
| A | surface area, mm2 |
| K | coefficient in correlation of Nusselt number |
| T | temperature, °C |
| tangential skin friction | |
| cR | exponent of Reynolds number |
| mlump | parameter in the lumped analysis |
| friction velocity, m/s | |
| R | radius of the disk, m |
| Bi | Biot number |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Re | Reynolds number |
| Greek Symbols | |
| thickness of the boundary layer, m | |
| perturbation parameter | |
| dynamic viscosity, Pa.s | |
| tangential coordinate, rad | |
| thermal diffusivity, m2/s | |
| kinematic viscosity, m2/s | |
| density, kg/m3 | |
| wall shear stress, MPa | |
| angular velocity, rad/s | |
| non-dimensional wall distance | |
| non-dimensional temperature | |
| Subscripts | |
| d | disk |
| w | wall |
| pix | pixel |
| turb | turbulent |
| ambient air | |
| Abbreviations | |
| FDM | Finite Difference Method |
| HWA | Hot-Wire Anemometer |
| ROI | Regin of Interest |
Appendix A. Raw (Uncalibrated) Thermal Images from ResearchIR Software
Sample raw thermal images taken from FLIR ResearchIR before calibrations in Python are shown below. The images are taken from experiment no. 6.

Figure A1.
Thermal image of the disk just before the start of motor.

Figure A2.
Thermal image of the disk just after the motor is stopped.
References
- Cobb, E.C.; Saunders, O.A. Heat Transfer from a Rotating Disk. Proc. R. Soc. Lond. A Math. Phys. Sci. 1956, 236, 343–351. [Google Scholar]
- Popiel, C.O.; Bogusławski, L. Local heat-transfer coefficients on the rotating disk in still air. Int. J. Heat. Mass. Transf. 1975, 18, 167–170. [Google Scholar] [CrossRef]
- Booth, G.L.; de Vere, A.P.C. Convective heat transfer from a rotating disc in a transverse air stream. In Proceedings of the Heat Transfer 1974, Fifth International Conference, Tokyo, Japan, 3–7 September 1974; Volume 2, pp. 30–34. [Google Scholar]
- Elkins, C.J.; Eaton, J.K. Turbulent heat and momentum transport on a rotating disk. J. Fluid. Mech. 2000, 402, 225–253. [Google Scholar] [CrossRef]
- Goldstein, S. On the Resistance to the Rotation of a Disc Immersed in a Fluid. Math. Proc. Camb. Philos. Soc. 1935, 31, 232–241. [Google Scholar] [CrossRef]
- Latour, B.; Bouvier, P.; Harmand, S. Convective heat transfer on a rotating disk with transverse air crossflow. J. Heat. Transf. 2011, 133, 021702. [Google Scholar] [CrossRef]
- Trinkl, C.-M.; Bardas, U.; Weyck, A.; der Wiesche, S.A. Experimental study of the convective heat transfer from a rotating disc subjected to forced air streams. Int. J. Therm. Sci. 2011, 50, 73–80. [Google Scholar] [CrossRef]
- Helcig, C.; der Wiesche, S.A.; Shevchuk, I.V. Prandtl Number Effect on the Laminar Convective Heat Transfer from a Rotating Disk. J. Heat Transf. 2017, 139, 101702. [Google Scholar] [CrossRef]
- de Vere, A.P.C. Convective Heat Transfer from a Rotating Disc in a Transverse Air Stream. Ph.D. Thesis, University of Leicester, Leicester, UK, 1975. [Google Scholar]
- LINGWOOD, R.J. An experimental study of absolute instability of the rotating-disk boundary-layer flow. J. Fluid. Mech. 1996, 314, 373405. [Google Scholar] [CrossRef]
- Malik, M.R.; Wilkinson, S.P.; Orszag, S.A. Instability and transition in rotating disk flow. AIAA J. 1981, 19, 1131–1138. [Google Scholar] [CrossRef]
- Kobayashi, R.; Kohama, Y.; Takamadate, C. Spiral vortices in boundary layer transition regime on a rotating disk. Acta Mech. 1980, 35, 71–82. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Herwig, H.; Wickern, G.; Gersten, K. Der Einfluß variabler Stoffwerte auf natürliche laminare Konvektionsströmungen. Wärme Stoffübertragung 1985, 19, 19–30. [Google Scholar] [CrossRef]
- Gersten, K.; Herwig, H. Impuls-und Wärmeübertragung bei variablen Stoffwerten für die laminare Plattenströmung. Wärme Stoffübertragung 1984, 18, 25–35. (In German) [Google Scholar] [CrossRef]
- Schäfer, P.; Severin, J.; Herwig, H. The effect of heat transfer on the stability of laminar boundary layers. Int. J. Heat Mass Transf. 1995, 38, 1855–1863. [Google Scholar] [CrossRef]
- der Wiesche, S.A.; Helcig, C. Effect of heating on the stability of the three-dimensional boundary layer flow over a rotating disk. E3S Web Conf. 2022, 345, 02007. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Miller, R.; Griffiths, P.T.; Hussain, Z.; Garrett, S.J. On the stability of a heated rotating-disk boundary layer in a temperature-dependent viscosity fluid. Phys. Fluids 2020, 32, 024105. [Google Scholar] [CrossRef]
- Cardone, G.; Astarita, T.; Carlomagno, G.M. Heat Transfer Measurements on a Rotating Disk. Int. J. Rotating Mach. 1997, 3, 912069. [Google Scholar] [CrossRef]
- Pellé, J.; Harmand, S. Heat transfer study in a rotor–stator system air-gap with an axial inflow. Appl. Therm. Eng. 2009, 29, 1532–1543. [Google Scholar] [CrossRef]
- Pellé, J.; Harmand, S. Heat transfer measurements in an opened rotor–stator system air-gap. Exp. Therm. Fluid. Sci. 2007, 31, 165–180. [Google Scholar] [CrossRef]
- Astarita, T.; Cardone, G.; Carlomagno, G.M. Spiral Vortices Detection on a Rotating Disk. In Proceedings of the Icas 2002 Congress, Toronto, ON, Canada, 8–13 September 2002; pp. 1–8. Available online: https://www.researchgate.net/publication/268386435 (accessed on 3 June 2024).
- Cati, Y.; der Wiesche, S.A.; Düzgün, M. Numerical Model of the Railway Brake Disk for the Temperature and Axial Thermal Stress Analyses. J. Therm. Sci. Eng. Appl. 2022, 14, 101014. [Google Scholar] [CrossRef]
- Kármán, T.V. Über laminare und turbulente Reibung. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Helcig, C. Experimentelle Untersuchung des Konvektiven Wärmeübergangs an Rotierenden Scheiben. Ph.D Thesis, University of Stuttgart, Stuttgart, Germany, 2018. [Google Scholar]
- Dorfman, L.A. Hydrodynamic Resistance and the Heat Loss of Rotating Solids; Oliver and Boyd: Edinburgh, UK, 1964. [Google Scholar] [CrossRef]
- der Wiesche, S.A.; Helcig, C. Convective Heat Transfer from Rotating Disks Subjected to Streams of Air; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Wilkinson, S.P.; Malik, M.R. Stability experiments in the flow over a rotating disk. AIAA J. 1985, 23, 588–595. [Google Scholar] [CrossRef]
- Watanabe, T. Effect of surface roughness on boundary layer transition in a rotating disk. Trans. Jpn. Soc. Mech. Eng. Ser. B 1989, 55, 1842–1846. [Google Scholar] [CrossRef][Green Version]
- Watanabe, T. Stability of Boundary Layers along a Rotating Disk with Uniform Suction. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 1988, 68, 21–24. [Google Scholar] [CrossRef]
- Shevchuk, I.V. Convective Heat and Mass Transfer in Rotating Disk Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Helcig, C.; der Wiesche, S.A. Convective Heat Transfer From a Free Rotating Disk Subjected to a Forced Crossflow. In Volume 5B: Heat Transfer; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Helcig, C.; Der Wiesche, S.A. The Effect of the Incidence Angle on the Flow Over a Rotating Disk Subjected to Forced Air Streams. In Proceedings of the ASME 2013 Fluids Engineering Division Summer Meeting, Incline Village, NV, USA, 7–11 July 2013. [Google Scholar]
- FLIR Systems Inc. ResearchIR 4 User’s Guide. 2022. Available online: www.flir.com (accessed on 3 June 2024).
- Ozisik, M.N. Heat Transfer: A Basic Approach; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Sutherland, W. The viscosity of gases and molecular force. Philos. Mag. Ser. 5 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Landau, L.; Lifchitz, E. Hydrodynamik; Akademie: Berlin, Germany, 1990. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).