Abstract
The use of a synthetic jet as the flow control technique to modulate a turbulent incompressible round jet was explored and assessed by numerical simulations. The flow response was characterised in terms of turbulent statistics and acoustic response in the far-field. A quasi-Direct Numerical Simulation (qDNS) strategy was used to predict the turbulent effects. The Ffowcs-Williams and Hawkings (FWH) acoustic analogy was employed to compute the far-field acoustic response. An amplification effect of the instabilities induced by the control jet was observed for some of the parameters explored. It was observed that the control technique allows controlling the axial distribution of the production and dissipation of turbulent kinetic energy, but with respect to the acoustic aspects, the appearance of a greater number of noise sources was observed, which in the far-field, resulted in an increase from 1 to 20 dB of the equivalent noise for the different operating parameters of the control technique studied.
1. Introduction
Injection by turbulent jet flows has multiple uses in industry including applications in heat transfer processes, drying, cleaning, aerodynamic stabilisation, combustion chambers, and propulsion systems, among others [1,2,3,4]. The noise generated by these sources has been widely studied, and noise generated in industrial environments is considered to be the third-most-damaging source of noise to the human hearing system [2]. The World Health Organisation (WHO) recommends the levels of exposure for noise generated by transportation systems, including aircraft propulsion systems. In the Environmental Noise Guidance [5], it is strongly recommended to reduce exposure to aircraft noise levels to less than 45 dB (day–evening–night-weighted sound pressure level) during the day and 40 dB at night. This is because exposure to higher noise levels is linked to adverse health effects and sleep problems.
Although there is no precise description of the nature of noise generated by turbulent jets, three noise components are associated with this phenomenon. These are known as turbulent mixing noise [6], broadband shock-associated noise [7], and screech tones. Nevertheless, the turbulent mixing noise is considered to be the main source of noise in subsonic jets. As the name suggests, it is generated by the turbulent mixing effects between the jet and a still medium [8], which occurs in an annular layer with high shear stress values, which increases in size as the jet advances into the medium. The region inside this annular region, where no rotational effects are present, is known as the potential core or cone of silence, and it extends until the mixing region completely fills the jet area [9]. In this way, turbulent mixing noise is composed of the noise generated by the small and large turbulent scales. The Fine-Scale Structures (FSSs) are predominant close to the nozzle; they have sizes of the order of magnitude of the thickness of the mixing layer and produce the high-frequency response in the noise spectrum. On the other hand, Large-Scale Structures (LSSs) occur further ahead of the potential jet core; they have sizes of the order of magnitude of the nozzle diameter and are the ones that provide the low-frequency effects [10]. Thus, for subsonic jets, the small turbulent scales are probably the most-predominant in terms of noise generation and the largest contributors at different emission angles. However, the noise generated by the large turbulent scales, which propagates in the jet direction, can become significant at small emission angles with respect to the jet axis [11].
In order to reduce jet noise in industrial applications, flow control techniques have been studied for more than 50 years [12]. These mainly seek to modify the mixing effects between the injected fluid and the still fluid [13], because noise jet arises from the turbulent effects created during fluid interaction. However, any alteration in the development or nature of the jet is reflected in the efficiency of the jet to generate thrust. A large number of control techniques seek to modify the flow patterns at the jet exit. Flow control strategies are classified into passive and active control techniques [14]. Passive control techniques focus on generating modifications on the nozzle geometry, and active control techniques do so by adding mass or energy to the jet and have the advantage of being able of adjust the control technique’s operation parameters during operation [15].
Chevron nozzles are amongst the most-commonly used passive control techniques. They are characterised by triangular grooves at the trailing edge of the nozzle, which introduce disturbances in the high gradient zones of the jet and enhance the mixing effects between the jet fluid and still medium. This enhances the presence of small turbulent scales in the initial zone of the jet and decreases turbulence levels in the downstream region [16,17]. These devices are the most-effective in terms of noise mitigation, and according to Sadeghian and Bandpy [4], their use has a minimal impact on the operation of the turbines in which they are installed.
On the other hand, some examples of active control techniques use injectors that add mass to the main jet, while also seeking to modify the flow patterns, as mentioned before. Active control techniques have been studied since the 1950s in aeronautical applications. Powell [18] studied the influence of the velocity profile at the exit of the turbulent jet on the noise generated and proposed the use of a lower velocity annular jet surrounding the main jet. The direct effect obtained with this technique was a reduction of the high velocity changes between layers of the jet. Subsequent studies focused on the use of auxiliary jets to reduce the high-velocity gradients at the jet exit. In Kurbjun [19], water was used as the injection fluid, and the jets were injected close to the nozzle with a radial orientation towards the longitudinal axis of the main jet. Although they found great efficiency in terms of noise reduction using water as the auxiliary injection fluid, they also pointed out the big practical challenge of auxiliary water jets, which would require large quantities of water to be injected into the engine jets during flight. In order to avoid the use of a different fluid, the Michael patent [20] proposes some modifications in the nozzle to make the auxiliary jets fed with the same fluid jet. These are evenly spaced on the periphery of the nozzle and can change their orientation from being fully parallel to the longitudinal axis of the jet to being slightly inclined towards the centre of the jet. These kinds of studies led to the use of active control techniques that feed from the jet fluid they are trying to control, facilitating their assembly, and also to the use of water as an injection fluid in launch applications, where noise reduction is required, especially at take-off. Recently, studies using these techniques have focused on studying the configurations, locations, and operating parameters of the auxiliary jets, such as Callender et al. [15] and Caeti and Kalkhoran [21], using fluidic injection, Rajput and Kumar [13], using downstream fluid injection, and Prasad and Morris [22] with fluid inserts.
An active control technique used in different applications is based on synthetic jets located outside of the flow boundaries and pointing across the mean flow. A synthetic jet is characterised for transfer momentum to the flow without net mass injection. It is produced by the periodic injection and subtraction of mass from an orifice induced by an oscillating diaphragm. Usually, the diaphragm’s resonance frequency is driven by a piezoceramic element [23]. However, there is also a special type of synthetic jet actuator driven thermodynamically by pulsed arc discharges, known as the plasma synthetic jet actuator [24]. Compared with the piezoelectric ones, plasma actuators are capable of producing high-velocity (>300 m/s) and high-frequency synthetic jets (>5 kHz) [25]. Among the different applications of these actuators are aerodynamic control [26], heat transfer [23], vectoring [27], and jet noise control [28,29]. Although related research has demonstrated the ability of this technique to perturb flow behaviour and control it depending on the parameters used, it is not yet clear which parameter plays an essential role in controlling flows in the most-efficient way. General parameters include the addition of momentum, the location of the actuator, and the frequency of excitation. Additionally, among the research focused on noise control using synthetic jets, it has not been possible to identify how the instabilities induced by the synthetic jets can influence the main jet flow and, thus, modify the sources of noise in the flow.
In this paper, we studied the modulation effects of the noise produced by a low-Mach-number and low-Reynolds-number subsonic turbulent jet, using as an active control technique a synthetic jet injected over an annular region located before the nozzle exit in different operating conditions, to understand the effect of the transport and propagation of ordered and synthetic instabilities by the round turbulent jet. In order to study the effect of the synthetic jet as a flow control technique, a number of flow features and properties were examined in detail, including turbulence statistics, the source term of the acoustic analogy of Lighthill [30], and the far-field noise using the acoustic analogy of Ffowcs Williams and Hawkings [31], also known as the Ffowcs-Williams and Hawkings (FWH) analogy.
The remainder of this paper is organised as follows. Section 2 describes the governing equations used as the mathematical model, as well as the details of the computational model used for the validation process and the main numerical experiments. Section 3 presents the results obtained by the model for both the validation case and the cases using the annular jet control technique. This section also presents the main conclusions on the flow field and the acoustic response at the sources and in the far-field. Finally, Section 4 presents the conclusions of the present study.
2. Materials and Methods
A three-dimensional computational model of a subsonic jet was produced based on the model presented by Brès et al. [32]. In particular, the convergent nozzle geometry and domain dimensions used in the present study match those used in Brès et al. [32]. The nozzle has a length of 10-times the diameter at the nozzle exit () and a size ratio of the inlet diameter to the outlet diameter of 10. At the inlet of the nozzle, the volumetric flow necessary to achieve the desired operating parameters at the outlet of the nozzle was configured. For the outer boundaries of the domain, the conditions of a fixed pressure of zero and a zero velocity gradient for the outflow and also for stability, and if recirculation occurs near the outlet, the normal wall velocity is applied. Additionally, a gradual increase of the size cells was applied in the regions away from the turbulent jet development region and in the direction of the domain exits, in order to increase the diffusive effects of the numerical methods used and to reduce any reflection effects that may occur. The nozzle tip was modelled as immersed within a domain that contains a still medium, as shown in Figure 1. The configuration employed allowed setting up a surface enclosing the acoustic sources, which, in turn, helped to reduce interference with the computational boundaries. Additionally, to avoid flow recirculation effects and to facilitate the entry of the jet into the domain, an exterior inlet flow was configured with a velocity 100-times lower than the jet velocity.
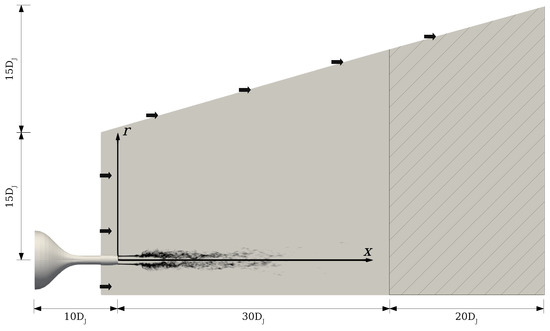
Figure 1.
Schematic view of the computational domain used and the model conditions.
The operating parameters of our test case were defined from one of the cases studied by Panchapakesan and Lumley [33], in which air was used as the injection fluid. These parameters are presented in Table 1.

Table 1.
Turbulent jet operating parameters.
2.1. Aerodynamic Computation
A quasi-Direct Numerical Simulation (qDNS) strategy was selected in this study to model the turbulent effects in the flow. This strategy is based on the idea of solving only the large turbulent scales using a reasonable fine mesh, as in classical Large Eddy Simulations (LES), but without explicitly modelling the smallest scales of the turbulence [34]. This was selected in order to avoid the high computational costs associated with simulating all turbulent scales by Direct Numerical Simulation (DNS) approximations, which requires the use of high-order numerical methods. Thus, the use of qDNS strategies reduces the space–temporal order of resolution of the phenomenon, but captures the trends of turbulent effects in the flows of interest. Although this simulation strategy under-predicts the intensity of the turbulent effects, it is able to capture the trend of the phenomenon with a more manageable associated computational cost [35,36,37]. Furthermore, another relatively well-known advantage of this strategy is that, unlike DNS approaches, where modelling flows in complex domains and situations is only feasible for moderate Reynolds numbers and simple flow geometries, the qDNS strategy allows modelling cases with complex geometries, with comparatively low computational costs, provided that a reasonable and efficient spatial discretisation is employed.
The numerical model selected for the present work was based on the Finite-Volume Method (FVM), using the weighted Crank–Nicholson method, employing a weight selected to ensure unconditional stability, and the gradient and divergence terms were discretised using the second-order Gaussian linear scheme, while the Laplacian terms were discretised using the Gaussian linear corrected scheme, which also aims to provideaccuracy for both interpolation and the surface normal gradient components required for the Laplacian terms. Finally, linear schemes were used for point-to-point interpolation. This model was solved using the open-source software OpenFOAM. To approximate the continuity and momentum equations for an incompressible flow in a transient state, the solver called pimpleFoam was selected. This is based on the PIMPLE algorithm, which is a combination of the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) and Pressure Implicit with Splitting of Operators (PISO) algorithms for pressure and velocity coupling and can be understood as the use of the SIMPLE algorithm to find a steady-state solution at each time step [38,39]. Convergence values for velocity and pressure of and 5 external correctors of the algorithm were used for the solver.
2.2. Aeroacoustic Computation
The noise at the sources and far-field was calculated using acoustic analogies intended to evaluate the acoustic response of the study cases. The acoustic sources were calculated using the right-hand side of the acoustic analogy of Lighthill [30], which is presented in Equation (1), an expression that is obtained from the manipulation of the conservation of mass and momentum equations.
Here, and denote the density and the velocity of sound in the fluid, p the acoustic pressure, the viscous stress tensor, and the Dirac delta function. If the flow is considered incompressible, the velocity fluctuations are dominated by turbulence and the viscous terms, represented by , can be neglected. Additionally, for isentropic flows, it is valid to assume that . Accordingly, it is possible to approximate the tensor to the term in Equation (2). After some simplifications and taking into account the conservation of mass for incompressible flows, the source term can be finally expressed as
On the other hand, the FWH equation was used to calculate the far-field acoustic response. This analogy model was implemented in OpenFOAM in the library libAcoustics, a computational tool developed by Epikhin et al. [40] that works in parallel with the fluid flow solvers. In this way, after a given number of iterations of the flow solver used, the sound pressure levels at the measurement points are calculated taking into account the time delay between the moment of noise generation from the turbulent flow and the moment it is perceived at the far-field.
The FWH equation was developed by Ffowcs Williams and Hawkings [31], and it has a generalised form in order to be able to describe the phenomenon of acoustic generation by turbulent flow in a domain with discontinuities, for instance when moving solid surfaces are immersed in a turbulent flow. The FWH equation is presented in Equation (4), and similar to the Lighthill acoustic analogy, it has an non-homogeneous wave equation form. The first term on the right-hand side represents the sources in the form of quadrupoles in the flux region. The second and third terms are typically known as the Loading Source Term (LST) and Thickness Source Term (TST). These terms represent the sources in the form of dipoles and monopoles, respectively. Furthermore, they are defined over the surface by a Dirac delta function, . The terms and are defined in Equations (5) and (6), respectively.
In these expressions, is the surface velocity, is the fluid velocity, is the step function that defines the surfaces that enclose the noise sources in the flow field, and the terms and are known as the loading source term and the thickness source term and represent the dipoles and monopoles sources, respectively. Equation (4) is the general form of the FWH equation and is also known as the formulation with permeable surfaces or control surface, where the acoustic sources are enclosed by the surface , which should not represent an obstacle in the flow. If corresponds to a solid surface, then , and the formulation of the FWH equation for moving impenetrable surfaces is obtained. If this surface is stationary, , and the FWH equation reduces to the equation of Curle [41].
In this approach, the calculation of the acoustic response of sources located at Y on points located at the far-field X is achieved by using the so-called integral formulation of the FWH analogy, shown in Equation (7). In this expression, the first term is evaluated within the volume where the turbulent flow develops, and the second and third terms are evaluated on the surface that separates the regions of the domain.
2.3. Computational Model
The computational domain was discretised using a structured mesh adapted to the shape of the nozzle aiming to obtain smaller cells in the regions close to the jet exit and the nozzle walls. This mesh was developed using the software Gmsh [42] and then imported into OpenFOAM.
The mesh has approximately million cells. In Figure 2, the cell sizes are presented over the line in the axial direction from the nozzle edge and over the radial line at the nozzle exit. To appreciate the quality of the prescribed computational mesh, our mesh density was compared with the meshes developed by Bogey et al. [43] and Brès et al. [32], which investigated turbulent jets using LES turbulence models with a number of and numbers of and , respectively.
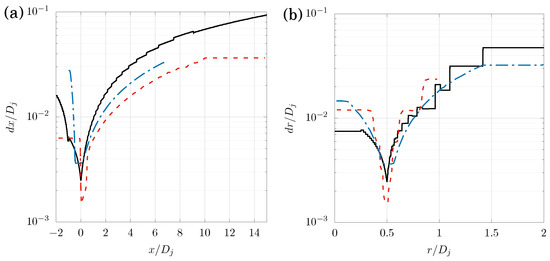
Figure 2.
Dimensionless cell sizes (a) in the axial direction from the nozzle edge and (b) in the radial direction at the nozzle outlet. —, , the present work; , , [43]; , , [32].
In the region closer to the nozzle, a mesh resolution similar to the one presented by the mentioned studies was achieved; however, it is important to note that the number used in this work is one order of magnitude smaller, and no turbulence model was used. In this way, it was inferred that the mesh employed was able to capture the turbulent effects in these regions in the same way as was performed in the mentioned investigations for higher turbulence levels. In addition, the necessary resolution was achieved for the region where the influence of the perturbations added by the synthetic jet was observed. Figure 3 shows a slice of the mesh at the initial part of the jet.
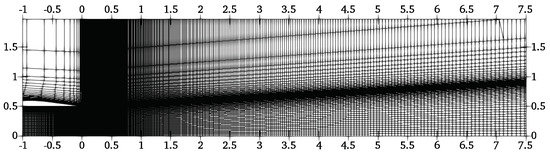
Figure 3.
Detail of computational mesh at the initial region of the jet in terms of nozzle diameters.
Additionally, in order to use the FWH analogy, the surface containing the turbulent flow was constructed with a cylindrical shape with a variable diameter, which was oriented in the direction of the jet and was located at the jet exit. The dimensions of the cylinder in terms of the nozzle diameter () were a length of , an initial diameter of , and a final diameter of . These characteristics were selected taking into account the information presented in Brès et al. [32] and the recommendations discussed by Mendez et al. [44]. The noise generated by the jet was computed on an array of points representing far-field locations according to Figure 4. Three arcs of 9 points each were configured, with distances of , , and from the jet exit and spanning angles from to .
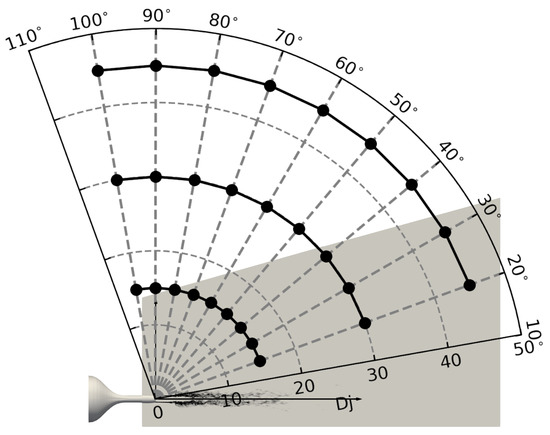
Figure 4.
Location of measurement points in the far-field.
2.4. Flow Control Technique
The proposed control technique consists of a synthetic jet injected over an annular region of the nozzle, located at a distance from the nozzle outlet. The location of the synthetic jet injection ring over the jet nozzle is shown in Figure 5.
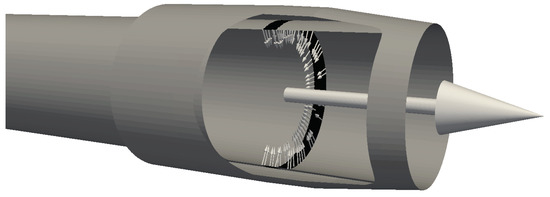
Figure 5.
Schematic of the synthetic jet configuration as a turbulent jet control technique.
Both round and fluctuating jets can be described using the Strouhal number (), a dimensionless number used to analyse oscillation phenomena in flows and representing the ratio between the inertial forces produced by the fluid instability and those produced by changes in velocity. In the present study, different operating conditions of the synthetic jet were explored, but only one operating condition of the main round jet. Thus, in order to simplify the analysis, a relationship between these dimensionless parameters was established, and all the analysis and presentation of the results were carried out using this relationship between the Strouhal numbers.
Equation (8) presents the Strouhal number for the round jet (), determined using the nozzle diameter (), the jet injection velocity (), and a frequency (), which was determined using the thickness of the boundary layer inside the nozzle () and the maximum value of the turbulent intensity () on the centerline of the jet.
On the other hand, Equation (9) presents the Strouhal number used for the synthetic jet () obtained using the oscillation frequency of the synthetic jet, the thickness of the injection ring (), and the oscillation amplitude of the synthetic jet (). Factor represents the ratio between the injection ring thickness and the nozzle diameter, whereas is the ratio between the oscillation amplitude of the synthetic jet and the injection velocity of the round jet. Therefore, the Strouhal number for the synthetic jet can be expressed as
Using the previous definitions for the Strouhal number for the round jet and the synthetic control jet, the ratio of can be expressed as a frequencies ratio, as presented in Equation (10).
In the present work, constant values were used for the parameters , and , specifically , , and , with representing the round jet diameter at the exit of the nozzle. The numerical experiments were established by varying the oscillation frequency of the synthetic jet. In this way, the value was reduced to the ratio between the frequencies of the synthetic jet and the round jet. Table 2 presents the values and their corresponding frequencies employed in the numerical experiments.

Table 2.
Oscillation frequencies of the synthetic jet.
3. Results and Discussion
The results presented below were obtained from the instantaneous, spatially averaged, or time-averaged values of the cases studied once they reached a quasi-steady-state, where a periodic behaviour was present. For this purpose, the simulations were allowed to run for more than 30 jet times, which in terms of the period of the oscillation in the lowest frequency-controlled case means 25 oscillations of the synthetic jet.
3.1. Validation
In order to determine the validity of the results achieved with our computational model, the behaviour of the turbulent jet was compared with experimental investigations and numerical results obtained by previous works using LES and DNS. The typical profiles included the mean velocity, the average velocity fluctuations, and the production and dissipation terms of the turbulent kinetic energy transport equation. These profiles were obtained over the axial lines at and and over radial lines located at different axial positions. The radial profiles were normalised using the velocity at of each axial location and the value of the radial distance at which the velocity decays to half of its value (). The normalisation can be performed based on the self-similarity characteristic of turbulent jets in the developed region of the jet.
The profiles of the axial component of the time-averaged velocity over the axial jet direction are presented in Figure 6. It can be observed for the centerline that the case captured the trend of the reference profiles; it presented a potential core length similar to those reported by Brès et al. [32] and Shin et al. [45] and presented a similar decay behaviour at , as presented by the cases of Todde et al. [46]. On the other hand, the profile on the lip line (Figure 6b) showed a similar behaviour to the jet with from .
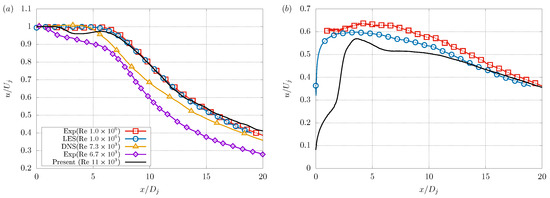
Figure 6.
Time-averaged centerline (a) and lip line (b) axial component of velocity. Data from Brès et al. [32] (red and blue), Shin et al. [45] (yellow), and Todde et al. [46] (purple).
The behaviour of the axial component over the radial direction of the jet is presented in Figure 7 and was compared with the analytical function proposed by Sautet and Stepowski [47], which is presented in Equation (11). It can be seen that the result obtained presented a profile that, after , had an increase of approximately , which was a consequence of the low velocity external flow, which had a considerable value when it was compared to the profiles in the last axial positions.
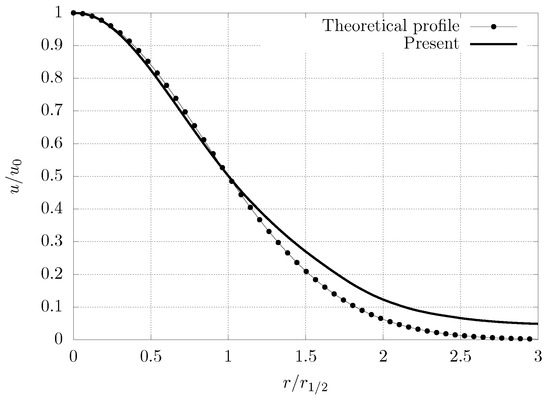
Figure 7.
Mean streamwise velocity radial profiles in similarity coordinates. Theoretical profile obtained from Equation (11).
The turbulent intensity over the lines in the axial direction located at and are presented in Figure 8 and compared with the cases of and of Brès et al. [32], and of Bonelli et al. [48], and of Shin et al. [45], and and of Todde et al. [46]. As can be seen, even in the cases reported in the literature, there were considerable differences in the shape of the profiles and the magnitudes reached, especially for values of smaller than 10. For the profile on the central line (Figure 8a), a peak at is observed, which coincides in position with the cases explored by Todde et al. [46] and presents closer values to those reported by the case of Bonelli et al. [48]. Similarly, for the line that goes from the edge of the nozzle (Figure 8b), there is a similarity with the case of Bonelli et al. [48].
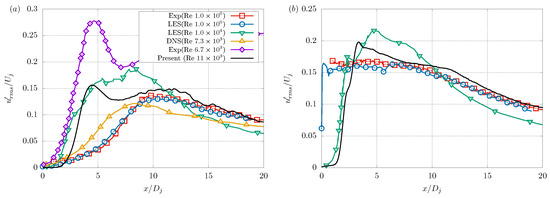
Figure 8.
Normalised turbulence intensities over centerline (a) and lip line (b). Description in the legend of Figure 6; green lines from Bonelli et al. [48].
With respect to the velocity fluctuations, the components of the Reynolds stress tensor over the radial direction of the jet were calculated, and the self-similarity profiles were constructed. These were compared with the data reported by Hussein et al. [49] and Panchapakesan and Lumley [33]. The profiles of the four components of this symmetric tensor are presented in Figure 9. As can be seen, there are similarities in the shape of the profiles, but they under-predict the reported values. This was a consequence of the way in which the turbulent effects were modelled in this work. Although a sufficiently fine mesh was developed in the critical zones of the jet to capture the large-scale turbulent effects, the failure to capture all turbulent scales with the mesh and the use of low-order schemes led to the attenuation of the turbulent effects and, thus, to a decrease in the values reporting the turbulence intensity.
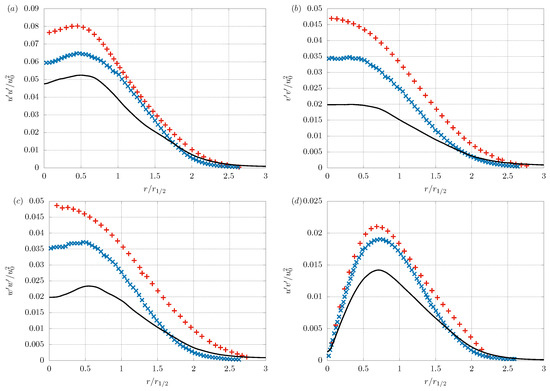
Figure 9.
Profiles of Reynolds stresses in self-similar region. Axial (a), radial (b), azimuthal (c), and shear (d) velocity fluctuations across the jet. Experimental data from Hussein et al. [49] (+) and Panchapakesan and Lumley [33] (×).
An additional measure of the prediction capabilities of the implemented model was performed in terms of the profiles of the production and dissipation terms of the Turbulent Kinetic Energy (TKE) transport equation. These profiles are presented in Figure 10a and were normalised using the value . As can be seen, the TKE production term was under-predicted, although it exhibits a similar shape to the profile reported by Panchapakesan and Lumley [33]. Interestingly, the dissipation term presented values approximately one order of magnitude lower than those reported experimentally. Noteworthy also, regarding the profile shape, there seemed to be a loss of the trend near the jet centre and at .
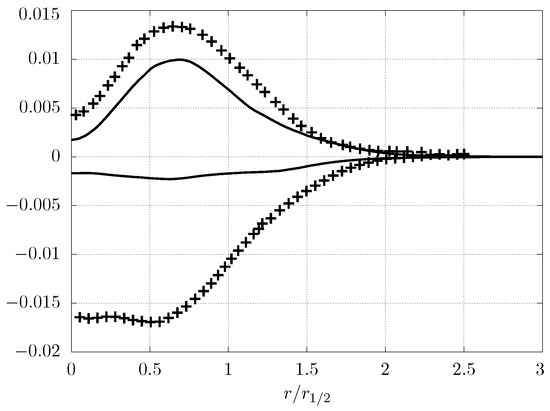
Figure 10.
Production (positive part) and dissipation (negative part) of turbulent kinetic energy in self-similar region. Experimental data from Panchapakesan and Lumley [33] (+).
Subsequently, the FWH acoustic analogy was used to compute the far-field noise for the round jet studied () and for another case with . The case was used to validate the model with the results presented in related studies, which generally explored jets with . Additionally, the self-similarity profiles of the acoustic spectra described by Viswanathan [50] fit the numbers of
Far-field noise spectra measured at , , and , with respect to the jet injection direction and located from the jet exit are presented in Figure 11 and compared with self-similarity acoustic spectra and data reported using from Jordan et al. [51]. As can be seen, the spectra obtained at the three measurement points show very similar behaviour. This indicated that, in the prediction phase of the turbulent effects, not all the existing scales were captured. Consequently, only the large turbulent scales generated sources of noise that tended to propagate uniformly in the far-field. However, for the case of (see Figure 11) at the range between and , the obtained spectra presented a similar slope and magnitudes close to the comparison spectra.
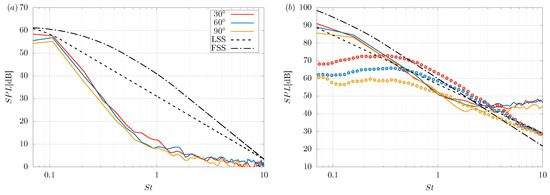
Figure 11.
Noise spectra on three measurement points located at for subsonic turbulent jets at (a) and (b) (∘ experimental data from Jordan et al. [51]; dashed lines are the self-similar functions developed by Tam et al. [10]).
From the validation analysis, it is possible to see that the model under-predicted the magnitude of the fluctuations caused by the turbulence phenomena, but it provided results that allow understanding the flow characteristics and energy transfer at the main flow scales. In addition, the model predicted the trend of the acoustic spectra in the far-field, and it showed sound pressure levels consistent with those presented in related studies. In this way, we proceeded to use the developed model as a comparative tool by applying the control technique with different operating parameters.
3.2. Flow Field
The instantaneous flow fields allow appreciating the nature of the jet when applying the control technique, as we can identify the mixing layer that is generated between the jet and the stationary fluid, and how such a layer is modified depending on the operating parameters of the control technique. In the Supplementary Materials section there are 3 videos that allow to visualize the instantaneous behavior when the control technique is applied. The magnitude of the velocity gradient is presented in Figure 12. As can be seen, the mixing layer of the non-controlled round jet case is stable up to . After this point, the first characteristic instabilities of the jet start to appear, inducing the onset of vortices, which increase in size until they dissipate in small turbulent scales in the attenuation region of the jet.
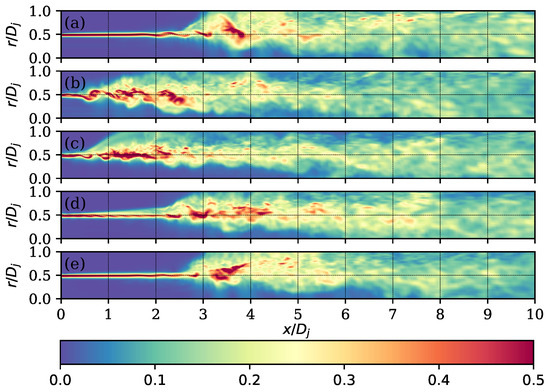
Figure 12.
Instantaneous magnitude of velocity gradient normalised with . Round case (a) and cases with (b), (c), (d), and (e).
When applying the control technique using the lowest value of the parameter, it was observed that the mixing layer was no longer stable, and instabilities appeared from . Thus, the instabilities that initiated the turbulence processes were not generated by the interaction of the injection fluid with the stationary fluid, but by the synthetic perturbations introduced by the control technique. However, as the parameter was increased, the initial mixing layer tended to be restored, and for , a more stable layer similar to that of the non-controlled round case was reached. For the case of , it was observed that the injected pulses tended to organise themselves into a thicker mixing layer with internal perturbations, but this was maintained up to . Thus, for low values of , the jet behaviour was significantly perturbed, and for higher values of , the control technique acted as a bulge in the jet nozzle, which did not have a considerable effect on the development of the jet, at least from the point of view of the instantaneous fields.
In order to visualise the coherent structures generated in the regions where vorticity effects are appreciable, the instantaneous fields of the Q-criterion were selected, and the iso-surfaces were plotted for the regions where the Q-criterion is higher than ; see Figure 13. The Q-criterion is one of the multiple methods used to identify vortices in the flow field. This criterion relates the rotation rate with the strain rate and is presented as a scalar field, where positive values represent regions where vorticity dominates and negative values where the strain rate is dominant.
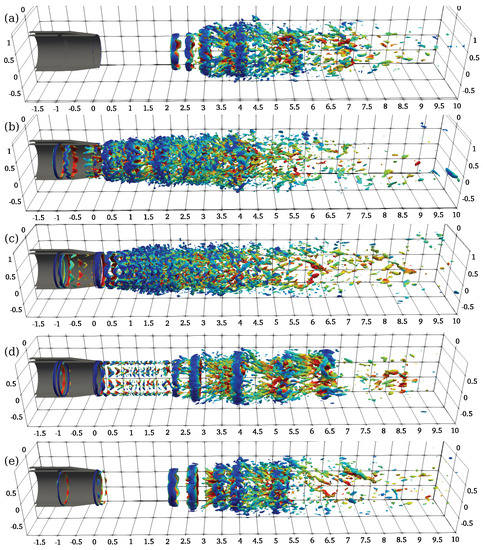
Figure 13.
Coherent structures obtained using Q-criterion with a threshold and coloured with the magnitude of the velocity. Lengths normalised using . (a) Non-controlled round jet case; (b) ; (c) ; (d) ; (e) .
As can be seen, these coherent structures appeared from for the non-controlled round case (Figure 13a) and initially had the shape of a ring, which increased in diameter as the jet developed. This particular structure was maintained until , where smaller structures started to be created, which tended to reduce in size, and eventually disappeared at . On the other hand, for the four cases where the control technique was used, the structures appeared in the injection region of the synthetic jet and, depending on the parameter , attenuated immediately or developed similarly to the non-controlled case. For the case of , the appearance of the smaller structures occurred before the jet left the nozzle. During the development of the jet, smaller structures were observed to appear and attenuated mostly before . In a similar way as occurred with , only in this case, a structure was formed outside the nozzle, which was maintained until , but from that point onwards, a behaviour similar to was observed. For the case , we observed the appearance of small structures in the region from to , which coincided with the internal perturbations of the mixing layer seen in Figure 12d. Thereafter, we observed a behaviour similar to the round case. Finally, something similar occurred for the case with , but in this case, there were no structures in the initial region of the jet, which in terms of the appearance of coherent structures, was very similar to the non-controlled case.
To visualise the effect of the use of the control technique on the intensity of the turbulent effects, the fields of the four Reynolds stress tensor terms were generated. This was performed by averaging the Reynolds stress tensor in cylindrical coordinates over 128 planes located uniformly in the angular direction. The fields of the , , , and terms are presented in Figure 14, Figure 15, Figure 16 and Figure 17, respectively.
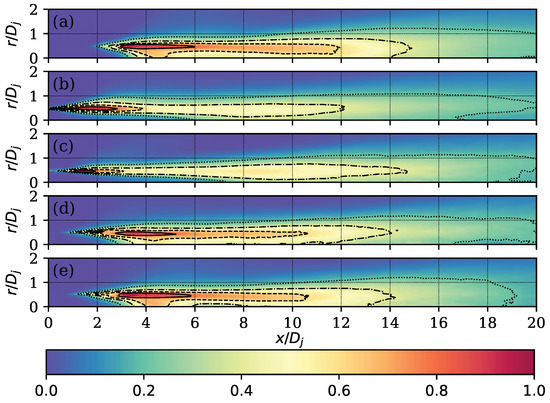
Figure 14.
Term of the Reynolds stress tensor normalised with . Contours on the values 0.8 (—), 0.6 (), 0.4 (), and 0.2 (⋯). Round case (a) and cases with (b), (c), (d), and (e).
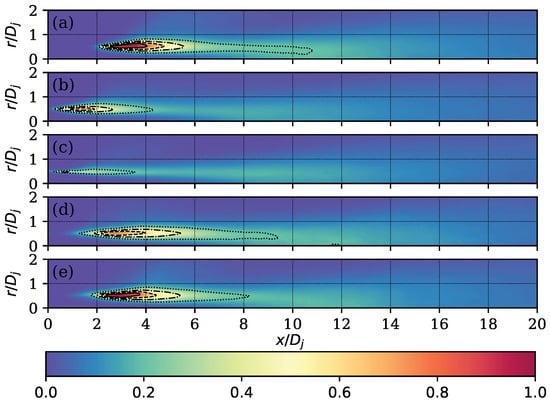
Figure 15.
Term of the Reynolds stress tensor normalised with . Contours on the values 0.8 (—), 0.6 (), 0.4 (), and 0.2 (⋯). Round case (a) and cases with (b), (c), (d), and (e).
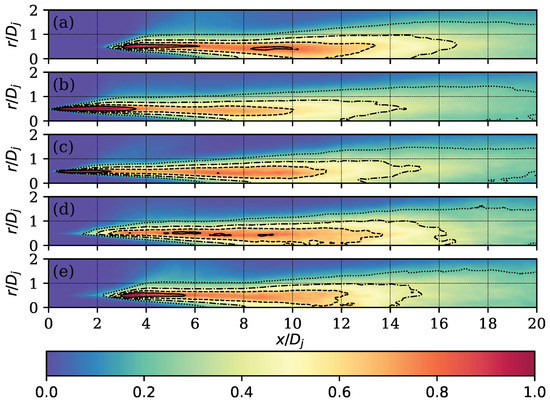
Figure 16.
Term of the Reynolds stress tensor normalised with . Contours on the values 0.8 (—), 0.6 (), 0.4 (), and 0.2 (⋯). Round case (a) and cases with (b), (c), (d), and (e).
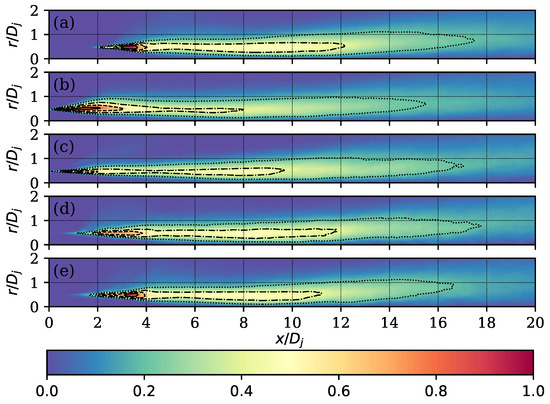
Figure 17.
Term of the Reynolds stress tensor normalised with . Contours on the values 0.8 (—), 0.6 (), 0.4 (), and 0.2 (⋯). Round case (a) and cases with (b), (c), (d), and (e).
As can be seen, the control technique produced fluctuations that appeared and subsequently attenuated at positions closer to the nozzle exit, especially for the cases of and . It is important to note that the control technique injected fluctuations into the flow, which depending on the parameter, made them behave as a jet at a more advanced stage of development, so that the interaction with the stationary surrounding fluid was more intense and at shorter distances.
It can be seen for the term plot (see Figure 14) how the fluctuations at the jet edge appeared at the nozzle exit, but in the centre of the jet, they were delayed to reach a value of at for and at for . This suggested that the synthetic fluctuations at the jet edge caused most of the jet energy to feed the high-intensity fluctuations at the edge and made them take longer to reach the jet centre. On the other hand, for the cases of and , the behaviour was similar to the round one, although a displacement of the region of fluctuations towards the jet exit was also observed.
In the term (see Figure 15), a significant attenuation of the intensity was observed, although the recovery effect of the round jet was still present for the highest value of . For the case of , the fluctuations in the radial direction were attenuated to the point of only perceiving the region with a value less than , suggesting that, for the oscillation frequency of this case, the instabilities tended to be organised in such a way that they were drastically reduced in the radial direction and compensated in other terms, such as and . This can be seen in Figure 16, where for the same case and for the case of , the region with higher intensity spans a larger region and, additionally, reaches higher values. This did not occur for the case of , where the attenuation of the magnitude was generated to the point of reducing the larger region of to three small regions spread between and . Finally, for the shear stress term , it can be observed how the above-mentioned appreciations for the normal stresses and were somehow reflected in this field and indicated the consistency of the post-processing.
The two terms considered in the turbulent kinetic energy transport equation were obtained using the same procedure used for the Reynolds stress tensor components. The production fields (P) obtained for the different cases explored are presented in Figure 18. The production in the round jet showed a shape of an annular region that spanned the region in the axial direction from to and in the radial direction from to . Using the control technique, the region enclosed by the contour maintained its shape and size, and for the cases with low , it shifted towards the jet exit. Similarly, the region enclosed by the value of had a larger size for the cases with a low value of , and for those with a larger , a similar location to the round case was observed with a similar behaviour.
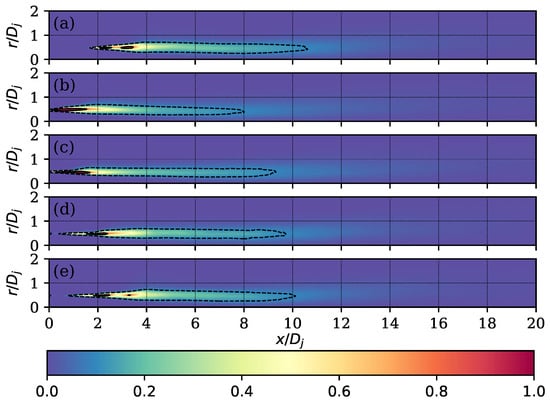
Figure 18.
Turbulent kinetic energy production normalised to . Contours on the values 0.8 (—) y 0.1 (). Round case (a) and cases with (b), (c), (d), and (e).
The dissipation term () is presented in Figure 19, and this term presented higher values for the cases with a low value of . For these cases, it can be observed how the contour enclosed by covers a region of approximately , unlike the round case and those with high values of , where this region has a smaller size and is located later in the development of the jet. This suggested that, for low values of , the transport processes of the turbulent kinetic energy towards the smaller scales and eventually towards internal energy occurred much faster and with greater intensity, generating after this zone a region with low dissipation values, which is maintained for a longer time.
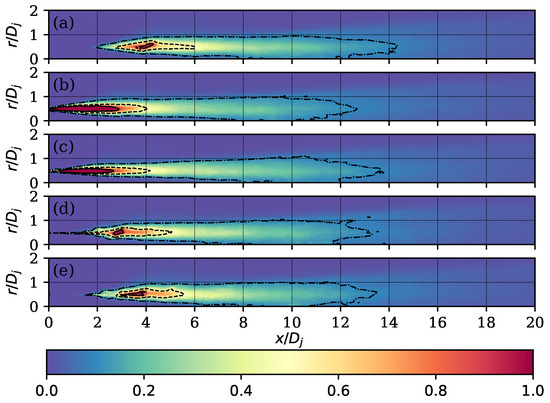
Figure 19.
Dissipation of the turbulent kinetic energy normalised with . Contours on the values 0.9 (—), 0.5 () y 0.1 (). Round case (a) and cases with (b), (c), (d), and (e).
3.3. Acoustic Response
The acoustic sources originating in the turbulent jet were calculated using the Lighthill equation (see Equation (3)). Their instantaneous value after the jets reached a fully developed quasi-steady-state, as presented in Figure 20.
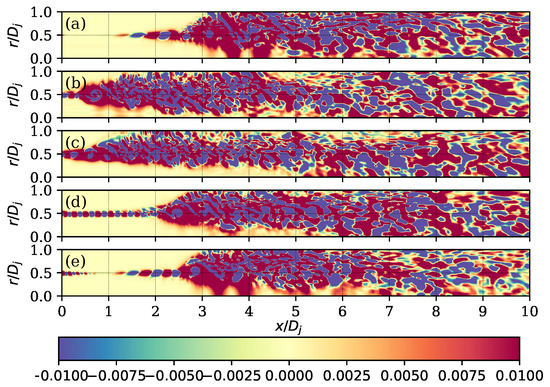
Figure 20.
Acoustic sources within the turbulent flow normalised with . Round case (a) and cases with (b), (c), (d), and (e).
For the different cases, there were two regions that differed in the way the acoustic sources were generated. In the initial part of the jets, there were source packages that fluctuated between positive and negative values, which coincided with the location of the mixing layer of the jets (see Figure 12). This was followed by the second zone, which was located in the region where the jet was fully developed. It was observed that the second zone approached the region closer to the nozzle in the cases with a low value of ( and ), and for the other two cases, it presented a behaviour similar to the round case.
Related to the acoustic source packages that were located on the initial mixing layer of the jet, it was observed that, for the round case, they appeared at , and when the control technique was used, acoustic sources appeared even before the jet exited the nozzle. For the cases with equal to and , these acoustic sources appeared as organised packages during the initial region of the jet. For the case of , three zones with different behaviour within the initial region of acoustic sources can be observed. First, there were organised packets with a thickness of approximately each, which changed sign and appeared up to . Then, there was a zone of silence up to and, finally, another zone with organised packages with a similar appearance as in the round jet case. This suggested that, for this particular case, there was a region of acoustic sources located near the nozzle exit, which was generated by the control technique and then another region of acoustic sources generated by the turbulent effects common for this type of flow.
The noise spectra obtained for some of the measurement points are presented in Figure 21. As can be seen, the use of the control technique generates a high-frequency pure tone and generally increases the sound pressure level captured at the different measurement points. It is also observed that the pure tone increases in frequency for higher values of . It can be observed that the noise captured by our model decreases with distance, although for the peaks of the pure tones, there is no clear decay effect. This is a typical behaviour of pure tones when propagated from different sources, because, depending on the separation of the sources, there may be points where the tone is attenuated or amplified, depending on the phase difference between the different sources.
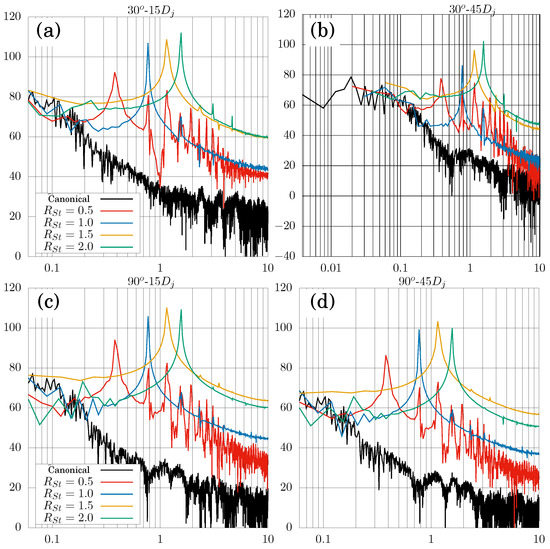
Figure 21.
Spectra of sound pressure levels in against the number at (a), (b), (c), and (d).
Additionally, we observed the appearance of peaks with frequencies of multiples of the pure tones and lower amplitude, which are known as harmonics. For the cases of and , up to 2 harmonics were captured, and for and , up to 10 harmonics were captured.
Taking into account that the additional noise added to the acoustic spectra by the control technique must be related to the oscillation frequency of the synthetic jet, the spectra were normalised with the oscillation frequency and are presented in Figure 22. It can be seen how the use of this control technique generated pure tones with a frequency of , the oscillation frequency of the synthetic jet. This suggested that injecting organised fluctuations into the jet promoted the appearance of acoustic sources that oscillated with the frequency of the control technique and with a greater amplitude than the rest of the sources that were generated by the turbulence phenomena typical of this type of flow.
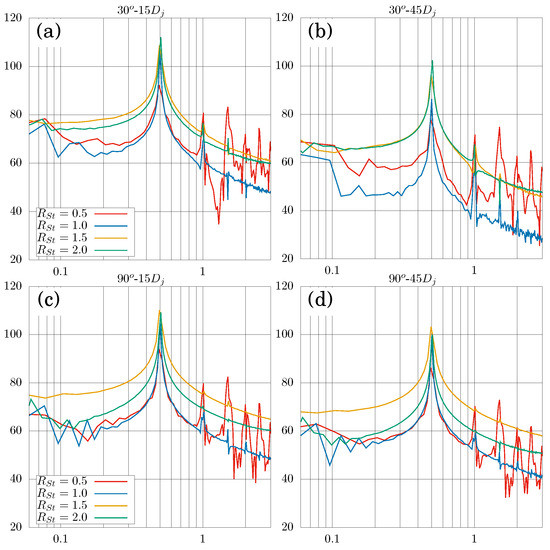
Figure 22.
Spectra of sound pressure levels in versus frequency normalised to the oscillation frequency of the synthetic jet in each case study at (a), (b), (c), and (d).
Figure 23 shows the directivity of the noise captured in the far-field. The figure was constructed by obtaining the equivalent noise for each of the 27 measurement points, and with the angular and radial position, the profiles were constructed for the three measurement distances.
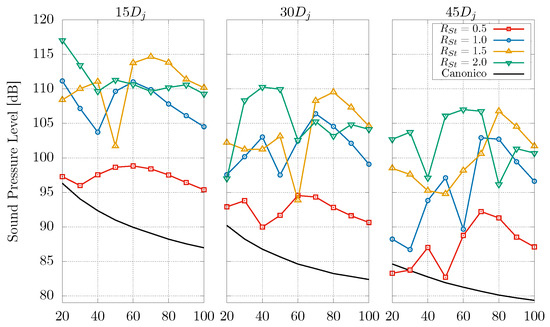
Figure 23.
Directivity of the noise captured in the far-field.
As can be seen, the round jet case presented a smooth profile with higher values at lower angles, as presented in the literature. On the other hand, the cases using the control technique presented an unusual behaviour. No attenuation of the signal was observed as the measurement distance increased; no smooth profiles increasing in magnitude at small angles were observed; below trend peaks appeared at different angles for different measurement distances.
4. Conclusions
In the present work, a computational model was built and validated with the aim of modelling the use of a synthetic annular jet as a flow control technique for an incompressible turbulent round jet. The results showed that the model employed had the ability to capture the tendency of the turbulent phenomenon, especially in the vicinity of the exit of the jets. The fluid was injected and subtracted alternately uniformly over the entire annular region, and taking into account that the fluid for the operating conditions was considered incompressible, a piston effect was generated in the region upstream of the nozzle outlet. This affected the portion of fluid at the end of the nozzle, which increased its velocity when it was in the injection phase of the synthetic jet, and on the contrary, it decreased its velocity when it was in the subtraction phase. In this way, the pulses injected inside the nozzle were immediately reflected throughout the jet exit area. Although it was found that this effect was most noticeable at the edge where the jet mixing layer was modified by the stationary fluid, at the jet centreline, these fluctuations were also noticeable (see Figure 14a), but those were quickly attenuated within the potential core of the jets.
The use of the control technique inside the nozzle caused the mixing layer to stop behaving in a stable way, and even a layer detachment seemingly appeared in the last section of the nozzle. This was noticeable for cases with low values of , where the oscillation period was longer and, therefore, the phase of positive and negative displacements injected and subtracted more fluid. For the cases with higher values of , it was observed that the control technique generated an alternating effect between throttling and flow relief, which was not sufficient to generate a significant modification effect of the initial mixing layer, at least from the point of view of the flow behaviour.
It was also observed that, depending on the value of , the location of the regions with high turbulence intensity values were modified. Thus, for the cases with low values of , the jets behaved similar to the ones presented in investigations related to higher numbers, which were characterised by instabilities in the initial annular region from the beginning of the jet injection. On the other hand, for the cases with higher values of , the behaviour was similar to the round case developed.
With respect to the acoustic response of the jets studied by applying the control technique, it was found that they all produced a higher sound pressure level in the far-field. This was true for the region of the spectrum where . The round jet was characterised by acoustic sources with considerable magnitude from the region where the mixing layer started to present instabilities. Using the control technique, the appearance of acoustic source packets was promoted. These acoustic source packets exhibited a size related to the wavelength of the oscillation frequency of the synthetic jet.
It was observed that the turbulent jet generated an amplification effect of the instabilities added before the jet exit. This amplification was reflected in the noise produced in the far-field. This coincides with the experiments mentioned in the discussion of Lighthill [30], where the high sensitivity of turbulent jets to sound waves from sources external to the flow was mentioned.
Additionally, it was identified that the noise added by the use of the control technique was presented as a pure tone with a frequency of -times the oscillation frequency of the synthetic jet. Although these pure tones tended to attenuate with increasing measurement distance, they also exhibited atypical behaviour in the directivity profiles. This was associated with the fact that acoustic sources with a given frequency propagated in the far-field, where the interaction with the signal coming from another source with the same frequency may present attenuation or amplification effects. It was observed that these attenuation effects (Figure 23) were associated with the appearance of at least one peak, which changed in steepness as the measurement distance increased for the different cases studied.
Finally, it is possible to conclude that synthetic annular jets can modulate the turbulence levels along round jets, which can be used in flow control strategies. In terms of noise emission, the control technique increased the noise levels generated by the jet, although this increase was smaller for lower values of . Further work is needed to explore the effect of other operating variables and geometrical constants, as well as the validity of our conclusions at higher Reynolds numbers and Mach numbers.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/fluids8040110/s1: Video S1: VelocityField. Video S2: GradVelocityField. Video S3: LighthillSourceTermField.
Author Contributions
Conceptualisation, J.M.-R. and C.D.-D.; validation, J.M.-R.; formal analysis, J.M.-R.; investigation, J.M.-R. and C.D.-D.; writing—original draft preparation, J.M.-R. and C.D.-D.; writing—review and editing, J.M.-R. and C.D.-D.; supervision, C.D.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kramer, C.; Gerhardt, H.; Knoch, M. Applications of jet flows in industrial flow circuits. J. Wind Eng. Ind. Aerodyn. 1984, 16, 173–188. [Google Scholar] [CrossRef]
- Gerges, S.; Sehrndt, G.; Parthey, W. 5 Noise Sources. In Occupational Exposure to Noise; World Health Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Sheen, S.C.; Hsiao, Y.H. On using multiple-jet nozzles to suppress industrial jet noise. J. Occup. Environ. Hyg. 2007, 4, 669–677. [Google Scholar] [CrossRef] [PubMed]
- Sadeghian, M.; Bandpy, M. Technologies for Aircraft Noise Reduction: Review Paper. J. Aeronaut. Aerosp. Eng. 2020, 9, 218. [Google Scholar]
- WHO. Environmental Noise Guidelines for the European Region; World Health Organization: Geneva, Switzerland, 2018.
- Ahuja, K.; Bushell, K. An experimental study of subsonic jet noise and comparison with theory. J. Sound Vib. 1973, 30, 317–IN1. [Google Scholar] [CrossRef]
- Tam, C.K.; Tanna, H. Shock associated noise of supersonic jets from convergent-divergent nozzles. J. Sound Vib. 1982, 81, 337–358. [Google Scholar] [CrossRef]
- Viswanathan, K. Investigation of noise source mechanisms in subsonic jets. AIAA J. 2008, 46, 2020–2032. [Google Scholar] [CrossRef]
- Howe, M.S.; Howe, M.S. Acoustics of Fluid-Structure Interactions; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Tam, C.; Golebiowski, M.; Seiner, J. On the two components of turbulent mixing noise from supersonic jets. In Proceedings of the Aeroacoustics Conference, State College, PA, USA, 6–8 May 1996; p. 1716. [Google Scholar]
- Camussi, R. Noise Sources in Turbulent Shear Flows: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 545. [Google Scholar]
- Henderson, B. Fifty years of fluidic injection for jet noise reduction. Int. J. Aeroacoust. 2010, 9, 91–122. [Google Scholar] [CrossRef]
- Rajput, P.; Kumar, S. Use of downstream fluid injection to reduce subsonic jet noise. Int. J. Aeroacoust. 2019, 18, 554–574. [Google Scholar] [CrossRef]
- Colonius, T.; Sinha, A.; Rodríguez, D.; Towne, A.; Liu, J.; Brès, G.; Appelö, D.; Hagstrom, T. Simulation and modeling of turbulent jet noise. In Direct and Large-Eddy Simulation IX; Springer: Berlin/Heidelberg, Germany, 2015; pp. 305–310. [Google Scholar]
- Callender, B.; Gutmark, E.; Martens, S. A comprehensive study of fluidic injection technology for jet noise reduction. In Proceedings of the 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference), Rome, Italy, 21–23 May 2007; p. 3608. [Google Scholar]
- Dhamankar, N.S.; Blaisdell, G.A.; Lyrintzis, A.S. Analysis of turbulent jet flow and associated noise with round and chevron nozzles using large eddy simulation. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; p. 3045. [Google Scholar]
- Stich, G.D.; Housman, J.A.; Ghate, A.S.; Kiris, C.C. Jet Noise Prediction with Large-Eddy Simulation for Chevron Nozzle Flows. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 January 2021; p. 1185. [Google Scholar]
- Powell, A. The influence of the exit velocity profile on the noise of a jet. Aeronaut. Q. 1954, 4, 341–360. [Google Scholar] [CrossRef]
- Kurbjun, M.C. Limited Investigation of Noise Suppression by Injection of Water into Exaust of Afterburning Jet Engine; National Advisory Committee for Aeronautics: Edwards, CA, USA, 1958; Volume 40. [Google Scholar]
- Michael, L.G. Jet Noise Suppression Means. U.S. Patent 2,990,905, 4 July 1961. [Google Scholar]
- Caeti, R.B.; Kalkhoran, I.M. Jet noise reduction via fluidic injection. AIAA J. 2014, 52, 26–32. [Google Scholar] [CrossRef]
- Prasad, C.; Morris, P.J. A study of noise reduction mechanisms of jets with fluid inserts. J. Sound Vib. 2020, 476, 115331. [Google Scholar] [CrossRef]
- Wang, J.; Feng, L. Synthetic Jet. In Flow Control Techniques and Applications; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2018; pp. 168–205. [Google Scholar] [CrossRef]
- Chedevergne, F.; Léon, O.; Bodoc, V.; Caruana, D. Experimental and numerical response of a high-Reynolds-number M = 0.6 jet to a Plasma Synthetic Jet actuator. Int. J. Heat Fluid Flow 2015, 56, 1–15. [Google Scholar] [CrossRef]
- Zong, H.; Chiatto, M.; Kotsonis, M.; De Luca, L. Plasma synthetic jet actuators for active flow control. Proc. Actuators 2018, 7, 77. [Google Scholar] [CrossRef]
- Glezer, A. Some aspects of aerodynamic flow control using synthetic-jet actuation. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 1476–1494. [Google Scholar] [CrossRef] [PubMed]
- Tamburello, D.A.; Amitay, M. Active control of a free jet using a synthetic jet. Int. J. Heat Fluid Flow 2008, 29, 967–984. [Google Scholar] [CrossRef]
- Léon, O.; Caruana, D.; Castelain, T. Increase and decrease of the noise radiated by high-Reynolds-number subsonic jets through plasma synthetic jet actuation. In Proceedings of the International Conference on Acoustic Climate Inside and Outside Buildings, Vilnius, Lithuania, 23–26 September 2014; pp. 23–26. [Google Scholar]
- Arafa, N.; Sullivan, P.E.; Ekmekci, A. Jet Velocity and Acoustic Excitation Characteristics of a Synthetic Jet Actuator. Fluids 2022, 7, 387. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Brès, G.; Jordan, P.; Jaunet, V.; Le Rallic, M.; Cavalieri, A.; Towne, A.; Lele, S.; Colonius, T.; Schmidt, O. Importance of the nozzle-exit boundary-layer state in subsonic turbulent jets. J. Fluid Mech. 2018, 851, 83–124. [Google Scholar] [CrossRef]
- Panchapakesan, N.R.; Lumley, J.L. Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 1993, 246, 197–223. [Google Scholar] [CrossRef]
- Moura, R.C.; Sherwin, S.J.; Peiró, J. Linear dispersion–diffusion analysis and its application to under-resolved turbulence simulations using discontinuous Galerkin spectral/hp methods. J. Comput. Phys. 2015, 298, 695–710. [Google Scholar] [CrossRef]
- Manneville, P.; Rolland, J. On modelling transitional turbulent flows using under-resolved direct numerical simulations: The case of plane Couette flow. Theor. Comput. Fluid Dyn. 2011, 25, 407–420. [Google Scholar] [CrossRef]
- Komen, E.; Shams, A.; Camilo, L.; Koren, B. Quasi-DNS capabilities of OpenFOAM for different mesh types. Comput. Fluids 2014, 96, 87–104. [Google Scholar] [CrossRef]
- Bosshard, C.; Deville, M.O.; Dehbi, A.; Leriche, E. UDNS or LES, that is the question. Open J. Fluid Dyn. 2015, 5, 339. [Google Scholar] [CrossRef]
- Ramirez-Pastran, J.; Duque-Daza, C. On the prediction capabilities of two SGS models for large-eddy simulations of turbulent incompressible wall-bounded flows in OpenFOAM. Cogent Eng. 2019, 6, 1679067. [Google Scholar] [CrossRef]
- LarKermani, E.; Roohi, E.; Porté-Agel, F. Evaluating the modulated gradient model in large eddy simulation of channel flow with OpenFOAM. J. Turbul. 2018, 19, 600–620. [Google Scholar] [CrossRef]
- Epikhin, A.; Evdokimov, I.; Kraposhin, M.; Kalugin, M.; Strijhak, S. Development of a Dynamic Library for Computational Aeroacoustics Applications Using the OpenFOAM Open Source Package. Procedia Comput. Sci. 2015, 66, 150–157. [Google Scholar] [CrossRef]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1955, 231, 505–514. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D Finite Element Mesh Generator with built-in Pre- and Post-Processing Facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Bogey, C.; Marsden, O.; Bailly, C. Influence of initial turbulence level on the flow and sound fields of a subsonic jet at a diameter-based Reynolds number of 10 (5). J. Fluid Mech. 2012, 701, 352–385. [Google Scholar] [CrossRef]
- Mendez, S.; Shoeybi, M.; Lele, S.; Moin, P. On the use of the Ffowcs Williams-Hawkings equation to predict far-field jet noise from large-eddy simulations. Int. J. Aeroacoust. 2013, 12, 1–20. [Google Scholar] [CrossRef]
- Shin, D.H.; Aparece-Scutariu, V.; Richardson, E. High Fidelity Simulation of Turbulent Jet and Identification of Acoustic Sources. Civ. Aircr. Des. Res. 2017, 3, 1–9. [Google Scholar] [CrossRef]
- Todde, V.; Spazzini, P.G.; Sandberg, M. Experimental analysis of low-Reynolds number free jets. Exp. Fluids 2009, 47, 279–294. [Google Scholar] [CrossRef]
- Sautet, J.; Stepowski, D. Dynamic behaviour of variable-density, turbulent jets in their near development fields. Phys. Fluids 1995, 7, 2796–2806. [Google Scholar] [CrossRef]
- Bonelli, F.; Viggiano, A.; Magi, V. High-speed turbulent gas jets: An LES investigation of Mach and Reynolds number effects on the velocity decay and spreading rate. Flow Turbul. Combust. 2021, 107, 519–550. [Google Scholar] [CrossRef]
- Hussein, H.J.; Capp, S.P.; George, W.K. Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 1994, 258, 31–75. [Google Scholar] [CrossRef]
- Viswanathan, K. Aeroacoustics of hot jets. In Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference & Exhibit, Breckenridge, CO, USA, 17–19 June 2004; p. 2481. [Google Scholar]
- Jordan, E.L.P.; Delville, J.; Bonnet, J.P. Source-mechanism identification by nearfield-farfield pressure correlations in subsonic jets. Int. J. Aeroacoust. 2008, 7, 41–68. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).